A Comprehensive Study of Water Resource–Environment Carrying Capacity via a Water-Socio-Ecological Framework and Differential Evolution-Based Projection Pursuit Modeling
Abstract
1. Introduction
2. Study Area and Data
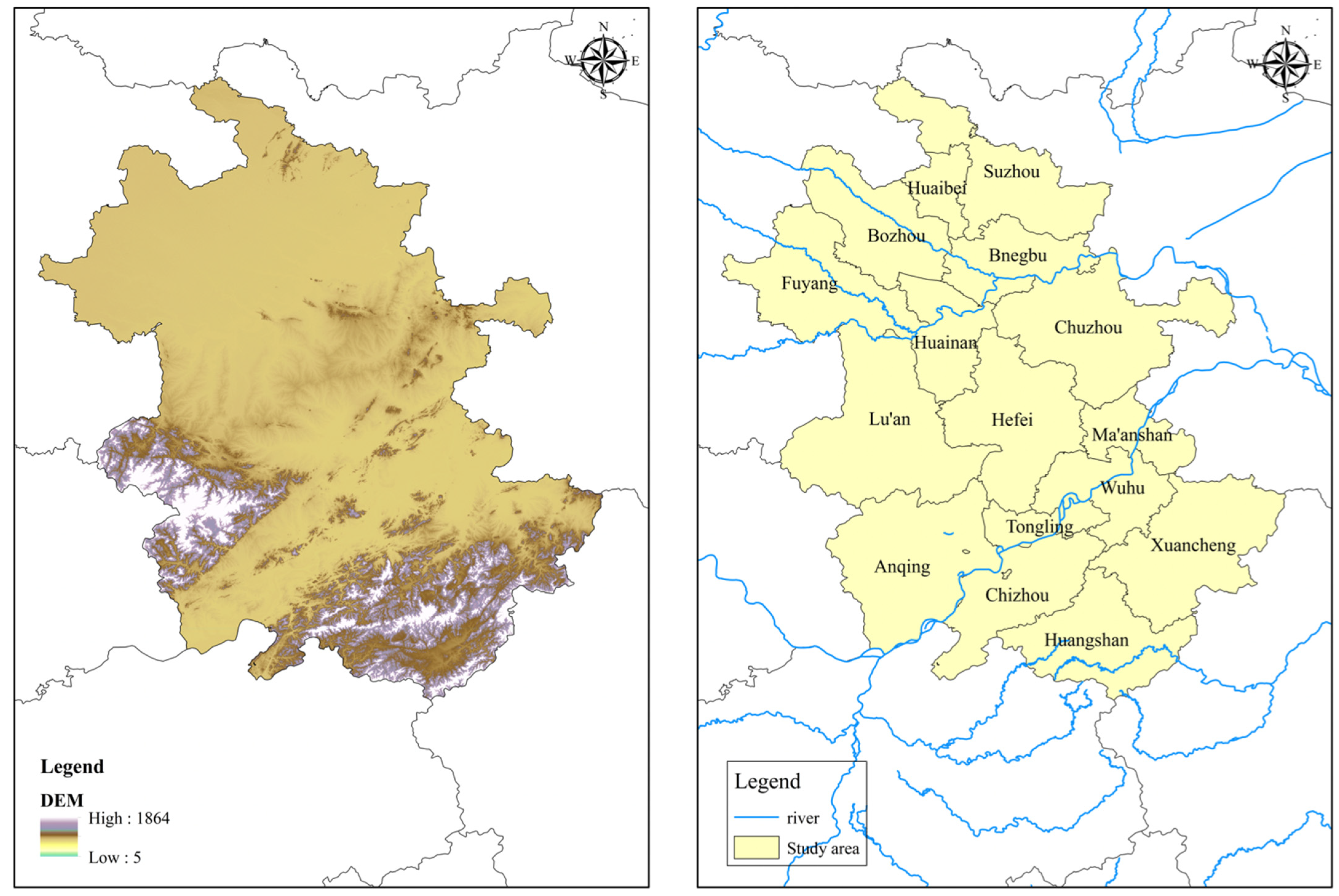
2.1. Study Area
2.2. Data Sources
2.3. The WR-WECC Evaluation System
3. Methods
3.1. Differential Evolution Projection Pursuit Modeling
- (1)
- Data preprocessing
- (2)
- Parameterization of the projection direction
- (3)
- Projective indicator function
- (4)
- Differential evolutionary algorithm
- (5)
- Convergence and stability analysis
3.2. Obstacle Degree Model
- (1)
- Data standardization
- (2)
- Comprehensive obstacle degree calculation
3.3. Coupling Coordination Degree Model (CCDM)
- (1)
- Calculation of the Composite Development Index for Systemswhere is the composite development index for the kth system. is the number of indicators for the kth system.
- (2)
- Calculate the degree of coupling
- (3)
- Calculation of the degree of coupling coordination
3.4. Autoregressive Integrated Moving Average
- (1)
- Data smoothing
- (2)
- Determine the model order (p, q)
- (3)
- Parameter estimation
- (4)
- Forecasting
4. Results
4.1. Horizontal Evaluation of WR-WECC in AP
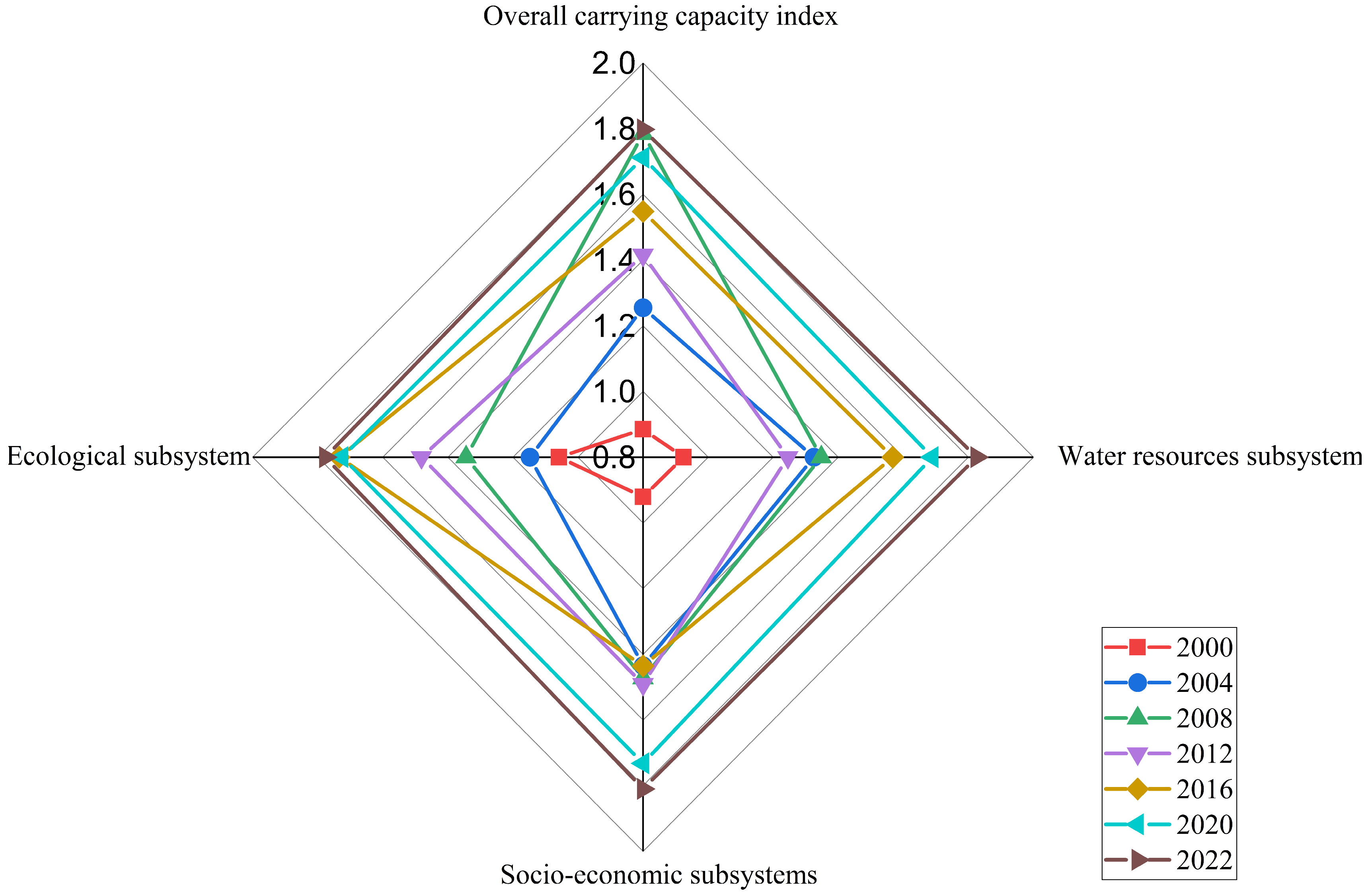
4.1.1. Overall WR-WECC Level Evaluation
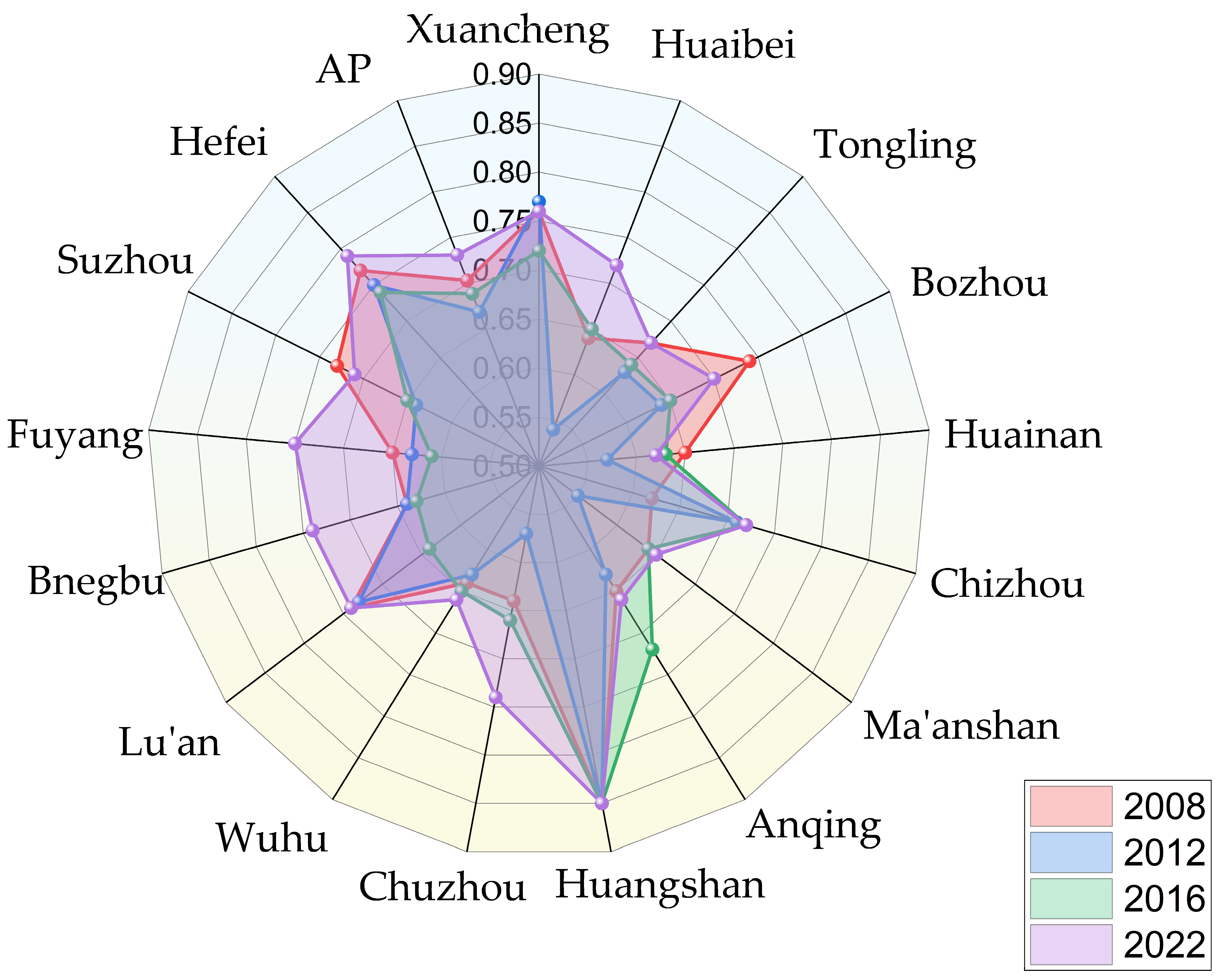
4.1.2. Evaluation of WR-WECC by Municipalities
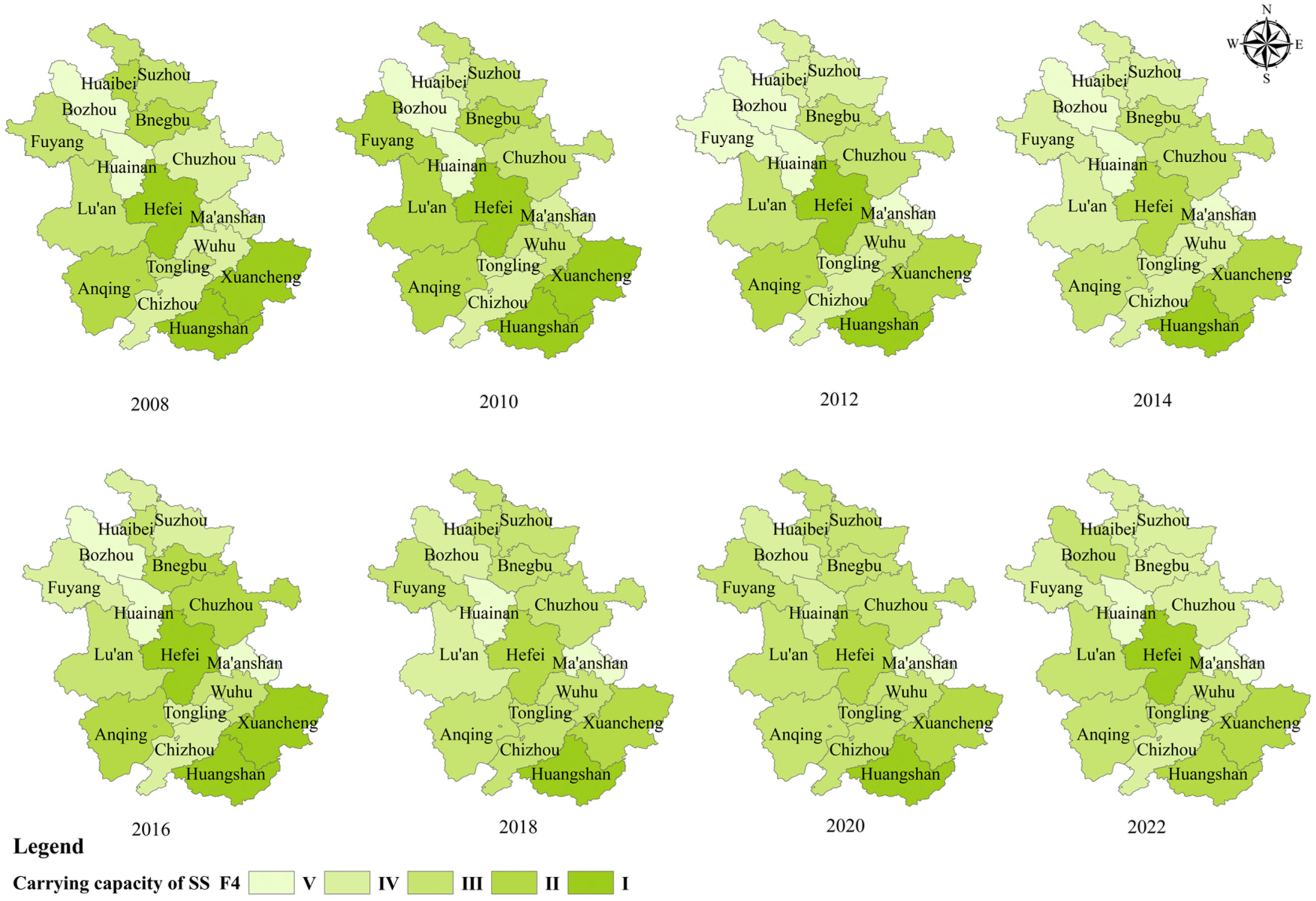
4.1.3. Carrying Capacity Analyses of WS by Municipality
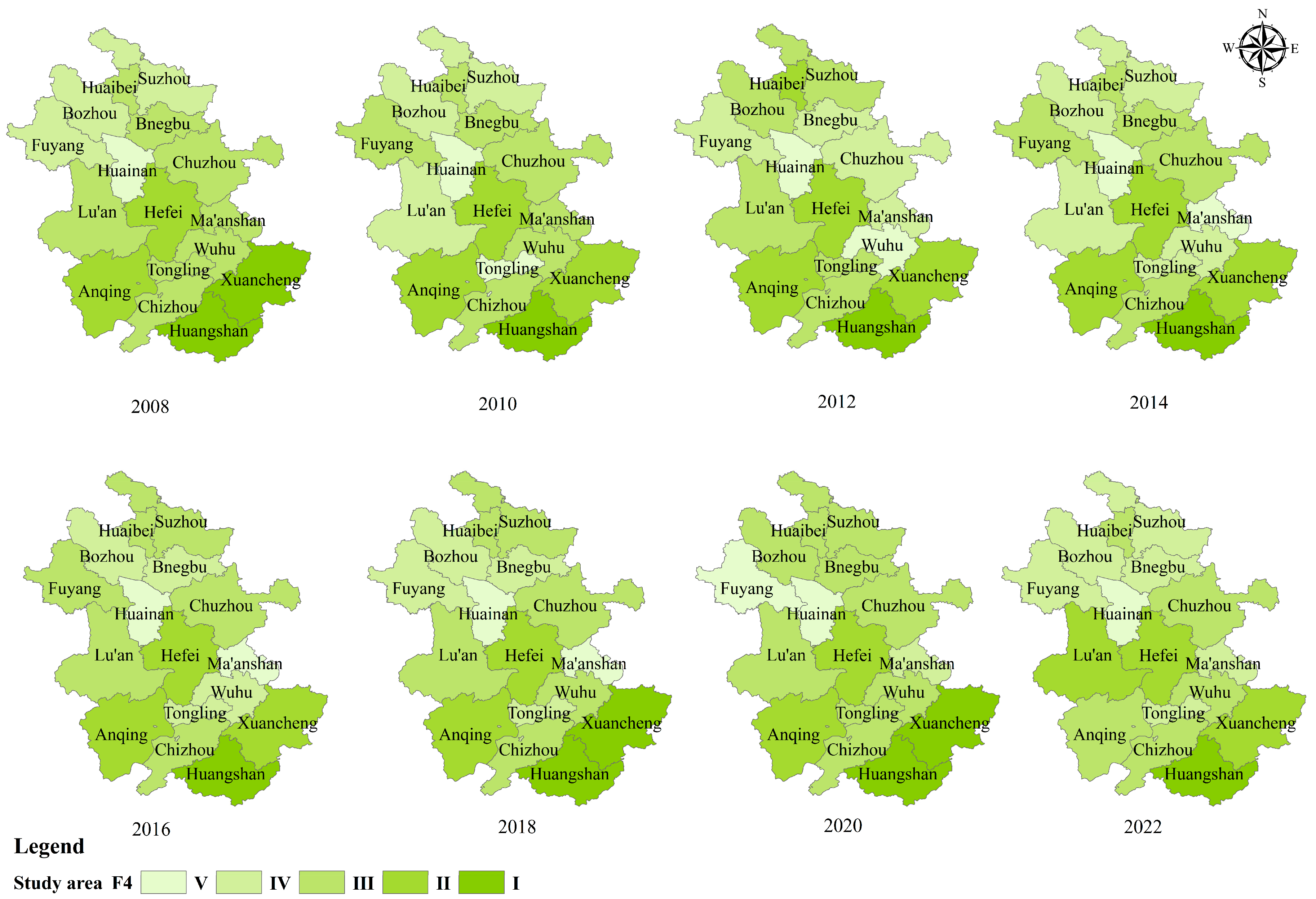
4.1.4. Carrying Capacity Analysis of SS by Municipality
4.1.5. Carrying Capacity Analysis of ES by Municipality
4.2. Analysis of the Coupled Coordination of WR-WECC in AP
4.3. OD Analysis of WR-WECC in AP
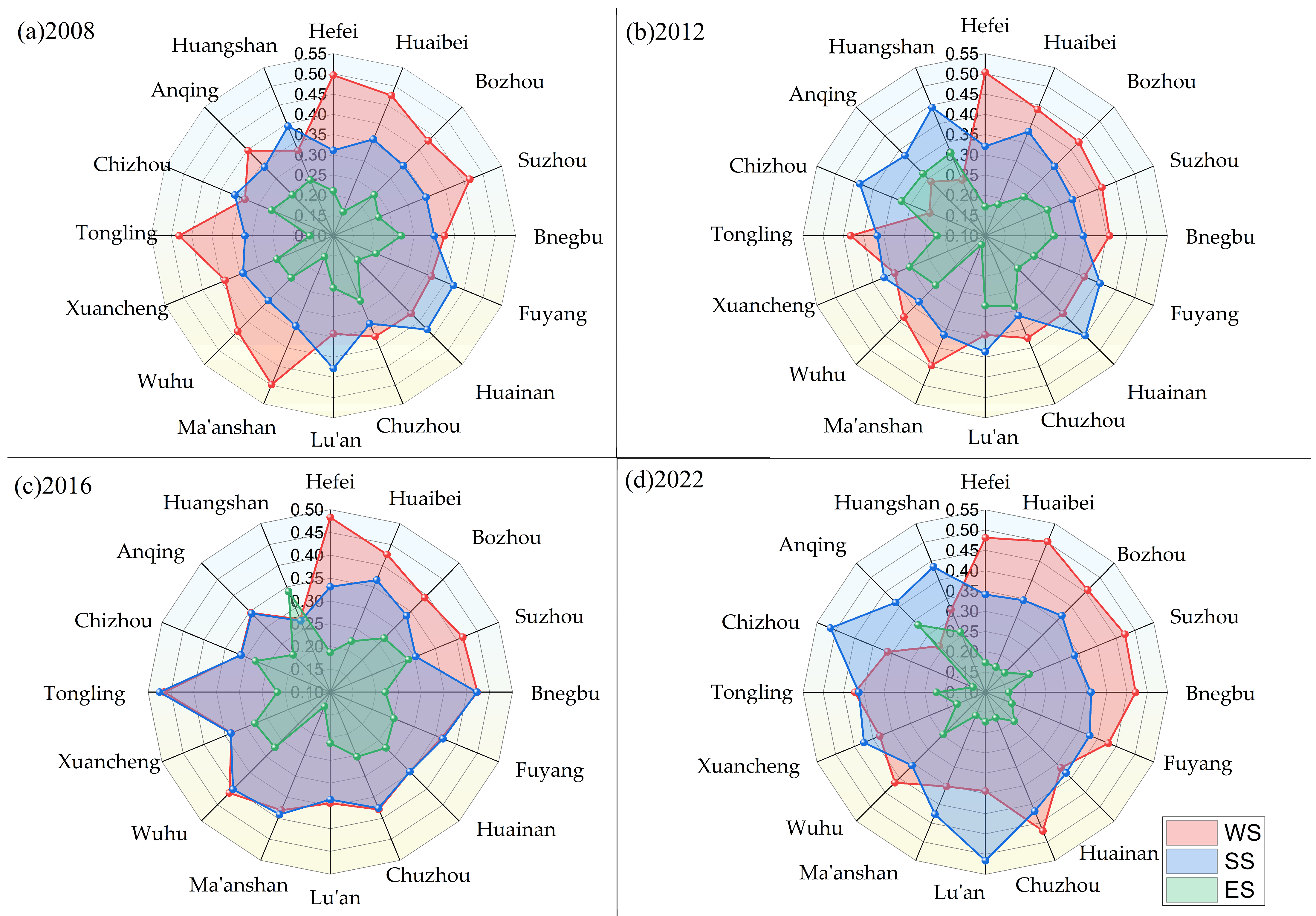
4.3.1. Factor Analysis of Obstacles at the Normative Level
4.3.2. Analysis of WR-WECC Guideline Layer Barrier Factors by Municipality
4.3.3. Factor Analysis of Obstacles at the Indicator Level
- (1)
- Provincial perspective
- (2)
- Municipal perspective
4.4. Forecast of WR-WECC Levels in AP
5. Discussion
- (1)
- The comprehensiveness of the evaluation system is constrained. Owing to the delayed disclosure of government data, this study was unable to incorporate critical indicators such as the soil erosion control area and water quality compliance rate in the ES assessment, potentially introducing bias in evaluating the ES carrying capacity.
- (2)
- The research is limited by the spatial scale of the study area. Currently, the study focuses on the 16 prefecture-level cities of AP, which does not adequately capture the variations in water resources and water environment carrying capacity (WR-WECC) across the Yangtze River, Huaihe River, and Xin’an River Basins within AP.
- (3)
- There is a limited alignment between the forecasted years and policy frameworks. The model projects up to 2040, yet it is not dynamically integrated with specific projects and carbon emission peaking targets outlined in AP’s “14th Five-Year Plan” for water conservancy, which may impact the effectiveness of the forecast results in informing policy interventions.
- (1)
- Developing a comprehensive index system utilizing multi-source data. By integrating multi-source remote sensing and government data platforms, missing indicators such as river and lake health assessments and groundwater overextraction rates can be supplemented, thereby establishing a more precise indicator system for the AP WR-WECC.
- (2)
- Investigating watershed characteristics. Future studies should expand the study area to include the Yangtze River, Huaihe River, and Xin’an River Basins within AP to analyze the differences in the WR-WECC across these basins, thereby enhancing the assessment of the WR-WECC status in AP.
- (3)
- Aligning forecasts with policy frameworks. Implementing policies should be responsive to forecast results, thereby increasing the decision-support value of these forecasts.
6. Conclusions
- (1)
- From 2008 to 2022, the AP WR-WECC exhibited a consistent upward trend, with the three subsystems generally displaying a fluctuating upward trajectory, among which the ecological subsystem experienced the most rapid growth. The WR-WECC across various cities demonstrated an overall fluctuating upward trend, with a narrowing spatial gap.
- (2)
- The DCC of the WSE system’s carrying capacity also showed a fluctuating upward trend, gradually transitioning from level 6 to level 9. The level of Southern Anhui was greater than that of Central Anhui and Northern Anhui, with a more significant increase. The DCC of Central Anhui surpassed that of Northern Anhui.
- (3)
- The OD order of the criterion layer of WR-WECC is WS > SS > ES, where the OD of ES generally shows a downward trend, whereas the OD of WS and SS generally shows an upward trend. Northern Anhui is affected mainly by WS, whereas the central Anhui and southern Anhui regions are restricted by SS. At the index level, the water supply modulus, the water production modulus, and the proportion of tertiary industry are the main obstacle factors restricting the improvement of the AP WR-WECC. The water yield modulus, WR per capita, and forest coverage rate were the main factors influencing Northern Anhui. The restriction of Central Anhui was the same as that in Northern Anhui. The factors restricting the utilization rate of WRs, the proportion of the tertiary industry, and the forest coverage rate in the southern Anhui area are as follows.
- (4)
- The prediction results for 2025–2040 indicate that the WR-WECC level and the three subsystem levels of AP are expected to continue increasing.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AP | Anhui Province |
| WSE | Water-Socio-Ecological |
| WR-WECC | Water Resource-Water Environment Carrying Capacity |
| DE-PPM | Differential Evolution Projection Pursuit Modeling |
| DCCM | Degree of Coupled Coordination Model |
| SA | Southern Anhui |
| CA | Central Anhui |
| NA | Northern Anhui |
References
- Lu, L.; Lei, Y.; Wu, T.; Chen, K. Evaluating Water Resources Carrying Capacity: The Empirical Analysis of Hubei Province, China 2008–2020. Ecol. Indic. 2022, 144, 109454. [Google Scholar] [CrossRef]
- Yang, H.; Hu, D.; Xu, H.; Zhong, X. Assessing the Spatiotemporal Variation of NPP and Its Response to Driving Factors in Anhui Province, China. Environ. Sci. Pollut. Res. 2020, 27, 14915–14932. [Google Scholar] [CrossRef]
- He, L.; Du, Y.; Wu, S.; Zhang, Z. Evaluation of the Agricultural Water Resource Carrying Capacity and Optimization of a Planting-Raising Structure. Agric. Water Manag. 2021, 243, 106456. [Google Scholar] [CrossRef]
- Alamanos, A.; Mylopoulos, N.; Loukas, A.; Gaitanaros, D. An Integrated Multicriteria Analysis Tool for Evaluating Water Resource Management Strategies. Water 2018, 10, 1795. [Google Scholar] [CrossRef]
- Gohari, A.; Mirchi, A.; Madani, K. System Dynamics Evaluation of Climate Change Adaptation Strategies for Water Resources Management in Central Iran. Water Resour. Manag. 2017, 31, 1413–1434. [Google Scholar] [CrossRef]
- Zou, D.; Cong, H. Evaluation and Influencing Factors of China’s Industrial Water Resource Utilization Efficiency from the Perspective of Spatial Effect. Alex. Eng. J. 2021, 60, 173–182. [Google Scholar] [CrossRef]
- Liu, P.; Lue, S.; Han, Y.; Wang, F.; Tang, L. Comprehensive Evaluation on Water Resources Carrying Capacity Based on Water-Economy-Ecology Concept Framework and EFAST-Cloud Model: A Case Study of Henan Province, China. Ecol. Indic. 2022, 143, 109392. [Google Scholar] [CrossRef]
- Wang, G.; Xiao, C.; Qi, Z.; Meng, F.; Liang, X. Development Tendency Analysis for the Water Resource Carrying Capacity Based on System Dynamics Model and the Improved Fuzzy Comprehensive Evaluation Method in the Changchun City, China. Ecol. Indic. 2021, 122, 107232. [Google Scholar] [CrossRef]
- Kang, J.; Zi, X.; Wang, S.; He, L. Evaluation and Optimization of Agricultural Water Resources Carrying Capacity in Haihe River Basin, China. Water 2019, 11, 999. [Google Scholar] [CrossRef]
- Ren, L.; Gao, J.; Song, S.; Li, Z.; Ni, J. Evaluation of Water Resources Carrying Capacity in Guiyang City. Water 2021, 13, 2155. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y.; Su, X.; Qi, L.; Liu, M. Evaluation of the Comprehensive Carrying Capacity of Interprovincial Water Resources in China and the Spatial Effect. J. Hydrol. 2019, 575, 794–809. [Google Scholar] [CrossRef]
- Deng, L.; Yin, J.; Tian, J.; Li, Q.; Guo, S. Comprehensive Evaluation of Water Resources Carrying Capacity in the Han River Basin. Water 2021, 13, 249. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, Y.; Wang, Y. Comprehensive Evaluation and Influencing Factors of Urban Agglomeration Water Resources Carrying Capacity. J. Clean. Prod. 2021, 288, 125097. [Google Scholar] [CrossRef]
- Wang, Y.; Cheng, H.; Huang, L. Water Resources Carrying Capacity Evaluation of a Dense City Group: A Comprehensive Water Resources Carrying Capacity Evaluation Model of Wuhan Urban Agglomeration. Urban. Water J. 2018, 15, 615–625. [Google Scholar] [CrossRef]
- Wu, L.; Su, X.; Ma, X.; Kang, Y.; Jiang, Y. Integrated Modeling Framework for Evaluating and Predicting the Water Resources Carrying Capacity in a Continental River Basin of Northwest China. J. Clean. Prod. 2018, 204, 366–379. [Google Scholar] [CrossRef]
- Cao, F.; Lu, Y.; Dong, S.; Li, X. Evaluation of Natural Support Capacity of Water Resources Using Principal Component Analysis Method: A Case Study of Fuyang District, China. Appl. Water Sci. 2020, 10, 192. [Google Scholar] [CrossRef]
- Mohamed, M.M.; El-Shorbagy, W.; Kizhisseri, M.I.; Chowdhury, R.; McDonald, A. Evaluation of Policy Scenarios for Water Resources Planning and Management in an Arid Region. J. Hydrol. Reg. Stud. 2020, 32, 100758. [Google Scholar] [CrossRef]
- He, L.; Du, X.; Zhao, J.; Chen, H. Exploring the Coupling Coordination Relationship of Water Resources, Socio-Economy and Eco-Environment in China. Sci. Total Environ. 2024, 918, 170705. [Google Scholar] [CrossRef]
- Wang, A.; Liang, S.; Wang, S. Coupling Coordination Development of Water Resources-Economy-Ecology System in Shanxi Province Based on System Dynamics. Sci. Rep. 2025, 15, 7370. [Google Scholar] [CrossRef]
- Zhang, Y.; Khan, S.U.; Swallow, B.; Liu, W.; Zhao, M. Coupling Coordination Analysis of China’s Water Resources Utilization Efficiency and Economic Development Level. J. Clean. Prod. 2022, 373, 133874. [Google Scholar] [CrossRef]
- Xu, L.; Chen, S.S. Coupling Coordination Degree between Social-Economic Development and Water Environment: A Case Study of Taihu Lake Basin, China. Ecol. Indic. 2023, 148, 110118. [Google Scholar] [CrossRef]
- Bai, S.; Abulizi, A.; Mamitimin, Y.; Wang, J.; Yuan, L.; Zhang, X.; Yu, T.; Akbar, A.; Shen, F. Coordination Analysis and Evaluation of Population, Water Resources, Economy, and Ecosystem Coupling in the Tuha Region of China. Sci. Rep. 2024, 14, 17517. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Shen, J.; He, R.; Fan, B.; Han, H. Dynamic Analysis of the Coupling Coordination Relationship between Urbanization and Water Resource Security and Its Obstacle Factor. Int. J. Environ. Res. Public Health 2019, 16, 4765. [Google Scholar] [CrossRef] [PubMed]
- Qiao, R.; Li, H.; Han, H. Spatio-Temporal Coupling Coordination Analysis between Urbanization and Water Resource Carrying Capacity of the Provinces in the Yellow River Basin, China. Water 2021, 13, 376. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, Y.; Kong, Q.; Huang, H. Coupling Coordination Analysis and Key Factors between Urbanization and Water Resources in Ecologically Fragile Areas: A Case Study of the Yellow River Basin, China. Environ. Sci. Pollut. Res. 2024, 31, 10818–10837. [Google Scholar] [CrossRef]
- Ma, H.; Chou, N.-T.; Wang, L. Dynamic Coupling Analysis of Urbanization and Water Resource Utilization Systems in China. Sustainability 2016, 8, 1176. [Google Scholar] [CrossRef]
- Wan, H.; He, G.; Li, B.; Zeng, J.; Cai, Y.; Shen, X.; Yang, Z. Coupling Coordination Relationship between Urbanization and Water Environment in China. J. Clean. Prod. 2024, 472, 143423. [Google Scholar] [CrossRef]
- Chen, L.; Wang, X.; Lv, M.; Su, J.; Yang, B. Coupling Coordination and Spatial–Temporal Evolution of the Water–Land–Ecology System in the North China Plain. Agriculture 2024, 14, 1636. [Google Scholar] [CrossRef]
- Lv, C.; Xu, W.; Ling, M.; Wang, S.; Hu, Y. Evaluation of Synergetic Development of Water and Land Resources Based on a Coupling Coordination Degree Model. Water 2023, 15, 1491. [Google Scholar] [CrossRef]
- Ren, D.; Hu, Z.; Cao, A. Evaluation and Prediction of the Coordination Degree of Coupling Water-Energy-Food-Land Systems in Typical Arid Areas. Sustainability 2024, 16, 6996. [Google Scholar] [CrossRef]
- Zhang, Q.; Cao, Z.; Wang, Y.; Huang, Y. Carrying Capacity and Coupling Coordination of Water and Land Resources Systems in Arid and Semi-Arid Areas: A Case Study of Yulin City, China. Chin. Geogr. Sci. 2024, 34, 931–950. [Google Scholar] [CrossRef]
- Zhao, L.; Yu, J.; Song, X.; Niu, Y.; Xie, J.; Zhang, L.; Li, X. Impact of Land-Use Change on Coupling Coordination Degree of Regional Water–Food–Carbon System. Front. Sustain. Food Syst. 2024, 8. [Google Scholar] [CrossRef]
- Luo, W.; Jiang, Y.; Chen, Y.; Yu, Z. Coupling Coordination and Spatial-Temporal Evolution of Water-Land-Food Nexus: A Case Study of Hebei Province at a County-Level. Land 2023, 12, 595. [Google Scholar] [CrossRef]
- Cheng, Y.; Wang, J.; Shu, K. The Coupling and Coordination Assessment of Food-Water-Energy Systems in China Based on Sustainable Development Goals. Sustain. Prod. Consum. 2023, 35, 338–348. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, C.; Li, L.; Jiang, E.; Zhao, H. The Coupling Coordination Degree and Its Driving Factors for Water–Energy–Food Resources in the Yellow River Irrigation Area of Shandong Province. Sustainability 2024, 16, 8473. [Google Scholar] [CrossRef]
- Han, C.; Han, X.; Ma, B.; Li, D.; Wang, Z.; Hao, Z.; Zhang, X. Research on the Coupling Coordination Relationship and Spatial Equilibrium Measurement of the Water–Energy–Food Nexus System in China. Water 2025, 17, 527. [Google Scholar] [CrossRef]
- Gao, J.; Xu, J. Research on the Spatiotemporal Characteristics of the Coupling Coordination Relationship of the Energy–Food–Water System in the Xinjiang Subregion. Sustainability 2024, 16, 3491. [Google Scholar] [CrossRef]
- Fu, N.; Liu, D.; Liu, H.; Pan, B.; Ming, G.; Huang, Q. Evaluation of the Coupled Coordination of the Water–Energy–Food–Ecology System Based on the Sustainable Development Goals in the Upper Han River of China. Agronomy 2024, 14, 706. [Google Scholar] [CrossRef]
- Gao, X.; Wang, K.; Lo, K.; Wen, R.; Mi, X.; Liu, K.; Huang, X. An Evaluation of Coupling Coordination between Rural Development and Water Environment in Northwestern China. Land 2021, 10, 405. [Google Scholar] [CrossRef]
- Zhao, J.; Li, M.; Guo, P.; Zhang, C.; Tan, Q. Agricultural Water Productivity Oriented Water Resources Allocation Based on the Coordination of Multiple Factors. Water 2017, 9, 490. [Google Scholar] [CrossRef]
- Miao, C.; Sun, L.; Yang, L. The Studies of Ecological Environmental Quality Assessment in Anhui Province Based on Ecological Footprint. Ecol. Indic. 2016, 60, 879–883. [Google Scholar] [CrossRef]
- Han, W.; Chen, D.; Li, H.; Chang, Z.; Chen, J.; Ye, L.; Liu, S.; Wang, Z. Spatiotemporal Variation of NDVI in Anhui Province from 2001 to 2019 and Its Response to Climatic Factors. Forests 2022, 13, 1643. [Google Scholar] [CrossRef]
- Xi, M.; Xu, Y.; Li, Z.; Hu, R.; Cheng, T.; Zhou, Y.; Tu, D.; Ji, Y.; Xu, X.; Sun, X.; et al. Progress and Challenges of Rice Ratooning Technology in Anhui Province, China. Crop Environ. 2023, 2, 81–86. [Google Scholar] [CrossRef]
- Ren, B.; Sun, B.; Shi, X.; Zhao, S.; Wang, X. Analysis of the Cooperative Carrying Capacity of Ulan Suhai Lake Based on the Coupled Water Resources–Water Environment–Water Ecology System. Water 2022, 14, 3102. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, J.; Song, Y. Comprehensive Comparison and Assessment of Three Models Evaluating Water Resource Carrying Capacity in Beijing, China. Ecol. Indic. 2022, 143, 109305. [Google Scholar] [CrossRef]
- Kong, Y.; He, W.; Gao, X.; Yuan, L.; Peng, Q.; Li, S.; Zhang, Z.; Degefu, D.M. Dynamic Assessment and Influencing Factors Analysis of Water Environmental Carrying Capacity in the Yangtze River Economic Belt, China. Ecol. Indic. 2022, 142, 109214. [Google Scholar] [CrossRef]
- Su, Y.; Xu, X.; Dai, M.; Hu, Y.; Li, Q.; Shu, S. A Comprehensive Evaluation of Water Resource Carrying Capacity Based on the Optimized Projection Pursuit Regression Model: A Case Study from China. Water 2024, 16, 2650. [Google Scholar] [CrossRef]
- Deng, W.; Shang, S.; Cai, X.; Zhao, H.; Song, Y.; Xu, J. An Improved Differential Evolution Algorithm and Its Application in Optimization Problem. Soft Comput. 2021, 25, 5277–5298. [Google Scholar] [CrossRef]
- Xia, X.; Gui, L.; Zhang, Y.; Xu, X.; Yu, F.; Wu, H.; Wei, B.; He, G.; Li, Y.; Li, K. A Fitness-Based Adaptive Differential Evolution Algorithm. Inf. Sci. 2021, 549, 116–141. [Google Scholar] [CrossRef]
- Yildizdan, G.; Baykan, Ö.K. A Novel Modified Bat Algorithm Hybridizing by Differential Evolution Algorithm. Expert. Syst. Appl. 2020, 141, 112949. [Google Scholar] [CrossRef]
- Su, Y.; Liu, Y.; Zhou, Y.; Liu, J. Research on the Coupling and Coordination of Land Ecological Security and High-Quality Agricultural Development in the Han River Basin. Land 2024, 13, 1666. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, M. Quality Evaluation of Enterprise Environmental Accounting Information Disclosure Based on Projection Pursuit Model. J. Clean. Prod. 2021, 279, 123679. [Google Scholar] [CrossRef]
- Zhi, G.; Liao, Z.; Tian, W.; Wu, J. Urban Flood Risk Assessment and Analysis with a 3D Visualization Method Coupling the PP-PSO Algorithm and Building Data. J. Environ. Manag. 2020, 268, 110521. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Li, Y.; Yang, X.; Zhang, Z.; Gao, S.; Zhou, Q.; Zhuo, Y.; Wen, X.; Guo, Z. Evaluating Urban Ecological Civilization and Its Obstacle Factors Based on Integrated Model of PSR-EVW-TOPSIS: A Case Study of 13 Cities in Jiangsu Province, China. Ecol. Indic. 2021, 133, 108431. [Google Scholar] [CrossRef]
- Fan, Y.; Fang, C. Evolution Process and Obstacle Factors of Ecological Security in Western China, a Case Study of Qinghai Province. Ecol. Indic. 2020, 117, 106659. [Google Scholar] [CrossRef]
- Bai, X.; Jin, J.; Zhou, R.; Wu, C.; Zhou, Y.; Zhang, L.; Cui, Y. Coordination Evaluation and Obstacle Factors Recognition Analysis of Water Resource Spatial Equilibrium System. Environ. Res. 2022, 210, 112913. [Google Scholar] [CrossRef]
- Dong, Q.; Zhong, K.; Liao, Y.; Xiong, R.; Wang, F.; Pang, M. Coupling Coordination Degree of Environment, Energy, and Economic Growth in Resource-Based Provinces of China. Resour. Policy 2023, 81, 103308. [Google Scholar] [CrossRef]
- Qi, Y.; Farnoosh, A.; Lin, L.; Liu, H. Coupling Coordination Analysis of China’s Provincial Water-Energy-Food Nexus. Environ. Sci. Pollut. Res. 2022, 29, 23303–23313. [Google Scholar] [CrossRef]
- Lee, Y.-S.; Tong, L.-I. Forecasting Time Series Using a Methodology Based on Autoregressive Integrated Moving Average and Genetic Programming. Knowl.-Based Syst. 2011, 24, 66–72. [Google Scholar] [CrossRef]
- Alharbi, F.R.; Csala, D. A Seasonal Autoregressive Integrated Moving Average with Exogenous Factors (SARIMAX) Forecasting Model-Based Time Series Approach. Inventions 2022, 7, 94. [Google Scholar] [CrossRef]
- Sheikh Khozani, Z.; Barzegari Banadkooki, F.; Ehteram, M.; Najah Ahmed, A.; El-Shafie, A. Combining Autoregressive Integrated Moving Average with Long Short-Term Memory Neural Network and Optimisation Algorithms for Predicting Ground Water Level. J. Clean. Prod. 2022, 348, 131224. [Google Scholar] [CrossRef]
- Peng, T.; Jin, Z.; Xiao, L. Assessing Carrying Capacity of Regional Water Resources in Karst Areas, Southwest China: A Case Study. Environ. Dev. Sustain. 2023, 25, 15139–15162. [Google Scholar] [CrossRef]
- Wang, X.; Liu, L.; Zhang, S.; Gao, C. Dynamic Simulation and Comprehensive Evaluation of the Water Resources Carrying Capacity in Guangzhou City, China. Ecol. Indic. 2022, 135, 108528. [Google Scholar] [CrossRef]
- Gan, L.; Shi, H.; Hu, Y.; Lev, B.; Lan, H. Coupling Coordination Degree for Urbanization City-Industry Integration Level: Sichuan Case. Sustain. Cities Soc. 2020, 58, 102136. [Google Scholar] [CrossRef]
- Huang, Y.; Li, X.; Liu, D.; Duan, B.; Huang, X.; Chen, S. Evaluation of Vegetation Restoration Effectiveness along the Yangtze River Shoreline and Its Response to Land Use Changes. Sci. Rep. 2024, 14, 7611. [Google Scholar] [CrossRef]
- Wu, J.; Cheng, S.; Li, Z.; Guo, W.; Zhong, F.; Yin, D. Case Study on Rehabilitation of a Polluted Urban Water Body in Yangtze River Basin. Environ. Sci. Pollut. Res. 2013, 20, 7038–7045. [Google Scholar] [CrossRef]
- Li, J.; Chen, X.; Zhang, X.; Huang, Z.; Xiao, L.; Huang, L.; Kano, Y.; Sato, T.; Shimatani, Y.; Zhang, C. Fish Biodiversity Conservation and Restoration, Yangtze River Basin, China, Urgently Needs ‘Scientific’ and ‘Ecological’ Action. Water 2020, 12, 3043. [Google Scholar] [CrossRef]
- Chen, M.; Tan, Y.; Xu, X.; Lin, Y. Identifying Ecological Degradation and Restoration Zone Based on Ecosystem Quality: A Case Study of Yangtze River Delta. Appl. Geogr. 2024, 162, 103149. [Google Scholar] [CrossRef]
- Chen, Q.; Zhu, M.; Zhang, C.; Zhou, Q. The Driving Effect of Spatial-Temporal Difference of Water Resources Carrying Capacity in the Yellow River Basin. J. Clean. Prod. 2023, 388, 135709. [Google Scholar] [CrossRef]



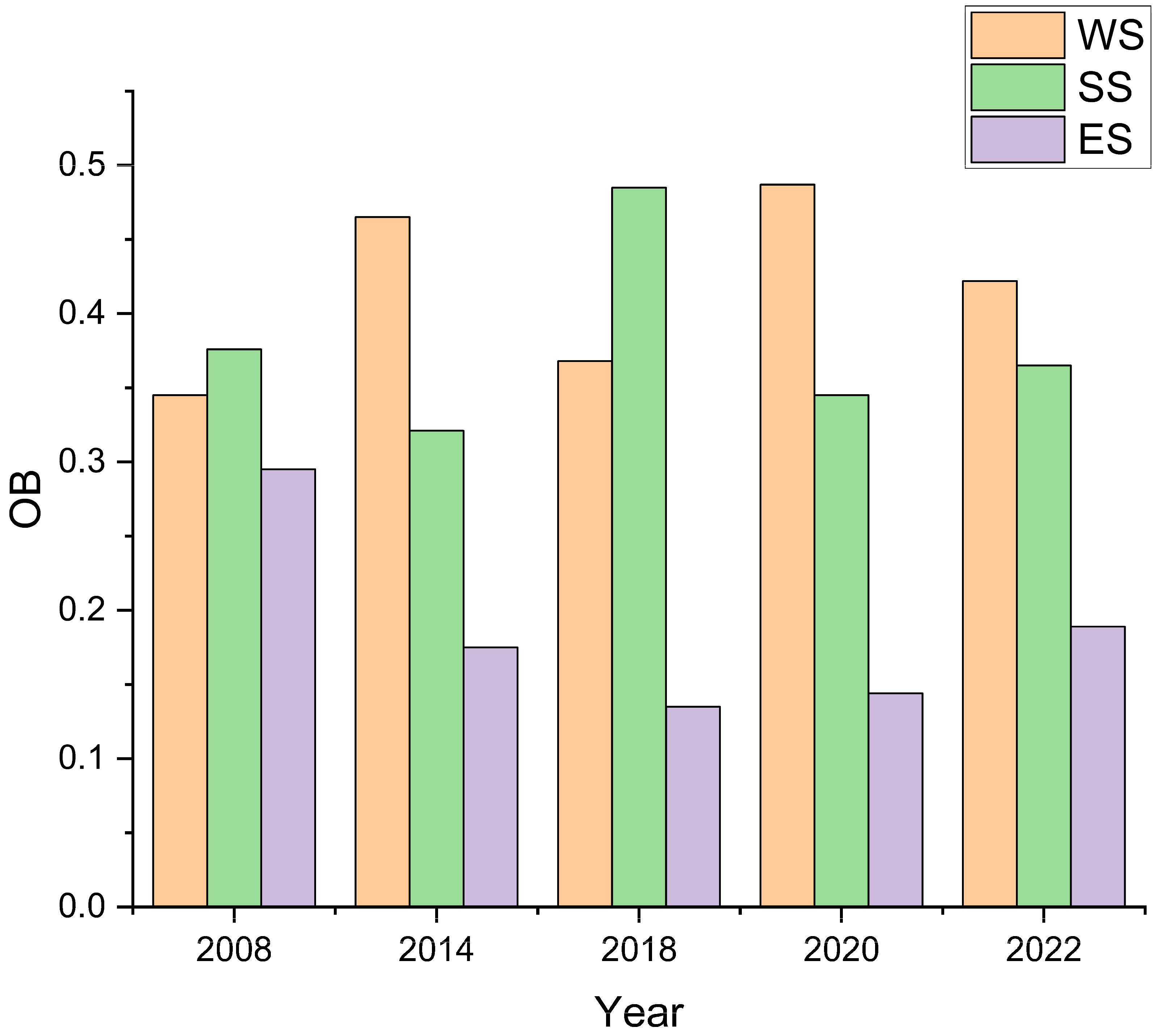
| Criterion Layer | Index Layer | Unit | Attribute |
|---|---|---|---|
| WS | X1 Total water resources (Billion) | m3 | + |
| X2 Water resources per capita | m3/person | + | |
| X3 Water consumption per capita | m3/person | − | |
| X4 Precipitation | mm | + | |
| X5 Modulus of water production | m3/km2 | + | |
| X6 Modulus of water supply | m3/km2 | − | |
| X7 Water resources development | % | + | |
| SS | X8 Population density | person/km2 | − |
| X9 Natural population growth rate | % | − | |
| X10 Urbanization level | % | − | |
| X11 GDP per capita | Yuan | + | |
| X12 Water consumption of 10,000 Yuan | GDP m3/CNY 10,000 | − | |
| X13 Water consumption of 10,000 Yuan of industrial added value | m3/million Yuan | − | |
| X14 Irrigation water consumption rate | % | − | |
| X15 Industrial water consumption rate | % | − | |
| X16 Tertiary industry | % | + | |
| ES | X17 Ecological water guarantee rate | % | + |
| X18 Centralized urban wastewater treatment rate | % | + | |
| X19 10,000 Yuan of Industrial Output Value COD Emission Intensity | kg/million Yuan | − | |
| X20 10,000 Yuan GDP Chemical Oxygen Demand Emission Intensity | kg/million Yuan | − | |
| X21 Forest cover rate | % | + | |
| X22 Greening coverage rate of built-up area | % | + |
| City/Level | 2008 | 2012 | 2016 | 2022 |
|---|---|---|---|---|
| Xuancheng | MC | MC | MC | MC |
| Huaibei | PC | BC | PC | MC |
| Tongling | PC | PC | PC | PC |
| Bozhou | MC | PC | PC | MC |
| Huainan | PC | BC | PC | PC |
| Chizhou | PC | MC | MC | MC |
| Ma’anshan | PC | BC | PC | PC |
| Anqing | PC | PC | MC | PC |
| Huangshan | GC | GC | GC | GC |
| Chuzhou | PC | MC | PC | MC |
| Wuhu | PC | PC | PC | MC |
| Lu’an | MC | MC | PC | MC |
| Bnegbu | PC | PC | PC | MC |
| Fuyang | PC | PC | PC | MC |
| Suzhou | MC | PC | PC | MC |
| Hefei | MC | MC | MC | MC |
| AP | MC | PC | PC | MC |
| Year | Obstacle Factor | |||||
|---|---|---|---|---|---|---|
| 2008 | X5 | X21 | X12 | X19 | X1 | X2 |
| 12.75 | 10.15 | 9.48 | 8.45 | 8.32 | 7.15 | |
| 2012 | X6 | X16 | X3 | X14 | X21 | X11 |
| 15.62 | 14.25 | 12.26 | 9.15 | 8.81 | 7.97 | |
| 2016 | X16 | X5 | X6 | X1 | X2 | X3 |
| 12.27 | 10.02 | 9.74 | 9.22 | 8.46 | 7.72 | |
| 2020 | X6 | X8 | X5 | X9 | X10 | X3 |
| 13.35 | 11.24 | 10.87 | 9.15 | 8.3 | 7.19 | |
| 2022 | X7 | X8 | X10 | X6 | X17 | X3 |
| 15.66 | 14.15 | 13.77 | 11.33 | 9.41 | 8.89 | |
| City | Obstacle Factor | |||||
|---|---|---|---|---|---|---|
| Huaibei | X5 | X1 | X2 | X21 | X4 | X16 |
| 13.44 | 10.15 | 9.48 | 8.45 | 8.32 | 7.15 | |
| Bozhou | X5 | X2 | X21 | X1 | X9 | X11 |
| 13.25 | 12.04 | 11.24 | 10.14 | 9.27 | 9.11 | |
| Suzhou | X5 | X2 | X1 | X21 | X16 | X11 |
| 12.27 | 10.02 | 9.74 | 9.54 | 9.41 | 8.84 | |
| Bengbu | X5 | X2 | X21 | X1 | X16 | X14 |
| 14.41 | 13.84 | 12.91 | 11.04 | 10.22 | 9.19 | |
| Fuyang | X5 | X2 | X21 | X1 | X16 | X11 |
| 13.27 | 12.17 | 10.75 | 9.24 | 9.1 | 8.47 | |
| Huainan | X21 | X5 | X12 | X2 | X1 | X22 |
| 12.74 | 11.4 | 10.26 | 9.81 | 9.23 | 8.61 | |
| Chuzhou | X16 | X5 | X2 | X14 | X21 | X1 |
| 12.02 | 11.44 | 11.2 | 10.26 | 9.76 | 9.24 | |
| Hefei | X2 | X5 | X21 | X10 | X9 | X1 |
| 13.52 | 12.19 | 11.16 | 10.54 | 9.84 | 9.24 | |
| Anqing | X19 | X16 | X7 | X21 | X2 | X12 |
| 11.05 | 10.74 | 10.64 | 9.84 | 9.26 | 8.89 | |
| Lu’an | X12 | X14 | X7 | X16 | X11 | X2 |
| 12.46 | 12.1 | 11.72 | 11.2 | 10.43 | 10.12 | |
| Ma’anshan | X6 | X21 | X3 | X2 | X12 | X16 |
| 12.47 | 11.61 | 11.4 | 10.54 | 10.11 | 9.77 | |
| Wuhu | X21 | X2 | X16 | X12 | X15 | X3 |
| 11.25 | 11.01 | 10.64 | 10.02 | 9.24 | 9.1 | |
| Xuancheng | X16 | X7 | X14 | X5 | X2 | X12 |
| 13.29 | 12.14 | 11.29 | 10.73 | 9.46 | 9.01 | |
| Tongling | X21 | X12 | X2 | X16 | X13 | X1 |
| 11.13 | 10.46 | 10.29 | 9.74 | 9.53 | 8.77 | |
| Chizhou | X16 | X7 | X12 | X3 | X11 | X13 |
| 11.23 | 10.95 | 9.7 | 9.26 | 9.11 | 8.49 | |
| Huangshan | X7 | X13 | X14 | X18 | X11 | X10 |
| 13.56 | 13.24 | 12.04 | 11.46 | 10.21 | 9.54 | |
| Year | True Value | Predicted Value | Residual Value |
|---|---|---|---|
| 2000 | 0.885 | 0.897 | −0.012 |
| 2003 | 1.314 | 1.113 | 0.201 |
| 2006 | 1.350 | 1.343 | 0.007 |
| 2009 | 1.349 | 1.680 | −0.331 |
| 2012 | 1.415 | 1.475 | −0.059 |
| 2015 | 1.429 | 1.483 | −0.054 |
| 2018 | 1.432 | 1.553 | −0.121 |
| 2021 | 1.736 | 1.666 | 0.070 |
| 2022 | 1.798 | 1.770 | 0.028 |
| 2025 | 1.890 | ||
| 2028 | 2.016 | ||
| 2031 | 2.127 | ||
| 2034 | 2.247 | ||
| 2037 | 2.361 | ||
| 2040 | 2.479 |
| Year | True Value | Predicted Value | Residual Value |
|---|---|---|---|
| 2000 | 0.924 | 0.923 | 0.001 |
| 2003 | 1.284 | 1.265 | 0.019 |
| 2006 | 1.414 | 1.427 | −0.013 |
| 2009 | 1.246 | 1.418 | −0.172 |
| 2012 | 1.245 | 1.215 | 0.030 |
| 2015 | 1.338 | 1.322 | 0.016 |
| 2018 | 1.348 | 1.457 | −0.109 |
| 2021 | 1.743 | 1.623 | 0.120 |
| 2022 | 1.825 | 1.914 | −0.089 |
| 2025 | 1.851 | ||
| 2028 | 2.026 | ||
| 2031 | 2.099 | ||
| 2034 | 2.249 | ||
| 2037 | 2.340 | ||
| 2040 | 2.476 |
| Year | True Value | Predicted Value | Residual Value |
|---|---|---|---|
| 2000 | 0.921 | 0.959 | −0.038 |
| 2003 | 1.330 | 1.454 | −0.124 |
| 2006 | 1.429 | 1.407 | 0.022 |
| 2009 | 1.433 | 1.485 | −0.052 |
| 2012 | 1.491 | 1.594 | −0.103 |
| 2015 | 1.452 | 1.463 | −0.011 |
| 2018 | 1.521 | 1.625 | −0.104 |
| 2021 | 1.784 | 1.820 | −0.036 |
| 2022 | 1.810 | 1.820 | −0.010 |
| 2025 | 1.879 | ||
| 2028 | 1.994 | ||
| 2031 | 2.108 | ||
| 2034 | 2.223 | ||
| 2037 | 2.338 | ||
| 2040 | 2.453 |
| Year | True Value | Predicted Value | Residual Value |
|---|---|---|---|
| 2000 | 1.059 | 1.092 | −0.033 |
| 2003 | 1.141 | 1.188 | −0.047 |
| 2006 | 1.182 | 1.264 | −0.082 |
| 2009 | 1.405 | 1.424 | −0.019 |
| 2012 | 1.481 | 1.523 | −0.042 |
| 2015 | 1.643 | 1.645 | −0.002 |
| 2018 | 1.712 | 1.736 | −0.024 |
| 2021 | 1.748 | 1.807 | −0.059 |
| 2022 | 1.777 | 1.807 | −0.030 |
| 2025 | 1.923 | ||
| 2028 | 2.025 | ||
| 2031 | 2.125 | ||
| 2034 | 2.224 | ||
| 2037 | 2.324 | ||
| 2040 | 2.424 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, Q.; Su, Y.; Geng, J.; Shu, S.; Liu, Y. A Comprehensive Study of Water Resource–Environment Carrying Capacity via a Water-Socio-Ecological Framework and Differential Evolution-Based Projection Pursuit Modeling. Water 2025, 17, 1624. https://doi.org/10.3390/w17111624
Fang Q, Su Y, Geng J, Shu S, Liu Y. A Comprehensive Study of Water Resource–Environment Carrying Capacity via a Water-Socio-Ecological Framework and Differential Evolution-Based Projection Pursuit Modeling. Water. 2025; 17(11):1624. https://doi.org/10.3390/w17111624
Chicago/Turabian StyleFang, Quan, Yuelong Su, Jie Geng, Shumiao Shu, and Yucheng Liu. 2025. "A Comprehensive Study of Water Resource–Environment Carrying Capacity via a Water-Socio-Ecological Framework and Differential Evolution-Based Projection Pursuit Modeling" Water 17, no. 11: 1624. https://doi.org/10.3390/w17111624
APA StyleFang, Q., Su, Y., Geng, J., Shu, S., & Liu, Y. (2025). A Comprehensive Study of Water Resource–Environment Carrying Capacity via a Water-Socio-Ecological Framework and Differential Evolution-Based Projection Pursuit Modeling. Water, 17(11), 1624. https://doi.org/10.3390/w17111624






