A New Method for Calculating the Roughness Coefficient of Salt Marsh Vegetation Based on Field Flow Observation
Abstract
1. Introduction
2. Methods
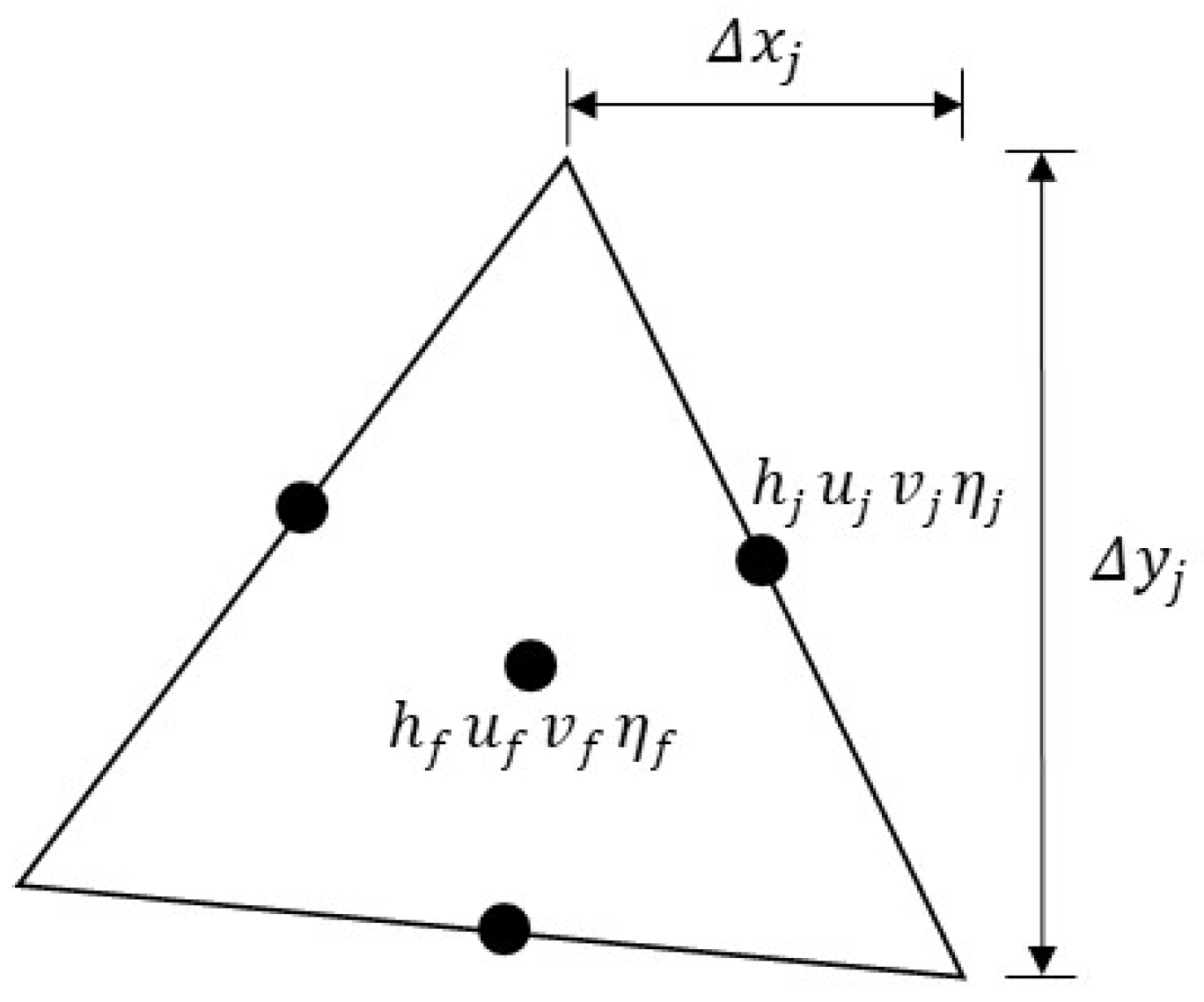
2.1. Theoretical Formulas
2.2. Field Observation
3. Results
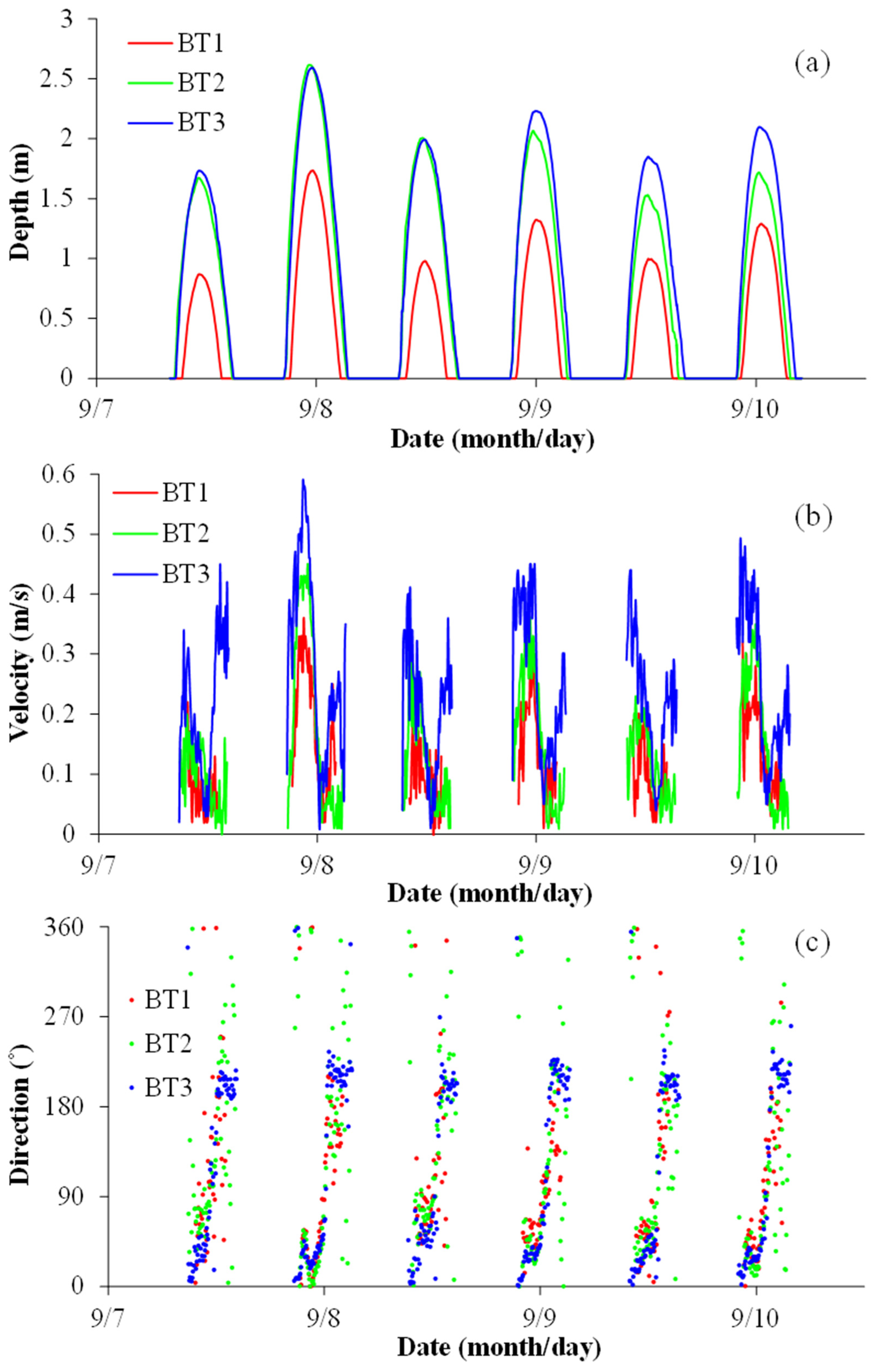
3.1. Spatio-Temporal Variations in Hydrodynamics
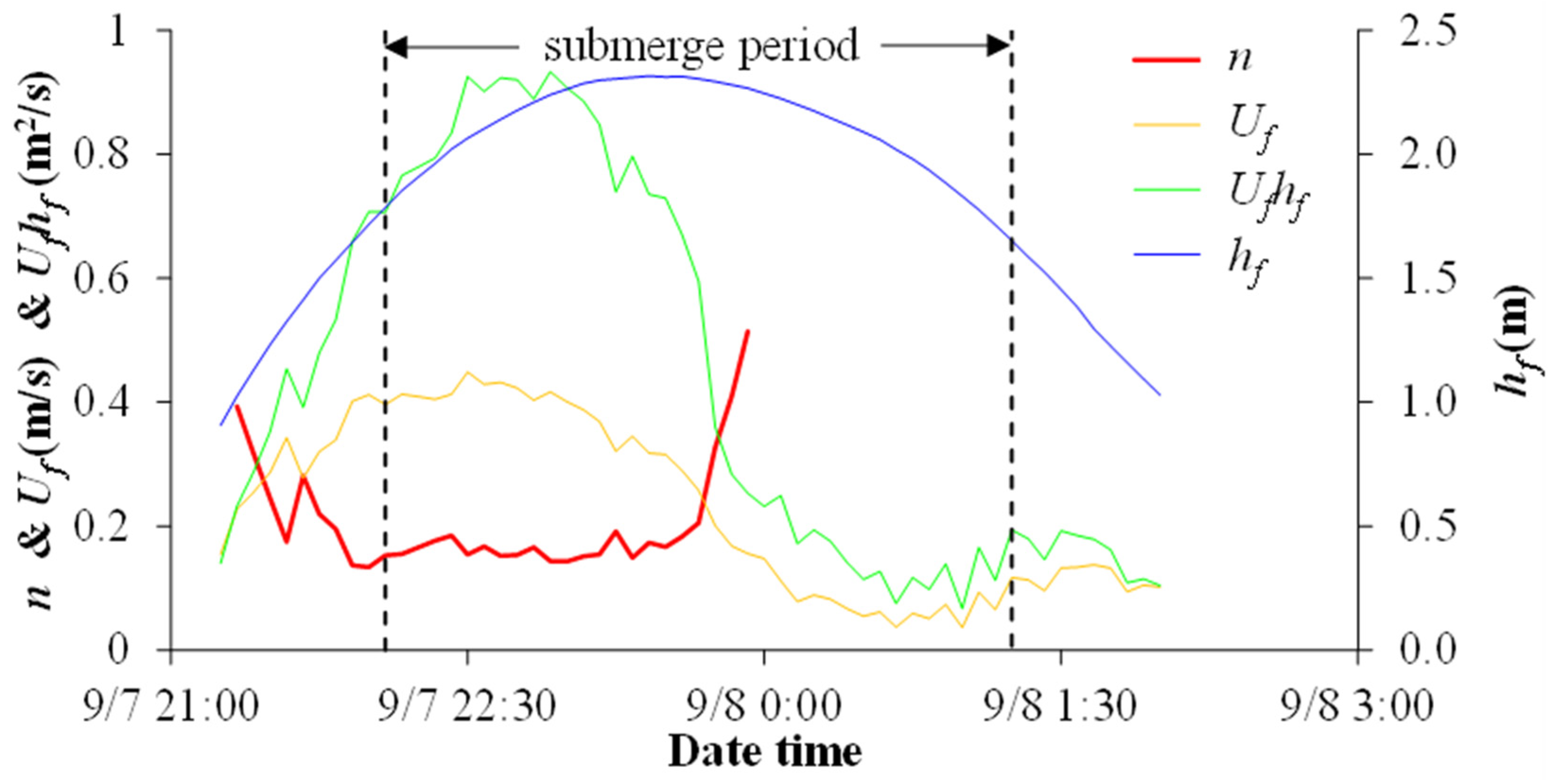
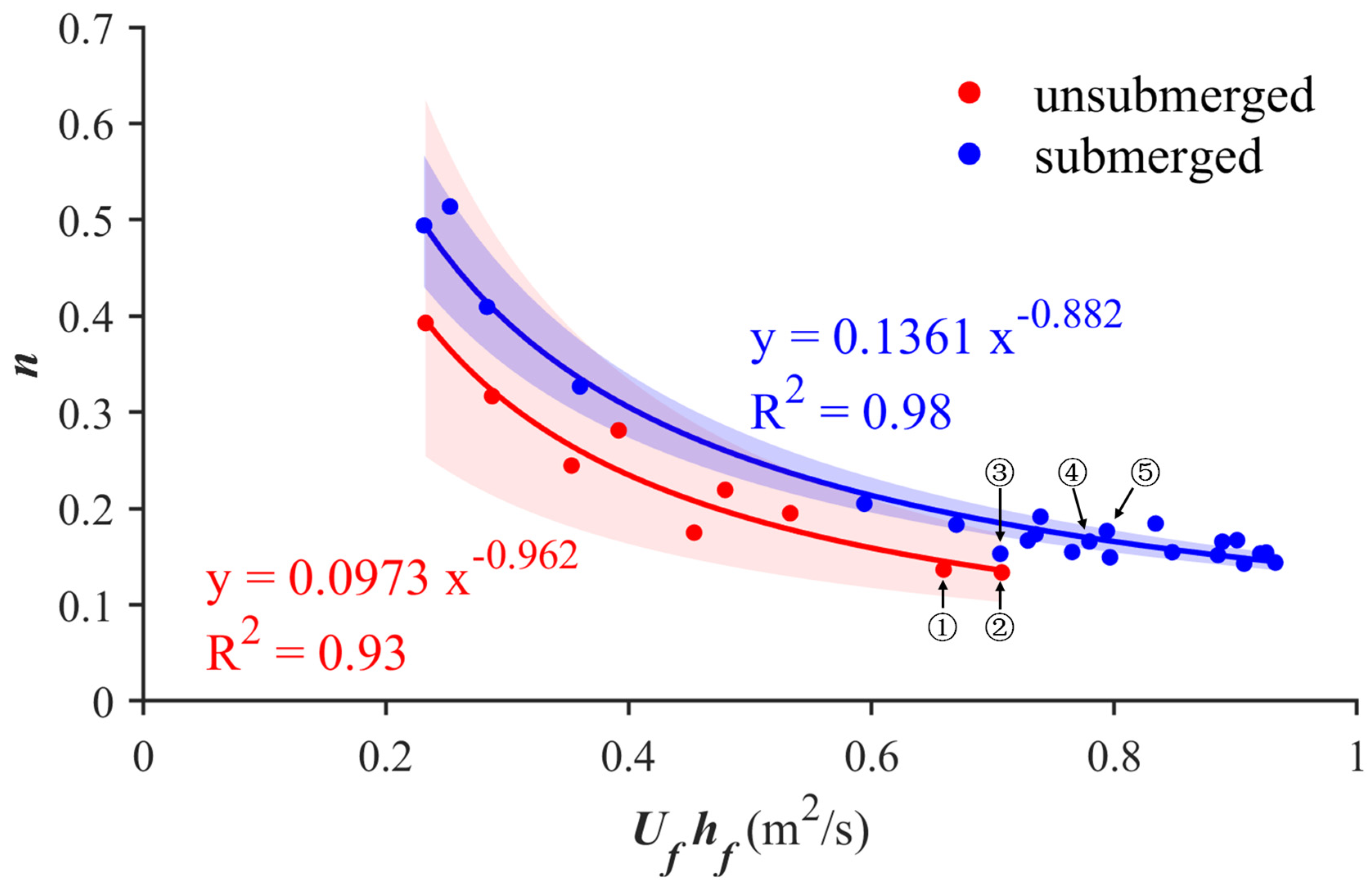
3.2. Variation Characteristics of Manning’s Roughness Coefficient
4. Discussion
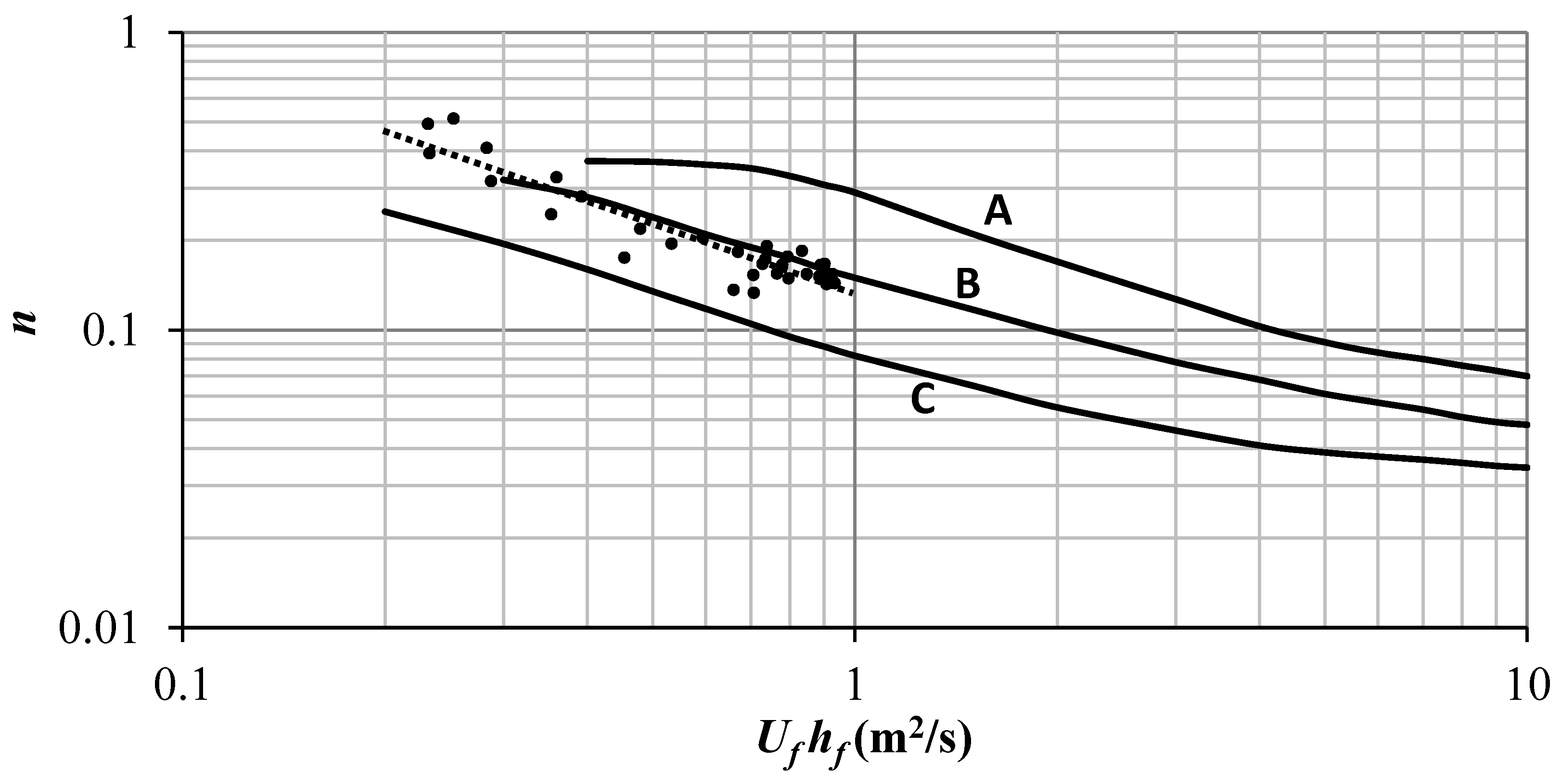
4.1. Verification of Calculation Results
4.2. Differences Between Submerged and Unsubmerged Conditions
4.3. Applications and Limitations of New Method
5. Conclusions
- (1)
- For the salt marsh vegetated zone, the formula of the roughness coefficient under the condition of two-dimensional unsteady flow can be derived by coupling the flow resistance equation with the discretized momentum conservation equation. This formula, in combination with field observation data, could obtain temporal variations in the roughness coefficient.
- (2)
- Flooding currents are dominant in the salt marsh vegetated zone of the Jiuduansha Wetland, whereas ebbing currents are less dominant. Both flooding and ebbing currents are significantly influenced by vegetation. Specifically, flooding currents show characteristics of overland flow along the elevation gradient, and the flooding velocity exhibits a notable decrease after passing through the vegetated zone.
- (3)
- The vegetation flow roughness coefficient shows an inverse power-law relationship with the product of flow velocity and water depth at the center of the control volume. Additionally, the submerged vegetation condition significantly influences the flow resistance. The roughness coefficient n slightly increases when the vegetation is nearly submerged, and its value is greater during the submerged period than during the non-submerged period.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- D’Alpaos, A.; Toffolon, M.; Camporeale, C. Ecogeomorphological feedbacks of water fluxes, sediment transport and vegetation dynamics in rivers and estuaries. Adv. Water Resour. 2016, 93, 151–155. [Google Scholar] [CrossRef]
- Gran, K.; Paola, C. Riparian vegetation controls on braided stream dynamics. Water Resour. Res. 2001, 37, 3275–3283. [Google Scholar] [CrossRef]
- Gong, Z.; Chen, X.; Zhou, Z.; Ge, R.; Chen, X.; Yu, X.; Zhang, C. The roles of biological factors in coastal sediment transport: A review. Chin. Sci. Bull. 2020, 66, 53–62. [Google Scholar] [CrossRef]
- Crooks, S.; Sutton-Grier, A.E.; Troxler, T.G.; Herold, N.; Bernal, B.; Schile-Beers, L.; Wirth, T. Coastal wetland management as a contribution to the US National Greenhouse Gas Inventory. Nat. Clim. Change 2018, 8, 1109–1112. [Google Scholar] [CrossRef]
- Huai, W.X.; Li, S.; Katul, G.G.; Liu, M.Y.; Yang, Z.H. Flow dynamics and sediment transport in vegetated rivers: A review. J. Hydrodyn. 2021, 33, 400–420. [Google Scholar] [CrossRef]
- Belluco, E.; Camuffo, M.; Ferrari, S.; Modenese, L.; Silvestri, S.; Marani, A.; Marani, M. Mapping salt-marsh vegetation by multispectral and hyperspectral remote sensing. Remote Sens. Environ. 2006, 105, 54–67. [Google Scholar] [CrossRef]
- Boorman, L. Saltmarsh Review: An Overview of Coastal Saltmarshes, Their Dynamic and Sensitivity Characteristics for Conservation and Management; JNCC: Peterborough, UK, 2003.
- Wu, F.S.; Wang, W.Y.; Jiang, S.H. Hydrodynamics development in vegetated open channel. Adv. Water Sci. 2007, 18, 456–461. [Google Scholar]
- Chen, H.; Ni, Y.; Li, Y.; Liu, F.; Ou, S.; Su, M.; Peng, Y.; Hu, Z.; Uijttewaal, W.; Suzuki, T. Deriving vegetation drag coefficients in combined wave-current flows by calibration and direct measurement methods. Adv. Water Resour. 2018, 122, 217–227. [Google Scholar] [CrossRef]
- Tsujimoto, T. Fluvial processes in streams with vegetation. J. Hydraul. Res. 1999, 37, 789–803. [Google Scholar] [CrossRef]
- D’Alpaos, A.; Lanzoni, S.; Mudd, S.M.; Fagherazzi, S. Modeling the influence of hydroperiod and vegetation on the cross-sectional formation of tidal channels. Estuar. Coast. Shelf Sci. 2006, 69, 311–324. [Google Scholar] [CrossRef]
- Li, H.; Yang, S.L. A Review of Influences of Saltmarsh Vegetation on Physical Processes in Intertidal Wetlands. Adv. Earth Sci. 2007, 26, 583–591. [Google Scholar]
- D’Alpaos, A.; Lanzoni, S.; Marani, M.; Rinaldo, A. On the O’Brien–Jarrett–Marchi law. Rend. Lincei 2009, 20, 225–236. [Google Scholar] [CrossRef][Green Version]
- Zheng, S.; Wu, Y.H.; Bai, Y.; Bao, L.; Mu, X.P. Experimental research on Manning’s roughness coefficient of an open channel with aquatic vegetation. J. Hydraul. Eng. 2017, 48, 874–881. [Google Scholar] [CrossRef]
- Lei, J.; Fan, D.; Angera, A.; Liu, Y.; Nepf, H. Drag force and reconfiguration of cultivated Saccharina latissima in current. Aquac. Eng. 2021, 94, 102169. [Google Scholar] [CrossRef]
- Luhar, M.; Nepf, H.M. From the blade scale to the reach scale: A characterization of aquatic vegetative drag. Adv. Water Resour. 2013, 51, 305–316. [Google Scholar] [CrossRef]
- Järvelä, J. Flow resistance of flexible and stiff vegetation: A flume study with natural plants. J. Hydrol. 2002, 269, 44–54. [Google Scholar] [CrossRef]
- Tang, H.W.; Yan, J.; Xiao, Y.; Lu, S.Q. Manning’s roughness coefficient of vegetated channels. J. Hydraul. Eng. 2007, 38, 1347–1353. [Google Scholar]
- Chow, V.T. Open-Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Kouwen, N.; Fathi-Moghadam, M. Friction Factors for Coniferous Trees along Rivers. J. Hydraul. Eng. 2000, 126, 732–740. [Google Scholar] [CrossRef]
- Kumar, B.; Patra, S.; Pandey, M. Experimental Investigation on Flow Configuration in Flexible and Rigid Vegetated Streams. Water Resour. Manag. 2023, 37, 6005–6019. [Google Scholar] [CrossRef]
- Iqbal, K.; Ghani, U.; Pasha, G.A.; Murtaza, N.; Kaleem Ullah, M.; Anjum, N. Laboratory investigation of flow behavior in an open channel with emerged porous rigid and flexible vegetation. J. Hydrodyn. 2025, 36, 1181–1199. [Google Scholar] [CrossRef]
- Wilson, C.A.M.E.; Stoesser, T.; Bates, P.D.; Pinzen, A.B. Open Channel Flow through Different Forms of Submerged Flexible Vegetation. J. Hydraul. Eng. 2003, 129, 847–853. [Google Scholar] [CrossRef]
- Zhang, C.; Tang, H.; Shi, B.; Wang, C.; Yin, Z.; Zhao, L. Roughness coeficent relations of open channel with flexible submerged vegetation. In Proceedings of the 16th IAHR-APD Congress and 3rd Symposium of IAHR-ISHS, Nanjing, China, 20–23 October 2008; p. 4. [Google Scholar]
- Shucksmith, J.D.; Boxall, J.B.; Guymer, I. Bulk Flow Resistance in Vegetated Channels: Analysis of Momentum Balance Approaches Based on Data Obtained in Aging Live Vegetation. J. Hydraul. Eng. 2011, 137, 1624–1635. [Google Scholar] [CrossRef]
- Gu, F.F.; Ni, H.G.; Qi, D.M. Roughness coefficient for unsubmerged and submerged reed. J. Hydrodyn. Ser.B 2007, 19, 421–428. [Google Scholar] [CrossRef]
- Zhang, J.; Lei, J.; Huai, W.; Nepf, H. Turbulence and Particle Deposition Under Steady Flow Along a Submerged Seagrass Meadow. J. Geophys. Res. Oceans 2020, 125, e2019JC015985. [Google Scholar] [CrossRef]
- Mohamed, S.A.E.; Samman, T.A.E. Manning roughness coefficient in vegetated open channels. Water Sci. 2020, 34, 124–131. [Google Scholar]
- Zhang, W.; Zhong, C.X.; Ying, H.H. Experimental study on hydraulic roughness of revetment with grass cover. Adv. Water Sci. 2007, 18, 483–489. [Google Scholar]
- Yang, F.; Li, H.; Cao, M. Roughness coefficient of seabuckthorn plant flexible dam under field water-flow experiment. Bull. Soil. Water Conserv. 2011, 31, 94–98. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, P.; Cheng, J.; Wang, W.J.; Zeng, L.; Wang, B. Drag Coefficient of Emergent Flexible Vegetation in Steady Nonuniform Flow. Water Resour. Res. 2020, 56, e2020WR027613. [Google Scholar] [CrossRef]
- Cui, H.; Felder, S.; Kramer, M. Predicting flow resistance in open-channel flows with submerged vegetation. Environ. Fluid Mech. 2023, 23, 757–778. [Google Scholar] [CrossRef]
- van Veelen, T.J.; Fairchild, T.P.; Reeve, D.E.; Karunarathna, H. Experimental study on vegetation flexibility as control parameter for wave damping and velocity structure. Coast. Eng. 2020, 157, 103648. [Google Scholar] [CrossRef]
- Tsihrintzis, V.A.; Madiedo, E.E. Hydraulic Resistance Determination in Marsh Wetlands. Water Resour. Manag. 2000, 14, 285–309. [Google Scholar] [CrossRef]
- Kirwan, M.L.; Guntenspergen, G.R. Feedbacks between inundation, root production, and shoot growth in a rapidly submerging brackish marsh. J. Ecol. 2012, 100, 764–770. [Google Scholar] [CrossRef]
- Lei, J.; Nepf, H. Evolution of flow velocity from the leading edge of 2-D and 3-D submerged canopies. J. Fluid Mech. 2021, 916, A36. [Google Scholar] [CrossRef]
- Lesser, G.R.; Roelvink, J.A.; van Kester, J.A.T.M.; Stelling, G.S. Development and validation of a three-dimensional morphological model. Coast. Eng. 2004, 51, 883–915. [Google Scholar] [CrossRef]
- Le Hir, P.; Monbet, Y.; Orvain, F. Sediment erodability in sediment transport modelling: Can we account for biota effects? Cont. Shelf Res. 2007, 27, 1116–1142. [Google Scholar] [CrossRef]
- Maanen, B.V.; Coco, G.; Bryan, K.R. Modelling the effects of tidal range and initial bathymetry on the morphological evolution of tidal embayments. Geomorphology 2013, 191, 23–34. [Google Scholar] [CrossRef]
- Lightbody, A.F.; Nepf, H.M. Prediction of velocity profiles and longitudinal dispersion in salt marsh vegetation. Limnol. Oceanogr. 2006, 51, 218–228. [Google Scholar] [CrossRef]
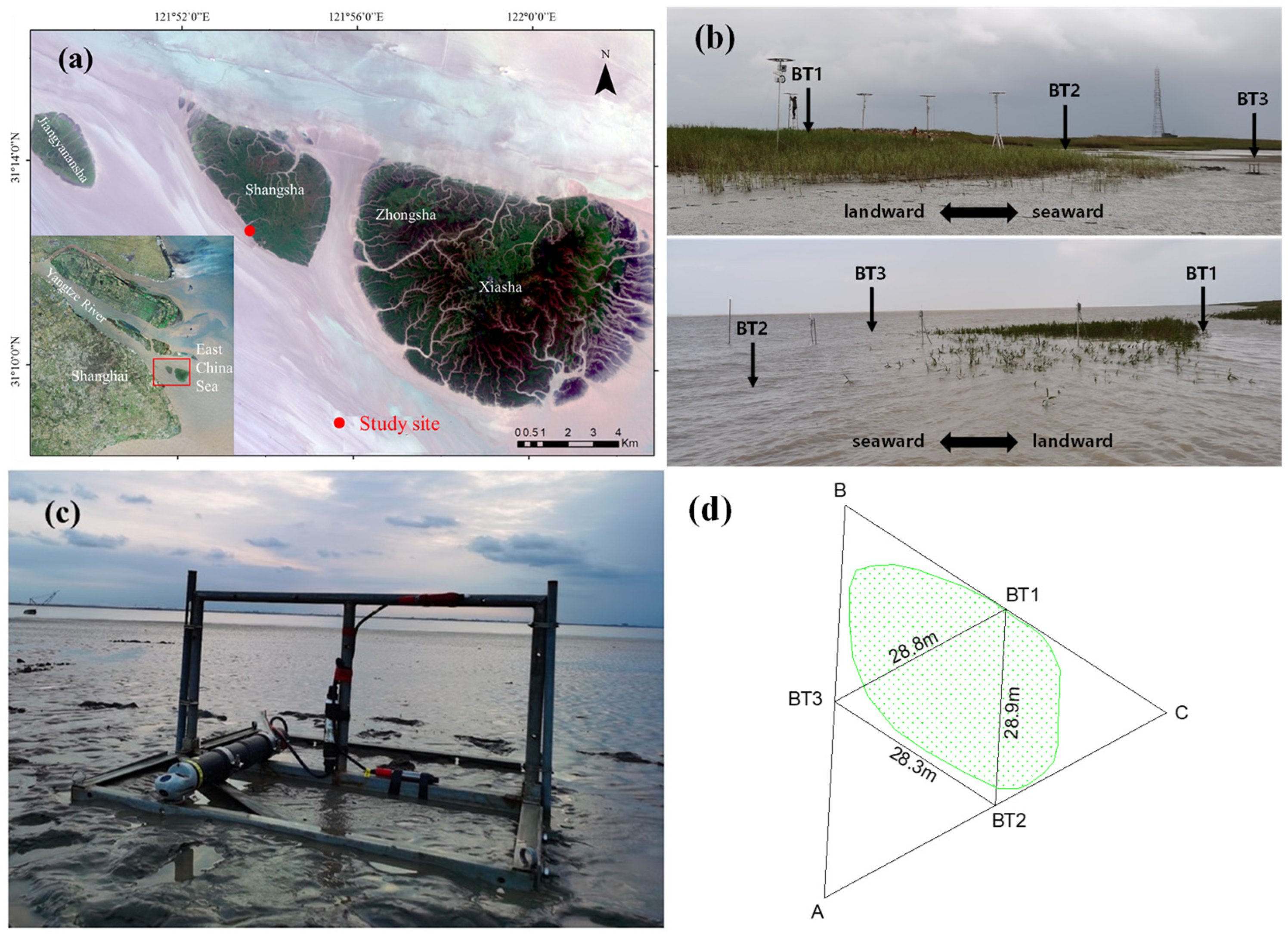


| Station | Elevation (m) | Maximum Water Depth (m) | Maximum Flow Velocity (m/s) |
|---|---|---|---|
| BT1 | 1.30 | 1.74 | 0.36 |
| BT2 | 0.54 | 2.62 | 0.45 |
| BT3 | 0.40 | 2.60 | 0.59 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, H.; Gu, F.; Zhao, L.; Zhang, W.; Zuo, Y.; Wang, Y. A New Method for Calculating the Roughness Coefficient of Salt Marsh Vegetation Based on Field Flow Observation. Water 2025, 17, 1490. https://doi.org/10.3390/w17101490
Cheng H, Gu F, Zhao L, Zhang W, Zuo Y, Wang Y. A New Method for Calculating the Roughness Coefficient of Salt Marsh Vegetation Based on Field Flow Observation. Water. 2025; 17(10):1490. https://doi.org/10.3390/w17101490
Chicago/Turabian StyleCheng, Haifeng, Fengfeng Gu, Leihua Zhao, Wei Zhang, Yin Zuo, and Yuanye Wang. 2025. "A New Method for Calculating the Roughness Coefficient of Salt Marsh Vegetation Based on Field Flow Observation" Water 17, no. 10: 1490. https://doi.org/10.3390/w17101490
APA StyleCheng, H., Gu, F., Zhao, L., Zhang, W., Zuo, Y., & Wang, Y. (2025). A New Method for Calculating the Roughness Coefficient of Salt Marsh Vegetation Based on Field Flow Observation. Water, 17(10), 1490. https://doi.org/10.3390/w17101490




