1. Introduction
Fringing coral reefs, prevalent in tropical and subtropical oceans, are characterized by a steep seaward fore-reef slope transitioning into a shallow, flat reef platform near the back-reef shore. Waves withstand momentous transformations as they pass over the steep slopes of fringing reefs and the related hydrodynamics are much more complicated than those on unprotected coastal beaches in many respects [
1,
2]. In the process of waves propagating from the oceanic to reef flats, the waves undergo transformation along the reef slope and break intensity around the reef edge, leading to a significant wave energy loss and wave height decrease [
3,
4,
5]. Accurate modeling of wave breaking and its associated hydrodynamic processes are crucial for understanding and predicting wave behavior over fringing reefs.
Numerical simulations, in addition to field observations and laboratory experiments [
6], play an increasingly important role in hydrodynamics research. Various numerical wave models have been employed to simulate the interactions of waves and currents with coral reefs [
1,
7,
8,
9,
10,
11,
12,
13,
14]. Among these, Boussinesq-type wave models are most extensively used in coral reef systems because they are efficient and effective, while able to simulate infragravity waves, crucial for simulating wave setup and run-up on reef flats [
15,
16,
17,
18].
Although Boussinesq models are widely employed for their efficiency in simulating wave nonlinearity and dispersion, it is crucial to acknowledge their inherent limitations stemming from the mild-slope and irrotational flow assumptions. Furthermore, as depth-integrated models, they simplify the vertical velocity structure. These characteristics may impose certain constraints when applied to steep or complex topographies.
Depth-integrated Boussinesq-type models assume irrotational flow, necessitating the introduction of extra mechanisms to model wave breaking. Wave breaking can be modeled using either an empirical model or the shock-capturing method. Prior studies have successfully coupled Boussinesq models with empirical breaking models to simulate regular and random wave transformation on coral reefs [
19,
20]. However, empirical breaking models require additional parameters to characterize wave onset, stoppage, and magnitude, which must be tuned for the terrain and break type. In contrast, Boussinesq models have been rapidly developed to exploit their shock-capturing capabilities [
21,
22,
23,
24,
25,
26]; this approach models wave breaking by locally switching to nonlinear shallow water equations (NSWE) by omitting dispersive terms, which enables wave breaking to be described as a discontinuous hydraulic jump by the NSWE. In these models, the Boussinesq equations are solved using hybrid finite-volume and finite-difference TVD (total variation diminishing)-type schemes, therefore this is called the hybrid wave breaking model [
27]. The hybrid wave breaking model has relatively few adjustable parameters, and the key to accurately simulating wave breaking is to detect wave breaking as accurately as possible [
28].
The hybrid wave breaking model, which assesses when to ignore dispersive terms based on wave breaking criteria, has been applied with several criteria to detect wave breaking [
24,
25,
26,
29,
30,
31]. The wave breaking criterion introduced by Tonelli and Petti [
32], using the wave height/local water depth ratio as the index, has become popular due to its simplicity and efficiency; it was adopted by the open source Boussinesq wave model FUNWAVE-TVD. Previous numerical experiments showed that simulations using different criteria accurately capture wave transformation on gentle slopes [
33]. However, as slopes steepen, simulation precision decreases significantly [
4]. Precision can be improved by tuning the thresholds of the wave breaking criteria to some extent [
34], but this is often arbitrary, and the thresholds remain fixed after tuning, rendering them unsuitable for composite slopes or multi-breaking of waves.
Therefore, to specifically address the identified limitations of the standard hybrid breaking model (
) on steep coral reefs, this study proposes and implements an enhanced hybrid breaking module within the FUNWAVE-TVD framework. The core innovation lies in a two-pronged approach designed for improved physical realism and adaptability: (1) we replace the fixed, empirically-derived threshold with a dynamic, slope-sensitive wave breaking criterion based on the Modified Goda formula (MGO) [
35], which inherently accounts for local bathymetry and wave conditions without manual tuning; (2) crucially, we develop and apply a practical methodology utilizing wave profile asymmetry relations [
36] to convert the MGO criterion’s physically-based breaking wave height (
) into an equivalent breaking surface elevation threshold (
). This conversion step is essential for seamlessly integrating the physically-based
criterion into FUNWAVE-TVD’s existing η-based switching mechanism, thereby overcoming the inaccuracies associated with the direct
approximation. The primary contribution of this work is thus the development, implementation, and rigorous validation (against steep slope experiments) of this synergistic approach, offering a more robust and physically-grounded tool for simulating wave breaking dynamics in challenging steep reef environments.
2. The Modified Model
In this section, the cause of decreasing simulation precision in the hybrid wave breaking model on steep coral reefs was investigated and, based on that analysis, a modified model was introduced and subsequently implemented.
2.1. Baseline Hybrid Breaking Model and Its Limitations on Steep Slopes
The numerical simulations presented in this study were conducted using FUNWAVE-TVD, a Boussinesq-type model engineered to solve the fully nonlinear Boussinesq equations [
25]. The model employs a hybrid finite-volume/finite-difference numerical scheme possessing Total Variation Diminishing (TVD) properties, rendering it suitable for shock-capturing applications inherent in wave breaking [
25]. To simulate the complex hydrodynamics of wave breaking, FUNWAVE-TVD incorporates the hybrid methodology originally proposed by Tonelli and Petti [
32]. Within this framework, the Boussinesq equations are reformulated into constituent components representing the Nonlinear Shallow Water Equations (NSWE) and additional dispersive terms.
The standard hybrid breaking mechanism implemented in FUNWAVE-TVD involves selectively neglecting these dispersive terms. This procedure effectively switches the governing equations locally from the Boussinesq system to the NSWE upon the detection of incipient breaking. Such an approach enables the model to capture the sharp variations in water surface elevation and the associated energy dissipation characteristic of breaking waves, which are treated computationally as moving hydraulic jumps or bores accommodated by the shock-capturing capabilities of the NSWE solver. In the widely adopted configuration of FUNWAVE-TVD, the criterion responsible for triggering this numerical switch relies on the ratio of the instantaneous free surface elevation
η to the total local water depth
d. Specifically, the switch to NSWE is activated when
, where
represents a predefined, constant threshold, canonically assigned a value of 0.8 in numerous applications [
17,
21,
22,
25,
32,
37,
38,
39,
40].
While this standard hybrid approach offers computational efficiency and has demonstrated considerable effectiveness in simulations pertaining to wave propagation over mild bathymetric slopes or within deeper water regions, its direct application to environments characterized by steep coral reef slopes encounters significant limitations. These limitations frequently manifest as a demonstrable reduction in simulation accuracy [
4], primarily attributable to the following deficiencies:
Lack of Physical Sensitivity: The invariant threshold
fails to inherently accommodate the well-established physical dependencies of wave breaking initiation (often parameterized by the ratio
, where
is the breaking wave height and
is the breaking depth) on critical local parameters. These parameters include the bottom slope (
m) and incident wave characteristics such as wavelength (
) or period (
T). In contrast, breaking criteria derived from theoretical considerations and extensive experimental data, exemplified by the Modified Goda formula (MGO), explicitly incorporate terms reflecting these physical dependencies [
35]. Consequently, on steep slopes where the onset and evolution of wave breaking exhibit heightened sensitivity to such local conditions, the insensitivity of the fixed
criterion emerges as a principal source of simulation error.
Inaccuracy of η as a Proxy for Wave Height: The utilization of the instantaneous free surface elevation η within the switching criterion () constitutes a computational proxy for a condition more fundamentally related to the local wave height (e.g., , where H is the wave height and is the breaking index). Although this substitution is convenient for implementation within the model’s time-stepping procedure, η quantifies only the crest elevation relative to SWL, neglecting the trough contribution to the full wave height (H). This approximation inherently introduces inaccuracies, the magnitude of which can become substantial for the highly nonlinear and asymmetric wave profiles typically observed immediately prior to the breaking point.
Amplified Errors in Steep Reef Environments: Coral reef systems frequently feature steep foreslopes that transition abruptly to shallow reef flats. This morphology results in spatially compressed shoaling regions and consequently confined surf zones. Within these specific bathymetric settings, the accurate prediction of both the wave breaking point (inception) and the spatial extent of the ensuing surf zone (, the region governed by NSWE where primary dissipation occurs) is paramount for correctly modeling wave transformation and energy decay onto the reef flat. The inaccuracies stemming from both the physically insensitive fixed threshold () and the inherent limitations of the η-proxy are often exacerbated under these steep slope conditions. This amplification can manifest as the model incorrectly predicting the location of breaking onset (often delayed) or prematurely reverting from the NSWE solver back to the Boussinesq equations within the surf zone. Such miscalculations lead to insufficient energy dissipation being modeled, culminating in erroneous (typically overestimated) wave height predictions on the reef flat.
Collectively, these identified factors contribute significantly to the observed reduction in the predictive accuracy of the standard FUNWAVE-TVD hybrid breaking model when applied to challenging steep reef topographies. This underscores the necessity for the development and implementation of a more physically grounded and adaptive wave breaking criterion tailored to the specific hydrodynamic complexities of such environments.
2.2. Implementation of the Enhanced Hybrid Breaking Module
Based on the analysis in
Section 2.1, we propose and implement an enhanced hybrid breaking module within FUNWAVE-TVD. This involves two core modifications: replacing the fixed breaking criterion with a dynamic, slope-aware criterion, and developing a method to integrate this criterion seamlessly into the model’s
η-based switching mechanism.
2.2.1. Dynamic Wave Breaking Criterion (MGO)
Instead of the fixed
, we adopt a dynamic breaking criterion based on the Modified Goda formula (MGO) proposed by Rattanapitikon and Shibayama [
35]. This formula predicts the breaking wave height (H
b) as a function of the deep-water wavelength (
), local breaking depth (
), and local bottom slope (m). It was shown to provide improved accuracy over the original Goda formula, particularly for steeper slopes (up to
or 1:2.3). The MGO formula is given by:
This formula provides a physically-based estimate of the maximum wave height () that can be sustained at a location with depth and slope m before breaking occurs. is calculated from the incident wave period T using the linear dispersion relation. In the model implementation, the local depth d and local slope m are used instead of and the breaking slope, assuming breaking is imminent.
2.2.2. Converting Threshold to Threshold Using Wave Asymmetry
A direct implementation challenge arises because the MGO criterion (Equation (2)) provides a threshold in terms of wave height (
), whereas the FUNWAVE-TVD hybrid mechanism requires a threshold based on surface elevation (
η) relative to depth (
d) to trigger the switch. Directly substituting
η for
would reintroduce the inaccuracies discussed in
Section 2.1.
To bridge this gap, we employ the concept of vertical wave profile asymmetry at the breaking point. The relationships between wave crest elevation (
), wave trough elevation (
), and wave height (
) are influenced by local wave conditions. Yu and Li [
36] proposed an empirical relationship for the vertical asymmetry ratio (
; see
Figure 1) based on relative depth (
), showing minimal influence from the bottom slope:
Using and Equation (2), we can relate the breaking wave height (calculated from MGO, Equation (1)) to the corresponding breaking crest elevation (which is the relevant η value for the η/d criterion):
From Equation (2), let
. Then
Substituting into
gives
. Therefore, the breaking crest elevation
(equivalent to
at breaking) can be calculated from
as:
This equation allows us to convert the physically-based breaking wave height threshold (from MGO) into an equivalent surface elevation threshold needed for the model’s switching logic.
2.2.3. Implementation Within FUNWAVE-TVD’s Hybrid Framework
The enhanced breaking module is implemented within the FUNWAVE-TVD code as follows, executed at each grid point (i, j) and each time step:
Obtain the current local water depth and the instantaneous free surface elevation from the model solution.
Calculate the local bottom slope from the bathymetry grid.
Calculate the deep-water wavelength based on the incident wave period T.
Calculate the theoretical breaking wave height using the MGO formula (Equation (1)) with local , and
Calculate the asymmetry ratio using Equation (2) with local and .
Calculate the equivalent breaking surface elevation threshold using Equation (3) with and .
Calculate the dynamic breaking criterion threshold .
Compare the model’s current normalized surface elevation () with the dynamic threshold .
If , activate the switch to NSWE by neglecting the dispersive terms in the Boussinesq equations at that grid point for the current time step. Otherwise, solve the full Boussinesq equations.
This implementation replaces the static criterion (η/d > 0.8) with a dynamic, physically-informed criterion (η/d > η < sub > b < /sub > /d) that adapts to local slope and wave conditions, while utilizing the existing hybrid switching mechanism of FUNWAVE-TVD.
3. Numerical Tests and Results
The original FUNWAVE-TVD performs with high precision on gentle slopes, as validated by numerous numerical experiments. Therefore, we only need to test the modified model on steep slopes. Four laboratory experiments recreating wave breaking on coral reefs were utilized to validate the modified model. Separate tests were conducted with slope gradients of 1:10, 1:6, 1:5, and 1:3.
3.1. Wave Breaking over a 1:10 Slope
Tsai et al. [
41] tested the breaking wave height formula through laboratory experiments using three different topographies and multiple wave depths and incident waves.
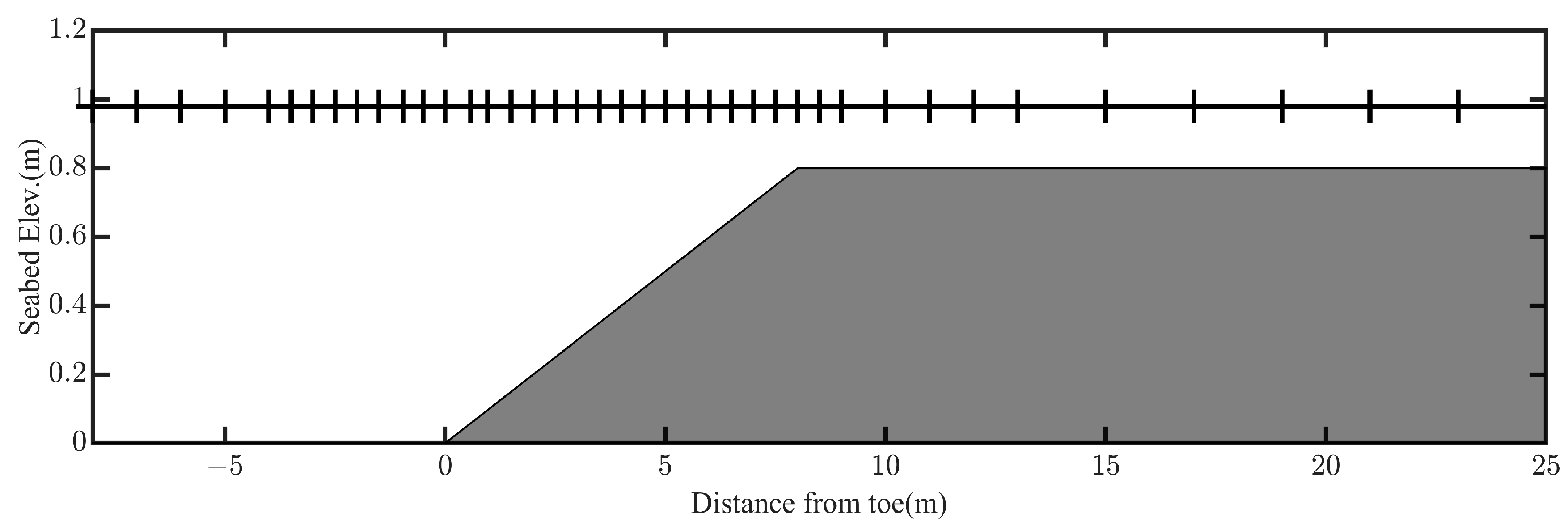
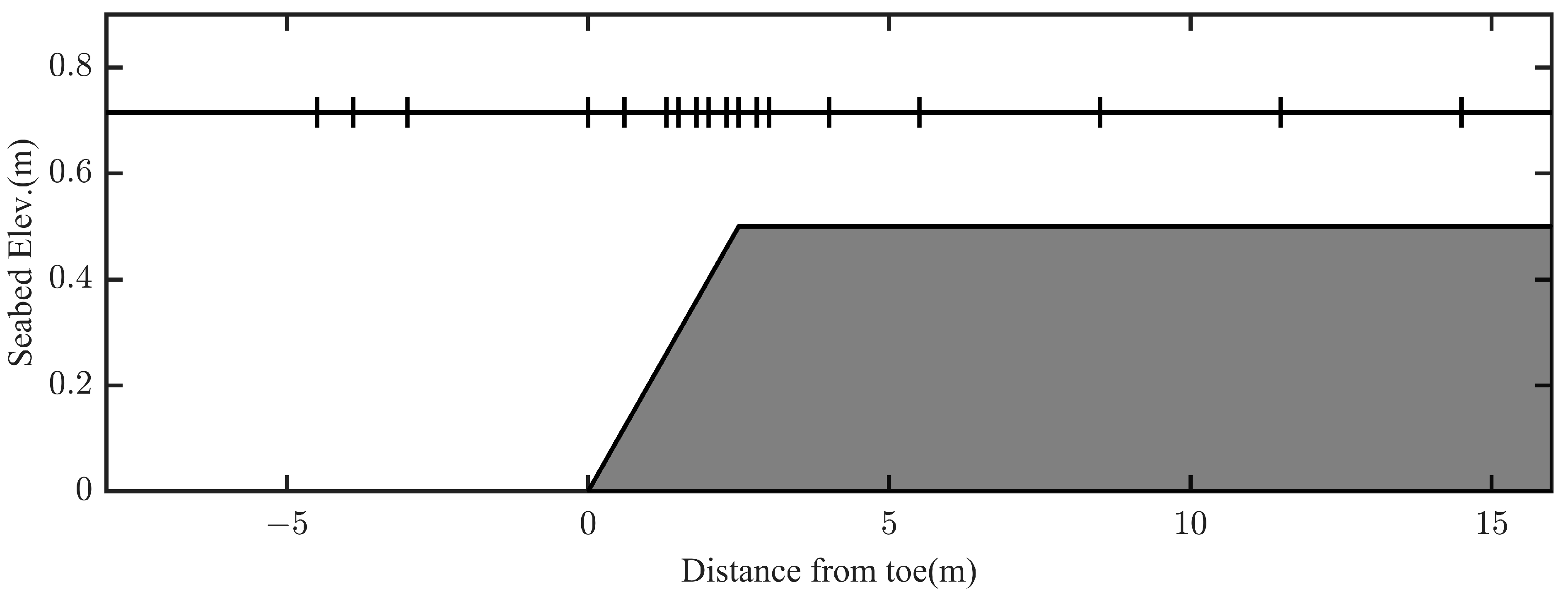
Figure 2 shows a sketch of the experimental bathymetry with the 1:10 slope and wave gauge locations. In this figure, the abscissa represents distance from the toe of the reef, while the ordinate represents seabed altitude and wave gauge locations are labeled with vertical short line on the static water table.
A slope of 1:10 is considered the threshold dividing steep and gentle slopes. The seaward water depth was 0.98 m, the reef flat was 0.8 m high, and the water depth over the reef flat was 0.18 m. The incident wave height was 0.213 m and the wave period was 2.6 s. An internal wave maker located 8 m in front of the toe was used. A space step of was set in this simulation.
The model was executed for 60 wave periods, and average of the last five waves was used to compute the wave height. For the modified model, the new threshold for the wave breaking criterion was computed by Equation (4); the new threshold and the original threshold (
) used in FUNWAVE-TVD are compared in
Figure 3.
Figure 4 compares measured wave data with wave heights calculated using FUNWAVE-TVD with the modified model; the zone in which the Boussinesq model switches to the NSWE during the simulation process is also shown. For convenience, the horizontal length governed by NSWE is expressed as
in this paper. The red area represents
from the modified model, while the gray area represents
from unmodified FUNWAVE-TVD. Wave height decreased rapidly after breaking, and the computed wave heights of both models agreed with the measured data, but small differences became apparent downstream of the breaking point. To the left of the two models’
boundary, wave heights are identical, therefore the breaking points were the same; these indeed corresponded to the wave breaking threshold criterion presented in
Figure 3, meaning the breaking point thresholds were almost equal. However, on the reef flat, the threshold for the modified model was smaller, therefore its
was wider, allowing sustained dissipation of wave energy. Model skill was used to evaluate model performance.
where
represents the observed value,
the calculated value, and
the number of the wave gauges. The skill value equals 1 for an almost perfect model result. The model skills of the original and modified FUNWAVE-TVD models were nearly identical, at 0.921 and 0.924, respectively. The original FUNWAVE-TVD already exhibits high precision in this case, and the improvement resulting from the modification was negligible.
3.2. Wave Breaking over a 1:6 Slope
Yao et al. [
42] conducted a series of experiments to investigate wave propagation over coral reefs. This study selects the case of examining wave transformation and breaking on an idealized coral reef without a ridge.
Figure 5 shows a sketch of the experimental bathymetry and the locations of wave gauges, totaling 12. The seaward water depth was 0.45 m, the fore-reef slope was 1:6, and the water depth over the reef flat was 0.1 m. Sponge absorbing layers were installed at both ends of the computational domain. The incident wave was generated by an internal wave maker with a height of 0.095 m and period of 1.25 s. The simulation used a space step of
m and a time step of
s.
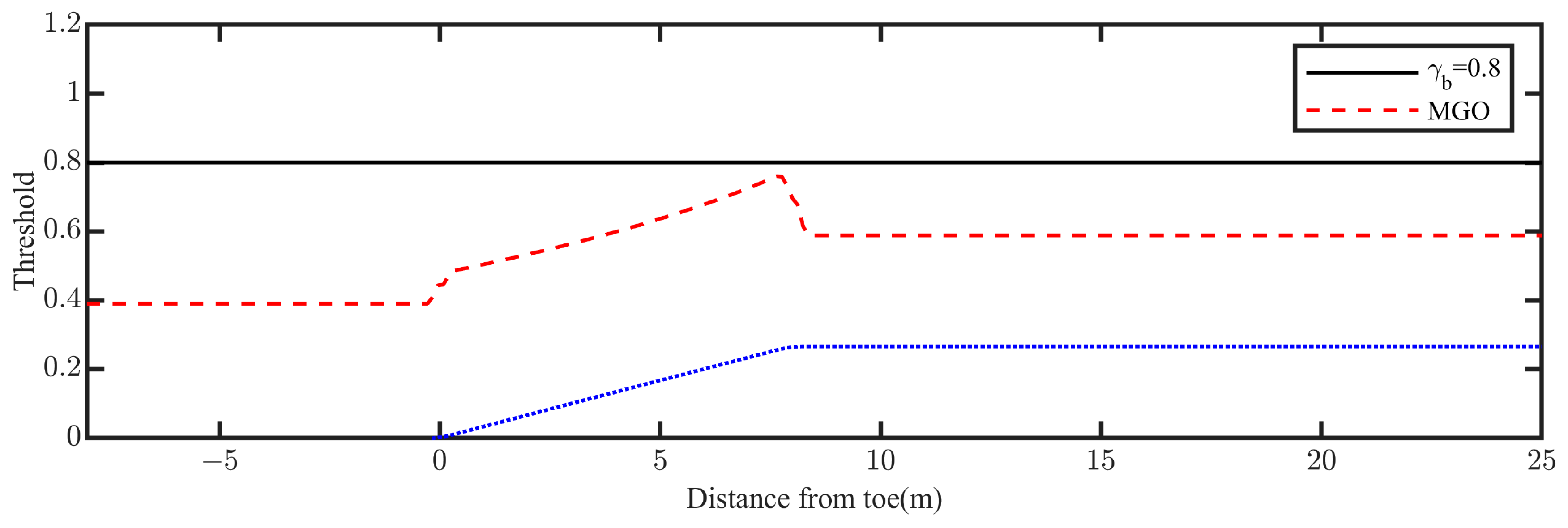
Figure 6 compares the thresholds from the modified model and the original threshold of FUNWAVE-TVD. The threshold value increased as the wave progressed up the slope and reached its maximum at the edge of the reef flat, equaling 0.75. The wave breaking threshold of the modified model was consistently lower than the original FUNWAVE-TVD threshold.
Figure 7 compares the wave heights from the original FUNWAVE-TVD and the modified model with the measured value, along with the
from the different models. The precision of the modified model was significantly higher than the original FUNWAVE-TVD. The breaking point predicted by the original FUNWAVE-TVD lagged behind the measured data and the
from the original FUNWAVE-TVD was too narrow to dissipate enough wave energy, reducing the precision of the original model’s wave breaking and height predictions. From the calculation, the original FUNWAVE-TVD’s model skill for wave height was 0.506, while the model skill of the modified model was 0.721, increasing the precision by 42.49%. Although the modified model was still imprecise, particularly in the surf zone, its precision was significantly improved compared to the original model.
3.3. Wave Breaking over a 1:5 Slope
Liu et al. [
43] conducted a series of comprehensive physical experiments at Dalian University of Technology to investigate wave breaking characteristics over reef terrains. The experimental setup, including the modeled reef terrain and wave gauge positions, is illustrated in
Figure 8. A representative scenario simulating wave breaking along the fore-reef slope was analyzed in detail. The water tank was 69 m long, with an offshore water depth of 0.715 m, a reef flat of 0.5 m, and a depth of 0.215 m over the reef flat. The incident wave had a period of
and height of
. A total of 18 wave gauges were strategically deployed throughout the experimental domain to capture detailed wave dynamics. An internal source wave maker, placed 10.5 m in front of the toe, was employed. Numerical simulations were carried out using a grid resolution of
, with sponge layers incorporated at both ends of the computational domain to minimize boundary reflections.
The reliability of the wave breaking criterion was scrutinized by comparing the original FUNWAVE-TVD model with a modified version, as shown in
Figure 9. Notably, the threshold values for wave breaking predicted by the modified model were substantially lower than those of the original version, with the maximum threshold reaching 0.68 near the reef’s edge.
Figure 10 compares the wave heights and
of the original and modified models. It is evident that the original FUNWAVE-TVD model failed to accurately predict the location of wave breaking, with its simulated breaking point lagging significantly behind the observed breaking point. Moreover, the
predicted by the original model was too narrow, resulting in insufficient dissipation of wave energy and a poor representation of the surf zone dynamics over the reef flat. In contrast, the modified model demonstrated improved performance, with the predicted breaking point and wave energy dissipation agreeing closely with the measured data. This substantial improvement highlights the enhanced ability of the modified model to simulate wave processes over reef terrains.
Quantitatively, the wave height model skill of the original FUNWAVE-TVD was 0.788, whereas the modified model achieved a higher skill score of 0.912, reflecting an improvement of 15.74%. This significant enhancement underscores the effectiveness of the modifications in improving the model’s precision and reliability in simulating wave dynamics in the reef flat and surf zone regions.
3.4. Wave Breaking over a 1:3 Slope
Another laboratory experiment conducted by Tsai, Chen, Hwung and Huang [
41] simulated wave breaking over a reef terrain with a fore-reef slope gradient of 1:3. The experimental setup, including the terrain configuration and wave gauge locations, is depicted in
Figure 11. The offshore water depth was set at 0.97 m, transitioning from a steep 1:3 fore-reef slope to a flat reef top, where the water depth was reduced to 0.17 m. Regular incident waves with a period of
T = 1.8 s and a wave height of
H = 0.202 m were employed. Numerical simulations utilized a grid spacing of
dx = 0.075 m and a time step of
dt = 0.008 s. The bottom friction was parameterized using Manning’s coefficient, set to a value of 0.01. The model was executed for 60 wave periods, with the averaged results from the final five wave cycles used for data analysis.
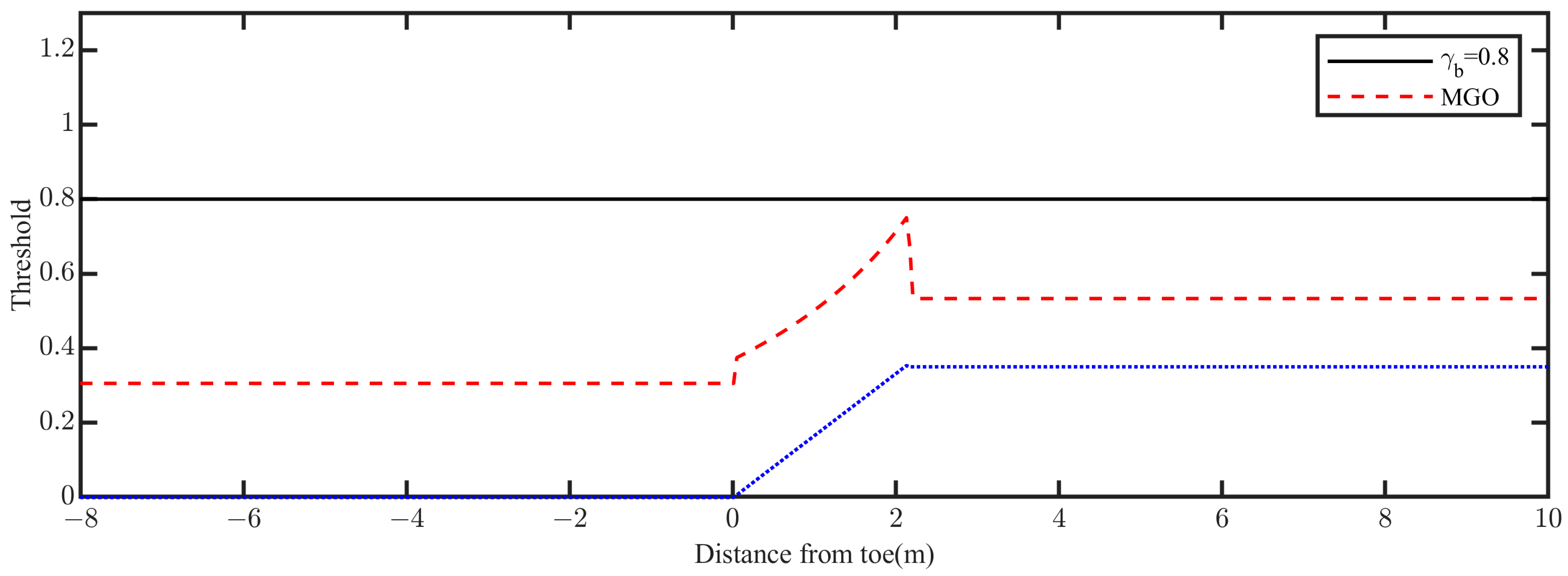
Figure 12 presents a comparison of the threshold values for the wave breaking criterion between the original FUNWAVE-TVD model and the modified model. The modified model exhibited lower threshold values compared to the original FUNWAVE-TVD, with the maximum threshold (0.73) occurring near the reef edge.
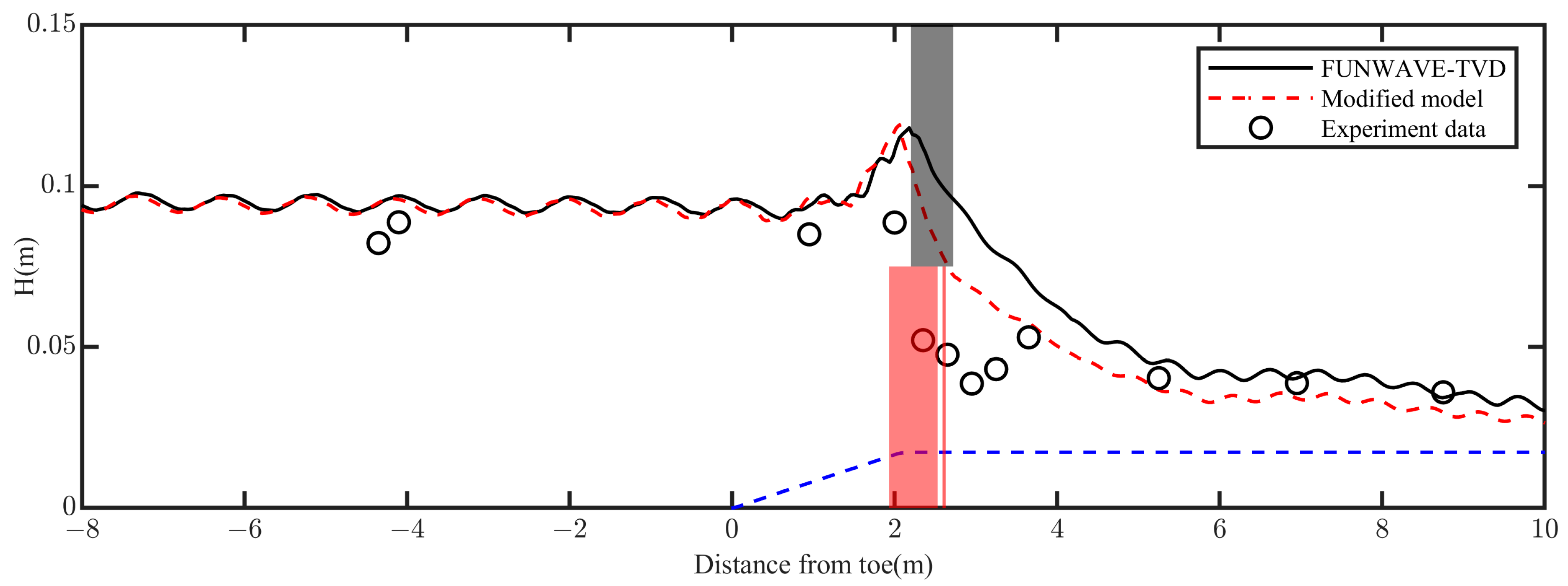
The computed wave heights and
values from the original FUNWAVE-TVD model and the modified model are presented in
Figure 13. The breaking points predicted by the two models were found to be close to each other, primarily due to the relatively minor differences in their wave breaking threshold values. However, the
predicted by the modified model exhibited a wider breaking zone, enabling more effective dissipation of wave energy and thereby offering a more accurate representation of the reef flat surf dynamics.
Furthermore, the modified model consistently demonstrated superior predictive accuracy. Quantitative evaluation of the model skill for wave height predictions revealed scores of 0.827 for the original FUNWAVE-TVD and 0.911 for the modified model, reflecting an improvement of 10.16%. This enhancement underscores the higher precision achieved by the modified model in simulating wave breaking and energy dissipation on steep coral reef terrains.
4. Discussion
Wave breaking on steep slopes, such as those formed by coral reefs, poses unique challenges for numerical modeling due to the short shoaling distance and narrow surf zone. These conditions amplify the complexity of accurately simulating wave dynamics, particularly when using traditional wave breaking criteria with fixed thresholds [
26]. The findings from this study, along with insights from previous research, highlight the limitations of existing approaches and suggest avenues for improvement.
Addressing these challenges, a key objective of the present study is to refine the numerical model’s description of the wave breaking process, particularly the breaking criterion itself. To effectively evaluate the sensitivity and performance of the proposed modifications, validation efforts were primarily focused on regular wave simulations. Regular waves, characterized by relatively well-defined breaking points, provide a more sensitive testbed for assessing the accuracy of breaking criteria compared to random waves, whose wider surf zones and reliance on statistical parameters tend to average out inaccuracies in individual wave breaking predictions. Indeed, previous work utilizing the baseline FUNWAVE-TVD model has already demonstrated its capability to accurately simulate random wave propagation over typical reef geometries [
4]. For instance, simulations of the Nwogu case (slope 1:10.2) and the Smith case (slope 1:5) yielded high model skill scores (skill > 0.9) for significant wave height prediction against experimental data. Given this established proficiency for random wave scenarios, the current study strategically concentrates on regular wave cases. These cases pose a more stringent test for evaluating improvements to the breaking mechanism, as the model’s performance is more directly influenced by the precise formulation of the breaking criterion.
4.1. Limitations of Fixed Thresholds and Grid Resolution
The widely used wave breaking criterion η/d = 0.8, effective for gentle slopes, fails to account for variability introduced by steep slopes. Steep slopes weaken the shoaling effect, reducing the increase in wave height and non-linearity. This results in an overly large threshold that fails to capture surf zone dynamics, leading to significant errors in simulation. Furthermore, the narrow surf zone demands higher precision in detecting wave breaking, exacerbating the limitations of fixed thresholds.
Two potential approaches exist for improving simulation precision: increasing grid resolution or implementing a more physically representative wave breaking criterion that better accounts for bathymetric influences [
44]. However, our investigations, in agreement with previous studies, revealed that excessively fine grid resolutions often lead to numerical instability and oscillations, particularly on steep slopes. Rather than improving accuracy, overly refined grids introduce errors that undermine model stability. These findings are consistent with those of Tissier et al. (2012) [
26], who observed similar shortcomings in Boussinesq-type models when applied to complex bathymetries. In light of these limitations, implementing a terrain-sensitive wave breaking criterion emerged as a more practical and effective solution for improving simulation reliability.
Beyond the issues with breaking criteria, the mild slope assumption of Boussinesq models may approach its applicability limits when applied to steep coral reef slopes, affecting the precise simulation of wave shoaling processes. Additionally, the irrotational flow assumption and depth-integrated characteristics limit the model’s ability to capture complex three-dimensional turbulent structures generated by breaking. Nevertheless, the comparative results of this study demonstrate that, through targeted improvements to the breaking module, model accuracy has been significantly enhanced, suggesting that under the current hybrid model framework the adaptability of breaking criteria is a particularly prominent factor affecting simulation accuracy on steep slopes.
4.2. Advantages of the Modified Wave Breaking Criterion
The modified Goda’s formula (MGO) introduced in this study provides a terrain-sensitive wave breaking criterion that significantly improves simulation precision on steep slopes. By incorporating the influence of slope gradients and wave profiles, the MGO adapts to the unique hydrodynamic conditions of coral reef environments. Numerical experiments demonstrated that the modified model performed well on slopes with gradients below 1:2.3, achieving improvements in precision from 10.16% to 42.49%, as shown in
Table 1. This underscores the importance of employing adaptable criteria that reflect terrain physical characteristics.
The integration of the MGO into the hybrid wave breaking model also addresses the issue of narrow surf zones. By widening , the modified model allows for sustained dissipation of wave energy, better capturing surf zone dynamics. This approach aligns with the principle of treating wave breaking as shocks within the NSWE framework, ensuring that the seaward boundary of remains ahead of the physical breaking point.
4.3. Challenges and Future Directions
The modified model showed significant improvements in prediction accuracy for slopes ranging from 1:6 to 1:3. However, as noted by the MGO formula’s creators, its application is not recommended for slopes steeper than 1:2.3 [
35].
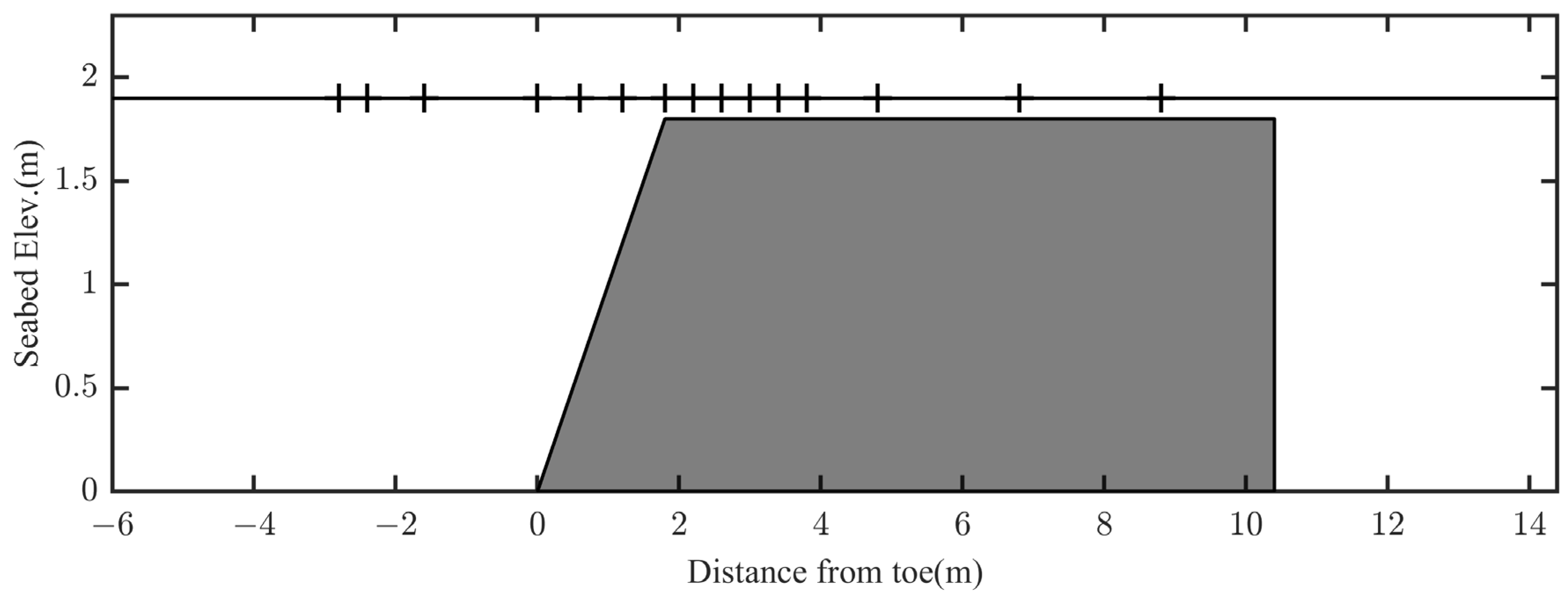
To further probe the model’s limitations on extremely steep slopes, an additional case study involving a 1:1 slope, based on the experiments by Wen et al. [
8], was conducted. Wen et al. experimentally and numerically investigated wave propagation and transformation over steep coral reef topographies. The idealized reef geometry and wave gauge locations used in their experiments are illustrated in
Figure 14. One representative case from their study was selected for validation here. The experimental setup featured a fore-reef water depth of 1.9 m, a reef flat height of 1.8 m (resulting in a water depth of 0.1 m over the reef flat), and a steep 1:1 fore-reef slope. The horizontal reef flat extended for 8.6 m, followed by a lagoon with a water depth of 1.9 m, which was connected to the fore-reef region. An absorbing boundary condition was applied at the shoreward end. Incident regular waves had a height of
and a period of
.
For numerical stability in the FUNWAVE-TVD simulation, the sharp transition between the reef flat and the lagoon was smoothed to a 1:1 slope. The simulation utilized a grid resolution of
and a time step of
. The bottom friction coefficient was set to
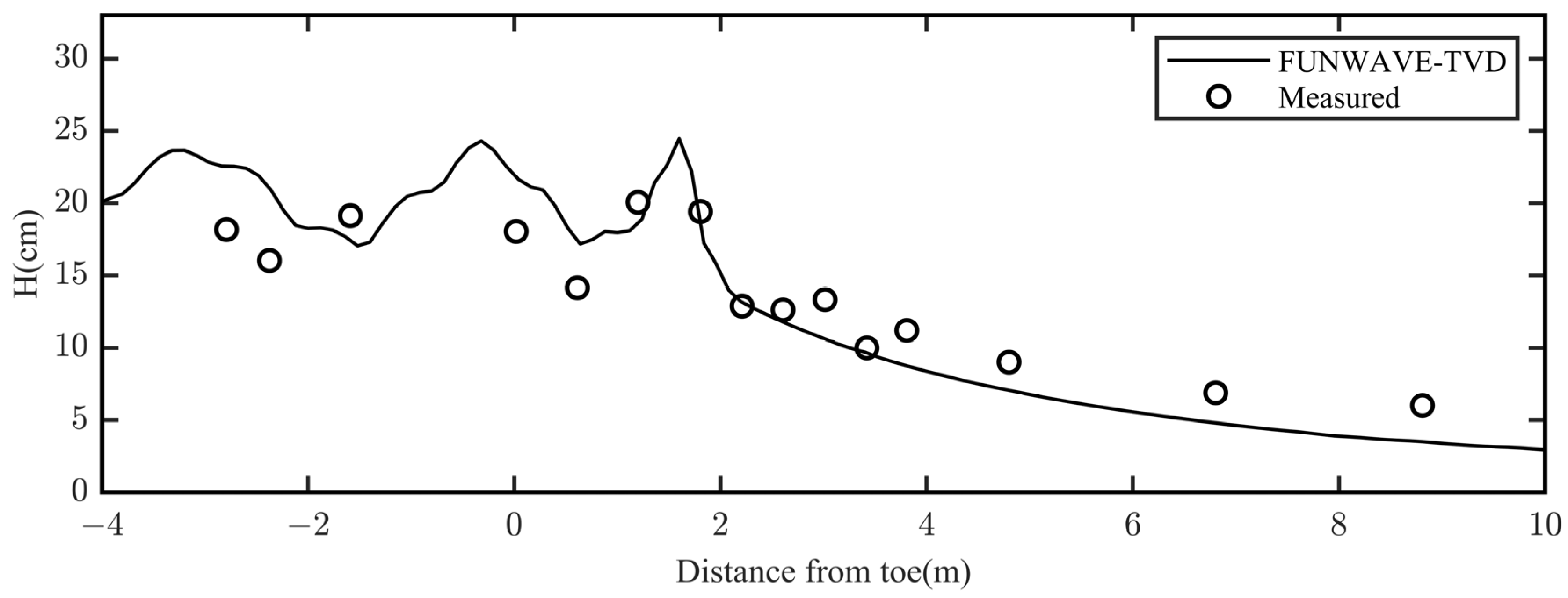
. A comparison between the wave heights computed by the original FUNWAVE-TVD model and the measured data is shown in
Figure 15. As seen in the figure, the original FUNWAVE-TVD model reasonably captured the wave breaking location and the general trend of wave height variation along the profile. However, it tended to overestimate wave reflection seaward of the reef and underestimate wave heights on the reef flat. The calculated model skill for wave height was 0.82.
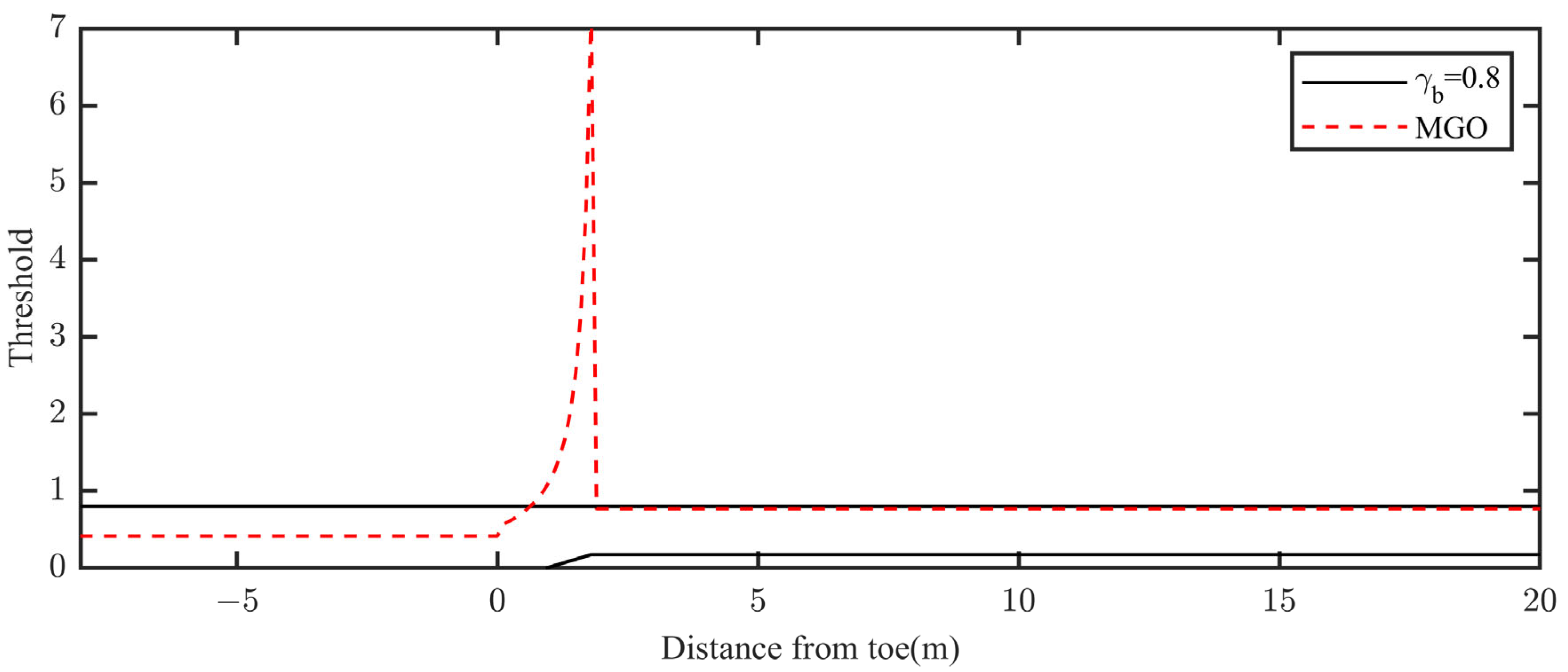
Figure 16 compares the wave breaking threshold calculated by the modified model (using the MGO criterion) with the original fixed threshold used in FUNWAVE-TVD. Crucially, the threshold predicted by the modified model exhibited abnormally large, non-physical peaks near the reef edge. This is a direct consequence of the inherent limitations of the MGO formula, which was empirically derived using data primarily from slopes gentler than m = 1:2.3 [
35]. Applying it to the extreme 1:1 slope in this case clearly exceeds its range of validity. This finding reinforces the conclusion that, while the MGO criterion enhances performance on moderately steep slopes, it is unsuitable for extremely steep gradients like 1:1, highlighting the need for further research to develop or identify more broadly applicable breaking criteria for such conditions.
4.4. Broader Implications
This study’s findings could potentially be applied to other steep coastal terrains like rocky shorelines or seawalls. The terrain-sensitive approach to wave breaking criteria could help in developing models for predicting coastal inundation under extreme weather. The modified hybrid wave breaking model can improve the precision of wave dynamics in complex coastal environments. Future research should focus on refining these criteria and exploring their applicability to broader coastal systems.
5. Conclusions
This study proposed a modified hybrid wave breaking model, designed to improve simulation accuracy across varying slope gradients, particularly for steep coral reefs. Through a detailed cause analysis, it was identified that the original wave breaking criterion failed to meet precision requirements on steep slopes, primarily due to its reliance on fixed thresholds and simplified assumptions. To address these limitations, the hybrid model was enhanced by incorporating two key modifications: (1) the adoption of the modified Goda’s formula to account for the influence of terrain on the wave breaking threshold, and (2) accounting for wave profile asymmetry when applying the wave breaking criterion, which eliminated errors introduced by the direct substitution of η/d for H/d in traditional implementations.
Upon integration into FUNWAVE-TVD, comprehensive performance evaluation across multiple experimental configurations demonstrated the efficacy of our approach. For gentler slopes with gradients less than 1:10, both the original and modified models accurately predicted wave height variations across reef profiles. However, for steeper slopes (/6), where the original model exhibited significant precision deficiencies, the modified model achieved substantial improvements in simulation accuracy, with precision enhancements ranging from 10.16% to 42.49%.
It is important to note that the MGO-based wave breaking criterion implemented in this study performs optimally for slopes with gradients gentler than 1:2.3. For extremely steep slopes beyond this threshold, alternative criteria would need to be developed, as our attempts to apply the MGO to gradients approaching 1:1 produced physically unrealistic results. Despite this limitation, the modifications introduced in this study represent a significant step forward in improving the robustness and applicability of hybrid wave breaking models.
While our implementation focused on FUNWAVE-TVD, the methodology developed here is fundamentally applicable to other hybrid wave breaking models. This study thus provides a valuable framework for improving the applicability and reliability of numerical wave models in steep coral reef environments, contributing to more accurate predictions of wave transformation, breaking processes, and associated hydrodynamics in these complex coastal systems.