An Explainable Machine Learning Framework for Forecasting Lake Water Equivalent Using Satellite Data: A 20-Year Analysis of the Urmia Lake Basin
Abstract
1. Introduction
- To compile and analyze a comprehensive 20-year dataset (2003–2023) of satellite-derived climatic and hydrological variables influencing Lake Urmia, including GRACE/GRACE-FO and GLDAS products.
- To assess historical groundwater storage trends using statistical techniques such as the Mann-Kendall trend test and Spearman correlation analysis, capturing both long-term and decadal changes.
- To develop an explainable ensemble-based predictive framework for forecasting LWE that incorporates lag features, temporal encodings, and feature re-weighting using XGBoost importance scores.
- To integrate SHAP for both global and local interpretability, providing transparent insights into the climatic drivers of groundwater storage dynamics.
- To evaluate and compare the predictive performance of the proposed model against baseline models (Persistence, Standard Ridge Regression, Random Forest, and XGBoost), demonstrating its superiority through statistical metrics (RMSE and ).
- To offer a scalable, interpretable, and data-driven forecasting tool that supports sustainable groundwater resource management under conditions of climatic uncertainty and environmental stress.
2. Literature Review
2.1. Remote Sensing and Hydrological Monitoring of Lake Urmia
2.2. Advancements in Modeling Techniques
2.3. Machine Learning Applications in Water Storage Forecasting and Lake Urmia Studies
2.4. Contribution of the Present Study
3. Materials and Methods
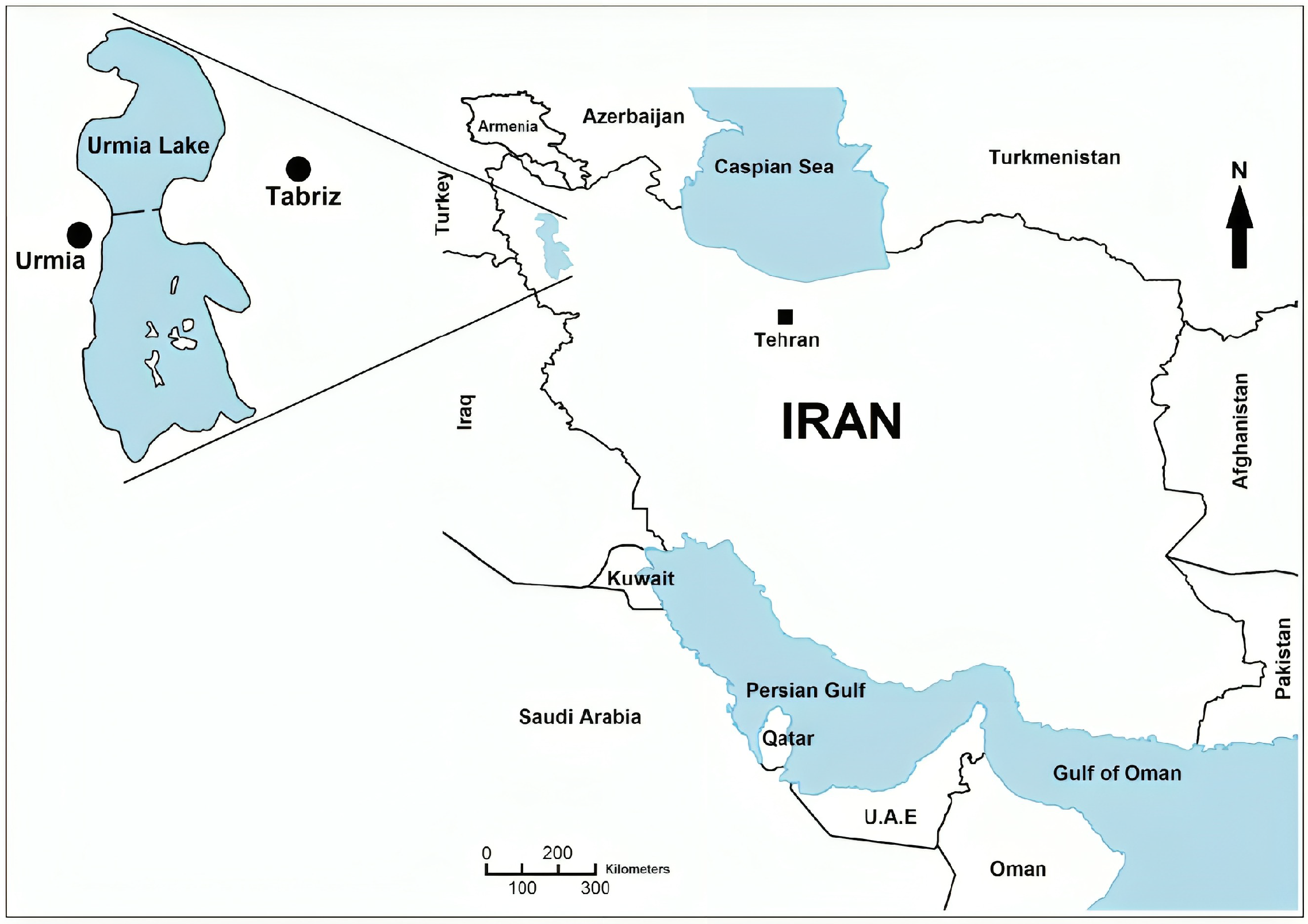
3.1. Case Study
3.2. Changes in Lake Urmia’s Surface Area
3.3. Trends of Climatic Variables in the Region (2003–2023)
4. Methods
4.1. Statistical Summary of Key Parameters (2003–2023)
4.2. Assessment of Normality for Climatic Variables and Groundwater Storage Changes
4.3. Spearman Correlation Analysis
4.4. Analysis of Groundwater Storage Trends
- 2003–2013: A significant decreasing trend in groundwater storage was detected, with a slope of units per month. The p-value () confirms strong statistical significance, and the negative test statistic () reflects a consistent decline over this decade.
- 2014–2023: In contrast, a significant increasing trend emerged in the later decade, with a positive slope of units per month. The p-value () indicates strong significance, and the positive test statistic () reflects substantial groundwater recovery during this period.
- 2003–2023: When considering the entire period, a significant decreasing trend was observed, with an overall negative slope of units per month. Although groundwater levels improved after 2014, the earlier substantial decline between 2003 and 2013 outweighed the later recovery, resulting in a net downward trend for the full 21-year period.
4.5. Regression and Forecasting Methods
Multiple Regression Analysis
- Multicollinearity: The presence of correlations among the explanatory variables (as seen in the correlation matrix) may inflate standard errors and obscure the individual effects of predictors, particularly for pressure and soil moisture, which show potential importance.
- Nonlinearity and Interactions: The assumption of linearity may not adequately capture the complex relationships between hydrometeorological variables and LWE. Interactions or threshold effects could exist, which linear models would fail to detect. The superior performance of nonlinear models such as Random Forest and XGBoost in our study supports this idea.
- Omitted Variables: Key influencing factors such as groundwater withdrawals, vegetation indices, and human interventions were not included in this model. Their absence may limit the model’s explanatory power and obscure the role of existing variables.
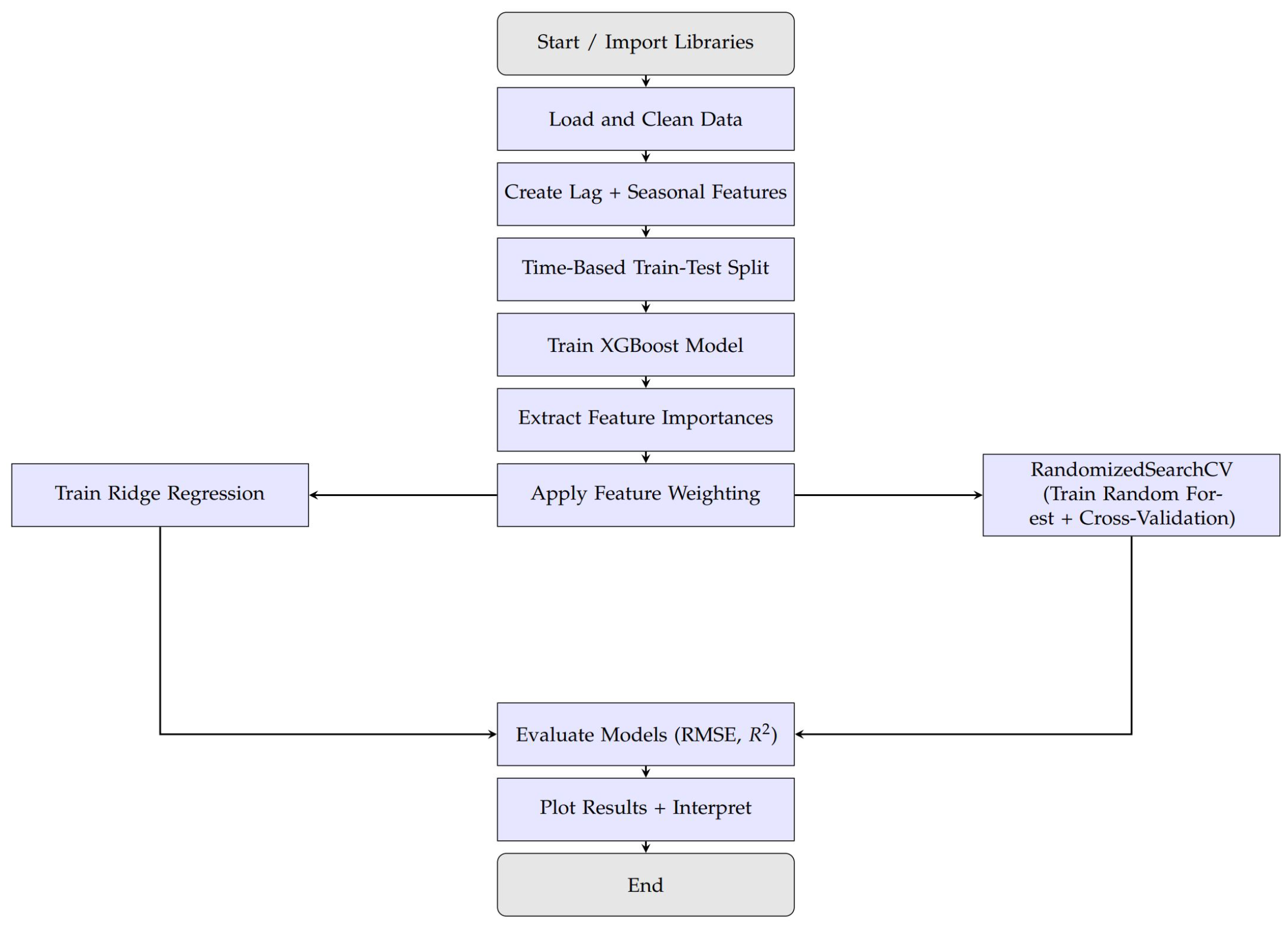
4.6. Predictive Modeling Framework Using Ensemble Learning and SHAP-Based Explainability
| Algorithm 1 LWE Prediction and Explainability Framework |
|
4.7. Performance Comparison Against Baseline Methods
4.8. Managerial Insights
4.9. Limitations and Future Research Directions
- Limited Feature Scope: While the current model uses key hydroclimatic variables, it does not yet include land use changes, human interventions (e.g., irrigation or dam operations), or groundwater extraction data, which can significantly impact LWE.
- Fixed Temporal Resolution: This study is based on monthly aggregates. Exploring models with finer temporal resolution (e.g., weekly or daily) or adaptive time windows could better capture short-term fluctuations and improve responsiveness.
- Geographic Generalizability: The proposed framework was trained and evaluated only on data for Lake Urmia. Extending the model to other basins or performing transfer learning could test its generalizability and broader applicability.
- Model Ensemble Optimization: Although Random Forest and Ridge Regression were used, future work could investigate more advanced hybrid or deep learning architectures (e.g., LSTM networks) while preserving interpretability via SHAP or surrogate models.
- Uncertainty Quantification: The current setup only provides point estimates; integrating probabilistic modeling or Bayesian machine learning could additionally offer confidence intervals and risk-aware forecasting.
- Physical-Model Fusion: Combining data-driven approaches with physical hydrological models could enhance accuracy and interpretability, especially under unseen extreme conditions.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. JavaScript Code for Visualizing Water Bodies Around Lake Urmia
| Listing A1. JavaScript code for extracting and visualizing water bodies around Lake Urmia using NDWI and Landsat 8 imagery. |
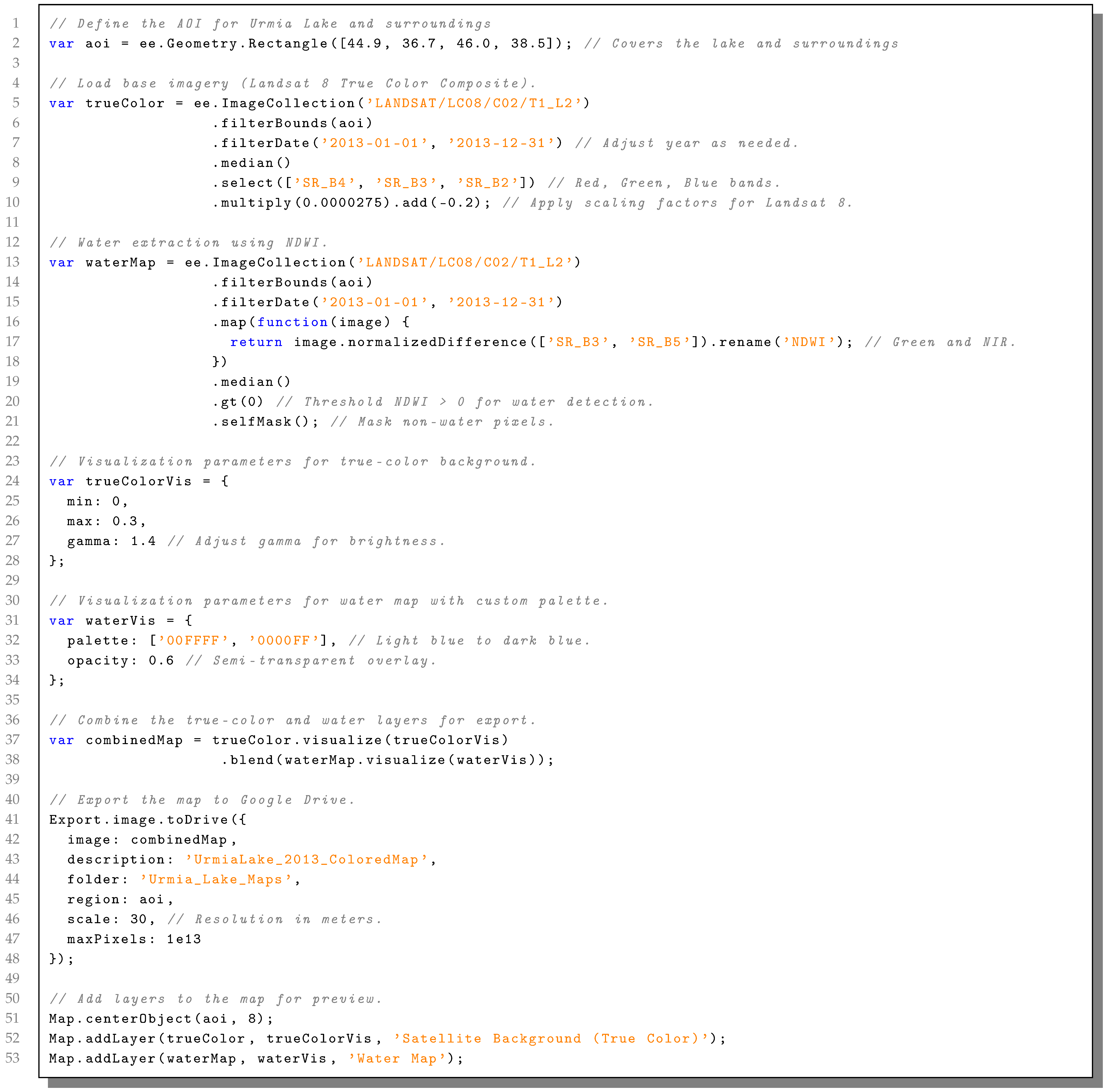 |
Appendix A.2. Python Script for Visualizing Raster Files
| Listing A2. Python script used for visualizing raster data and adding a legend via Matplotlib. |
 |
References
- Ahmadaali, J.; Barani, G.-A.; Qaderi, K.; Hessari, B. Analysis of the effects of water management strategies and climate change on the environmental and agricultural sustainability of Urmia Lake Basin, Iran. Water 2018, 10, 160. [Google Scholar] [CrossRef]
- Kazemi Garajeh, M.; Haji, F.; Tohidfar, M.; Sadeqi, A.; Ahmadi, R.; Kariminejad, N. Spatiotemporal monitoring of climate change impacts on water resources using an integrated approach of remote sensing and Google Earth Engine. Sci. Rep. 2024, 14, 5469. [Google Scholar] [CrossRef]
- Ghazi, B.; Dutt, S.; Torabi Haghighi, A. Projection of future meteorological droughts in Lake Urmia Basin, Iran. Water 2023, 15, 1558. [Google Scholar] [CrossRef]
- Habibi, S. A long-term study of the effects of wastewater on some chemical and physical properties of soil. J. Appl. Res. Water Wastewater 2019, 6, 156–161. [Google Scholar]
- Garousi, V.; Najafi, A.; Samadi, A.; Rasouli, K.; Khanaliloo, B. Environmental crisis in Lake Urmia, Iran: A systematic review of causes, negative consequences and possible solutions. In Proceedings of the 6th International Perspective on Water Resources & the Environment (IPWE), Izmir, Turkey, 7–9 January 2013. [Google Scholar]
- Ahrari, A.; Sharifi, A.; Haghighi, A.T. Anthropogenic vs. climatic drivers: Dissecting lake desiccation on the Iranian plateau. J. Environ. Manag. 2024, 368, 122103. [Google Scholar] [CrossRef]
- Mosavi, A.; Ozturk, P.; Chau, K.-W. Flood prediction using machine learning models: Literature review. Water 2018, 10, 1536. [Google Scholar] [CrossRef]
- Sit, M.; Demir, I. A comprehensive review of deep learning applications in hydrology and water resources. J. Hydrol. 2020, 588, 125096. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat, F. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef]
- Molnar, C. Interpretable Machine Learning. Leanpub. 2022. Available online: https://christophm.github.io/interpretable-ml-book/ (accessed on 11 April 2025).
- Lundberg, S.M.; Lee, S.-I. A unified approach to interpreting model predictions. Adv. Neural Inf. Process. Syst. 2017, 30, 4765–4774. [Google Scholar]
- Lundberg, S.M.; Erion, G.G.; Lee, S.-I. From local explanations to global understanding with explainable AI for trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef]
- Dehghanipour, A.H.; Moshir Panahi, D.; Mousavi, H.; Kalantari, Z.; Tajrishy, M. Effects of Water Level Decline in Lake Urmia, Iran, on Local Climate Conditions. Water 2020, 12, 2153. [Google Scholar] [CrossRef]
- Zarinmehr, H.; Tizro, A.T.; Fryar, A.E.; Pour, M.K.; Fasihi, R. Prediction of groundwater level variations based on gravity recovery and climate experiment (GRACE) satellite data and a time-series analysis: A case study in the Lake Urmia Basin, Iran. Environ. Earth Sci. 2022, 81, 180. [Google Scholar] [CrossRef]
- Tourian, M.J.; Elmi, O.; Chen, Q.; Devaraju, B.; Roohi, S.; Sneeuw, N. A spaceborne multisensor approach to monitor the desiccation of Lake Urmia in Iran. Remote Sens. Environ. 2015, 156, 349–360. [Google Scholar] [CrossRef]
- Aghayi, M.M.; Tajrishy, M.; Guan, H. Assessing mountain block water storage changes in river basins using water balance and GRACE: A case study on Lake Urmia Basin of Iran. J. Hydrol. Reg. Stud. 2023, 49, 101511. [Google Scholar] [CrossRef]
- Saemian, P.; Elmi, O.; Vishwakarma, B.D.; Tourian, M.J.; Sneeuw, N. Analyzing the Lake Urmia restoration progress using ground-based and spaceborne observations. Sci. Total Environ. 2020, 739, 139857. [Google Scholar] [CrossRef]
- Khorrami, B.; Ali, S.; Sahin, O.G.; Gunduz, O. Model-coupled GRACE-based analysis of hydrological dynamics of drying Lake Urmia and its basin. Hydrol. Process. 2023, 37, e14893. [Google Scholar] [CrossRef]
- Issazadeh, V.; Argany, M. Changes in water surface of aquifers using GRACE satellite data in the Google Earth Engine: A study of the Urmia Lake watershed from 2002 to 2017. Town Country Plan. 2021, 13. [Google Scholar] [CrossRef]
- Sabzehee, F.; Amiri-Simkooei, A.; Kerachian, R.; Sharifi, M. CNN-based reconstruction of water storage anomaly gaps in Urmia Lake Basin during the GRACE and GRACE-FO transition. Preprint or Unpublished Work.
- Radman, A.; Akhoondzadeh, M.; Hosseiny, B. Monitoring and predicting temporal changes of Urmia Lake and its basin using satellite multi-sensor data and deep-learning algorithms. PFG J. Photogramm. Remote Sens. Geoinf. Sci. 2022, 90, 319–335. [Google Scholar] [CrossRef]
- Chaudhari, S. Modeling and Remote Sensing of Water Storage Change in Lake Urmia Basin, Iran; Michigan State University: East Lansing, MI, USA, 2017. [Google Scholar]
- Moghim, S. Assessment of water storage changes using GRACE and GLDAS. Water Resour. Manag. 2020, 34, 685–697. [Google Scholar] [CrossRef]
- Hosseini-Moghari, S.M.; Araghinejad, S.; Tourian, M.J.; Ebrahimi, K.; Döll, P. Quantifying the impacts of human water use and climate variations on recent drying of Lake Urmia basin: The value of different sets of spaceborne and in situ data for calibrating a global hydrological model. Hydrol. Earth Syst. Sci. 2020, 24, 1939–1956. [Google Scholar] [CrossRef]
- Taheri Dehkordi, A.; Valadan Zoej, M.J.; Ghasemi, H.; Jafari, M.; Mehran, A. Monitoring long-term spatiotemporal changes in Iran surface waters using Landsat imagery. Remote Sens. 2022, 14, 4491. [Google Scholar] [CrossRef]
- Shiri, J.; Shamshirband, S.; Kisi, O.; Karimi, S.; Bateni, S.M.; Hosseini Nezhad, S.H.; Hashemi, A. Prediction of water-level in the Urmia Lake using the extreme learning machine approach. Water Resour. Manag. 2016, 30, 5217–5229. [Google Scholar] [CrossRef]
- Asadollah, S.B.H.S.; Sharafati, A.; Saeedi, M.; Shahid, S. Estimation of soil moisture from remote sensing products using an ensemble machine learning model: A case study of Lake Urmia Basin, Iran. Earth Sci. Inform. 2024, 17, 385–400. [Google Scholar] [CrossRef]
- Azizi, S. Drought and Environmental Transformations of Lake Urmia: An Integrated Analysis Using Machine Learning and GIS. Eur. J. Appl. Sci. 2024, 12. [Google Scholar] [CrossRef]
- Sakizadeh, M.; Milewski, A. Quantifying LULC changes in Urmia Lake Basin using machine learning techniques, intensity analysis and a combined method of cellular automata (CA) and artificial neural networks (ANN)(CA-ANN). Model. Earth Syst. Environ. 2024, 10, 2011–2030. [Google Scholar] [CrossRef]
- Soltani, K.; Azari, A. Terrestrial water storage anomaly estimating using machine learning techniques and satellite-based data (a case study of Lake Urmia Basin). Irrig. Drain. 2024, 73, 215–229. [Google Scholar] [CrossRef]
- Raheli, B.; Talebbeydokhti, N.; Saadat, S.; Nourani, V. Uncertainty assessment of surface water salinity using standalone, ensemble, and deep machine learning methods: A case study of Lake Urmia. Iran. J. Sci. Technol. Trans. Civ. Eng. 2024, 48, 1029–1047. [Google Scholar] [CrossRef]
- Hou, X.; Zhu, Y.; Guo, H.; Yang, D.; Guo, J.; Zhou, Y. Water clarity mapping of global lakes using a novel hybrid deep-learning-based recurrent model with Landsat OLI image. Water Res. 2022, 218, 118536. [Google Scholar]
- Zhou, Y.; Hou, X.; Guo, J.; Yang, D.; Zhu, Y.; Guo, H. An optical mechanism-based deep learning approach for deriving water trophic state of China’s lakes from Landsat images. Water Res. 2024, 260, 120301. [Google Scholar]
- Choopan, Y.; Emami, S. Optimal operation of dam reservoir using gray wolf optimizer algorithm (case study: Urmia Shaharchay Dam in Iran). J. Soft Comput. Civ. Eng. 2019, 3, 47–61. [Google Scholar]
- Asem, A.; Eimanifar, A.; Djamali, M.; De los Rios, P.; Wink, M. Biodiversity of the hypersaline Urmia Lake National Park (NW Iran). Diversity 2014, 6, 102–132. [Google Scholar] [CrossRef]
- Li, H.; Sheffield, J.; Wood, E.F. Bias correction of monthly precipitation and temperature fields from Intergovernmental Panel on Climate Change AR4 models using equidistant quantile matching. J. Geophys. Res. Atmos. 2010, 115, D10101. [Google Scholar] [CrossRef]
- Schafer, J.L.; Graham, J.W. Missing data: Our view of the state of the art. Psychol. Methods 2002, 7, 147–177. [Google Scholar] [CrossRef] [PubMed]
- Nygren, M.; Barthel, R.; Allen, D.M.; Giese, M. Exploring groundwater drought responsiveness in lowland post-glacial environments. Hydrogeol. J. 2022, 30, 1937–1961. [Google Scholar] [CrossRef]
- Saqr, A.M.; Kartal, V.; Karakoyun, E.; Abd-Elmaboud, M.E. Improving the accuracy of groundwater level forecasting by coupling ensemble machine learning model and Coronavirus Herd Immunity Optimizer. Water Resour. Manag. 2025; In Press. 1–28. [Google Scholar]


| Statistics | Temperature (°C) | Precipitation (in) | Sea Level Pressure (hPa) | Soil Moisture (%) | LWE (in) |
|---|---|---|---|---|---|
| Mean | 12.32005 | 317.86 | 25.55719 | 23.78035 | |
| Median | 12.20000 | 309.00 | 25.58818 | 23.89875 | |
| Std. Deviation | 0.58088 | 76.241 | 0.07890 | 1.65669 | 8.68347 |
| Minimum | 11.000 | 157 | 25.360 | 19.8283 | |
| Maximum | 13.800 | 505 | 25.655 | 26.6019 | 5.483 |
| Category | Statistic | Temperature (°C) | Precipitation (in) | Sea Level Pressure (hPa) | Soil Moisture (%) | LWE (in) |
|---|---|---|---|---|---|---|
| Normal Parameters a,b | Mean | 12.32005 | 317.86 | 25.55719 | 23.78035 | |
| Std. Deviation | 0.58088 | 76.241 | 0.07890 | 1.65669 | 8.68347 | |
| Most Extreme Differences | Absolute | 0.147 | 0.182 | 0.249 | 0.146 | 0.241 |
| Positive | 0.124 | 0.182 | 0.116 | 0.106 | 0.122 | |
| Negative | ||||||
| Test Statistic | 0.147 | 0.182 | 0.249 | 0.146 | 0.241 | |
| Asymp. Sig. (2-tailed) c | 0.200 d | 0.069 | 0.001 | 0.200 d | 0.002 | |
| Monte Carlo Sig. (2-tailed) e | Sig. | 0.261 | 0.065 | 0.001 | 0.266 | 0.002 |
| 99% CI Lower Bound | 0.249 | 0.059 | 0.000 | 0.255 | 0.001 | |
| 99% CI Upper Bound | 0.272 | 0.072 | 0.002 | 0.278 | 0.003 | |
| Variables | Temperature (°C) | Precipitation (in) | Sea Level Pressure (hPa) | Soil Moisture (%) | LWE (in) |
|---|---|---|---|---|---|
| Temperature (°C) | 1.000 | 0.634 ** | −0.601 ** | −0.300 | |
| Sig. (2-tailed) | 0.375 | 0.002 | 0.004 | 0.186 | |
| Precipitation (in) | 1.000 | 0.181 | |||
| Sig. (2-tailed) | 0.375 | 0.927 | 0.559 | 0.433 | |
| Sea Level Pressure (hPa) | 0.634 ** | 1.000 | −0.684 ** | −0.527 * | |
| Sig. (2-tailed) | 0.002 | 0.927 | 0.014 | ||
| Soil Moisture (%) | −0.601 ** | −0.684 ** | 1.000 | 0.155 | |
| Sig. (2-tailed) | 0.004 | 0.559 | 0.504 | ||
| LWE (in) | 0.181 | −0.527 * | 0.155 | 1.000 | |
| Sig. (2-tailed) | 0.186 | 0.433 | 0.014 | 0.504 |
| Parameter | 2003–2013 | 2014–2023 | 2003–2023 |
|---|---|---|---|
| Trend | Decreasing | Increasing | Decreasing |
| Slope | −0.1721 | 0.1648 | −0.0239 |
| p-value | 0.0000 | 0.0000 | 0.0133 |
| Test Statistic (S) | −4424.0 | 2778.0 | −3312.0 |
| Model | Variables Entered | Variables Removed | Method | ||
|---|---|---|---|---|---|
| 1 | Soil Moisture (%), Precipitation (in), Temperature (°C), Sea Level Pressure (hPa) | None | Enter (All predictors entered together) | ||
| Model Summary | |||||
| Model | R | R Square | Adjusted R Square | Std. Error of Estimate | |
| 1 | 0.603 | 0.363 | 0.204 | 7.748 | |
| ANOVA Results | |||||
| Model | Sum of Squares | df | Mean Square | F | Sig. |
| Regression | 547.477 | 4 | 136.869 | 2.280 | 0.106 |
| Residual | 960.576 | 16 | 60.036 | ||
| Total | 1508.052 | 20 | |||
| Coefficients | |||||
| Predictor | B | Std. Error | Beta | t | Sig. |
| (Constant) | 1583.779 | 811.373 | - | 1.952 | 0.069 |
| Temperature (°C) | −1.830 | 4.252 | −0.122 | −0.430 | 0.673 |
| Precipitation (in) | 0.025 | 0.027 | 0.222 | 0.938 | 0.362 |
| Sea Level Pressure (hPa) | −60.337 | 31.724 | −0.548 | −1.902 | 0.075 |
| Soil Moisture (%) | −1.340 | 1.554 | −0.256 | −0.862 | 0.401 |
| Model | RMSE | Score |
|---|---|---|
| Persistence Model | 11.79 | −0.42 |
| Ridge Regression (No Feature Weighting) | 3.91 | 0.93 |
| Random Forest (Simple, No Cross-Validation) | 3.82 | 0.89 |
| XGBoost Model Alone | 3.85 | 0.90 |
| Ridge Regression (Weighted + Cross-Validated) | 3.65 | 0.86 |
| Random Forest (Weighted + Cross-Validated) | 3.31 | 0.89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Habibi, S.; Tasouji Hassanpour, S. An Explainable Machine Learning Framework for Forecasting Lake Water Equivalent Using Satellite Data: A 20-Year Analysis of the Urmia Lake Basin. Water 2025, 17, 1431. https://doi.org/10.3390/w17101431
Habibi S, Tasouji Hassanpour S. An Explainable Machine Learning Framework for Forecasting Lake Water Equivalent Using Satellite Data: A 20-Year Analysis of the Urmia Lake Basin. Water. 2025; 17(10):1431. https://doi.org/10.3390/w17101431
Chicago/Turabian StyleHabibi, Sara, and Saeed Tasouji Hassanpour. 2025. "An Explainable Machine Learning Framework for Forecasting Lake Water Equivalent Using Satellite Data: A 20-Year Analysis of the Urmia Lake Basin" Water 17, no. 10: 1431. https://doi.org/10.3390/w17101431
APA StyleHabibi, S., & Tasouji Hassanpour, S. (2025). An Explainable Machine Learning Framework for Forecasting Lake Water Equivalent Using Satellite Data: A 20-Year Analysis of the Urmia Lake Basin. Water, 17(10), 1431. https://doi.org/10.3390/w17101431






