A Network-Based Clustering Method to Ensure Homogeneity in Regional Frequency Analysis of Extreme Rainfall
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Data Sources
2.2. Index Flood Procedure Based on L-Moments
2.3. Multivariate Analysis and Clustering Techniques
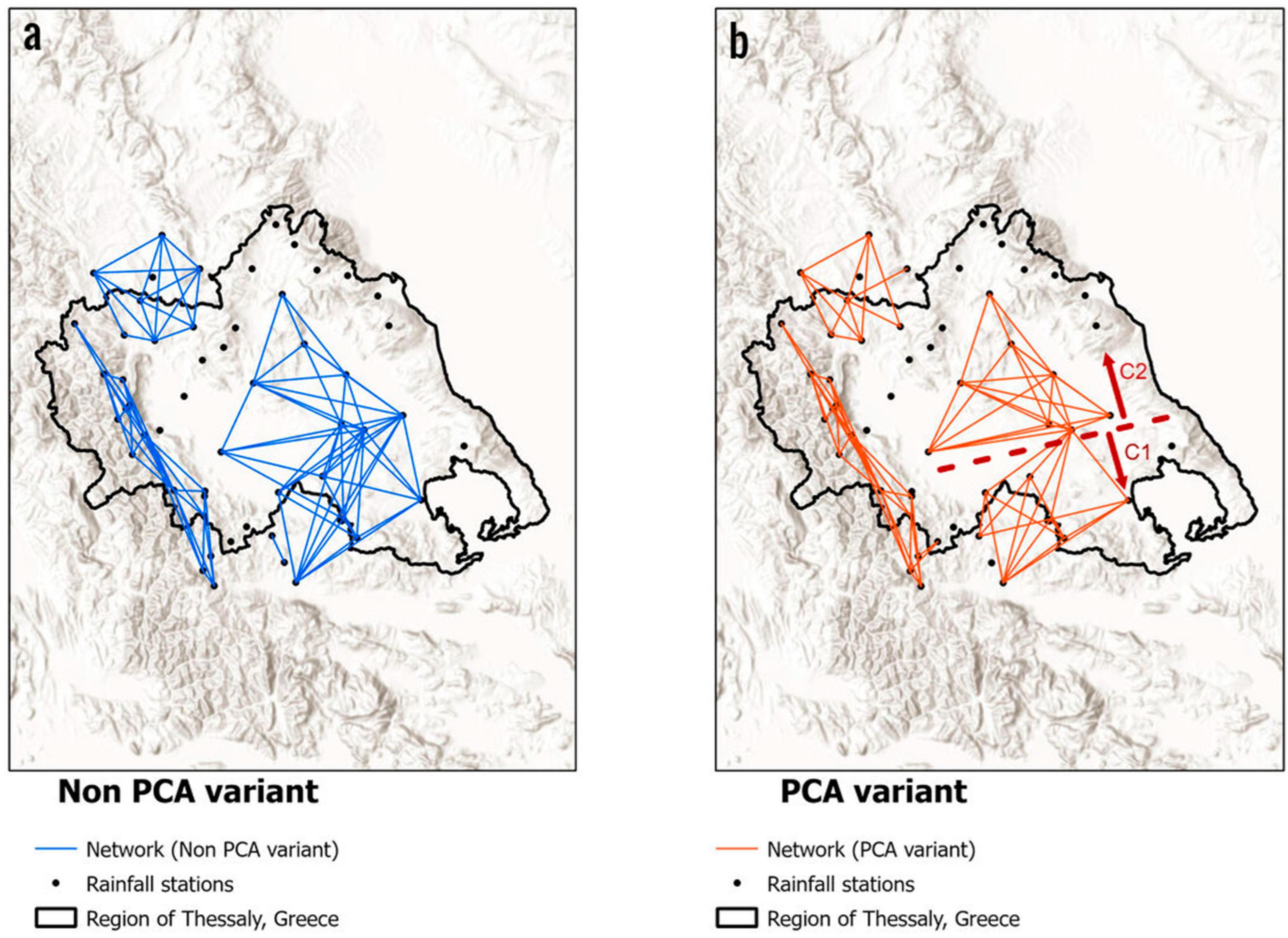
2.4. Network Analysis and Community Detection
2.5. Regional Frequency Analysis
2.5.1. Heterogeneity Measures
2.5.2. Selection of the Appropriate Probability Distribution
2.5.3. Uncertainty Analysis
- Fit an appropriate distribution to the original data using the L-moments method.
- Generate a sample of equal size from the fitted distribution.
- Refit the distribution to the generated sample and calculate the desired quantiles.
- Repeat this process multiple times (N = 10,000 in this study).
- Determine the 5–95% CIs for the target quantiles.
2.6. Methodology Application
3. Results
3.1. Multivariate Analysis and Clustering Results
3.2. Distribution Fitting
3.3. Quantile Estimation and Confidence Intervals
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Name | X | Y | Z | Mean Annual Precipitation | Mean of Maximun Annual Daily Rainfall | Lca |
|---|---|---|---|---|---|---|
| Agchialos | 396,203.00 | 4,341,105.00 | 15.00 | 501.72 | 55.31 | 0.24 |
| Agiofyllo | 291,669.00 | 4,415,392.00 | 600.00 | 790.78 | 59.40 | 0.15 |
| Agrelia | 322,649.00 | 4,397,952.00 | 700.00 | 548.35 | 48.60 | 0.14 |
| Amarantos | 315,620.00 | 4,342,587.00 | 800.00 | 1159.08 | 86.97 | −0.02 |
| Anavra | 372,326.70 | 4,327,101.00 | 208.00 | 735.11 | 73.81 | 0.21 |
| Argithea | 288,679.00 | 4,358,079.00 | 992.00 | 1649.70 | 80.02 | 0.12 |
| Chrysomilia | 285,140.00 | 4,385,948.00 | 940.00 | 1238.19 | 95.38 | 0.02 |
| Drakotrypa | 293,185.00 | 4,365,363.00 | 680.00 | 1336.82 | 81.95 | 0.24 |
| Elassona | 344,494.00 | 4,417,838.00 | 314.00 | 538.81 | 59.04 | 0.41 |
| ElatiDEH | 313,872.20 | 4,427,213.00 | 663.60 | 734.38 | 65.96 | 0.14 |
| ElatiYPEKA | 287,748.00 | 4,376,618.00 | 900.00 | 1630.37 | 99.38 | 0.24 |
| Farkadona | 333,800.00 | 4,384,747.00 | 87.00 | 548.58 | 55.74 | 0.24 |
| Farsala | 359,598.90 | 4,350,003.00 | 250.00 | 627.10 | 62.56 | 0.19 |
| FragmaPlastira | 304,154.00 | 4,344,717.00 | 850.00 | 1241.14 | 84.85 | 0.00 |
| Giannota | 333,296.00 | 4,427,329.00 | 500.00 | 583.38 | 57.70 | 0.20 |
| Kallipeyki | 368,844.00 | 4,424,784.00 | 1050.00 | 710.89 | 97.11 | 0.45 |
| Karditsa | 321,757.00 | 4,359,103.00 | 103.00 | 607.73 | 62.90 | 0.36 |
| Karpero | 296,204.00 | 4,424,125.00 | 504.40 | 638.67 | 45.50 | 0.25 |
| Kipourgio | 274,279.30 | 4,425,745.00 | 828.20 | 916.37 | 49.46 | 0.07 |
| Koniskos | 311,401.00 | 4,405,624.00 | 860.00 | 800.00 | 62.84 | 0.23 |
| Kryovrisi | 357,491.00 | 4,426,838.00 | 1030.00 | 679.91 | 59.75 | 0.33 |
| Larisa | 368,210.00 | 4,387,785.00 | 79.00 | 414.67 | 48.11 | 0.38 |
| Liopraso | 314,719.40 | 4,393,282.00 | 688.00 | 713.12 | 60.87 | 0.03 |
| LivadiYPEKA | 342,182.00 | 4,443,797.00 | 1179.00 | 718.00 | 64.14 | 0.17 |
| LivadiYPGE | 342,182.00 | 4,443,797.00 | 1179.00 | 718.49 | 62.70 | 0.29 |
| Loutsopigh | 331,211.00 | 4,331,131.00 | 730.00 | 916.89 | 72.95 | 0.28 |
| Magoyla | 343,054.60 | 4,343,956.00 | 170.00 | 581.52 | 51.10 | 0.14 |
| Makrinitsa | 412,260.00 | 4,361,258.00 | 690.00 | 836.88 | 103.59 | 0.16 |
| Makryraxh | 340,690.60 | 4,327,788.00 | 602.90 | 777.98 | 60.35 | 0.18 |
| Malakasio | 267,150.00 | 4,406,840.00 | 842.00 | 1209.57 | 67.39 | 0.08 |
| Megalh_kerasia | 285,604.00 | 4,402,599.00 | 500.00 | 889.16 | 67.71 | 0.10 |
| Meteora | 296,980.00 | 4,400,438.00 | 596.00 | 809.63 | 69.17 | 0.19 |
| Moloha | 315,446.00 | 4,335,188.00 | 790.00 | 1092.66 | 89.76 | 0.13 |
| Moyzaki | 298,972.00 | 4,367,063.00 | 226.00 | 1128.61 | 64.78 | −0.07 |
| Myra | 375,034.00 | 4,367,317.00 | 320.00 | 535.48 | 55.65 | 0.19 |
| Neoxori | 314,969.00 | 4,314,839.00 | 800.00 | 1100.05 | 80.68 | 0.13 |
| Paleioxori | 278,037.00 | 4,388,000.00 | 1050.00 | 1166.62 | 88.84 | 0.14 |
| Pitsiota | 317,985.00 | 4,320,322.00 | 800.00 | 1287.63 | 61.45 | 0.30 |
| Pyloroi | 299,745.90 | 4,439,832.00 | 715.10 | 793.03 | 40.12 | 0.13 |
| Pyrgetos | 380,116.00 | 4,417,196.00 | 31.00 | 797.63 | 81.07 | 0.04 |
| Pythio | 349,135.00 | 4,436,253.00 | 750.00 | 648.67 | 60.42 | 0.39 |
| Raxhoyla | 315,664.00 | 4,344,437.00 | 330.00 | 1122.11 | 72.34 | −0.09 |
| Redina | 325,324.00 | 4,325,708.00 | 903.00 | 1253.70 | 66.23 | 0.31 |
| Skopia | 367,299.00 | 4,334,140.00 | 450.00 | 547.24 | 57.29 | 0.27 |
| Sphlia | 384,223.00 | 4,406,031.00 | 813.00 | 848.79 | 103.41 | 0.20 |
| Stoyrnaraiika | 283,294.00 | 4,371,187.00 | 860.00 | 1849.46 | 113.00 | 0.18 |
| Swthrio | 389,455.00 | 4,372,649.00 | 54.00 | 409.02 | 63.07 | 0.36 |
| Trikala | 307,901.00 | 4,379,795.00 | 114.00 | 697.73 | 54.79 | 0.04 |
| Trilofo | 345,367.00 | 4,317,887.00 | 580.00 | 632.52 | 52.54 | 0.08 |
| Tymfristos | 319,174.00 | 4,309,189.00 | 850.00 | 1005.41 | 67.24 | 0.02 |
| Tyrnavos | 352,688.00 | 4,399,169.00 | 92.00 | 528.02 | 60.86 | 0.48 |
| Verdikoysa | 327,102.00 | 4,405,255.00 | 863.00 | 799.62 | 66.72 | 0.10 |
| Vrontero | 286,305.10 | 4,375,195.00 | 853.00 | 1542.36 | 111.90 | 0.15 |
| Zappeio | 366,461.00 | 4,369,310.00 | 170.00 | 499.96 | 57.03 | 0.32 |
| Zileyto | 349,557.00 | 4,310,404.00 | 120.00 | 712.53 | 50.28 | 0.14 |
| Name | Min | 1st Qu | Median | 3rd Qu | Max |
|---|---|---|---|---|---|
| Agchialos | 21.13 | 34.64 | 47.07 | 70.37 | 159.78 |
| Agiofyllo | 24.30 | 44.89 | 54.41 | 72.01 | 108.48 |
| Agrelia | 15.82 | 27.12 | 45.20 | 64.98 | 92.66 |
| Amarantos | 37.29 | 66.67 | 91.19 | 100.23 | 141.25 |
| Anavra | 25.61 | 51.87 | 67.80 | 83.62 | 180.80 |
| Argithea | 16.05 | 57.18 | 82.15 | 94.13 | 183.51 |
| Chrysomilia | 41.06 | 75.77 | 100.57 | 108.48 | 176.85 |
| Drakotrypa | 27.12 | 63.51 | 74.58 | 91.53 | 165.54 |
| Elassona | 20.57 | 35.29 | 47.97 | 69.42 | 279.11 |
| ElatiDEH | 27.70 | 47.05 | 68.60 | 73.95 | 128.10 |
| ElatiYPEKA | 47.00 | 73.50 | 91.85 | 111.50 | 312.50 |
| Farkadona | 24.86 | 40.68 | 49.15 | 66.28 | 127.69 |
| Farsala | 32.88 | 45.85 | 57.63 | 76.92 | 107.35 |
| FragmaPlastira | 37.29 | 73.45 | 85.32 | 96.90 | 124.30 |
| Giannota | 22.94 | 45.85 | 54.52 | 64.52 | 102.83 |
| Kallipeyki | 36.65 | 66.66 | 76.74 | 112.69 | 329.44 |
| Karditsa | 13.45 | 41.98 | 54.81 | 71.76 | 298.32 |
| Karpero | 20.90 | 31.60 | 40.15 | 56.93 | 90.50 |
| Kipourgio | 30.00 | 38.50 | 47.75 | 58.08 | 81.50 |
| Koniskos | 26.44 | 40.23 | 53.68 | 78.82 | 118.65 |
| Kryovrisi | 37.52 | 46.90 | 52.55 | 67.91 | 124.30 |
| Larisa | 16.16 | 29.02 | 39.33 | 52.91 | 159.44 |
| Liopraso | 14.24 | 48.87 | 63.28 | 69.44 | 116.39 |
| LivadiYPEKA | 21.81 | 44.52 | 61.02 | 75.99 | 175.15 |
| LivadiYPGE | 40.23 | 48.31 | 55.94 | 73.45 | 102.83 |
| Loutsopigh | 25.69 | 42.07 | 62.32 | 90.30 | 178.77 |
| Magoyla | 27.35 | 40.68 | 47.18 | 62.61 | 81.36 |
| Makrinitsa | 33.33 | 70.17 | 98.31 | 127.86 | 220.35 |
| Makryraxh | 27.91 | 45.34 | 57.18 | 69.89 | 122.04 |
| Malakasio | 29.15 | 51.87 | 66.56 | 81.14 | 139.78 |
| Megalh_kerasia | 30.96 | 51.64 | 68.14 | 82.61 | 113.45 |
| Meteora | 30.85 | 54.13 | 64.97 | 81.36 | 163.85 |
| Moloha | 35.60 | 73.56 | 83.62 | 105.99 | 186.45 |
| Moyzaki | 17.48 | 39.84 | 70.63 | 88.65 | 114.02 |
| Myra | 21.47 | 40.82 | 51.42 | 68.08 | 110.18 |
| Neoxori | 49.20 | 62.60 | 80.20 | 94.80 | 135.50 |
| Paleioxori | 51.08 | 67.80 | 84.75 | 105.20 | 142.38 |
| Pitsiota | 42.00 | 51.20 | 57.80 | 66.40 | 124.60 |
| Pyloroi | 21.00 | 32.35 | 37.00 | 49.30 | 70.00 |
| Pyrgetos | 20.11 | 54.72 | 85.20 | 99.04 | 156.51 |
| Pythio | 29.04 | 37.86 | 50.85 | 74.02 | 155.94 |
| Raxhoyla | 43.39 | 65.99 | 74.13 | 77.52 | 95.37 |
| Redina | 30.85 | 51.14 | 60.68 | 71.81 | 216.73 |
| Skopia | 20.34 | 40.12 | 51.08 | 63.38 | 124.30 |
| Sphlia | 36.84 | 74.41 | 98.54 | 118.31 | 300.24 |
| Stoyrnaraiika | 67.91 | 91.73 | 110.18 | 127.86 | 276.29 |
| Swthrio | 20.79 | 36.16 | 50.28 | 75.03 | 203.40 |
| Trikala | 13.33 | 44.21 | 52.94 | 66.27 | 129.05 |
| Trilofo | 19.21 | 39.33 | 51.64 | 62.15 | 110.74 |
| Tymfristos | 13.56 | 53.09 | 67.35 | 81.70 | 133.11 |
| Tyrnavos | 28.48 | 42.38 | 51.30 | 65.54 | 292.22 |
| Verdikoysa | 22.94 | 49.89 | 63.73 | 81.93 | 123.06 |
| Vrontero | 68.93 | 89.02 | 103.06 | 136.17 | 178.54 |
| Zappeio | 23.73 | 43.40 | 51.42 | 62.77 | 169.50 |
| Zileyto | 10.62 | 37.26 | 47.86 | 57.97 | 113.00 |
References
- Forestieri, A.; Lo Conti, F.; Blenkinsop, S.; Cannarozzo, M.; Fowler, H.J.; Noto, L.V. Regional Frequency Analysis of Extreme Rainfall in Sicily (Italy). Int. J. Climatol. 2018, 38, e698–e716. [Google Scholar] [CrossRef]
- Das, S.; Zhu, D.; Yin, Y. Comparison of Mapping Approaches for Estimating Extreme Precipitation of Any Return Period at Ungauged Locations. Stoch. Environ. Res. Risk Assess. 2020, 34, 1175–1196. [Google Scholar] [CrossRef]
- Hailegeorgis, T.T.; Thorolfsson, S.T.; Alfredsen, K. Regional Frequency Analysis of Extreme Precipitation with Consideration of Uncertainties to Update IDF Curves for the City of Trondheim. J. Hydrol. 2013, 498, 305–318. [Google Scholar] [CrossRef]
- Liang, Y.; Liu, S.; Guo, Y.; Hua, H. L-Moment-Based Regional Frequency Analysis of Annual Extreme Precipitation and Its Uncertainty Analysis. Water Resour. Manag. 2017, 31, 3899–3919. [Google Scholar] [CrossRef]
- Bharath, R.; Srinivas, V.V. Regionalization of Extreme Rainfall in India. Int. J. Climatol. 2015, 35, 1142–1156. [Google Scholar] [CrossRef]
- Dalrymple, T. Flood-Frequency Analyses, Manual of Hydrology: Part 3; U.S. Government Publishing Office: Washington, DC, USA, 1960. [Google Scholar]
- Fundamentals of Statistical Hydrology; Naghettini, M., Ed.; Springer International Publishing: Cham, Switzerland, 2017; ISBN 978-3-319-43560-2. [Google Scholar]
- Deidda, R.; Hellies, M.; Langousis, A. A Critical Analysis of the Shortcomings in Spatial Frequency Analysis of Rainfall Extremes Based on Homogeneous Regions and a Comparison with a Hierarchical Boundaryless Approach. Stoch. Environ. Res. Risk Assess. 2021, 35, 2605–2628. [Google Scholar] [CrossRef]
- Hosking, J.R.M.; Wallis, J.R. Regional Frequency Analysis: An Approach Based on L-Moments; Cambridge University Press: Cambridge, UK, 1997; ISBN 978-0-521-43045-6. [Google Scholar]
- Leščešen, I.; Šraj, M.; Basarin, B.; Pavić, D.; Mesaroš, M.; Mudelsee, M. Regional Flood Frequency Analysis of the Sava River in South-Eastern Europe. Sustainability 2022, 14, 9282. [Google Scholar] [CrossRef]
- Prahadchai, T.; Busababodhin, P.; Park, J.-S. Regional Flood Frequency Analysis of Extreme Rainfall in Thailand, Based on L-Moments. Commun. Stat. Appl. Methods 2024, 31, 37–53. [Google Scholar] [CrossRef]
- Zhang, Z.; Stadnyk, T.A. Investigation of Attributes for Identifying Homogeneous Flood Regions for Regional Flood Frequency Analysis in Canada. Water 2020, 12, 2570. [Google Scholar] [CrossRef]
- Ghafori, V.; Sedghi, H.; Sharifan, R.A.; Nazemosadat, S.M.J. Regional Frequency Analysis of Droughts Using Copula Functions (Case Study: Part of Semiarid Climate of Fars Province, Iran). Iran. J. Sci. Technol. Trans. Civ. Eng. 2020, 44, 1223–1235. [Google Scholar] [CrossRef]
- Li, M.; Liu, M.; Cao, F.; Wang, G.; Chai, X.; Zhang, L. Application of L-Moment Method for Regional Frequency Analysis of Meteorological Drought across the Loess Plateau, China. PLoS ONE 2022, 17, e0273975. [Google Scholar] [CrossRef] [PubMed]
- Parvizi, S.; Eslamian, S.; Gheysari, M.; Gohari, A.; Kopai, S.S. Regional Frequency Analysis of Drought Severity and Duration in Karkheh River Basin, Iran Using Univariate L-Moments Method. Environ. Monit. Assess. 2022, 194, 336. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Zhu, D.; Wang, M.; Liao, Y. Regional Precipitation Frequency Analysis for 24-h Duration Using GPM and L-Moments Approach in South China. Theor. Appl. Clim. 2023, 152, 709–722. [Google Scholar] [CrossRef]
- Fowler, H.J.; Kilsby, C.G. A Regional Frequency Analysis of United Kingdom Extreme Rainfall from 1961 to 2000. Int. J. Climatol. 2003, 23, 1313–1334. [Google Scholar] [CrossRef]
- Jin, H.; Chen, X.; Zhong, R.; Duan, K. Frequency Analysis of Extreme Precipitation in Different Regions of the Huaihe River Basin. Int. J. Climatol. 2022, 42, 3517–3536. [Google Scholar] [CrossRef]
- Mahmoudi, M.R.; Eslamian, S.; Soltani, S.; Tahanian, M. Regionalization of Rainfall Intensity–Duration–Frequency (IDF) Curves with L-Moments Method Using Neural Gas Networks. Theor. Appl. Clim. 2023, 151, 1–11. [Google Scholar] [CrossRef]
- Gall, P.L.; Favre, A.-C.; Naveau, P.; Prieur, C. Improved Regional Frequency Analysis of Rainfall Data. Weather Clim. Extrem. 2022, 36, 100456. [Google Scholar] [CrossRef]
- Nain, M.; Hooda, B.K. Regional Frequency Analysis of Maximum Monthly Rainfall in Haryana State of India Using L-Moments. J. Reliab. Stat. Stud. 2021, 14, 33–56. [Google Scholar] [CrossRef]
- Ul Hassan, M.; Noreen, Z.; Ahmed, R. Regional Frequency Analysis of Annual Daily Rainfall Maxima in Skane, Sweden. Int. J. Climatol. 2021, 41, 4307–4320. [Google Scholar] [CrossRef]
- García-Marín, A.P.; Morbidelli, R.; Saltalippi, C.; Cifrodelli, M.; Estévez, J.; Flammini, A. On the Choice of the Optimal Frequency Analysis of Annual Extreme Rainfall by Multifractal Approach. J. Hydrol. 2019, 575, 1267–1279. [Google Scholar] [CrossRef]
- Srivastava, A.; Grotjahn, R.; Ullrich, P.A.; Risser, M. A Unified Approach to Evaluating Precipitation Frequency Estimates with Uncertainty Quantification: Application to Florida and California Watersheds. J. Hydrol. 2019, 578, 124095. [Google Scholar] [CrossRef]
- Ibrahim, M.N. Assessment of the Uncertainty Associated with Statistical Modeling of Precipitation Extremes for Hydrologic Engineering Applications in Amman, Jordan. Sustainability 2022, 14, 17052. [Google Scholar] [CrossRef]
- Hailegeorgis, T.T.; Alfredsen, K. Regional Flood Frequency Analysis and Prediction in Ungauged Basins Including Estimation of Major Uncertainties for Mid-Norway. J. Hydrol. Reg. Stud. 2017, 9, 104–126. [Google Scholar] [CrossRef]
- Dinpashoh, Y.; Fakheri-Fard, A.; Moghaddam, M.; Jahanbakhsh, S.; Mirnia, M. Selection of Variables for the Purpose of Regionalization of Iran’s Precipitation Climate Using Multivariate Methods. J. Hydrol. 2004, 297, 109–123. [Google Scholar] [CrossRef]
- Feidas, H.; Karagiannidis, A.; Keppas, S.; Vaitis, M.; Kontos, T.; Zanis, P.; Melas, D.; Anadranistakis, M. Modeling and Mapping Temperature and Precipitation Climate Data in Greece Using Topographical and Geographical Parameters. Theor. Appl. Climatol. 2013, 118, 133–146. [Google Scholar] [CrossRef]
- Iliopoulou, T.; Malamos, N.; Koutsoyiannis, D. Regional Ombrian Curves: Design Rainfall Estimation for a Spatially Diverse Rainfall Regime. Hydrology 2022, 9, 67. [Google Scholar] [CrossRef]
- Loukas, A.; Vasiliades, L. Streamflow Simulation Methods for Ungauged and Poorly Gauged Watersheds. Nat. Hazards Earth Syst. Sci. 2014, 14, 1641–1661. [Google Scholar] [CrossRef]
- Vasiliades, L. Drought Spatiotemporal Analysis, Modelling and Forecasting in Pinios River Basin of Thessaly, Greece. Ph.D. Thesis, Department of Civil Engineering, School of Engineering, University of Thessaly, Volos, Greece, 2010. [Google Scholar]
- Pereira, P.; Oliva, M.; Misiune, I. Spatial Interpolation of Precipitation Indexes in Sierra Nevada (Spain): Comparing the Performance of Some Interpolation Methods. Theor. Appl. Clim. 2016, 126, 683–698. [Google Scholar] [CrossRef]
- Baeriswyl, P.-A.; Rebetez, M. Regionalization of Precipitation in Switzerland by Means of Principal Component Analysis. Theor. Appl. Clim. 1997, 58, 31–41. [Google Scholar] [CrossRef]
- Burn, D.H. Evaluation of Regional Flood Frequency Analysis with a Region of Influence Approach. Water Resour. Res. 1990, 26, 2257–2265. [Google Scholar] [CrossRef]
- Gaál, L.; Kysely, J.; Szolgay, J. Region-of-Influence Approach to a Frequency Analysis of Heavy Precipitation in Slovakia. Hydrol. Earth Syst. Sci. 2008, 12, 825–839. [Google Scholar] [CrossRef]
- Guttman, N.B. The Use of L-Moments in the Determination of Regional Precipitation Climates. J. Clim. 1993, 6, 2309–2325. [Google Scholar] [CrossRef]
- Hassan, B.G.H.; Ping, F. Regional Rainfall Frequency Analysis for the Luanhe Basin–by Using L-Moments and Cluster Techniques. APCBEE Procedia 2012, 1, 126–135. [Google Scholar] [CrossRef]
- Lin, G.; Chen, L. Identification of Homogeneous Regions for Regional Frequency Analysis Using the Self-Organizing Map. J. Hydrol. 2006, 324, 1–9. [Google Scholar] [CrossRef]
- Pineda-Martínez, L.F.; Carbajal, N.; Medina-Roldán, E. Regionalization and Classification of Bioclimatic Zones in the Central-Northeastern Region of México Using Principal Component Analysis (PCA). Atmósfera 2007, 20, 133–145. [Google Scholar]
- Ramos, M.C. Divisive and Hierarchical Clustering Techniques to Analyse Variability of Rainfall Distribution Patterns in a Mediterranean Region. Atmos. Res. 2001, 57, 123–138. [Google Scholar] [CrossRef]
- Santos, E.B.; Lucio, P.S.; Silva, C.M.S. e Precipitation Regionalization of the Brazilian Amazon. Atmos. Sci. Lett. 2015, 16, 185–192. [Google Scholar] [CrossRef]
- Yang, T.; Shao, Q.; Hao, Z.-C.; Chen, X.; Zhang, Z.; Xu, C.-Y.; Sun, L. Regional Frequency Analysis and Spatio-Temporal Pattern Characterization of Rainfall Extremes in the Pearl River Basin, China. J. Hydrol. 2010, 380, 386–405. [Google Scholar] [CrossRef]
- Hao, W.; Hao, Z.; Yuan, F.; Ju, Q.; Hao, J. Regional Frequency Analysis of Precipitation Extremes and Its Spatio-Temporal Patterns in the Hanjiang River Basin, China. Atmosphere 2019, 10, 130. [Google Scholar] [CrossRef]
- Warren, R.A.; Jakob, C.; Hitchcock, S.M.; White, B.A. Heavy versus Extreme Rainfall Events in Southeast Australia. Q. J. R. Meteorol. Soc. 2021, 147, 3201–3226. [Google Scholar] [CrossRef]
- Sivakumar, B. Networks: A Generic Theory for Hydrology? Stoch. Environ. Res. Risk Assess. 2015, 29, 761–771. [Google Scholar] [CrossRef]
- Agarwal, A.; Marwan, N.; Ozturk, U.; Maheswaran, R. Unfolding Community Structure in Rainfall Network of Germany Using Complex Network-Based Approach. In Proceedings of the Water Resources and Environmental Engineering II; Rathinasamy, M., Chandramouli, S., Phanindra, K.B.V.N., Mahesh, U., Eds.; Springer: Singapore, 2019; pp. 179–193. [Google Scholar]
- Kim, K.; Joo, H.; Han, D.; Kim, S.; Lee, T.; Kim, H.S. On Complex Network Construction of Rain Gauge Stations Considering Nonlinearity of Observed Daily Rainfall Data. Water 2019, 11, 1578. [Google Scholar] [CrossRef]
- Han, X.; Ouarda, T.B.M.J.; Rahman, A.; Haddad, K.; Mehrotra, R.; Sharma, A. A Network Approach for Delineating Homogeneous Regions in Regional Flood Frequency Analysis. Water Resour. Res. 2020, 56, e2019WR025910. [Google Scholar] [CrossRef]
- Joo, H.; Lee, M.; Kim, J.; Jung, J.; Kwak, J.; Kim, H.S. Stream Gauge Network Grouping Analysis Using Community Detection. Stoch. Environ. Res. Risk Assess. 2021, 35, 781–795. [Google Scholar] [CrossRef]
- Rocha, R.V.; Souza Filho, F.D.A.D. Stream Gauge Clustering and Analysis for Non-Stationary Time Series through Complex Networks. J. Hydrol. 2023, 616, 128773. [Google Scholar] [CrossRef]
- Newman, M.E.J. Networks, 2nd ed.; Oxford University Press: Oxford, UK; New York, NY, USA, 2018; ISBN 978-0-19-880509-0. [Google Scholar]
- Fang, K.; Sivakumar, B.; Woldemeskel, F.M. Complex Networks, Community Structure, and Catchment Classification in a Large-Scale River Basin. J. Hydrol. 2017, 545, 478–493. [Google Scholar] [CrossRef]
- Donges, J.F.; Zou, Y.; Marwan, N.; Kurths, J. Complex Networks in Climate Dynamics. Eur. Phys. J. Spec. Top. 2009, 174, 157–179. [Google Scholar] [CrossRef]
- Newman, M.E.J. Analysis of Weighted Networks. Phys. Rev. E 2004, 70, 056131. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.E.J.; Girvan, M. Finding and Evaluating Community Structure in Networks. Phys. Rev. E 2004, 69, 026113. [Google Scholar] [CrossRef] [PubMed]
- Mpillios, M.; Vasiliades, L. Regional Frequency Estimates of Annual Rainfall Maxima and Sampling Uncertainty Quantification. In Proceedings of the 8th International Electronic Conference on Water Sciences, Basel, Switzerland, 14–16 October 2024. [Google Scholar]
- Loukas, A.; Mylopoulos, N.; Vasiliades, L. A Modeling System for the Evaluation of Water Resources Management Strategies in Thessaly, Greece. Water Resour Manag. 2007, 21, 1673–1702. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Landwehr, J.M.; Matalas, N.C.; Wallis, J.R. Probability Weighted Moments: Definition and Relation to Parameters of Several Distributions Expressable in Inverse Form. Water Resour. Res. 1979, 15, 1049–1054. [Google Scholar] [CrossRef]
- Hosking, J.R.M. L-Moments: Analysis and Estimation of Distributions Using Linear Combinations of Order Statistics. J. R. Stat. Soc. Ser. B (Methodol.) 1990, 52, 105–124. [Google Scholar] [CrossRef]
- Bayazit, M.; Önöz, B. Robustness Analysis of Regional Flood Frequency Models: A Case Study. In Coping with Floods; Rossi, G., Harmancioğlu, N., Yevjevich, V., Eds.; Springer: Dordrecht, The Netherlands, 1994; pp. 243–255. ISBN 978-94-011-1098-3. [Google Scholar]
- Saf, B. Regional Flood Frequency Analysis Using L-Moments for the West Mediterranean Region of Turkey. Water Resour Manag. 2009, 23, 531–551. [Google Scholar] [CrossRef]
- Zafirakou-Koulouris, A.; Vogel, R.M.; Craig, S.M.; Habermeier, J. L Moment Diagrams for Censored Observations. Water Resour. Res. 1998, 34, 1241–1249. [Google Scholar] [CrossRef]
- Vogel, R.M.; Fennessey, N.M. L Moment Diagrams Should Replace Product Moment Diagrams. Water Resour. Res. 1993, 29, 1745–1752. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Principal Component Analysis; Springer Science & Business Media: New York, NY, USA, 2002; ISBN 978-0-387-95442-4. [Google Scholar]
- Abdi, H.; Williams, L.J. Principal Component Analysis. WIREs Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Shlens, J. A Tutorial on Principal Component Analysis 2014. arXiv 2024, arXiv:1404.1100. [Google Scholar]
- Ikotun, A.M.; Ezugwu, A.E.; Abualigah, L.; Abuhaija, B.; Heming, J. K-Means Clustering Algorithms: A Comprehensive Review, Variants Analysis, and Advances in the Era of Big Data. Inf. Sci. 2023, 622, 178–210. [Google Scholar] [CrossRef]
- Steinley, D. K-Means Clustering: A Half-Century Synthesis. Br. J. Math. Stat. Psychol. 2006, 59, 1–34. [Google Scholar] [CrossRef]
- Sahu, R.T.; Verma, M.K.; Ahmad, I. Regional Frequency Analysis Using L-Moment Methodology—A Review. In Proceedings of the Recent Trends in Civil Engineering; Pathak, K.K., Bandara, J.M.S.J., Agrawal, R., Eds.; Springer: Singapore, 2021; pp. 811–832. [Google Scholar]
- Na, S.; Xumin, L.; Yong, G. Research on K-Means Clustering Algorithm: An Improved k-Means Clustering Algorithm. In Proceedings of the 2010 Third International Symposium on Intelligent Information Technology and Security Informatics, Jinggangshan, China, 2–4 April 2010; pp. 63–67. [Google Scholar]
- Wang, J.; Su, X. An Improved K-Means Clustering Algorithm. In Proceedings of the 2011 IEEE 3rd International Conference on Communication Software and Networks, Xi’an, China, 27–29 May 2011; pp. 44–46. [Google Scholar]
- Bock, H.-H. Clustering Methods: A History of k-Means Algorithms. In Selected Contributions in Data Analysis and Classification; Brito, P., Cucumel, G., Bertrand, P., de Carvalho, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 161–172. ISBN 978-3-540-73560-1. [Google Scholar]
- Newman, M.E.J. The Structure and Function of Complex Networks. SIAM Rev. 2003, 45, 167–256. [Google Scholar] [CrossRef]
- Fortunato, S. Community Detection in Graphs. Phys. Rep. 2010, 486, 75–174. [Google Scholar] [CrossRef]
- Javed, M.A.; Younis, M.S.; Latif, S.; Qadir, J.; Baig, A. Community Detection in Networks: A Multidisciplinary Review. J. Netw. Comput. Appl. 2018, 108, 87–111. [Google Scholar] [CrossRef]
- Clauset, A.; Newman, M.E.J.; Moore, C. Finding Community Structure in Very Large Networks. Phys. Rev. E 2004, 70, 066111. [Google Scholar] [CrossRef]
- Newman, M.E.J. Modularity and Community Structure in Networks. Proc. Natl. Acad. Sci. USA 2006, 103, 8577–8582. [Google Scholar] [CrossRef] [PubMed]
- Girvan, M.; Newman, M.E.J. Community Structure in Social and Biological Networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef]
- Brandes, U.; Delling, D.; Gaertler, M.; Gorke, R.; Hoefer, M.; Nikoloski, Z.; Wagner, D. On Modularity Clustering. IEEE Trans. Knowl. Data Eng. 2008, 20, 172–188. [Google Scholar] [CrossRef]
- Viglione, A.; Laio, F.; Claps, P. A Comparison of Homogeneity Tests for Regional Frequency Analysis. Water Resour. Res. 2007, 43, W03428. [Google Scholar] [CrossRef]
- Nguyen, T.-H.; El Outayek, S.; Lim, S.H.; Nguyen, V.-T.-V. A Systematic Approach to Selecting the Best Probability Models for Annual Maximum Rainfalls—A Case Study Using Data in Ontario (Canada). J. Hydrol. 2017, 553, 49–58. [Google Scholar] [CrossRef]
- Hansen, C.R. Comparison of Regional and At-Site Frequency Analysis Methods for the Estimation of Southern Alberta Extreme Rainfall. Can. Water Resour. J./Rev. Can. Ressour. Hydr. 2015, 40, 325–342. [Google Scholar] [CrossRef]
- Blanchet, J.; Ceresetti, D.; Molinié, G.; Creutin, J.-D. A Regional GEV Scale-Invariant Framework for Intensity–Duration–Frequency Analysis. J. Hydrol. 2016, 540, 82–95. [Google Scholar] [CrossRef]
- Mascaro, G. Comparison of Local, Regional, and Scaling Models for Rainfall Intensity–Duration–Frequency Analysis. J. Appl. Meteorol. Climatol. 2020, 59, 1519–1536. [Google Scholar] [CrossRef] [PubMed]
- Yue, S.; Hashino, M. Probability Distribution of Annual, Seasonal and Monthly Precipitation in Japan. Hydrol. Sci. J. 2007, 52, 863–877. [Google Scholar] [CrossRef]
- Das, S. An Assessment of Using Subsampling Method in Selection of a Flood Frequency Distribution. Stoch. Environ. Res. Risk Assess. 2017, 31, 2033–2045. [Google Scholar] [CrossRef]
- Das, S. Assessing the Regional Concept with Sub-Sampling Approach to Identify Probability Distribution for at-Site Hydrological Frequency Analysis. Water Resour. Manag. 2020, 34, 803–817. [Google Scholar] [CrossRef]
- Laio, F. Cramer–von Mises and Anderson-Darling Goodness of Fit Tests for Extreme Value Distributions with Unknown Parameters. Water Resour. Res. 2004, 40, W09308. [Google Scholar] [CrossRef]
- Kyselý, J. A Cautionary Note on the Use of Nonparametric Bootstrap for Estimating Uncertainties in Extreme-Value Models. J. Appl. Meteorol. Climatol. 2008, 47, 3236–3251. [Google Scholar] [CrossRef]
- Gabor, C.; Tamas, N. The Igraph Software Package for Complex Network Research. Inter J. Complex Syst. 2006, 1695, 1–9. [Google Scholar]
- Viglione, A. nsRFA: Non-Supervised Regional Frequency Analysis 2024. R Package Version 0.7-17. Available online: https://CRAN.R-project.org/package=nsRFA (accessed on 21 December 2024).
- Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer Science & Business Media: New York, NY, USA, 2013; ISBN 978-1-4471-3675-0. [Google Scholar]
- Schendel, T.; Thongwichian, R. Flood Frequency Analysis: Confidence Interval Estimation by Test Inversion Bootstrapping. Adv. Water Resour. 2015, 83, 1–9. [Google Scholar] [CrossRef]
- Lima, A.O.; Lyra, G.B.; Abreu, M.C.; Oliveira-Júnior, J.F.; Zeri, M.; Cunha-Zeri, G. Extreme Rainfall Events over Rio de Janeiro State, Brazil: Characterization Using Probability Distribution Functions and Clustering Analysis. Atmos. Res. 2021, 247, 105221. [Google Scholar] [CrossRef]
- Wilks, D.S. Chapter 13—Principal Component (EOF) Analysis. In Statistical Methods in the Atmospheric Sciences, 4th ed.; Wilks, D.S., Ed.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 617–668. ISBN 978-0-12-815823-4. [Google Scholar]
- Ngongondo, C.S.; Xu, C.-Y.; Tallaksen, L.M.; Alemaw, B.; Chirwa, T. Regional Frequency Analysis of Rainfall Extremes in Southern Malawi Using the Index Rainfall and L-Moments Approaches. Stoch. Environ. Res. Risk Assess. 2011, 25, 939–955. [Google Scholar] [CrossRef]
- Jones, M.R.; Blenkinsop, S.; Fowler, H.J.; Kilsby, C.G. Objective Classification of Extreme Rainfall Regions for the UK and Updated Estimates of Trends in Regional Extreme Rainfall. Int. J. Climatol. 2014, 34, 751–765. [Google Scholar] [CrossRef]
- Blenkinsop, S.; Fowler, H.J.; Dubus, I.G.; Nolan, B.T.; Hollis, J.M. Developing Climatic Scenarios for Pesticide Fate Modelling in Europe. Environ. Pollut. 2008, 154, 219–231. [Google Scholar] [CrossRef]
- Ahmed, A.; Khan, Z.; Rahman, A. Searching for Homogeneous Regions in Regional Flood Frequency Analysis for Southeast Australia. J. Hydrol. Reg. Stud. 2024, 53, 101782. [Google Scholar] [CrossRef]
- Pansera, W.; Gomes, B.; Boas, M.; Mello, E. Clustering Rainfall Stations Aiming Regional Frequency Analysis. J. Food Agric. Environ. 2013, 11, 877–885. [Google Scholar]
- Jingyi, Z.; Hall, M.J. Regional Flood Frequency Analysis for the Gan-Ming River Basin in China. J. Hydrol. 2004, 296, 98–117. [Google Scholar] [CrossRef]
- Chang, C.-H.; Rahmad, R.; Wu, S.-J.; Hsu, C.-T. Spatial Frequency Analysis by Adopting Regional Analysis with Radar Rainfall in Taiwan. Water 2022, 14, 2710. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Iliopoulou, T.; Koukouvinos, A.; Malamos, N.; Mamassis, N.; Dimitriadis, P.; Tepetidis, N.; Markantonis, D. Technical Report, Production of Maps with Updated Parameters of the Ombrian Curves at Country Level (Impementation of the EU Directive 2007/60/EC in Greece); Department of Water Resources and Environmental Engineering, National Technical University of Athens: Athens, Greece, 2023. [Google Scholar]
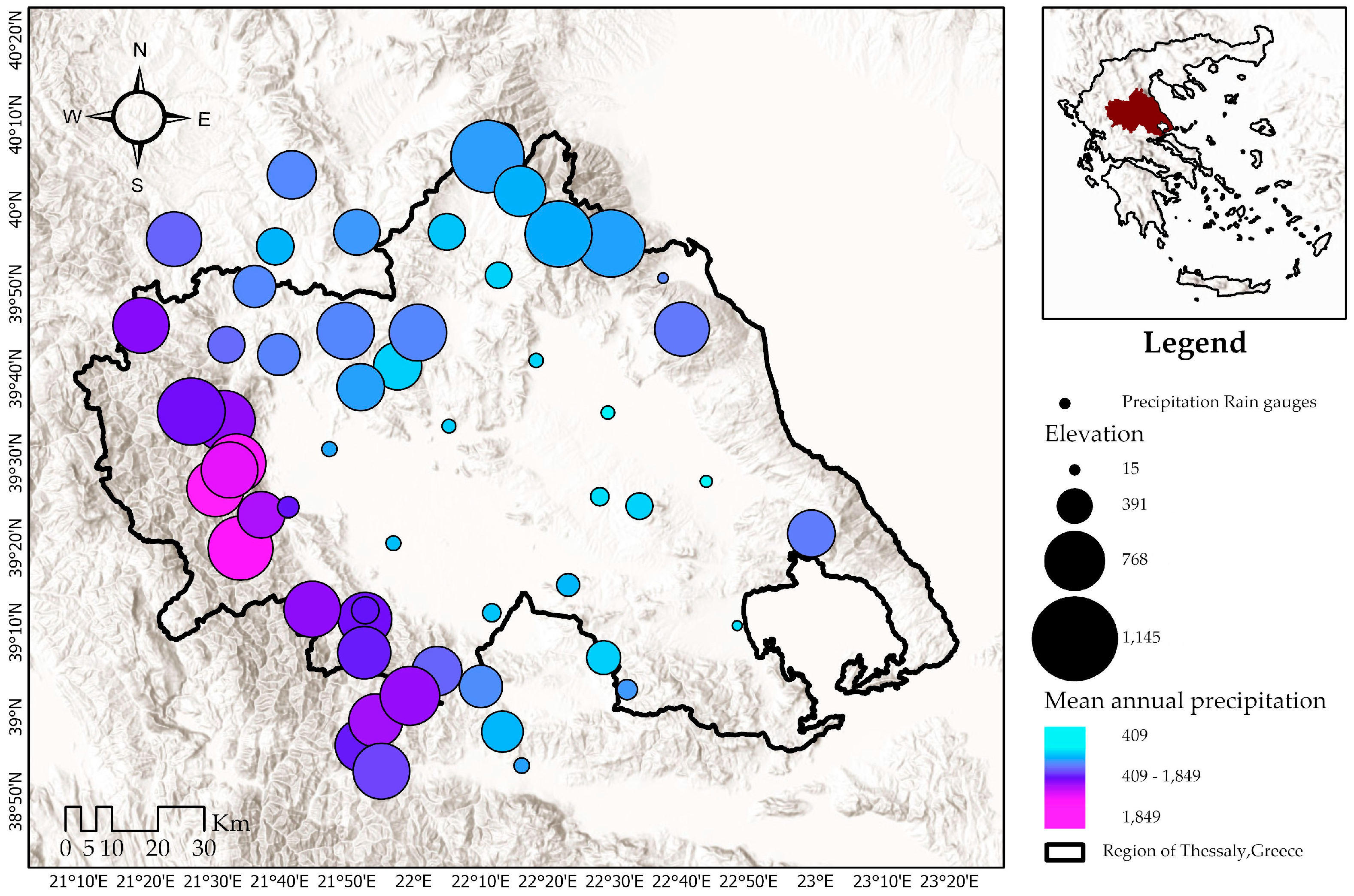
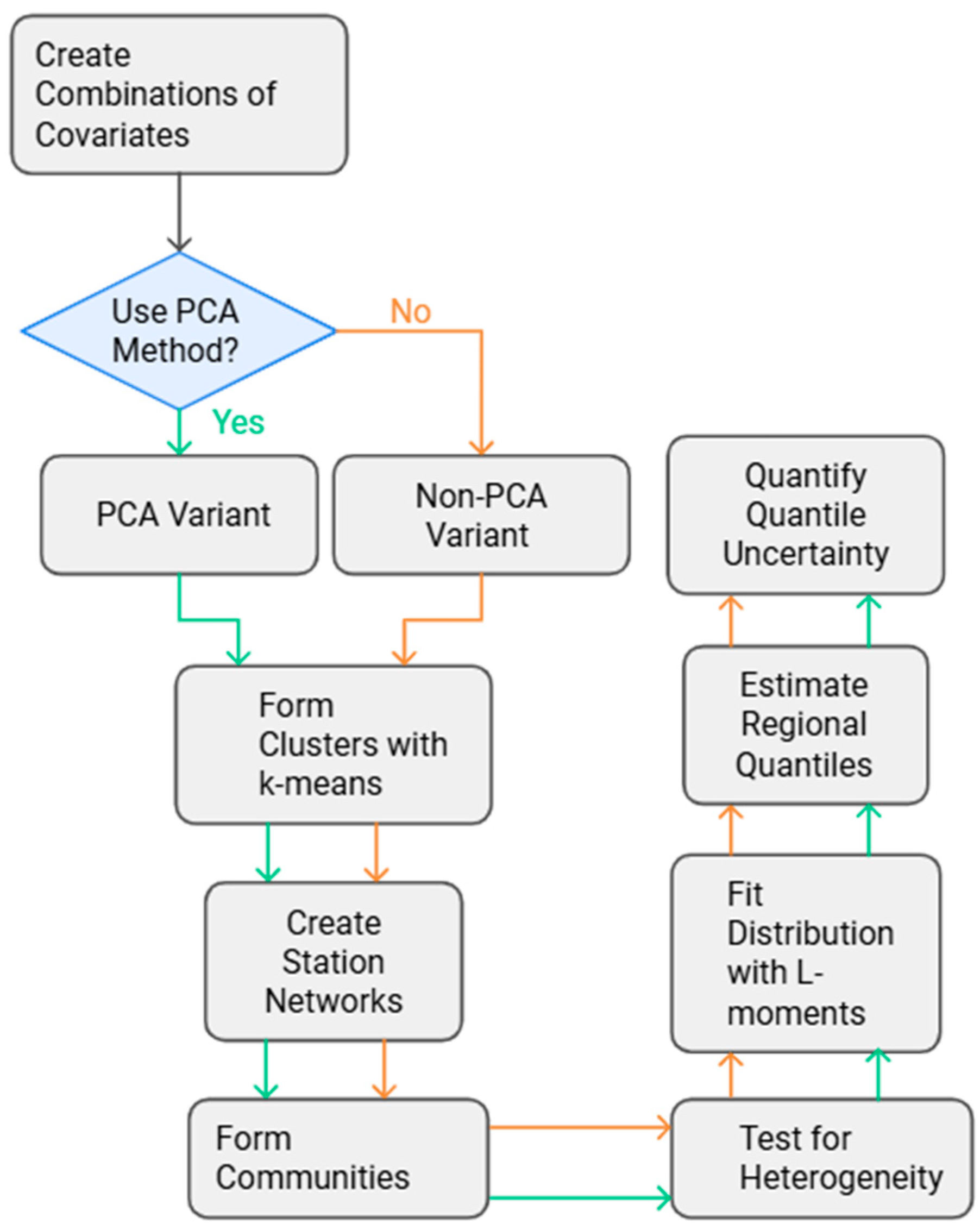


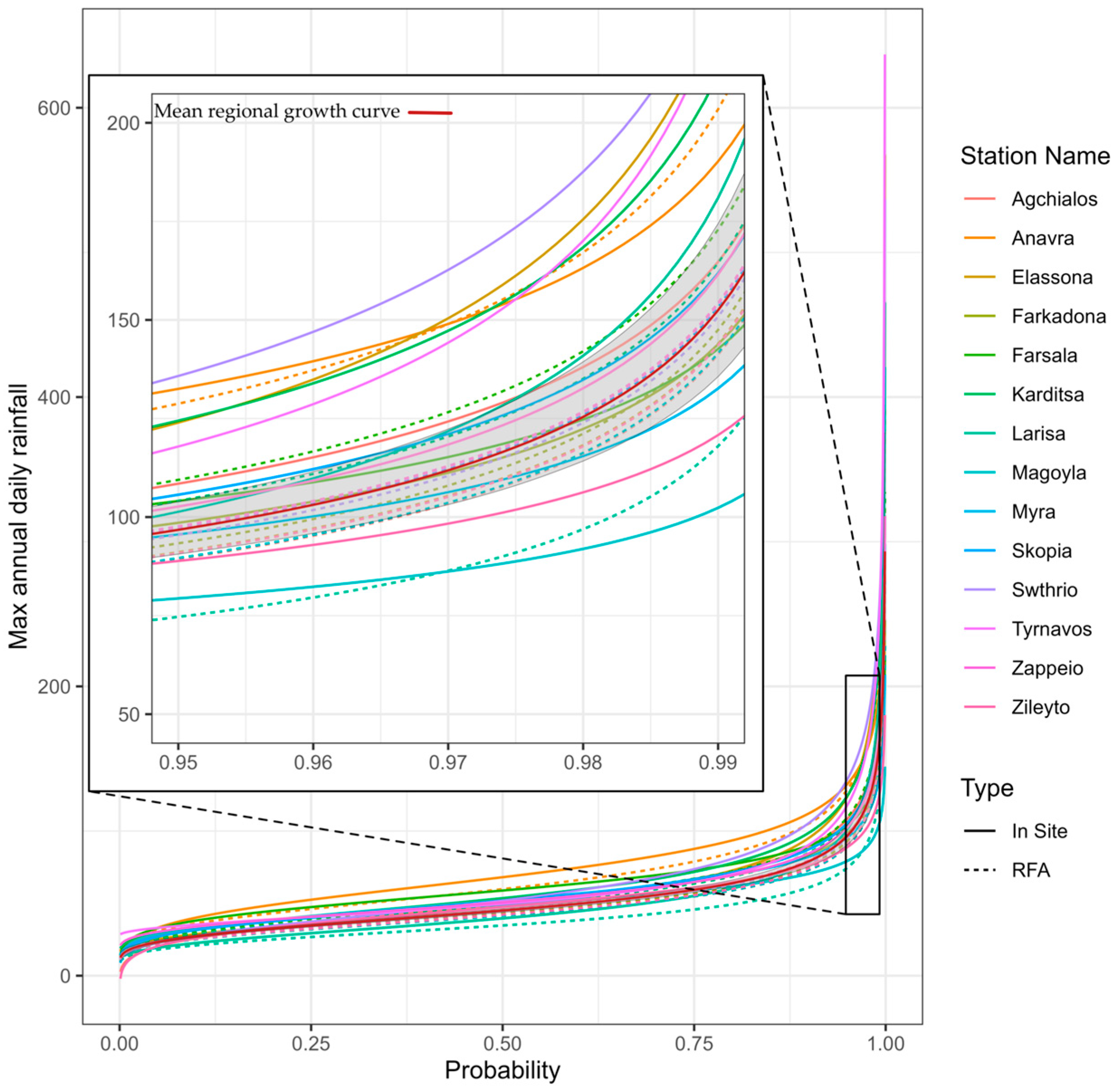
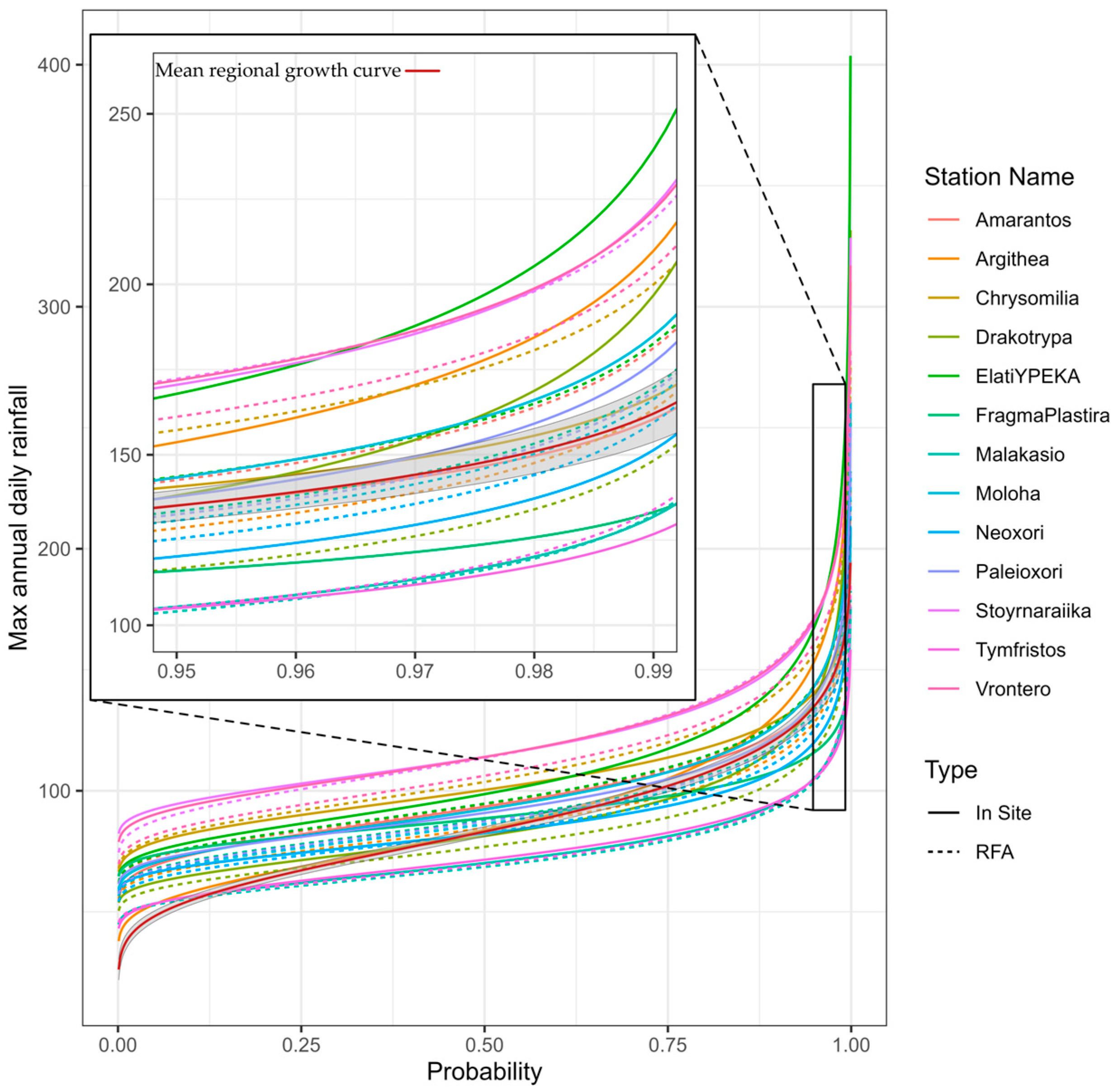




| Min | Max | ||||
|---|---|---|---|---|---|
| Elevation (m) | 15 | 282 | 688 | 850 | 1179 |
| Number of data (years) | 15 | 31 | 44 | 62 | 69 |
| PCA Variant | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| C 1 | C 2 | C 3 | C 4 | C 5 | C 6 | C 7 | C 8 | C 9 | |
| k = 2 | 1.089 | 0.067 | 2.579 | 1.926 | 0.389 | 1.118 | |||
| k = 3 | 0.438 | 2.846 | 2.055 | 1.027 | 0.158 | 0.543 | 0.928 | ||
| k = 4 | 1.621 | −1.047 | 0.318 | 1.748 | −0.757 | 1.037 | 0.158 | 0.615 | 1.106 |
| k = 5 | 0.797 | −0.113 | 2.157 | 0.264 | 0.846 | 0.829 | 0.881 | 1.234 | |
| k = 6 | 2.021 | −0.040 | 6.074 | 1.047 | |||||
| k = 7 | 1.981 | 0.334 | 0.999 | 0.968 | 0.619 | 1.170 | |||
| Non PCA Variant | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| C 1 | C 2 | C 3 | C 4 | C 5 | C 6 | C 7 | C 8 | C 9 | |
| k = 2 | 0.847 | 2.660 | 1.930 | 0.278 | 0.561 | 1.065 | |||
| k = 3 | 0.442 | 3.142 | 1.915 | 0.867 | 0.120 | 0.601 | 6.071 | 1.075 | |
| k = 4 | 1.634 | 3.756 | 1.980 | 1.015 | −0.820 | −0.186 | 0.859 | 0.882 | |
| k = 5 | 0.788 | −0.463 | 1.893 | −0.285 | 0.270 | 0.919 | 0.870 | 1.011 | |
| k = 6 | 0.427 | 2.138 | −0.815 | 0.283 | 1.131 | 1.560 | |||
| k = 7 | 2.071 | 0.241 | 0.870 | 0.920 | 0.699 | 0.897 | |||
| Station Names | |||
|---|---|---|---|
| PCA Communities | Non PCA Communities | ||
| C 1 (8) | Anavra, Agchialos, Makryraxh, Zileyto, Farsala, Magoyla, Skopia, Trilofo | C 1 (14) | Anavra, Agchialos, Zileyto, Farsala, Magoyla, Skopia, Myra, Farkadona, Elassona, Larisa, Tyrnavos, Karditsa, Swthrio, Zappeio |
| C 2 (8) | Myra, Farkadona, Elassona, Larisa, Tyrnavos, Karditsa, Swthrio, Zappeio | ||
| C 3 (7) | ElatiDEH, Agiofyllo, KipourgioKoniskos, Megalh_kerasia, Meteora, Pyloroi | C 2 (7) | ElatiDEH, Agiofyllo, Kipourgio, Koniskos, Megalh_kerasia, Meteora, Pyloroi |
| C 4 (13) | Drakotrypa, Amarantos, FragmaPlastira, Neoxori, Tymfristos, Argithea, ElatiYPEKA, Paleioxori, Chrysomilia, Moloha, Stoyrnaraiika, Vrontero, Malakasio | C 3 (13) | Drakotrypa, Amarantos, FragmaPlastira, Neoxori, Tymfristos, Argithea, ElatiYPEKA, Paleioxori, Chrysomilia, Moloha, Stoyrnaraiika, Vrontero, Malakasio |
| C 5 (2) | LivadiYPGE, LivadiYPEKA | C 4 (2) | LivadiYPGE, LivadiYPEKA |
| C 6 (2) | Redina, Pitsiota | C 5 (2) | Trilofo, Makryraxh |
| C 6 (2) | Redina, Pitsiota | ||
| AD Test | Normal | Log-Normal | Generalized Extreme Value | P3 | Generalized Pareto | GLO | |
|---|---|---|---|---|---|---|---|
| C 1 | A2 | 29.04 | 1.58 | 0.48 | 25.86 | 44.86 | 0.14 |
| P(A2) | 1 | 0.98 | 0.86 | 1 | 1 | 0.03 | |
| C 2 | A2 | 3.08 | 0.23 | 0.22 | 0.26 | 12.19 | 0.59 |
| P(A2) | 1 | 0.41 | 0.38 | 0.37 | 1 | 0.95 | |
| C 3 | A2 | 3.88 | 0.68 | 0.74 | 0.88 | 21.36 | 0.51 |
| P(A2) | 1 | 0.98 | 0.99 | 0.99 | 1 | 0.91 |
| Xi | Alpha | Kappa | |
|---|---|---|---|
| C 1-GLO | 0.882 | 0.216 | −0.296 |
| C 2-GEV | 0.845 | 0.286 | 0.040 |
| C 3-GLO | 0.967 | 0.168 | −0.115 |
| Communities | InSite 5–95% CI Range | RFA 5–95% CI Range | Absolute Error of Estimation | |
|---|---|---|---|---|
| Mean | 122.46 | 57.14 | 32.17 | |
| C 1 | Max | 223.98 | 76.43 | 75.03 |
| Min | 39.34 | 44.42 | 2.00 | |
| Mean | 45.63 | 19.37 | 15.84 | |
| C 2 | Max | 87.83 | 23.70 | 56.39 |
| Min | 16.96 | 12.60 | 0.96 | |
| Mean | 73.59 | 25.41 | 21.87 | |
| C 3 | Max | 138.97 | 31.84 | 50.61 |
| Min | 30.23 | 19.98 | 0.28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Billios, M.; Vasiliades, L. A Network-Based Clustering Method to Ensure Homogeneity in Regional Frequency Analysis of Extreme Rainfall. Water 2025, 17, 38. https://doi.org/10.3390/w17010038
Billios M, Vasiliades L. A Network-Based Clustering Method to Ensure Homogeneity in Regional Frequency Analysis of Extreme Rainfall. Water. 2025; 17(1):38. https://doi.org/10.3390/w17010038
Chicago/Turabian StyleBillios, Marios, and Lampros Vasiliades. 2025. "A Network-Based Clustering Method to Ensure Homogeneity in Regional Frequency Analysis of Extreme Rainfall" Water 17, no. 1: 38. https://doi.org/10.3390/w17010038
APA StyleBillios, M., & Vasiliades, L. (2025). A Network-Based Clustering Method to Ensure Homogeneity in Regional Frequency Analysis of Extreme Rainfall. Water, 17(1), 38. https://doi.org/10.3390/w17010038







