Abstract
As critical equipment in nuclear power systems, the stability of circulating water pumps (CWP) directly impacts the efficiency of power plants. To investigate the impact mechanisms of the unsteady flow characteristics and flow-induced forces on the rotation system, numerical simulation methods were employed to calculate the internal flow of a volute mixed-flow CWP under different flow rates (0.8Qd, 1.0Qd, 1.2Qd). The flow field results indicate that, under the part-load condition, the flow within the volute is chaotic with high energy losses, while under the over-load condition, there is a significant velocity gradient within the impeller, leading to relatively severe flow losses. Additionally, the rotor–stator interface is a major factor in flow-induced pulsations, and the asymmetric pressure distribution within the volute results in radial force imbalance. The finite element method (FEM) results indicate that the position of maximum stress on the pump shaft is closely related to the ratio of radial and axial force. Increasing the flow rate appropriately has been noted to be advantageous in reducing flow-induced forces and their amplitude, consequently diminishing the forces on the rotation system and improving the long-term operational stability of the CWP.
1. Introduction
Climate change resulting from global warming is one of the most urgent and critical challenges facing the world today, with extreme weather events posing serious impacts on global ecosystems and human societies. To address this challenge, countries around the world are promoting the development of clean energy and reducing their reliance on fossil fuels [1]. Nuclear energy, as a clean and reliable source of energy, holds significant potential in providing essential baseload power, hence attracting considerable attention from decision-makers [2]. Nowadays, nuclear energy technology is developing rapidly, and nuclear electricity accounts for 11% of the global electricity generation [3]. The Circulating Water Pump (CWP) is an important facility in the cooling system of nuclear power plants, which is used to pump seawater into a condenser for cooling steam [4,5]. Unstable flow can exacerbate pump vibration and flow-induced force pulsation, while excessive loads can lead to damage in the rotor system, thereby impacting the long-term stable operation of the CWP and reducing the efficiency of the power generation system. Hence, maintaining the stable operation of the CWP is crucial for nuclear power plants.
In nuclear power plants, CWPs generally use mixed-flow pumps, which are characterized by high flow rates and high efficiency. There has been extensive research on the hydraulic design and optimization of these pumps [6,7]. Researchers have investigated and outlined the impact mechanisms of different parameters, such as impeller meridional shape and blade thickness, on the performance and internal flow characteristics of mixed-flow pumps [8,9,10]. Researchers have also utilized methods like the design of experiments and intelligent algorithms (such as the response surface method, genetic algorithms, and artificial intelligence algorithms) to optimize the pump performance [11,12].
However, the long-term stable operation of CWPs is also affected by factors such as pressure pulsation and transient flow-induced force. Researchers have conducted detailed studies on pressure pulsations within mixed-flow pumps, revealing the influencing mechanisms of variables, such as gas volume fraction [13], flow rate [14,15], and cavitation [16], on pressure pulsations. Researchers have also focused on studying the flow-induced force of mixed-flow pumps. Van Esch [17] studied the performance and flow-induced forces of the mixed-flow pump under a non-uniform suction flow based on experiment results. He found that slight non-uniform flows have a minor impact on the head and axial force. Hao et al. [18] investigated the radial forces of mixed-flow pumps with different tip clearances, finding that unsymmetrical tip clearances significantly enhance radial force fluctuations. Li et al. [19] analyzed the flow-induced forces of mixed-flow pumps using numerical simulation methods and discussed the influence of the blade rotation angle on the radial and axial force.
Excessive flow-induced forces and severe fluctuations can lead to excessive loads on the shaft system, resulting in consequences such as bearing damage. Therefore, research that combines the study of unstable flow, flow-induced forces, and rotation system structures is of significant importance for the stable operation of CWPs. However, research in this field is not yet comprehensive.
In this paper, the Reynolds-averaged Navier–Stokes (RANS) method is employed to simulate the internal flow and flow-induced force of a CWP at different flow rates (0.8Qd, 1.0Qd, 1.2Qd). Based on the unsteady flow, the Finite Element Method (FEM) is employed to calculate the flow-induced structural response of the rotation system. Then, the transient flow-induced forces and unstable flow inside the pump at different flow rates are analyzed and the stress distribution of the rotation system under transient loads is studied. Finally, the paper summarizes the impact of an unstable flow on the rotation system.
2. Numerical Simulation Methods
2.1. Governing Equation
The Reynolds-Averaged Navier–Stokes (RANS) method is one of the most widely used methods in numerical simulations of pumps currently [20]. The fundamental principle of the RANS method involves the temporal averaging of physical quantities within the flow field, followed by the solution of the resulting time-averaged governing equations. The Shear Stress Transport (SST) turbulence model, a hybrid model that merges the k-w and k-ε models, stands out for its ability to predict a broad spectrum of flows accurately. As a preferred two-equation model in pump simulations, it provides superior predictive capabilities [20,21,22,23]. Hence, the SST turbulence model is employed for numerical simulations. The governing equations for the SST turbulence model are as follows [24]:
2.2. Research Model
The research model of this paper is a volute mixed-flow CWP, with the following main performance parameters: the rated flow rate (Qd) is 110,880 m3/h, the head (Hd) is 16 m, and the speed (n) is 137 r/min. The flow domain used in this paper includes the inlet pipe, impeller, volute, and outlet pipe, with the lengths of the inlet and outlet pipes being 7 times their diameters, as shown in Figure 1.
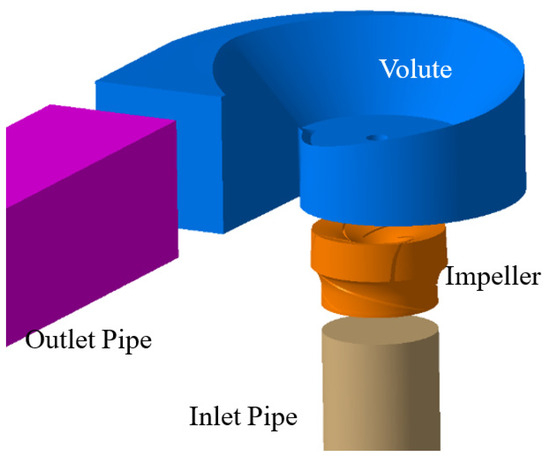
Figure 1.
The research model.
2.3. Numerical Simulation
In this paper, the SST turbulence model is chosen for the simulation, with a convergence criterion of Root Mean Square (RMS) set to 10−5. The impeller domain is set as rotating, while the other domains are set as stationary. The frozen rotor mode is used on the rotor–stator interfaces. The inlet boundary is set as the total pressure inlet (1 atm), and the outlet boundary is set as the mass flow outlet. All wall conditions are set as no-slip walls, with a roughness of 0.02 mm applied to the impeller walls. The unsteady settings are as follows: the time step is 0.002433 s, meaning a calculation is performed every 2° of impeller rotation, and the total simulation time is 4.379562 s, covering ten revolutions.
To ensure computational accuracy, grid independence validation is required [25]. The performance of the CWP with different grid numbers has been calculated, as shown in Table 1. From the table, it can be observed that as the number of grids increases, the difference in head between the cases decreases significantly. Considering both computational accuracy and efficiency, the mesh with 7 million grids is ultimately used for further simulations. Figure 2 shows the mesh used for the impeller and volute.

Table 1.
The mesh independence validation.

Figure 2.
The mesh of the research model (a) Impeller; (b) Volute.
2.4. Experimental Verification
Given the substantial size of the CWP, a scaled-down model pump was used for experimentation, and then the hydraulic performance of the full-scale pump was calculated using the pump affinity law. The pump affinity law has been validated as an effective approach for estimating pump performance [26,27]. The scaled-down model is only used for performance estimation, not for flow analysis. The experiments were conducted on a closed test rig, with the following experimental precision: flow rates (1%), head (1%), torque (1%), and rotational speed (0.1%). Figure 3 shows the experimental results and the numerical simulation results. It can be observed from the figure that the head and efficiency from the numerical simulation are slightly higher than the experimental results. However, the deviation between the numerical simulation and the experimental results is within 5%, and the performance curves show a similar trend. Therefore, the numerical simulation method is reliable.
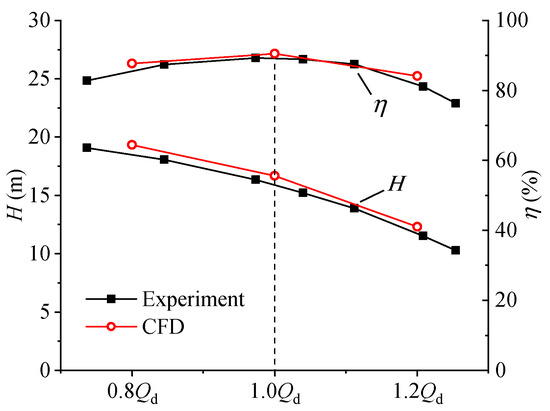
Figure 3.
The performance curves.
3. Internal Flow Analysis
3.1. Unsteady Flow
Entropy production theory is a valuable method for identifying and quantifying energy losses. By analyzing entropy production, this theory provides insights into the amount and location of energy dissipation, making it a powerful tool for understanding energy losses in complex systems such as pumps [28]. The entropy production theory, as an analytical method that visualizes energy loss, is an effective tool for analyzing hydraulic losses induced by the unsteady flow inside the pump. Many studies have applied it to analyze the flow inside pumps for understanding the energy dissipation mechanisms occurring within the pump [29,30]. Therefore, we employed the Entropy production theory to analyze and locate the energy losses within the CWP. Subsequently, a detailed analysis of energy loss mechanisms was conducted, based on entropy production distribution, in conjunction with velocity and pressure distributions.
The equation for entropy production is as follows:
where μ represents dynamic viscosity, T is temperature, u, v, and w is the velocity components, and represents the wall shear stress.
Figure 4 illustrates the entropy production of the impeller and volute of the CWP under different flow rates. It can be observed from the figure that the total entropy production of the CWP is the lowest at 1.0Qd, with similar entropy generation at 0.8Qd and 1.2Qd. Upon comparing the entropy generation of different components, it is evident that as the flow rate increases, the entropy production of the impeller steadily rises, while the proportion of entropy production within the volute gradually decreases.
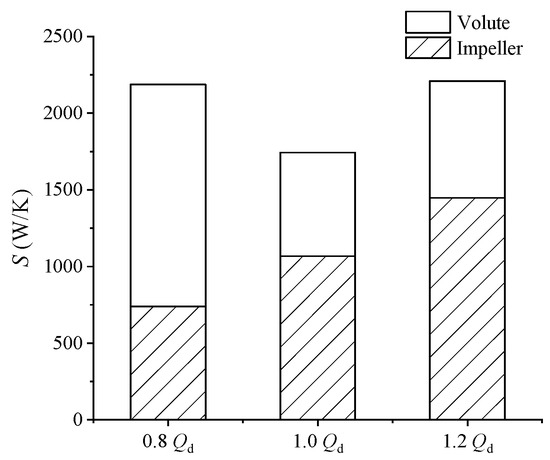
Figure 4.
Distribution of entropy production in the CWP.
For further analysis of energy loss distribution within the CWP, the entropy production rate (EPR) at the mid-section of the pump is illustrated in Figure 5. It exhibits the high-energy loss region within the CWP under different conditions. From the figure, it is evident that energy losses in the CWP primarily occur around the impeller blades and the tongue of the volute. Rotor–stator interaction and high-velocity gradients have resulted in significant energy losses at the impeller and volute tongue.
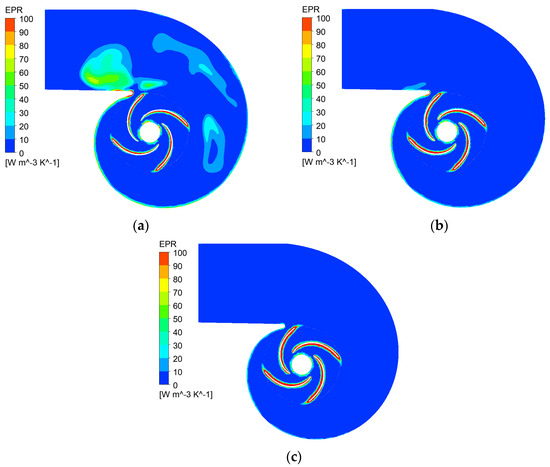
Figure 5.
Distribution of EPR at the mid−section of the CWP. (a) 0.8 Qd; (b) 1.0 Qd; (c) 1.2 Qd.
It is observed that at 0.8Qd, a significant region of high EPR appears in the volute, and predominantly concentrates towards the rear of the tongue. As the flow rate increases, the high EPR area inside the volute rapidly decreases. At 1.0Qd, the high EPR area within the volute spiral section essentially disappears, but there is still a certain high-EPR area near the tongue. When the flow rate increases to 1.2Qd, the high EPR area inside the volute essentially disappears. As the flow rate increases, the high EPR region on the suction side of the impeller blades continues to expand.
Figure 6 shows the velocity distribution at the corresponding location within the CWP under different conditions. The unsteady flow characteristics within the CWP, such as vortices and high velocity gradients, are the primary reasons for energy loss. It can be seen from the figure that, at 0.8Qd, the flow in the volute is turbulent and irregular in direction (pointed by arrows), and the cross-sectional shape of the volute does not match the 0.8Qd, leading to significant energy losses. In contrast, at 1.0Qd and 1.2Qd, the flow within the volute casing shows a significant enhancement, with a continuous decrease in the low-speed region area and a decreasing trend in the velocity gradient observed.
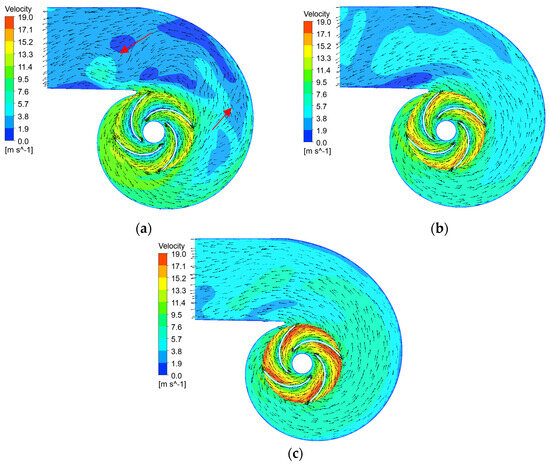
Figure 6.
Distribution of velocity at the mid-section of the CWP. (a) 0.8Qd; (b) 1.0Qd; (c) 1.2Qd.
From the figure, it is evident that as the flow rate increases, the velocity inside the impeller continuously rises, with a noticeable increase in the velocity gradient as well. Additionally, the significant velocity gradient at 1.2Qd causes flow losses around the blades. Meanwhile, a significant flow impact can be observed at the leading edge of the impeller blade, which also contributes to flow losses.
Figure 7 shows the pressure distribution at the mid-section of the CWP. The pressure distribution in the pump remains consistent across different conditions, with pressure increasing continuously from the impeller inlet to the volute outlet. As the flow rate increases, the internal pressure decreases, reflected in the reduced head at higher flow rates. Additionally, the pressure distribution within the impeller is axially symmetric about the pump shaft, while the pressure distribution within the volute is notably unbalanced, a characteristic attributed to the volute’s structural design. The imbalance in pressure in the volute results in a significant and relatively stable biasing force acting on the impeller, leading to an imbalance in radial forces. From the figure, it can be observed that, at 0.8Qd and 1.0Qd, the pressure in the first quadrant is obviously higher and that in the third quadrant, the differential pressure results in a biasing force, as indicated by the arrow. Similarly, at 1.2Qd, the pressure is high in the second quadrant and low in the fourth quadrant, leading to a biasing force.
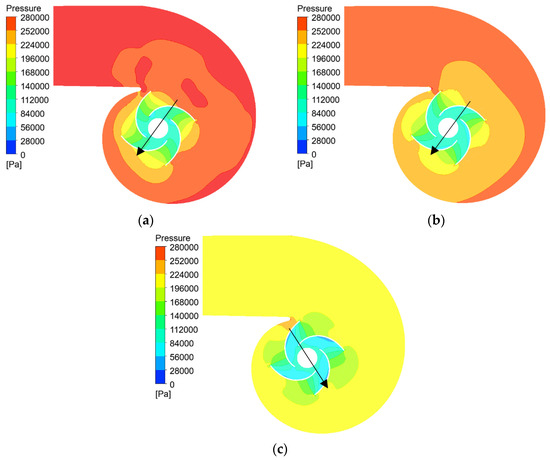
Figure 7.
Pressure distribution at the mid-section of the. (a) 0.8Qd; (b) 1.0Qd; (c) 1.2Qd.
3.2. Unsteady Flow-Induced Forces
During the operation of the pumps, the flow-induced forces on the impeller can be decomposed into radial forces and axial forces. These forces are transmitted directly to the pump shaft through the impeller. Therefore, the magnitude and pulsation of flow-induced forces directly impacts the long-term stable operation and safety of the CWP.
Figure 8 shows the radial force vector distribution of the CWP within one cycle under different conditions. It is apparent from the figure that the radial forces of the pump do not exhibit symmetry about the origin under all conditions. The radial forces predominantly point towards the third and fourth quadrants. By comparing the pressure distribution in the volute (refer to Figure 7) to the direction of the radial forces, it can be observed that the imbalance in radial forces is attributed to the differential pressure in the volute. The unequal pressures acting on both sides of the impeller lead to the fluid pushing the impeller towards one side, resulting in an unbalanced axial force. The imbalance in radial force will result in uneven loading on the bearing, eventually leading to premature bearing failure.
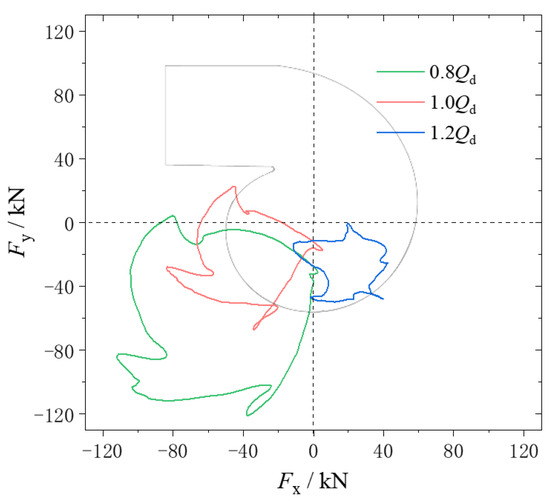
Figure 8.
The radial force vector distribution of the CWP.
From Figure 8, it can be obvious that there is a significant variation in the radial force of the pump under different conditions, with the radial forces on the impeller notably decreasing as the flow rate increases. Additionally, the direction of radial force varies across different flow rates.
Figure 9 shows the time-domain graph of the radial forces’ X and Y components of the CWP under conditions. From the graph, it is evident that the X and Y components of the radial forces exhibit distinct periodicity. This period is consistent with the impeller rotation period. Notably, there is a discernible disparity in the mean radial forces observed at different flow rates. And, as the flow rate increases from 0.8Qd to 1.2Qd, the peak-to-peak value of the radial force significantly decreases. Furthermore, the variation in flow rate also causes changes in the phase of the X and Y directional forces, consequently influencing the direction of the radial force.
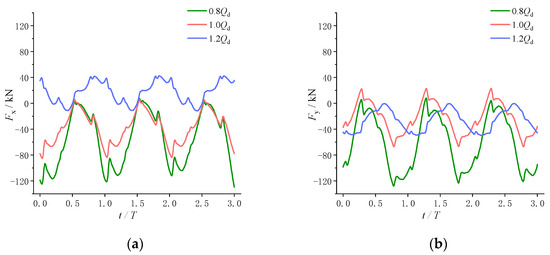
Figure 9.
The radial force time-domain graph of the CWP (a) X direction; (b) Y direction.
To further analyze the fluctuation intensity and frequency characteristics of the radial force, the Fourier transform was performed on the radial force, as shown in Figure 10. It can be observed that the predominant frequency of the radial force is 2.3 Hz (shaft frequency), and it is not influenced by the flow rate. This indicates that the rotor–stator interaction between the impeller and volute is the main cause of radial force fluctuations. The amplitude of the predominant frequency decreases significantly, by more than 60%, as the flow rate increases from 0.8Qd to 1.2Qd. This indicates that the radial force is significantly affected by the flow rate. The results point out that increasing the flow rate appropriately can effectively reduce the magnitude and pulsation intensity of radial forces, improve the loading conditions of the rotation system, and contribute to enhancing the long-term stable operation of the CWP.
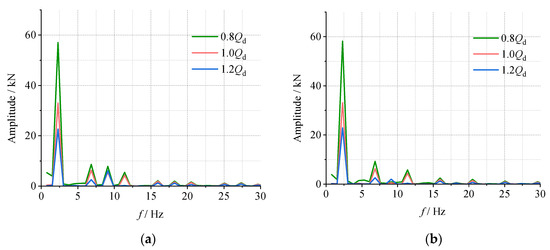
Figure 10.
The radial force frequency-domain graph of the CWP (a) X direction; (b) Y direction.
Figure 11 shows the time-domain and frequency-domain distributions of axial forces of the CWP under the stated conditions. From the time-domain graph, it is evident that the axial force exhibits significant periodic variations over time. The flow rate has a considerable impact on the average value of axial force. As the flow rate increases, the axial force decreases. The axial force at 0.8Qd is more than twice that of 1.2Qd. However, the direction of the axial force remains unaffected by the flow rate, consistently pointing along the shaft towards the impeller inlet. From the frequency-domain graph, it can be observed that the predominant frequency of the axial force is 9.1 Hz (blade passing frequency), and this is not influenced by the flow rate, indicating that the axial force is primarily fluctuating due to the rotor–stator interaction. As the flow rate increases from 0.8Qd to 1.2Qd, the amplitude of the predominant frequency significantly decreases, and there is also a substantial reduction in the amplitude of the low-frequency (0–2 Hz). From the perspective of axial force, increasing the flow rate is also beneficial for the long-term stable operation of the CWP.
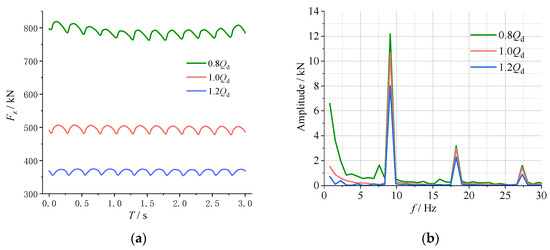
Figure 11.
The time-domain and frequency-domain graph of axial force (a) Time-domain; (b) Frequency-domain.
The comparative analysis of axial force and radial force reveals that, across all conditions, the maximum and average values of the radial force are lower than those of the axial force. However, the fluctuation amplitude of the radial force significantly exceeds that of the axial force. The operational stability of the CWP is mainly influenced by the fluctuation of flow-induced forces, hence weakening the fluctuation of the radial force is a more effective measure to improve the operational stability of the CWP. And, increasing the flow rate can effectively reduce the magnitude of flow-induced forces and pulsations.
4. Structural Response Analysis of Rotation System
The preceding passage provides a detailed analysis of the unsteady flow and the flow-induced forces acting on the CWP. To further investigate the long-term stability of the CWP, a structural analysis of the pump rotation system was carried out using the finite element method (FEM).
4.1. Finite Element Method
The finite element method is a commonly used numerical analysis technique in structural computations. Utilizing the discretization of structures, the establishment of mathematical models, and the solution of equation systems enables the simulation and analysis of mechanical behaviors of various complex structures.
The FEM setup and mesh for the CWP rotation system are shown in Figure 12. Figure A represents the gravitational acceleration (9.8 m/s2), Figure B represents the rotational speed of the rotor system (137 r/min), and Figure C represents the junction of the rotor shaft and the motor, set as a fixed support. Figures D, E, and F correspond to the bearing supports, and Figure G is the flow-induced force acting on the impeller.
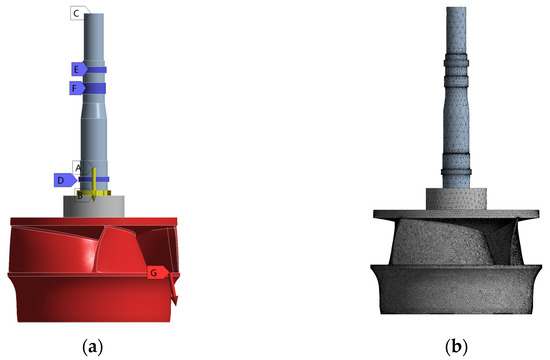
Figure 12.
FEM setting and mesh. (a) Boundary condition; (b) Mesh.
4.2. Modal Analysis
Modal analysis can provide the natural frequencies and mode shapes of the rotation system. Table 2 presents the first four natural frequencies of the rotation system. It can be observed from the table that the critical speed of the rotation system (1379.6 rpm) is significantly higher than the operating speed of the CWP (137 rpm), indicating that the CWP will not experience resonance due to its natural frequencies during operation.

Table 2.
Rotation system natural frequency.
Figure 13 shows the first and second mode shapes of the rotation system. Due to the periodic symmetry of the structure and boundary conditions, modes with similar shapes are displayed. It can be observed from the figure that the first- and second-order modes of the rotor system exhibit transverse bending, but in opposite directions.
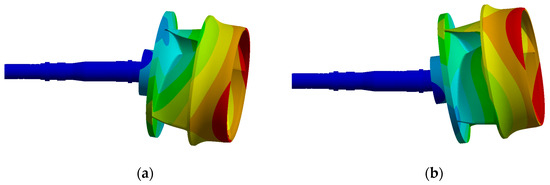
Figure 13.
Rotation system first- and second-order mode shape. (a) First order; (b) Second order.
4.3. Stress Analysis
Figure 14, Figure 15 and Figure 16 show the stress distribution of the impeller and pump shaft of the CWP. It can be observed from Figure 14 that at 0.8Qd, the maximum stress on the pump shaft occurs at the lower guide bearing position, and the stress at the thrust bearing location is relatively high. According to Figure 15 and Figure 16, at 1.0Qd and 1.2Qd, the maximum stress on the pump shaft occurs at the thrust bearing position. According to Figure 9 and Figure 11, it can be observed that as the flow rate increases, the ratio of axial force to radial force continuously increases, indicating that the axial force relative to radial force acting on the rotor system is continuously increasing. This explains the shift of the maximum stress on the rotor shaft from the guide bearing (radially loaded) to the thrust bearing (axially loaded). These results indicate that changes in flow rate affect the location of maximum stress on the pump shaft, which is closely related to the proportion of radial and axial forces in the flow-induced force.
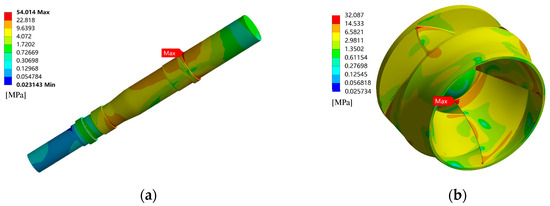
Figure 14.
Stress distribution of the rotation system at 0.8Qd. (a) Pump shaft; (b) Impeller.
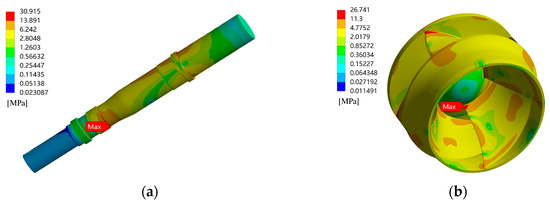
Figure 15.
Stress distribution of the rotation system at 1.0Qd. (a) Pump shaft; (b) Impeller.
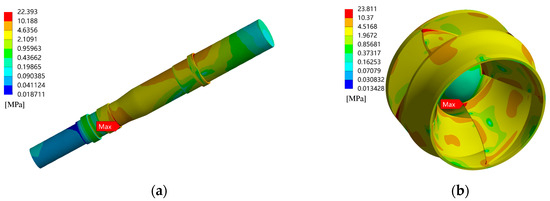
Figure 16.
Stress distribution of the rotation system at 1.2Qd. (a) Pump shaft; (b) Impeller.
It can be observed that, under all conditions, the maximum stress on the impeller is at the root of the blade’s leading edge, and significant stress is at the root of the blade’s trailing edge. The flow rate does not exhibit a significant influence on the location of maximum stress on the impeller.
Further analysis of the maximum stress under all conditions revealed that, as the flow rate increased, the maximum stress on the rotation system decreased accordingly. The maximum stress on the pump shaft decreased by 31.6 MPa (58.4%) and the maximum stress on the impeller decreased by 8.3 MPa (25.8%) as the flow rate increased from 0.8Qd to 1.2Qd, indicating a significant influence of flow rate on the forces acting on the pump rotation system.
5. Conclusions
The unsteady numerical simulation of CWP under different flow rates was conducted using the SST k-w turbulence model. Flow field information, such as entropy production, velocity, and pressure distribution, were analyzed, and the unsteady flow-induced forces under different flow rates were compared. The stress analysis of the CWP rotor system under these conditions was calculated using FEM. The impact mechanism of flow rates on internal flow characteristics of CWP and stress in the CWP rotor system was summarized. The following conclusions were drawn:
- (1)
- The flow rate has a significant impact on the ratio of energy loss of the CPW. Under the part-load condition, the volute has severe energy loss due to the unsteady flow, while under the over-load condition, the impeller suffers from significant flow losses due to large velocity gradients. Additionally, the asymmetrical pressure distribution within the volute is a primary factor in causing radial force imbalance.
- (2)
- The average radial force of the CWP under all conditions is lower than the axial force, but the fluctuation amplitude of the radial force is significantly higher. As the flow rate increases, both the radial and axial forces of the CWP show a decreasing trend. Therefore, increasing the flow rate is an effective approach for enhancing the stability of the CWP.
- (3)
- The FEM results indicate that the main force position on the rotation system is at the bearing and the root of the impeller blade leading edge. Additionally, the maximum stress position of the pump shaft varies at different flow rates, with a close relationship between the ratio of the radial force and the axial force.
Author Contributions
Conceptualization, J.L. and X.Y. (Xueliang Yao); methodology, J.L. and T.W.; software, H.Z.; validation, X.Y. (Xiaowei Yan) and H.L.; formal analysis, X.Y. (Xueliang Yao); investigation, T.W.; resources, J.L. and H.L.; data curation, T.W.; writing—original draft preparation, J.L.; writing—review and editing, X.Y. (Xueliang Yao) and X.Y. (Xiaowei Yan); visualization, T.W.; supervision, H.L. and H.Z.; project administration, H.L.; funding acquisition, J.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 52179084.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
Authors Jinqi Lu, Xueliang Yao, Haixia Zheng, Xiaowei Yan were employed by the company Shanghai Apollo Machinery Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Danish; Ulucak, R.; Erdogan, S. The effect of nuclear energy on the environment in the context of globalization: Consumption vs production-based CO2 emissions. Nucl. Eng. Technol. 2022, 54, 1312–1320. [Google Scholar] [CrossRef]
- Mahmood, N.; Wang, Z.; Zhang, B. The role of nuclear energy in the correction of environmental pollution: Evidence from Pakistan. Nucl. Eng. Technol. 2020, 52, 1327–1333. [Google Scholar] [CrossRef]
- Mathew, M.D. Nuclear energy: A pathway towards mitigation of global warming. Prog. Nucl. Energy 2022, 143, 104080. [Google Scholar] [CrossRef]
- Xia, L.; Liu, D.; Zhou, L.; Wang, F.; Wang, P. Optimal number of circulating water pumps in a nuclear power plant. Nucl. Eng. Des. 2015, 288, 35–41. [Google Scholar] [CrossRef]
- Ma, Y.Y.; Yan, S.; Yang, Z.G.; Qi, G.S.; He, X.Y. Failure analysis on circulating water pump of duplex stainless steel in 1000 MW ultra-supercritical thermal power unit. Eng. Fail. Anal. 2015, 47, 162–177. [Google Scholar] [CrossRef]
- Bing, H.; Tan, L.; Cao, S.; Lu, L. Prediction method of impeller performance and analysis of loss mechanism for mixed-flow pump. Sci. China Technol. Sci. 2012, 55, 1988–1998. [Google Scholar] [CrossRef]
- Wu, X.F.; Tian, X.; Tan, M.G.; Liu, H.L. Multi-Parameter Optimization and Analysis on Performance of a Mixed Flow Pump. J. Appl. Fluid Mech. 2020, 13, 199–209. [Google Scholar] [CrossRef]
- Bing, H.; Cao, S.; Tan, L.; Zhu, B. Effects of meridional flow passage shape on hydraulic performance of mixed-flow pump impellers. Chin. J. Mech. Eng. 2013, 26, 469–475. [Google Scholar] [CrossRef]
- Lei, T.; Zhiyi, Y.; Yun, X.; Yabin, L.; Shuliang, C. Role of blade rotational angle on energy performance and pressure fluctuation of a mixed-flow pump. Proc. Inst. Mech. Eng. Part A J. Power Energy 2017, 231, 227–238. [Google Scholar] [CrossRef]
- Ji, L.; Li, W.; Shi, W.; Tian, F.; Agarwal, R. Effect of blade thickness on rotating stall of mixed-flow pump using entropy generation analysis. Energy 2021, 236, 121381. [Google Scholar] [CrossRef]
- Kim, S.; Kim, Y.I.; Kim, J.H.; Choi, Y.S. Three-objective optimization of a mixed-flow pump impeller for improved suction performance and efficiency. Adv. Mech. Eng. 2019, 11, 1687814019898969. [Google Scholar] [CrossRef]
- Wang, M.; Li, Y.; Yuan, J.; Meng, F.; Appiah, D.; Chen, J. Comprehensive Improvement of Mixed-Flow Pump Impeller Based on Multi-Objective Optimization. Processes 2020, 8, 905. [Google Scholar] [CrossRef]
- Zhang, W.; Yu, Z.Y.; Zhu, B.S. Numerical Study of Pressure Fluctuation in a Gas- Liquid Two-Phase Mixed-Flow Pump. Energies 2017, 10, 634. [Google Scholar] [CrossRef]
- Zheng, Y.; Chen, Y.; Mao, X.; Wang, H.; Shi, W.; Kan, K.; Zhang, Y. Pressure pulsation characteristics and its impact on flow-induced noise in mixed-flow pump. Trans. Chin. Soc. Agric. Eng. 2015, 31, 67–73. [Google Scholar]
- Shen, X.; Zhang, D.; Xu, B.; Zhao, R.; Jin, Y.; Chen, J.; Shi, W. Numerical and experimental investigation of the pressure fluctuation in a mixed-flow pump under low flow conditions. Proc. Inst. Mech. Eng. Part A J. Power Energy 2020, 234, 46–57. [Google Scholar] [CrossRef]
- Zhang, H.; Meng, F.; Zheng, Y.; Li, Y. The Cavitation-Induced Pressure Fluctuations in a Mixed-Flow Pump under Impeller Inflow Distortion. Machines 2021, 9, 326. [Google Scholar] [CrossRef]
- Van Esch, B.P.M. Performance and Radial Loading of a Mixed-Flow Pump Under Non-Uniform Suction Flow. J. Fluids Eng. 2009, 131, 051101. [Google Scholar] [CrossRef]
- Hao, Y.; Tan, L. Symmetrical and unsymmetrical tip clearances on cavitation performance and radial force of a mixed flow pump as turbine at pump mode. Renew. Energy 2018, 127, 368–376. [Google Scholar] [CrossRef]
- Li, Y.; Sun, D.; Meng, F.; Zheng, Y.; Zhong, Y. Study Regarding the Influence of Blade Rotation Angle Deviations on the Hydraulic Pulsation Characteristics of a Mixed-Flow Pump. J. Mar. Sci. Eng. 2023, 11, 530. [Google Scholar] [CrossRef]
- Shah, S.R.; Jain, S.V.; Patel, R.N.; Lakhera, V.J. CFD for Centrifugal Pumps: A Review of the State-of-the-Art. Procedia Eng. 2013, 51, 715–720. [Google Scholar] [CrossRef]
- Shi, L.; Zhang, W.; Jiao, H.; Tang, F.; Wang, L.; Sun, D.; Shi, W. Numerical simulation and experimental study on the comparison of the hydraulic characteristics of an axial-flow pump and a full tubular pump. Renew. Energy 2020, 153, 1455–1464. [Google Scholar] [CrossRef]
- Al-Azawy, M.G.; Turan, A.; Revell, A. Assessment of turbulence models for pulsatile flow inside a heart pump. Comput. Methods Biomech. Biomed. Eng. 2016, 19, 271–285. [Google Scholar] [CrossRef] [PubMed]
- Fu, Q.; Yang, D.; Zhang, J.; Zhu, R.; Shi, W. Study on Unsteady Flow Characteristics of Cooling Water Pump for Nuclear Power Plant Equipment under Low Flow Rate Conditions. Water 2023, 15, 3780. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Xie, C.; Zhang, C.; Fu, T.; Zhang, T.; Feng, A.; Jin, Y. Numerical Analysis and Model Test Verification of Energy and Cavitation Characteristics of Axial Flow Pumps. Water 2022, 14, 2853. [Google Scholar] [CrossRef]
- Chen, K.; Zhang, F.; Liu, R.; Adu-Pokua, K.A.; Yuan, S.; Hong, Q. Experimental and Numerical Evaluation of Affinity Law of Single-Stage and Multistage Side Channel Pumps at Variable Rotating Speeds. J. Fluids Eng. 2023, 145, 101201. [Google Scholar] [CrossRef]
- Chang, L.; Yang, C.; Su, X.; Dai, X.; Xu, Q.; Guo, L. Investigations on affinity law under gas–liquid conditions in multistage radial and mixed-flow multiphase pumps. Int. J. Fluid Eng. 2024, 1, 013503. [Google Scholar] [CrossRef]
- Zhou, L.; Hang, J.; Bai, L.; Krzemianowski, Z.; El-Emam, M.A.; Yasser, E.; Agarwal, R. Application of entropy production theory for energy losses and other investigation in pumps and turbines: A review. Appl. Energy 2022, 318, 119211. [Google Scholar] [CrossRef]
- Wu, D.; Zhu, Z.; Ren, Y.; Gu, Y.; Zhou, P. Influence of blade profile on energy loss of sewage self-priming pump. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 470. [Google Scholar] [CrossRef]
- Hou, H.; Zhang, Y.; Zhou, X.; Zuo, Z.; Chen, H. Optimal hydraulic design of an ultra-low specific speed centrifugal pump based on the local entropy production theory. Proc. Inst. Mech. Eng. Part A J. Power Energy 2019, 233, 715–726. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).