Modeling of Biofoam Destabilization by Biodefoamers in Poultry Slaughterhouse Wastewater Treatment Activated Sludge
Abstract
1. Introduction
Theory: Kinetic Models
2. Materials and Methods
2.1. Batch Culture Experiments to Produce Biodefoamers
2.2. Set-Up for Foaming Potential (Foamability) of the Activated Sludge Samples
2.3. Foam Destabilization Kinetic Parameter Assessments during Poultry Slaughterhouse Treatment
2.4. Regression and Statistical Analysis
3. Results and Discussion
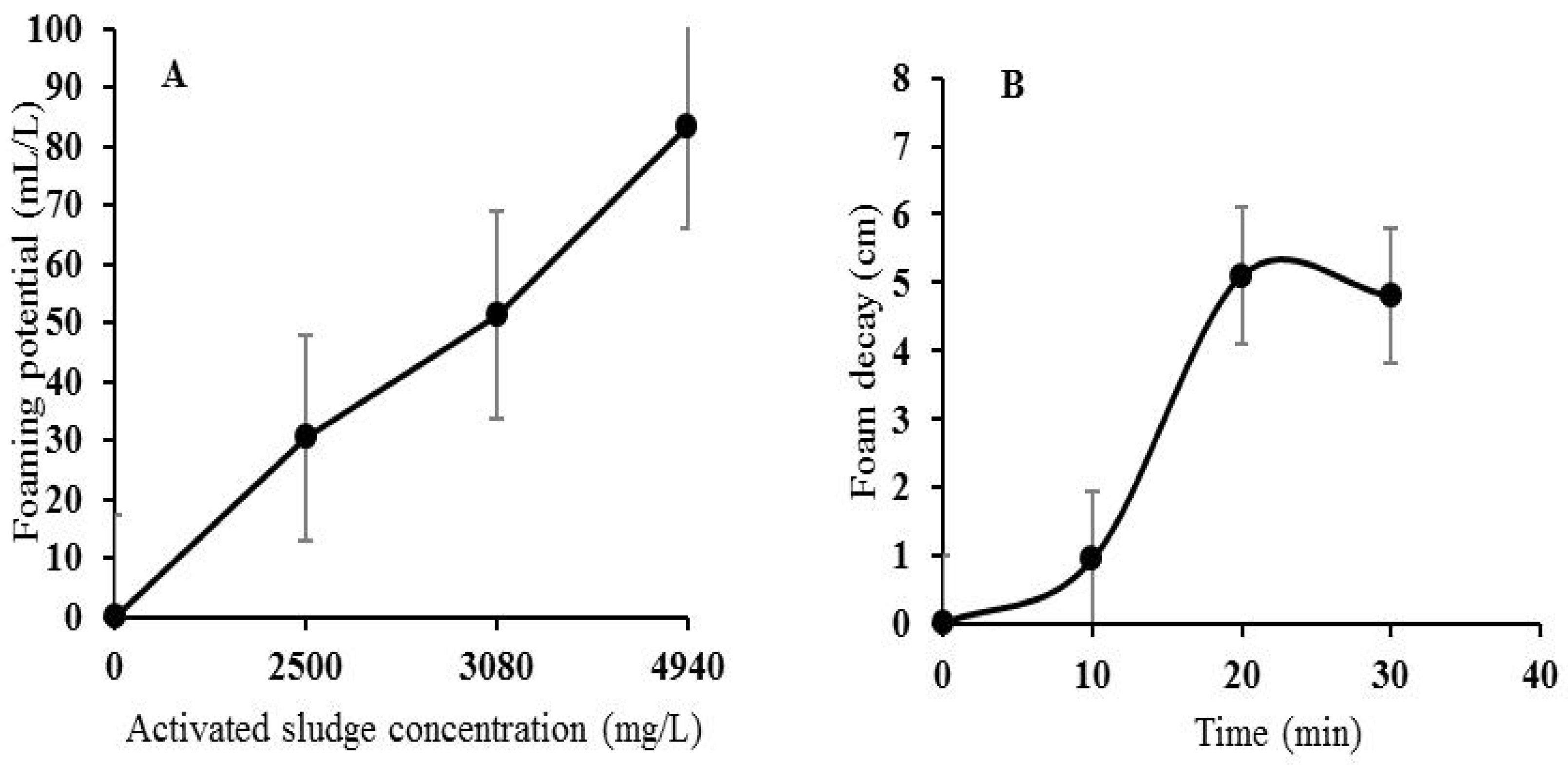
3.1. Foaming Potential (Foamability) of the Activated Sludge
3.2. Foam Drainage (Collapse) Kinetics
3.3. Foam Decay Kinetics
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Garg, A.; Stensel, H.D.; Bucher, B.; Sukapanpotharam, P.; Winkler, M.K.H. Effect of Waste Activated Sludge Pretreatment Methods to Mitigate Gordonia Foaming Potential in Anaerobic Digestion. Water Environ. J. 2020, 35, 381–389. [Google Scholar] [CrossRef]
- Alizad Oghyanous, F.; Etemadi, H.; Yegani, R. Foaming Control and Determination of Biokinetic Coefficients in Membrane Bioreactor System under Various Organic Loading Rate and Sludge Retention Time. Biochem. Eng. J. 2020, 157, 107491. [Google Scholar] [CrossRef]
- Collivignarelli, M.C.; Carnevale Miino, M.; Caccamo, F.M.; Baldi, M. Evaluation of Foaming Potential for Water Treatment: Limits and Developments. Environ. Sci. Pollut. Res. 2020, 27, 27952–27960. [Google Scholar] [CrossRef] [PubMed]
- Trybala, A.; Koursari, N.; Johnson, P.; Arjmandi-Tash, O.; Starov, V. Interaction of Liquid Foams with Porous Substrates. Curr. Opin. Colloid Interface Sci. 2019, 39, 212–219. [Google Scholar] [CrossRef]
- Panizzolo, L.A.; Mussio, L.E.; Añón, M.C. A Kinetic Description for the Destabilization Process of Protein Foams. Int. J. Food Prop. 2012, 15, 60–68. [Google Scholar] [CrossRef]
- Dlangamandla, C.; Basitere, M.; Okeleye, B.I.; Chidi, B.S.; Karabo Obed Ntwampe, S. Biofoam Formation and Defoamation in Global Wastewater Treatment Systems. Water Pract. Technol. 2020, 16, 1–18. [Google Scholar] [CrossRef]
- James, M. Optimisation of Defoamer in a Bio-Reactor, University of the Witwatersrand, Johannesburg. 2017. Available online: http://hdl.handle.net/10539/24961 (accessed on 15 April 2024).
- Kozhukhova, E.; Litvinova, M.; Makarevich, E.; Malaeva, A. Biodegradation of Petroleum Hydrocarbons by Bioflocculant-Producing Microorganisms of the Aquatic Ecosystems in the Arctic Region. IOP Conf. Ser. Earth Environ. Sci. 2020, 539, 012192. [Google Scholar] [CrossRef]
- Liu, M.; Gill, J.J.; Young, R.; Summer, E.J. Bacteriophages of Wastewater Foaming-Associated Filamentous Gordonia Reduce Host Levels in Raw Activated Sludge. Sci. Rep. 2015, 5, 13754. [Google Scholar] [CrossRef] [PubMed]
- Dyson, Z.A.; Tucci, J.; Seviour, R.J.; Petrovski, S. Isolation and Characterization of Bacteriophage SPI1, Which Infects the Activated-Sludge-Foaming Bacterium Skermania Piniformis. Arch. Virol. 2015, 161, 149–158. [Google Scholar] [CrossRef]
- Ji, M.; Liu, Z.; Sun, K.; Li, Z.; Fan, X.; Li, Q. Bacteriophages in Water Pollution Control: Advantages and Limitations. Front. Environ. Sci. Eng. 2020, 15, 84. [Google Scholar] [CrossRef]
- Pajdak-Stós, A.; Kocerba-Soroka, W.; Fyda, J.; Sobczyk, M.; Fiałkowska, E. Foam-Forming Bacteria in Activated Sludge Effectively Reduced by Rotifers in Laboratory- and Real-Scale Wastewater Treatment Plant Experiments. Environ. Sci. Pollut. Res. 2017, 24, 13004–13011. [Google Scholar] [CrossRef] [PubMed]
- Dlangamandla, C.; Ntwampe, S.K.O.; Basitere, M.; Chidi, B.S.; Okeleye, B.I.; Mukandi, M.R. Production, Application, and Efficacy of Biodefoamers from Bacillus, Aeromonas, Klebsiella, Comamonas spp. Consortium for the Defoamation of Poultry Slaughterhouse Wastewater. Water 2023, 15, 655. [Google Scholar] [CrossRef]
- Ross, J.; Miles, G.D. An Apparatus for Comparison of Foaming Properties of Soaps and Detergents. Oil Soap 1941, 18, 99–102. [Google Scholar] [CrossRef]
- Nakajima, J.; Mishima, I. Measurement of Foam Quality of Activated Sludge in MBR Process. Acta Hydrochim. Hydrobiol. 2005, 33, 232–239. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, H.; Chen, H. Response of Aerobic Activated Sludge to Edible Oil Exposure: Extracellular Polymeric Substance (EPS) Characteristics and Microbial Community. J. Environ. Manag. 2023, 335, 117571. [Google Scholar] [CrossRef] [PubMed]
- Dunkel, T.; de León Gallegos, E.L.; Bock, C.; Lange, A.; Hoffmann, D.; Boenigk, J.; Denecke, M. Illumina Sequencing for the Identification of Filamentous Bulking and Foaming Bacteria in Industrial Activated Sludge Plants. Int. J. Environ. Sci. Technol. 2017, 15, 1139–1158. [Google Scholar] [CrossRef]
- Li, B.-B.; Peng, Z.-Y.; Zhi, L.-L.; Li, H.-B.; Zheng, K.-K.; Li, J. Distribution and Diversity of Filamentous Bacteria in Wastewater Treatment Plants Exhibiting Foaming of Taihu Lake Basin, China. Environ. Pollut. 2020, 267, 115644. [Google Scholar] [CrossRef] [PubMed]
- Blackall, L.L.; Seviour, E.M.; Bradford, D.; Rossetti, S.; Tandoi, V.; Seviour, R.J. “Candidatus Nostocoida Limicola”, a Filamentous Bacterium from Activated Sludge. Int. J. Syst. Evol. Microbiol. 2000, 50, 703–709. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Nierychlo, M.; Andersen, K.S.; Xu, Y.; Green, N.; Jiang, C.; Albertsen, M.; Dueholm, M.S.; Nielsen, P.H. MiDAS 3: An Ecosystem-Specific Reference Database, Taxonomy and Knowledge Platform for Activated Sludge and Anaerobic Digesters Reveals Species-Level Microbiome Composition of Activated Sludge. Water Res. 2020, 182, 115955. [Google Scholar] [CrossRef]
- Salager, J.L.; Antón, R.; Bracho, C.L.; Briceño, M.I.; Peña, A.; Rondón, M.; Salager, S. Attainment of emulsion properties on design, a typical case of formulation engineering. In Proceedings of the Second European Congress of Chemical Engineering, Montpellier, France, 5–7 October 1999. [Google Scholar]
- Pal, P.; Khairnar, K.; Paunikar, W.N. Causes and remedies for filamentous foaming in activated sludge treatment plant. Glob. NEST J. 2014, 16, 762–772. [Google Scholar]
- Wang, J.; Nguyen, A.V.; Farrokhpay, S. Foamability of Sodium Dodecyl Sulfate Solutions: Anomalous Effect of Dodecanol Unexplained by Conventional Theories. Colloids Surf. A Physicochem. Eng. Asp. 2016, 495, 110–117. [Google Scholar] [CrossRef]
- Polyuzhyn, L.; Bura, K.; Shapoval, Y.; Polyuzhyn, I. Concentration effect of silicone defoamer with trade name BYK-037 on foam destruction rate for water solution of polyacrylamide and sodium laureth sulfate. In Proceedings of the International Youth Science Forum “Litteris et Artibus”, Lviv, Ukraine, 24–26 November 2016. [Google Scholar]
- Verma, A.; Chauhan, G.; Ojha, K. Characterization of α-Olefin Sulfonate Foam in Presence of Cosurfactants: Stability, Foamability and Drainage Kinetic Study. J. Mol. Liq. 2018, 264, 458–469. [Google Scholar] [CrossRef]


| Model | km | ki | ky | n | R2 | Variance |
|---|---|---|---|---|---|---|
| Rate law | - | 9 | - | −14.62 | 1 | 6.99 × 10−19 |
| Monod’s | −0.988 | - | 0.099 | - | 0.99 | 0.015 |
| Model | km | ki | ky | n | R2 | Variance |
|---|---|---|---|---|---|---|
| Rate law | - | 0.00011 | - | 0.781 | 0.98 | 0.0148 |
| Monod’s | 5.96 | - | 0.439 | - | 0.62 | 0.038 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dlangamandla, C.; Mpongwana, N.; Ntwampe, S.K.O.; Basitere, M.; Chidi, B.S. Modeling of Biofoam Destabilization by Biodefoamers in Poultry Slaughterhouse Wastewater Treatment Activated Sludge. Water 2024, 16, 1293. https://doi.org/10.3390/w16091293
Dlangamandla C, Mpongwana N, Ntwampe SKO, Basitere M, Chidi BS. Modeling of Biofoam Destabilization by Biodefoamers in Poultry Slaughterhouse Wastewater Treatment Activated Sludge. Water. 2024; 16(9):1293. https://doi.org/10.3390/w16091293
Chicago/Turabian StyleDlangamandla, Cynthia, Ncumisa Mpongwana, Seteno K. O. Ntwampe, Moses Basitere, and Boredi S. Chidi. 2024. "Modeling of Biofoam Destabilization by Biodefoamers in Poultry Slaughterhouse Wastewater Treatment Activated Sludge" Water 16, no. 9: 1293. https://doi.org/10.3390/w16091293
APA StyleDlangamandla, C., Mpongwana, N., Ntwampe, S. K. O., Basitere, M., & Chidi, B. S. (2024). Modeling of Biofoam Destabilization by Biodefoamers in Poultry Slaughterhouse Wastewater Treatment Activated Sludge. Water, 16(9), 1293. https://doi.org/10.3390/w16091293









