Daily Streamflow Forecasting Using Networks of Real-Time Monitoring Stations and Hybrid Machine Learning Methods
Abstract
1. Introduction
1.1. Streamflow Prediction Models
1.2. Advancements in Streamflow Forecasting through Deep Learning
2. Materials and Methods
2.1. The Correlation of Discharge, Groundwater Level, and Precipitation
2.2. Concepts and Evaluation Measures of the Models
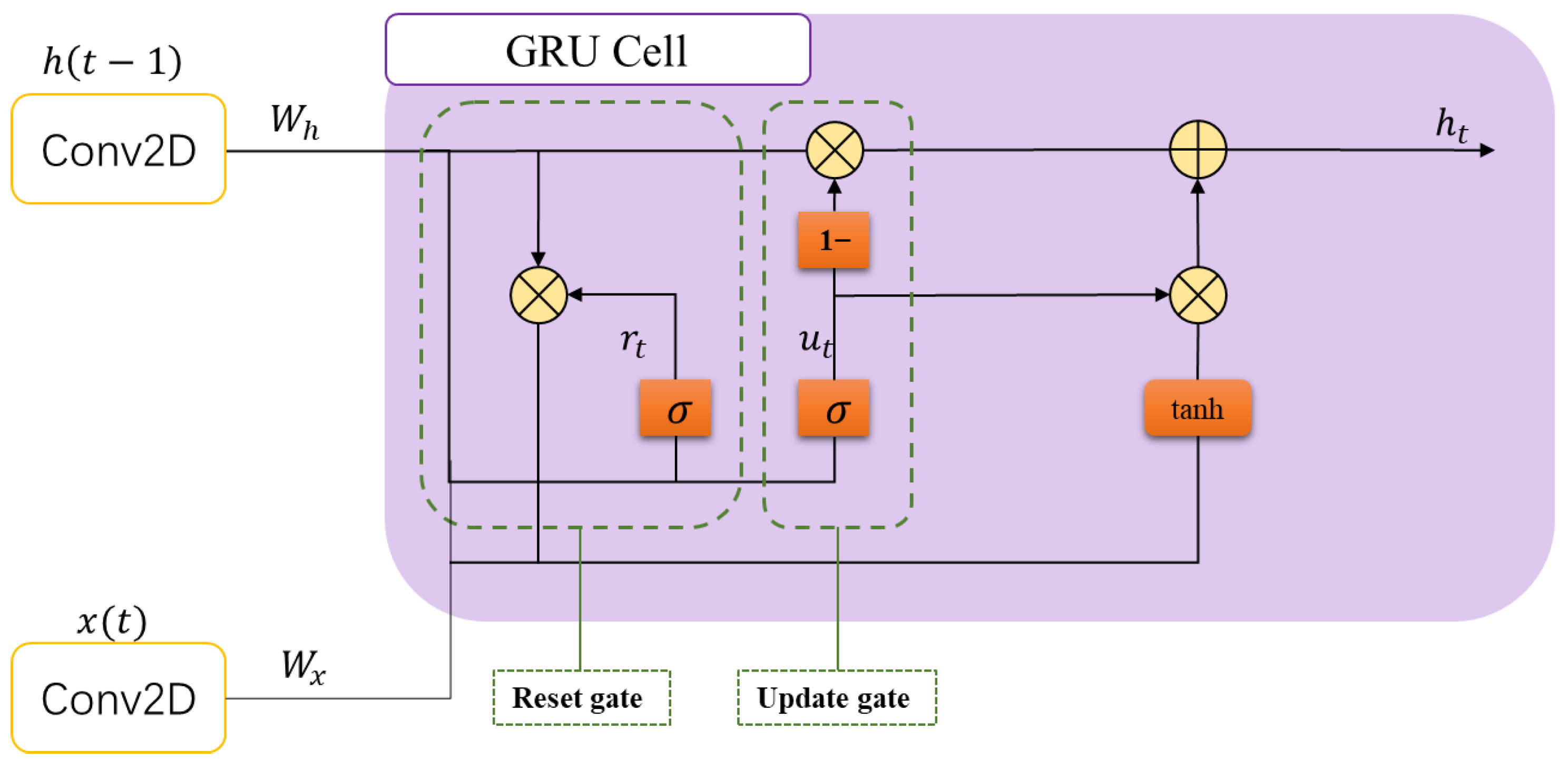
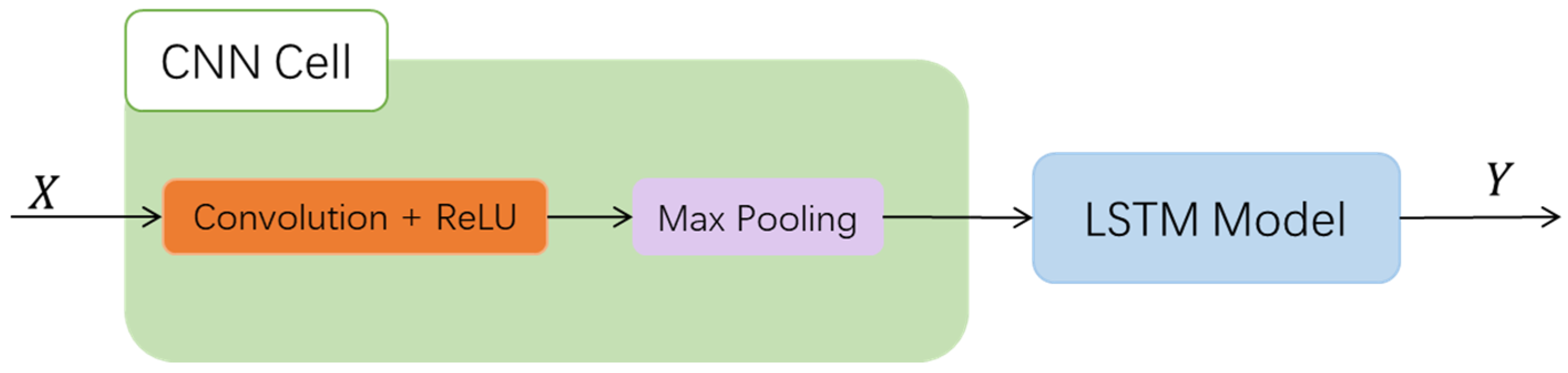
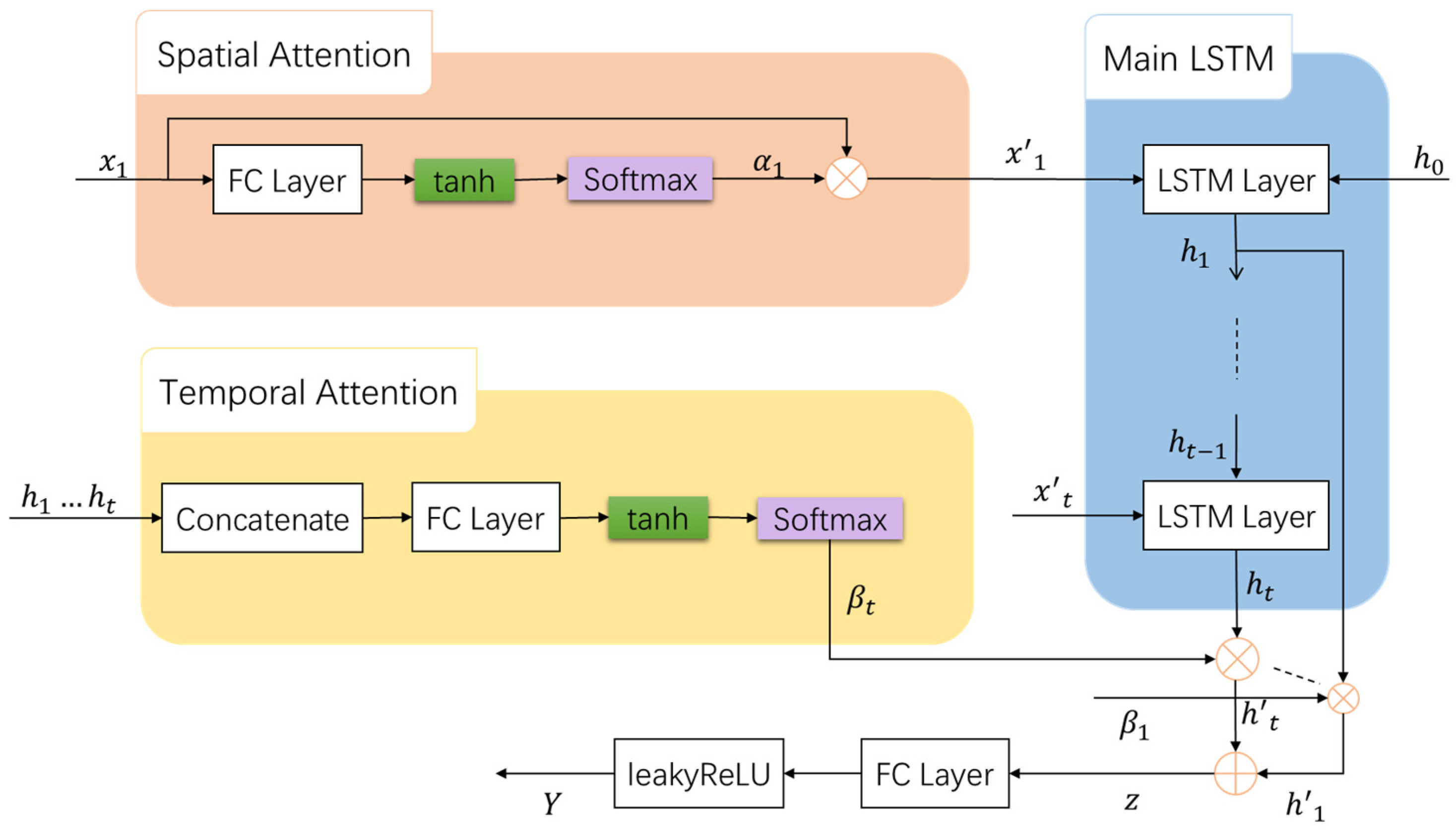
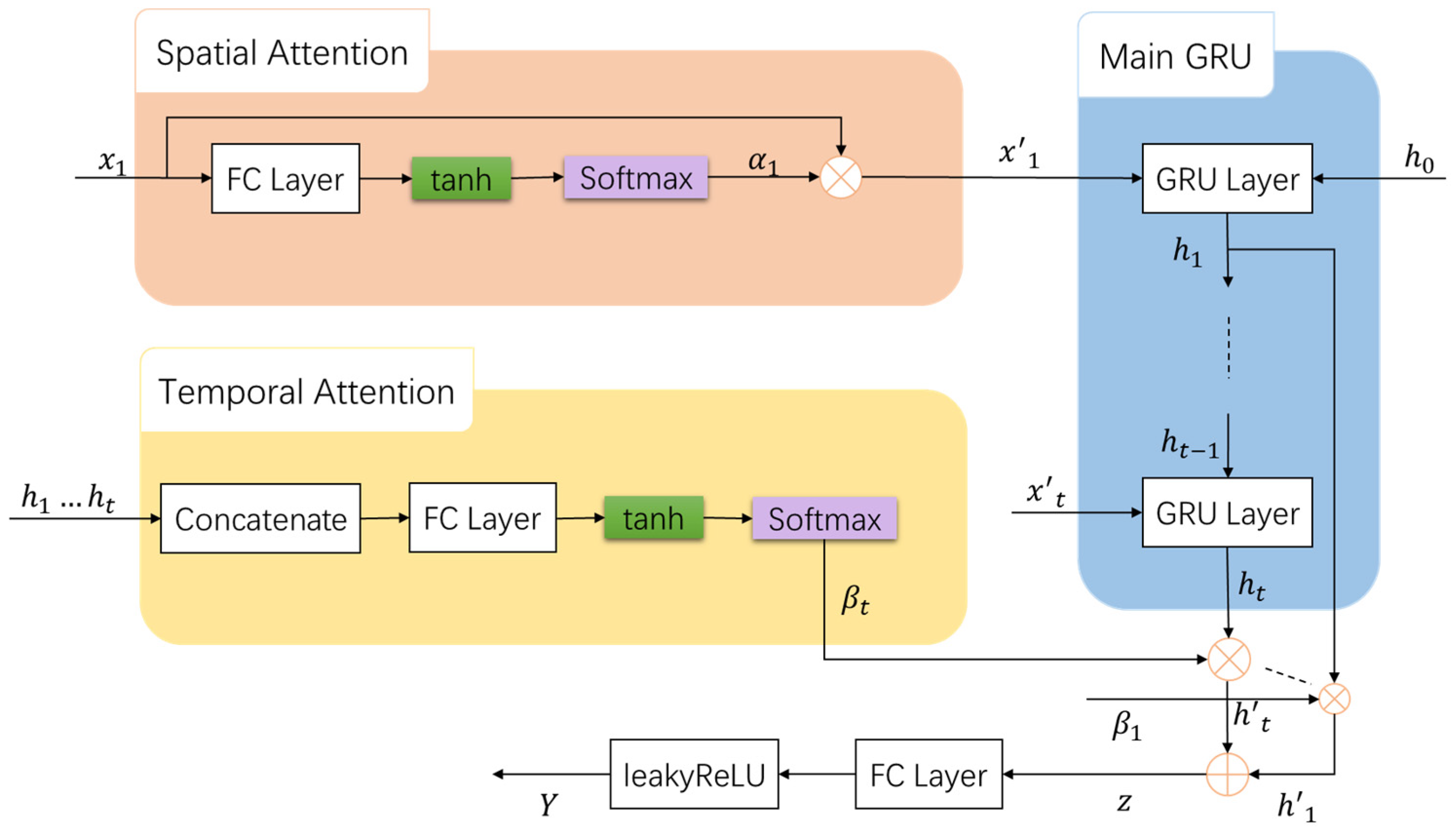
2.2.1. STA-GRU Models
2.2.2. Evaluation Measures
- The RMSE quantifies the average of the squares of the differences between predicted and actual observed values. It serves as a widely used metric for evaluating the accuracy of predictions.where n is the number of observations, is the actual observed value, and is the predicted value.
- The MAE represents the average absolute deviation between predicted values and actual observations, offering an intuitive gauge of predictive accuracy.
- The MAPE is a measure that expresses the accuracy of a predictive model as a percentage. It calculates the average absolute deviation between the observed values and the predictions relative to the actual values, thereby providing a clear and interpretable indication of the model’s prediction error in terms of proportionate accuracy.
- is a measure that expresses the accuracy of a predictive model as a percentage. It calculates the average absolute deviation between the observed values and the predictions relative to the actual values, thereby providing a clear and interpretable indication of the model’s prediction error in terms of proportionate accuracy.
3. Results and Discussion
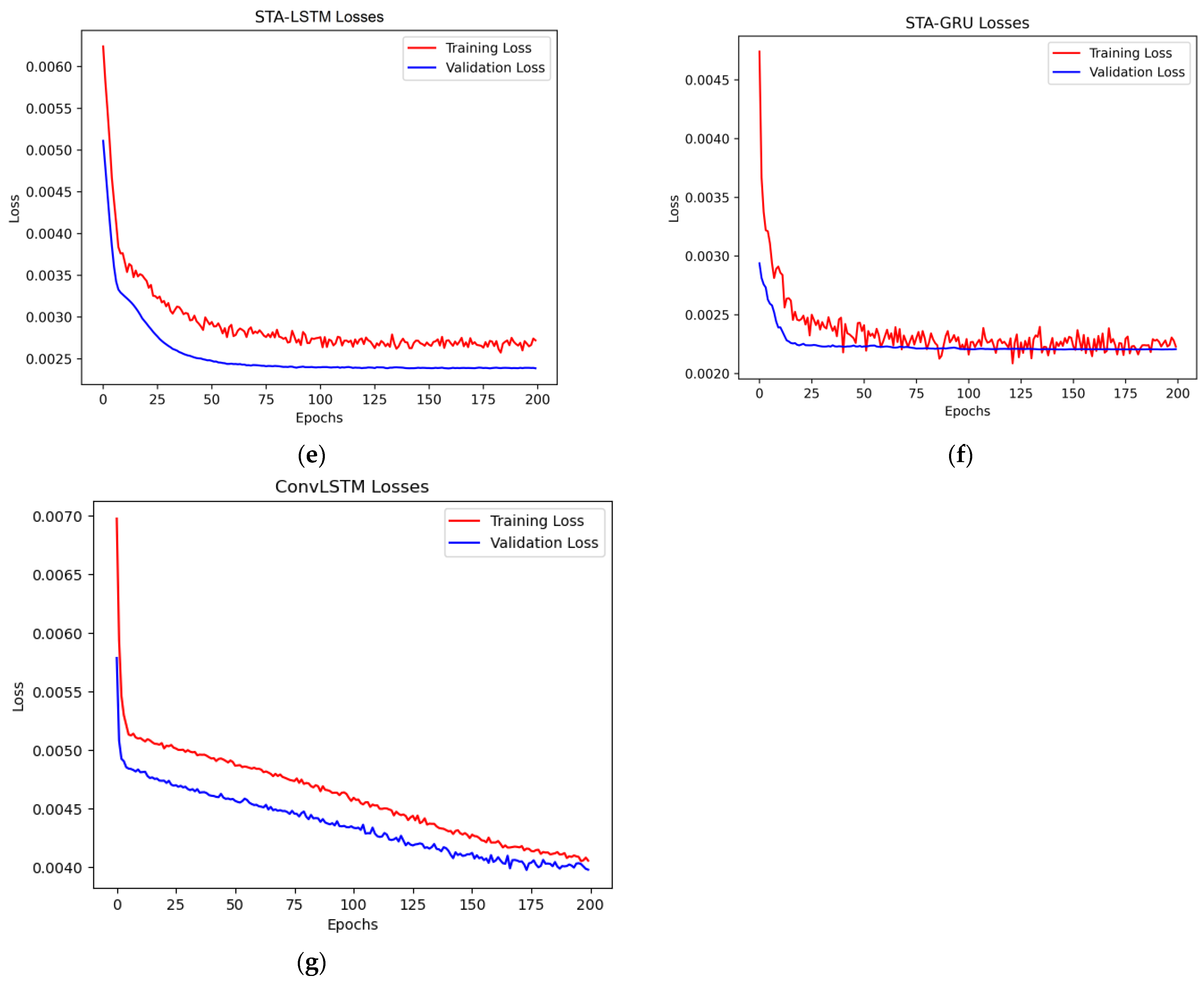
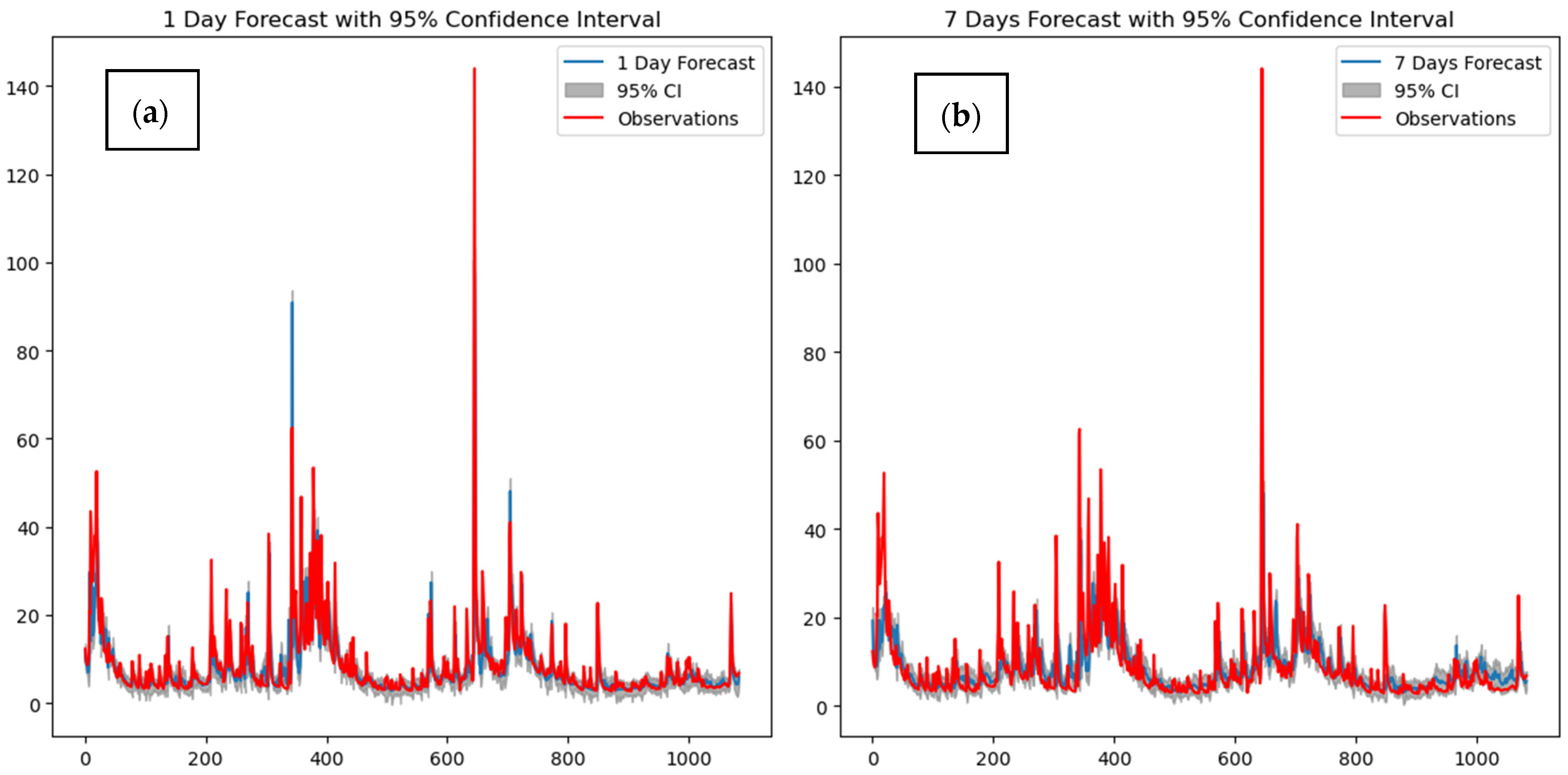
3.1. Results and Analysis
3.2. Discussions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bhasme, P.; Bhatia, U. Improving the interpretability and predictive power of hydrological models: Applications for daily streamflow in managed and unmanaged catchments. J. Hydrol. 2024, 628, 130421. [Google Scholar] [CrossRef]
- Drisya, J.; Kumar, D.S.; Roshni, T. Hydrological drought assessment through streamflow forecasting using wavelet enable artificial neural networks. Environ. Dev. Sustain. 2021, 23, 3653–3672. [Google Scholar] [CrossRef]
- Tan, M.L.; Gassman, P.W.; Yang, X.; Haywood, J. A review of SWAT applications, performance and future needs for simulation of hydro-climatic extremes. Adv. Water Resour. 2020, 143, 103662. [Google Scholar] [CrossRef]
- Jahangir, M.S.; Quilty, J. Generative deep learning for probabilistic streamflow forecasting: Conditional variational auto-encoder. J. Hydrol. 2024, 629, 130498. [Google Scholar] [CrossRef]
- Kumar, V.; Kedam, N.; Sharma, K.V.; Mehta, D.J.; Caloiero, T. Advanced machine learning techniques to improve hydrological prediction: A comparative analysis of streamflow prediction models. Water 2023, 15, 2572. [Google Scholar] [CrossRef]
- Sabale, R.; Venkatesh, B.; Jose, M. Sustainable water resource management through conjunctive use of groundwater and surface water: A review. Innov. Infrastruct. Solut. 2023, 8, 17. [Google Scholar] [CrossRef]
- Tripathy, K.P.; Mishra, A.K. Deep Learning in Hydrology and Water Resources Disciplines: Concepts, Methods, Applications, and Research Directions. J. Hydrol. 2023, 628, 130458. [Google Scholar] [CrossRef]
- Yildirim, I.; Aksoy, H. Intermittency as an indicator of drought in streamflow and groundwater. Hydrol. Process. 2022, 36, e14615. [Google Scholar] [CrossRef]
- Wang, T.; Wu, Z.; Wang, P.; Wu, T.; Zhang, Y.; Yin, J.; Yu, J.; Wang, H.; Guan, X.; Xu, H.; et al. Plant-groundwater interactions in drylands: A review of current research and future perspectives. Agric. For. Meteorol. 2023, 341, 109636. [Google Scholar] [CrossRef]
- Meng, F.; Luo, M.; Sa, C.; Wang, M.; Bao, Y. Quantitative assessment of the effects of climate, vegetation, soil and groundwater on soil moisture spatiotemporal variability in the Mongolian Plateau. Sci. Total Environ. 2022, 809, 152198. [Google Scholar] [CrossRef] [PubMed]
- Han, Z.; Huang, S.; Huang, Q.; Bai, Q.; Leng, G.; Wang, H.; Zhao, J.; Wei, X.; Zheng, X. Effects of vegetation restoration on groundwater drought in the Loess Plateau, China. J. Hydrol. 2020, 591, 125566. [Google Scholar] [CrossRef]
- Marchionni, V.; Daly, E.; Manoli, G.; Tapper, N.; Walker, J.; Fatichi, S. Groundwater buffers drought effects and climate variability in urban reserves. Water Resour. Res. 2020, 56, e2019WR026192. [Google Scholar] [CrossRef]
- Gavrilescu, M. Water, soil, and plants interactions in a threatened environment. Water 2021, 13, 2746. [Google Scholar] [CrossRef]
- Ondrasek, G.; Rengel, Z. Environmental salinization processes: Detection, implications & solutions. Sci. Total Environ. 2021, 754, 142432. [Google Scholar] [PubMed]
- Mukhopadhyay, R.; Sarkar, B.; Jat, H.S.; Sharma, P.C.; Bolan, N.S. Soil salinity under climate change: Challenges for sustainable agriculture and food security. J. Environ. Manag. 2021, 280, 111736. [Google Scholar] [CrossRef]
- Stavi, I.; Thevs, N.; Priori, S. Soil salinity and sodicity in drylands: A review of causes, effects, monitoring, and restoration measures. Front. Environ. Sci. 2021, 9, 712831. [Google Scholar] [CrossRef]
- Lee, S.; Hyun, Y.; Lee, S.; Lee, M.J. Groundwater potential mapping using remote sensing and GIS-based machine learning techniques. Remote Sens. 2020, 12, 1200. [Google Scholar] [CrossRef]
- Abdelkareem, M.; Al-Arifi, N. The use of remotely sensed data to reveal geologic, structural, and hydrologic features and predict potential areas of water resources in arid regions. Arab. J. Geosci. 2021, 14, 1–15. [Google Scholar] [CrossRef]
- Gholami, V.; Booij, M. Use of machine learning and geographical information system to predict nitrate concentration in an unconfined aquifer in Iran. J. Clean. Prod. 2022, 360, 131847. [Google Scholar] [CrossRef]
- Drogkoula, M.; Kokkinos, K.; Samaras, N. A Comprehensive Survey of Machine Learning Methodologies with Emphasis in Water Resources Management. Appl. Sci. 2023, 13, 12147. [Google Scholar] [CrossRef]
- Ntona, M.M.; Busico, G.; Mastrocicco, M.; Kazakis, N. Modeling groundwater and surface water interaction: An overview of current status and future challenges. Sci. Total Environ. 2022, 846, 157355. [Google Scholar] [CrossRef] [PubMed]
- Haque, A.; Salama, A.; Lo, K.; Wu, P. Surface and groundwater interactions: A review of coupling strategies in detailed domain models. Hydrology 2021, 8, 35. [Google Scholar] [CrossRef]
- Condon, L.E.; Kollet, S.; Bierkens, M.F.; Fogg, G.E.; Maxwell, R.M.; Hill, M.C.; Fransen, H.J.H.; Verhoef, A.; Van Loon, A.F.; Sulis, M.; et al. Global groundwater modeling and monitoring: Opportunities and challenges. Water Resour. Res. 2021, 57, e2020WR029500. [Google Scholar] [CrossRef]
- Wang, W.; Van Gelder, P.H.; Vrijling, J.; Ma, J. Forecasting daily streamflow using hybrid ANN models. J. Hydrol. 2006, 324, 383–399. [Google Scholar] [CrossRef]
- Rasouli, K.; Hsieh, W.W.; Cannon, A.J. Daily streamflow forecasting by machine learning methods with weather and climate inputs. J. Hydrol. 2012, 414, 284–293. [Google Scholar] [CrossRef]
- Cheng, M.; Fang, F.; Kinouchi, T.; Navon, I.; Pain, C. Long lead-time daily and monthly streamflow forecasting using machine learning methods. J. Hydrol. 2020, 590, 125376. [Google Scholar] [CrossRef]
- Chu, H.; Wei, J.; Wu, W.; Jiang, Y.; Chu, Q.; Meng, X. A classification-based deep belief networks model framework for daily streamflow forecasting. J. Hydrol. 2021, 595, 125967. [Google Scholar] [CrossRef]
- Essam, Y.; Huang, Y.F.; Ng, J.L.; Birima, A.H.; Ahmed, A.N.; El-Shafie, A. Predicting streamflow in Peninsular Malaysia using support vector machine and deep learning algorithms. Sci. Rep. 2022, 12, 3883. [Google Scholar] [CrossRef] [PubMed]
- Ibrahim, K.S.M.H.; Huang, Y.F.; Ahmed, A.N.; Koo, C.H.; El-Shafie, A. A review of the hybrid artificial intelligence and optimization modelling of hydrological streamflow forecasting. Alex. Eng. J. 2022, 61, 279–303. [Google Scholar] [CrossRef]
- Riahi-Madvar, H.; Dehghani, M.; Memarzadeh, R.; Gharabaghi, B. Short to long-term forecasting of river flows by heuristic optimization algorithms hybridized with ANFIS. Water Resour. Manag. 2021, 35, 1149–1166. [Google Scholar] [CrossRef]
- Sit, M.; Demiray, B.Z.; Xiang, Z.; Ewing, G.J.; Sermet, Y.; Demir, I. A comprehensive review of deep learning applications in hydrology and water resources. Water Sci. Technol. 2020, 82, 2635–2670. [Google Scholar] [CrossRef] [PubMed]
- Ardabili, S.; Mosavi, A.; Dehghani, M.; Várkonyi-Kóczy, A.R. Deep learning and machine learning in hydrological processes climate change and earth systems a systematic review. In Proceedings of the Engineering for Sustainable Future: Selected Papers of the 18th International Conference on Global Research and Education Inter-Academia–2019 18, Budapest and Balatonfüred, Hungary, 4–7 September 2019; Springer: Berlin/Heidelberg, Germany, 2020; pp. 52–62. [Google Scholar]
- Ruma, J.F.; Adnan, M.S.G.; Dewan, A.; Rahman, R.M. Particle swarm optimization based LSTM networks for water level forecasting: A case study on Bangladesh river network. Results Eng. 2023, 17, 100951. [Google Scholar] [CrossRef]
- Xiang, Z.; Yan, J.; Demir, I. A rainfall-runoff model with LSTM-based sequence-to-sequence learning. Water Resour. Res. 2020, 56, e2019WR025326. [Google Scholar] [CrossRef]
- Song, X.; Liu, Y.; Xue, L.; Wang, J.; Zhang, J.; Wang, J.; Jiang, L.; Cheng, Z. Time-series well performance prediction based on Long Short-Term Memory (LSTM) neural network model. J. Pet. Sci. Eng. 2020, 186, 106682. [Google Scholar] [CrossRef]
- Duan, J.; Zhang, P.F.; Qiu, R.; Huang, Z. Long short-term enhanced memory for sequential recommendation. World Wide Web 2023, 26, 561–583. [Google Scholar] [CrossRef]
- Sagheer, A.; Hamdoun, H.; Youness, H. Deep LSTM-based transfer learning approach for coherent forecasts in hierarchical time series. Sensors 2021, 21, 4379. [Google Scholar] [CrossRef] [PubMed]
- Feng, D.; Fang, K.; Shen, C. Enhancing streamflow forecast and extracting insights using long-short term memory networks with data integration at continental scales. Water Resour. Res. 2020, 56, e2019WR026793. [Google Scholar] [CrossRef]
- Fu, M.; Fan, T.; Ding, Z.; Salih, S.Q.; Al-Ansari, N.; Yaseen, Z.M. Deep learning data-intelligence model based on adjusted forecasting window scale: Application in daily streamflow simulation. IEEE Access 2020, 8, 32632–32651. [Google Scholar] [CrossRef]
- Li, G.; Zhu, H.; Jian, H.; Zha, W.; Wang, J.; Shu, Z.; Yao, S.; Han, H. A combined hydrodynamic model and deep learning method to predict water level in ungauged rivers. J. Hydrol. 2023, 625, 130025. [Google Scholar] [CrossRef]
- Ghimire, S.; Yaseen, Z.M.; Farooque, A.A.; Deo, R.C.; Zhang, J.; Tao, X. Streamflow prediction using an integrated methodology based on convolutional neural network and long short-term memory networks. Sci. Rep. 2021, 11, 17497. [Google Scholar] [CrossRef] [PubMed]
- Vatanchi, S.M.; Etemadfard, H.; Maghrebi, M.F.; Shad, R. A comparative study on forecasting of long-term daily streamflow using ANN, ANFIS, BiLSTM and CNN-GRU-LSTM. Water Resour. Manag. 2023, 37, 4769–4785. [Google Scholar] [CrossRef]
- Soltani, K.; Ebtehaj, I.; Amiri, A.; Azari, A.; Gharabaghi, B.; Bonakdari, H. Mapping the spatial and temporal variability of flood susceptibility using remotely sensed normalized difference vegetation index and the forecasted changes in the future. Sci. Total Environ. 2021, 770, 145288. [Google Scholar] [CrossRef]
- Mohammed, A.; Corzo, G. Spatiotemporal convolutional long short-term memory for regional streamflow predictions. J. Environ. Manag. 2024, 350, 119585. [Google Scholar] [CrossRef] [PubMed]
- Baek, S.S.; Pyo, J.; Chun, J.A. Prediction of water level and water quality using a CNN-LSTM combined deep learning approach. Water 2020, 12, 3399. [Google Scholar] [CrossRef]
- Verma, S.; Srivastava, K.; Tiwari, A.; Verma, S. Deep learning techniques in extreme weather events: A review. arXiv 2023, arXiv:2308.10995. [Google Scholar]
- Dehghani, A.; Moazam, H.M.Z.H.; Mortazavizadeh, F.; Ranjbar, V.; Mirzaei, M.; Mortezavi, S.; Ng, J.L.; Dehghani, A. Comparative evaluation of LSTM, CNN, and ConvLSTM for hourly short-term streamflow forecasting using deep learning approaches. Ecol. Inform. 2023, 75, 102119. [Google Scholar] [CrossRef]
- Ding, Y.; Zhu, Y.; Feng, J.; Zhang, P.; Cheng, Z. Interpretable spatio-temporal attention LSTM model for flood forecasting. Neurocomputing 2020, 403, 348–359. [Google Scholar] [CrossRef]
- Cho, M.; Kim, C.; Jung, K.; Jung, H. Water level prediction model applying a long short-term memory (lstm)–gated recurrent unit (gru) method for flood prediction. Water 2022, 14, 2221. [Google Scholar] [CrossRef]
- Xu, W.; Chen, J.; Zhang, X.J. Scale effects of the monthly streamflow prediction using a state-of-the-art deep learning model. Water Resour. Manag. 2022, 36, 3609–3625. [Google Scholar] [CrossRef]
- Alizadeh, B.; Bafti, A.G.; Kamangir, H.; Zhang, Y.; Wright, D.B.; Franz, K.J. A novel attention-based LSTM cell post-processor coupled with bayesian optimization for streamflow prediction. J. Hydrol. 2021, 601, 126526. [Google Scholar] [CrossRef]
- Zhao, X.; Lv, H.; Wei, Y.; Lv, S.; Zhu, X. Streamflow forecasting via two types of predictive structure-based gated recurrent unit models. Water 2021, 13, 91. [Google Scholar] [CrossRef]
- Wegayehu, E.B.; Muluneh, F.B. Multivariate streamflow simulation using hybrid deep learning models. Comput. Intell. Neurosci. 2021, 2021, 5172658. [Google Scholar] [CrossRef] [PubMed]
- Jamei, M.; Jamei, M.; Ali, M.; Karbasi, M.; Farooque, A.A.; Malik, A.; Cheema, S.J.; Esau, T.J.; Yaseen, Z.M. Quantitative improvement of streamflow forecasting accuracy in the Atlantic zones of Canada based on hydro-meteorological signals: A multi-level advanced intelligent expert framework. Ecol. Inform. 2024, 80, 102455. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, Z.; Van Griensven Thé, J.; Yang, S.X.; Gharabaghi, B. Flood Forecasting Using Hybrid LSTM and GRU Models with Lag Time Preprocessing. Water 2023, 15, 3982. [Google Scholar] [CrossRef]
- Tarekegn, A.N.; Ullah, M.; Cheikh, F.A. Deep Learning for Multi-Label Learning: A Comprehensive Survey. arXiv 2024, arXiv:2401.16549. [Google Scholar]
- Mhedhbi, R. Integrating Precipitation Nowcasting in a Deep Learning-Based Flash Flood Prediction Framework and Assessing the Impact of Rainfall Forecasts Uncertainties. Master’s Thesis, York University, Toronto, ON, Canada, 2022. [Google Scholar]
- Suthar, T.; Shah, T.; Raja, M.K.; Raha, S.; Kumar, A.; Ponnusamy, M. Predicting Weather Forecast Uncertainty based on Large Ensemble of Deep Learning Approach. In Proceedings of the 2023 International Conference on Self Sustainable Artificial Intelligence Systems (ICSSAS), Erode, India, 18–20 October 2023; pp. 1–6. [Google Scholar]
- Landi, F.; Baraldi, L.; Cornia, M.; Cucchiara, R. Working memory connections for LSTM. Neural Netw. 2021, 144, 334–341. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Gu, Z.; Thé, J.V.G.; Yang, S.X.; Gharabaghi, B. The discharge forecasting of multiple monitoring station for humber river by hybrid LSTM models. Water 2022, 14, 1794. [Google Scholar] [CrossRef]
- Niu, Z.; Zhong, G.; Yu, H. A review on the attention mechanism of deep learning. Neurocomputing 2021, 452, 48–62. [Google Scholar] [CrossRef]
- Li, X.; Zhang, W.; Ding, Q. Understanding and improving deep learning-based rolling bearing fault diagnosis with attention mechanism. Signal Process. 2019, 161, 136–154. [Google Scholar] [CrossRef]
- Ficklin, D.L.; Abatzoglou, J.T.; Robeson, S.M.; Null, S.E.; Knouft, J.H. Natural and managed watersheds show similar responses to recent climate change. Proc. Natl. Acad. Sci. USA 2018, 115, 8553–8557. [Google Scholar] [CrossRef] [PubMed]
- Ficklin, D.L.; Luo, Y.; Luedeling, E.; Zhang, M. Climate change sensitivity assessment of a highly agricultural watershed using SWAT. J. Hydrol. 2009, 374, 16–29. [Google Scholar] [CrossRef]
- Heerspink, B.P.; Kendall, A.D.; Coe, M.T.; Hyndman, D.W. Trends in streamflow, evapotranspiration, and groundwater storage across the Amazon Basin linked to changing precipitation and land cover. J. Hydrol. Reg. Stud. 2020, 32, 100755. [Google Scholar] [CrossRef]
- Kumar, S.; Kolekar, T.; Kotecha, K.; Patil, S.; Bongale, A. Performance evaluation for tool wear prediction based on Bi-directional, Encoder–Decoder and Hybrid Long Short-Term Memory models. Int. J. Qual. Reliab. Manag. 2022, 39, 1551–1576. [Google Scholar] [CrossRef]
- Zhang, Y.; Pan, D.; Van Griensven, J.; Yang, S.X.; Gharabaghi, B. Intelligent flood forecasting and warning: A survey. Intell. Robot 2023, 3, 190–212. [Google Scholar] [CrossRef]


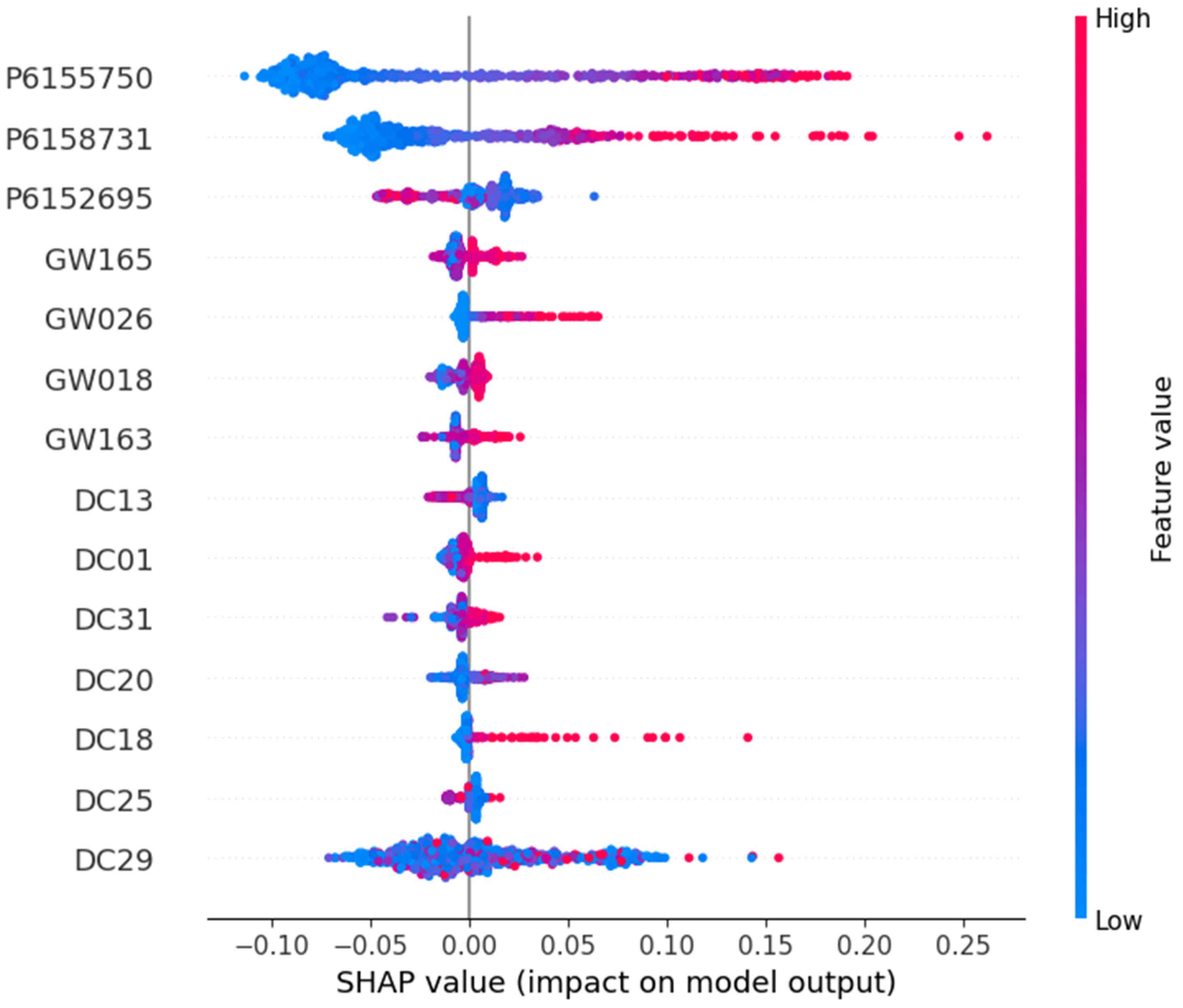




| Reference | Model | RMSE | MAE | |
|---|---|---|---|---|
| Chu, Haibo et al. (2021) [27] | DBN | 43.04 | 12.42 | 0.82 |
| FCN-PMI-DBN | 26.51 | 8.08 | 0.95 | |
| Wegayehu et al. (2021) [53] | GRU | 46.63 | 20.89 | 0.55 |
| CNNGRU | 45.61 | 21.79 | 0.57 | |
| LSTM | 48.64 | 22.79 | 0.51 | |
| CNNLSTM | 45.38 | 21.85 | 0.57 | |
| Vatanchi et al. (2023) [42] | ANFIS | N/A | 26.17 | 0.93 |
| BiLSTM | N/A | 32.15 | 0.92 |
| Stations | Max | Min | Mean | Std | Std/Mean |
|---|---|---|---|---|---|
| DC29 | 144.00 | 2.00 | 9.06 | 8.68 | 0.958 |
| DC25 | 101.00 | 1.92 | 7.47 | 6.69 | 0.896 |
| DC18 | 60.80 | 1.70 | 4.94 | 3.74 | 0.757 |
| DC20 | 6.32 | 0.21 | 0.51 | 0.31 | 0.608 |
| DC31 | 1.48 | 0.11 | 0.17 | 0.05 | 0.294 |
| DC01 | 27.10 | 0.66 | 2.10 | 1.57 | 0.748 |
| DC13 | 9.33 | 0.20 | 0.69 | 0.54 | 0.783 |
| GW163 | 426.13 | 422.27 | 424.44 | 0.79 | 0.002 |
| GW018 | 449.77 | 447.67 | 448.84 | 0.31 | 0.001 |
| GW026 | 390.20 | 386.37 | 387.33 | 0.64 | 0.002 |
| GW165 | 281.53 | 279.92 | 280.77 | 0.30 | 0.001 |
| P6152695 | 73.60 | 0.00 | 1.32 | 4.27 | 3.235 |
| P6158731 | 126.00 | 0.00 | 2.21 | 5.61 | 2.538 |
| P6155750 | 62.80 | 0.00 | 2.22 | 5.67 | 2.554 |
| Forecast | Algorithm | RMSE (Train) | RMSE (Test) | MAE (Train) | MAE (Test) | MAPE (Train) | MAPE (Test) | (Train) | (Test) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | LSTM | 7.225 | 7.448 | 3.502 | 3.817 | 46.7% | 47.5% | 30.1% | 21.2% |
| 1 | GRU | 7.101 | 7.198 | 3.473 | 3.775 | 43.6% | 46.7% | 32.9% | 22.8% |
| 1 | CNNLSTM | 6.796 | 7.742 | 3.211 | 3.879 | 37.4% | 48.0% | 40.6% | 14.9% |
| 1 | CNNGRU | 6.678 | 6.896 | 2.284 | 2.490 | 37.0% | 47.5% | 39.8% | 22.6% |
| 1 | ConvLSTM | 4.026 | 4.575 | 1.965 | 1.993 | 19.6% | 23.0% | 74.3% | 68.5% |
| 1 | STA-LSTM | 4.263 | 4.939 | 2.196 | 2.439 | 23.1% | 25.1% | 78.6% | 71.6% |
| 1 | STA-GRU | 3.731 | 4.214 | 2.016 | 2.362 | 19.2% | 21.5% | 80.2% | 74.4% |
| 7 | LSTM | 7.578 | 7.755 | 3.789 | 3.905 | 49.1% | 52.8% | 20.2% | 14.5% |
| 7 | GRU | 7.531 | 7.703 | 3.699 | 3.871 | 47.3% | 51.3% | 24.2% | 17.8% |
| 7 | CNNLSTM | 7.796 | 7.935 | 3.481 | 4.117 | 40.9% | 53.1% | 28.9% | 10.1% |
| 7 | CNNGRU | 7.351 | 7.636 | 3.459 | 3.679 | 39.6% | 41.9% | 29.1% | 16.7% |
| 7 | ConvLSTM | 7.081 | 7.453 | 3.437 | 3.744 | 41.5% | 46.9% | 32.9% | 20.9% |
| 7 | STA-LSTM | 6.749 | 6.899 | 3.401 | 3.533 | 38.6% | 40.6% | 36.0% | 28.3% |
| 7 | STA-GRU | 6.591 | 6.727 | 3.450 | 3.653 | 32.0% | 35.6% | 37.7% | 31.2% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Zhou, Z.; Deng, Y.; Pan, D.; Van Griensven Thé, J.; Yang, S.X.; Gharabaghi, B. Daily Streamflow Forecasting Using Networks of Real-Time Monitoring Stations and Hybrid Machine Learning Methods. Water 2024, 16, 1284. https://doi.org/10.3390/w16091284
Zhang Y, Zhou Z, Deng Y, Pan D, Van Griensven Thé J, Yang SX, Gharabaghi B. Daily Streamflow Forecasting Using Networks of Real-Time Monitoring Stations and Hybrid Machine Learning Methods. Water. 2024; 16(9):1284. https://doi.org/10.3390/w16091284
Chicago/Turabian StyleZhang, Yue, Zimo Zhou, Ying Deng, Daiwei Pan, Jesse Van Griensven Thé, Simon X. Yang, and Bahram Gharabaghi. 2024. "Daily Streamflow Forecasting Using Networks of Real-Time Monitoring Stations and Hybrid Machine Learning Methods" Water 16, no. 9: 1284. https://doi.org/10.3390/w16091284
APA StyleZhang, Y., Zhou, Z., Deng, Y., Pan, D., Van Griensven Thé, J., Yang, S. X., & Gharabaghi, B. (2024). Daily Streamflow Forecasting Using Networks of Real-Time Monitoring Stations and Hybrid Machine Learning Methods. Water, 16(9), 1284. https://doi.org/10.3390/w16091284









