Abstract
With the increasing demand for energy and the depletion of traditional resources, the development of alternative energy sources has become a critical issue. Shale gas, as an abundant and widely distributed resource, has great potential as a substitute for conventional natural gas. However, due to the low permeability of shale-gas reservoirs, efficient extraction poses significant challenges. The application of hydraulic fracturing technology has been proven to effectively enhance rock permeability, but the influence of environmental factors on its efficiency remains unclear. In this study, we investigate the impact of gas fracturing on shale-gas extraction efficiency under varying environmental conditions using numerical simulations. Our simulations provide a comprehensive analysis of the physical changes that occur during the fracturing process, allowing us to evaluate the effects of gas fracturing on rock mechanics and permeability. We find that gas fracturing can effectively induce internal fractures within the rock, and the magnitude of tensile stress decreases gradually during the process. The boundary pressure of the rock mass is an important factor affecting the effectiveness of gas fracturing, as it exhibits an inverse relationship with the gas content present within the rock specimen. Furthermore, the VL constant demonstrates a direct correlation with gas content, while the permeability and PL constant exhibit an inverse relationship with it. Our simulation results provide insights into the optimization of gas fracturing technology under different geological parameter conditions, offering significant guidance for its practical applications.
1. Introduction
For decades, petroleum and natural gas reserves have served as the backbone of global energy supplies, facilitating the daily activities of humanity. However, the relentless march of technological progress and modernization has led to an unprecedented surge in demand for these finite resources [1]. As we navigate the pressing imperative to diminish our reliance on traditional energy sources and align with sustainable development objectives, the quest for alternative energy reservoirs has assumed paramount importance. Among these alternatives, unconventional natural gas resources emerge as a beacon of promise, holding immense potential for diversifying our energy portfolio. Shale gas, in particular, stands out as one of the most abundant geological resources among unconventional oil and gas reserves, offering compelling opportunities for technological development [2]. Renowned for its cleanliness and high energy quality, shale gas is considered a key player in reducing greenhouse gas emissions [3]. Considering that conventional natural gas is a non-renewable resource, the development and utilization of shale-gas resources will play a crucial role in addressing current energy shortages.
Shale gas, typically stored within rock matrices, presents formidable challenges for exploration and extraction due to the high hardness and poor permeability of rocks. Hydraulic fracturing technology has emerged as indispensable for enhancing shale-gas extraction efficiency [4]. However, the utilization of hydraulic pressure exerts significant strain on water resources, potentially generating noise and triggering seismic activity during post-fracturing backflow [5,6]. Moreover, hydraulic fracturing may damage reservoir permeability, resulting in a notable decrease in oil and gas permeability, known as the water-blocking effect, which obstructs gas desorption and migration, leading to adverse outcomes [7]. With growing concerns regarding reservoir disturbance, environmental pollution, and water consumption associated with hydraulic fracturing, these issues have gained prominence in academic discourse. Researchers such as Anderson [8], Bahrami [9], and Zhang [10] have conducted comprehensive investigations into various aspects of hydraulic fracturing’s environmental impact and damage mechanisms, seeking environmentally friendly methods for shale-gas extraction. Anhydrous fracturing technology, including carbon dioxide, nitrogen, liquefied petroleum pressure, and liquid nitrogen fracturing, has thus become a focal point for unconventional natural gas development [11,12]. This innovative approach aims to mitigate the environmental footprint of shale gas extraction while bolstering its viability as a sustainable energy source.
Gas fracturing technology traces its roots back to the 1960s in the United States, marking the beginning of a transformative journey in the field of energy extraction. Initially, engineers relied on high-explosive materials like TNT to initiate explosive fracturing of gas reservoirs. However, the indiscriminate force exerted by these explosives often resulted in substantial damage to wellbores and reservoir formations, prompting a quest for safer alternatives. Subsequently, researchers explored the use of milder explosive materials such as nitrocellulose, aiming to mitigate the adverse effects of blasting operations while ensuring desirable fracturing outcomes. Despite the evident advantages of gas fracturing technology over traditional hydraulic fracturing, particularly in terms of applicability and efficiency, a definitive consensus regarding the mechanism of natural gas pressure cracking remains elusive. Hence, there is an urgent need for the integration of extensive experimental research and numerical simulation to advance our understanding of this mechanism, especially in the context of shale-gas extraction.
In recent years, a substantial body of research has explored the efficacy of gas fracturing as a means of enhancing rock permeability. Notably, Cai et al. [13] have conducted comprehensive investigations into the impact of gas fracturing on reservoirs, employing advanced techniques such as nuclear magnetic resonance and acoustic emission testing. Their findings highlight the positive influence of gas fracturing on micro-pore expansion and coal-pore connectivity, ultimately leading to improved reservoir permeability. Numerous scholars have conducted extensive research on the fracturing of rocks induced by liquid nitrogen. Ultimately, comprehensive analyses of rock fracture properties have been conducted through mechanical experiments and equipment such as acoustic emission instruments [14,15]. Studies by researchers such as Hou et al. [16] and Zhang et al. [17] have delved into the intricacies of rock fracturing under varying gas filtration conditions, offering valuable insights into the behavior of formations during hydraulic fracturing. Additionally, these scholars have proposed mathematical models for estimating stimulated reservoir volume (SRV), a crucial parameter in evaluating the effectiveness of fracturing operations. Meanwhile, Rogala and Wang [18,19] have provided comprehensive summaries of the technology behind shale-gas extraction through anhydrous fracturing methods. Li et al. [20] researched the influence of gas fracturing on micro cracks in coal. Zhai et al. [21], on the other hand, investigated the changes in pore structures within coal over time after gas fracturing. Shao et al. [22] performed experiments to investigate the impact of gas fracturing on the propagation of acoustic waves in coal rock, revealing a substantial decrease in both the velocity and amplitude of sound waves after treatment. This indicates that gas fracturing can result in notable alterations to the internal structure and mechanical strength of coal rock. Zhang et al. [23,24] studied the effect of gas fracturing on the enlargement of primary cracks and the crushing resistance of coal rock. They found that gas fracturing promotes the development of rock cracks.
Gas fracturing technology has emerged as a promising method for enhancing rock permeability in shale formations, as evidenced by numerous laboratory studies [25,26,27]. However, these indoor experiments often fail to fully replicate the complex stress state of reservoir rocks, leading to gaps in our understanding of how gas fracturing precisely influences rock permeability. Hence, this article aims to provide a comprehensive overview of the past work conducted in terms of methodology and key findings. By critically analyzing existing research, we can identify areas where the understanding of gas fracturing’s impact on rock permeability remains incomplete. Building upon this groundwork, our study employs advanced numerical simulations to accurately model the underground rock environment and investigate the changes in physical parameters during the gas fracturing process. Specifically, we analyzed the evolution of stress, strain, permeability, PL constant, and gas content within shale formations. By simulating the development of internal damage and micro fractures, we aim to uncover underlying patterns that contribute to changes in rock permeability. Moreover, our research assesses the impact of various physical parameters of rock formations on gas content during extraction. By conducting sensitivity analyses and exploring different scenarios, we seek to provide a robust scientific foundation for the utilization of gas fracturing methods in shale-gas development.
2. Mechanism and Model of Gas Fracturing in Coupled Fluid–Solid Systems
Fluid–solid interaction (FSI) belongs to the field of mechanics that encompasses the intersection between fluid dynamics and solid mechanics. It explores the behavior of deformed solids under the influence of fluid flow and the impact of solid configurations on fluid dynamics. The fundamental characteristic of fluid–solid interaction is the mutual interaction between the two-phase media. Under the influence of fluid loading, deformed solids experience deformation or displacement; as a result, they impact the flow of fluids, leading to changes in the distribution and intensity of fluid forces. Under diverse conditions, this mutual interaction leads to a range of FSI phenomena [28].
The fluid–solid coupling problem can be defined by its coupling equations, which are a set of equations. The definition domain includes both the fluid domain and the solid domain. These equations accurately describe the interaction at the interface between fluid and solid regions. The unknown variables in fluid–solid interaction problems consist of variables that contain both fluid and solid phenomena. These variables possess two key characteristics: Firstly, it is not possible to solve the fluid and solid domains independently since their behaviors are inherently coupled. The deformation of the solid structure influences the surrounding fluid flow, while the fluid forces exerted on the solid surface induce solid deformation or motion. Secondly, it is not possible to explicitly eliminate the independent variables that describe fluid motion and solid behavior.
From a holistic perspective, fluid–solid interaction problems can be generally divided into two groups according to their coupling mechanisms:
The initial group of problems associated with fluid–solid interaction is characterized by coupling effects occurring solely at the boundary separating the fluid and solid regions. The second group of issues related to fluid–solid interaction is characterized by the partial or complete overlap of the fluid and solid domains, making it challenging to clearly separate the two [29]. In these cases, the equations governing the physical phenomena, especially the constitutive equations, need to be established specifically for the given physical phenomenon being studied. The coupling effects in these problems are manifested through a system of differential equations that describe the problem at hand.
2.1. Heterogeneity of Rock Materials
To accurately capture the inherent heterogeneity of rock materials, discrete finite element representation is employed in numerical simulations. This approach allows for a closer alignment of the mechanical parameters with real-world conditions. For instance, rock materials’ Young’s modulus and strength are described by a probability density function called the Weibull distribution, as shown in Equation (1).
where represents the parameter of the unit cell, is the size parameter that is linked to the mean value of material parameters, and the shape parameter represents the degree of homogeneity.
2.2. The Mechanical Equilibrium and Damage Evolution Equations of Rock Masses
In simulating the aerodynamic fracturing process, it is assumed that the loading on the fracturing rock mass occurs in two stages: the first stage involves transient dynamic stress waves, while the second stage entails sustained quasi-static gas pressurization over a longer duration. Given these loading conditions, the modified Navier equation can be employed to depict the mechanical equilibrium of the rock under dynamic loading and quasi-static pressure, as shown in Equation (2) [30].
where represents the shear modulus, ; denotes the displacements occurring in each direction; represents the material’s Poisson’s ratio; represents the Biot coefficient; represents the forces acting within the body in each specific direction; represents the density of the solid; is the pressure coefficient; and represents time. During the loading phase under dynamic loads, the coefficient is zero. Throughout the stage of gas pressurization under quasi-static conditions, the coefficients representing air pressure, denoted as and , are considered to be zero. During the process of gas discharge resulting from high-pressure pneumatic fracturing, the coefficient representing gas pressure, denoted as , as well as the expression found on the right side of the equation, denoted as , are considered to be zero. In this given condition, considering the slow flow velocity of coalbed gas, numerical analysis can only be conducted in the quasi-static stage.
In this numerical simulation calculation, the evaluation of damage caused by tensile and shear stresses in brittle media (specifically referring to shale-gas reservoirs) is determined using the criterion for maximum tensile stress and the Mohr–Coulomb strength criterion. The calculations can be performed using the following equation [31]:
where and refer to the magnitude of forces calculated by two theories, is the ultimate pressure, is the stress in all directions, and is the internal friction angle.
When rock mass experiences damage and failure, its elastic modulus also undergoes changes accordingly, which can be mathematically formulated as equations or expressions as follows:
where is the elastic modulus, is the initial elastic modulus, and is the damage variable.
Furthermore, the damage variable can be quantitatively defined or represented based on the constitutive relationship diagram in Figure 1 using the following equation:
where is the damage variable, and are the magnitude of the force calculated by two methods, and represents the strain in all directions.
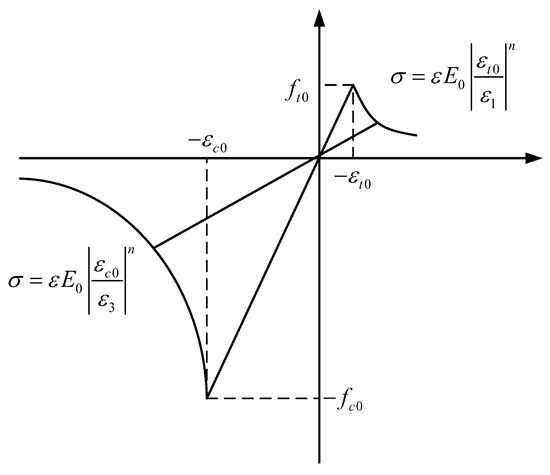
Figure 1.
Schematic diagram of the constitutive relationship of the element based on elastic damage under uniaxial stress conditions.
2.3. The Gas Equilibrium Equation
Shale-gas reservoirs are commonly regarded as porous media consisting of pore spaces and a solid matrix. During the hydraulic fracturing process, high-pressure air can be injected into the fractures and pores, leading to the further expansion of existing fractures.
The gas flow in porous media is described by [32]:
where represents the porosity of rock fractures or pores, is the density of the flowing gas, is the Darcy velocity of the flowing gas, is the total gas mass sources, and represents the gas flow time.
Gas density can be determined using the following equation:
where and represent gas pressure and gas density, respectively.
The Darcy velocity can be derived using the following equation:
where denotes the permeability of the medium and represents the dynamic viscosity. By substituting Equations (7) and (8) into Equation (6), we can derive:
When gas pressure and porosity changes occur in shale-gas reservoirs, adsorption or desorption of shale gas takes place. To account for the effects of gas adsorption or desorption, the following equation can be used to describe gas flow in the reservoir:
where represents the compression factor, denotes the Langmuir volume constant, and denotes the pressure coefficient of the gas.
The relationship between stress and porosity in gas reservoirs is as follows:
where represents the porosity at zero stress, denotes the porosity of rock under high pressure, and signifies the stress sensitivity coefficient of the rock, while indicates the average effective stress applied to the rock.
Additionally, the degree of damage to the rock can also have an effect on its permeability, which can be calculated using the following equation:
where represents the permeability under no stress conditions and is the coefficient that accounts for the damage-induced permeability effect.
To summarize, when subjected to dynamic loading, Equation (2) describes the dynamic mechanical conditions, while Equation (5) is utilized to solve the unit cell’s damage-evolution process. In the phase of quasi-static gas pressurization, when the term representing acceleration in Equation (2) is set to zero, Equations (9) and (2) are employed to calculate the quasi-static air pressure and stress conditions. Equation (5) is then employed again to compute the damage evolution of the unit cell. Finally, various parameters, including effective porosity and permeability, as well as the distribution of damage obtained during the quasi-static stage, will be transferred to the numerical analysis of gas extraction. Equations (9) and (10) will be utilized to calculate the process of gas extraction.
3. Construction of Geometric Model
Rock is a typical porous medium material that includes fracture and matrix. A schematic diagram of shale-reservoir exploitation is shown in Figure 2. Considering the challenges associated with conducting physical experiments using solid models, this study utilized the COMSOL 6.1 software to simulate the behavior of a shale-gas reservoir during hydraulic fracturing, also known as fracking, in a horizontal well. In this simulation, a 1 × 1 × 1 cubic unit cell was employed as a substitute for the physical model. Within the unit cell, a circular hole with a radius of 0.1 m was incorporated to mimic the fractures induced by the pressure of the gas. The shale gas was approximated as a fluid, following the principles of Darcy’s law. Boundary conditions were applied to the surfaces of the unit cell, with pressure simulated at the wellhead to represent the hydraulic pressure exerted, as shown in Figure 3. As time progressed, the pressure-induced fractures gradually propagated from the perimeter of the circular hole towards the outer boundaries of the unit cell, eventually resulting in its failure. Through the aforementioned simulation experiment, it is possible to observe the gradual depletion of shale gas within the unit cell as fractures propagate. This simulation approach can be used to investigate the relationship between gas content and instantaneous production rate, and various parameters such as rock permeability, gas density, and temperature can be modified during the simulation to gain insights into the speed and process of shale-gas extraction under different conditions. By obtaining comparative data through the manipulation of these parameters, it is possible to determine the variation patterns in the interaction between fluids and solids during gas fracturing operations.
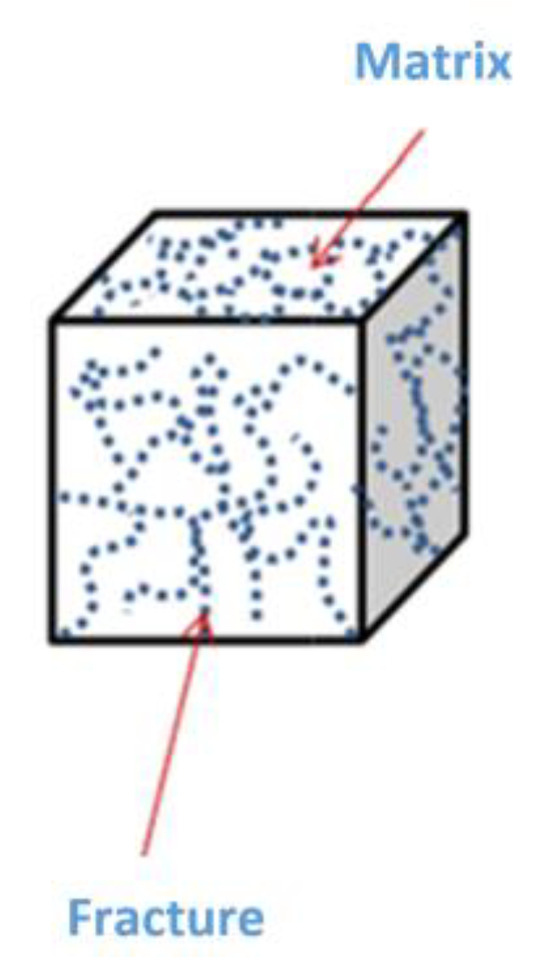
Figure 2.
Schematic diagram of shale-gas-reservoir exploitation.
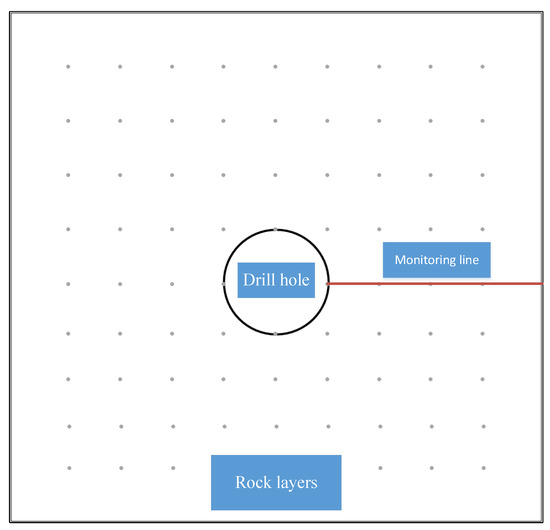
Figure 3.
Schematic diagram of numerical simulation model of gas fracturing of rock specimen.
4. Results of Numerical Calculations
4.1. Development of Rock Mass Damage under Gas Fracture
In the present simulation, a certain level of pressure was applied around the borehole to simulate the hydraulic fracturing pressure. Due to the presence of permeable fractures within the rock, the high-pressure gas flowing through these pores generates pressure at the periphery of the fractures, causing them to gradually expand during the fracturing process until the rock is fully damaged. Figure 4 illustrates the development process of rock fractures around the borehole, as simulated by the software.
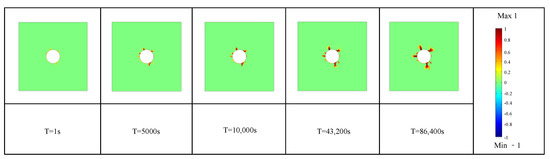
Figure 4.
Schematic diagram of the development of crack damage in simulated rock mass specimens.
As can be observed in the figure, the fractures within the rock gradually expand along the periphery of the borehole due to the high-pressure gas, eventually leading to the failure of the test specimen.
During the process of hydraulic-fracturing-induced rock damage, certain physical and mechanical parameters within the rock layer undergo significant changes as the damage progresses. By selecting several time steps during the simulation process and analyzing the corresponding parameters, one can observe the changes in various rock parameters as the damage evolves.
Understanding the evolution of stress distribution within the rock mass is crucial for assessing the effectiveness and safety of hydraulic fracturing operations. This detailed analysis provides insights into the temporal progression of fracture formation and its impact on the optimization of hydraulic fracturing processes. By elucidating the mechanisms governing fracture initiation and propagation, it enables a deeper understanding of how the rock responds to applied pressures over time. This understanding aids in predicting the extent of damage and identifying potential failure points, thus facilitating the optimization of hydraulic fracturing techniques for the safe and efficient extraction of shale gas and other unconventional resources.
The fluctuations of the maximum principal stress in the specimens are depicted in Figure 5 and Figure 6, where positive stress values denote tensile stress, and negative values indicate compressive stress. This description elucidates that during the hydraulic fracturing process, the rock primarily experiences tensile stress near the wellbore. Furthermore, with the progression of time, the maximum tensile stress gradually decreases. This observed phenomenon can be attributed to several inherent factors in the hydraulic fracturing process. Initially, the substantial injection of gas into the surrounding region of the wellbore increases the pore pressure within the rock, resulting in an elevation of tensile stress. However, as fractures extend and propagate, the injected gas provides a pathway for pressure relief, consequently lowering the overall stress state within the rock mass. Additionally, as the fracturing process proceeds, the formation of new fractures and the redistribution of stresses within the rock alter the mechanical behavior of the formation. The initiation and propagation of fractures aid in stress dissipation, particularly in the vicinity of the wellbore where tensile stress is most prominent. Thus, the gradual decrease in maximum tensile stress reflects the dynamic interplay between gas injection, fracture propagation, and stress redistribution within the rock mass during the hydraulic fracturing process. This understanding underscores the complexity of rock behavior under fracturing conditions and emphasizes the importance of continually optimizing fracturing parameters to enhance operational efficiency and mitigate associated risks. In summary, a comprehensive analysis of stress evolution can enhance our understanding of rock behavior under fracturing conditions, enabling the optimization of fracturing parameters and mitigation of potential risks associated with the process.
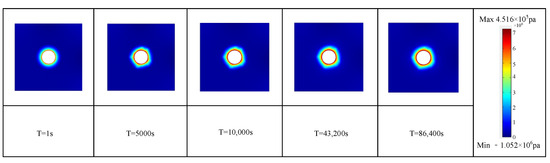
Figure 5.
Schematic diagram of the damage process caused by the first principal stress.
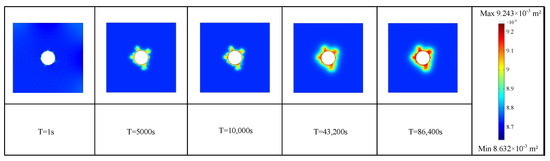
Figure 6.
Schematic diagram of permeability during the damage process.
By comparing the stress around the borehole before and after damage, it is evident that the mechanical properties of the rock significantly decrease during gas fracturing. After the damage begins, the stress in the surrounding area of the borehole significantly increases compared to the state before the damage. This increase indicates that due to gas fracturing, more internal cracks are generated within the rock matrix. The increase in the number of cracks reduces the bearing capacity of the rock. This analysis provides valuable insights into the impact of pneumatic fracturing on the mechanical properties of rock masses. It emphasizes the necessity of carefully considering fracturing parameters and their potential impact on rock stability. By optimizing these parameters, engineers and researchers can mitigate potential risks associated with hydraulic fracturing operations and ensure safe and efficient extraction of shale gas and other unconventional resources.
4.2. Characteristics of Gas Content during the Extraction Process
Given the abundance of points and lines within the unit cell, conducting a simulation analysis at each position individually is an infeasible task. To simplify the calculation process, one may choose to select a straight line along the boundary of the unit cell and borehole, and represent the simulation results at any position within the unit cell by analyzing the data along this line. The selected line segment within the unit cell is illustrated in Figure 3.
Assuming that shale gas follows Darcy’s law and can be treated as a fluid, it can be inferred that there is an airflow with Darcy velocity in the sample. When natural gas is extracted from shale, it will move outward from the borehole. By integrating the gas velocity around the borehole, the instantaneous gas recovery rate of shale gas can be obtained, as shown in Equation (13). In addition, the accumulation of instantaneous natural gas extraction rates over time can determine how shale-gas extraction rates change over time. Gas extraction operations may cause changes in gas content within rock formations. In addition, the physical parameters of different rock layers can also affect the gas content during the extraction process. Therefore, simulations and analyses were conducted to investigate the changes in gas content in rock samples under different parameters and times. Through these simulations and analyses, we can observe how the gas content in rock samples changes over time under different parameter settings. These pieces of information provide valuable insights into the natural gas extraction behavior in rock formations and help us understand the factors that affect the efficiency of natural gas production. By studying the changes in gas content, the extraction process can be optimized by adjusting parameters such as injection pressure, well spacing, and fracturing fluid properties. This can maximize natural gas production, while minimizing potential operational issues and environmental impacts related to shale-gas extraction.
where is the shale-gas extraction volume, is the gas velocity, and is the cross-sectional area of the borehole.
Numerical simulations can be conducted to analyze the gas content within shale gas under various permeability conditions. As shown in Figure 7, these simulations reveal a general trend: as permeability increases, the gas content of rock samples at a given location gradually decreases. This phenomenon is a result of higher permeability within the rock, which implies the existence of more interconnected pores. During gas fracturing, a significant amount of gas flows into these interconnected pores, causing an increase in gas pressure within the pores. As a result, the pores expand and their connectivity is enhanced. This leads to even higher permeability in rock samples with initially higher permeability at the same location after gas fracturing. Consequently, these rock samples experience increased gas leakage and a gradual decrease in gas content. This observed trend highlights the importance of monitoring and optimizing permeability during gas extraction operations. By understanding the impact of permeability on gas-content variation, engineers and researchers can adjust the fracturing parameters to achieve optimal gas production efficiency. Furthermore, accurate permeability measurements can assist in identifying potential gas-rich zones for drilling, leading to improved resource utilization and reduced exploration costs.
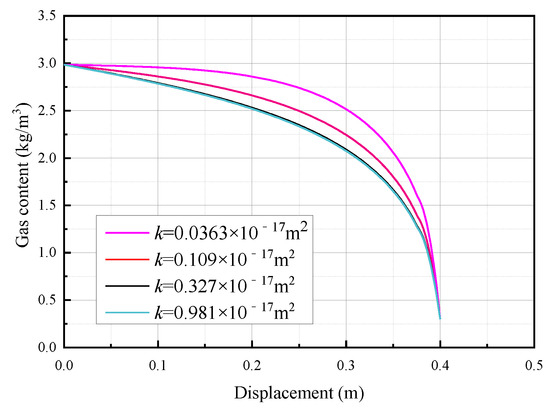
Figure 7.
Schematic diagram of the variation relationship of gas content of rock mass specimens under different permeabilities.
The analysis of gas content within the specimens unveils a consistent trend, as depicted in Figure 8 and Figure 9: there is a notable decrease in gas content as the analysis position moves further away from the drilling borehole. Additionally, parameters such as the pressure parameter (PL) and volume constant (VL) exert significant influence on gas content. Of particular note is the substantial impact of the PL parameter on gas content. As the PL parameter increases, there is a discernible decrease in gas content at a given position. This suggests that higher pressure conditions lead to lower gas content, indicating reduced gas extraction efficiency. Similarly, the volume constant (VL) of the specimen plays a pivotal role in determining gas content. A decrease in the VL value corresponds with a reduction in gas content at the same position, implying lower gas extraction efficiency for specimens with smaller volume constants. These observations underscore the importance of the physical characteristics of the experimental parameters in gas extraction efficiency. Specifically, variations in the PL parameter and volume constant VL closely correlate with gas extraction efficiency. Notably, when the PL value is small and the VL value is large, gas extraction efficiency tends to be relatively high. This analysis suggests that optimizing the pressure parameter and volume constant of the specimens could significantly enhance gas extraction efficiency. Future research endeavors could focus on identifying the optimal range of these parameters to maximize gas extraction in practical applications. Additionally, further investigation into the underlying mechanisms driving the observed trends in gas-content variation with respect to these parameters would provide valuable insights for improving gas extraction processes.
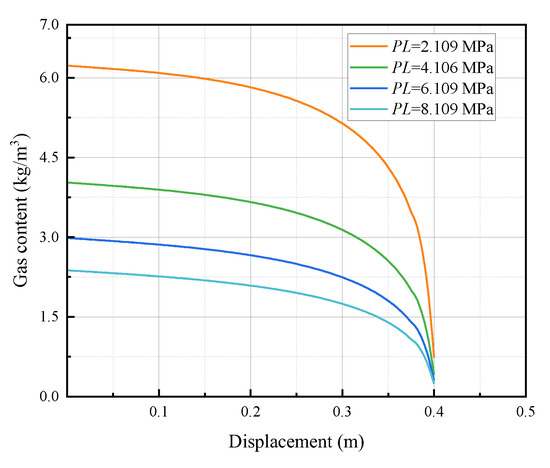
Figure 8.
Schematic diagram of the variation of gas content of rock mass specimens under different Langmuir pressure PL constants.
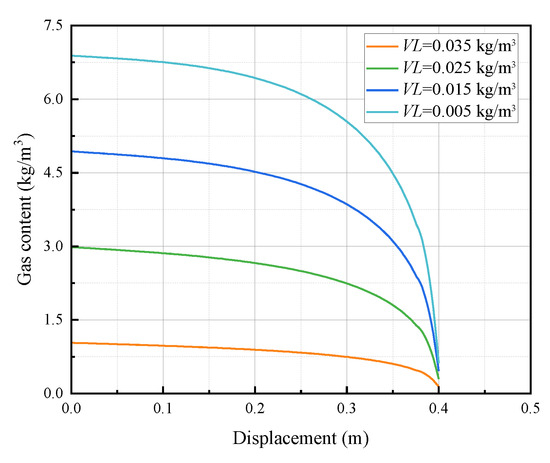
Figure 9.
Schematic diagram of the variation relationship of gas content of rock mass specimens under different Langmuir volume constants (VLs).
Figure 10a indicates minimal disparity in gas content. To address subtle variations in gas-content analysis under diverse boundary conditions, an expansion of the analysis was undertaken, as depicted in Figure 10b. Specifically, attention was focused on the segment between 0.274 and 0.280 m from the borehole. This targeted approach allows for meticulous scrutiny and analysis of any slight changes or patterns in gas content at that precise location. Upon enlarging the segment for detailed analysis, it becomes apparent that boundary conditions exert a significant influence on the gas content of rock samples. With an increase in the load imposed by boundary conditions, the gas content of the rock sample proportionately escalates. This observation validates the initial hypothesis that heightened boundary loads pose greater challenges to shale-gas extraction. This pivotal analysis yields valuable insights into the correlation between boundary conditions and gas content, indicating that the magnitude of the boundary load directly impacts gas content, with higher loads resulting in increased gas content. These findings have profound implications for shale-gas extraction endeavors, underscoring the imperative of carefully deliberating and managing boundary conditions to optimize the efficiency of natural gas extraction. Subsequent research endeavors can delve into exploring the specific mechanisms underlying the influence of boundary conditions on gas content. Understanding these mechanisms aids in devising strategies and technologies to mitigate the challenges posed by heightened boundary loads and enhance the efficiency of shale-gas extraction.
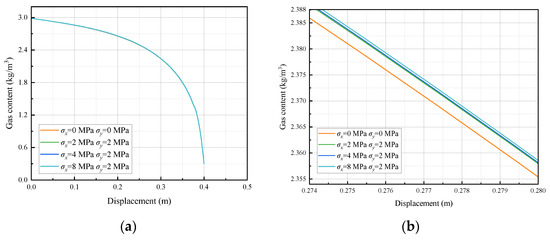
Figure 10.
Schematic diagram of the gas-content change relationship of rock mass specimens under different rock boundary conditions. (a) overall diagram and (b) partial enlarged image.
Based on the numerical simulation analysis of shale-gas production under different permeability conditions, as shown in Figure 11 and Figure 12, it has been observed that the gas extraction rate of the specimen shows a rising trend as the simulation time extends. This indicates that, over time, more gas is being extracted from the rock specimen. Furthermore, when the permeability set for the specimen is increased, there is an observed increasing trend in the gas extraction rate over the same period. This suggests that a higher initial permeability of the rock leads to better gas fracturing effects. As a result, the efficiency of shale-gas production improves, leading to a higher shale-gas production rate. These findings have important implications for shale-gas extraction operations. Increasing the permeability of the rock can enhance the effectiveness of the gas fracturing process, allowing for greater gas extraction rates. This understanding can inform decision-making processes when selecting areas for shale-gas production and designing extraction techniques. However, it is important to note that there may be an optimal permeability range beyond which further increases may not significantly improve gas extraction rates. Future research could focus on identifying this optimal range and exploring additional factors that may influence the gas extraction process. In summary, the numerical simulation analysis reveals that increasing the permeability of the rock specimen positively impacts the gas extraction rate and overall efficiency of shale-gas production. This insight can guide efforts to optimize extraction techniques and maximize the production of shale-gas resources.
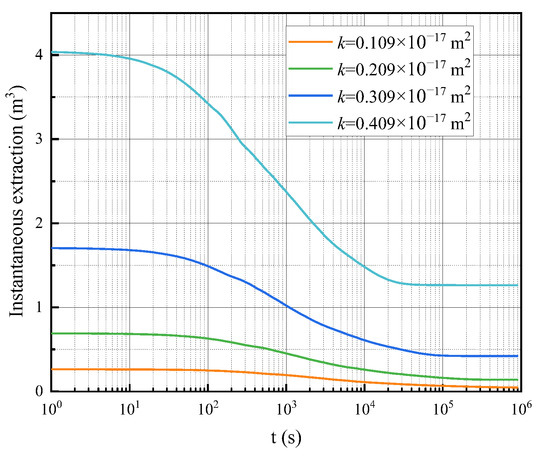
Figure 11.
Schematic diagram of instantaneous extraction of shale gas at different permeabilities.
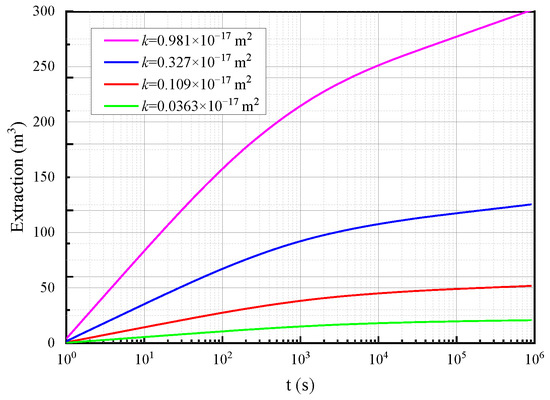
Figure 12.
Schematic diagram of total shale-gas extraction at different permeabilities.
5. Conclusions
- (1)
- Gas fracturing technology has shown promising potential in enhancing fracture propagation in rocks. This study conducted numerical experiments to examine the influence of different permeability levels on the extraction rates of gas from shale. The results indicated a direct relationship between the initial permeability of the rock and the efficacy of gas fracturing, thus leading to a significant improvement in shale-gas extraction efficiency.
- (2)
- Through software simulation, the objective of this study was to analyze the evolution of fractures in the surrounding rock mass near a borehole. Several parameters were selected and analyzed at different time steps during the damage simulation process. The findings highlight that the primary influence on rock failure in the vicinity of the borehole is tensile stress, with the maximum stress gradually decreasing over time. After the evolution of damage, a noteworthy reduction in stress around the borehole was observed, indicating the generation of additional fractures within the rock mass due to gas fracturing.
- (3)
- The boundary pressure of the rock mass is a crucial factor influencing the effectiveness of gas fracturing. The applied load at the boundary exhibits an inverse relationship with the gas content of the rock specimens. In the context of shale-gas extraction, selecting geologically soft soil conditions can maximize the optimization of fracturing outcomes.
- (4)
- The effectiveness of shale-gas extraction is influenced not only by boundary pressure but also by parameters such as rock porosity. This study investigates the impact of different physical parameters of rock formations on gas content during extraction. Through simulations and analysis of gas content variations in rock specimens under varying parameters and timeframes, the effects of factors such as permeability, Langmuir pressure constant (PL), and Langmuir volume constant (VL) on gas content are explored. The simulation results demonstrate an inverse relationship between permeability and PL constant with gas content in the rock specimens, while a direct proportionality is observed between VL constant and gas content. Therefore, it is essential to take into account the impact of different rock parameters on extraction efficiency during the gas fracturing process and employ appropriate measures and techniques to effectively enhance shale-gas extraction performance.
Author Contributions
Conceptualization, E.Q. and F.X.; methodology, L.W. and Y.Z.; data curation, Y.X. and Y.F. All authors have read and agreed to the published version of the manuscript.
Funding
The authors are grateful for the financial support of the Key Research and Development Program of Shaanxi Province, China (2022ZDLSF07-06 and 2023-YBSF-369) and the Natural Science Basic Research Program of Shaanxi (2022JM-216 and 2022JC-LHJJ-08).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare that there are no conflicts of interest regarding the publication of this paper.
References
- Salmachi, A.; Karacan, C.Ö. Cross-formational flow of water into coalbed methane reservoirs: Controls on relative permeability curve shape and production profile. Environ. Earth Sci. 2017, 76, 200. [Google Scholar] [CrossRef]
- Dong, D.; Zou, C.; Dai, J.; Huang, S.; Zheng, J.; Gong, J.; Wang, Y.; Li, X.; Guan, Q.; Zhang, C.; et al. Suggestions on the development strategy of shale gas in China. J. Nat. Gas Geosci. 2016, 1, 413–423. [Google Scholar] [CrossRef]
- Mac Kinnon, M.A.; Brouwer, J.; Samuelsen, S. The role of natural gas and its infrastructure in mitigating greenhouse gas emissions, improving regional air quality, and renewable resource integration. Prog. Energy Combust. Sci. 2018, 64, 62–92. [Google Scholar] [CrossRef]
- Chong, Z.; Yao, Q.; Li, X.; Liu, J. Investigations of seismicity induced by hydraulic fracturing in naturally fractured reservoirs based on moment tensors. J. Nat. Gas Sci. Eng. 2020, 81, 103448. [Google Scholar] [CrossRef]
- Hu, Y.; Wu, X. Research on coalbed methane reservoir water blocking damage mechanism and anti-water blocking. J. China Coal Soc. 2014, 39, 1107–1111. [Google Scholar]
- Wang, L.; Xue, Y.; Cao, Z.; Kong, H.; Han, J.; Zhang, Z. Experimental study on mode I fracture characteristics of granite after low temperature cooling with liquid nitrogen. Water 2023, 15, 3442. [Google Scholar] [CrossRef]
- Yan, C.; Chen, Y.; Chen, T.; Cheng, Y.; Yan, X. Experimental study of hydraulic fracturing for unconsolidated reservoirs. Rock Mech. Rock Eng. 2022, 55, 3399–3424. [Google Scholar] [CrossRef]
- Anderson, R.L.; Ratcliffe, I.; Greenwell, H.C.; Williams, P.A.; Cliffe, S.; Coveney, P.V. Clay swelling—A challenge in the oilfield. Earth-Sci. Rev. 2010, 98, 201–216. [Google Scholar] [CrossRef]
- Bahrami, H.; Rezaee, R.; Clennell, B. Water blocking damage in hydraulically fractured tight sand gas reservoirs: An example from Perth Basin, Western Australia. J. Pet. Sci. Eng. 2012, 88, 100–106. [Google Scholar] [CrossRef]
- Zhang, D.; Yang, T. Environmental impacts of hydraulic fracturing in shale gas development in the United States. Pet. Explor. Dev. 2015, 42, 876–883. [Google Scholar] [CrossRef]
- Zhang, X.; Lu, Y.; Tang, J.; Zhou, Z.; Liao, Y. Experimental study on fracture initiation and propagation in shale using supercritical carbon dioxide fracturing. Fuel 2017, 190, 370–378. [Google Scholar] [CrossRef]
- Cao, Z.; Sun, Q.; Li, Z.; Du, F. Abnormal ore pressure mechanism of working face under the influence of overlying concentrated coal pillar. Sci. Rep. 2024, 14, 626. [Google Scholar]
- Cai, C.; Li, G.; Huang, Z.; Tian, S.; Shen, Z.; Fu, X. Experiment of coal damage due to super-cooling with liquid nitrogen. J. Nat. Gas Sci. Eng. 2015, 22, 42–48. [Google Scholar] [CrossRef]
- Xue, Y.; Wang, L.; Liu, J.; Ranjith, P.G.; Gao, F.; Cai, C.; Xie, H. Experimental study on the effect of heating and liquid nitrogen-cooling cyclic treatment on mechanical properties and fracturing characteristics of granite. Int. J. Rock Mech. Min. Sci. 2024, 176, 105691. [Google Scholar] [CrossRef]
- Cai, Y.; Ma, Y.; Teng, T.; Xue, Y.; Wang, L.; Cao, Z.; Zhang, Z. Risk Assessment and Analysis of Rock Burst under High-Temperature Liquid Nitrogen Cooling. Water 2024, 16, 516. [Google Scholar] [CrossRef]
- Hou, P.; Gao, F.; Gao, Y.; Yang, Y.; Cai, C. Effect of pore pressure distribution on fracture behavior of sandstone in nitrogen fracturing. Energy Explor. Exploit. 2017, 35, 609–626. [Google Scholar] [CrossRef]
- Zhang, H.; Sheng, J. Optimization of horizontal well fracturing in shale gas reservoir based on stimulated reservoir volume. J. Pet. Sci. Eng. 2020, 190, 107059. [Google Scholar] [CrossRef]
- Rogala, A.; Krzysiek, J.; Bernaciak, M.; Hupka, J. Non-aqueous fracturing technologies for shale gas recovery. Physicochem. Probl. Miner. Process. 2013, 49, 313–322. [Google Scholar]
- Wang, L.; Yao, B.; Cha, M.; Alqahtani, N.B.; Patterson, T.W.; Kneafsey, T.J.; Miskimins, J.L.; Yin, X.; Wu, Y.S. Waterless fracturing technologies for unconventional reservoirs-opportunities for liquid nitrogen. J. Nat. Gas Sci. Eng. 2016, 35, 160–174. [Google Scholar] [CrossRef]
- Li, H.; Wang, L.; Zhang, C.; Du, W.; Li, J. Experimental study of the fatigue crack extension influences of liquid nitrogen on water cut coal sample. J. Exp. Mech. 2016, 31, 119–126. [Google Scholar]
- Zhai, C.; Qin, L.; Liu, S.; Xu, J.; Tang, Z.; Wu, S. Pore structure in coal: Pore evolution after cryogenic freezing with cyclic liquid nitrogen injection and its implication on coalbed methane extraction. Energy Fuels 2016, 30, 6009–6020. [Google Scholar] [CrossRef]
- Shao, Z.; Ye, S.; Tao, S.; Feng, X.; Wang, Y. Experimental study of the effect of liquid nitrogen penetration on damage and fracture characteristics in dry and saturated coals. J. Pet. Sci. Eng. 2021, 201, 108374. [Google Scholar] [CrossRef]
- Zhang, Z.; Mao, J.; Yang, X.; Zhao, J.; Smith, G.S. Advances in waterless fracturing technologies for unconventional reservoirs. Energy Sources Part A Recovery Util. Environ. Eff. 2019, 41, 237–251. [Google Scholar] [CrossRef]
- Gao, H.; Li, H.A. Pore structure characterization, permeability evaluation and enhanced gas recovery techniques of tight gas sandstones. J. Nat. Gas Sci. Eng. 2016, 28, 536–547. [Google Scholar] [CrossRef]
- Hemmati-Sarapardeh, A.; Mohagheghian, E. Modeling interfacial tension and minimum miscibility pressure in paraffin-nitrogen systems: Application to gas injection processes. Fuel 2017, 205, 80–89. [Google Scholar] [CrossRef]
- Qi, E.; Xiong, F.; Cao, Z.; Zhang, Y.; Xue, Y.; Zhang, Z.; Ji, M. Simulation of Gas Fracturing in Reservoirs Based on a Coupled Thermo-Hydro-Mechanical-Damage Model. Appl. Sci. 2024, 14, 1763. [Google Scholar] [CrossRef]
- Wang, B.; Li, H.; Shao, Z.; Chen, S.; Li, X. Investigating the mechanism of rock fracturing induced by high-pressure gas blasting with a hybrid continuum-discontinuum method. Comput. Geotech. 2021, 140, 104445. [Google Scholar] [CrossRef]
- Das, V.; Mukerji, T.; Mavko, G. Numerical simulation of coupled fluid-solid interaction at the pore scale: A digital rock-physics technology. Geophysics 2019, 84, WA71–WA81. [Google Scholar] [CrossRef]
- Cao, Z.; Wang, P.; Li, Z.; Du, F. Migration mechanism of grouting slurry and permeability reduction in mining fractured rock mass. Sci. Rep. 2024, 14, 3446. [Google Scholar]
- Hosking, L.J.; Chen, M.; Thomas, H.R. Numerical analysis of dual porosity coupled thermo-hydro-mechanical behaviour during CO2 sequestration in coal. Int. J. Rock Mech. Min. Sci. 2020, 135, 104473. [Google Scholar] [CrossRef]
- Ogata, S.; Yasuhara, H.; Kinoshita, N.; Inui, T.; Nishira, E.; Kishida, K. Numerical analyses of coupled thermal–hydraulic–mechanical–chemical processes for estimating permeability change in fractured rock induced by alkaline solution. Geomech. Energy Environ. 2022, 31, 100372. [Google Scholar] [CrossRef]
- Teng, T.; Zhao, Y.; Gao, F.; Wang, J.G.; Wang, W. A fully coupled thermo-hydro-mechanical model for heat and gas transfer in thermal stimulation enhanced coal seam gas recovery. Int. J. Heat Mass Transf. 2018, 125, 866–875. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).