Prediction of Diffuse Attenuation Coefficient Based on Informer: A Case Study of Hangzhou Bay and Beibu Gulf
Abstract
1. Introduction
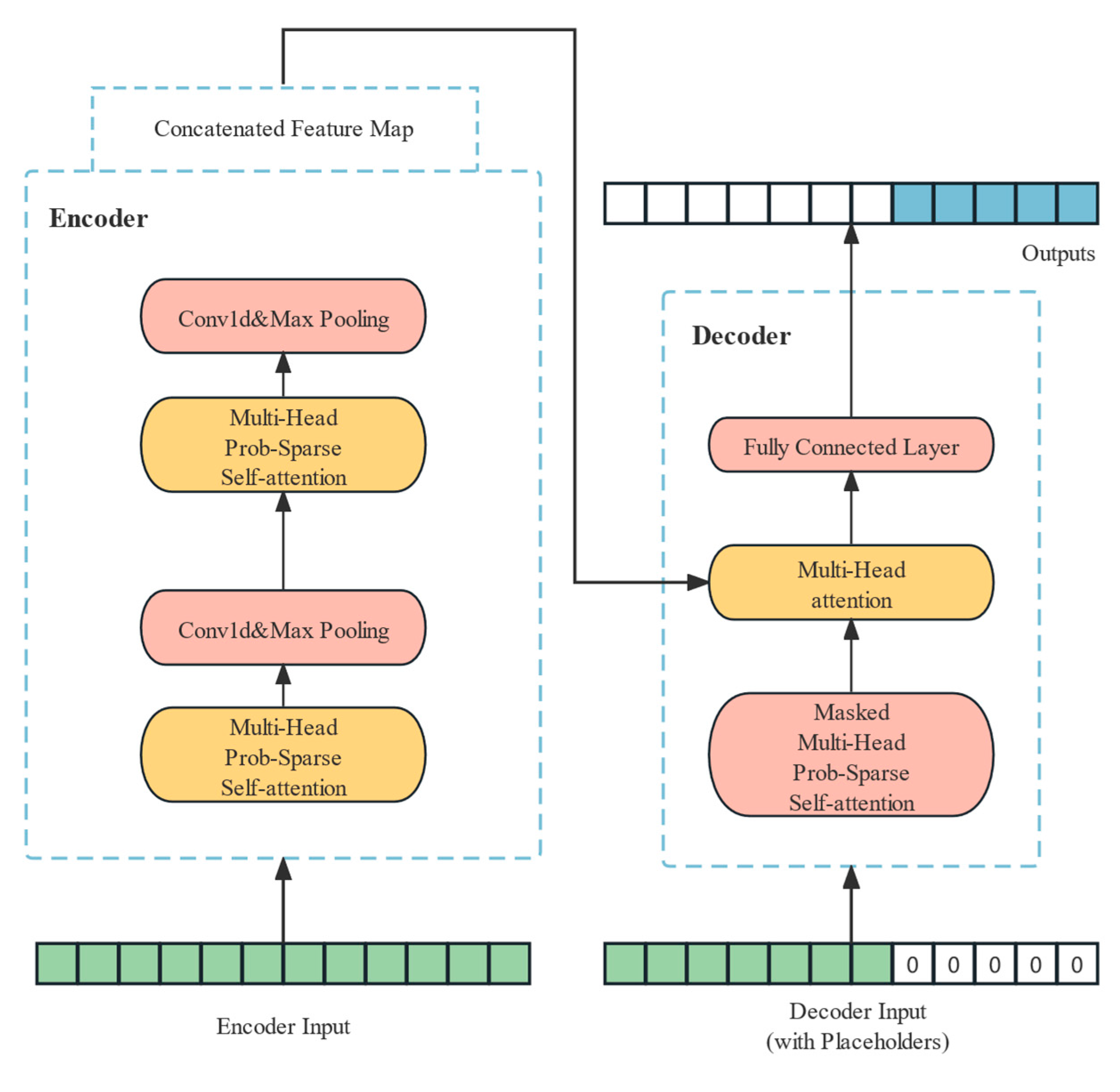
2. Methodology of Informer
2.1. Encoder
2.2. Decoder
3. Experimental Methods
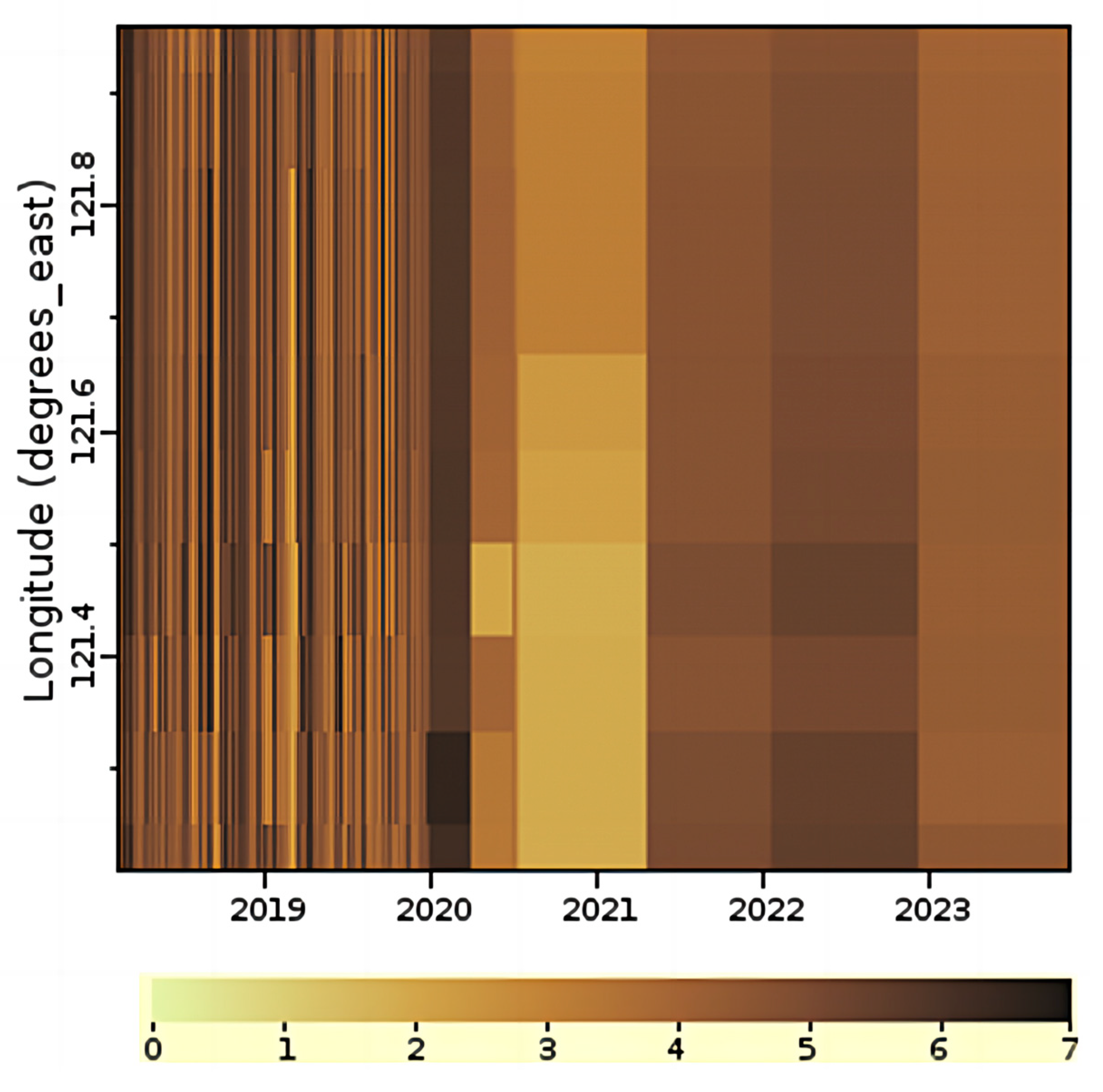
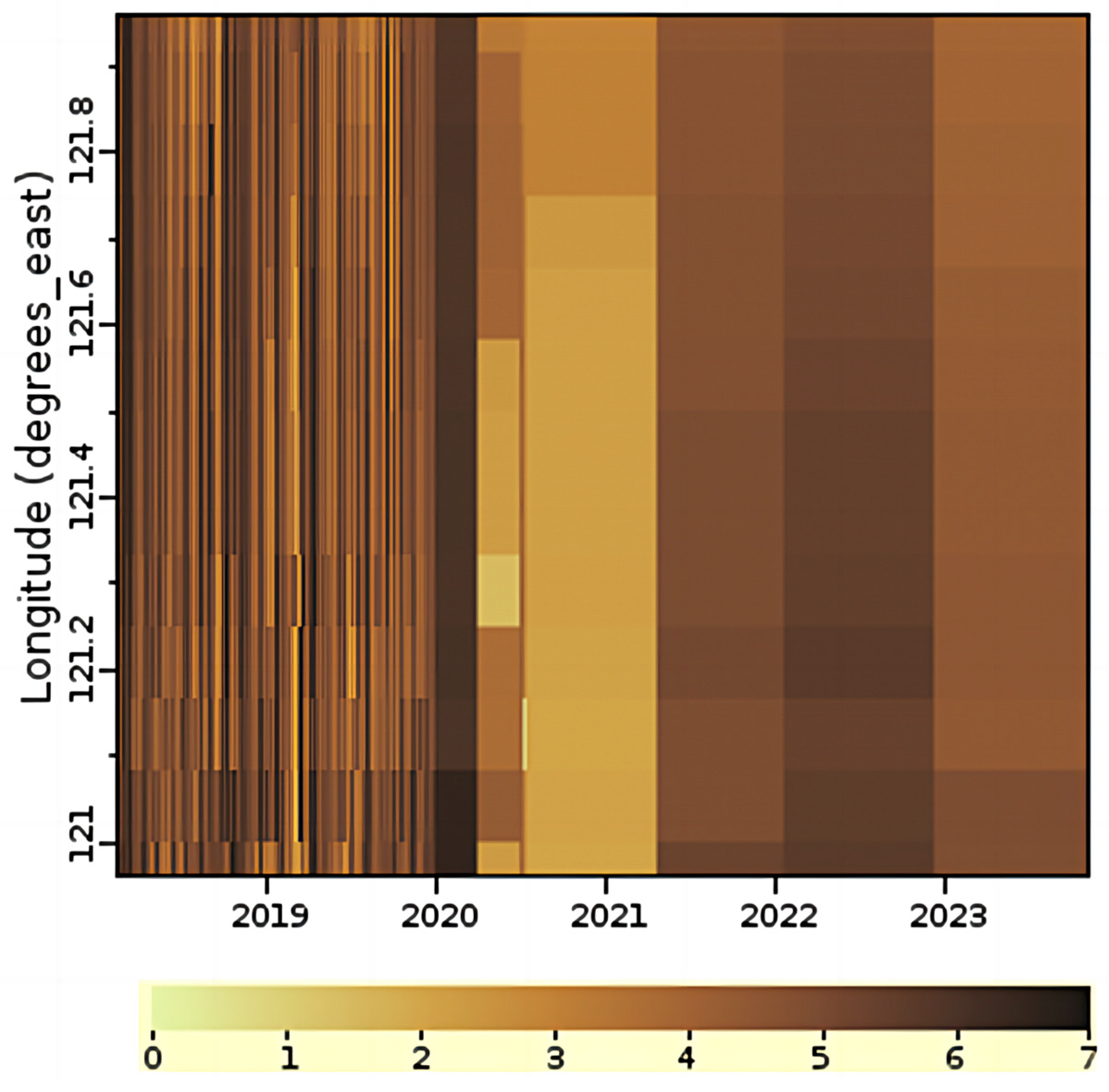
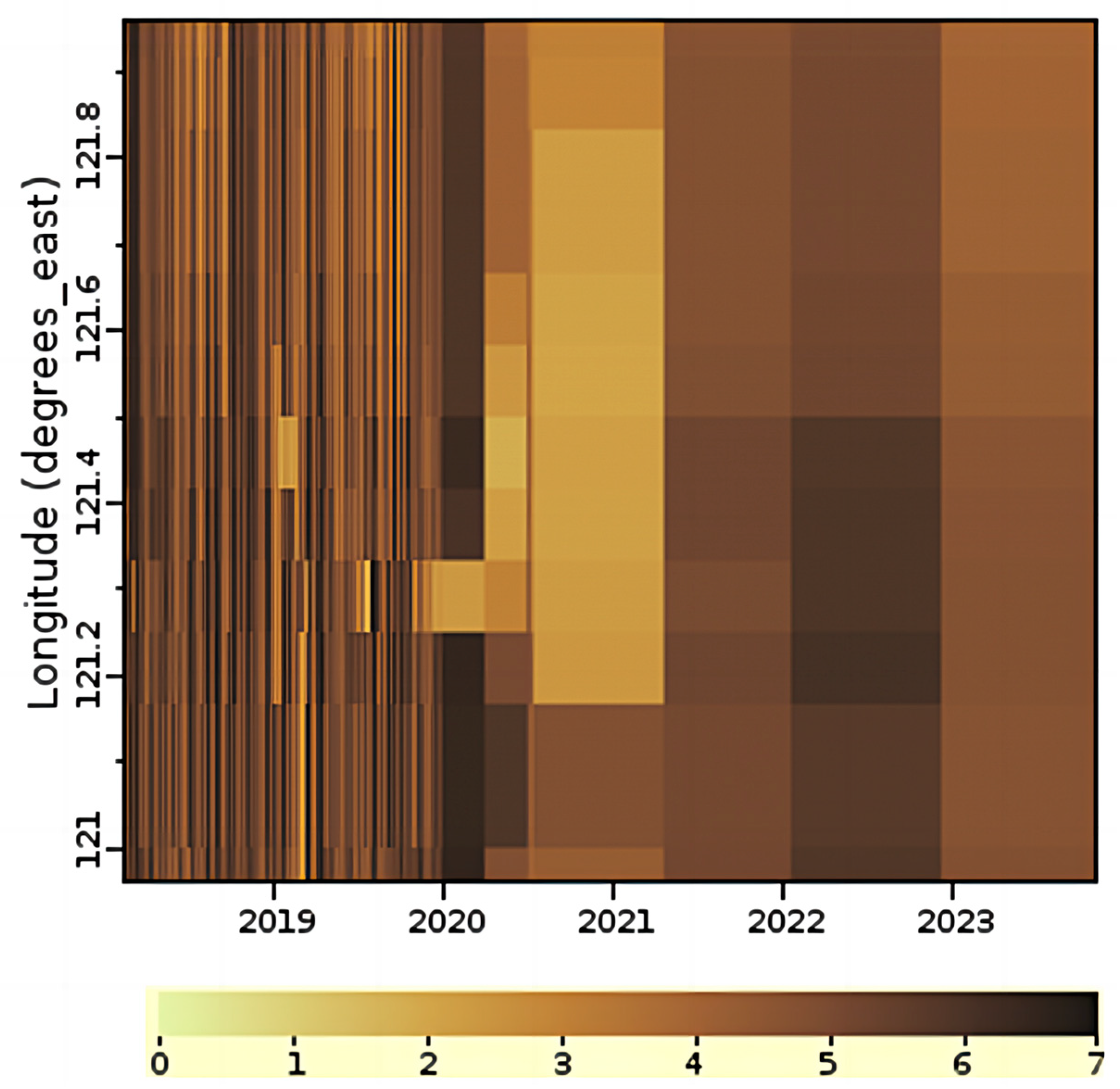
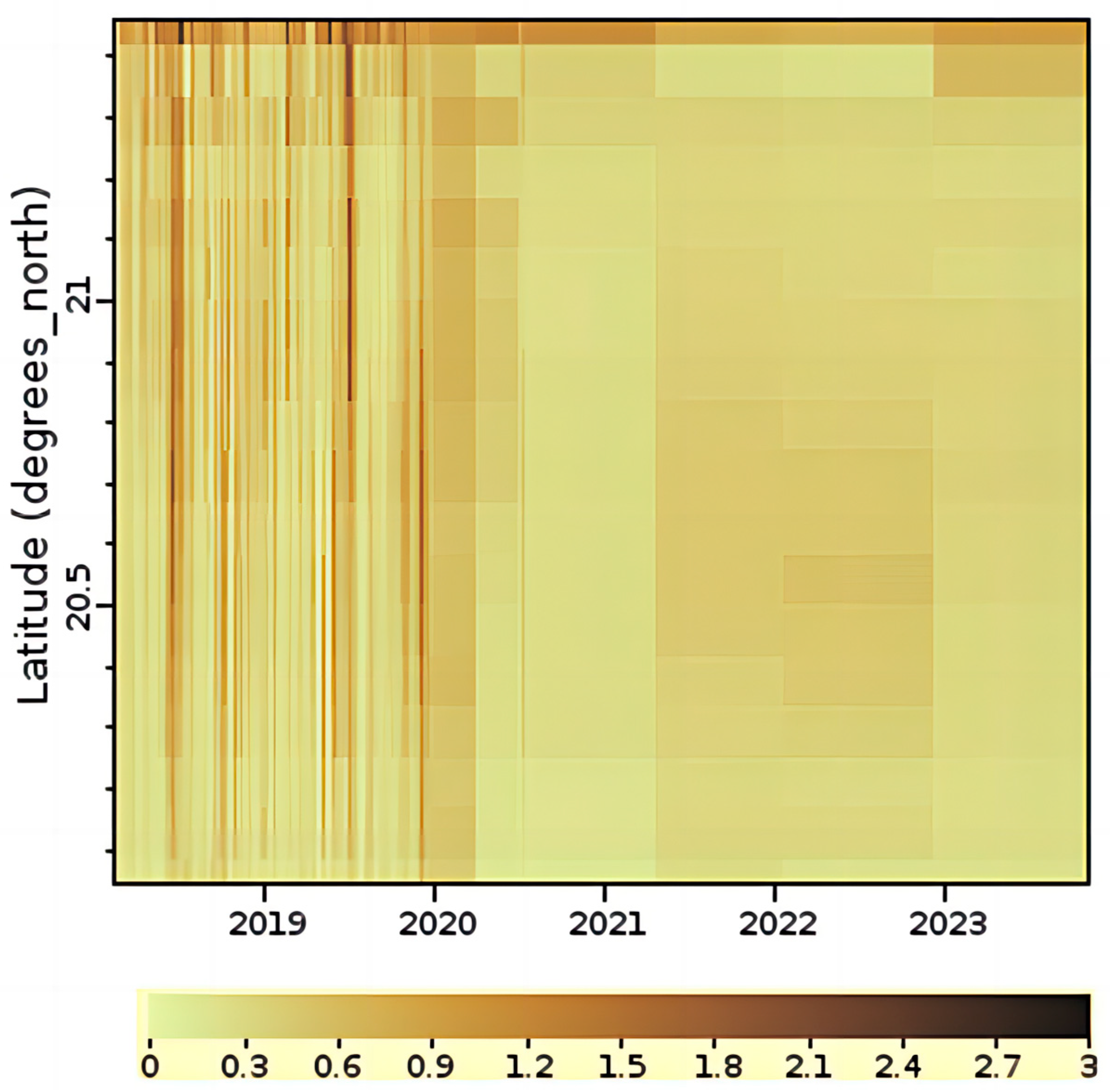
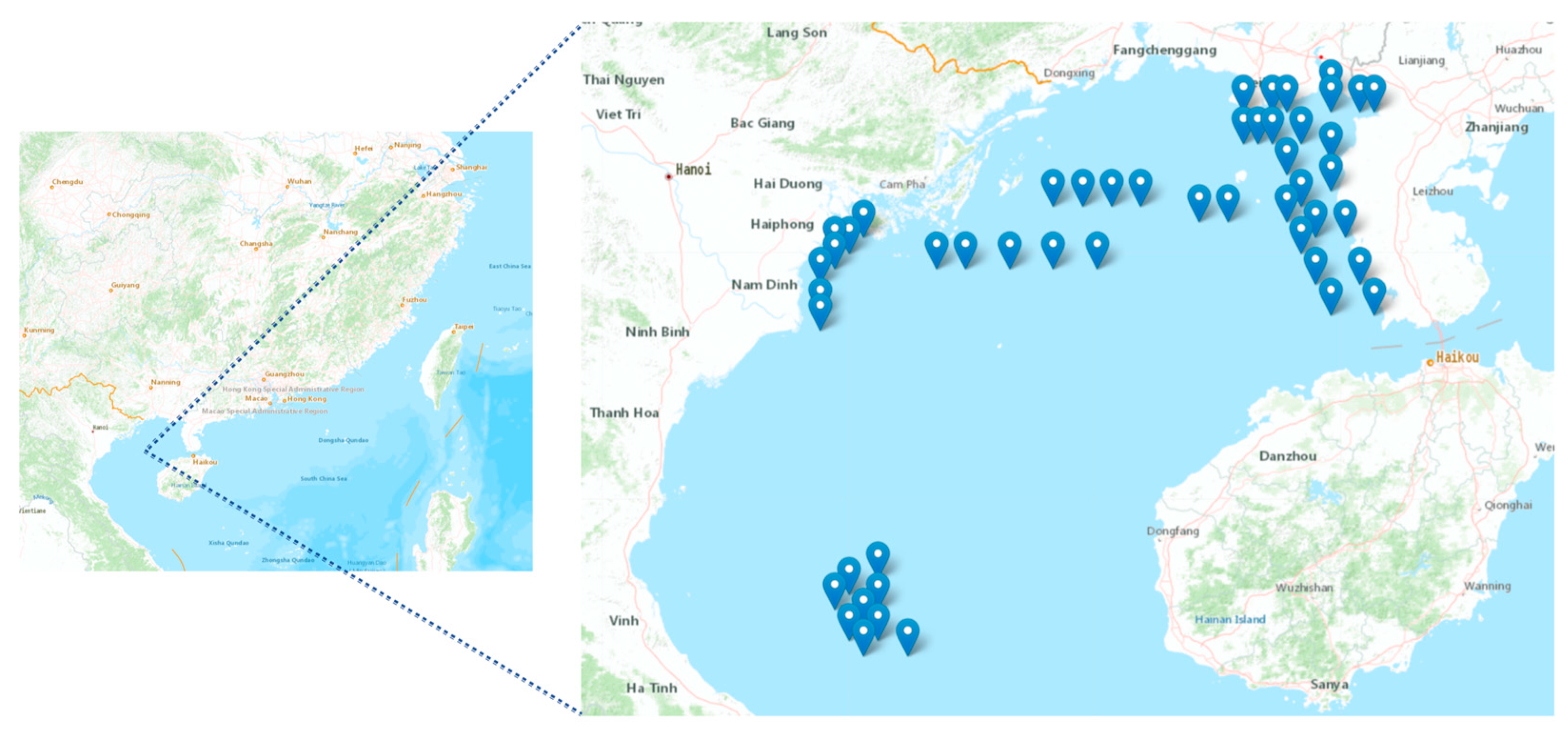
3.1. Study Area
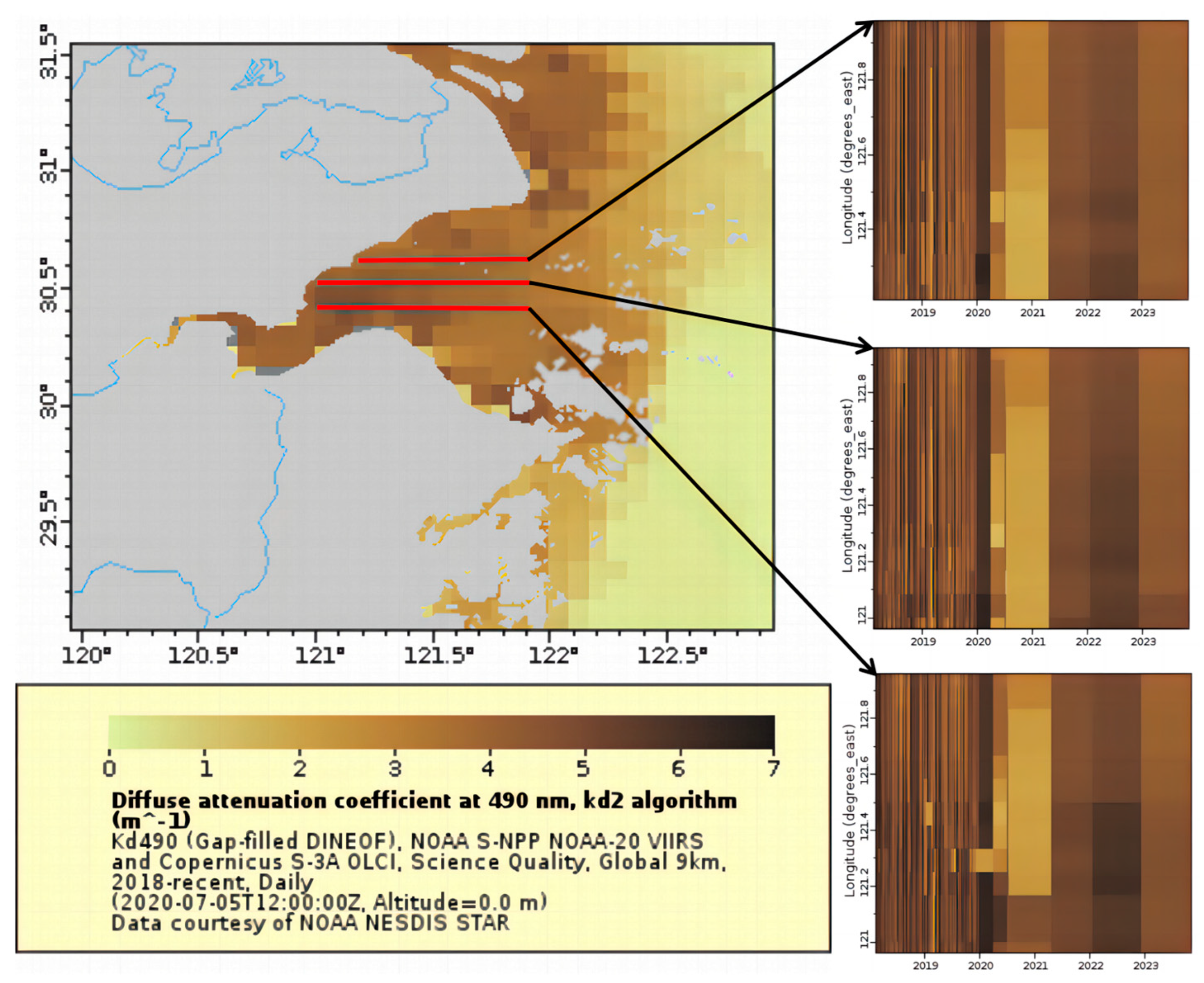
3.1.1. Hangzhou Bay
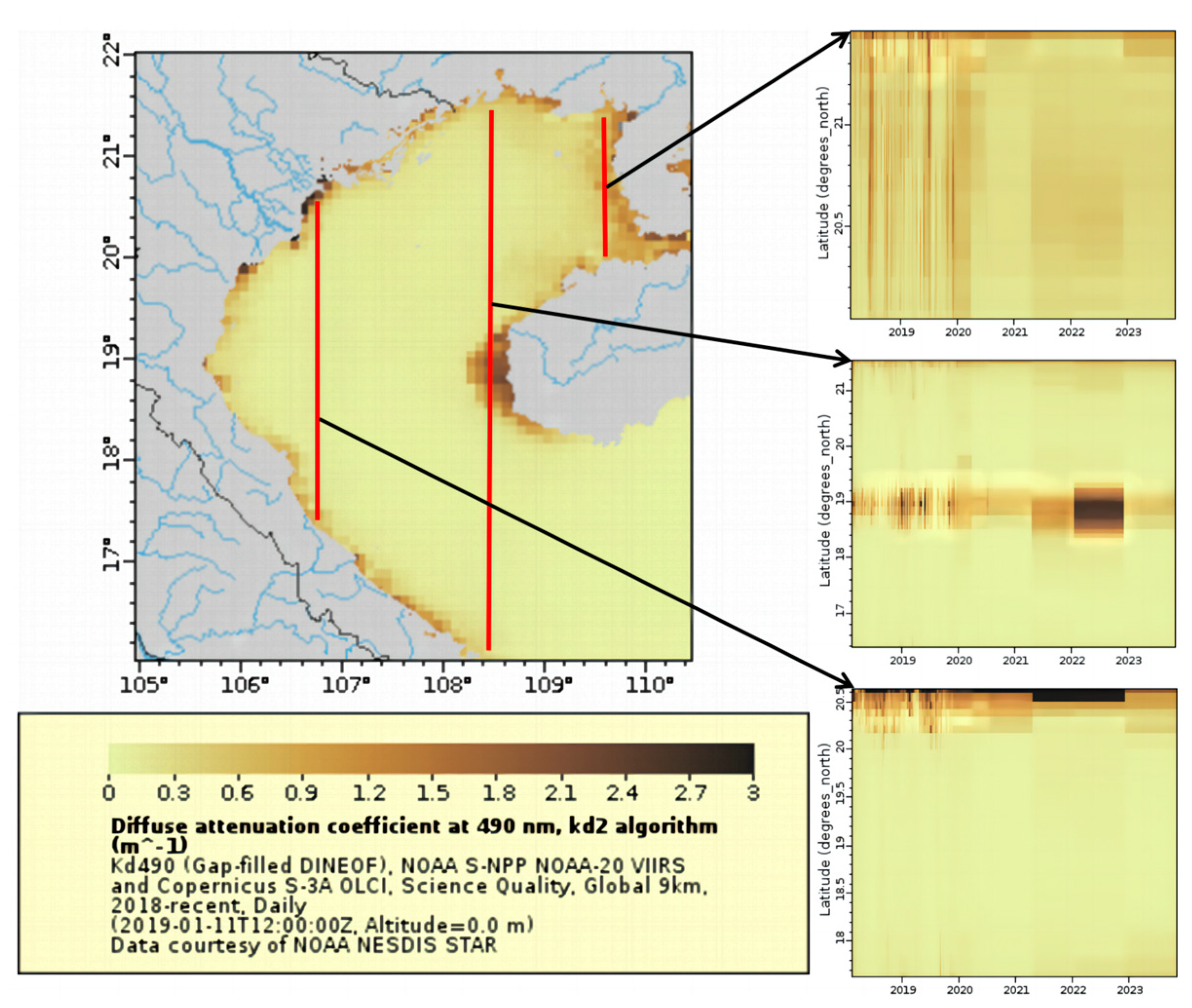
3.1.2. Beibu Gulf
3.2. Experimental Framework
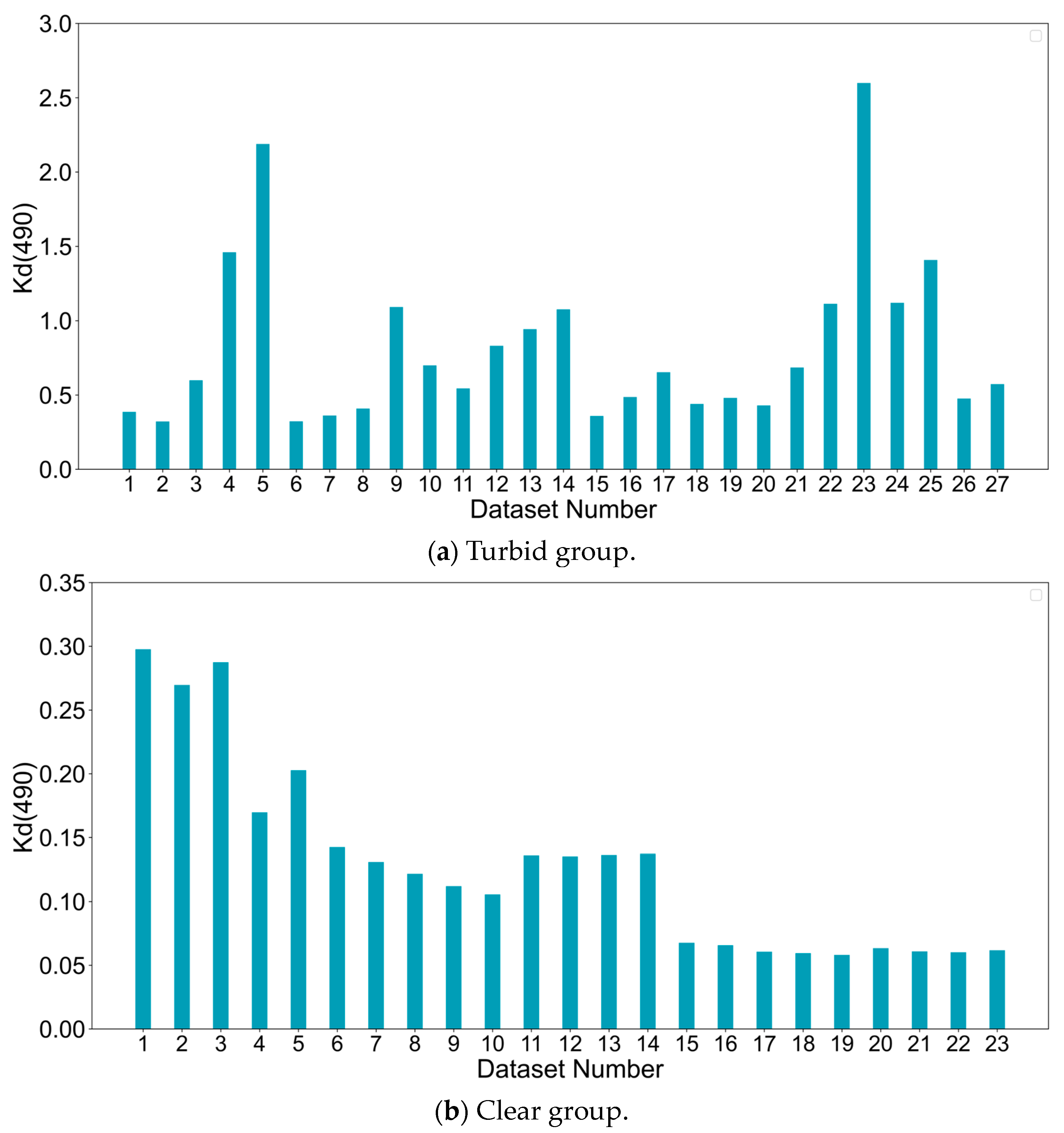
- Data preprocessing: The global daily gap-free Kd(490) product used in this study covers the period from 9 February 2018 to 2 October 2023. The daily global Kd(490) data products are sampled based on the selected study areas. The time-series datasets for Kd(490) are obtained for each study area. The datasets are categorized into 3 groups based on the area location and daily mean Kd(490), i.e., the Hangzhou Bay dataset group, the Beibu Gulf turbid dataset group, and the Beibu Gulf clear dataset group. To address missing values in individual datasets, we use temporal linear interpolation. Additionally, we standardize the time-series data to facilitate model training.
- Data splitting: In this study, we divide the training, validation set, and test set according to the ratio of 7:1:2. The length of the test set spans over a year, which enhances the reliability of the test results to some extent.
- Model training: The RSIKP, ANN, CNN, GRU, LSTM-RNN, and LSTM models are analyzed and compared on the 3 dataset groups mentioned above at 15-day, 30-day, and 60-day prediction steps. It is conducted to identify the model that demonstrates optimal performance.
- Model evaluation: Mean Absolute Error (MAE), Mean Square Error (MSE), and Mean Absolute Percentage Error (MAPE) are commonly used error evaluation metrics. MAE represents the real error between actual values and predicted values and is solely dependent on the data size. MSE guarantees that each term is positive and possesses differentiability. MAPE, which is expressed as a percentage, serves as a valuable metric for comparing predictions across various proportions. The 3 error metrics are expressed aswhere is the i-th actual Kd(490), is the i-th predicted Kd(490), and is the total number of predicted points.
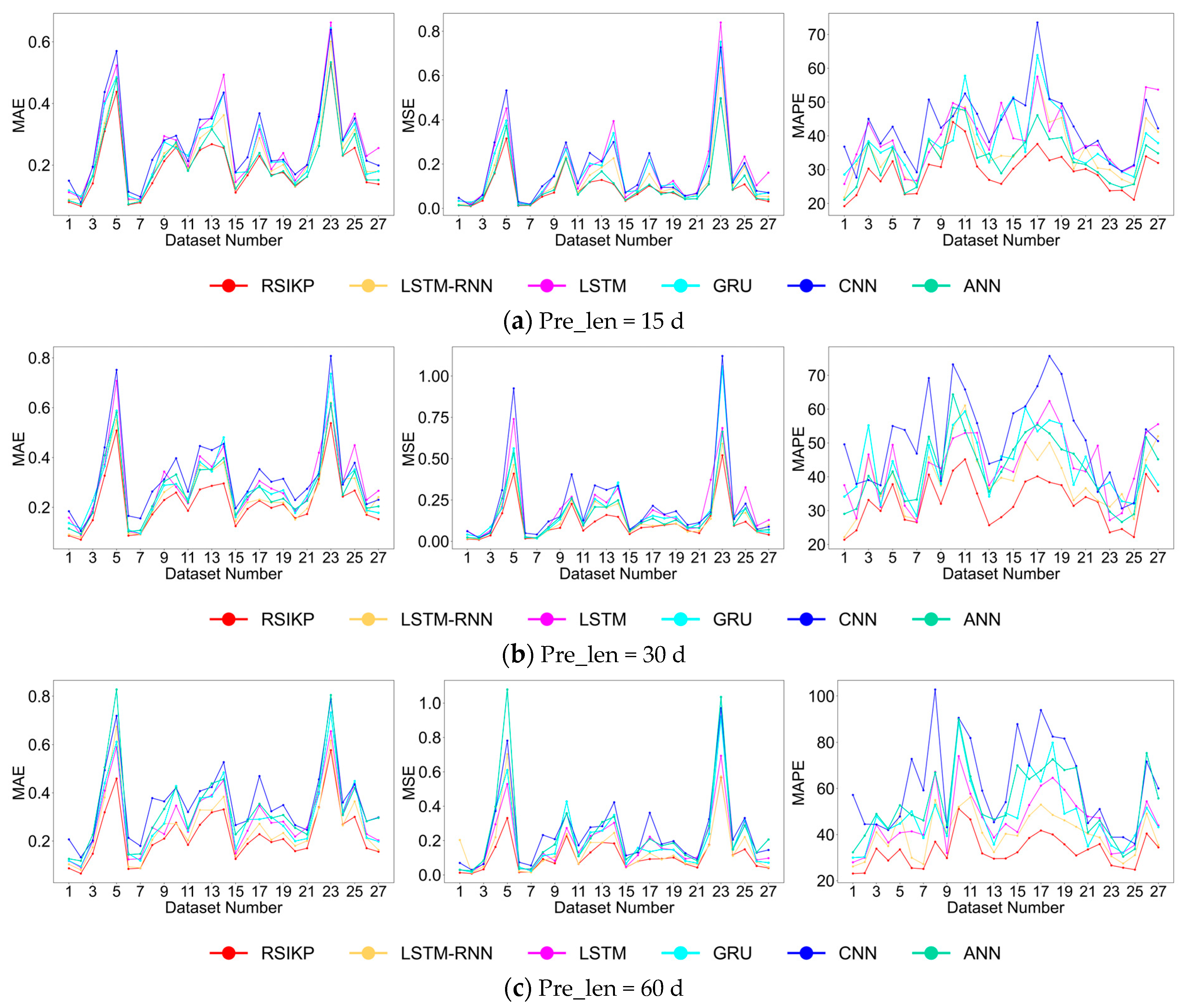
- Results analysis: We visualized the error metrics of each model on different dataset groups. We could then more intuitively compare and analyze the performance of the models. In addition, we analyzed the variation in prediction performance of models as the prediction step increased.
4. Results and Discussion
4.1. Analysis of Error Metrics
4.2. Effect of Prediction Step on Performance
5. Conclusions and Prospects
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Sea Location | Number | Latitude | Longitude |
|---|---|---|---|
| Hangzhou Bay | 1 | 30.792° N | 121.875° E |
| 2 | 30.542° N | 121.875° E | |
| 3 | 30.292° N | 121.875° E | |
| 4 | 30.125° N | 121.875° E | |
| 5 | 30.792° N | 121.708° E | |
| 6 | 30.625° N | 121.708° E | |
| 7 | 30.458° N | 121.708° E | |
| 8 | 30.292° N | 121.708° E | |
| 9 | 30.125° N | 121.708° E | |
| 10 | 30.708° N | 121.542° E | |
| 11 | 30.541° N | 121.542° E | |
| 12 | 30.292° N | 121.542° E | |
| 13 | 30.708° N | 121.458° E | |
| 14 | 30.458° N | 121.458° E | |
| 15 | 30.625° N | 121.375° E | |
| 16 | 30.375° N | 121.375° E | |
| 17 | 30.625° N | 121.292° E | |
| 18 | 30.542° N | 121.208° E | |
| 19 | 30.458° N | 121.042° E | |
| 20 | 30.291° N | 120.875° E | |
| Beibu Gulf | 21 | 21.375° N | 109.125° E |
| 22 | 21.375° N | 109.292° E | |
| 23 | 21.375° N | 109.375° E | |
| 24 | 21.375° N | 109.625° E | |
| 25 | 21.375° N | 109.792° E | |
| 26 | 21.375° N | 109.875° E | |
| 27 | 21.208° N | 109.125° E | |
| 28 | 21.208° N | 109.208° E | |
| 29 | 21.208° N | 109.292° E | |
| 30 | 21.208° N | 109.458° E | |
| 31 | 20.792° N | 108.875° E | |
| 32 | 20.792° N | 109.042° E | |
| 33 | 20.792° N | 109.375° E | |
| 34 | 20.542° N | 107.375° E | |
| 35 | 20.542° N | 107.542° E | |
| 36 | 20.542° N | 107.792° E | |
| 37 | 20.542° N | 108.042° E | |
| 38 | 20.542° N | 108.292° E | |
| 39 | 21.458° N | 109.625° E | |
| 40 | 21.125° N | 109.625° E | |
| 41 | 20.958° N | 109.625° E | |
| 42 | 20.708° N | 109.708° E | |
| 43 | 20.458° N | 109.792° E | |
| 44 | 20.292° N | 109.875° E | |
| 45 | 21.042° N | 109.375° E | |
| 46 | 20.875° N | 109.458° E | |
| 47 | 20.708° N | 109.542° E | |
| 48 | 20.625° N | 109.458° E | |
| 49 | 20.458° N | 109.542° E | |
| 50 | 20.292° N | 109.625° E | |
| 51 | 20.708° N | 106.958° E | |
| 52 | 20.625° N | 106.875° E | |
| 53 | 20.625° N | 106.792° E | |
| 54 | 20.542° N | 106.792° E | |
| 55 | 20.458° N | 106.708° E | |
| 56 | 20.292° N | 106.708° E | |
| 57 | 20.208° N | 106.708° E | |
| 58 | 20.875° N | 108.042° E | |
| 59 | 20.875° N | 108.208° E | |
| 60 | 20.875° N | 108.375° E | |
| 61 | 20.875° N | 108.542° E | |
| 62 | 18.708° N | 106.792° E | |
| 63 | 18.542° N | 106.875° E | |
| 64 | 18.625° N | 106.958° E | |
| 65 | 18.708° N | 107.042° E | |
| 66 | 18.458° N | 107.208° E | |
| 67 | 18.792° N | 106.875° E | |
| 68 | 18.875° N | 107.042° E | |
| 69 | 18.542° N | 107.042° E | |
| 70 | 18.458° N | 106.958° E |


References
- Kumar, L.; Afzal, M.S.; Ahmad, A. Prediction of water turbidity in a marine environment using machine learning: A case study of Hong Kong. Reg. Stud. Mar. Sci. 2022, 52, 102260. [Google Scholar] [CrossRef]
- Ahmed, A.N.; Othman, F.B.; Afan, H.A.; Ibrahim, R.K.; Fai, C.M.; Hossain, M.S.; Ehteram, M.; Elshafie, A. Machine learning methods for better water quality prediction. J. Hydrol. 2019, 578, 124084. [Google Scholar] [CrossRef]
- Noori, N.; Kalin, L.; Isik, S. Water quality prediction using SWAT-ANN coupled approach. J. Hydrol. 2020, 590, 125220. [Google Scholar] [CrossRef]
- Dritsas, E.; Trigka, M. Efficient Data-Driven Machine Learning Models for Water Quality Prediction. Computation 2023, 11, 16. [Google Scholar] [CrossRef]
- García-Alba, J.; Bárcena, J.F.; Ugarteburu, C.; García, A. Artificial neural networks as emulators of process-based models to analyse bathing water quality in estuaries. Water Res. 2019, 150, 283–295. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Yang, Y.; Nishiura, H.; Saitoh, M. Deep learning for epidemiological predictions. In Proceedings of the 41st International ACM SIGIR Conference on Research and Development in Information Retrieval, Ann Arbor, MI, USA, 8–12 July 2018; pp. 1085–1088. [Google Scholar]
- Zhou, J.; Wang, Y.; Xiao, F.; Wang, Y.; Sun, L. Water quality prediction method based on IGRA and LSTM. Water 2018, 10, 1148. [Google Scholar] [CrossRef]
- Arepalli, P.G.; Akula, M.; Kalli, R.S.; Kolli, A.; Popuri, V.P.; Chalichama, S. Water quality prediction for salmon fish using gated recurrent unit (GRU) model. In Proceedings of the 2022 Second International Conference on Computer Science, Engineering and Applications (ICCSEA), Gunupur, India, 8 September 2022; pp. 1–5. [Google Scholar]
- Liu, X.; Wang, M. Global daily gap-free ocean color products from multi-satellite measurements. Int. J. Appl. Earth Obs. Geoinf. 2022, 108, 102714. [Google Scholar] [CrossRef]
- Lund-Hansen, L.C. Diffuse attenuation coefficients Kd (PAR) at the estuarine North Sea–Baltic Sea transition: Time-series, partitioning, absorption, and scattering. Estuar. Coast. Shelf Sci. 2004, 61, 251–259. [Google Scholar] [CrossRef]
- Wang, W.; Zhao, J. Variation of Diffuse Attenuation Coefficient of Downwelling Irradiance in the Arctic Ocean. Acta Oceanol. Sin. 2014, 33, 53–62. [Google Scholar] [CrossRef]
- Prieur, L.; Sathyendranath, S. An optical classification of coastal and oceanic waters based on the specific spectral absorption curves of phytoplankton pigments, dissolved organic matter, and other particulate materials. Limnol. Oceanogr. 1981, 26, 671–689. [Google Scholar] [CrossRef]
- Pope, R.M.; Fry, E.S. Absorption spectrum (380–700 nm) of pure water. II. Integrating cavity measurements. Appl. Opt. 1997, 36, 8710–8723. [Google Scholar] [CrossRef] [PubMed]
- Shi, W.; Wang, M. Characterization of global ocean turbidity from Moderate Resolution Imaging Spectroradiometer ocean color observations. J. Geophys. Res. Ocean. 2010, 115, C11022. [Google Scholar] [CrossRef]
- Rodríguez-López, L.; González-Rodríguez, L.; Duran-Llacer, I.; García, W.; Cardenas, R.; Urrutia, R. Assessment of the Diffuse Attenuation Coefficient of Photosynthetically Active Radiation in a Chilean Lake. Remote Sens. 2022, 14, 4568. [Google Scholar] [CrossRef]
- Bardaji, R.; Sánchez, A.-M.; Simon, C.; Wernand, M.R.; Piera, J. Estimating the underwater diffuse attenuation coefficient with a low-cost instrument: The KdUINO DIY buoy. Sensors 2016, 16, 373. [Google Scholar] [CrossRef] [PubMed]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st Annual Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of the Thirty-Fifth AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021. [Google Scholar]
- Rahhal, M.M.A.; Bazi, Y.; Alsharif, N.A.; Bashmal, L.; Alajlan, N.; Melgani, F. Multilanguage Transformer for Improved Text to Remote Sensing Image Retrieval. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 9115–9126. [Google Scholar] [CrossRef]
- Bi, C.; Ren, P.; Yin, T.; Zhang, Y.; Li, B.; Xiang, Z. An Informer Architecture-Based Ionospheric foF2 Model in the Middle Latitude Region. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1005305. [Google Scholar] [CrossRef]
- Fang, Z.; Feng, T.; Qin, G.; Meng, Y.; Zhao, S.; Yang, G.; Wang, L.; Sun, W. Simulations of water pollutants in the Hangzhou Bay, China: Hydrodynamics, characteristics, and sources. Mar. Pollut. Bull. 2024, 200, 116140. [Google Scholar] [CrossRef]
- Qinghui, M.; Lin, W.; Zhihua, M. Preliminary study on the application of HJ CCD imagery to water quality assessment for Hangzhou Bay. Guangxi Sci. 2015, 22, 322–328. [Google Scholar]
- Luo, Z.L.; Yang, C.P.; Wang, L.M.; Liu, Y.; Shan, B.B.; Liu, M.T.; Chen, C.; Guo, T.; Sun, D. Relationships between Fish Community Structure and Environmental Factors in the Nearshore Waters of Hainan Island, South China. Diversity 2023, 15, 901. [Google Scholar] [CrossRef]
- Haghiabi, A.H.; Nasrolahi, A.H.; Parsaie, A. Water quality prediction using machine learning methods. Water Qual. Res. J. Can. 2018, 25, 23–28. [Google Scholar] [CrossRef]
- Qiu, Z.; Wu, T.; Su, Y. Retrieval of diffuse attenuation coefficient in the China seas from surface reflectance. Opt. Express 2013, 21, 15287–15297. [Google Scholar] [CrossRef] [PubMed]






| Parameters | Description | Value |
|---|---|---|
| gpu | GPU | cuda1 |
| loss | loss function | “mse” |
| patience | early stopping patience | 3 |
| inverse | inverse of data | True |
| enc_in | encoder input size | 1 |
| dec_in | decoder input size | 1 |
| dec_out | decoder output size | 1 |
| n_heads | numbers of heads | 8 |
| d_model | model dimension | 512 |
| dropout | dropout | 0.05 |
| batch_size | Batch size | 32 |
| enc_layers | layers of encoder | 2 |
| dec_layers | layers of decoder | 1 |
| seq_length | sequence length | 15–90 |
| lab_length | lable length | 7–60 |
| pre_length | prediction length | 7–60 |
| train_epochs | train epochs | 500 |
| learning_rate | leaning rate | 0.0001 |
| pre_len Model | RSIKP | ANN | CNN | GRU | LSTM-RNN | LSTM | |
|---|---|---|---|---|---|---|---|
| 15 d | MAE | 0.5219 | 0.5302 | 0.6615 | 0.6487 | 0.5808 | 0.6552 |
| MSE | 0.4471 | 0.4604 | 0.7124 | 0.6912 | 0.5582 | 0.7147 | |
| MAPE | 13.0709 | 13.5310 | 16.7819 | 16.4885 | 14.8375 | 16.5615 | |
| 30 d | MAE | 0.5517 | 0.6107 | 0.7285 | 0.6795 | 0.6104 | 0.7061 |
| MSE | 0.4763 | 0.5993 | 0.8511 | 0.7442 | 0.6036 | 0.7867 | |
| MAPE | 13.8742 | 15.6400 | 18.4566 | 17.4800 | 15.5915 | 18.0747 | |
| 60 d | MAE | 0.5437 | 0.7433 | 0.8087 | 0.7312 | 0.6629 | 0.7106 |
| MSE | 0.4676 | 0.8845 | 1.0333 | 0.8273 | 0.6986 | 0.8046 | |
| MAPE | 14.3187 | 19.0921 | 20.7217 | 19.2146 | 17.2930 | 18.6928 | |
| pre_len Model | RSIKP | ANN | CNN | GRU | LSTM-RNN | LSTM | |
|---|---|---|---|---|---|---|---|
| 15 d | MAE | 0.2023 | 0.2137 | 0.2740 | 0.2530 | 0.2317 | 0.2667 |
| MSE | 0.0973 | 0.1046 | 0.1682 | 0.1578 | 0.1258 | 0.1733 | |
| MAPE | 29.5971 | 33.3157 | 42.6953 | 38.3391 | 35.8097 | 39.6464 | |
| 30 d | MAE | 0.2217 | 0.2687 | 0.3237 | 0.2812 | 0.2546 | 0.2922 |
| MSE | 0.1132 | 0.1536 | 0.2234 | 0.1811 | 0.1404 | 0.1929 | |
| MAPE | 32.5673 | 42.2344 | 51.6866 | 43.4737 | 39.4721 | 43.6236 | |
| 60 d | MAE | 0.2262 | 0.3373 | 0.3635 | 0.3028 | 0.2588 | 0.2941 |
| MSE | 0.1168 | 0.2372 | 0.2483 | 0.2000 | 0.1525 | 0.1815 | |
| MAPE | 32.9484 | 53.8294 | 61.9271 | 48.2803 | 40.1906 | 46.1878 | |
| pre_len Model | RSIKP | ANN | CNN | GRU | LSTM-RNN | LSTM | |
|---|---|---|---|---|---|---|---|
| 15 d | MAE | 0.0284 | 0.0295 | 0.0374 | 0.0340 | 0.0311 | 0.0346 |
| MSE | 0.0038 | 0.0040 | 0.0063 | 0.0062 | 0.0048 | 0.0051 | |
| MAPE | 18.6176 | 19.6451 | 24.9659 | 22.2344 | 20.7147 | 22.9925 | |
| 30 d | MAE | 0.0324 | 0.0395 | 0.0489 | 0.0391 | 0.0355 | 0.0434 |
| MSE | 0.0045 | 0.0063 | 0.0089 | 0.0057 | 0.0051 | 0.0081 | |
| MAPE | 22.1245 | 27.1191 | 34.1425 | 28.6891 | 25.3383 | 30.1258 | |
| 60 d | MAE | 0.0313 | 0.0532 | 0.0635 | 0.0426 | 0.0378 | 0.0426 |
| MSE | 0.0039 | 0.0096 | 0.0126 | 0.0065 | 0.0059 | 0.0071 | |
| MAPE | 22.1100 | 39.3913 | 47.4426 | 31.3254 | 28.1619 | 30.0850 | |
| Dataset Group | Change Rate | RSIKP | ANN | LSTM-RNN | |
|---|---|---|---|---|---|
| Hangzhou Bay | 15–30 d | GMAE | 5.7099 | 15.1829 | 5.0964 |
| GMSE | 6.5310 | 30.1694 | 8.1333 | ||
| GMAPE | 6.1457 | 15.5864 | 5.0817 | ||
| 30–60 d | GMAE | −1.4501 | 21.7128 | 8.6009 | |
| GMSE | −1.8266 | 47.5889 | 15.7389 | ||
| GMAPE | 3.2038 | 22.0723 | 10.9130 | ||
| 15–60 d | GMAE | 4.1770 | 40.1924 | 14.1357 | |
| GMSE | 4.5851 | 92.1156 | 25.1523 | ||
| GMAPE | 9.5464 | 41.0990 | 16.5493 | ||
| Beibu Gulf turbid | 15–30 d | GMAE | 9.5897 | 25.7370 | 9.8835 |
| GMSE | 16.3412 | 46.8451 | 11.6057 | ||
| GMAPE | 10.0354 | 26.7703 | 10.2274 | ||
| 30–60 d | GMAE | 2.0298 | 25.5303 | 1.6496 | |
| GMSE | 3.1802 | 54.4271 | 8.6182 | ||
| GMAPE | 1.1702 | 27.4539 | 1.8203 | ||
| 15–60 d | GMAE | 11.8141 | 57.8381 | 11.6962 | |
| GMSE | 20.0411 | 126.7686 | 21.2242 | ||
| GMAPE | 11.3231 | 61.5737 | 12.2338 | ||
| Beibu Gulf clear | 15–30 d | GMAE | 14.0845 | 33.8983 | 14.1479 |
| GMSE | 18.4211 | 57.5000 | 6.2500 | ||
| GMAPE | 18.8365 | 38.0451 | 22.3204 | ||
| 30–60 d | GMAE | −3.3951 | 34.6835 | 6.4789 | |
| GMSE | −13.3333 | 52.3810 | 15.6863 | ||
| GMAPE | −0.0655 | 45.2530 | 11.1436 | ||
| 15–60 d | GMAE | 10.2113 | 80.3390 | 21.5434 | |
| GMSE | 2.6316 | 140.0000 | 22.9167 | ||
| GMAPE | 18.7586 | 100.5146 | 35.9513 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, R.; Hu, M.; Geng, X.; Ibrahim, M.K.; Wang, C. Prediction of Diffuse Attenuation Coefficient Based on Informer: A Case Study of Hangzhou Bay and Beibu Gulf. Water 2024, 16, 1279. https://doi.org/10.3390/w16091279
Cai R, Hu M, Geng X, Ibrahim MK, Wang C. Prediction of Diffuse Attenuation Coefficient Based on Informer: A Case Study of Hangzhou Bay and Beibu Gulf. Water. 2024; 16(9):1279. https://doi.org/10.3390/w16091279
Chicago/Turabian StyleCai, Rongyang, Miao Hu, Xiulin Geng, Mohammed K. Ibrahim, and Chunhui Wang. 2024. "Prediction of Diffuse Attenuation Coefficient Based on Informer: A Case Study of Hangzhou Bay and Beibu Gulf" Water 16, no. 9: 1279. https://doi.org/10.3390/w16091279
APA StyleCai, R., Hu, M., Geng, X., Ibrahim, M. K., & Wang, C. (2024). Prediction of Diffuse Attenuation Coefficient Based on Informer: A Case Study of Hangzhou Bay and Beibu Gulf. Water, 16(9), 1279. https://doi.org/10.3390/w16091279







