Application of One-Dimensional Hydrodynamic Coupling Model in Complex River Channels: Taking the Yongding River as an Example
Abstract
1. Introduction
2. Materials and Methods
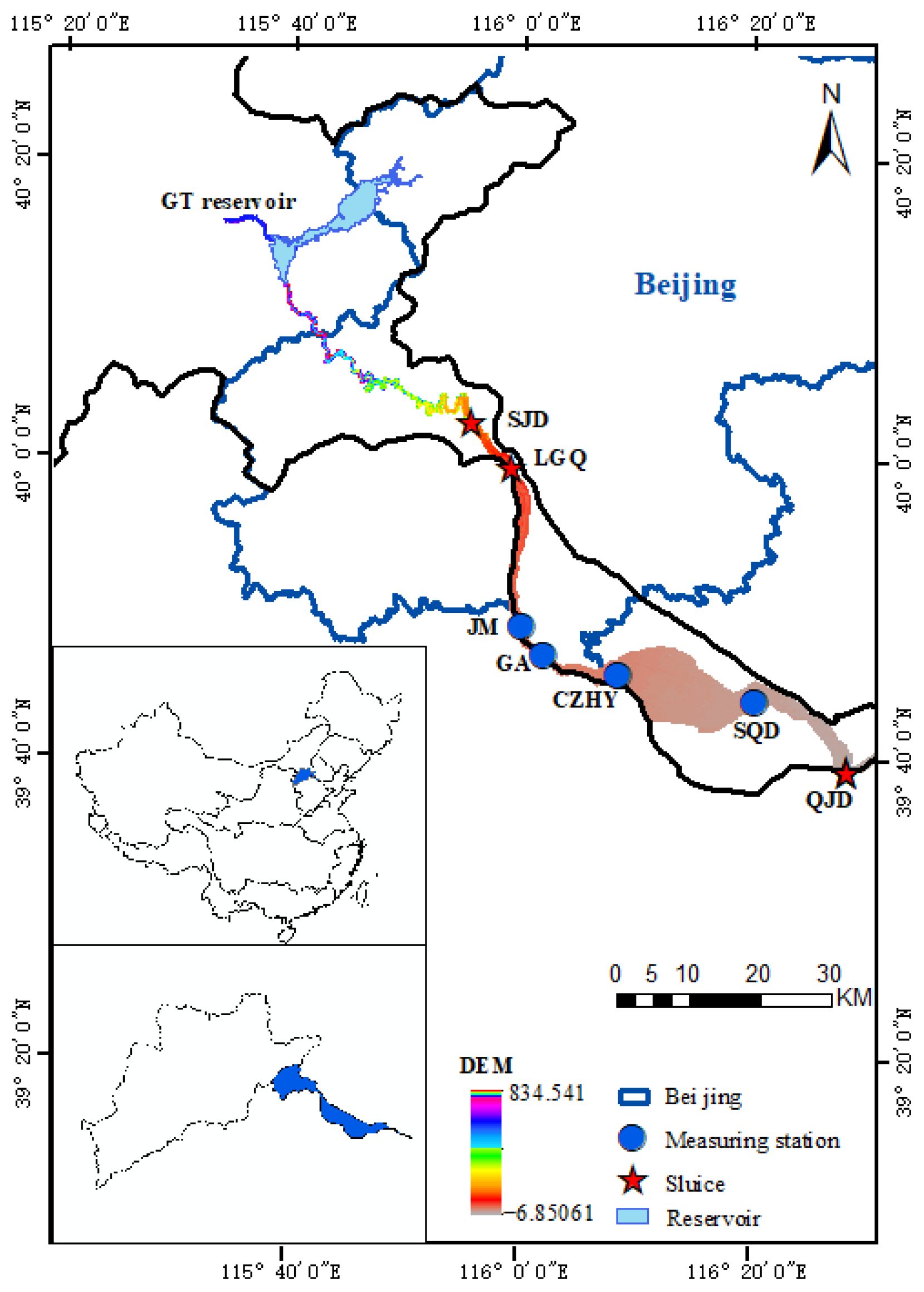
2.1. Study Area
2.2. Basic Data
2.3. Methods
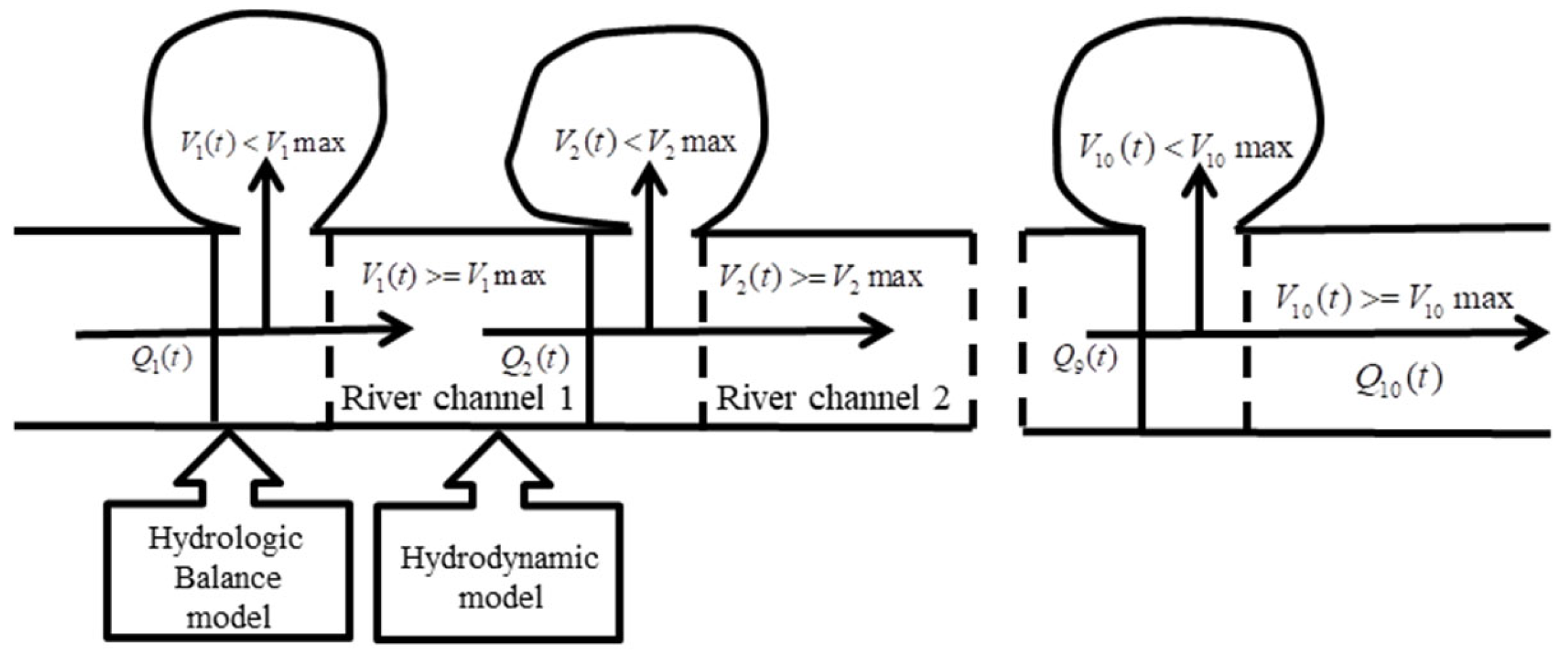
2.3.1. One-Dimensional Hydrodynamic Modelling of Natural River Channels
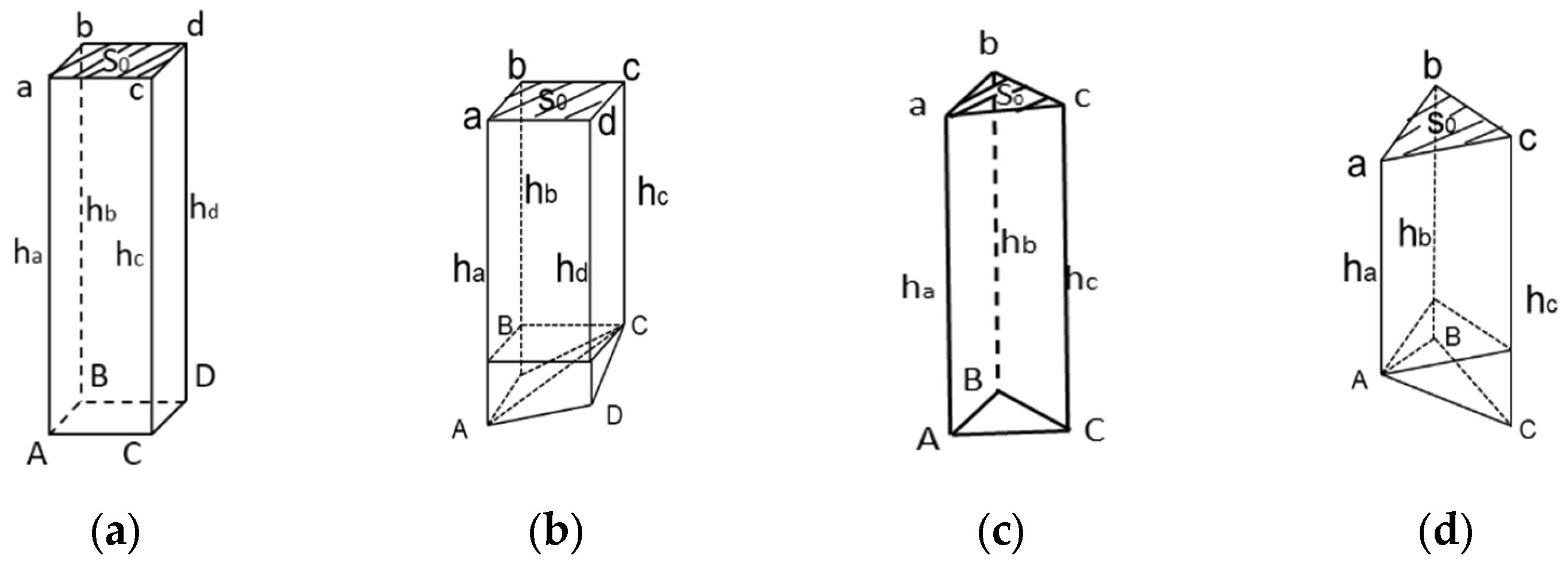
2.3.2. Modelling Water Level and Storage Curve Calculations
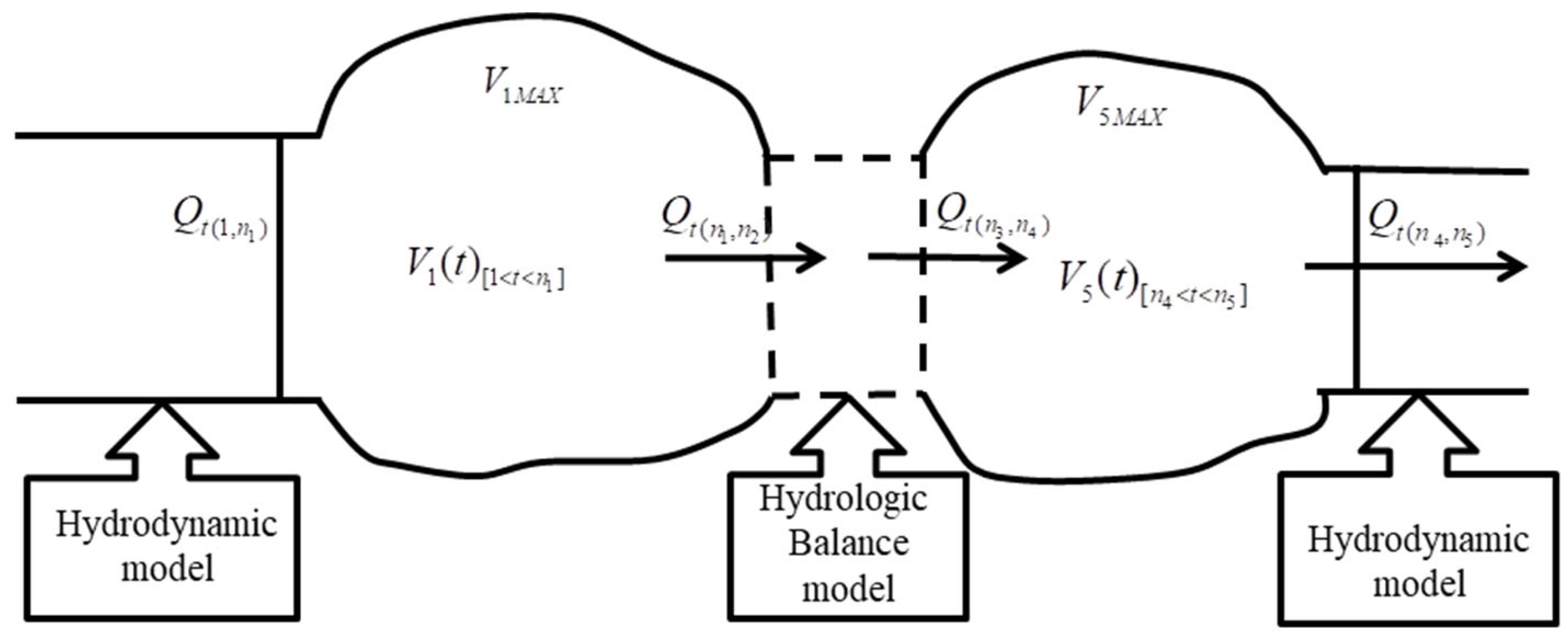
2.3.3. One-Dimensional Hydrodynamic Model with Coupled Control Project Rules
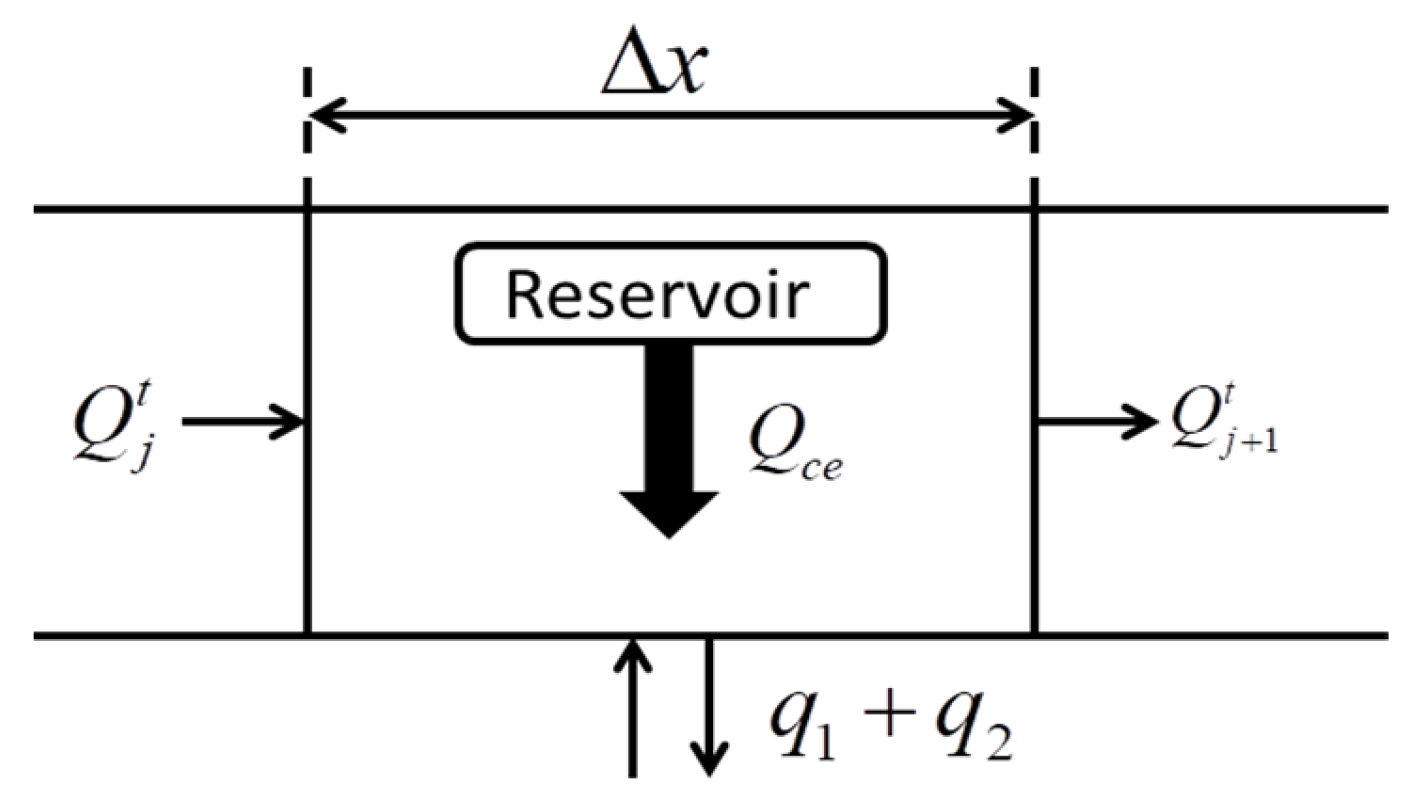
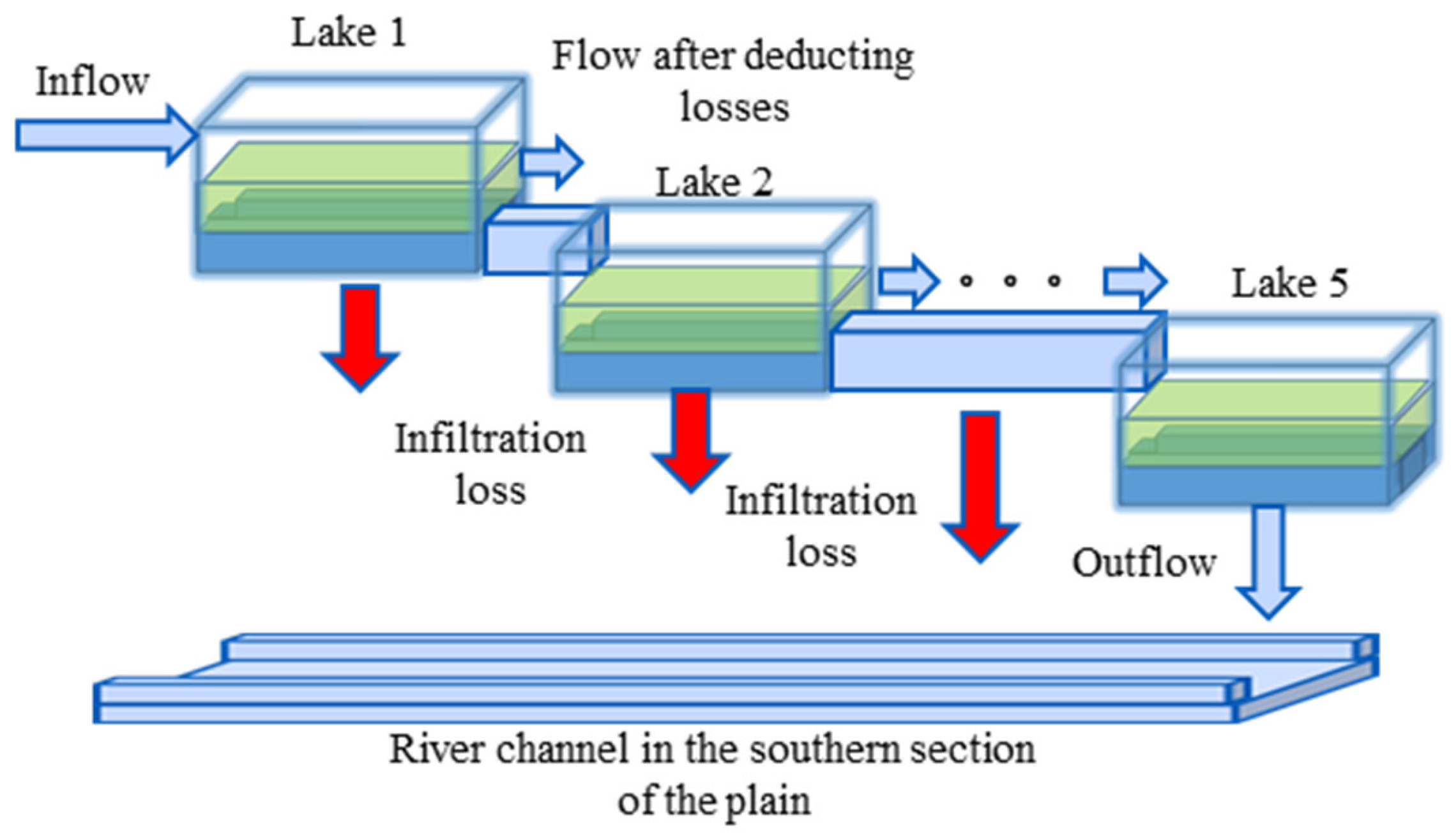
2.3.4. One-Dimensional Hydrodynamic Modelling of Coupled Water Balance
2.3.5. Spatial Coupling of Nodes
3. Results
3.1. Sectional Roughness Calibration for River Channel
3.2. River Infiltration Calibration
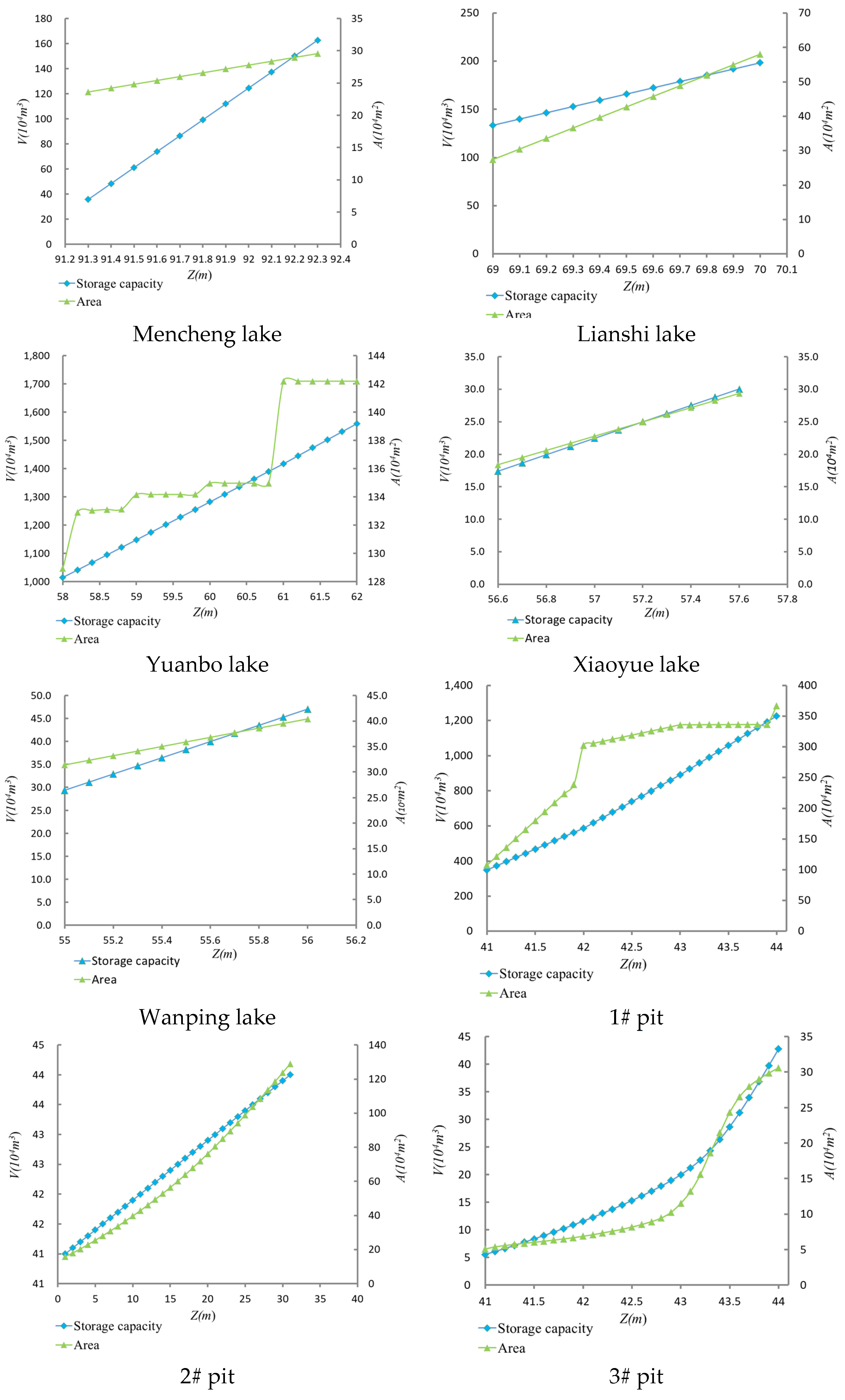
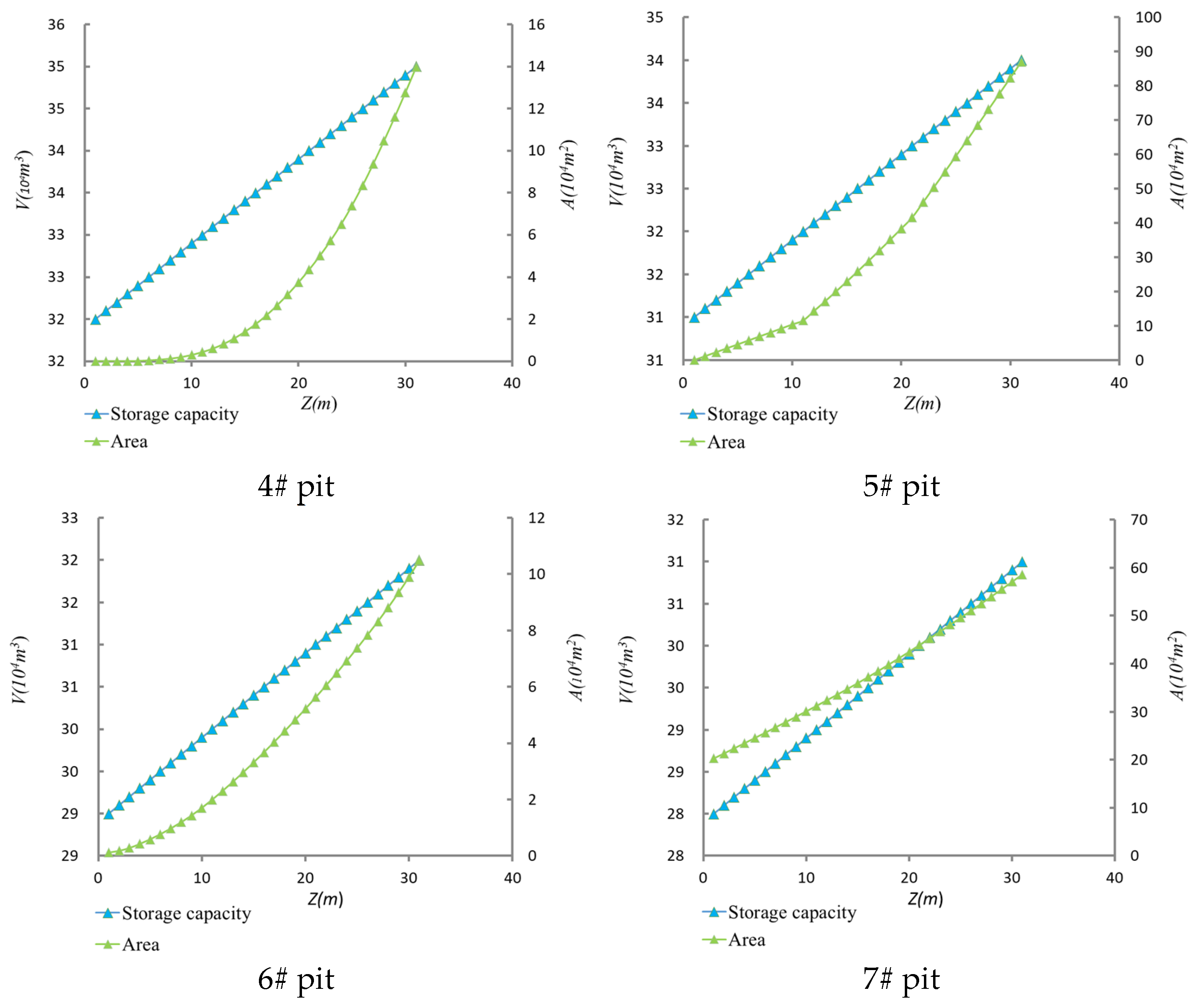
3.3. Water Level Storage Curves of Lakes and Gravel Pits
4. Discussion
4.1. Simulation Results of Water Flow Time
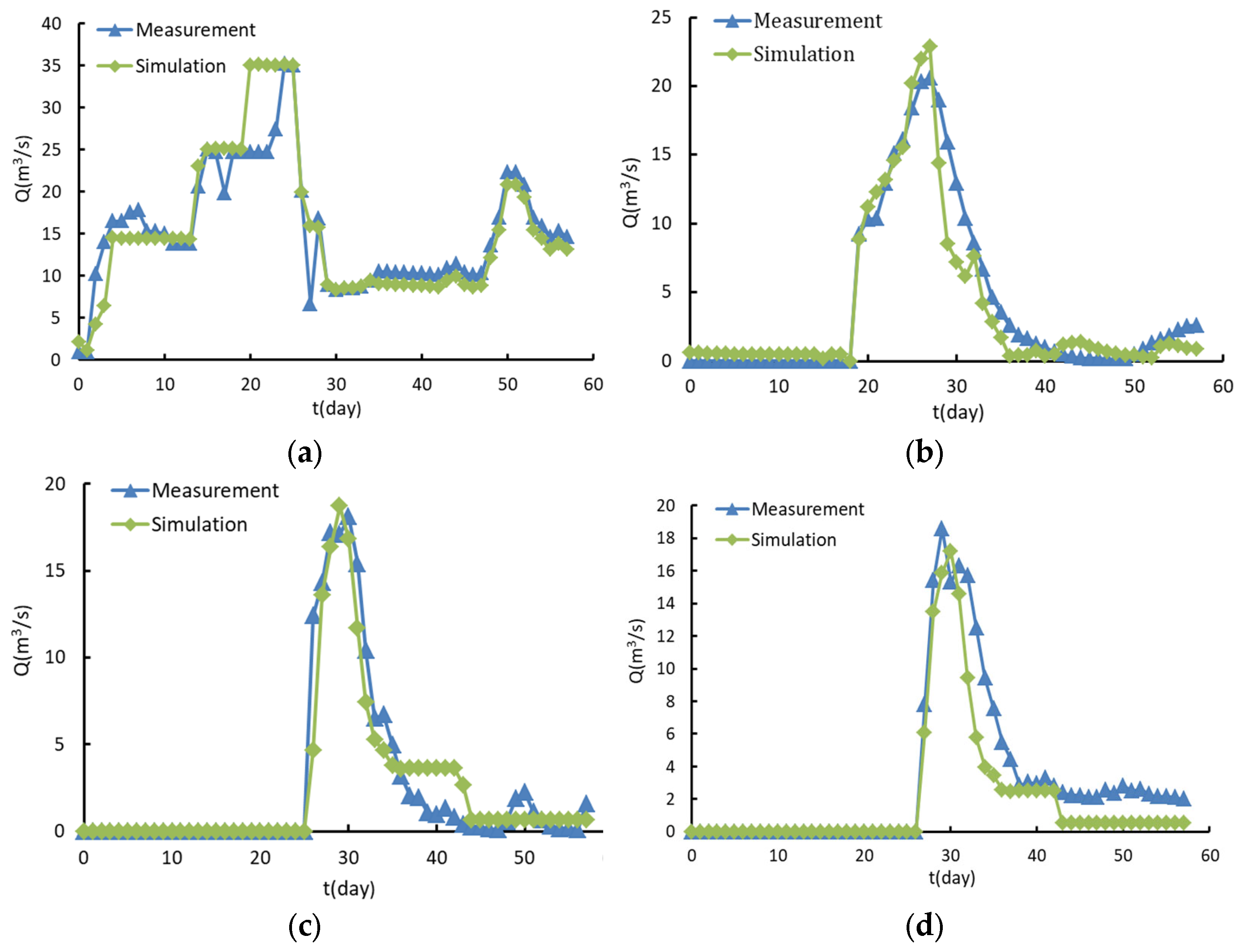
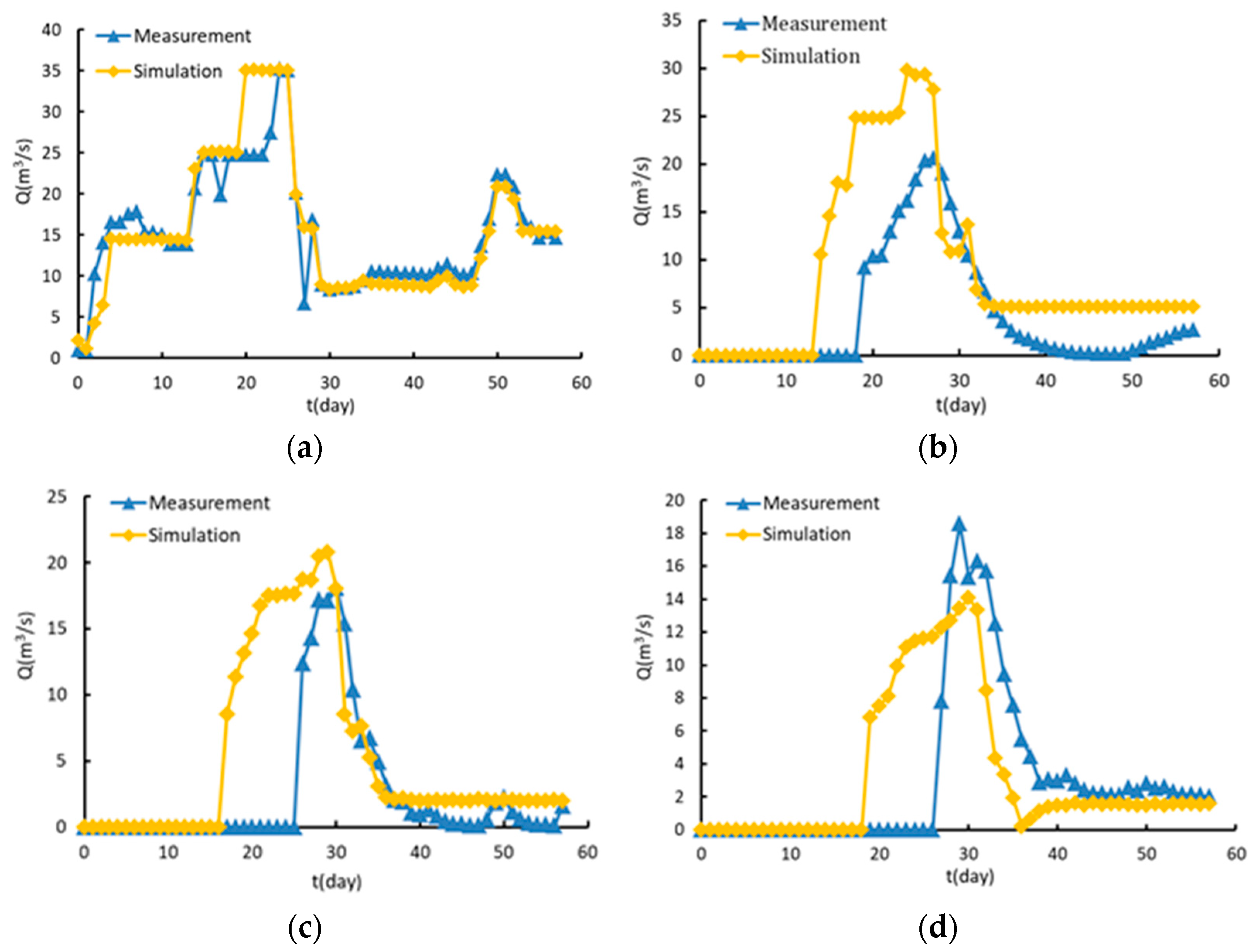
4.2. Simulation Results of Key Cross-Section Flow Process
4.3. Simulation Results of Total Flow Rate of Key Sections
5. Conclusions and Prospects
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ferreira, D.M.; Fernandes, C.V.S.; Kaviski, E.; Bleninger, T. Calibration of river hydrodynamic models: Analysis from the dynamic component in roughness coefficients. J. Hydrol. 2021, 598, 126136. [Google Scholar] [CrossRef]
- Yu, H.; Huang, G. A coupled 1D and 2D hydrodynamic model for free-surface flows. Proc. Inst. Civ. Eng. Water Manag. 2020, 167, 523–531. [Google Scholar] [CrossRef]
- Atabay, S. Accuracy of the ISIS Bridge Methods for prediction of afflux at high flows. Water Environ. J. 2008, 22, 64–73. [Google Scholar] [CrossRef]
- Pareo, S.; Chatterjee, C.; Mohanty, S. Flood inundation modeling using MIKE FLOOD and remote sensing data. J. Indian Soc. Remote Sens. 2009, 37, 107–118. [Google Scholar]
- Brunner, G.W. HEC-RAS River Analysis System. Hydraulic Reference Manual; Hydrologic Engineering Center: Davis, CA, USA, 1995.
- Wang, C.; Li, G. Practical River Network Flow Calculation; Department of Water Resources and Hydrology, Hohai University: Nanjing, China, 2003. [Google Scholar]
- Morin, E.; Grodek, T.; Dahan, O.; Benito, G.; Enzel, Y. Flood routing and alluvial aquifer recharge along the ephemeral arid Kuiseb River, Namibia. J. Hydrol. 2009, 36, 262–275. [Google Scholar] [CrossRef]
- Feng, D.; Tan, Z.; He, Q. Physics-Informed Neural Networks of the Saint-Venant Equations for Downscaling a Large-Scale River Model. Water Resour. Res. 2022, 59, e2022WR033168. [Google Scholar] [CrossRef]
- Kong, L. Predictive control for the operation of cascade pumping stations in water supply canal systems considering energy consumption and costs. Appl. Energy 2023, 341, 121103. [Google Scholar] [CrossRef]
- Peng, A.; Liu, K.; Hu, Q.; Wang, Y.; Zhang, X.; Jiang, W. Allocation of Multiple Water Sources and Optimal Operation of Reservoir Groups in the Yongding River Basin. Adv. Water Sci. 2023, 34, 418–430. (In Chinese) [Google Scholar]
- Li, H. Impact analysis of historical forest change on Yongding River. China Water Resour. 2005, 18, 56–58. (In Chinese) [Google Scholar]
- Li, X.; Ye, X.; Yuan, C.; Xu, C. Can water release from local reservoirs cope with the droughts of downstream lake in a large river-lake system? J. Hydrol. 2023, 625, 130172. [Google Scholar] [CrossRef]
- Saleh, F.; Ducharne, A.; Flipo, N.; Oudin, L.; Ledoux, E. Impact of river bed morphology on discharge and water levels simulated by a 1D Saint–Venant hydraulic model at regional scale. J. Hydrol. 2013, 476, 169–177. [Google Scholar] [CrossRef]
- Gomes, M.N.; Rápalo, L.M.C.; Oliveira, P.T.S.; Giacomoni, H.A.; do Lago, C.A.F.; Mendiondo, E.M. Modeling unsteady and steady 1D hydrodynamics under different hydraulic conceptualizations: Model/Software development and case studies. Environ. Model. Softw. Vol. 2023, 167, 105733. [Google Scholar] [CrossRef]
- Yong, D.; Bao, A.; Zhang, T.; Ding, W. Quantifying the impacts of climate change and human activities on seasonal runoff in the Yongding River basin. Ecol. Indic. 2023, 154, 110839. [Google Scholar]
- Jiang, B.; Wong, C.P.; Lu, F.; Ouyang, Z.; Wang, Y. Drivers of drying on the Yongding River in Beijing. J. Hydrol. 2014, 519, 69–79. [Google Scholar] [CrossRef]
- Yue, D.; Liu, Y.; Wang, J.; Li, H.; Cui, W. Physical principle of wind erosion on sandy land surface in southern Beijing. J. Geogr. Sci. 2006, 16, 487–494. [Google Scholar] [CrossRef]
- Dong, J. Sandstorms in Beijing—Occurrence, Protection and Control. Master’s Thesis, Royal Institute of Technology, Stockholm, Sweden, 2002. [Google Scholar]
- Zhang, S.; Zhu, J.; Yi, Y.; Wu, Y.; Zhao, Y. The dynamic capacity calculation method and the flood control ability of the Three Gorges Reservoir. J. Hydrol. 2017, 555, 361–370. [Google Scholar] [CrossRef]
- Lu, Y.; Tan, D.; Liang, D. A rapid and accurate computation method of three gorges reservoir storage. J. Yangtze River. Acad. Sci. 2010, 27, 80. [Google Scholar]
- Box, W.; Järvelä, J.; Västilä, K. Flow resistance of floodplain vegetation mixtures for modelling river flows. J. Hydrol. 2021, 601, 126593. [Google Scholar] [CrossRef]
- Kim, J.-S.; Lee, C.-J.; Kim, W.; Kim, Y.-J. Roughness coefficient and its uncertainty in gravel-bed river. Water Sci. Eng. 2010, 3, 217–232. [Google Scholar]
- Anderson, B.G.; Rutherfurd, I.D.; Western, A.W. An analysis of the influence of riparian vegetation on the propagation of flood waves. Environ. Model. Softw. 2006, 21, 1290–1296. [Google Scholar] [CrossRef]
- Yu, Y.; Hua, T.; Chen, L.; Zhang, Z.; Pereira, P. Divergent Changes in Vegetation Greenness, Productivity, and Rainfall Use Efficiency Are Characteristic of Ecological Restoration towards High-Quality Development in the Yellow River Basin, China. Engineering 2023, 1–3. [Google Scholar] [CrossRef]
- Wang, Z.; Cheng, L.; Wang, Y.; Liu, K. River Network Flood Simulation Considering River Infiltration under High Intensity Human Activities. J. Hydraul. Eng. 2015, 46, 11. (In Chinese) [Google Scholar]
- Cheng, W.; Xi, H.; Chen, Y.; Zhao, X.; Zhao, J.; Ma, K. Infiltration mechanism of the sandy riverbed in the arid inland region of China. J. Hydrol. 2022, 42, 12–13. [Google Scholar] [CrossRef]
- Long, Y.; Chen, W.; Jiang, C.; Huang, Z.; Yan, S.; Wen, X. Improving streamflow simulation in Dongting Lake Basin by coupling hydrological and hydrodynamic models and considering water yields in data-scarce areas. J. Hydrol. 2023, 47, 101420. [Google Scholar] [CrossRef]
- Yu, Y.; Feng, J.; Liu, H.; Wu, C.; Zhang, J.; Wang, Z.; Liu, C.; Zhao, J.; Rodrigo-Comino, J. Linking hydrological connectivity to sustainable watershed management in the Loess Plateau of China. Curr. Opin. Environ. Sci. Health 2023, 35, 100493. [Google Scholar] [CrossRef]
- Yu, Y.; Zhu, R.; Ma, D.; Liu, D.; Liu, Y.; Gao, Z.; Yin, M.; Bandala, E.R.; Rodrigo-Comino, J. Multiple surface runoff and soil loss responses by sandstone morphologies to land-use and precipitation regimes changes in the Loess Plateau, China. Catena 2022, 217, 106477. [Google Scholar] [CrossRef]

| Name | Data Precision | Corresponding Model | Data Purpose |
|---|---|---|---|
| River cross-sectional data | Interval 500 m | Hydrodynamic model | Basic data |
| Digital elevation model | 2 m | Hydrodynamic model and water balance model | Improving the accuracy of river cross-sectional data |
| Measured data | Daily flow rate at 8:00 a.m., daily average flow rate (m3/s) | Hydrodynamic model | Basic data |
| Remote sensing images | 2 m (before and after ecological replenishment) | Water balance model | Inverting the initial conditions of lakes and gravel pits |
| Storage capacity curve | Water level and storage curve | Water balance model | Improving the simulation accuracy of coupled models |
| River Type | Underlying Surface Condition | Minimum Value | Maximum Value |
|---|---|---|---|
| Plain rivers | Clean, straight, without beaches or depressions | 0.025 | 0.033 |
| Clean, straight, without beaches or depressions, with a small amount of vegetation and gravel | 0.03 | 0.04 | |
| Clean, straight, with a small amount of beach and depression | 0.033 | 0.045 | |
| Clean, straight, with a small amount of beach and depression, and a small amount of vegetation and gravel | 0.035 | 0.05 | |
| Clean, straight, with a small amount of beach and depression, a small amount of vegetation and gravel, shallow water depth, and variable bank slopes | 0.04 | 0.05 | |
| Clean, straight, flat, and low-lying areas, with a small amount of vegetation and gravel | 0.05 | 0.08 | |
| Clean, straight, with more beaches and depressions, more vegetation and gravel | 0.075 | 0.15 | |
| Mountain rivers (without vegetation, with steep banks) | With a small amount of gravel, pebbles, and stones | 0.025 | 0.05 |
| With a lot of gravel, pebbles, and stones | 0.04 | 0.07 |
| Segment Name | Underlying Surface Condition | Roughness Value |
|---|---|---|
| Guaniting–Sanjiadian | With a small amount of gravel, pebbles, and stones | 0.033 |
| Sanjiadian–Jingliang road | / | / |
| Jingliang road–Ethylene pipe bridge | Clean, straight, with more beaches and depressions, more vegetation and gravel | 0.7 |
| Ethylene pipe bridge–Jinmen | Clean, straight, flat, and low-lying areas, with a small amount of vegetation and gravel | 0.7 |
| Jinmen–Cuizhihui | Clean, straight, with a small amount of beach and depression, a small amount of vegetation and gravel, shallow water depth, and variable bank slopes | 0.065 |
| Cuizhihui–Shaoqidi | Clean, straight, with a small amount of beach and depression, and a small amount of vegetation and gravel | 0.4 |
| Shaoqidi–Qujiadian | Clean, straight, with a small amount of beach and depression, and a small amount of vegetation and gravel | 0.4 |
| Segment Name | Initial Infiltration Parameters (cm/day) | Stable Infiltration Parameters (cm/day) |
|---|---|---|
| Guaniting–Sanjiadian | 10 | 10 |
| Sanjiadian–Jingliang road | 6 | 6 |
| Jingliang road–Ethylene pipe bridge | 17 | 13 |
| Ethylene pipe bridge-Jinmen | 10 | 8 |
| Jinmen–Cuizhihui | 4 | 2 |
| Cuizhihui–Shaoqidi | 2 | 2 |
| Shaoqidi–Qujiadian | 2 | 2 |
| Name | Initial Water Level (m) | Initial Area (m2) | Initial Storage Capacity (m3) |
|---|---|---|---|
| Mencheng lake | 91.3 | 236,118.75 | 357,075.26 |
| Lianshi lake | 69 | 274,312.5 | 1,335,552 |
| Yuanbo lake | 58.4 | 1,330,143.32 | 10,680,207.94 |
| Xiaoyue lake | 56.6 | 184,040.6 | 174,015.9 |
| Wanping lake | 55 | 313,912.5 | 293,492.2 |
| 1# pit | 41.9 | 2,534,612.5 | 10,922,779.41 |
| 2# pit | 42.1 | 224,700 | 318,392.30 |
| 3# pit | 41.2 | 54,225 | 69,373.99 |
| 4# pit | 35.5 | 533,464.8 | 429,172.43 |
| 5# pit | 33.2 | 446,780.4 | 504,940.82 |
| 6# pit | 29.1 | 7298.72 | 1773.78 |
| 7# pit | 29 | 114,824.16 | 312,307.39 |
| Critical Cross-Section | Measured Water Flow Arrival Time | Time Interval (h) | Simulated Water Flow Arrival Time | Time Interval (h) | Interval Flow Time Error (h) | Absolute Error (h) |
|---|---|---|---|---|---|---|
| Sanjiadian | 27 February 8:00 | 72 | 27 February 10:00 | 74 | 2 | 2 |
| Lugouqiao | 6 March 8:00 | 168 | 6 March 7:00 | 165 | −3 | −1 |
| Jinmen | 13 March 12:00 | 172 | 13 March 9:00 | 170 | −2 | −3 |
| Guan | 14 March 16:00 | 28 | 14 March 10:00 | 25 | −3 | −6 |
| Cuizhihui | 17 March 16:00 | 72 | 17 March 12:00 | 74 | 2 | −4 |
| Shaoqidi | 19 March 17:30 | 49 | 19 March 12:00 | 48 | −1 | −5 |
| Qujiadian | 20 March 10:30 | 17 | 20 March 9:30 | 21 | 4 | −3 |
| Critical Cross-Section | Measured Water Head-Arrival Time | Time Interval (h) | Simulated Water Head-Arrival Time | Time Interval (h) | Interval Flow Time Error (h) | Absolute Error (h) |
|---|---|---|---|---|---|---|
| Sanjiadian | 27 February 8:00 | 72 | 27 February 5:00 | 69 | −3 | 2 |
| Lugouqiao | 6 March 8:00 | 168 | 28 February 8:00 | 27 | −141 | −144 |
| Jinmen | 13 March 12:00 | 172 | 9 March 9:00 | 49 | −123 | −99 |
| Guan | 14 March 16:00 | 28 | 10 March 7:00 | 22 | −6 | −105 |
| Cuizhihui | 17 March 16:00 | 72 | 11 March 6:00 | 23 | −49 | −154 |
| Shaoqidi | 19 March 17:30 | 49 | 13 March 7:00 | 49 | 0 | −154.5 |
| Qujiadian | 20 March 10:30 | 17 | 15 March 8:00 | 49 | 32 | −122.5 |
| Section Name | Measured Total Flow (1 × 104 m3) | Simulated Total Flow (1 × 104 m3) | Difference |
|---|---|---|---|
| Sanjiadian | 7753.54 | 7797.90 | 0.57% |
| Guan | 2068.17 | 1892.30 | −8.5% |
| Shaoqidi | 1244.84 | 1211.15 | −2.71% |
| Qujiadian | 1169.76 | 995.66 | −14.88% |
| Section Name | Measured Total Flow (1 × 104 m3) | Simulated Total Flow (1 × 104 m3) | Difference |
|---|---|---|---|
| Sanjiadian | 7753.54 | 8201.90 | 5.7% |
| Guan | 2068.17 | 4387.03 | 112.1% |
| Shaoqidi | 1244.84 | 2655.34 | 113.3% |
| Qujiadian | 1169.76 | 1667.30 | 42% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, P.; Kong, L.; Chuo, R.; Liu, H.; Cai, S.; Zhao, M. Application of One-Dimensional Hydrodynamic Coupling Model in Complex River Channels: Taking the Yongding River as an Example. Water 2024, 16, 1161. https://doi.org/10.3390/w16081161
Lv P, Kong L, Chuo R, Liu H, Cai S, Zhao M. Application of One-Dimensional Hydrodynamic Coupling Model in Complex River Channels: Taking the Yongding River as an Example. Water. 2024; 16(8):1161. https://doi.org/10.3390/w16081161
Chicago/Turabian StyleLv, Pingyu, Lingling Kong, Ruiyuan Chuo, Haijiao Liu, Siyu Cai, and Mengqi Zhao. 2024. "Application of One-Dimensional Hydrodynamic Coupling Model in Complex River Channels: Taking the Yongding River as an Example" Water 16, no. 8: 1161. https://doi.org/10.3390/w16081161
APA StyleLv, P., Kong, L., Chuo, R., Liu, H., Cai, S., & Zhao, M. (2024). Application of One-Dimensional Hydrodynamic Coupling Model in Complex River Channels: Taking the Yongding River as an Example. Water, 16(8), 1161. https://doi.org/10.3390/w16081161







