En-WBF: A Novel Ensemble Learning Approach to Wastewater Quality Prediction Based on Weighted BoostForest
Abstract
1. Introduction
2. Related Work
2.1. Machine Learning Methods
2.2. Deep Learning Methods
3. En-WBF Model Development
3.1. Problem Statement
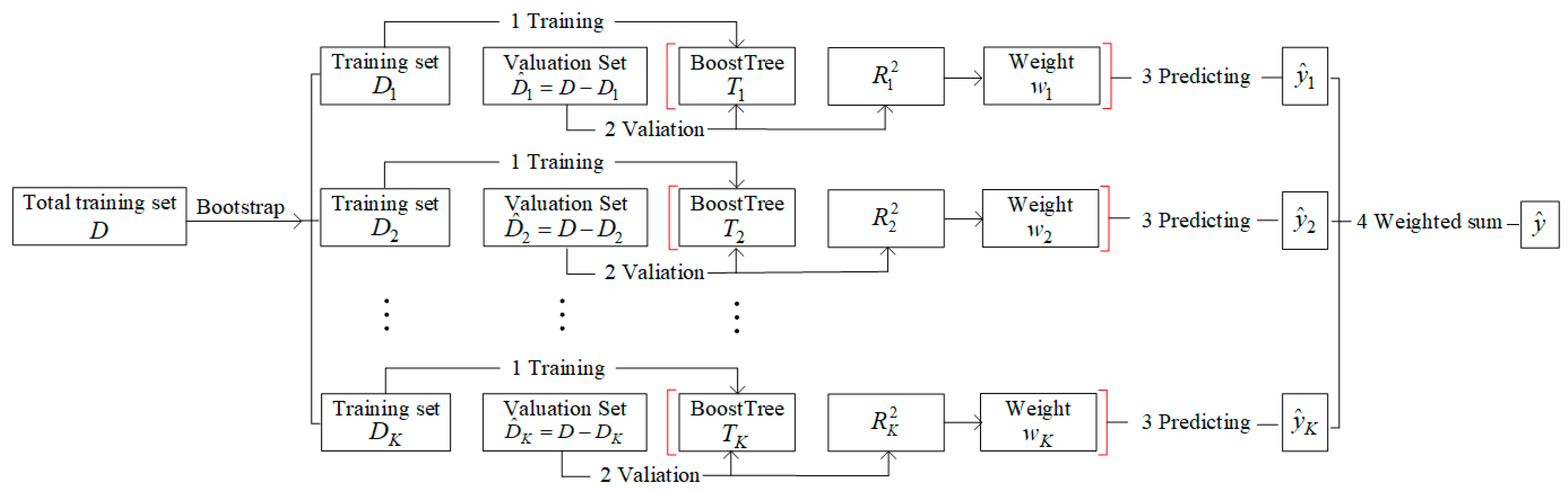
3.2. Overall Architecture of En-WBF
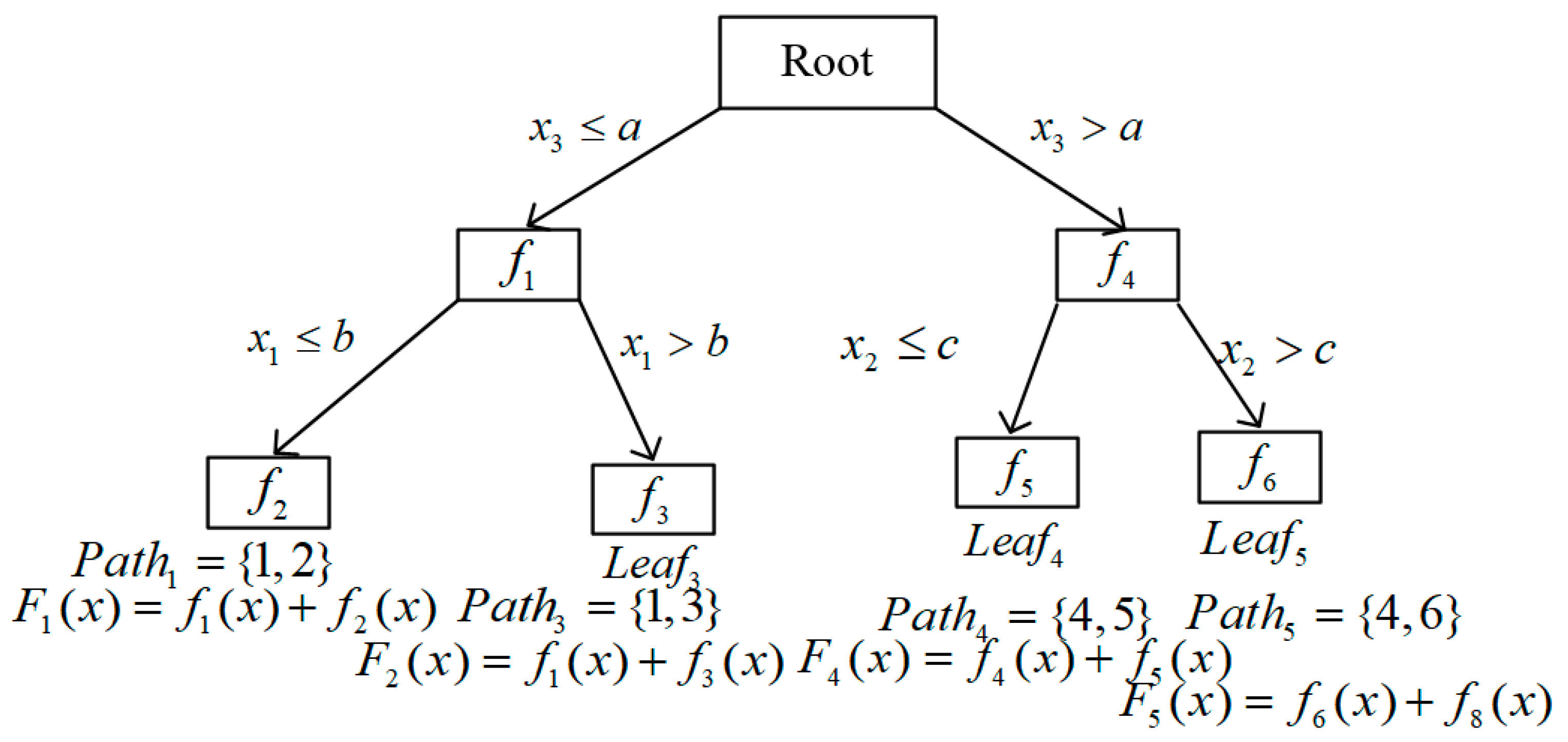
3.3. BoostTree
3.4. Weighted BoostForest
| Algorithm 1 Training process of WBF. |
| Input: , N is the number of training samples, is the number of BoostTree, is the sampling proportion; |
| Output: WeightedBoostForest |
| 1: Initialize WeightedBoostForest = {} |
| 2: For i = 1: do |
| 3: Sample from according to |
| 4: Train on |
| 5: Add to WeightedBoostForest |
| 6: End |
3.5. Research Questions
4. Experiment
4.1. Dataset
4.2. Evaluation Metrics
4.3. Experimental Results
4.3.1. RQ1: How Does the Performance of the Proposed WBF Approach Compare with That of Traditional Machine Learning Methods in Predicting Effluent BOD?
4.3.2. RQ2: Is Weighted Polymerization Better Than Average Polymerization for BoostForest?
4.3.3. RQ3: What Are the Optimal Parameter Settings of the Proposed En-WBF Approach?
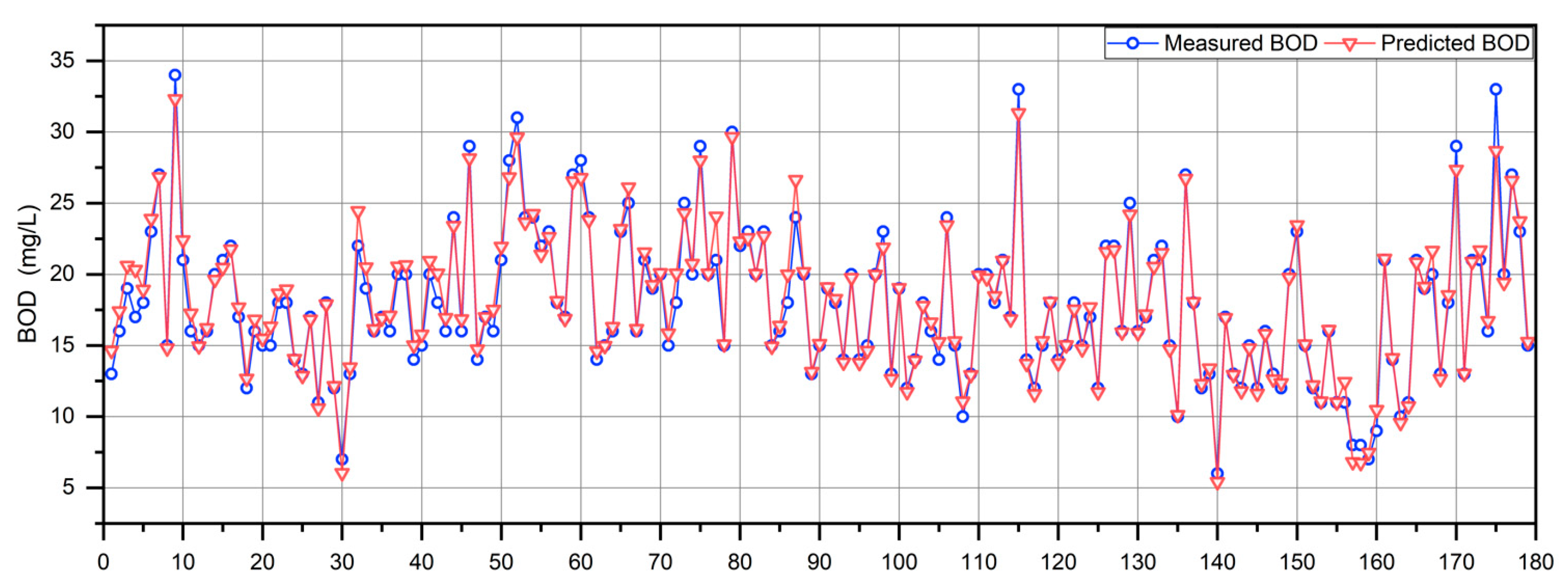
4.3.4. RQ4: How Does the Proposed En-WBF Approach Perform on Real Wastewater Treatment Data?
5. Discussion
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huang, J.; Qian, R.; Gao, J.; Bing, H.; Huang, Q.; Qi, L.; Huang, J. A novel framework to predict water turbidity using Bayesian modeling. Water Res. 2021, 202, 117406. [Google Scholar] [CrossRef] [PubMed]
- Saravanan, A.; Kumar, P.S.; Jeevanantham, S.; Karishma, S.; Tajsabreen, B.; Yaashikaa, P.R.; Reshma, B. Effective water/wastewater treatment methodologies for toxic pollutants removal: Processes and applications towards sustainable development. Chemosphere 2021, 280, 130595. [Google Scholar] [CrossRef] [PubMed]
- Tang, W.; Pei, Y.; Zheng, H.; Zhao, Y.; Shu, L.; Zhang, H. Twenty years of China’s water pollution control: Experiences and challenges. Chemosphere 2022, 295, 133875. [Google Scholar] [CrossRef] [PubMed]
- Fathollahi-Fard, A.M.; Ahmadi, A.; Al-e-Hashem, S.M. Sustainable closed-loop supply chain network for an integrated water supply and wastewater collection system under uncertainty. J. Environ. Manag. 2020, 275, 111277. [Google Scholar] [CrossRef] [PubMed]
- Luo, L.; Dzakpasu, M.; Yang, B.; Zhang, W.; Yang, Y.; Wang, X.C. A novel index of total oxygen demand for the comprehensive evaluation of energy consumption for urban wastewater treatment. Appl. Energy 2019, 236, 253–261. [Google Scholar] [CrossRef]
- Zhu, J.J.; Kang, L.; Anderson, P.R. Predicting influent biochemical oxygen demand: Balancing energy demand and risk management. Water Res. 2018, 128, 304–313. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Jia, Q.S.; Zhou, M.; Bi, J.; Qiao, J.; Abusorrah, A. Artificial neural networks for water quality soft-sensing in wastewater treatment: A review. Artif. Intell. Rev. 2022, 55, 565–587. [Google Scholar] [CrossRef]
- Zhang, W.; Li, R.; Zhao, J.; Wang, J.; Meng, X.; Li, Q. Miss-gradient boosting regression tree: A novel approach to imputing water treatment data. Appl. Intell. 2023, 53, 22917–22937. [Google Scholar] [CrossRef]
- Bahramian, M.; Dereli, R.K.; Zhao, W.; Giberti, M.; Casey, E. Data to intelligence: The role of data-driven models in wastewater treatment. Expert Syst. Appl. 2023, 217, 119453. [Google Scholar] [CrossRef]
- Park, J.; Lee, W.H.; Kim, K.T.; Park, C.Y.; Lee, S.; Heo, T.Y. Interpretation of ensemble learning to predict water quality using explainable artificial intelligence. Sci. Total Environ. 2022, 832, 155070. [Google Scholar] [CrossRef] [PubMed]
- El-Rawy, M.; Abd-Ellah, M.K.; Fathi, H.; Ahmed, A.K.A. Forecasting effluent and performance of wastewater treatment plant using different machine learning techniques. J. Water Process Eng. 2021, 44, 102380. [Google Scholar] [CrossRef]
- Sharafati, A.; Asadollah, S.B.H.S.; Hosseinzadeh, M. The potential of new ensemble machine learning models for effluent quality parameters prediction and related uncertainty. Process Saf. Environ. Prot. 2020, 140, 68–78. [Google Scholar] [CrossRef]
- Nourani, V.; Asghari, P.; Sharghi, E. Artificial intelligence based ensemble modeling of wastewater treatment plant using jittered data. J. Clean. Prod. 2021, 291, 125772. [Google Scholar] [CrossRef]
- Zhan, C.; Zhang, X.; Yuan, J.; Chen, X.; Zhang, X.; Fathollahi-Fard, A.M.; Wang, C.; Wu, J.; Tian, G. A hybrid approach for low-carbon transportation system analysis: Integrating CRITIC-DEMATEL and deep learning features. Int. J. Environ. Sci. Technol. 2024, 21, 791–804. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Zhang, Y.; Huang, M.; Liu, H. Adaptive dynamic prediction of effluent quality in wastewater treatment processes using partial least squares embedded with relevance vector machine. J. Clean. Prod. 2021, 314, 128076. [Google Scholar] [CrossRef]
- Yang, B.; Xiao, Z.; Meng, Q.; Yuan, Y.; Wang, W.; Wang, H.; Feng, X. Deep learning-based prediction of effluent quality of a constructed wetland. Environ. Sci. Ecotechnol. 2023, 13, 100207. [Google Scholar] [CrossRef]
- Yang, Y.; Kim, K.R.; Kou, R.; Li, Y.; Fu, J.; Zhao, L.; Liu, H. Prediction of effluent quality in a wastewater treatment plant by dynamic neural network modeling. Process Saf. Environ. Prot. 2022, 158, 515–524. [Google Scholar] [CrossRef]
- Abou Houran, M.; Bukhari SM, S.; Zafar, M.H.; Mansoor, M.; Chen, W. COA-CNN-LSTM: Coati optimization algorithm-based hybrid deep learning model for PV/wind power forecasting in smart grid applications. Appl. Energy 2023, 349, 121638. [Google Scholar] [CrossRef]
- Cui, S.; Yin, Y.; Wang, D.; Li, Z.; Wang, Y. A stacking-based ensemble learning method for earthquake casualty prediction. Appl. Soft Comput. 2021, 101, 107038. [Google Scholar] [CrossRef]
- Zhao, C.; Wu, D.; Huang, J.; Yuan, Y.; Zhang, H.T.; Peng, R.; Shi, Z. BoostTree and BoostForest for ensemble learning. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 8110–8126. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Yang, C.H.; Han, J.; Yi, Y.G. Forward variable selection method based on k-nearest neighbor mutual information and its application on soft sensor modeling of water quality parameters. Syst. Eng. Theory Pract. 2022, 42, 253–261. (In Chinese) [Google Scholar]
- Wang, Y.; Lu, W.; Zuo, C.H.; Bao, M.Y. Research on Water Quality BOD Prediction Based on Improved Random Forest Model. Chin. J. Sens. Actuators 2021, 34, 1482–1488. (In Chinese) [Google Scholar]
- Ching PM, L.; Zou, X.; Wu, D.; So, R.H.Y.; Chen, G.H. Development of a wide-range soft sensor for predicting wastewater BOD5 using an eXtreme gradient boosting (XGBoost) machine. Environ. Res. 2022, 210, 112953. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Yang, C.; Huang, M.; Yoo, C. Soft sensor modeling of industrial process data using kernel latent variables-based relevance vector machine. Appl. Soft Comput. 2020, 90, 106149. [Google Scholar] [CrossRef]
- Foschi, J.; Turolla, A.; Antonelli, M. Soft sensor predictor of E. coli concentration based on conventional monitoring parameters for wastewater disinfection control. Water Res. 2021, 191, 116806. [Google Scholar] [CrossRef] [PubMed]
- Wongburi, P.; Park, J.K. Prediction of Wastewater Treatment Plant Effluent Water Quality Using Recurrent Neural Network (RNN) Models. Water 2023, 15, 3325. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Q.; Liu, Z.; Wu, T. A deep learning interpretable model for river dissolved oxygen multi-step and interval prediction based on multi-source data fusion. J. Hydrol. 2024, 629, 130637. [Google Scholar] [CrossRef]
- Satish, N.; Anmala, J.; Rajitha, K.; Varma, M.R. A stacking ANN ensemble model of ML models for stream water quality prediction of Godavari River Basin, India. Ecol. Inform. 2024, 80, 102500. [Google Scholar] [CrossRef]
- Ha, N.T.; Manley-Harris, M.; Pham, T.D.; Hawes, I. The use of radar and optical satellite imagery combined with advanced machine learning and metaheuristic optimization techniques to detect and quantify above ground biomass of intertidal seagrass in a New Zealand estuary. Int. J. Remote Sens. 2021, 42, 4712–4738. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, S.; Wang, Q. KSAP: An approach to bug report assignment using KNN search and heterogeneous proximity. Inf. Softw. Technol. 2016, 70, 68–84. [Google Scholar] [CrossRef]
| ID | Question |
|---|---|
| RQ1 | How are the performances of the proposed WBF approach compared with that of traditional machine learning methods in predicting effluent BOD? |
| RQ2 | Is weighted polymerization better than average polymerization for BoostForest? |
| RQ3 | What are the optimal parameter settings for the proposed En-WBF approach? |
| RQ4 | How does the proposed En-WBF approach perform on actual wastewater treatment data? |
| Notation | Description |
|---|---|
| DBO-D | Input biological demand of oxygen to secondary settler |
| SS-D | Input suspended solids to secondary settler |
| CONE-D | Input conductivity to secondary settler |
| DQO-S | Output chemical demand of oxygen |
| SED-S | Output sediments |
| RD-DBO-S | Performance input biological demand of oxygen to secondary settler |
| RD-SS-G | Global performance input suspended solids |
| Method | Parameter | Description |
|---|---|---|
| SVR | SVRc = 1, SVRKernel = ‘rbf’ | SVRc is the regularization parameter of SVR; SVRKernel is the kernel type of SVR; |
| GBRT | n_estimators = 100, min_samples_leaf = 5 | n_estimators is the number of estimators of GBRT; min_samples_leaf is the minimum sample number of GBRT leaf nodes; |
| RF | n_estimators = 110, min_samples_leaf = 5 | n_estimators is the number of estimators of RF; min_samples_leaf is the minimum sample number of RF leaf nodes; |
| XG-Boost | n_estimators = 100, max_depth = 4, max_leaves = 5 | n_estimators is the number of estimators of XG-Boost; max_depth is the maximum depth of XG-Boost; max_leaves is the maximum number of leaf nodes per tree of XG-Boost; |
| RVM | RVMKernel = ‘linear’ | RVMKernel is the kernel type of RVM; |
| ANN | nfirst = 32, nsecond = 16 | nfirst is the number of hidden units in the first dense layer; nsecond is the number of hidden units in the second dense layer; |
| LSTM | nlstm = 32 | nlstm is the number of hidden units in the LSTM layer. |
| Method | MAE | MAPE | MSE | RMSE | R2 | AIC | BIC |
|---|---|---|---|---|---|---|---|
| En-WBF | 0.2573 | 0.0171 | 0.1869 | 0.4323 | 0.9938 | 147.7845 | 861.7589 |
| SVR | 0.3667 | 0.0241 | 0.2610 | 0.5109 | 0.9713 | 99.5610 | 641.4165 |
| GBRT | 0.8821 | 0.0586 | 1.6393 | 1.2803 | 0.9452 | 572.4742 | 1343.8216 |
| RF | 1.0001 | 0.0778 | 2.9375 | 1.7139 | 0.9018 | 1128.8830 | 2620.5796 |
| XG-Boost | 0.8734 | 0.0559 | 1.7999 | 1.3416 | 0.9398 | 1029.2039 | 2501.7761 |
| RVM | 1.2383 | 0.0771 | 2.5810 | 1.6066 | 0.9137 | 183.7237 | 206.0354 |
| ANN | 0.8454 | 0.0491 | 1.5282 | 1.1577 | 0.9467 | 1677.9122 | 4231.0082 |
| LSTM | 0.8373 | 0.0447 | 1.4913 | 1.2211 | 0.9501 | 2469.7556 | 6348.8042 |
| Method | MAE | MAPE | MSE | RMSE | R2 | AIC | BIC |
|---|---|---|---|---|---|---|---|
| En-WBF | 0.2573 | 0.0171 | 0.1869 | 0.4323 | 0.9938 | 147.7845 | 861.7589 |
| ABF | 0.2612 | 0.0174 | 0.1927 | 0.4390 | 0.9889 | 151.6813 | 879.7123 |
| n_estimators | MAE | MSE |
|---|---|---|
| 10 | 0.3263 | 0.3134 |
| 20 | 0.3085 | 0.2819 |
| 30 | 0.2910 | 0.2612 |
| 40 | 0.2718 | 0.2108 |
| 50 | 0.2744 | 0.2176 |
| 60 | 0.2789 | 0.2178 |
| 70 | 0.2884 | 0.2223 |
| Bootstrap_rate | MAE | MSE |
|---|---|---|
| 0.60 | 0.3478 | 0.3896 |
| 0.65 | 0.2909 | 0.2713 |
| 0.70 | 0.3027 | 0.2408 |
| 0.75 | 0.2675 | 0.1996 |
| 0.80 | 0.2775 | 0.2018 |
| 0.85 | 0.2847 | 0.2040 |
| 0.90 | 0.2886 | 0.2060 |
| min_samples_leaf | MAE | MSE |
|---|---|---|
| 1 | 0.4268 | 0.3449 |
| 2 | 0.3892 | 0.2905 |
| 3 | 0.3384 | 0.2453 |
| 4 | 0.3032 | 0.2209 |
| 5 | 0.2573 | 0.1869 |
| 6 | 0.2738 | 0.2184 |
| 7 | 0.2828 | 0.2223 |
| Notation | Description |
|---|---|
| Q-E | Effluent flow rate |
| MLSS | Mixed liquor suspended solids |
| COD-I | Influent biological demand of oxygen |
| BOD-I | Influent chemical demand of oxygen |
| SS-I | Influent suspended solids |
| P-I | Influent phosphorus |
| P-E | Effluent phosphorus |
| Method | MAE | MAPE | MSE | RMSE | R2 | AIC | BIC |
|---|---|---|---|---|---|---|---|
| En-WBF | 3.0647 | 0.2272 | 17.9724 | 4.2392 | 0.6838 | 637.1084 | 1113.9190 |
| SVR | 3.3431 | 0.2494 | 20.5808 | 4.5366 | 0.6738 | 500.2910 | 835.2406 |
| GBRT | 3.3529 | 0.2502 | 20.8585 | 4.5671 | 0.6529 | 697.0014 | 1225.0396 |
| RF | 3.3678 | 0.2498 | 21.2829 | 4.6133 | 0.6501 | 1010.0689 | 1845.4727 |
| XG-Boost | 3.4259 | 0.2548 | 21.5569 | 4.6429 | 0.6233 | 1138.0689 | 2099.5714 |
| RVM | 3.6679 | 0.2749 | 23.7362 | 4.8720 | 0.5991 | 171.1084 | 188.8410 |
| ANN | 3.3542 | 0.2496 | 20.9333 | 4.5752 | 0.6317 | 1763.1911 | 3341.3949 |
| LSTM | 3.4317 | 0.2559 | 21.7285 | 4.6613 | 0.6091 | 2597.1671 | 4995.0124 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, B.; Zhang, W.; Li, R.; Bai, Y.; Chang, J. En-WBF: A Novel Ensemble Learning Approach to Wastewater Quality Prediction Based on Weighted BoostForest. Water 2024, 16, 1090. https://doi.org/10.3390/w16081090
Su B, Zhang W, Li R, Bai Y, Chang J. En-WBF: A Novel Ensemble Learning Approach to Wastewater Quality Prediction Based on Weighted BoostForest. Water. 2024; 16(8):1090. https://doi.org/10.3390/w16081090
Chicago/Turabian StyleSu, Bojun, Wen Zhang, Rui Li, Yongsheng Bai, and Jiang Chang. 2024. "En-WBF: A Novel Ensemble Learning Approach to Wastewater Quality Prediction Based on Weighted BoostForest" Water 16, no. 8: 1090. https://doi.org/10.3390/w16081090
APA StyleSu, B., Zhang, W., Li, R., Bai, Y., & Chang, J. (2024). En-WBF: A Novel Ensemble Learning Approach to Wastewater Quality Prediction Based on Weighted BoostForest. Water, 16(8), 1090. https://doi.org/10.3390/w16081090





