Deformation and Strength of Unsaturated Loess—Hydraulic Coupling Effects under Loads
Abstract
1. Introduction
2. Materials and Methods
2.1. Samples
2.2. Testing Procedures
3. Basic Model Features
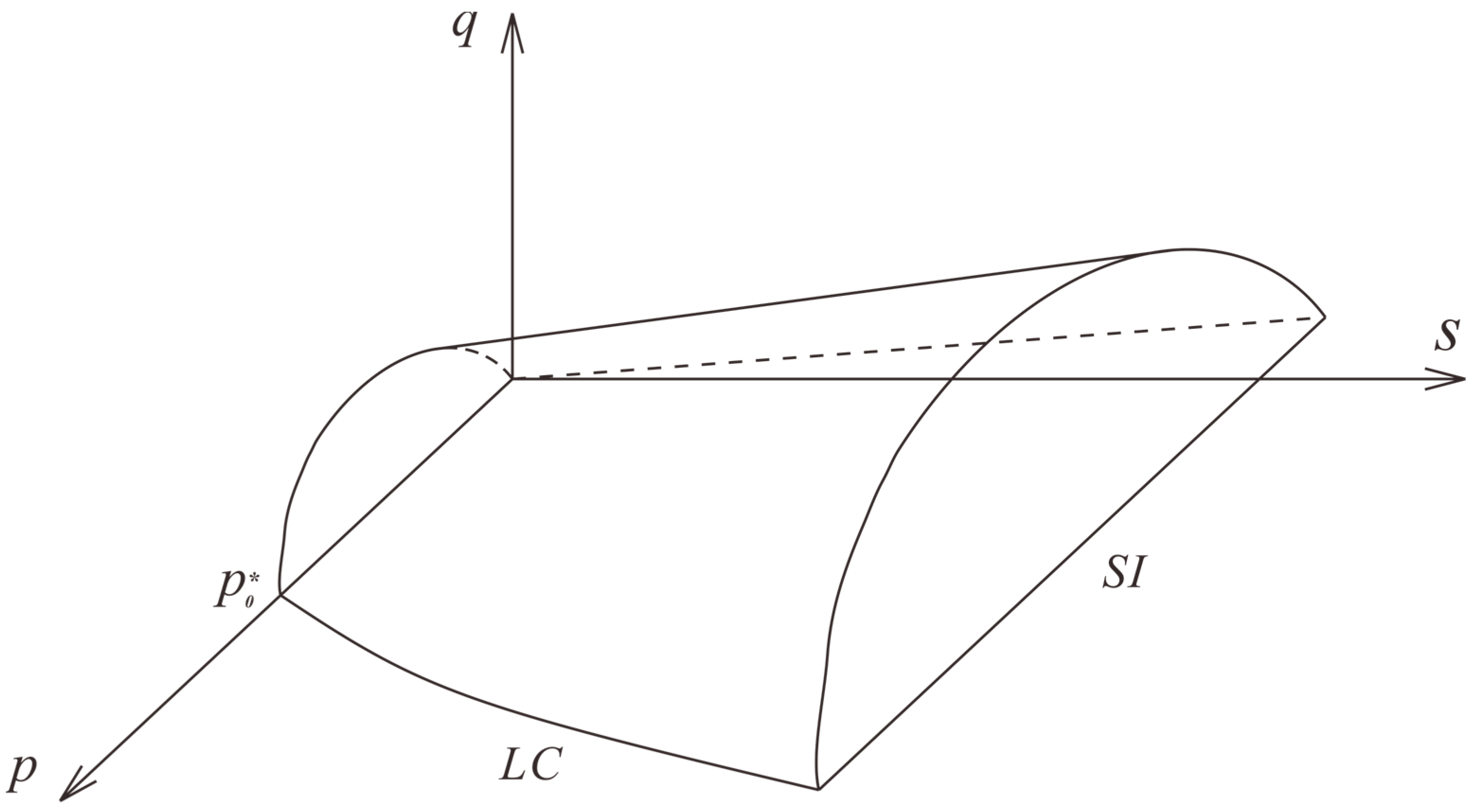
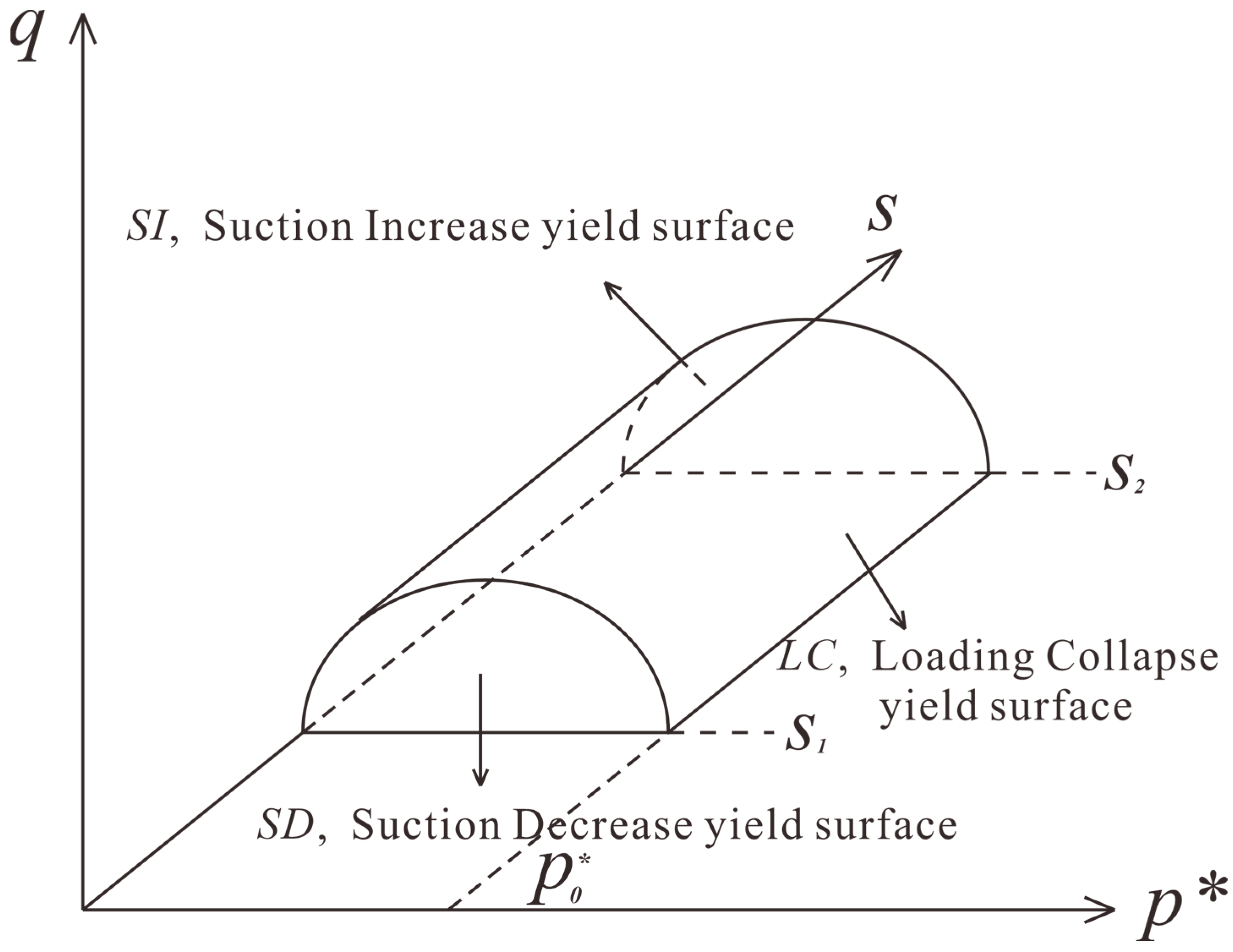
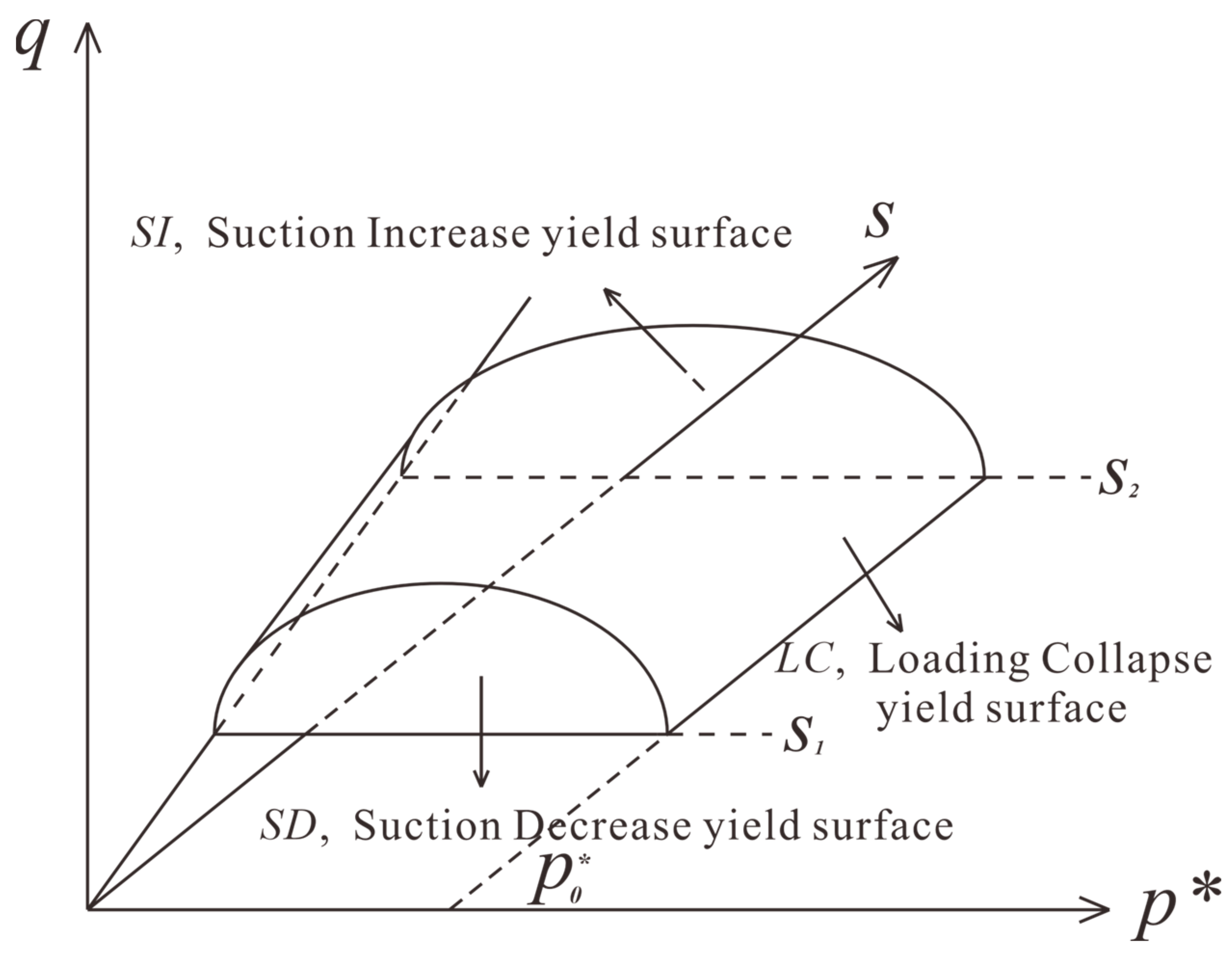
3.1. The Expanded Barcelona Basic Model
3.2. Glasgow Coupled Model
4. Results
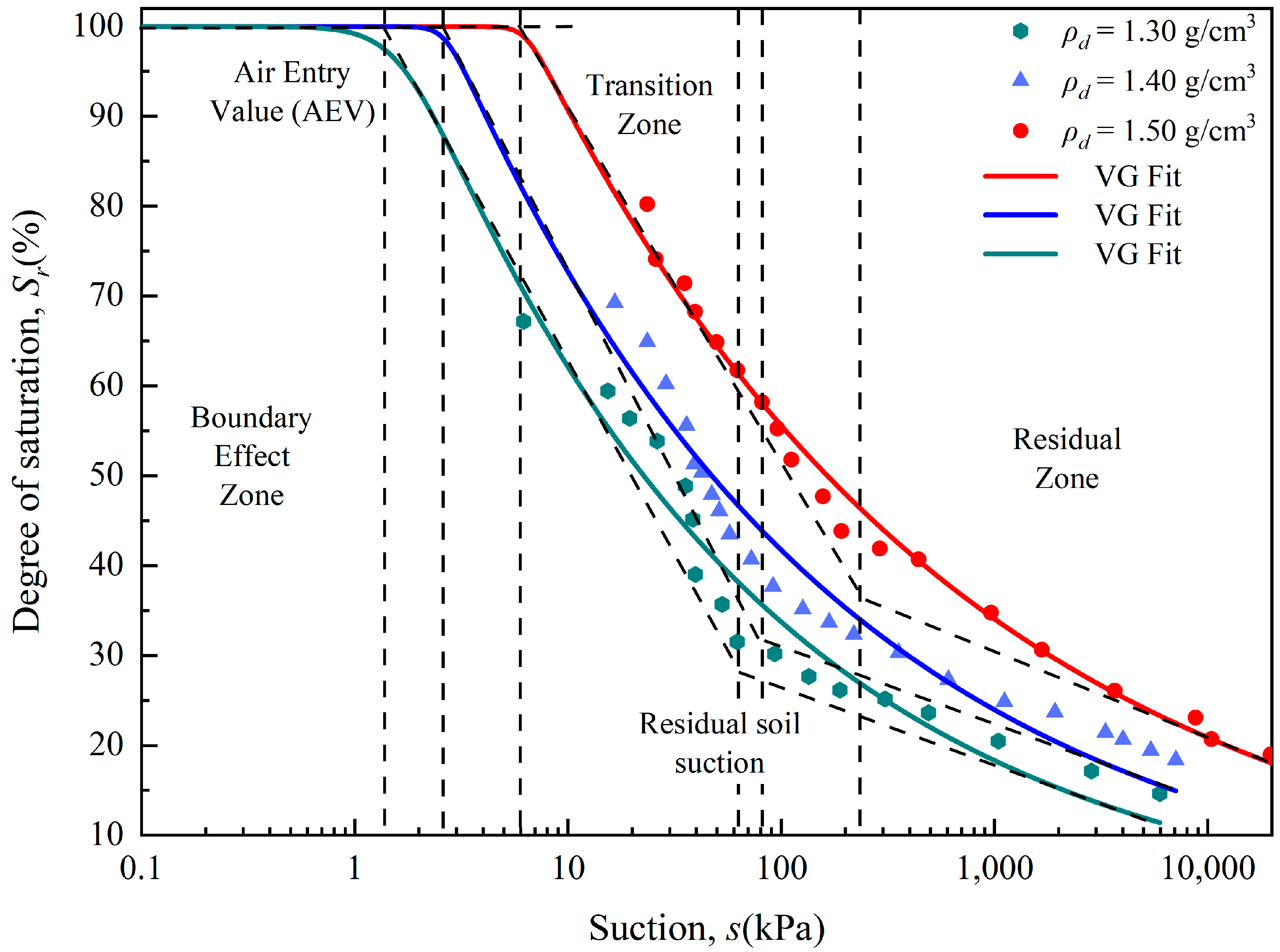
4.1. Soil–Water Characteristic Curve
4.2. Model Parameter Selection
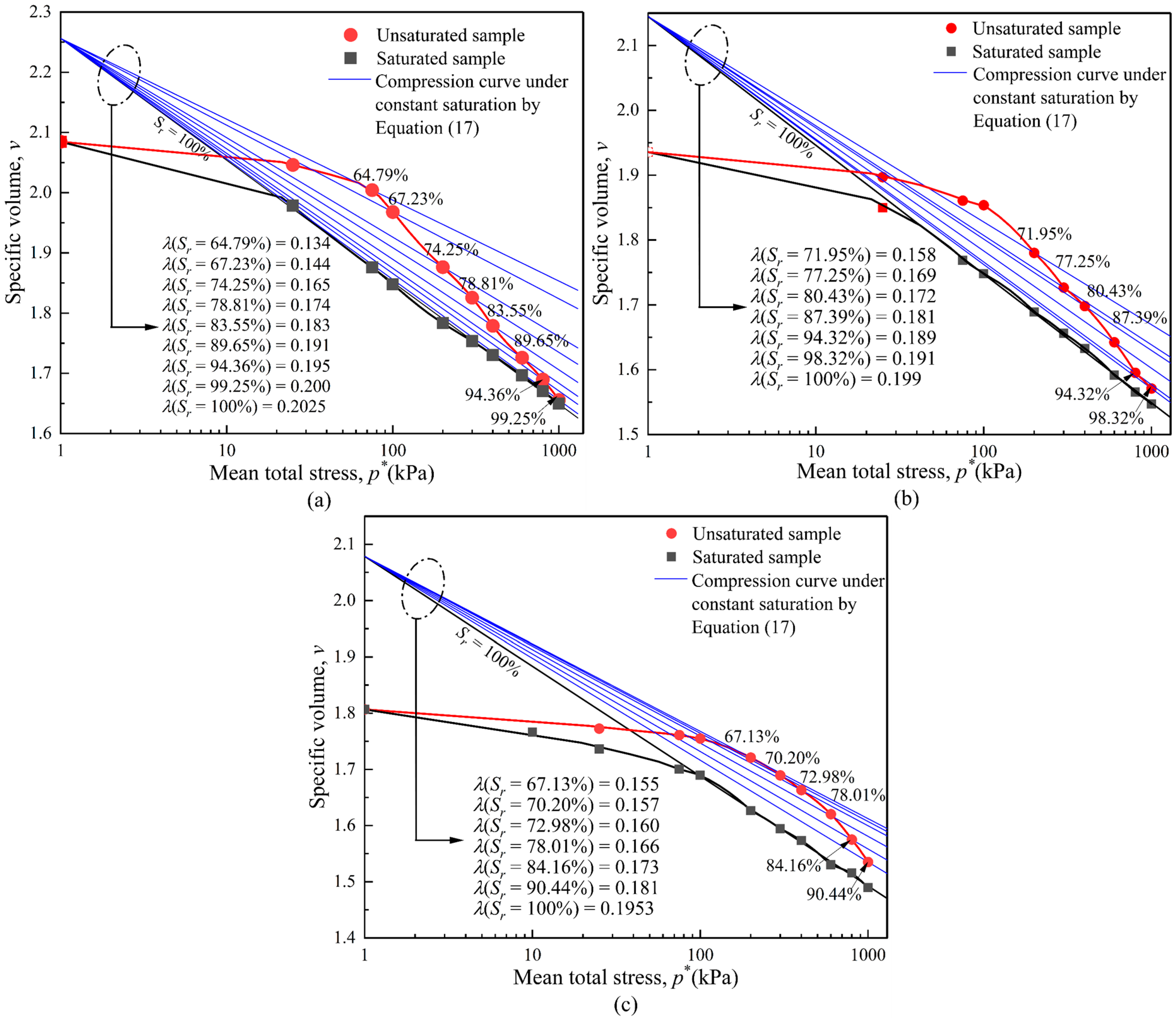
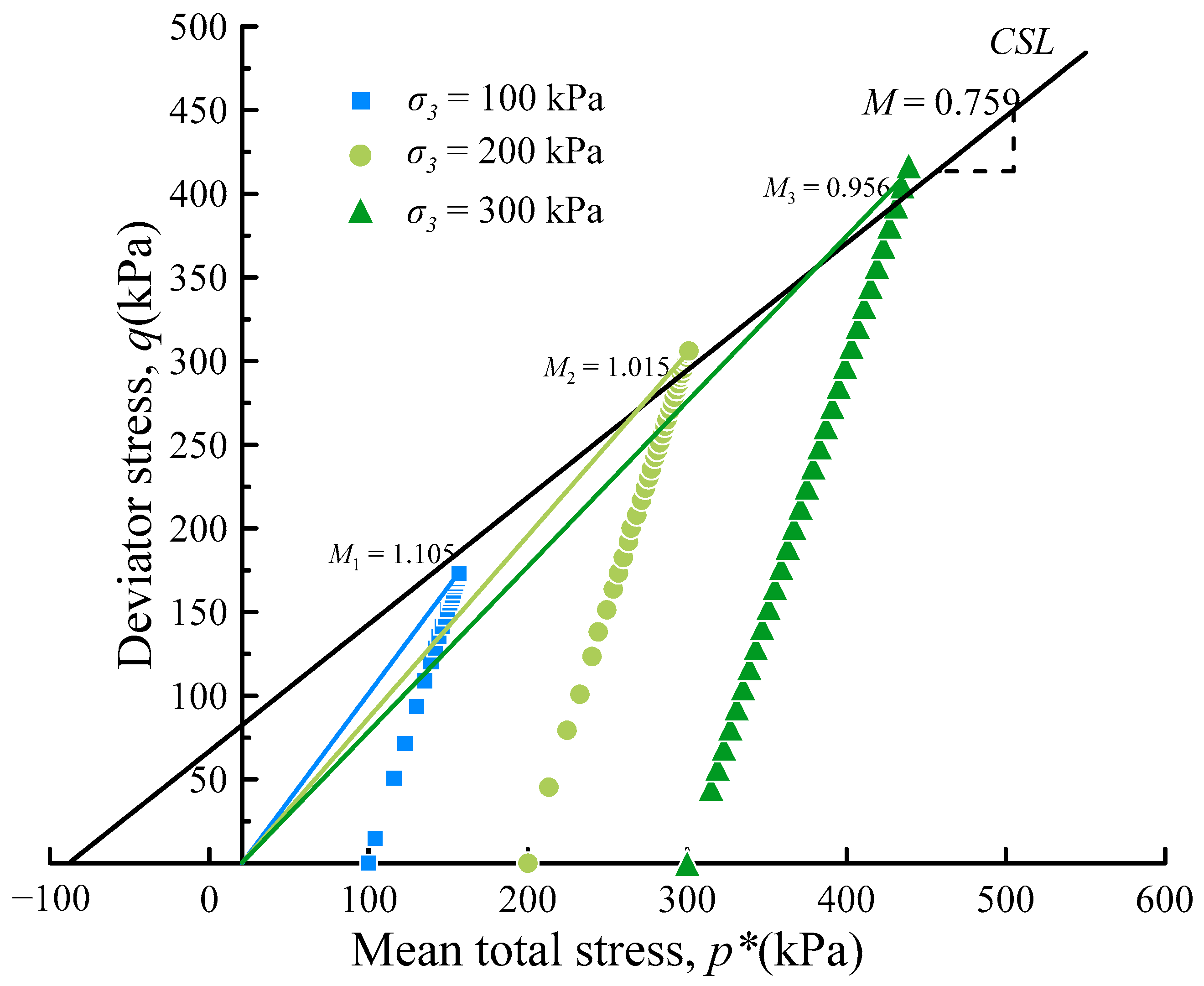
4.3. The Normal Consolidation Curve of Unsaturated Loess
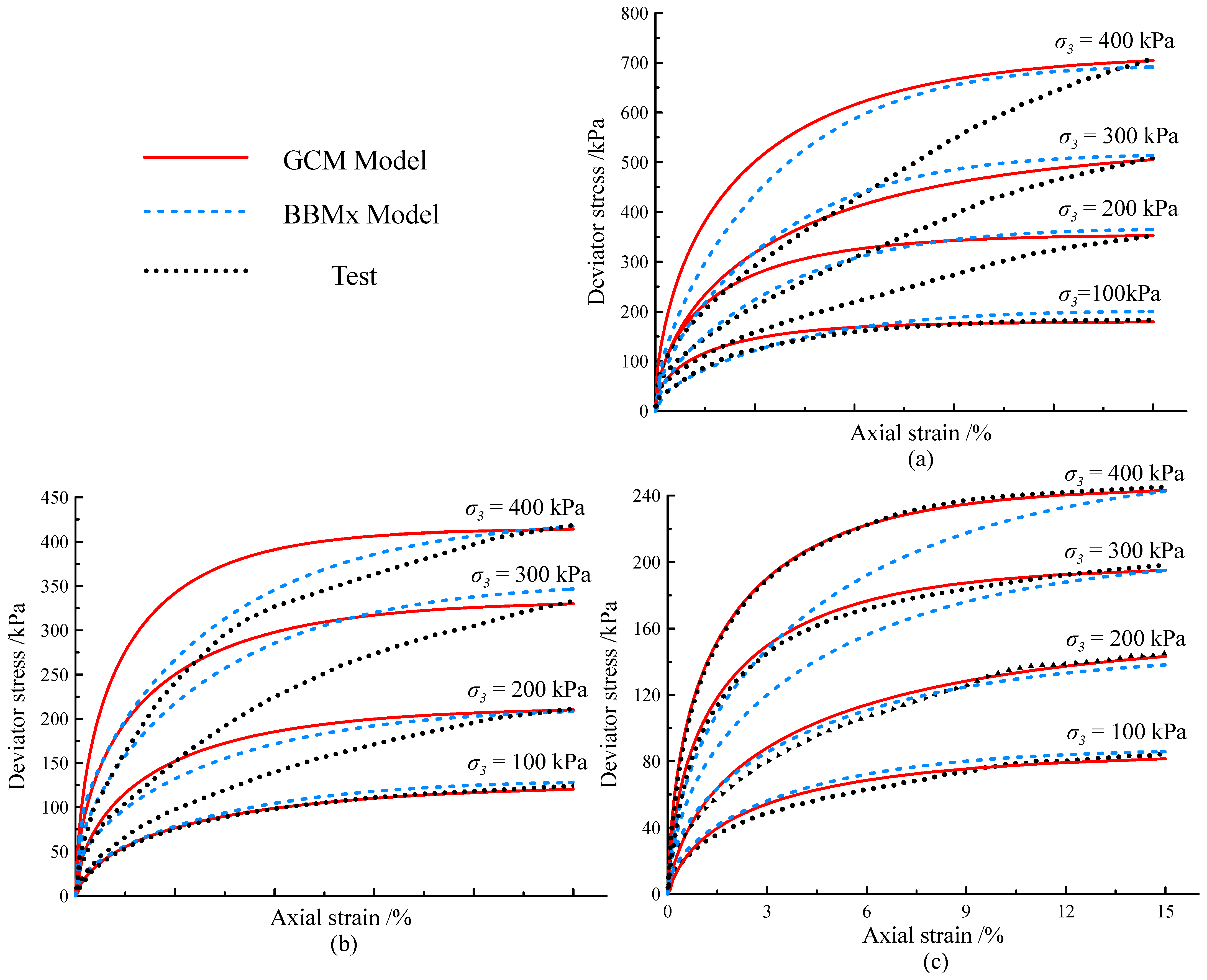
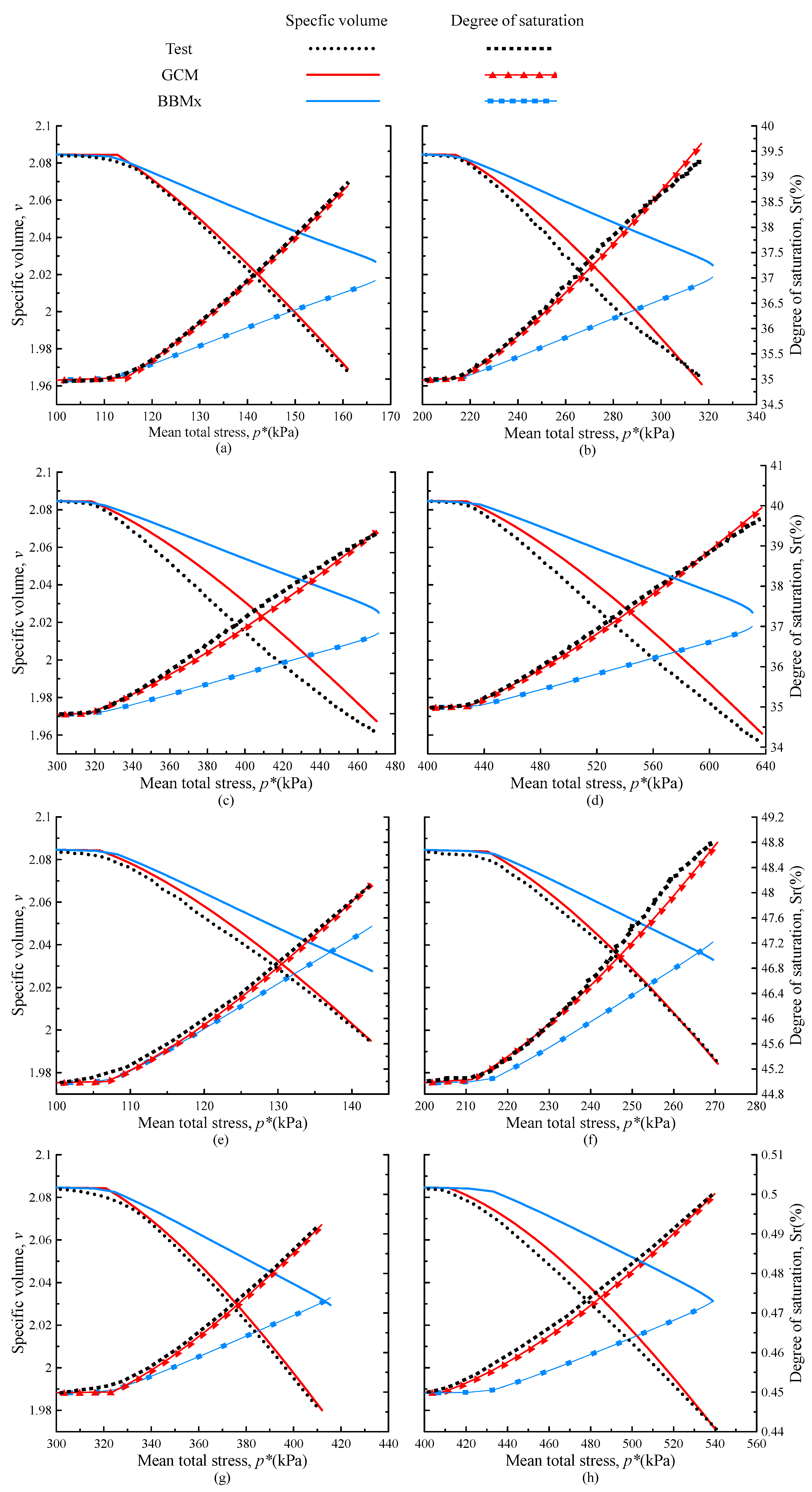
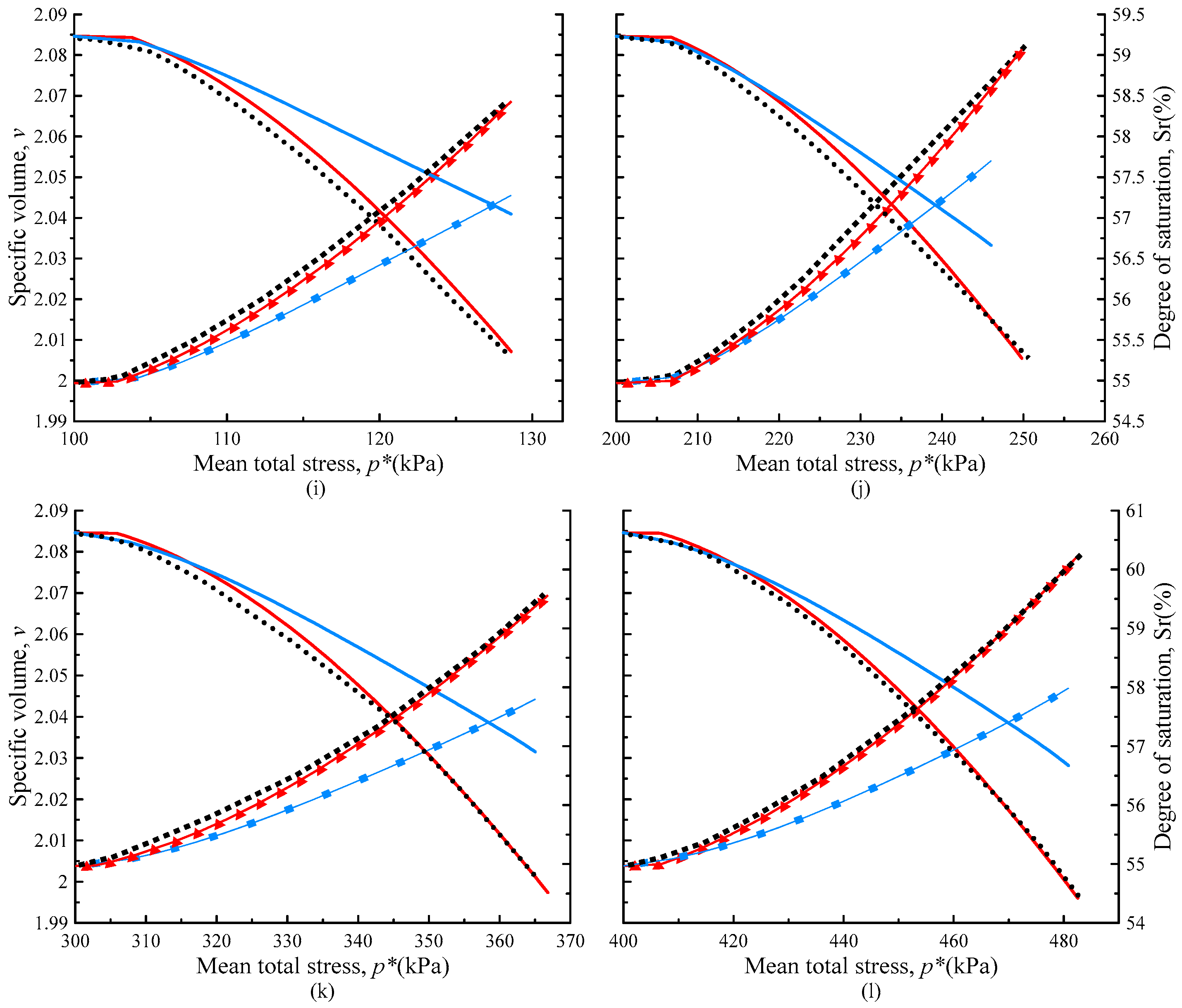
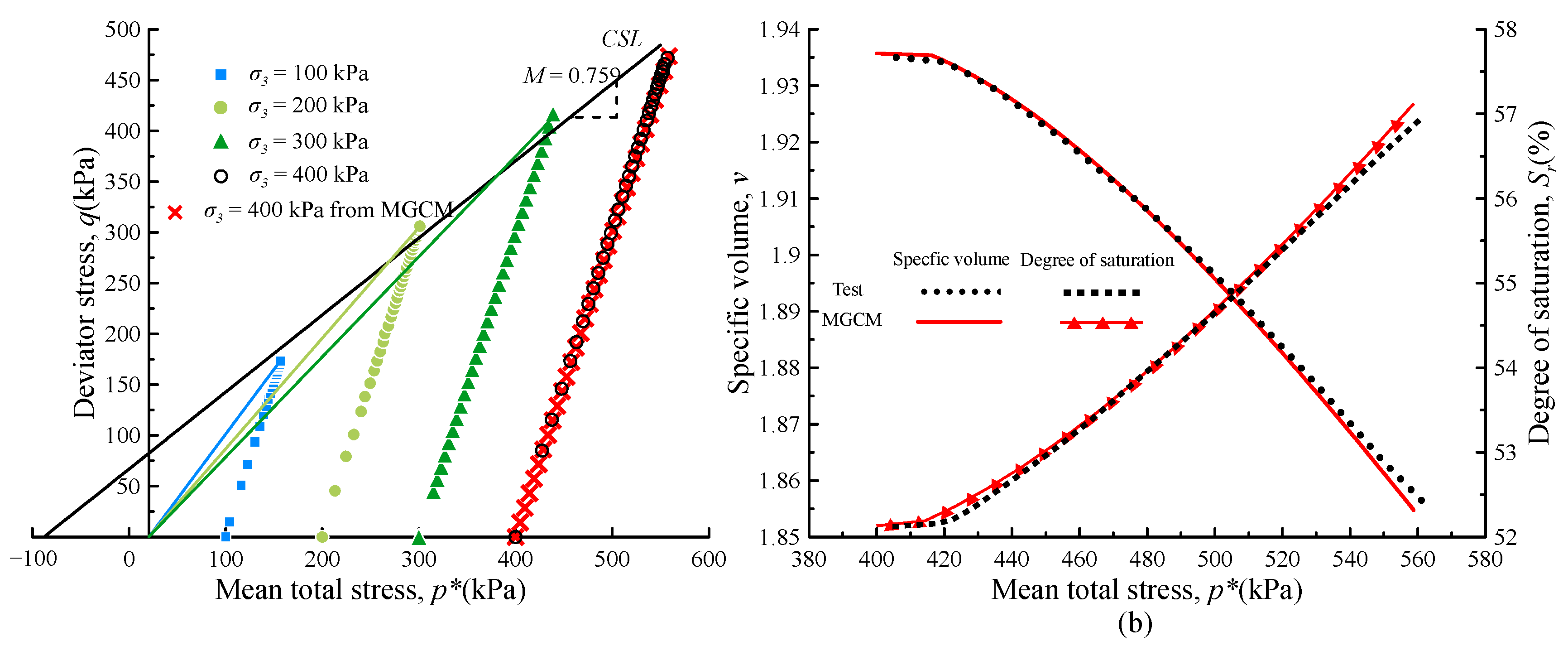
4.4. Analysis of Simulation and Test Results
4.5. The Hydraulic Coupling Effect during Shearing
4.6. The Proposal of the Strength Parameter η
5. Discussion
6. Conclusions
- (1)
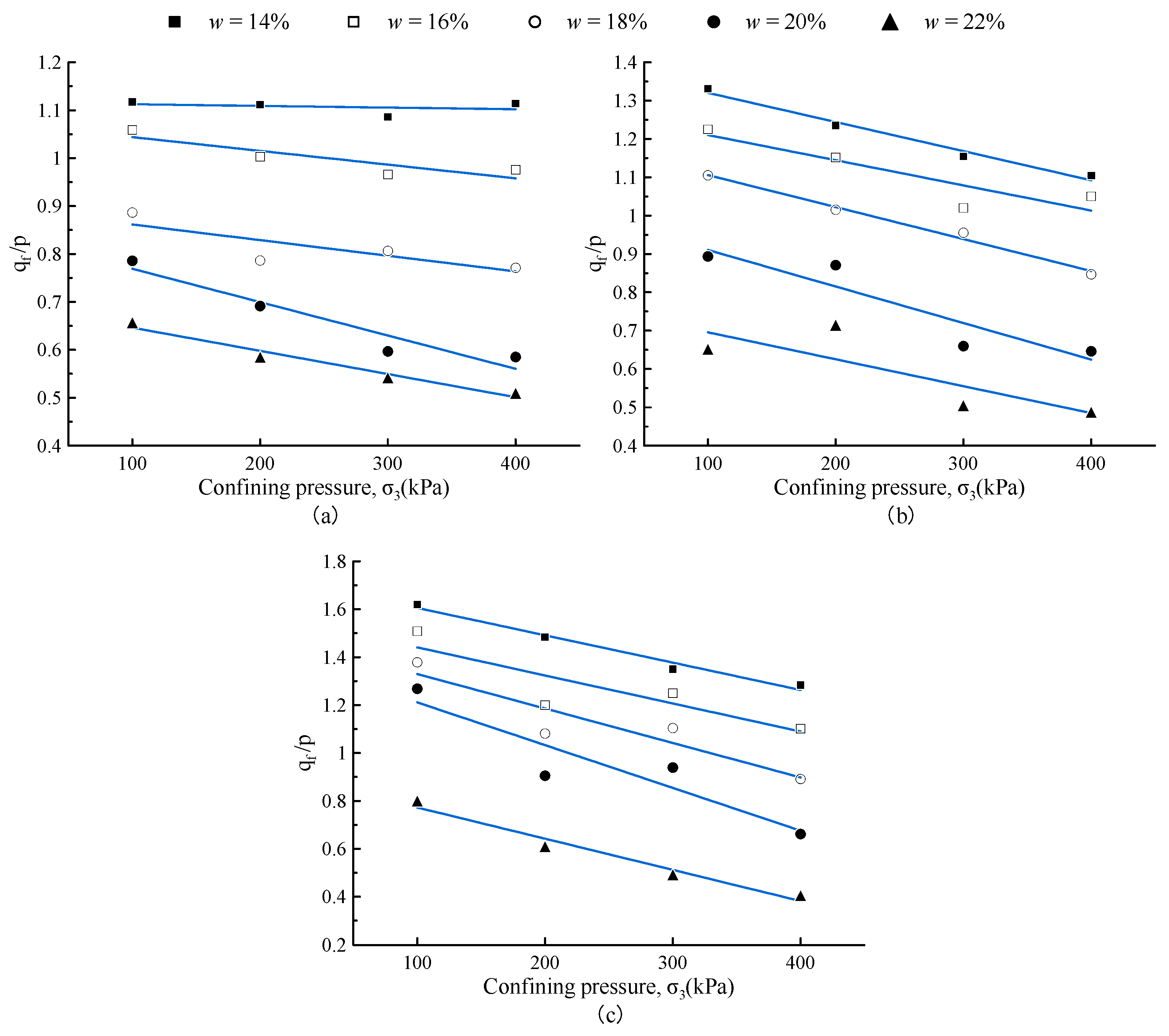
- The mechanical impact of increased saturation with constant water content influences the mechanical properties of unsaturated loess. Under constant water content, volume compression reduces the strength of unsaturated compacted loess. This is evident both in isotropic consolidation, where the compression index can be expressed as a function of saturation, and in triaxial shearing, where increasing water content leads to higher confining pressure, which in turn increases saturation and intensifies the trend of M reduction and strain softening. This illustrates the hydraulic coupling effect of the mechanical increase in saturation on the mechanical characteristics of unsaturated loess.
- (2)
- The hydro-mechanical coupling model (GCM), considering the mechanical changes in saturation, can better reflect the hydro-mechanical response of loess under load conditions. As the water content increases, the influence of hydraulic factors on the model’s performance gradually weakens. The model (BBMx) that does not consider hydraulic effects shows an increased response of loess properties under high water content, indicating a reduced dependence of the mechanical properties of loess on saturation with high water content.
- (3)
- The introduction of the strength parameter η, which characterizes the decay of initial strength as saturation increases during shearing, reveals the hydraulic–mechanical coupling effect of strength decay with increasing saturation during shearing and makes the critical state line of the same sample unique, thus improving the GCM. The improved model not only enhances the accuracy of model calculations but also improves predictive capability for the same initial state. The results of the constitutive model calculations indicate that the hydraulic coupling effect reveals the variation laws of specific volumes and saturations of unsaturated loess with average stress.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, Y.; Shi, W.; Aydin, A.; Beroya-Eitner, M.A.; Gao, G. Loess genesis and worldwide distribution. Earth-Sci. Rev. 2020, 201, 102947. [Google Scholar] [CrossRef]
- Pu, C.; Xu, Q.; Zhao, K.; Jiang, Y.; Hao, L.; Liu, J.; Chen, W.; Kou, P. Characterizing the Topographic Changes and Land Subsidence Associated with the Mountain Excavation and City Construction on the Chinese Loess Plateau. Remote Sens. 2021, 13, 1556. [Google Scholar] [CrossRef]
- Li, J.; Zhao, S.; Wang, X.; Hao, J.; Zhi, B.; Zhang, H.; Deng, B.; Xu, J. Experimental Study on Consolidation Characteristics of Compacted Loess. Adv. Civ. Eng. 2021, 2021, 6687858. [Google Scholar] [CrossRef]
- Lai, J.; Liu, Y.; Xiang, Y.; Wang, W.; Xu, J.; Cao, B.; Zhao, D.; Wei, W.; Bao, H.; Yan, C.; et al. Experimental study on shear strength of saturated remolded loess. PLoS ONE 2022, 17, e0271266. [Google Scholar] [CrossRef] [PubMed]
- Leng, Y.; Peng, J.; Wang, S.; Lu, F. Development of water sensitivity index of loess from its mechanical properties. Eng. Geol. 2021, 280, 105918. [Google Scholar] [CrossRef]
- Xing, Y.; Gao, D.; Jin, S.; Zhang, A.; Guo, M. Study on Mechanical Behaviors of Unsaturated Loess in terms of Moistening Level. KSCE J. Civ. Eng. 2019, 23, 1055–1063. [Google Scholar] [CrossRef]
- Shao, S.; Shao, S.; Wang, J. True triaxial mechanical properties of unsaturated loess in foundation pit engineering. Bull. Eng. Geol. Environ. 2021, 80, 4751–4772. [Google Scholar] [CrossRef]
- Sheng, D. Review of fundamental principles in modelling unsaturated soil behaviour. Comput. Geotech. 2011, 38, 757–776. [Google Scholar] [CrossRef]
- Niu, L.; Niu, H.; Zhao, Y.; Ge, L.; Guo, M.; Ren, W.; Wang, Y.; Zhang, A. Study on the Unified Mechanical Properties of Ili Undisturbed Loess under the Influence of Soluble Salt. Sustainability 2023, 15, 14717. [Google Scholar] [CrossRef]
- Zhang, Z.; Fu, Y.; Zhou, A.; Hou, X.; Zhang, M.; Fan, Z. Coupled Hydromechanical Behavior of Compacted Loess during Isotropic Compression. Int. J. Geomech. 2023, 23, 04023167. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, J.; Chen, C.; Wang, S. The compression and collapse behaviour of intact loess in suction-monitored triaxial apparatus. Acta Geotech. 2019, 15, 529–548. [Google Scholar] [CrossRef]
- Bai, J.; Diao, Y.; Jia, C.; Liu, C.; Zhang, M.; Wang, C. A Review of Advances in Triaxial Tests: Instruments, Test Techniques and Prospects. KSCE J. Civ. Eng. 2022, 26, 3325–3341. [Google Scholar] [CrossRef]
- Yates, K.; Russell, A.R. The unsaturated characteristics of natural loess in slopes, New Zealand. Géotechnique 2022, 73, 871–884. [Google Scholar] [CrossRef]
- Zhang, J.W.; Mu, Q.Y.; Garg, A.; Liu, F.L.; Cao, J. Shear behavior of unsaturated intact and compacted loess: A comparison study. Environ. Earth Sci. 2020, 79, 79. [Google Scholar] [CrossRef]
- Gao, B.; Su, L. Triaxial Mechanical Testing of Undisturbed Unsaturated Loess. Soil Mech. Found. Eng. 2020, 57, 57–64. [Google Scholar] [CrossRef]
- Zhong, Z.-L.; Liu, Y.-X.; Liu, X.-R.; Li, X.-Y.; Wang, S. Influence of moisture content on shearing strength of unsaturated undisturbed quaternary system middle pleistocene. J. Cent. South Univ. 2015, 22, 2776–2782. [Google Scholar] [CrossRef]
- Zheng, F.; Shao, S.; Wang, J.; Shao, S. Experimental Study on the Mechanical Behaviour of Natural Loess Based on Suction-Controlled True Triaxial Tests. KSCE J. Civ. Eng. 2020, 24, 2304–2321. [Google Scholar] [CrossRef]
- Wong, C.K.; Lun, M.C.H.; Wong, R.C.K. Interpretation of undrained shear strength observed in confined triaxial compression tests on compacted clay. Can. Geotech. J. 2021, 58, 1690–1702. [Google Scholar] [CrossRef]
- Yan, G.; Li, Z.; Galindo Torres, S.A.; Scheuermann, A.; Li, L. Transient Two-Phase Flow in Porous Media: A Literature Review and Engineering Application in Geotechnics. Geotechnics 2022, 2, 32–90. [Google Scholar] [CrossRef]
- Yan, G.; Li, Z.; Bore, T.; Galindo Torres, S.A.; Scheuermann, A.; Li, L. A lattice Boltzmann exploration of two-phase displacement in 2D porous media under various pressure boundary conditions. J. Rock Mech. Geotech. Eng. 2022, 14, 1782–1798. [Google Scholar] [CrossRef]
- Pujiastuti, H. The Effect of Matric Suction on the Shear Strength of Unsaturated Sandy Clay. Int. J. GEOMATE 2018, 14, 112–119. [Google Scholar] [CrossRef]
- Onyelowe, K.C.; Ebid, A.M.; Ramani Sujatha, E.; Fazel-Mojtahedi, F.; Golaghaei-Darzi, A.; Kontoni, D.N.; Nooralddin-Othman, N. Extensive overview of soil constitutive relations and applications for geotechnical engineering problems. Heliyon 2023, 9, e14465. [Google Scholar] [CrossRef]
- Alonso, E.E.; Gens, A.; Josa, A. A constitutive model for partially saturated soils. Géotechnique 1990, 40, 405–430. [Google Scholar] [CrossRef]
- Pedroso, D.M.; Farias, M.M. Extended Barcelona Basic Model for unsaturated soils under cyclic loadings. Comput. Geotech. 2011, 38, 731–740. [Google Scholar] [CrossRef]
- Lloret-Cabot, M.; Sánchez, M.; Wheeler, S.J. Formulation of a three-dimensional constitutive model for unsaturated soils incorporating mechanical-water retention couplings. Int. J. Numer. Anal. Methods Geomech. 2013, 37, 3008–3035. [Google Scholar] [CrossRef]
- Yao, Y.-P.; Kong, Y.-X. Extended UH Model: Three-Dimensional Unified Hardening Model for Anisotropic Clays. J. Eng. Mech. 2012, 138, 853–866. [Google Scholar] [CrossRef]
- Wheeler, S.J.; Sharma, R.S.; Buisson, M.S.R. Coupling of hydraulic hysteresis and stress–strain behaviour in unsaturated soils. Géotechnique 2003, 53, 41–54. [Google Scholar] [CrossRef]
- Sheng, D.; Sloan, S.W.; Gens, A.; Smith, D.W. Finite element formulation and algorithms for unsaturated soils. Part I: Theory. Int. J. Numer. Anal. Methods Geomech. 2003, 27, 745–765. [Google Scholar] [CrossRef]
- Sheng, D.; Fredlund, D.G.; Gens, A. A new modelling approach for unsaturated soils using independent stress variables. Can. Geotech. J. 2008, 45, 511–534. [Google Scholar] [CrossRef]
- Khalili, N.; Habte, M.A.; Zargarbashi, S. A fully coupled flow deformation model for cyclic analysis of unsaturated soils including hydraulic and mechanical hystereses. Comput. Geotech. 2008, 35, 872–889. [Google Scholar] [CrossRef]
- Cardoso, R.; Han, B.; Cai, G.; Xie, L.; Li, J.; Zhao, C.; Jommi, C.; Romero, E. Bounding surface constitutive model for unsaturated soils considering microscopic pore structure and bonding effect. In E3S Web of Conferences, Proceedings of the 4th European Conference on Unsaturated Soils (E-UNSAT 2020), Lisbon, Portugal, 19–21 October 2020; EDP Sciences: Les Ulis, France, 2020; Volume 195. [Google Scholar] [CrossRef]
- Hu, R.; Liu, H.-H.; Chen, Y.; Zhou, C.; Gallipoli, D. A constitutive model for unsaturated soils with consideration of inter-particle bonding. Comput. Geotech. 2014, 59, 127–144. [Google Scholar] [CrossRef]
- Liu, W.-H.; Li, W.-G.; Zhang, H.-Y.; Lin, X.-Y.; Kong, G.-Q.; Wang, L.; Hu, P. A critical state constitutive model for unsaturated structured soils. Comput. Geotech. 2022, 152, 104993. [Google Scholar] [CrossRef]
- Gao, D.; Zhao, K.; Jin, S.; Xing, Y. Moistening Deformation Constitutive Model for Unsaturated Loess. Int. J. Geomech. 2022, 22. [Google Scholar] [CrossRef]
- Shao, S.J.; Yu, Q.G.; Long, J.Y. A stress-strain relationship with soil structural parameter of collapse loess. In Proceedings of the 3rd Sino-Japan Geotechnical Symposium, Chongqing, China, 4–7 November 2007; pp. 488–500. [Google Scholar]
- Yao, Z.; Chen, Z.; Fang, X.; Wang, W.; Li, W.; Su, L. Elastoplastic damage seepage–consolidation coupled model of unsaturated undisturbed loess and its application. Acta Geotech. 2019, 15, 1637–1653. [Google Scholar] [CrossRef]
- GB/T50123-2019; Standard for Geotechnical Testing Method. Ministry of Water Resources of the People’s Republic of China: Beijing, China, 2019.
- Lloret-Cabot, M.; Wheeler, S.J.; Sánchez, M. A unified mechanical and retention model for saturated and unsaturated soil behaviour. Acta Geotech. 2016, 12, 1–21. [Google Scholar] [CrossRef]
- van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Zhou, A.-N.; Sheng, D.; Sloan, S.W.; Gens, A. Interpretation of unsaturated soil behaviour in the stress—Saturation space, I: Volume change and water retention behaviour. Comput. Geotech. 2012, 43, 178–187. [Google Scholar] [CrossRef]
- Behbehani, F.; McCartney, J.S. Compression Response of Sedimented Unsaturated Soils. J. Geotech. Geoenviron. 2022, 148. [Google Scholar] [CrossRef]
- Liang, Q.; Wu, X.; Li, C.; Wang, L. Mechanical analysis using the unconfined penetration test on the tensile strength of Q3 loess around Lanzhou City, China. Eng. Geol. 2014, 183, 324–329. [Google Scholar] [CrossRef]
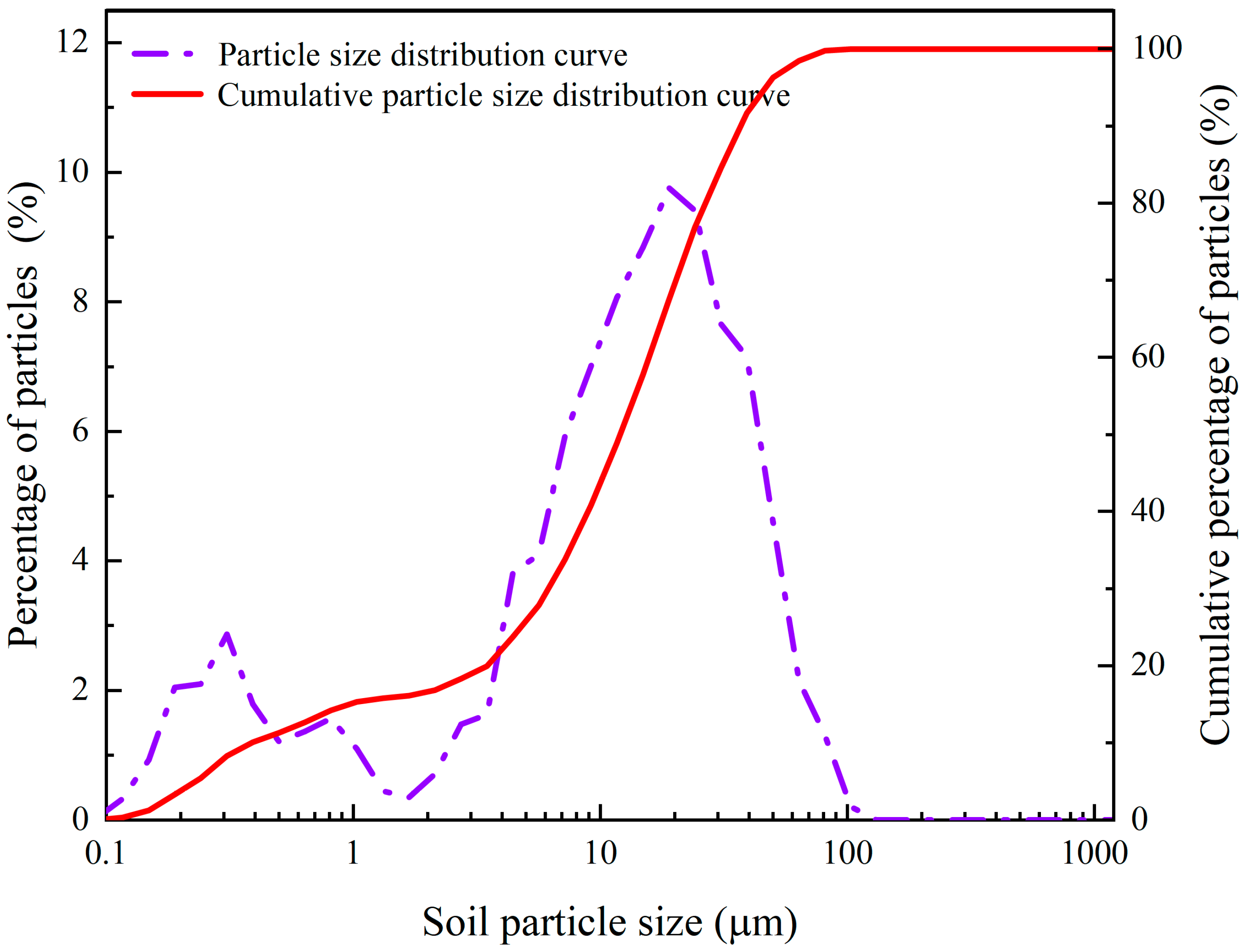





| Specific Gravity | Water Content | Dry Density (g/cm3) | Void Ratio | Size Composition | Liquid Limit (%) | Plastic Limit (%) | ||
|---|---|---|---|---|---|---|---|---|
| >0.075 mm | 0.075–0.005 mm | <0.005 mm | ||||||
| 2.71 | 11.21% | 1.43 | 1.09 | 0.29 | 73.92 | 25.79 | 35.12 | 19.96 |
| Samples | Dry Density | Confining Pressure | Water Content | Quantity |
|---|---|---|---|---|
| Loess 1 | 1.3 g/cm3 | 100 kPa, 200 kPa, 300 kPa, 400 kPa | 14%, 16%, 18%, 20%, 22% | 60 |
| Loess 2 | 1.4 g/cm3 | |||
| Loess 3 | 1.5 g/cm3 |
| Dry Density | α | n | m | R2 |
|---|---|---|---|---|
| 1.30 g/cm3 | 0.603 | 4 | 0.066 | 0.935 |
| 1.40 g/cm3 | 0.375 | 10.5 | 0.023 | 0.950 |
| 1.50 g/cm3 | 0.158 | 11 | 0.019 | 0.989 |
| Parameter | Dry Density 1.3 g/cm3 | Dry Density 1.4 g/cm3 | Dry Density 1.5 g/cm3 |
|---|---|---|---|
| ν | 0.4 | 0.4 | 0.4 |
| λ(0) | 0.2025 | 0.199 | 0.1953 |
| λ(s) | 0.1519–0.1547 | 0.1493–0.1497 | 0.1465–0.1469 |
| κ | 0.008–0.01 | 0.008–0.01 | 0.008–0.01 |
| κs | 0.008–0.01 | 0.008–0.01 | 0.008–0.01 |
| β | 0.18 | 0.18 | 0.18 |
| γ | 0.75 | 0.75 | 0.75 |
| sy | – | – | – |
| pref | 20–30 kPa | 25–45 kPa | 30–65 kPa |
| M | 0.456–1.106 | 0.400–1.013 | 0.236–1.122 |
| k | 0.1–3.95 | 0.5–5.21 | 0.46–13.45 |
| Parameter | Dry Density 1.3 g/cm3 | Dry Density 1.4 g/cm3 | Dry Density 1.5 g/cm3 |
|---|---|---|---|
| ν | 0.4 | 0.4 | 0.4 |
| λ(0) | 0.2025 | 0.199 | 0.1953 |
| κ | 0.008–0.01 | 0.008–0.01 | 0.008–0.01 |
| λw | 0.032 | 0.039 | 0.042 |
| κw | 0.01 | 0.018 | 0.032 |
| k1 | 0.1 | 0.2 | 0.2 |
| k2 | 0.8 | 0.8 | 0.8 |
| s1 | 8–44 kPa | 12–48 kPa | 26–233 kPa |
| s2 | – | – | – |
| M | 1.12–0.51 | 1.33–0.487 | 1.62–0.41 |
| ν | λ(0) | κ | λw | kw | k1 | k2 | ps | s2 | M | η0 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.4 | 0.48 | 0.008 | 0.039 | 0.018 | 0.2 | 0.8 | 41.3 kPa | 18.5 kPa | 0.759 | 3.52 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chai, H.; Li, X.; Qin, B.; Wang, W.; Axel, M. Deformation and Strength of Unsaturated Loess—Hydraulic Coupling Effects under Loads. Water 2024, 16, 997. https://doi.org/10.3390/w16070997
Chai H, Li X, Qin B, Wang W, Axel M. Deformation and Strength of Unsaturated Loess—Hydraulic Coupling Effects under Loads. Water. 2024; 16(7):997. https://doi.org/10.3390/w16070997
Chicago/Turabian StyleChai, Hao, Xi’an Li, Biao Qin, Weiping Wang, and Mani Axel. 2024. "Deformation and Strength of Unsaturated Loess—Hydraulic Coupling Effects under Loads" Water 16, no. 7: 997. https://doi.org/10.3390/w16070997
APA StyleChai, H., Li, X., Qin, B., Wang, W., & Axel, M. (2024). Deformation and Strength of Unsaturated Loess—Hydraulic Coupling Effects under Loads. Water, 16(7), 997. https://doi.org/10.3390/w16070997







