Judging Rainfall Intensity from Inter-Tip Times: Comparing ‘Straight-Through’ and Syphon-Equipped Tipping-Bucket Rain Gauge Performance
Abstract
1. Introduction
- (a)
- How does the presence of a syphon perturb the sequence of ITTs when the TBRG is fed with a constant, pumped water flow equivalent to rain of a constant intensity? By how much are the ITTs altered?
- (b)
- Does the presence of a syphon perceptibly perturb the recorded sequence of ITTs during natural rainfall of varying intensity?
- (c)
- What artefacts occur in the apparent rainfall intensities derived from the individual ITTs? (In other words, by how much are estimates of intensity perturbed by syphon operation?).
- (d)
- Given that when rain begins, a syphon may be empty or may already be partially filled owing to prior rainfall, or may remain partially filled at the cessation of rainfall, just as tipping buckets can, by how much can estimates of rainfall intensity and rainfall commencement and cessation times be perturbed by these combined effects?
Estimating Intensity from Unaggregated ITTs
2. Materials and Methods
2.1. Laboratory Tests at Constant Inflow Rates
2.2. Field Tests with Paired Gauges
3. Results
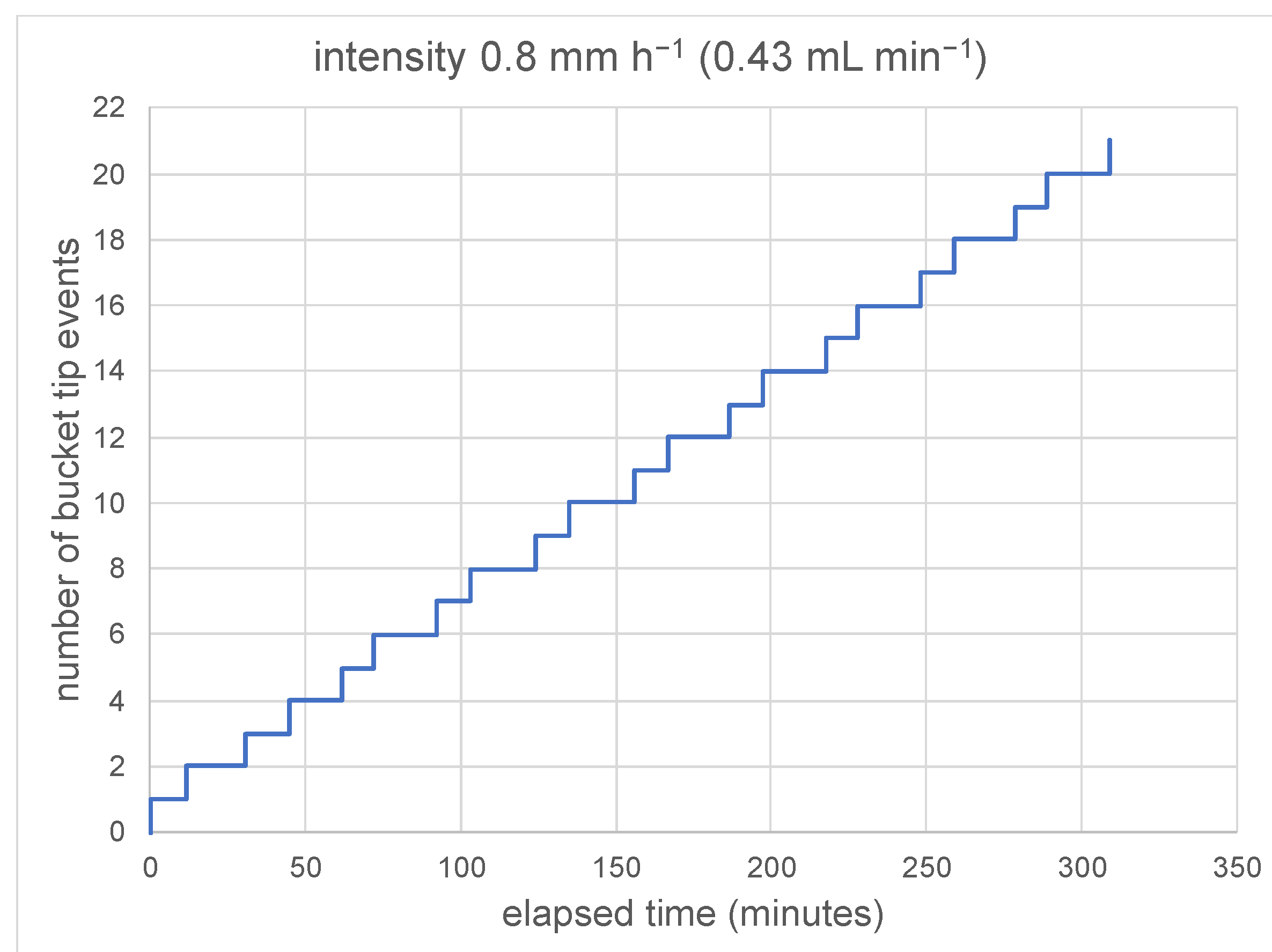
3.1. Lab Tests at Constant Pumped Flow Rates
3.2. Field Tests Using Two Co-Located Rain Gauges
4. Discussion
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Segovia-Cardozo, D.A.; Rodríguez-Sinobas, L.; Díez-Herrero, A.; Zubelzu, S.; Canales-Ide, F. Understanding the Mechanical Biases of Tipping-Bucket Rain Gauges: A Semi-Analytical Calibration Approach. Water 2021, 13, 2285. [Google Scholar] [CrossRef]
- Segovia-Cardozo, D.A.; Bernal-Basurco, C.; Rodríguez-Sinobas, L. Tipping Bucket Rain Gauges in Hydrological Research: Summary on Measurement Uncertainties, Calibration, and Error Reduction Strategies. Sensors 2023, 23, 5385. [Google Scholar] [CrossRef]
- Cauteruccio, A.; Colli, M.; Stagnaro, M.; Lanza, L.; Vuerich, E. In-situ precipitation measurements. In Springer Handbook of Atmospheric Measurements; Foken, T., Ed.; Springer Nature: Cham, Switzerland, 2021; pp. 359–400. [Google Scholar] [CrossRef]
- Saidi, H.; Ciampittiello, M.; Dresti, C.; Turconi, L. Extreme rainfall events: Evaluation with different instruments and measurement reliability. Environ. Earth Sci. 2014, 72, 4607–4616. [Google Scholar] [CrossRef]
- Costello, T.A.; Williams, H.J. Short duration rainfall intensity measured using calibrated time-of-tip data from a tipping bucket raingage. Agric. For. Meteorol. 1991, 57, 147–155. [Google Scholar] [CrossRef]
- Humphrey, M.D.; Istok, J.D.; Lee, J.Y.; Hevesi, J.A.; Flint, A.L. A New Method for Automated Dynamic Calibration of Tipping-Bucket Rain Gauges. J. Atmos. Ocean. Technol. 1997, 14, 1513–1519. [Google Scholar] [CrossRef]
- Santana, M.A.A.; Guimarães, P.L.O.; Lanza, L.G.; Vuerich, E. Metrological analysis of a gravimetric calibration system for tipping-bucket rain gauges. Meteorol. Appl. 2015, 22, 879–885. [Google Scholar] [CrossRef]
- Sypka, P. Dynamic real-time volumetric correction for tipping-bucket rain gauges. Agric. For. Meteorol. 2019, 271, 158–167. [Google Scholar] [CrossRef]
- Kimball, S.K.; Mulekar, M.S.; Cummings, S.; Stamates, J. The University of South Alabama Mesonet and Coastal Observing System: A Technical and Statistical Overview. J. Atmos. Ocean. Technol. 2010, 27, 1417–1439. [Google Scholar] [CrossRef]
- Cai, Z.; Liu, J.; Liao, A.; Li, X.; Liao, M. Numerical and Experimental Investigation on the Function of Siphons for Tipping-Bucket Rain Gauges. J. Atmos. Ocean. Technol. 2020, 37, 1189–1201. [Google Scholar] [CrossRef]
- Duchon, C.; Fiebrich, C.; Grimsley, D. Using High-Speed Photography to Study Undercatch in Tipping-Bucket Rain Gauges. J. Atmos. Ocean. Technol. 2014, 31, 1330–1336. [Google Scholar] [CrossRef]
- Liao, M.; Liao, A.; Liu, J.; Cai, Z.; Liu, H.; Ma, T. A novel method and system for the fast calibration of tipping bucket rain gauges. J. Hydrol. 2021, 597, 125782. [Google Scholar] [CrossRef]
- Parkin, D.A.; King, W.D.; Shaw, D.E. An Automatic Recording Raingage Network for a Cloud-Seeding Experiment. J. Appl. Meteorol. 1982, 21, 227–236. [Google Scholar] [CrossRef][Green Version]
- Maksimović, Č.; Bužek, L.; Petrović, J. Corrections of rainfall data obtained by tipping bucket rain gauge. Atmos. Res. 1991, 27, 45–53. [Google Scholar] [CrossRef]
- Harremoës, P.; Mikkelsen, P.S. Properties of extreme point rainfall I: Results from a rain gauge system in Denmark. Atmos. Res. 1995, 37, 277–286. [Google Scholar] [CrossRef]
- Overgaard, S.; El-Shaarawi, A.H.; Arnbjerg-Nielsen, K. Calibration of tipping bucket rain gauges. Water Sci. Technol. 1998, 37, 139–145. [Google Scholar] [CrossRef]
- Chwala, C.; Gmeiner, A.; Qiu, W.; Hipp, S.; Nienaber, D.; Siart, U.; Eibert, T.; Pohl, M.; Seltmann, J.; Fritz, J.; et al. Precipitation observation using microwave backhaul links in the alpine and pre-alpine region of Southern Germany. Hydrol. Earth Syst. Sci. 2012, 16, 2647–2661. [Google Scholar] [CrossRef]
- Colli, M.; Stagnaro, M.; Caridi, A.; Lanza, L.G.; Randazzo, A.; Pastorino, M.; Caviglia, D.D.; Delucchi, A. A Field Assessment of a Rain Estimation System Based on Satellite-to-Earth Microwave Links. IEEE Trans. Geosci. Remote Sens. 2019, 57, 2864–2875. [Google Scholar] [CrossRef]
- Adirosi, E.; Facheris, L.; Giannetti, F.; Scarfone, S.; Bacci, G.; Mazza, A.; Ortolani, A.; Baldini, L. Evaluation of Rainfall Estimation Derived from Commercial Interactive DVB Receivers Using Disdrometer, Rain Gauge, and Weather Radar. IEEE Trans. Geosci. Remote Sens. 2021, 59, 8978–8991. [Google Scholar] [CrossRef]
- Gianoglio, C.; Alyosef, A.; Colli, M.; Zani, S.; Caviglia, D.D. Rain Discrimination with Machine Learning Classifiers for Opportunistic Rain Detection System Using Satellite Micro-Wave Links. Sensors 2023, 23, 1202. [Google Scholar] [CrossRef]
- Yu, C.L.; Sin, K.C.; Chan, Y.W. Inter-comparison of 0.1-mm resolution raingauges in the measurement of rainfall amount and rainfall intensity. In Proceedings of the 27th Guangdong—Hong Kong—Macao Seminar on Meteorological Science and Technology, Shaoguan, China, 9–10 January 2013; 16p. [Google Scholar]
- Chan, Y.; Yu, C.; Tam, K. Inter-comparison of raingauges on rainfall amount and intensity measurements in a tropical environment. J. Geod. Geomat. Eng. 2015, 1, 12–25. [Google Scholar]
- Stagnaro, M.; Colli, M.; Lanza, L.G.; Chan, P.W. Performance of post-processing algorithms for rainfall intensity using measurements from tipping-bucket rain gauges. Atmos. Meas. Tech. 2016, 9, 5699–5706. [Google Scholar] [CrossRef]
- Stagnaro, M.; Colli, M.; Lanza, L.; Chan, P.W. Assessing rainfall intensity calculation algorithms for tipping bucket rain gauges at a field test site. In Proceedings of the European Geosciences Union, General Assembly, Vienna, Austria, 17–22 April 2016. [Google Scholar]
- Shedekar, V.S.; Brown, L.C.; Heckel, M.; King, K.W.; Fausey, N.R.; Daren Harmel, R. Measurement Errors in Tipping Bucket Rain Gauges under Different Rainfall Intensities and their implication to Hydrologic Models. In Proceedings of the 2009 ASABE Annual International Meeting, Grand Sierra Resort and Casino Reno, Reno, NV, USA, 21–24 June 2009; pp. 1–9. [Google Scholar]
- Rachmawati, L.M.; Mardiansyah, A.; Kinanti, I.W.; Ramadhan, A.; Adiwidya, A.S.; Jalasena, A.; Chandra, I. Natural, Meteorology, And Novel—IAP Data Processing Method for Tipping Bucket Based Rain Gauge. J. Phys. Conf. Ser. 2022, 2243, 012071. [Google Scholar] [CrossRef]
- Song, Y.; Han, D.; Rico-Ramirez, M.A. High temporal resolution rainfall rate estimation from rain gauge measurements. J. Hydroinform. 2017, 19, 930–941. [Google Scholar] [CrossRef]
- Dunkerley, D.L. Rainfall intensity bursts and the erosion of soils: An analysis highlighting the need for high temporal resolution rainfall data for research under current and future climates. Earth Surf. Dynam. 2019, 7, 345–360. [Google Scholar] [CrossRef]
- Dunkerley, D. Intra-event intermittency of rainfall: An analysis of the metrics of rain and no-rain periods. Hydrol. Process. 2015, 29, 3294–3305. [Google Scholar] [CrossRef]
- Dunkerley, D. What does I30 tell us? An assessment using high-resolution rainfall event data from two Australian locations. Catena 2019, 180, 320–332. [Google Scholar] [CrossRef]
- Dunkerley, D. Intermittency of rainfall at sub-daily timescales: New quantitative indices based on the number, duration, and sequencing of interruptions to rainfall. Atmos. Res. 2021, 253, 105475. [Google Scholar] [CrossRef]
- Mandeep, J.S.; Hassan, S.I.S. 60- to 1-Min Rainfall-Rate Conversion: Comparison of Existing Prediction Methods with Data Obtained in the Southeast Asia Region. J. Appl. Meteorol. Climatol. 2008, 47, 925–930. [Google Scholar] [CrossRef]
- Muñoz, P.; Celleri, R.; Feyen, J. Effect of the Resolution of Tipping-Bucket Rain Gauge and Calculation Method on Rainfall Intensities in an Andean Mountain Gradient. Water 2016, 8, 534. [Google Scholar] [CrossRef]
- Dunkerley, D. How does sub-hourly rainfall intermittency bias the climatology of hourly and daily rainfalls? Examples from arid and wet tropical Australia. Int. J. Climatol. 2019, 39, 2412–2421. [Google Scholar] [CrossRef]
- Connolly, R.D.; Schirmer, J.; Dunn, P.K. A daily rainfall disaggregation model. Agric. For. Meteorol. 1998, 92, 105–117. [Google Scholar] [CrossRef]
- Dunkerley, D. Sub-daily rainfall intermittency: Is it really stochastic? A test at two Australian locations. Int. J. Climatol. 2024, 44, 552–570. [Google Scholar] [CrossRef]
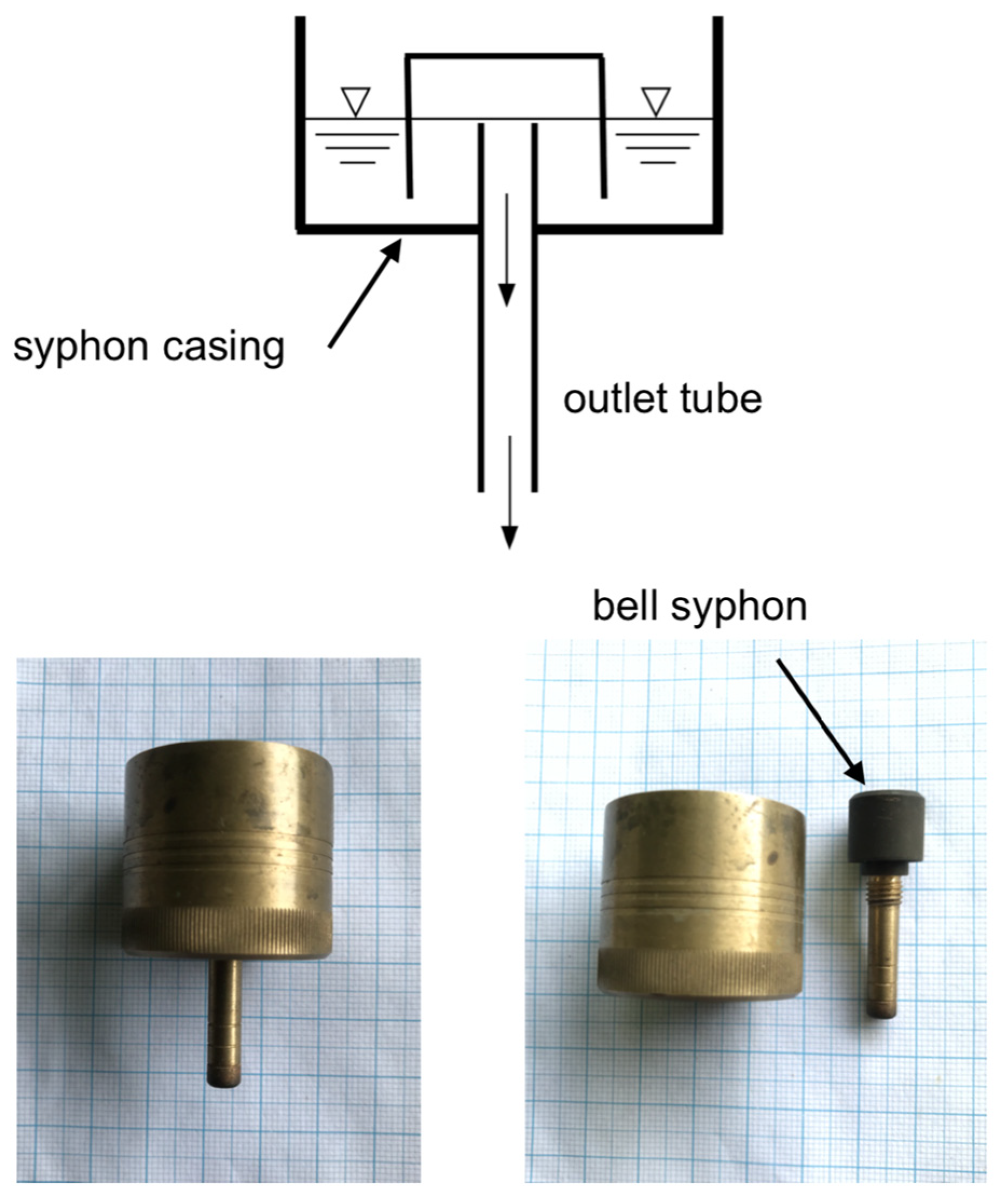


| Parameter | RIMCO Model 8020 |
|---|---|
| syphon casing outside diameter | 31.5 mm |
| syphon casing inside diameter | 22 mm |
| syphon casing height | 27.5 mm |
| bell syphon diameter | 12.5 mm |
| bell syphon height | 11 mm |
| bell syphon outlet tube length | 25 mm |
| bell syphon outlet tube outside diameter | 5 mm |
| bell syphon outlet tube inside diameter | 2.6 mm |
| Parameter | Syphon-Equipped (SE) Gauge | Straight-Through (ST) Gauge | |
|---|---|---|---|
| ITTs (units: seconds) | mean | 59.12 | 59.17 |
| std. deviation | 101.46 | 80.72 | |
| minimum | 11.0 | 11.0 | |
| maximum | 615.0 | 367.0 s | |
| median | 27.0 | 30.5 | |
| intensities (units: mm h−1) | mean | 26.19 | 24.77 |
| std. deviation | 15.32 | 14.97 | |
| minimum | 1.17 | 1.96 | |
| maximum | 65.45 | 65.45 | |
| median | 26.67 | 23.61 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dunkerley, D. Judging Rainfall Intensity from Inter-Tip Times: Comparing ‘Straight-Through’ and Syphon-Equipped Tipping-Bucket Rain Gauge Performance. Water 2024, 16, 998. https://doi.org/10.3390/w16070998
Dunkerley D. Judging Rainfall Intensity from Inter-Tip Times: Comparing ‘Straight-Through’ and Syphon-Equipped Tipping-Bucket Rain Gauge Performance. Water. 2024; 16(7):998. https://doi.org/10.3390/w16070998
Chicago/Turabian StyleDunkerley, David. 2024. "Judging Rainfall Intensity from Inter-Tip Times: Comparing ‘Straight-Through’ and Syphon-Equipped Tipping-Bucket Rain Gauge Performance" Water 16, no. 7: 998. https://doi.org/10.3390/w16070998
APA StyleDunkerley, D. (2024). Judging Rainfall Intensity from Inter-Tip Times: Comparing ‘Straight-Through’ and Syphon-Equipped Tipping-Bucket Rain Gauge Performance. Water, 16(7), 998. https://doi.org/10.3390/w16070998






