Figure 1.
Distribution of meteorological, rainfall, and hydrological stations throughout the Tuwei River Basin.
Figure 1.
Distribution of meteorological, rainfall, and hydrological stations throughout the Tuwei River Basin.
Figure 2.
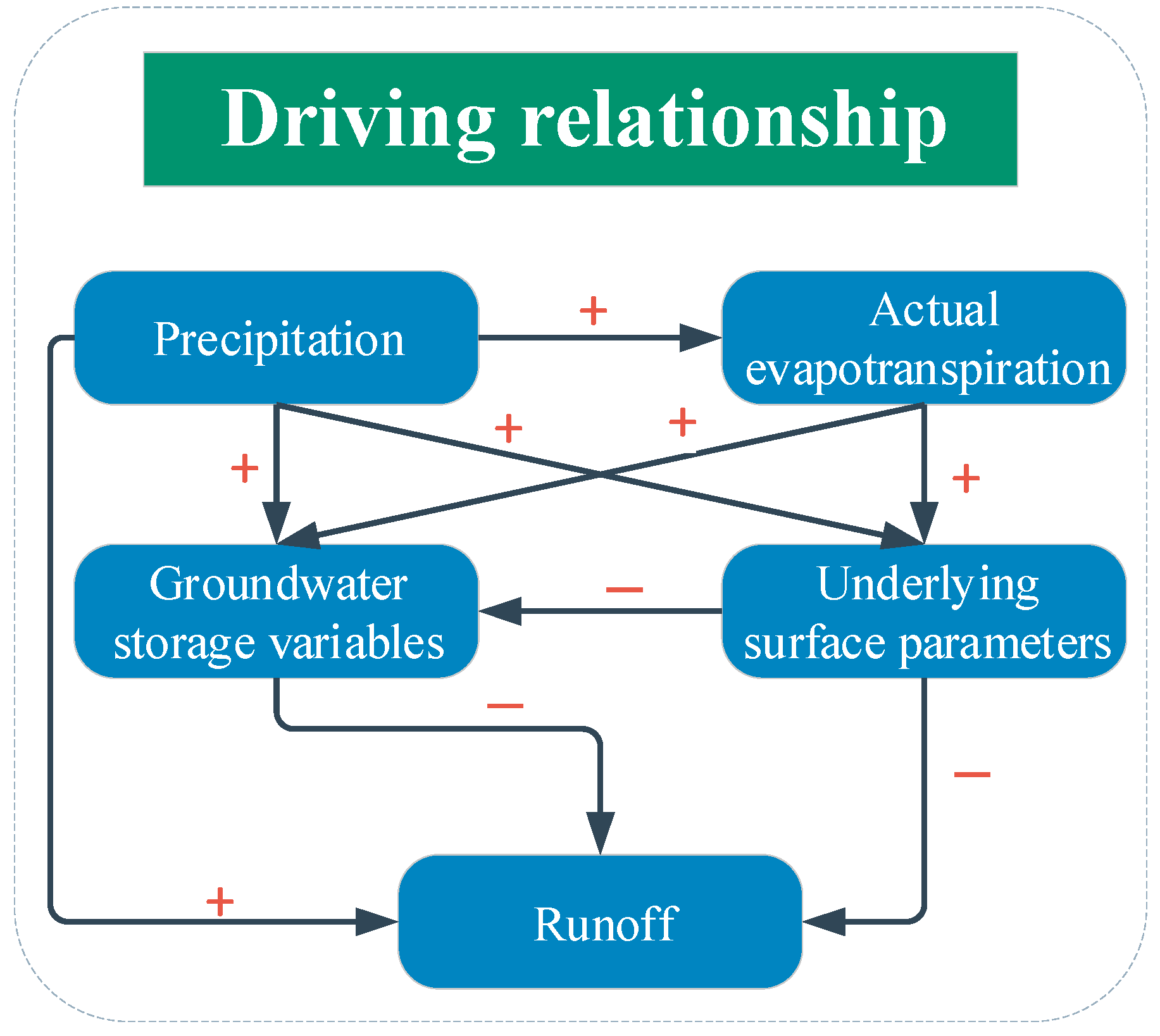
Interaction relationship between runoff and its physical driving elements. “+” represents positive driving effect, and “−” represents opposite driving effect.
Figure 2.
Interaction relationship between runoff and its physical driving elements. “+” represents positive driving effect, and “−” represents opposite driving effect.
Figure 3.
Five % (blue), fifty % (dark green), and ninety-five % (light green) quantile plots of the best non-stationary model for three distributions of annual groundwater storage variables, with P, E, and n as covariates.
Figure 3.
Five % (blue), fifty % (dark green), and ninety-five % (light green) quantile plots of the best non-stationary model for three distributions of annual groundwater storage variables, with P, E, and n as covariates.
Figure 4.
Worm plots of residuals from the best non-stationary models for three distributions of annual groundwater storage variables, with P, E, and n as covariates. For a satisfactory fit, the data points should be within the two gray lines (95% confidence interval).
Figure 4.
Worm plots of residuals from the best non-stationary models for three distributions of annual groundwater storage variables, with P, E, and n as covariates. For a satisfactory fit, the data points should be within the two gray lines (95% confidence interval).
Figure 5.
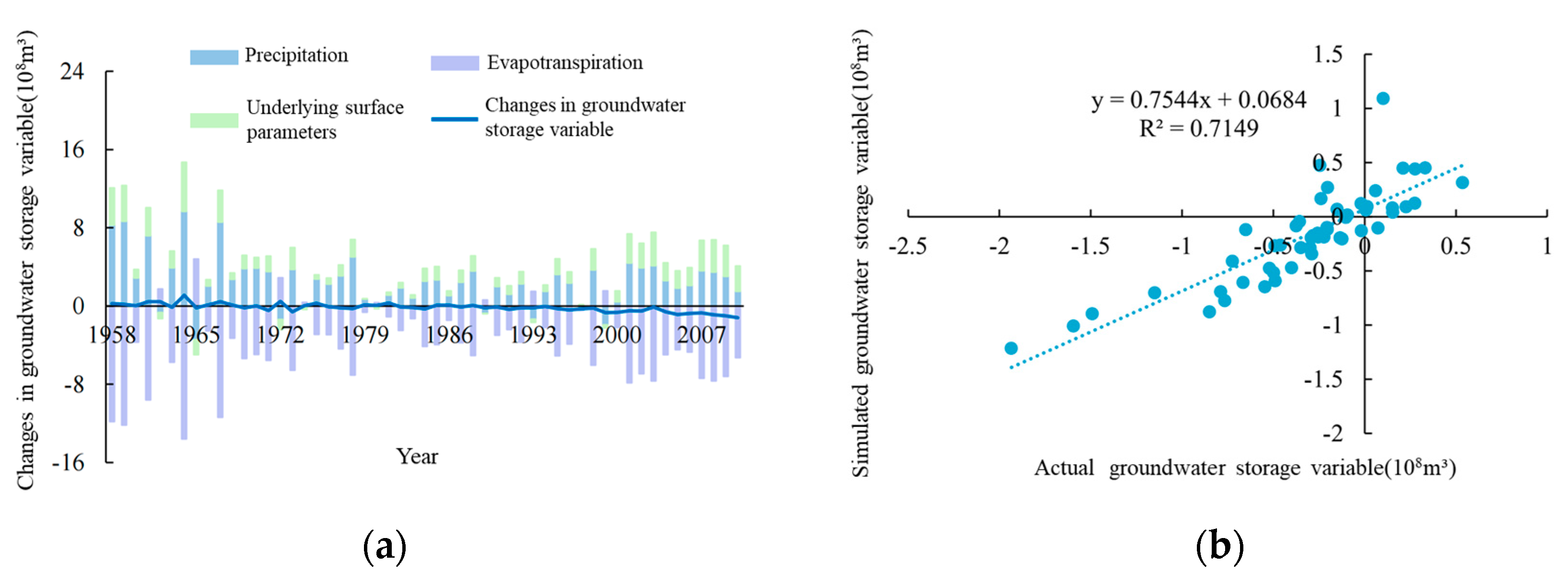
Contribution changes (a) of P, E, and n to groundwater storage variables, and correlation scatter plot (b) between simulated and actual change values.
Figure 5.
Contribution changes (a) of P, E, and n to groundwater storage variables, and correlation scatter plot (b) between simulated and actual change values.
Figure 6.
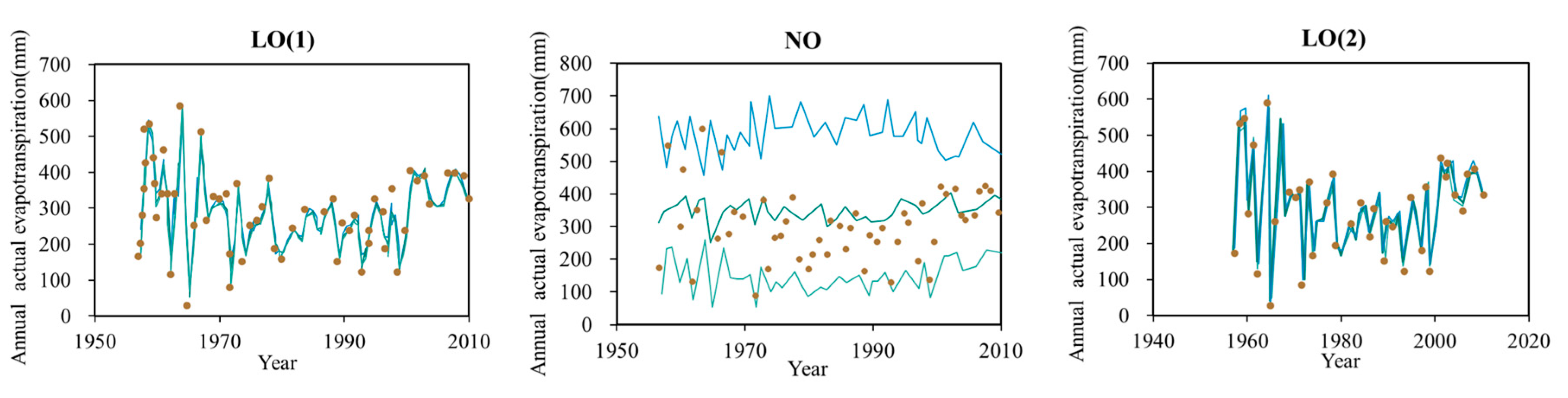
Five % (blue), fifty % (dark green), and ninety-five % (light green) quantile plots of the best non-stationary model for three distributions of actual evapotranspiration, with physical variables as covariates.
Figure 6.
Five % (blue), fifty % (dark green), and ninety-five % (light green) quantile plots of the best non-stationary model for three distributions of actual evapotranspiration, with physical variables as covariates.
Figure 7.
Worm plots of residuals from the best non-stationary models for three distributions of annual actual evapotranspiration, with P and n as covariates. For a satisfactory fit, the data points should be within the two gray lines (95% confidence interval).
Figure 7.
Worm plots of residuals from the best non-stationary models for three distributions of annual actual evapotranspiration, with P and n as covariates. For a satisfactory fit, the data points should be within the two gray lines (95% confidence interval).
Figure 8.
Contribution changes (a) in P and n to E and correlation scatter plot (b) between the changes in simulated and measured values.
Figure 8.
Contribution changes (a) in P and n to E and correlation scatter plot (b) between the changes in simulated and measured values.
Figure 9.
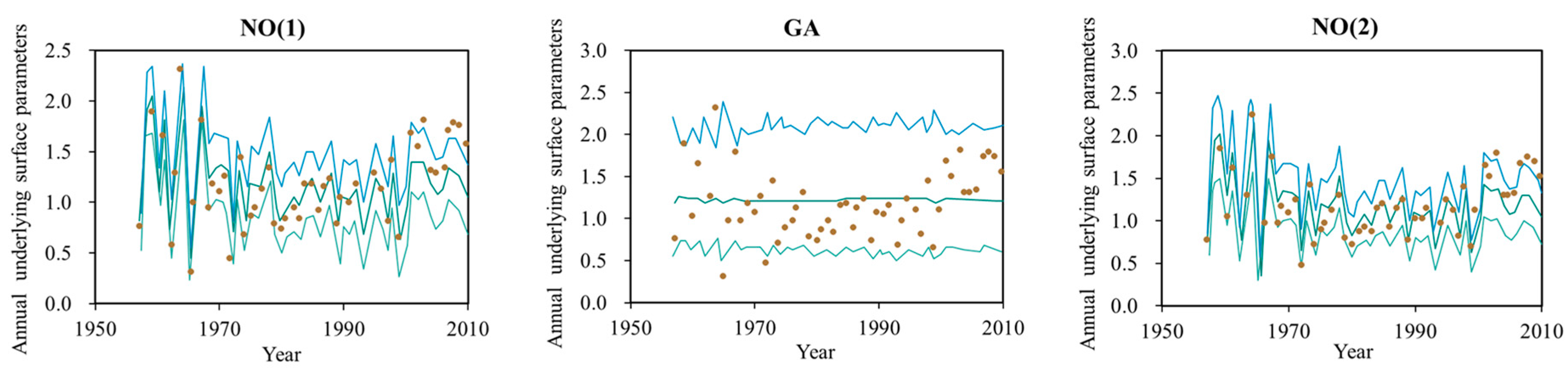
Five % (blue), fifty % (dark green), and ninety-five % (light green) quantile plots of the best non-stationary model for three distributions of underlying surface parameter, with P as the covariate.
Figure 9.
Five % (blue), fifty % (dark green), and ninety-five % (light green) quantile plots of the best non-stationary model for three distributions of underlying surface parameter, with P as the covariate.
Figure 10.
Worm plots of residuals from the best non-stationary models for three distributions of annual underlying surface parameter, with P as the covariate. For a satisfactory fit, the data points should be within the two gray lines (95% confidence interval).
Figure 10.
Worm plots of residuals from the best non-stationary models for three distributions of annual underlying surface parameter, with P as the covariate. For a satisfactory fit, the data points should be within the two gray lines (95% confidence interval).
Figure 11.
Contribution changes (a) of P to underlying surface parameter n and correlation scatter plot (b) between the changes in simulated and computed values.
Figure 11.
Contribution changes (a) of P to underlying surface parameter n and correlation scatter plot (b) between the changes in simulated and computed values.
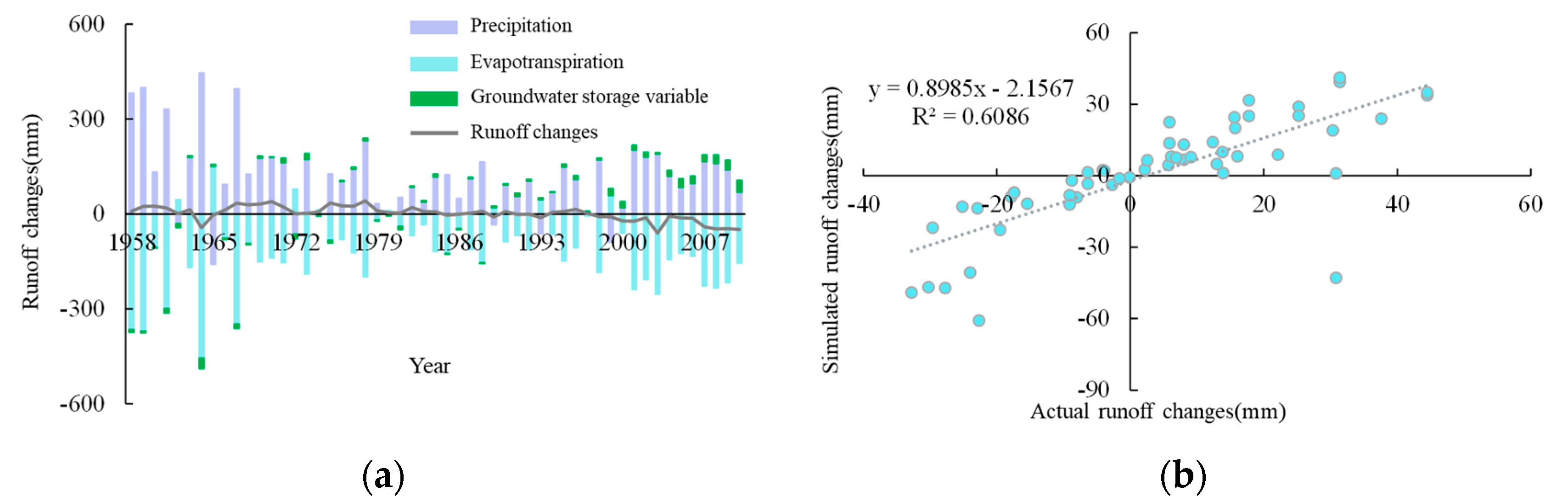
Figure 12.
Contribution changes (a) of P, E, and ΔG to runoff and correlation scatter plot (b) between the changes in observed and computed values.
Figure 12.
Contribution changes (a) of P, E, and ΔG to runoff and correlation scatter plot (b) between the changes in observed and computed values.
Table 1.
AIC values for the non-stationary GAMLSS of annual groundwater storage variable utilizing physical variables as covariates, with only the mean value μ changing.
Table 1.
AIC values for the non-stationary GAMLSS of annual groundwater storage variable utilizing physical variables as covariates, with only the mean value μ changing.
| Covariate Combination | GU | LO | NO |
|---|
| P | 64.21 | 69.98 | 76.48 |
| E | 64.71 | 70.10 | 75.71 |
| n | 64.02 | 67.22 | 71.45 |
| P + E | −0.27 | −0.24 | −1.59 |
| P + n | 30.19 | 26.10 | 24.33 |
| E + n | 54.38 | 47.07 | 47.27 |
| P + E + n | −9.33 | −6.02 | −6.28 |
Table 2.
Distribution parameter estimates and goodness-of-fit test for GU-GAMLSS with only the mean value μ changing.
Table 2.
Distribution parameter estimates and goodness-of-fit test for GU-GAMLSS with only the mean value μ changing.
| Distribution | Covariate Combination | Position Parameter | Scale Parameter | AIC | SBC |
|---|
| GU | P + E + n | 0.02P − 0.03E + 2.15n − 1.76 | logσ = −1.75 | −9.33 | 0.62 |
Table 3.
AIC values for the non-stationary GAMLSS of annual groundwater storage variable utilizing physical variables as covariates; only the mean square error σ varies with physical variables.
Table 3.
AIC values for the non-stationary GAMLSS of annual groundwater storage variable utilizing physical variables as covariates; only the mean square error σ varies with physical variables.
| Covariate Combination | GU | LO | NO |
|---|
| P | 64.77 | 70.13 | 76.69 |
| E | 63.92 | 70.13 | 76.69 |
| n | 61.66 | 58.56 | 61.40 |
| P + E | 56.86 | 48.33 | 47.06 |
| P + n | 55.33 | 47.34 | 45.80 |
| E + n | 54.41 | 48.06 | 46.27 |
| P + E + n | 56.02 | 49.34 | 47.79 |
Table 4.
Distribution parameter estimates and goodness-of-fit test for NO-GAMLSS with only the mean square error σ varying.
Table 4.
Distribution parameter estimates and goodness-of-fit test for NO-GAMLSS with only the mean square error σ varying.
| Distribution | Covariate Combination | Position Parameter | Scale Parameter | AIC | SBC |
|---|
| NO | P + n | 0.29 | logσ = −0.01P + 2.43n − 1.30 | 45.80 | 53.76 |
Table 5.
AIC values for the non-stationary GAMLSS of annual groundwater storage variable utilizing physical variables as covariates; both mean μ and mean square error σ change with physical variables.
Table 5.
AIC values for the non-stationary GAMLSS of annual groundwater storage variable utilizing physical variables as covariates; both mean μ and mean square error σ change with physical variables.
| Covariate Combination | GU | LO | NO |
|---|
| P | 64.77 | 70.13 | 76.69 |
| E | 63.92 | 70.13 | 76.69 |
| n | 61.66 | 58.56 | 61.40 |
| P + E | 56.86 | 48.33 | 47.06 |
| P + n | 55.33 | 47.34 | 45.80 |
| E + n | 54.41 | 48.06 | 46.27 |
| P + E + n | 56.02 | 49.34 | 47.79 |
Table 6.
Distribution parameter estimates and goodness-of-fit test for GU-GAMLSS, with both mean μ and mean square error σ changing with physical variables.
Table 6.
Distribution parameter estimates and goodness-of-fit test for GU-GAMLSS, with both mean μ and mean square error σ changing with physical variables.
| Distribution | Covariate Combination | Position Parameter | Scale Parameter | AIC | SBC |
|---|
| GU | P + E + n | 0.02P − 0.03E + 3.32n − 2.35 | = 0.02P − 0.03E + 6.01n − 4.85 | −11.45 | 4.46 |
Table 7.
Residual sequence statistical indicators and Filliben correlation coefficient of the best non-stationary model for three distributions of annual groundwater storage variables, with P, E, and n as covariates. ν represents the skewness coefficient, and τ refers to kurtosis coefficient.
Table 7.
Residual sequence statistical indicators and Filliben correlation coefficient of the best non-stationary model for three distributions of annual groundwater storage variables, with P, E, and n as covariates. ν represents the skewness coefficient, and τ refers to kurtosis coefficient.
| Distribution | Characteristics | Covariate Combination | μ | σ | ν | τ | Filliben Coefficient |
|---|
| GU−μ | μ changing, σ constant | P + E + n | −0.00 | 1.00 | 0.11 | 2.42 | 0.99 |
| NO−σ | μ constant, σ changing | P + n | −0.17 | 0.99 | 52 | 3.13 | 0.98 |
| GU−μσ | μ, σ changing | P + E + n | −0.02 | 1.02 | 60.8 | 2.37 | 0.99 |
Table 8.
Residual sequence statistical indicators and Filliben correlation coefficient of the best non-stationary model for three distributions of annual actual evapotranspiration, with P and n as covariates. ν represents the skewness coefficient, and τ refers to kurtosis coefficient.
Table 8.
Residual sequence statistical indicators and Filliben correlation coefficient of the best non-stationary model for three distributions of annual actual evapotranspiration, with P and n as covariates. ν represents the skewness coefficient, and τ refers to kurtosis coefficient.
| Distribution | Characteristics | Covariate Combination | μ | σ | ν | τ | Filliben Coefficient |
|---|
| LO−μ | μ changing, σ constant | P + n | −0.06 | 1.09 | −0.95 | 4.88 | 0.97 |
| NO−σ | μ constant, σ changing | P | −0.18 | 0.71 | 1.63 | 6.27 | 0.92 |
| LO−μσ | μ, σ changing | P + n | −0.06 | 1.03 | −0.44 | 2.90 | 0.98 |
Table 9.
Residual sequence statistical indicators and Filliben correlation coefficient of the best non-stationary model for three distributions of annual underlying surface parameter, with P as the covariate.
Table 9.
Residual sequence statistical indicators and Filliben correlation coefficient of the best non-stationary model for three distributions of annual underlying surface parameter, with P as the covariate.
| Distribution | Characteristics | Covariate Combination | μ | σ | ν | τ | Filliben Coefficient |
|---|
| NO−μ | μ changing, σ constant | P | 0.00 | 1.02 | 1.03 | 3.45 | 0.95 |
| GA−σ | μ constant, σ changing | P | −0.11 | 0.96 | 0.43 | 3.18 | 0.99 |
| NO−μσ | μ, σ changing | P | −0.00 | 1.02 | 1.05 | 3.58 | 0.96 |
Table 10.
Calculations of variable changes under baseline conditions.
Table 10.
Calculations of variable changes under baseline conditions.
| Driving Process | Calculated Variables | Change Value |
|---|
| P → n | n | 1.17 |
| P & n → E | E | 298.31 (mm) |
| P, n & E → ΔG | ΔG | 5.75 (mm) |
| P, n & ΔG → R | R | 88.14 (mm) |
Table 11.
Calculations of variable changes under a 10% increase in precipitation.
Table 11.
Calculations of variable changes under a 10% increase in precipitation.
| Driving Process | Calculated Variables | Change Value | Difference from Baseline Conditions |
|---|
| P → n | n | 1.29 | +0.12 |
| P & n → E | E | 336.61 (mm) | +38.3 (mm) |
| P, n & E → ΔG | ΔG | 5.44 (mm) | −0.31 (mm) |
| P, n & ΔG → R | R | 89.37 (mm) | +1.23 (mm) |
Table 12.
Calculations of variable changes under a 10% increase in underlying surface parameters.
Table 12.
Calculations of variable changes under a 10% increase in underlying surface parameters.
| Driving Process | Calculated Variables | Change Value | Difference from Baseline Conditions |
|---|
| P → n | n | 1.17 | |
| n increasing by 10% | Increase in n | 0.12 | +0.12 |
| Total change of n | n | 1.29 | |
| P & n → E | E | 316.39 (mm) | +18.08 (mm) |
| P, n & E → ΔG | ΔG | −0.57 (mm) | −6.32 (mm) |
| P, n & ΔG → R | R | 76.37 (mm) | −11.77 (mm) |
Table 13.
Calculations of variable changes under 10% increases in precipitation and underlying surface parameter simultaneously.
Table 13.
Calculations of variable changes under 10% increases in precipitation and underlying surface parameter simultaneously.
| Driving Process | Calculated Variables | Change Value | Difference from Baseline Conditions |
|---|
| P → n | n | 1.29 | |
| n increasing by 10% | Increase in n | 0.13 | +0.25 |
| Total change of n | n | 1.42 | |
| P & n → E | E | 356.57 (mm) | +58.26 (mm) |
| P, n & E → ΔG | ΔG | −1.53 (mm) | −7.28 (mm) |
| P, n & ΔG → R | R | 76.38 (mm) | −11.76 (mm) |