Multi-Objective Ecological Long-Term Operation of Cascade Reservoirs Considering Hydrological Regime Alteration
Abstract
1. Introduction
2. Methodology
2.1. Streamflow and Scenario Reduction Module
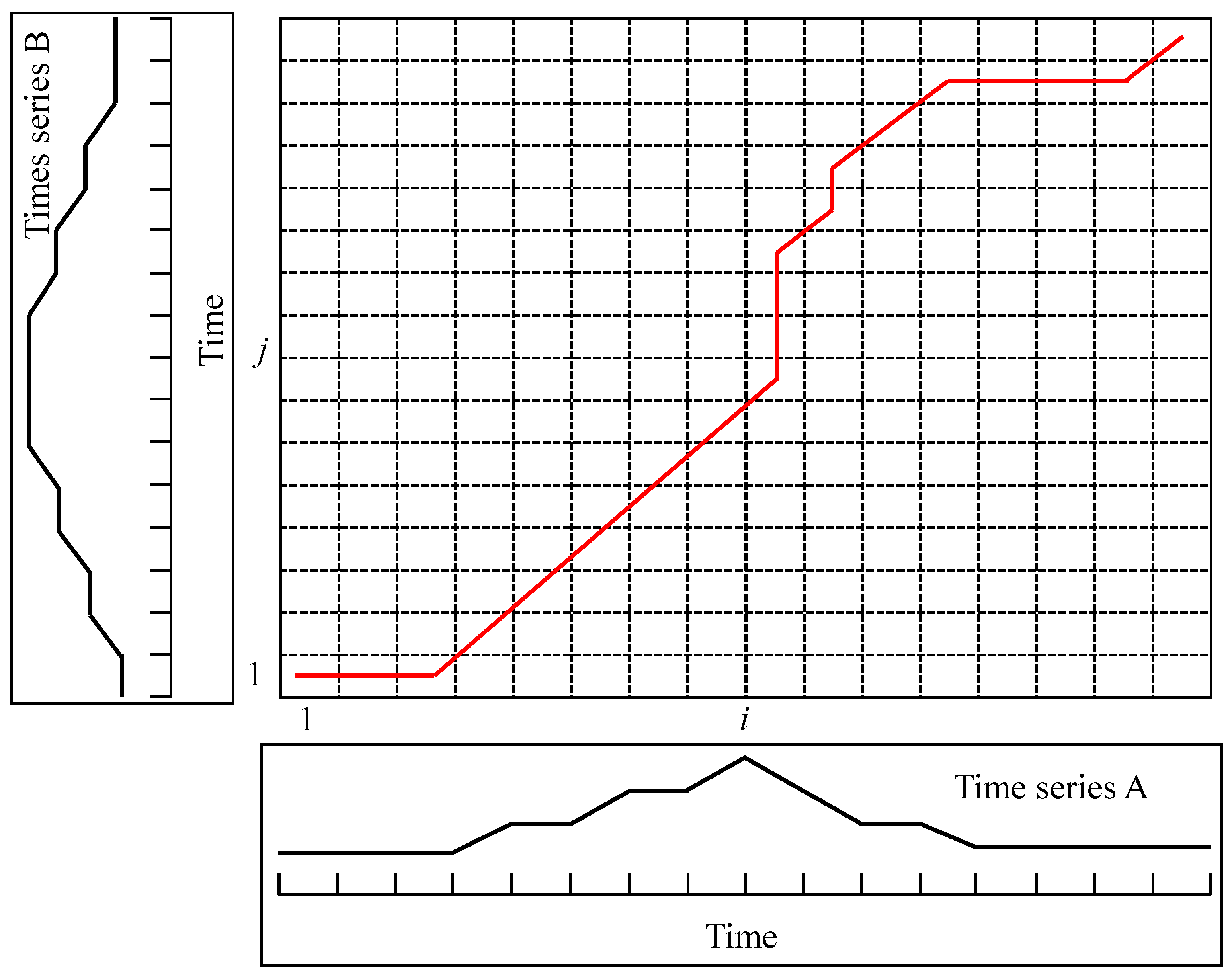
2.1.1. DTW-SBR Framework
2.1.2. Evaluation Indicators
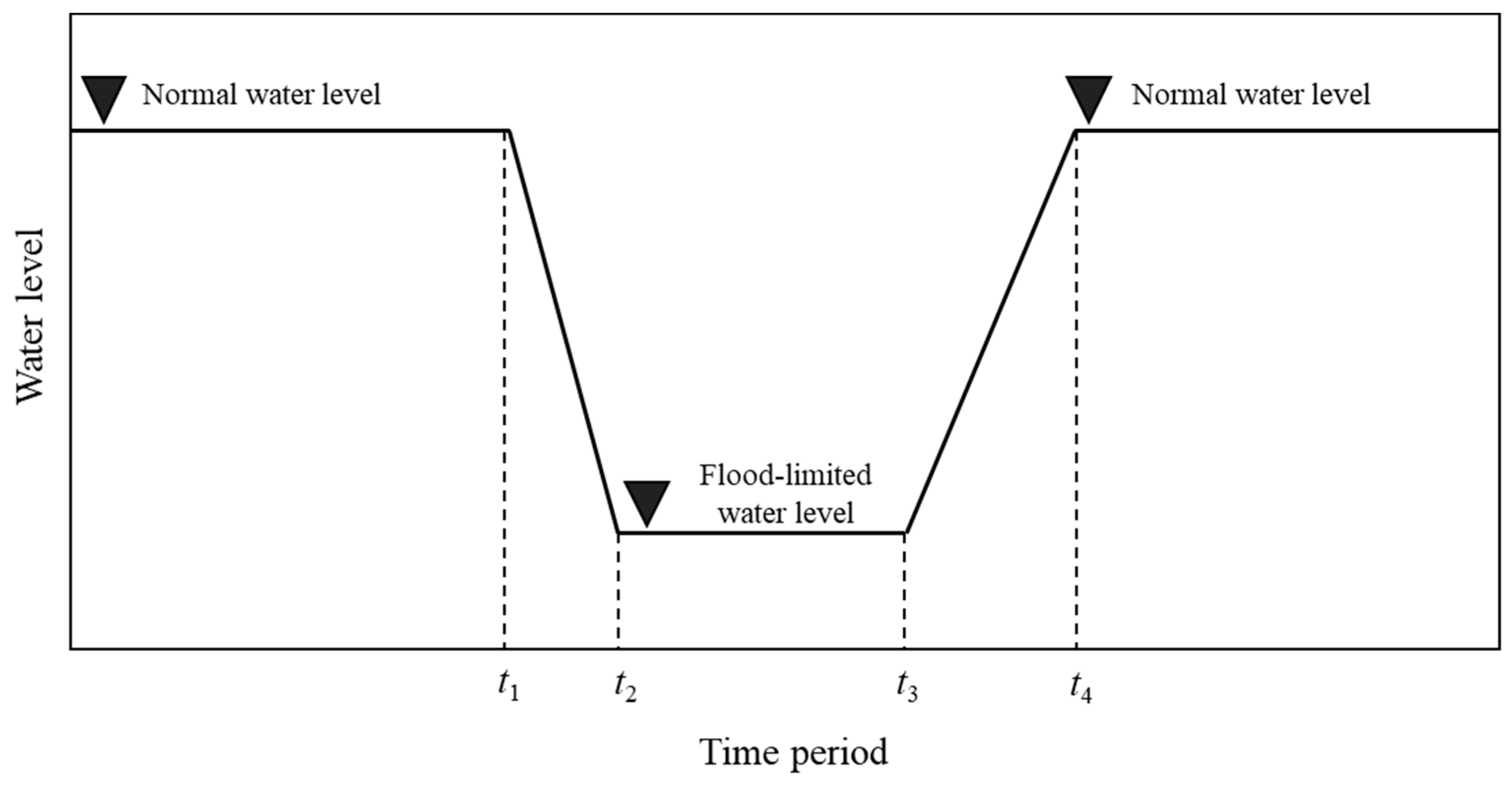
2.2. Hydroregime-Hydroelectricity Operation Mode
2.2.1. Multi-Objective Functions
2.2.2. Constraints
2.3. Multi-Objective Optimization Method for Long-Term Operation
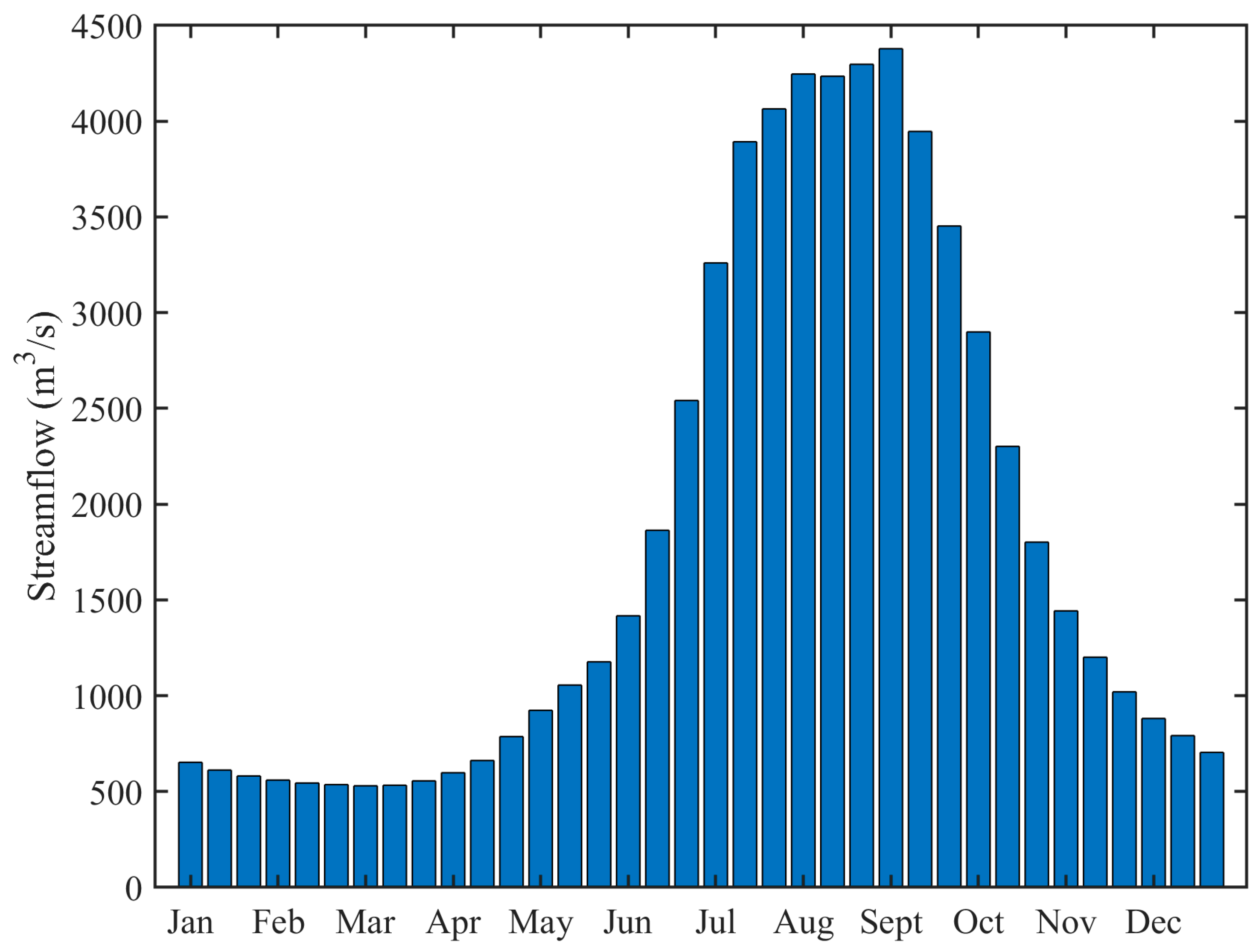
3. Materials
4. Results and Discussion
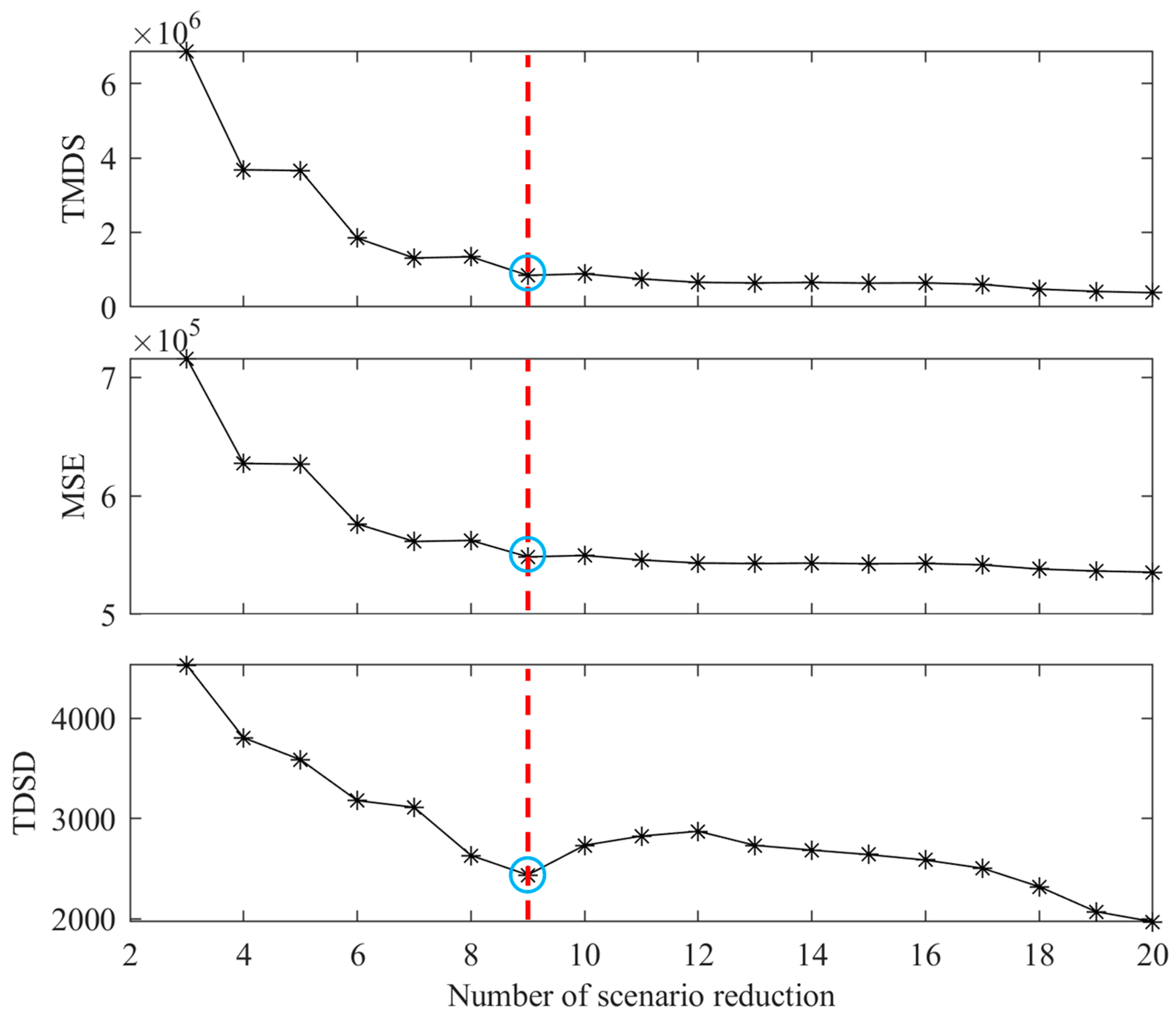
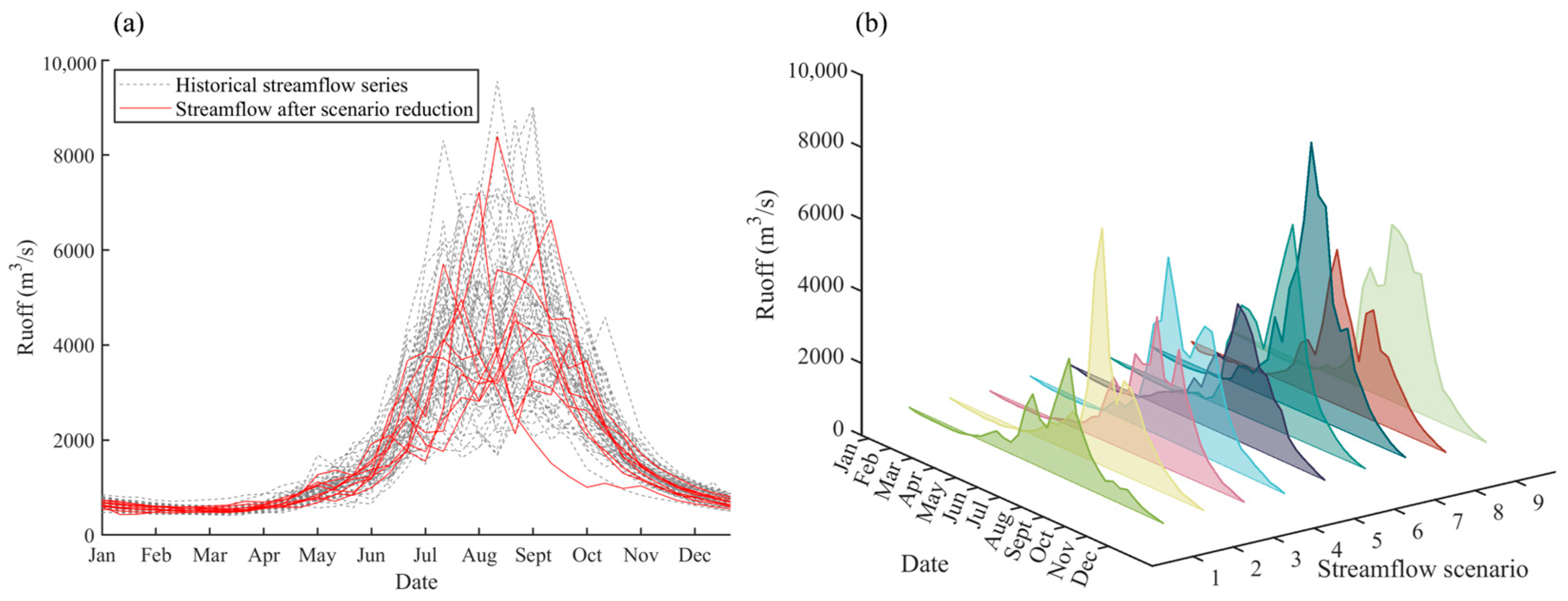
4.1. Streamflow Scenario Reduction
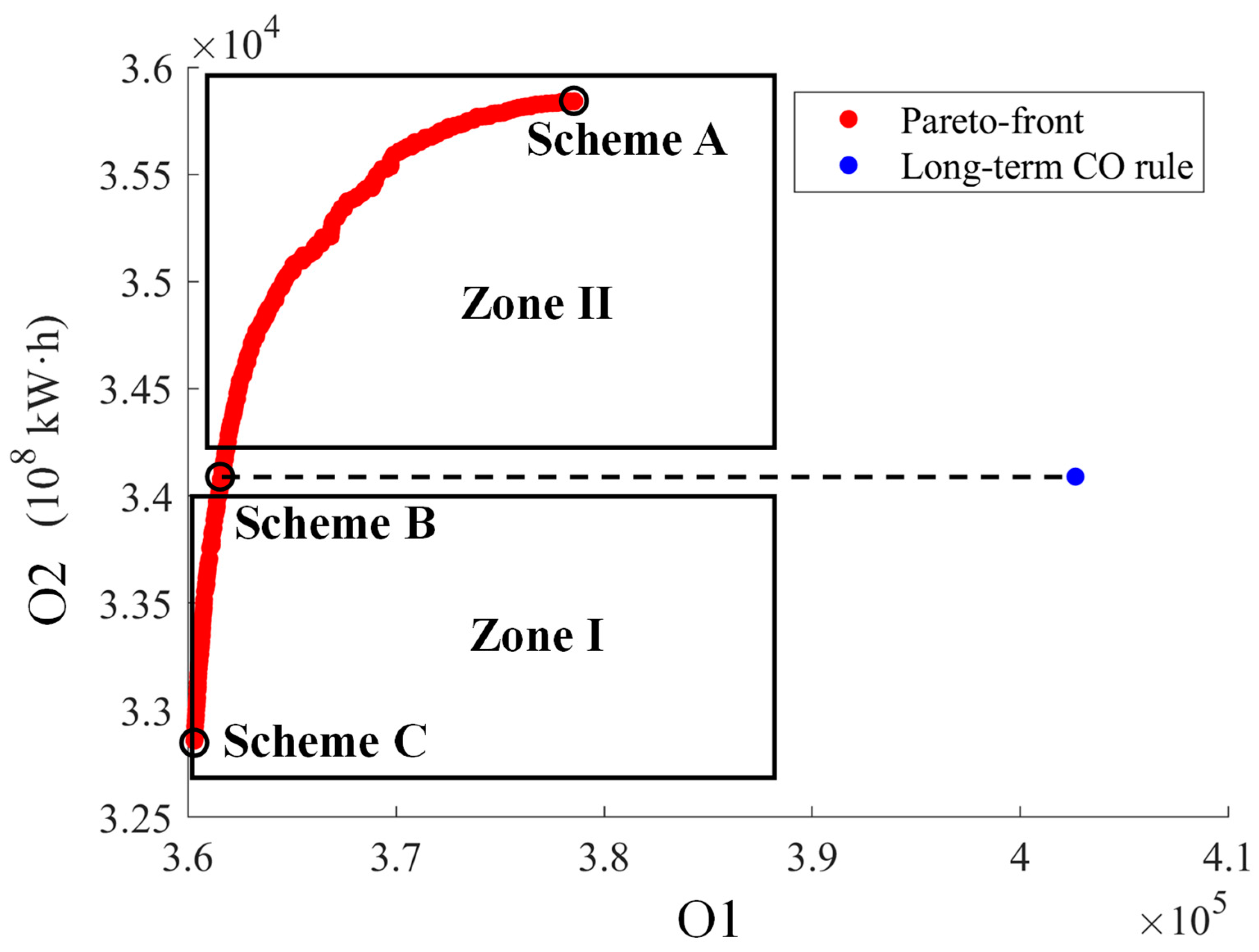
4.2. Optimization of the Two Objectives by NSGA-II
4.3. Analysis of Reservoir Operation Schemes
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, X.; Dong, Q.; Costa, V.; Wang, X. A hierarchical Bayesian model for decomposing the impacts of human activities and climate change on water resources in China. Sci. Total Environ. 2019, 665, 836–847. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Mei, Y.; Chen, J.; Hu, T.; Xiao, W. Attribution analysis of dry season runoff in the Lhasa River using an extended hydrological sensitivity method and a hydrological model. Water 2019, 11, 1187. [Google Scholar] [CrossRef]
- Xiong, F.; Guo, S.; Liu, P.; Xu, C.Y.; Zhong, Y.; Yin, J.; He, S. A general framework of design flood estimation for cascade reservoirs in operation period. J. Hydrol. 2019, 577, 124003. [Google Scholar] [CrossRef]
- Zhang, H.; Chang, J.; Gao, C.; Wu, H.; Wang, Y.; Lei, K.; Long, R.; Zhang, L. Cascade hydropower plants operation considering comprehensive ecological water demands. Energy Convers. Manag. 2019, 180, 119–133. [Google Scholar] [CrossRef]
- Javadinejad, S.; Ostad-Ali-Askari, K.; Jafary, F. Using simulation model to determine the regulation and to optimize the quantity of chlorine injection in water distribution networks. Model. Earth Syst. Environ. 2019, 5, 1015–1023. [Google Scholar] [CrossRef]
- Ding, Z.; Fang, G.; Wen, X.; Tan, Q.; Huang, X.; Lei, X.; Tian, Y.; Quan, J. A novel operation chart for cascade hydropower system to alleviate ecological degradation in hydrological extremes. Ecol. Model. 2018, 384, 10–22. [Google Scholar] [CrossRef]
- Ding, Z.; Fang, G.; Wen, X.; Tan, Q.; Lei, X.; Liu, Z.; Huang, X. Cascaded hydropower operation chart optimization balancing overall ecological benefits and ecological conservation in hydrological extremes under climate change. Water Resour. Manag. 2020, 34, 1231–1246. [Google Scholar] [CrossRef]
- Nafchi, R.F.; Vanani, H.R.; Pashaee, K.N.; Brojeni, H.S.; Ostad-Ali-Askari, K. Investigation on the effect of inclined crest step pool on scouring protection in erodible river beds. Nat. Hazards 2022, 110, 1495–1505. [Google Scholar] [CrossRef]
- Zhu, D.; Mei, Y.; Ben, Y.; Xu, X. Inter-and intra-annual trend analysis of water level and flow in the middle and lower reaches of the Ganjiang River, China. Hydrol. Sci. J. 2020, 65, 2128–2141. [Google Scholar] [CrossRef]
- Ostad-Ali-Askari, K.; Ghorbanizadeh Kharazi, H.; Shayannejad, M.; Zareian, M.J. Effect of management strategies on reducing negative impacts of climate change on water resources of the Isfahan–Borkhar aquifer using MODFLOW. River Res. Appl. 2019, 35, 611–631. [Google Scholar] [CrossRef]
- Yazdian, H.; Zahraie, B.; Jaafarzadeh, N. Multi—Objective Reservoir Operation Optimization by Considering Ecosystem Sustainability and Ecological Targets. Water Resour. Manag. 2024, 38, 881–892. [Google Scholar] [CrossRef]
- Zhu, D.; Zhou, Y.; Guo, S.; Chang, F.J.; Lin, K.; Deng, Z. Exploring a multi-objective optimization operation model of water projects for boosting synergies and water quality improvement in big river systems. J. Environ. Manag. 2023, 345, 118673. [Google Scholar] [CrossRef] [PubMed]
- Castelletti, A.; Pianosi, F.; Soncini-Sessa, R. Water reservoir control under economic, social and environmental constraints. Automatica 2008, 44, 1595–1607. [Google Scholar] [CrossRef]
- Yin, X.; Yang, Z.; Yang, W.; Zhao, Y.; Chen, H. Optimized reservoir operation to balance human and riverine ecosystem needs: Model development, and a case study for the Tanghe reservoir, Tang river basin, China. Hydrol. Process. 2010, 24, 461–471. [Google Scholar] [CrossRef]
- Li, Y.; Lin, J.; Liu, Y.; Yao, W.; Zhang, D.; Peng, Q.; Qian, S. Refined operation of cascade reservoirs considering fish ecological demand. J. Hydrol. 2022, 607, 127559. [Google Scholar] [CrossRef]
- Lu, X.; Wang, X.; Ban, X.; Singh, V.P. Considering ecological flow in multi-objective operation of cascade reservoir systems under climate variability with different hydrological periods. J. Environ. Manag. 2022, 309, 114690. [Google Scholar] [CrossRef] [PubMed]
- Ai, Y.; Ma, Z.; Xie, X.; Huang, T.; Cheng, H. Optimization of ecological reservoir operation rules for a northern river in China: Balancing ecological and socio-economic water use. Ecol. Indic. 2022, 138, 108822. [Google Scholar] [CrossRef]
- Feng, Z.K.; Niu, W.J.; Cheng, C.T. Optimization of hydropower reservoirs operation balancing generation benefit and ecological requirement with parallel multi-objective genetic algorithm. Energy 2018, 153, 706–718. [Google Scholar] [CrossRef]
- Jager, H.I.; Smith, B.T. Sustainable reservoir operation: Can we generate hydropower and preserve ecosystem values? River Res. Appl. 2008, 24, 340–352. [Google Scholar] [CrossRef]
- Cioffi, F.; Gallerano, F. Multi-objective analysis of dam release flows in rivers downstream from hydropower reservoirs. Appl. Math. Model. 2012, 36, 2868–2889. [Google Scholar] [CrossRef]
- Chen, W.; Olden, J.D. Designing flows to resolve human and environmental water needs in a dam-regulated river. Nat. Commun. 2017, 8, 2158. [Google Scholar] [CrossRef] [PubMed]
- Saadatpour, M.; Afshar, A.; Solis, S.S. Surrogate-based multiperiod, multiobjective reservoir operation optimization for quality and quantity management. J. Water Resour. Plan. Manag. ASCE 2020, 146, 04020053. [Google Scholar] [CrossRef]
- Yu, L.; Wu, X.; Wu, S.; Jia, B.; Han, G.; Xu, P.; Dai, J.; Zhang, Y.; Wang, F.; Yang, Q.; et al. Multi-objective optimal operation of cascade hydropower plants considering ecological flow under different ecological conditions. J. Hydrol. 2021, 601, 126599. [Google Scholar] [CrossRef]
- Jordan, S.; Quinn, J.; Zaniolo, M.; Giuliani, M.; Castelletti, A. Advancing reservoir operations modelling in SWAT to reduce socio-ecological tradeoffs. Environ. Modell. Softw. 2022, 157, 105527. [Google Scholar] [CrossRef]
- Richter, B.D.; Baumgartner, J.V.; Powell, J.; Braun, D.P. A method for assessing hydrologic alteration within ecosystems. Conserv. Biol. 1996, 10, 1163–1174. [Google Scholar] [CrossRef]
- Bunn, S.E.; Arthington, A.H. Basic principles and ecological consequences of altered flow regimes for aquatic biodiversity. Environ. Manag. 2002, 30, 492–507. [Google Scholar] [CrossRef]
- Yan, M.; Fang, G.H.; Dai, L.H.; Tan, Q.F.; Huang, X.F. Optimizing reservoir operation considering downstream ecological demands of water quantity and fluctuation based on IHA parameters. J. Hydrol. 2021, 600, 126647. [Google Scholar] [CrossRef]
- Poff, N.L.; Allan, J.D.; Bain, M.B.; Karr, J.R.; Prestegaard, K.L.; Richter, B.D.; Sparks, R.E.; Stromberg, J.C. The natural flow regime. Bioscience 1997, 47, 769–784. [Google Scholar] [CrossRef]
- Gao, Y.; Vogel, R.M.; Kroll, C.N.; Poff, N.L.; Olden, J.D. Development of representative indicators of hydrologic alteration. J. Hydrol. 2009, 374, 136–147. [Google Scholar] [CrossRef]
- Zhang, Q.; Gu, X.; Singh, V.P.; Chen, X. Evaluation of ecological instream flow using multiple ecological indicators with consideration of hydrological alterations. J. Hydrol. 2015, 529, 711–722. [Google Scholar] [CrossRef]
- Mohammed, H.; Hansen, A.T. Spatial heterogeneity of low flow hydrological alterations in response to climate and land use within the Upper Mississippi River basin. J. Hydrol. 2024, 632, 130872. [Google Scholar] [CrossRef]
- Avesani, D.; Zanfei, A.; Di Marco, N.; Galletti, A.; Ravazzolo, F.; Righetti, M.; Majone, B. Short-term hydropower optimization driven by innovative time-adapting econometric model. Appl. Energy 2022, 310, 118510. [Google Scholar] [CrossRef]
- Ahmad, S.K.; Hossain, F. Forecast-informed hydropower optimization at long and short-time scales for a multiple dam network. J. Renew. Sustain. Energy 2020, 12, 014501. [Google Scholar] [CrossRef]
- Dupačová, J.; Gröwe-Kuska, N.; Römisch, W. Scenario reduction in stochastic programming. Math. Program. 2003, 95, 493–511. [Google Scholar] [CrossRef]
- Heitsch, H.; Römisch, W. Scenario reduction algorithms in stochastic programming. Comput. Optim. Appl. 2003, 24, 187–206. [Google Scholar] [CrossRef]
- Heitsch, H.; Römisch, W. Scenario tree modeling for multistage stochastic programs. Math. Program. 2009, 118, 371–406. [Google Scholar] [CrossRef]
- Li, J.; Lan, F.; Wei, H. A scenario optimal reduction method for wind power time series. IEEE Trans. Power Syst. 2015, 31, 1657–1658. [Google Scholar] [CrossRef]
- Li, J.; Zhu, F.; Xu, B.; Yeh, W.W.G. Streamflow scenario tree reduction based on conditional Monte Carlo sampling and regularized optimization. J. Hydrol. 2019, 577, 123943. [Google Scholar] [CrossRef]
- Yin, Y.; Liu, T.; He, C. Day-ahead stochastic coordinated scheduling for thermal-hydro-wind-photovoltaic systems. Energy 2019, 187, 115944. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, F.; Nie, F.; Li, H.; Wang, J. Speed up dynamic time warping of multivariate time series. J. Intell. Fuzzy Syst. 2019, 36, 2593–2603. [Google Scholar] [CrossRef]
- Berndt, D.J.; Clifford, J. Using dynamic time warping to find patterns in time series. In Proceedings of the 3rd International Conference on Knowledge Discovery and Data Mining, Seattle, WA, USA, 31 July–1 August 1994; pp. 359–370. [Google Scholar]
- Yakowitz, S. Dynamic programming applications in water resources. Water Resour. Res. 1982, 18, 673–696. [Google Scholar] [CrossRef]
- Yang, Z.; Yang, K.; Wang, Y.; Su, L.; Hu, H. Long-term multi-objective power generation operation for cascade reservoirs and risk decision making under stochastic uncertainties. Renew. Energy 2021, 164, 313–330. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, P.; Chen, X.; Wang, L.; Ai, X.; Feng, M.; Liu, D.; Liu, Y. Optimal operation of multi-reservoir systems considering time-lags of flood routing. Water Resour. Manag. 2016, 30, 523–540. [Google Scholar] [CrossRef]
- Deb, K.; Agrawal, S.; Pratap, A.; Meyarivan, T. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II. In Parallel Problem Solving from Nature PPSN VI, Proceedings of the 6th International Conference, Paris, France, 18–20 September 2000; Springer: Berlin/Heidelberg, Germany, 2000; Proceedings 6. [Google Scholar]
- Hojjati, A.; Monadi, M.; Faridhosseini, A.; Mohammadi, M. Application and comparison of NSGA-II and MOPSO in multi-objective optimization of water resources systems. J. Hydrol. Hydromech. 2018, 66, 323–329. [Google Scholar] [CrossRef]
- Wu, L.; Bai, T.; Huang, Q.; Wei, J.; Liu, X. Multi-objective optimal operations based on improved NSGA-II for Hanjiang to Wei River Water Diversion Project, China. Water 2019, 11, 1159. [Google Scholar] [CrossRef]
- He, W.; Ma, C.; Zhang, J.; Lian, J.; Wang, S.; Zhao, W. Multi-objective optimal operation of a large deep reservoir during storage period considering the outflow-temperature demand based on NSGA-II. J. Hydrol. 2020, 586, 124919. [Google Scholar] [CrossRef]
- Gonzalez, J.M.; Tomlinson, J.E.; Harou, J.J.; Ceseña, E.A.M.; Panteli, M.; Bottacin-Busolin, A.; Hurford, A.; Olivares, M.A.; Siddiqui, A.; Erfani, T.; et al. Spatial and sectoral benefit distribution in water-energy system design. Appl. Energy 2020, 269, 114794. [Google Scholar] [CrossRef]
- He, Y.; Guo, S.; Zhou, Y.; Zhu, D.; Chen, H.; Xiong, L.; Liu, J.; Xu, C.Y. Boosting hydropower generation of mixed reservoirs for reducing carbon emissions by using a simulation–optimization framework. Hydrol. Res. 2024, 55, 144–160. [Google Scholar] [CrossRef]
- Zhu, D.; Chen, H.; Zhou, Y.; Xu, X.; Guo, S.; Chang, F.J.; Xu, C.Y. Exploring a multi-objective cluster-decomposition framework for optimizing flood control operation rules of cascade reservoirs in a river basin. J. Hydrol. 2022, 614, 128602. [Google Scholar] [CrossRef]
- Joint Operation Plan of Water Engineering in the Yangtze River Basin. Changjiang Water Resources Commission of the Ministry of Water Resources; Joint Operation Plan of Water Engineering in the Yangtze River Basin: Wuhan, China, 2023. [Google Scholar]

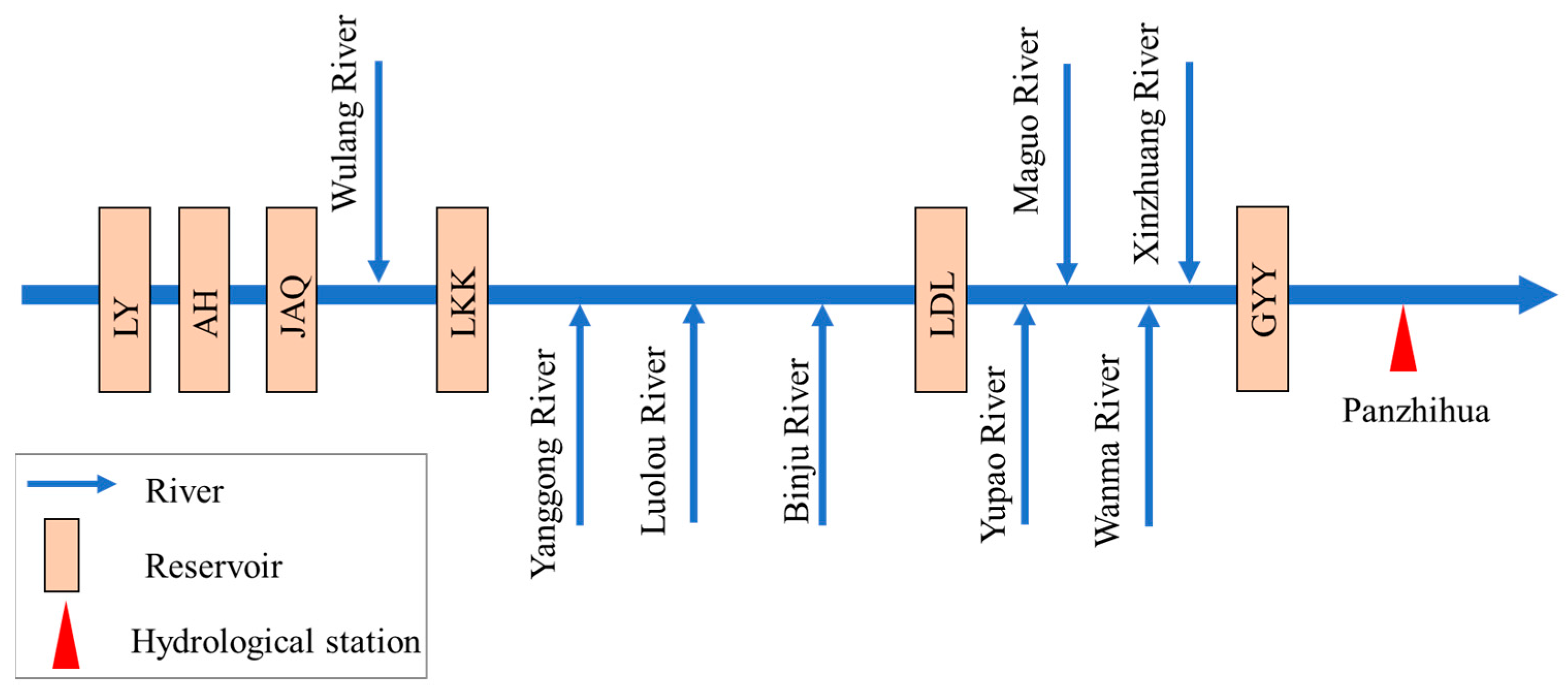
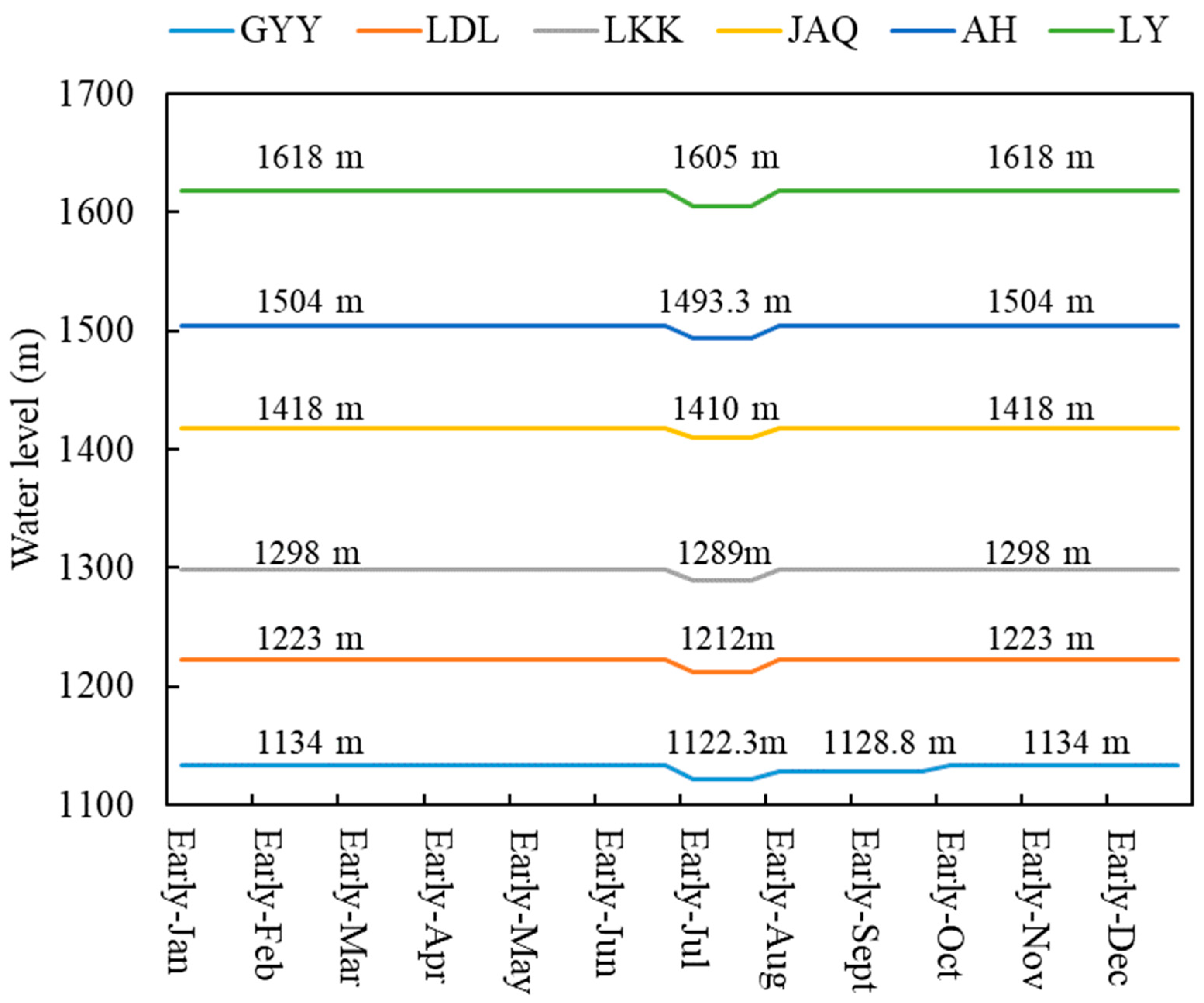

| Reservoir | Dam Height (m) | Dead Water Level (m) | Flood-Limited Water Level (m) | Normal Water Level (m) | Minimum Outflow * (m3/s) | Regulating Storage (108 m3) | Total Storage (108 m3) | Installed Capacity (MW) |
|---|---|---|---|---|---|---|---|---|
| LY | 155 | 1605 | 1605 | 1618 | 300 | 1.73 | 8.05 | 2400 |
| AH | 130 | 1492 | 1493.3 | 1504 | 350 | 2.38 | 8.85 | 2000 |
| JAQ | 160 | 1398 | 1410 | 1418 | 350 | 3.46 | 9.13 | 2400 |
| LKK | 119 | 1290 | 1289 | 1298 | 380 | 1.13 | 5.58 | 1800 |
| LDL | 140 | 1216 | 1212 | 1223 | 400 | 3.76 | 17.18 | 2160 |
| GYY | 159 | 1122.3 | 1122.3/1128.8 | 1134 | 439 | 5.55 | 22.50 | 3000 |
| Streamflow Scenario | Annual Maximum 10-Day Flow (m3/s) | Time of Annual Maximum 10-Day Flow | Annual Minimum 10-Day Flow (m3/s) | Annual Runoff (108 m3) | Probability (%) |
|---|---|---|---|---|---|
| 1 | 3959 | Mid-August | 514 | 384 | 12.70 |
| 2 | 7219 | Early August | 475 | 500 | 6.35 |
| 3 | 4677 | Late August | 465 | 487 | 14.29 |
| 4 | 5709 | Mid-July | 550 | 566 | 14.29 |
| 5 | 4515 | Late August | 572 | 513 | 7.94 |
| 6 | 6636 | Mid-September | 531 | 610 | 11.11 |
| 7 | 8388 | Mid-August | 592 | 712 | 12.70 |
| 8 | 4965 | Late July | 431 | 515 | 9.52 |
| 9 | 5587 | Mid-August | 490 | 585 | 11.11 |
| Scheme | O1 | O2 (108 kW·h) | Improvement rate of O1 (%) * | Improvement rate of O2 (%) ** |
|---|---|---|---|---|
| Long-term CO rules (Benchmark) | 402,638 | 34,089 | / | / |
| Scheme A | 378,673 | 35,841 | 5.95 | 5.14 |
| Scheme B | 361,678 | 34,083 | 10.17 | 0.00 |
| Scheme C | 360,326 | 32,837 | 10.51 | −3.67 |
| Reservoir | Long-Term CO Rule (108 kw·h) | Scheme A | Scheme B | Scheme C | |||
|---|---|---|---|---|---|---|---|
| Hydropower Generation (108 kw·h) | Increase Rate (%) * | Hydropower Generation (108 kw·h) | Increase Rate (%) * | Hydropower Generation (108 kw·h) | Increase Rate (%) * | ||
| LY | 5742 | 5910 | 2.93 | 5426 | −5.51 | 5271 | −8.21 |
| AH | 5414 | 5420 | 0.10 | 5211 | −3.75 | 5161 | −4.68 |
| JAQ | 6328 | 6690 | 5.72 | 6295 | −0.53 | 5914 | −6.55 |
| LKK | 4470 | 4700 | 5.14 | 4361 | −2.45 | 4043 | −9.56 |
| LDL | 5156 | 5480 | 6.29 | 5428 | 5.28 | 5274 | 2.29 |
| GYY | 6979 | 7641 | 9.48 | 7362 | 5.49 | 7176 | 2.82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, C.; Zhu, D.; Guo, W.; Ouyang, S.; Li, L.; Bu, H.; Wang, L.; Zuo, J.; Chen, J. Multi-Objective Ecological Long-Term Operation of Cascade Reservoirs Considering Hydrological Regime Alteration. Water 2024, 16, 1849. https://doi.org/10.3390/w16131849
Xu C, Zhu D, Guo W, Ouyang S, Li L, Bu H, Wang L, Zuo J, Chen J. Multi-Objective Ecological Long-Term Operation of Cascade Reservoirs Considering Hydrological Regime Alteration. Water. 2024; 16(13):1849. https://doi.org/10.3390/w16131849
Chicago/Turabian StyleXu, Changjiang, Di Zhu, Wei Guo, Shuo Ouyang, Liping Li, Hui Bu, Lin Wang, Jian Zuo, and Junhong Chen. 2024. "Multi-Objective Ecological Long-Term Operation of Cascade Reservoirs Considering Hydrological Regime Alteration" Water 16, no. 13: 1849. https://doi.org/10.3390/w16131849
APA StyleXu, C., Zhu, D., Guo, W., Ouyang, S., Li, L., Bu, H., Wang, L., Zuo, J., & Chen, J. (2024). Multi-Objective Ecological Long-Term Operation of Cascade Reservoirs Considering Hydrological Regime Alteration. Water, 16(13), 1849. https://doi.org/10.3390/w16131849






