Prediction of Soil Erosion Using 3D Point Scans and Acoustic Emissions
Abstract
1. Introduction
2. Methodology
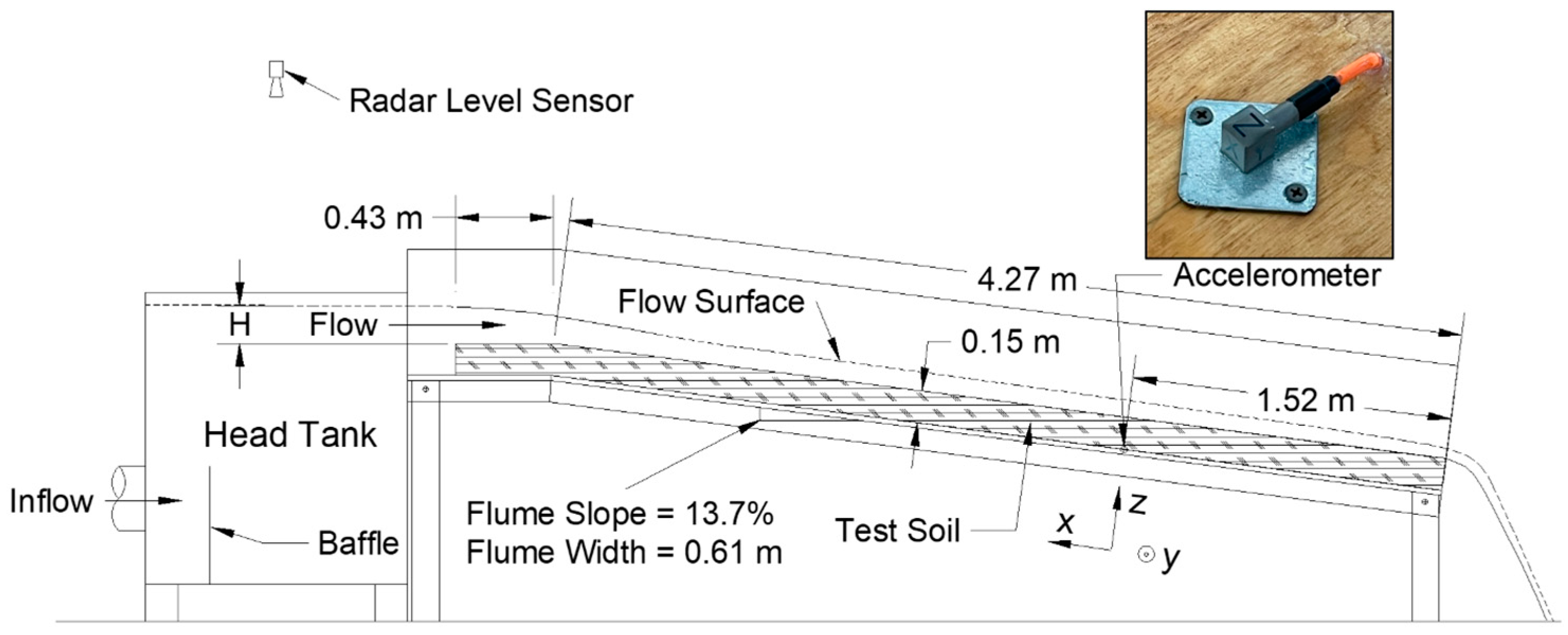
2.1. Experimental Apparatus
2.2. Vibration Data Analysis
3. Results
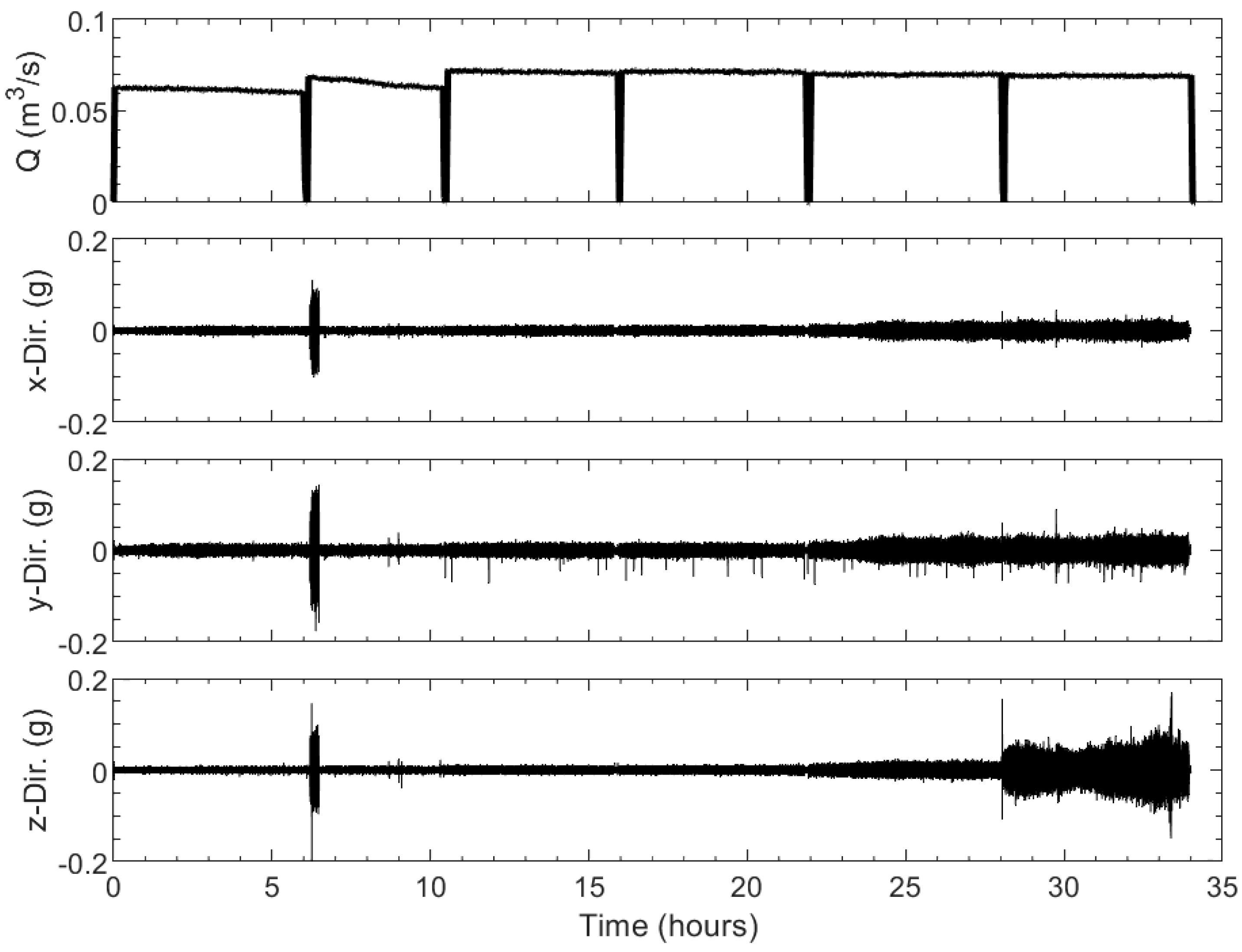
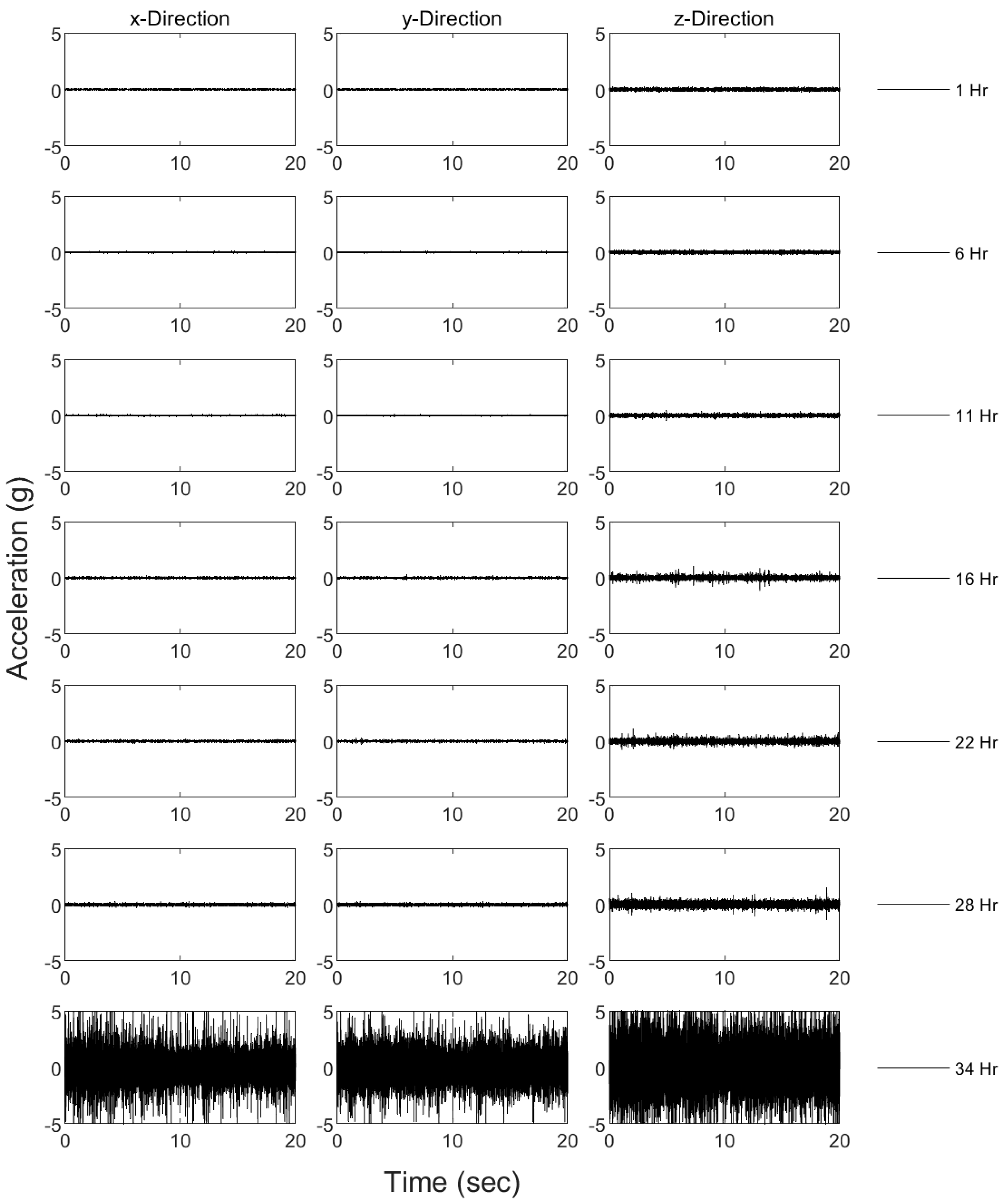
3.1. Raw Data
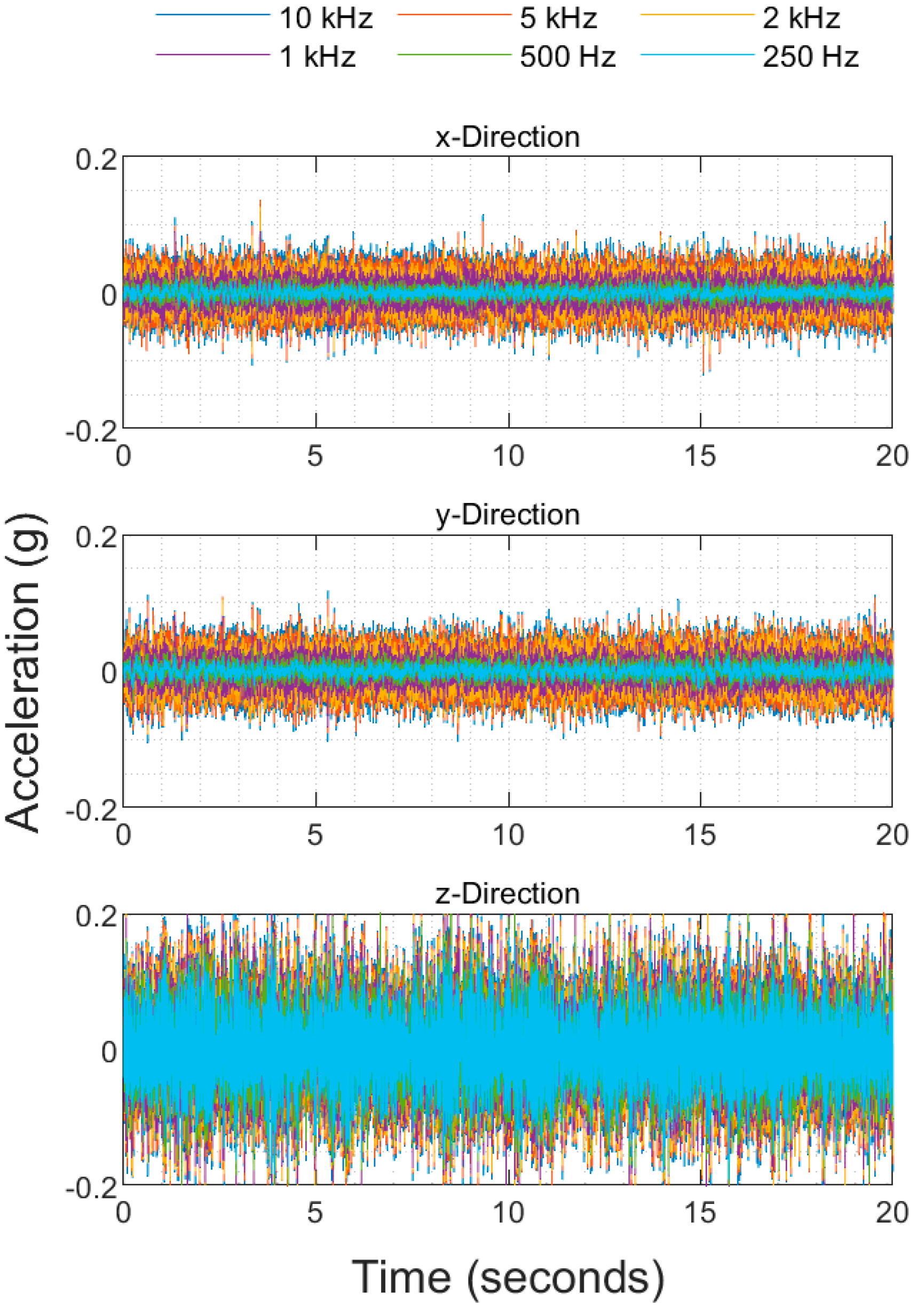
3.2. Sampling Rate Analysis
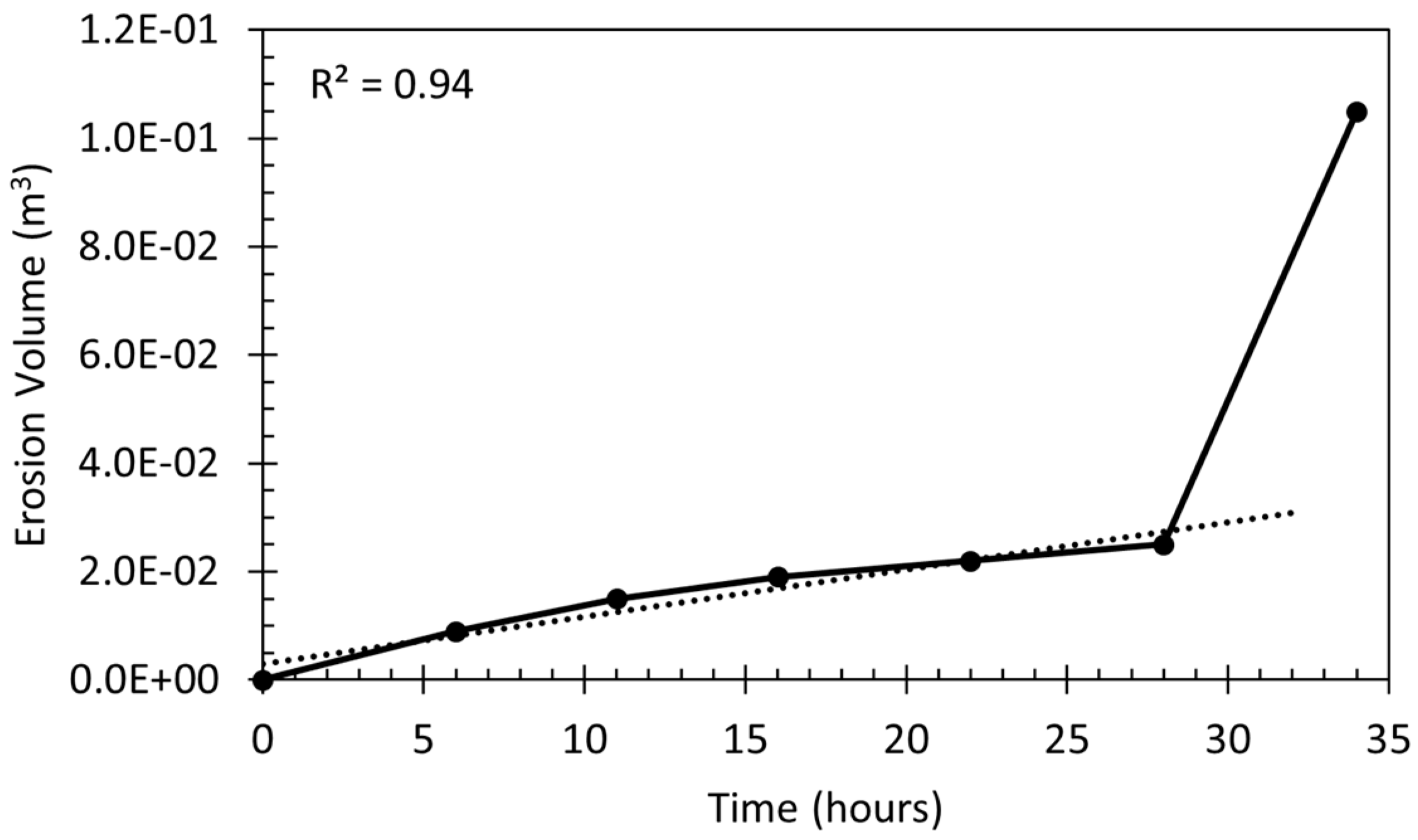
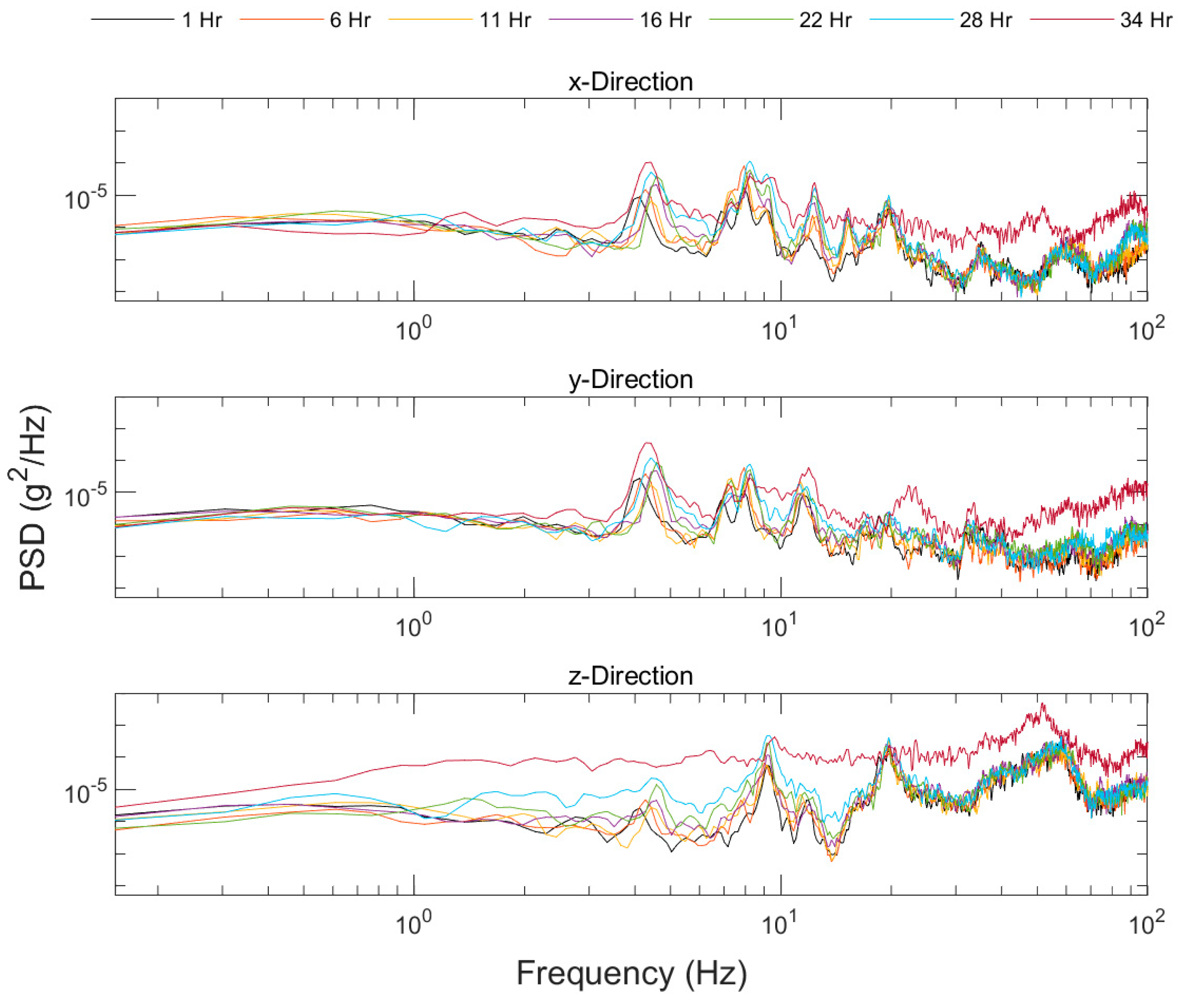
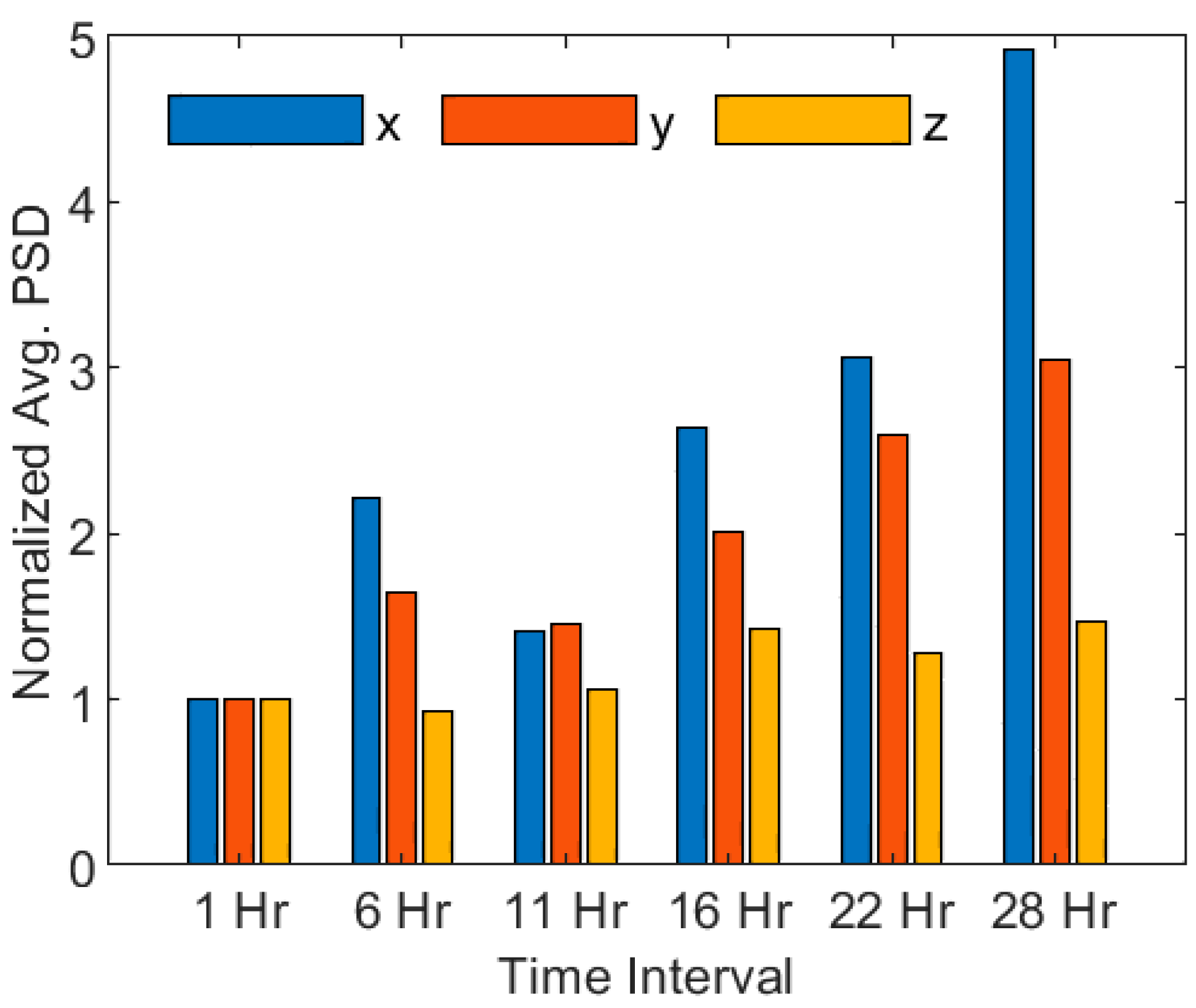
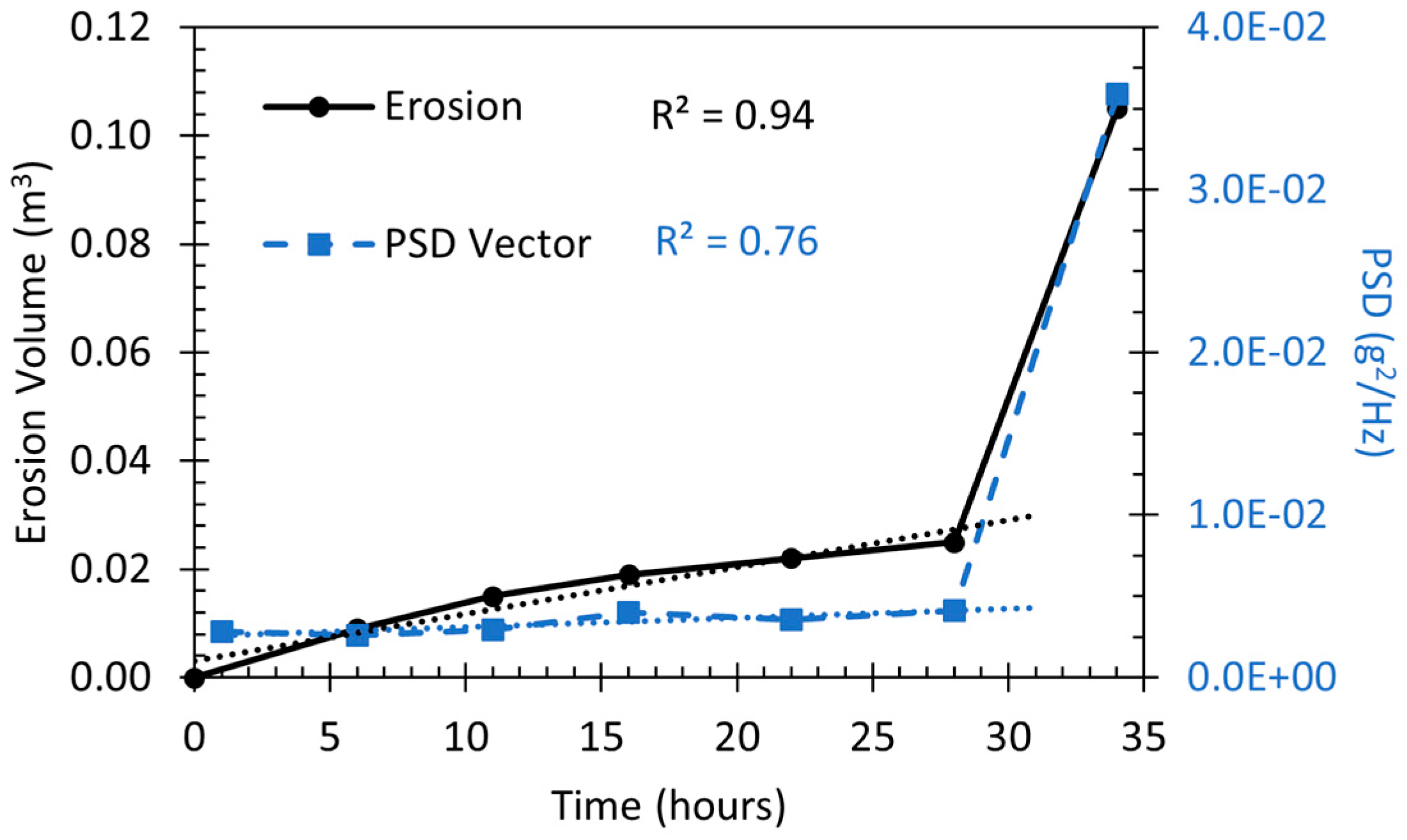
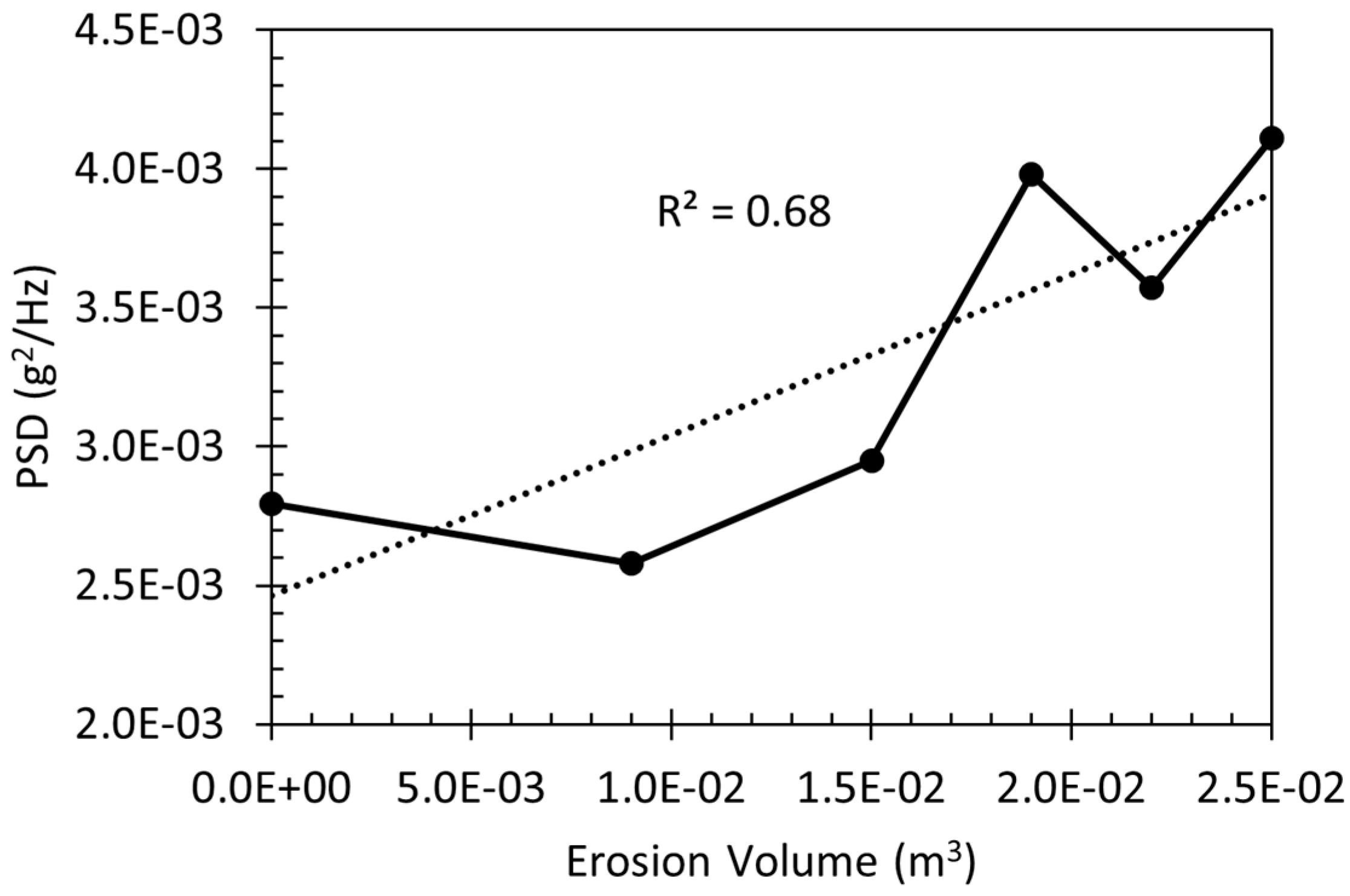
3.3. Erosion Vibration Response
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Association of State Dam Safety Officials (ASDSO). ASDSO Incident Database Input Form. 2024. Available online: https://www.damsafety.org/content/asdso-incident-database-input-form (accessed on 5 February 2024).
- Foster, M.; Fell, R.; Spannagle, M. The statistics of embankment dam failures and accidents. Can. Geotech. J. 2000, 37, 1000–1024. [Google Scholar] [CrossRef]
- Costa, J.E. Floods from Dam Failures; US Geological Survey: Reston, VA, USA, 1985; Volume 85, No. 560. [Google Scholar] [CrossRef]
- Caldwell, L. USDA Watershed Programs Facts and Figures: A Reservoir of Watershed Program Information; US Department of Agriculture Natural Resources Conservation Service (NRCS), Conservation Engineering Division: Washington, DC, USA, 2020. [Google Scholar]
- Anderson, N.L.; Ismael, A.M.; Thitimakorn, T. Ground-penetrating radar: A tool for monitoring bridge scour. Environ. Eng. Geosci. 2007, 13, 1–10. [Google Scholar] [CrossRef]
- Di Prinzio, M.; Bittelli, M.; Castellarin, A.; Pisa, P.R. Application of GPR to the monitoring of river embankments. J. Appl. Geophys. 2010, 71, 53–61. [Google Scholar] [CrossRef]
- Anchuela, Ó.P.; Frongia, P.; Di Gregorio, F.; Sainz, A.C.; Juan, A.P. Internal characterization of embankment dams using ground penetrating radar (GPR) and thermographic analysis: A case study of the Medau Zirimilis Dam (Sardinia, Italy). Eng. Geol. 2018, 237, 129–139. [Google Scholar] [CrossRef]
- Shin, S.; Park, S.; Kim, J.H. Time-lapse electrical resistivity tomography characterization for piping detection in earthen dam model of a sandbox. J. Appl. Geophys. 2019, 170, 103834. [Google Scholar] [CrossRef]
- Guo, Y.; Cui, Y.A.; Xie, J.; Luo, Y.; Zhang, P.; Liu, H.; Liu, J. Seepage detection in earth-filled dam from self-potential and electrical resistivity tomography. Eng. Geol. 2022, 306, 106750. [Google Scholar] [CrossRef]
- Sanuade, O.; Ismail, A. Geophysical and Geochemical Pilot Study to Characterize the Dam Foundation Rock and Source of Seepage in Part of Pensacola Dam in Oklahoma. Water 2023, 15, 4036. [Google Scholar] [CrossRef]
- Marescot, L.; Monnet, R.; Chapellier, D. Resistivity and induced polarization surveys for slope instability studies in the Swiss Alps. Eng. Geol. 2008, 98, 18–28. [Google Scholar] [CrossRef]
- Abdulsamad, F.; Revil, A.; Ahmed, A.S.; Coperey, A.; Karaoulis, M.; Nicaise, S.; Peyras, L. Induced polarization tomography applied to the detection and the monitoring of leaks in embankments. Eng. Geol. 2019, 254, 89–101. [Google Scholar] [CrossRef]
- Sazal, Z.; Sanuade, O.; Ismail, A. Geophysical characterization of the Carl Blackwell earth-fill dam: Stillwater, Oklahoma, USA. Pure Appl. Geophys. 2022, 179, 2853–2867. [Google Scholar] [CrossRef]
- Wise, J.; Hunt, S.; Al Dushaishi, M. Prediction of earth dam seepage using a transient thermal finite element model. Water 2023, 15, 1423. [Google Scholar] [CrossRef]
- Fadaei-Kermani, E.; Shojaee, S.; Memarzadeh, R.; Barani, G.A. Numerical simulation of seepage problem in porous media. Appl. Water Sci. 2019, 9, 79. [Google Scholar] [CrossRef]
- Aniskin, N.A.; Antonov, A.S. Using mathematical models to study the seepage conditions at the bases of tall dams. Power Technol. Eng. 2017, 50, 580–584. [Google Scholar] [CrossRef]
- Alekseevich, A.N.; Sergeevich, A.A. Numerical modelling of tailings dam thermal-seepage regime considering phase transitions. Model. Simul. Eng. 2017, 2017, 7245413. [Google Scholar] [CrossRef]
- Dardanelli, G.; Pipitone, C. Hydraulic models and finite elements for monitoring of an earth dam, by using GNSS techniques. Period. Polytech. Civ. Eng. 2017, 61, 421–433. [Google Scholar] [CrossRef]
- Zhou, W.; Li, S.; Zhou, Z.; Chang, X. InSAR observation and numerical modeling of the earth-dam displacement of Shuibuya Dam (China). Remote Sens. 2016, 8, 877. [Google Scholar] [CrossRef]
- Gordan, B.; Adnan, A.; Aida, M.A. Soil saturated simulation in embankment during strong earthquake by effect of elasticity modulus. Model. Simul. Eng. 2014, 2014, 191460. [Google Scholar] [CrossRef][Green Version]
- Kheiry, M.; Kalateh, F. Uncertainty Quantification of Steady-State Seepage Through Earth-fill Dams by Random Finite Element Method and Multivariate Adaptive Regression Splines. J. Hydraul. Struct. 2023, 9, 48–74. [Google Scholar] [CrossRef]
- Azimi Sardari, M.R.; Bazrafshan, O.; Panagopoulos, T.; Sardooi, E.R. Modeling the impact of climate change and land use change scenarios on soil erosion at the Minab Dam Watershed. Sustainability 2019, 11, 3353. [Google Scholar] [CrossRef]
- Kalateh, F.; Kheiry, M. A Review of Stochastic Analysis of the Seepage Through Earth Dams with a Focus on the Application of Monte Carlo Simulation. Arch. Comput. Methods Eng. 2024, 31, 47–72. [Google Scholar] [CrossRef]
- Vrieling, A. Satellite remote sensing for water erosion assessment: A review. Catena 2006, 65, 2–18. [Google Scholar] [CrossRef]
- Nasategay, F.F.U. Detection and Monitoring of Tailings Dam Surface Erosion Using UAV and Machine Learning. Ph.D. Thesis, University of Nevada, Reno, NV, USA, 2020. [Google Scholar]
- Slingerland, N.; Sommerville, A.; O’Leary, D.; Beier, N.A. Identification and quantification of erosion on a sand tailings dam. Geosystem Eng. 2020, 23, 131–145. [Google Scholar] [CrossRef]
- Rinehart, R.V.; Parekh, M.L.; Rittgers, J.B.; Mooney, M.A.; Revil, A. Preliminary implementation of geophysical techniques to monitor embankment dam filter cracking at the laboratory scale. In Proceedings of the ICSE6, Paris, France, 27–31 August 2012. ICSE6-103. [Google Scholar]
- Fisher, W.D.; Camp, T.K.; Krzhizhanovskaya, V.V. Anomaly detection in earth dam and levee passive seismic data using support vector machines and automatic feature selection. J. Comput. Sci. 2017, 20, 143–153. [Google Scholar] [CrossRef]
- Talwani, P.; Acree, S. Pore pressure diffusion and the mechanism of reservoir-induced seismicity. In Earthquake Prediction; Birkhäuser: Basel, Switzerland, 1985; pp. 947–965. [Google Scholar] [CrossRef]
- Talwani, P. Seismotectonics of the Koyna-Warna area, India. In Seismicity Associated with Mines, Reservoirs and Fluid Injections; Birkhäuser: Basel, Switzerland, 1998; pp. 511–550. [Google Scholar] [CrossRef]
- Larsen, D.C. Water Measurement; Issue 552 of Bulletin; University of Idaho, College of Agriculture: Moscow, ID, USA, 1976. [Google Scholar]



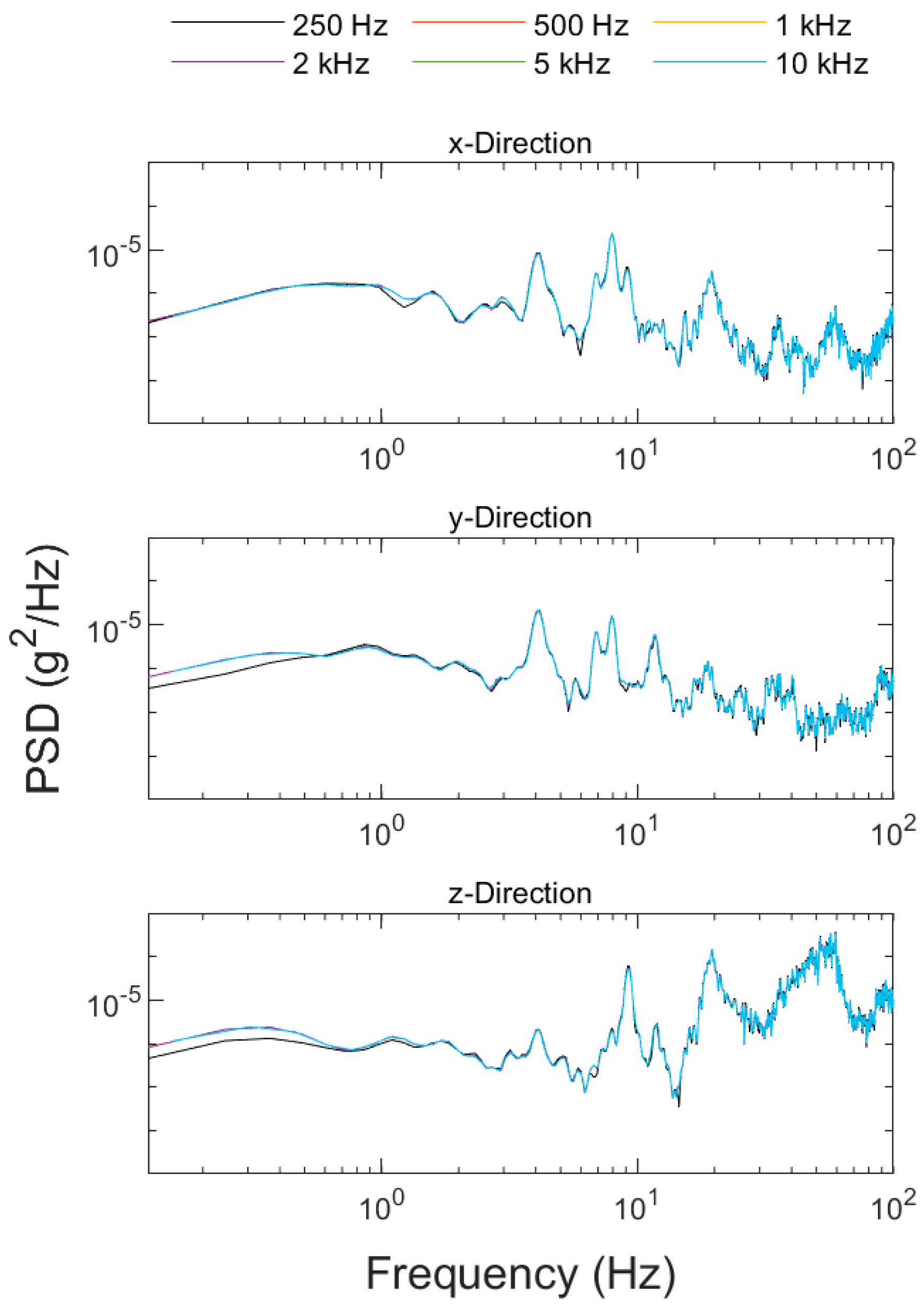


| Sampling | x-Axis | y-Axis | z-Axis |
|---|---|---|---|
| Rate | % Diff. | % Diff. | % Diff. |
| 250 Hz | 0.08% | 0.08% | 0.07% |
| 500 Hz | 0.05% | 0.04% | 0.04% |
| 1 kHz | 0.02% | 0.02% | 0.07% |
| 2 kHz | 0.01% | 0.02% | 0.04% |
| 5 kHz | 0.00% | 0.00% | −0.01% |
| 10 kHz | - | - | - |
| Sampling | x-Axis | y-Axis | z-Axis |
|---|---|---|---|
| Rate | % Diff. | % Diff. | % Diff. |
| 1 kHz | 0.02% | 0.02% | 0.08% |
| 5 kHz | −0.01% | −0.01% | −0.01% |
| 10 kHz | - | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wise, J.; Al Dushaishi, M.F. Prediction of Soil Erosion Using 3D Point Scans and Acoustic Emissions. Water 2024, 16, 1009. https://doi.org/10.3390/w16071009
Wise J, Al Dushaishi MF. Prediction of Soil Erosion Using 3D Point Scans and Acoustic Emissions. Water. 2024; 16(7):1009. https://doi.org/10.3390/w16071009
Chicago/Turabian StyleWise, Jarrett, and Mohammed F. Al Dushaishi. 2024. "Prediction of Soil Erosion Using 3D Point Scans and Acoustic Emissions" Water 16, no. 7: 1009. https://doi.org/10.3390/w16071009
APA StyleWise, J., & Al Dushaishi, M. F. (2024). Prediction of Soil Erosion Using 3D Point Scans and Acoustic Emissions. Water, 16(7), 1009. https://doi.org/10.3390/w16071009






