Numerical Study of Pore Water Pressure in Frozen Soils during Moisture Migration
Abstract
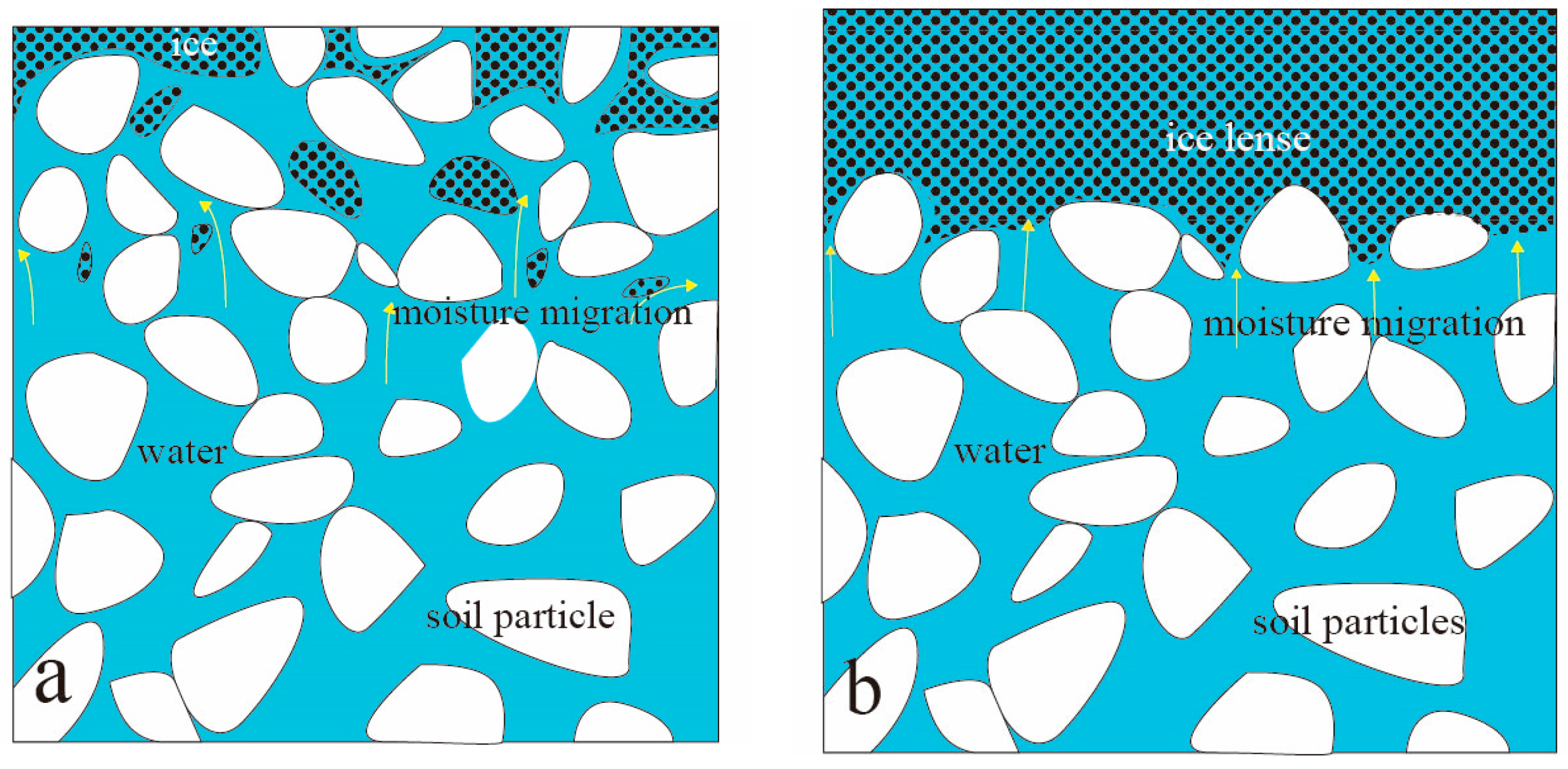
1. Introduction
2. Controlled Differential Equation Solving
2.1. Control Equations for Temperature Field and Water Splitting Field
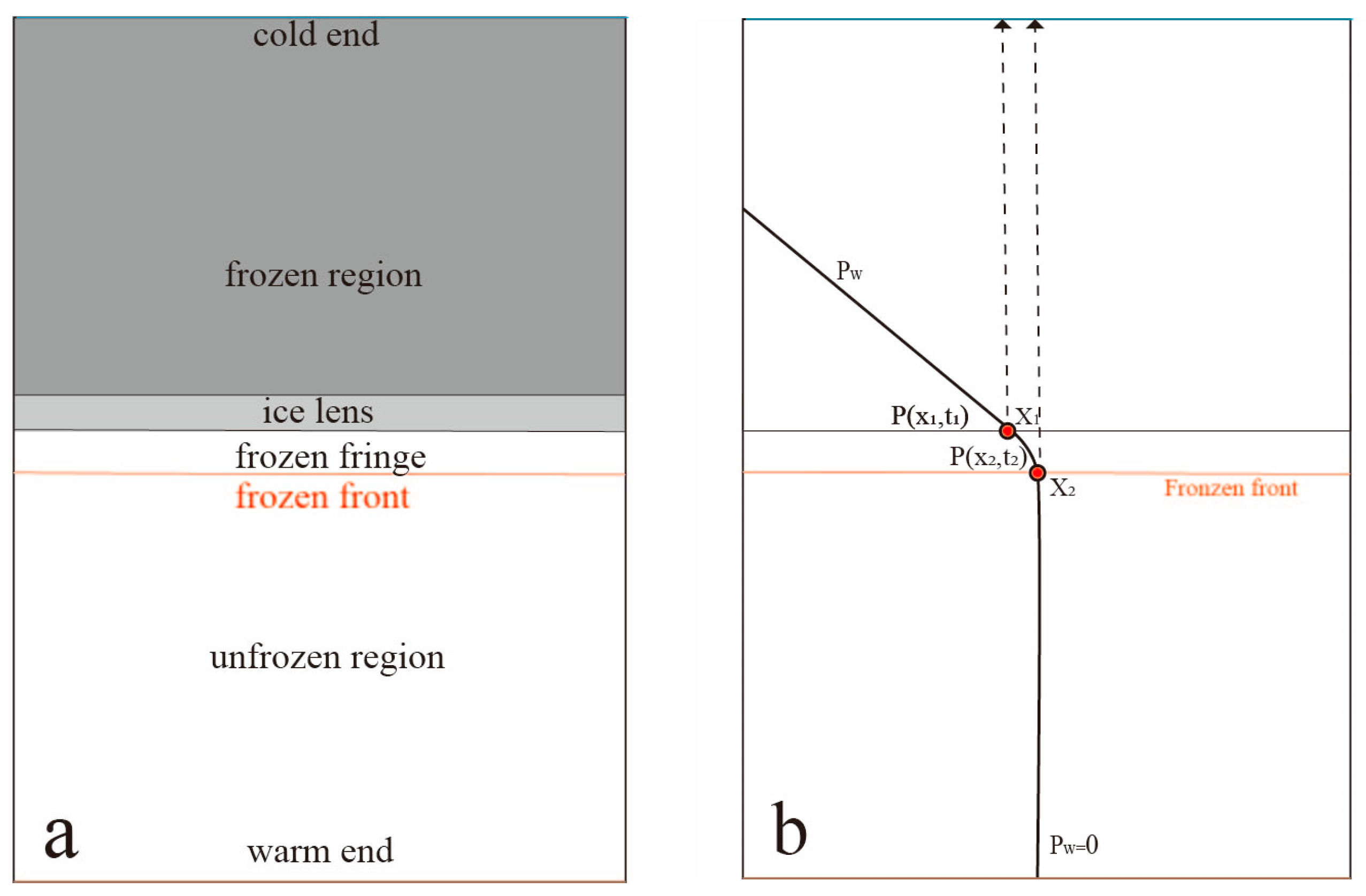
2.2. Pore Water Pressure Equation during Water Migration
2.3. Water Flow Equation
3. Model Construction
Model and Experiment Parameters
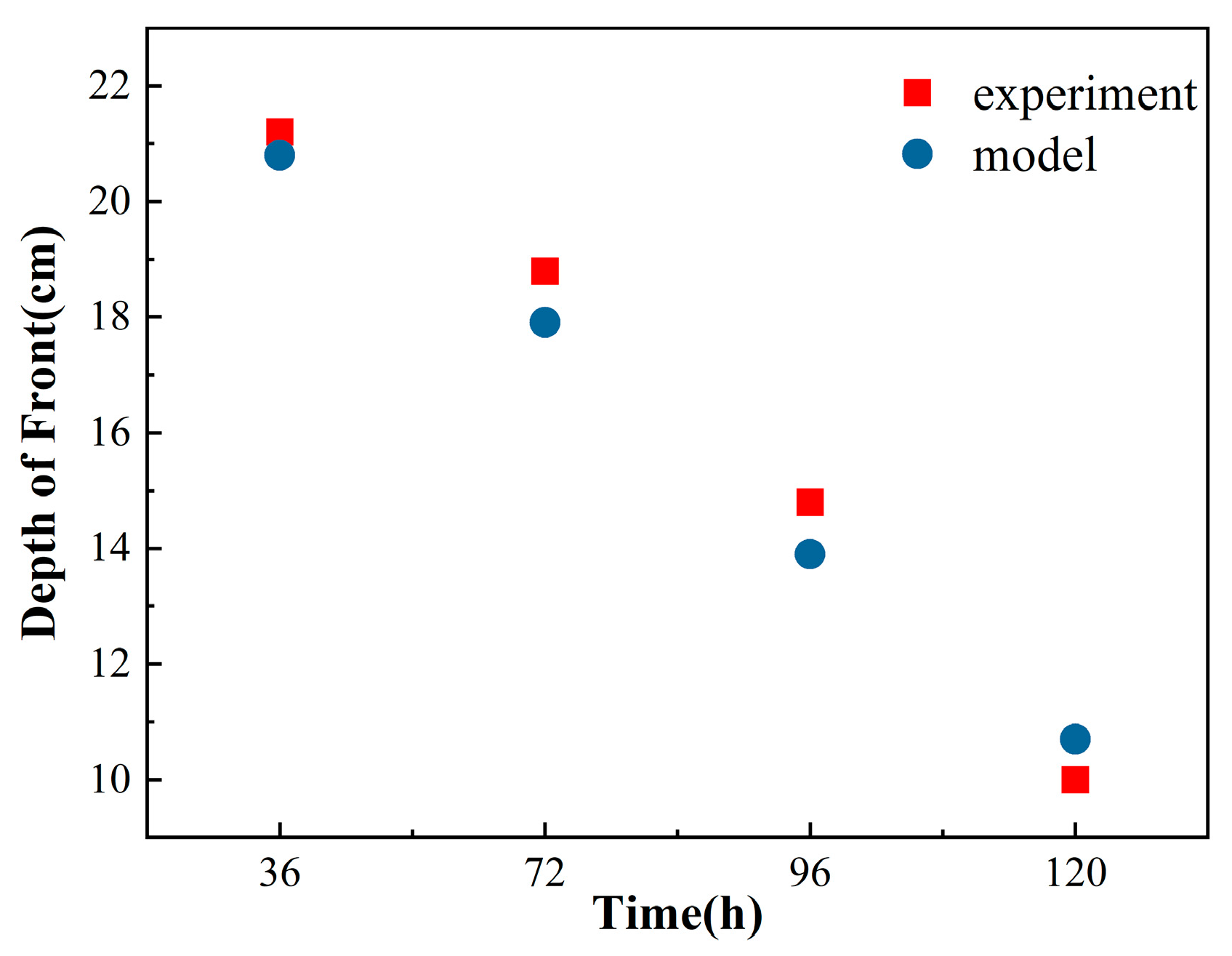
4. Numerical Simulation Results and Analysis
4.1. Temperature and Water Content Variation during Water Migration
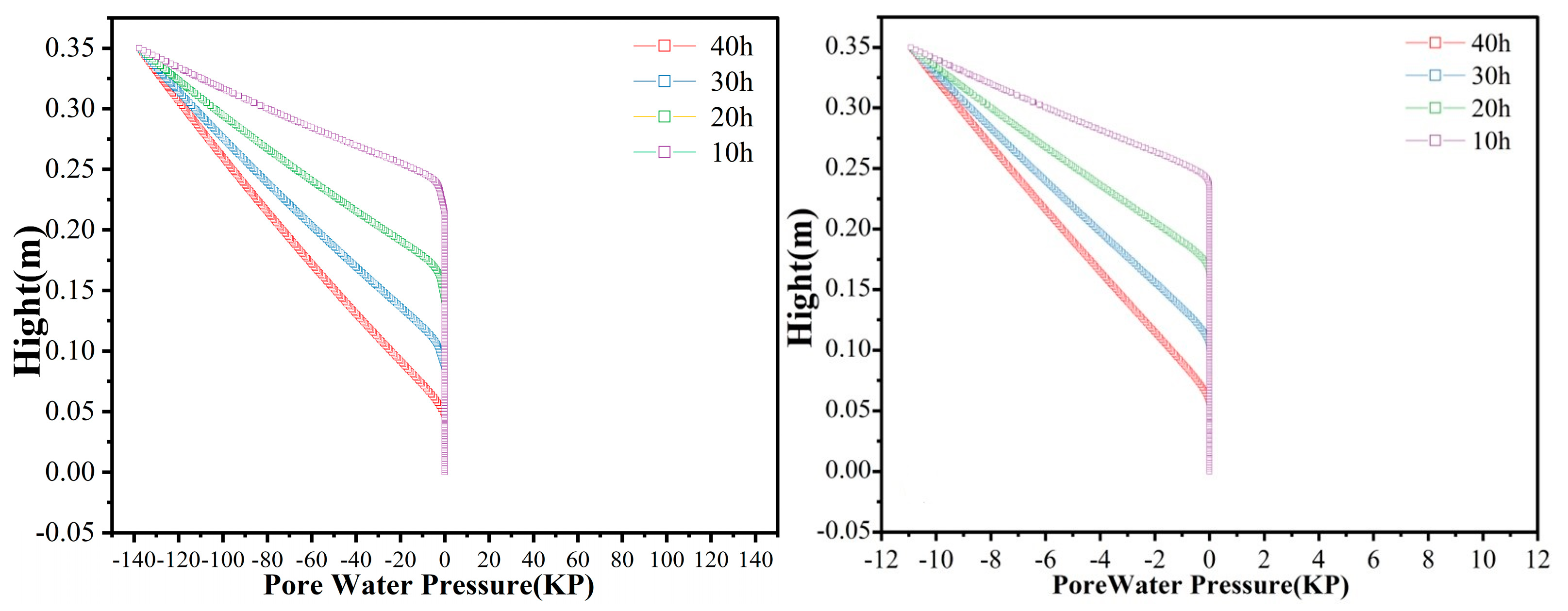
4.2. Pore Water Pressure Variation during Water Migration
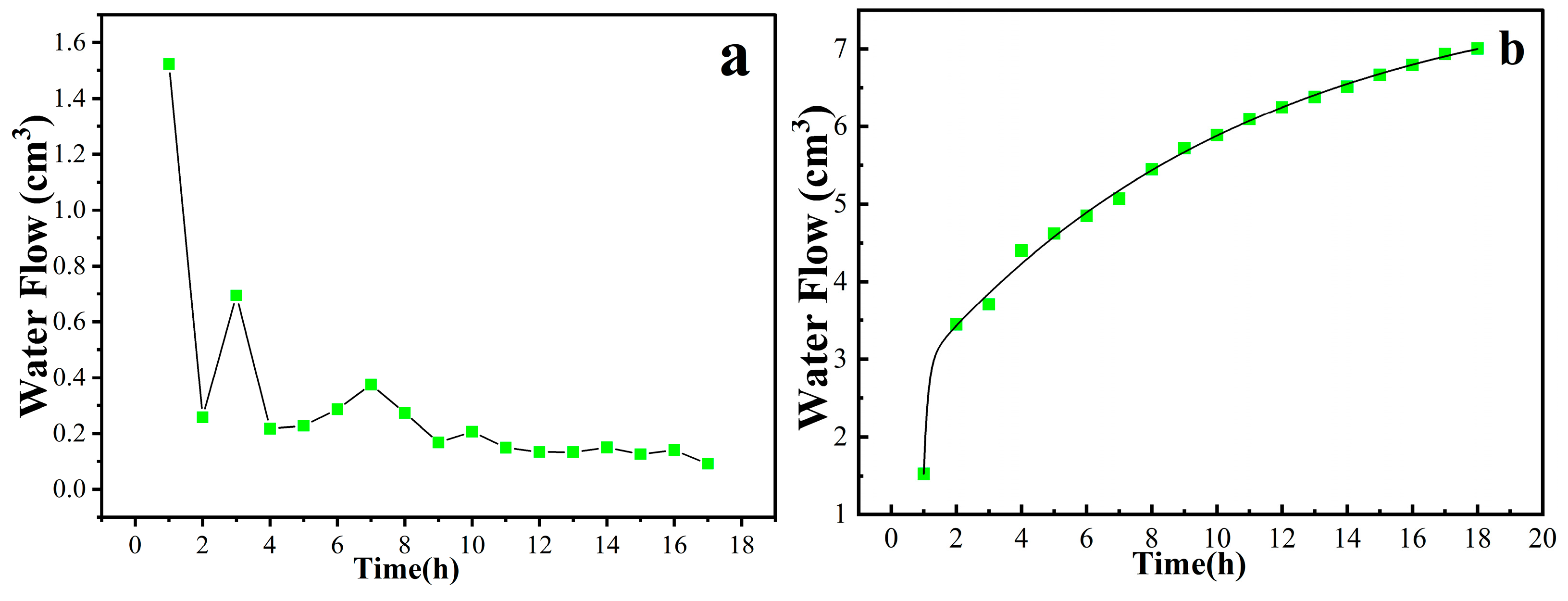
4.3. Water Flow after Water Migration
5. Conclusions
6. Discussions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| specific heat capacity of soil | |
| specific heat capacity of water | |
| specific heat capacity of ice | |
| thermal conductivity of soil | |
| thermal conductivity of water | |
| thermal conductivity of ice | |
| latent heat of fusion | |
| density of ice | |
| density of water | |
| density of soil | |
| pore ice pressure | |
| saturated moisture volume content | |
| residual moisture content | |
| Initial freezing temperature of soil | |
| coefficient related to solid–liquid ratio | |
| Permeability coefficient of saturated soils | |
| VG model parameters | |
| VG model parameters | |
| VG model parameters | |
| Initial Saturation | |
| permeability coefficient | |
| unfrozen water content | |
| specific water volume | |
| volume water content | |
| volume ice content | |
| impedance factor | |
| diffusion coefficient | |
| thermal conductivity | |
| ice-to-liquid ratio | |
| pore water pressure | |
| upper boundary temperature | |
| parameter related to pore water pressure | |
| ice saturation |
References
- Ma, W.; Zhang, L.; Yang, C. Discussion of the applicability of the generalized Clausius-Clapeyron equation and the frozen fringe process. Earth-Sci. Rev. 2015, 142, 47–59. [Google Scholar] [CrossRef]
- Taber, S. Frost heaving. J. Geol. 1929, 37, 428–461. [Google Scholar] [CrossRef]
- Li, A.; Niu, Y.; Niu, F.J.; Liu, H. Research status of frost heaving properties and controlling measures of coarse grained soil. J. Glaciol. Geocryol. 2015, 37, 202–210. [Google Scholar]
- Miller, R.D. Freezing and heaving of saturated and unsaturated soils. Highw. Res. Rec. 1972, 393, 1–11. [Google Scholar]
- Beskow, G.; Osterberg, J.O. Soil Freezing and Frost Heaving with Special Application to Roads and Railroads: With Special Supplement for the English Translation of Progress from 1935 to 1946; Technological Institute, Northwestern University: Evanston, IL, USA, 1947. [Google Scholar]
- Jackson, K.A.; Chalmers, B. Freezing of Liquids in Porous Media with Special Reference to Frost Heave in Soils. J. Appl. Phys. 1958, 29, 1178–1181. [Google Scholar] [CrossRef]
- Koopmans, R.W.R.; Miller, R.D. Soil freezing and soil water characteristic curves. Soil Sci. Soc. Am. J. 1966, 30, 680–685. [Google Scholar] [CrossRef]
- Everett, D.H. The thermodynamics of frost damage to porous solids. Trans. Faraday Soc. 1961, 57, 1541–1551. [Google Scholar] [CrossRef]
- Rempel, A.W. Frost heave. J. Glaciol. 2010, 56, 1122–1128. [Google Scholar] [CrossRef]
- Rempel, A.W. Hydromechanical Processes in Freezing Soils. Vadose Zone J. 2012, 11, vzj2012.0045. [Google Scholar] [CrossRef]
- Hoekstra, P. Moisture movement in soils under temperature gradients with the cold-side temperature below freezing. Water Resour. Res. 1996, 2, 241–250. [Google Scholar] [CrossRef]
- Loch, J.P.G.; Kay, B.D. Water Redistribution in Partially Frozen, Saturated silt Under Several Temperature Gradients and Overburden Loads. Soil Sci. Soc. Am. J. 1978, 42, 400–406. [Google Scholar] [CrossRef]
- Miller, R.D. Lens initiation in secondary heaving. In Proceedings of the International Symposium on Frost Action in Soils, Lulea, Sweden, 16–18 February 1977. [Google Scholar]
- Miller, R.D. Frost heaving in non-colloidal soils. In Proceedings of the Third International Conference in Permafrost, Edmonton, ALB, Canada, 10–13 July 1978. [Google Scholar]
- Gilpin, R.R. A Model for prediction of ice lensing and frost heave soils. Water Resour. Res. 1980, 16, 918–930. [Google Scholar] [CrossRef]
- O’Neill, K.; Miller, R.D. Exploration of a rigid ice model of frost heave. Water Resour. Res. 1985, 21, 281–296. [Google Scholar] [CrossRef]
- Konrad, J.M.; Morgenstern, N.R. A mechanistic theory of ice lens formation in fine-grained soils. Can. Geotech. J. 1980, 17, 473–486. [Google Scholar] [CrossRef]
- Zhou, J.Z.; Li, D. Numerical analysis of coupled water, heat and stress in saturated freezing soil. Cold Reg. Sci. Technol. 2012, 72, 43–49. [Google Scholar] [CrossRef]
- Harlan, R.L. Analysis of Coupled Heat-Fluid Transport in Partially Frozen Soil. Water Resour. Res. 1973, 9, 1314–1323. [Google Scholar] [CrossRef]
- Thomas, H.R.; Cleall, P.; Li, Y.C.; Harris, C.; Kern-Luetschg, M. Modelling of cryogenic processes in permafrost and seasonally frozen soils. Geotechnique 2009, 29, 173–184. [Google Scholar] [CrossRef]
- Lai, Y.; Pei, W.; Zhang, M.; Zhou, J. Study on theory model of hydro-thermal-mechanical interaction process in saturated freezing silty soil. Int. J. Heat Mass Transf. 2014, 78, 805–819. [Google Scholar] [CrossRef]
- Geng, L.; Tang, L.; Cong, S.Y.; Ling, X.Z.; Lu, J. Three-dimensional analysis of geosynthetic-encased granular columns for liquefaction mitigation. Geosynth. Int. 2016, 24, 45–59. [Google Scholar] [CrossRef]
- Zhao, C.; Liu, Z.; Shi, P.; Li, J.; Cai, G.; Wei, C. Average soil skeleton stress for saturated soils and discussion on effective stress. Int. J. Geomech. 2016, 16, D4015006. [Google Scholar] [CrossRef]
- Liu, Z.; Cai, G.; Kong, X.; Li, J.; Zhao, C. A thermodynamics-based mathematical model for the frost heave of unsaturated freezing soils. Cold Reg. Sci. Technol. 2020, 178, 103125. [Google Scholar] [CrossRef]
- Akagawa, S.; Hiasa, S.; Kanie, S.; Huang, S.L. Pore water and effective pressure in the frozen fringe during soil freezing. In Proceedings of the Ninth International Conference on Permafrost, Fairbanks, AK, USA, 28 June–3 July 2008; pp. 13–18. [Google Scholar]
- Lian-Hai, Z.; Wei, M.; Ya-Jun, S. The modes and its implications of water accumulation near the freezing front during soil freezing with considering ice segregation. J. Glaciol. Geocryol. 2022, 44, 1–11. [Google Scholar]
- TAO Wenquan. Heat Transfer; Northwestern Polytechnical University Press: Xi’An, China, 2006. [Google Scholar]
- Lu, N.; Likos, W.J. Unsaturated Soil Mechanics; Higher Education Press: Beijing, China, 2012; pp. 269–287. [Google Scholar]
- Taylor, G.S.; Luthin, J.N. A model for coupled heat and moisture transfer during soil freezing. Can. Geotech. J. 1978, 15, 548–555. [Google Scholar] [CrossRef]
- Bai, Q.; Li, X.; Tian, Y.; Fang, J. Equations and numerical simulation for coupled water and heat transfer in frozen soil. Chin. J. Geotech. Eng. 2015, 37, 131–136. [Google Scholar]
- Chen, F.; Li, N.; Cheng, G. The theoretical frame of multi-phase porous medium for the freezing soil. Chin. J. Geotech. Eng. 2002, 24, 213–217. [Google Scholar]
- O’Neill, K. The physics of mathematical frost heave models: A review. Cold Reg. Sci. Technol. 1983, 6, 275–291. [Google Scholar] [CrossRef]
- Konrad, J.M.; Duquennoi, C. A model for water transport and ice Lensing in freezing soils. Water Resour. Res. 1993, 29, 3109–3124. [Google Scholar] [CrossRef]
- GB/T 50123-2019; Standard for Geotechnical Experimental Methods. China Planning Press: Beijing, China, 2019.
- Zeng, G.; Zhang, M.; Li, Z.; Yuan, H. Review of mechanical criterion for formation of ice lens in freezing soil. J. Glaciol. Geocryol. 2015, 37, 192–201. [Google Scholar]



| 2.59 | 0.22 | 0.5 | 0.22 | 0.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, B.; Brouchkov, A.V.; Hu, J. Numerical Study of Pore Water Pressure in Frozen Soils during Moisture Migration. Water 2024, 16, 776. https://doi.org/10.3390/w16050776
Zhou B, Brouchkov AV, Hu J. Numerical Study of Pore Water Pressure in Frozen Soils during Moisture Migration. Water. 2024; 16(5):776. https://doi.org/10.3390/w16050776
Chicago/Turabian StyleZhou, Bicheng, Anatoly V. Brouchkov, and Jiabo Hu. 2024. "Numerical Study of Pore Water Pressure in Frozen Soils during Moisture Migration" Water 16, no. 5: 776. https://doi.org/10.3390/w16050776
APA StyleZhou, B., Brouchkov, A. V., & Hu, J. (2024). Numerical Study of Pore Water Pressure in Frozen Soils during Moisture Migration. Water, 16(5), 776. https://doi.org/10.3390/w16050776






