Modeling of a Jet Pipe Servovalve Considering Nonlinear Flow Forces Acting on the Spool
Abstract
1. Introduction
2. Theoretical Model
2.1. Linear Model
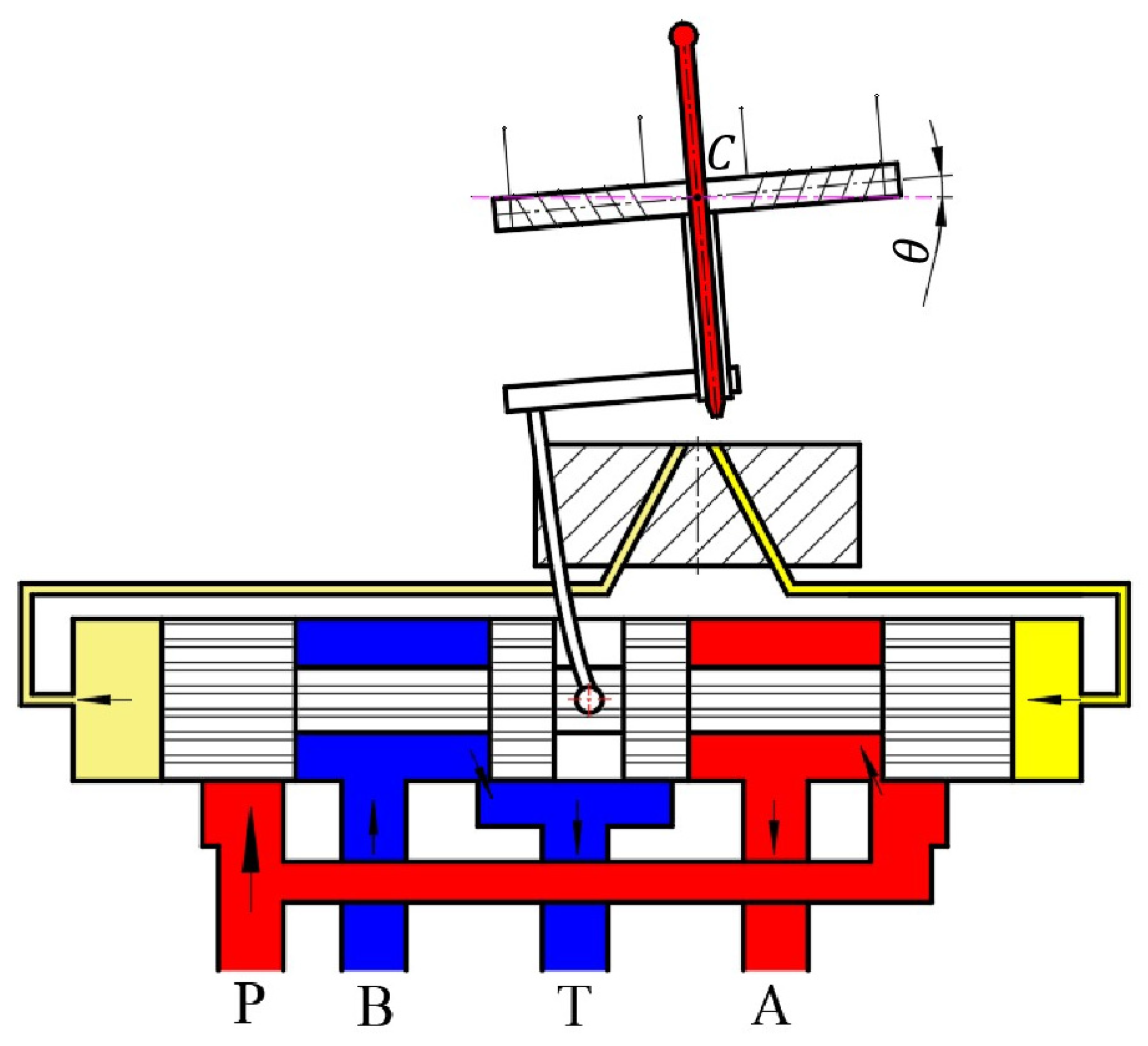
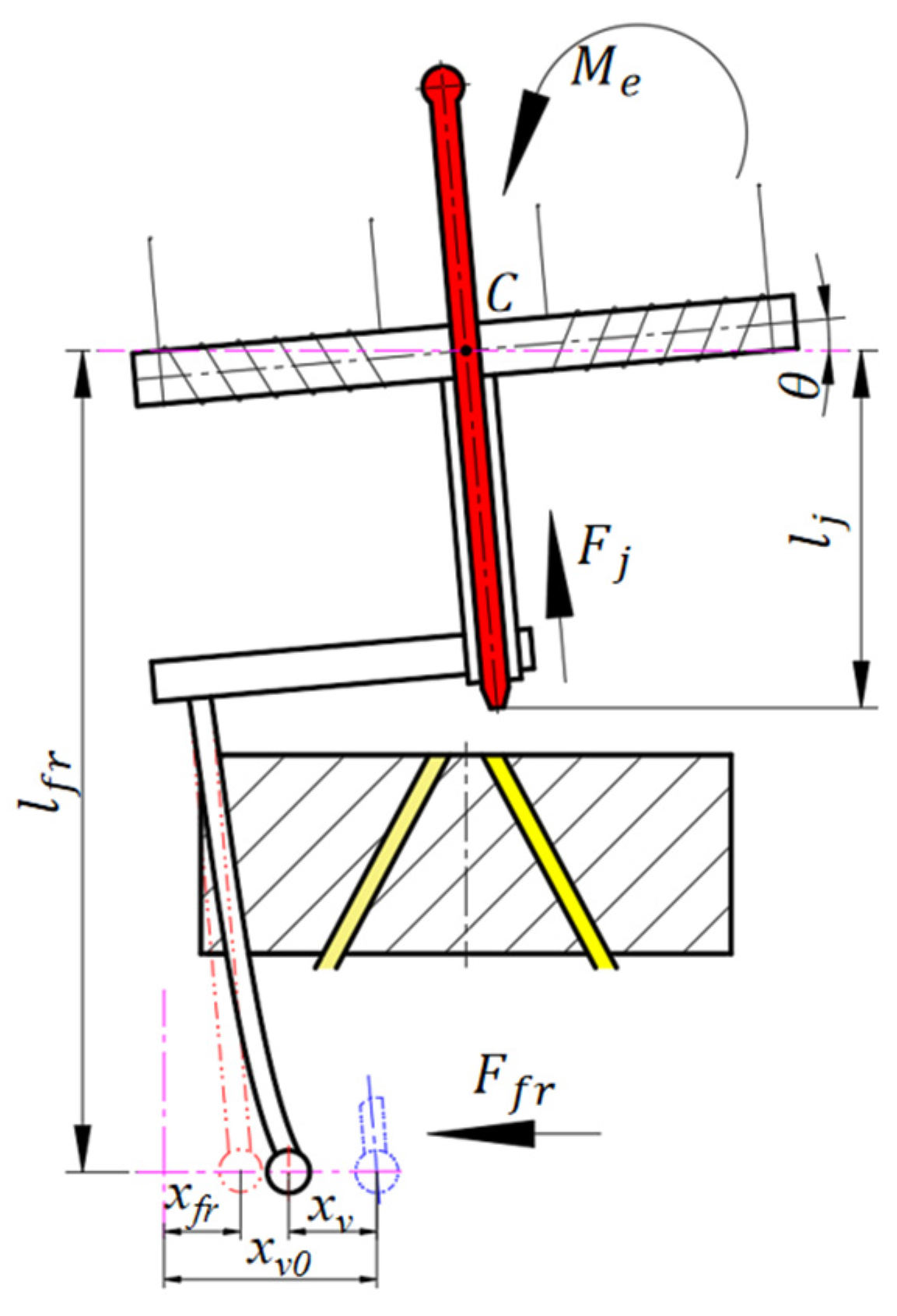
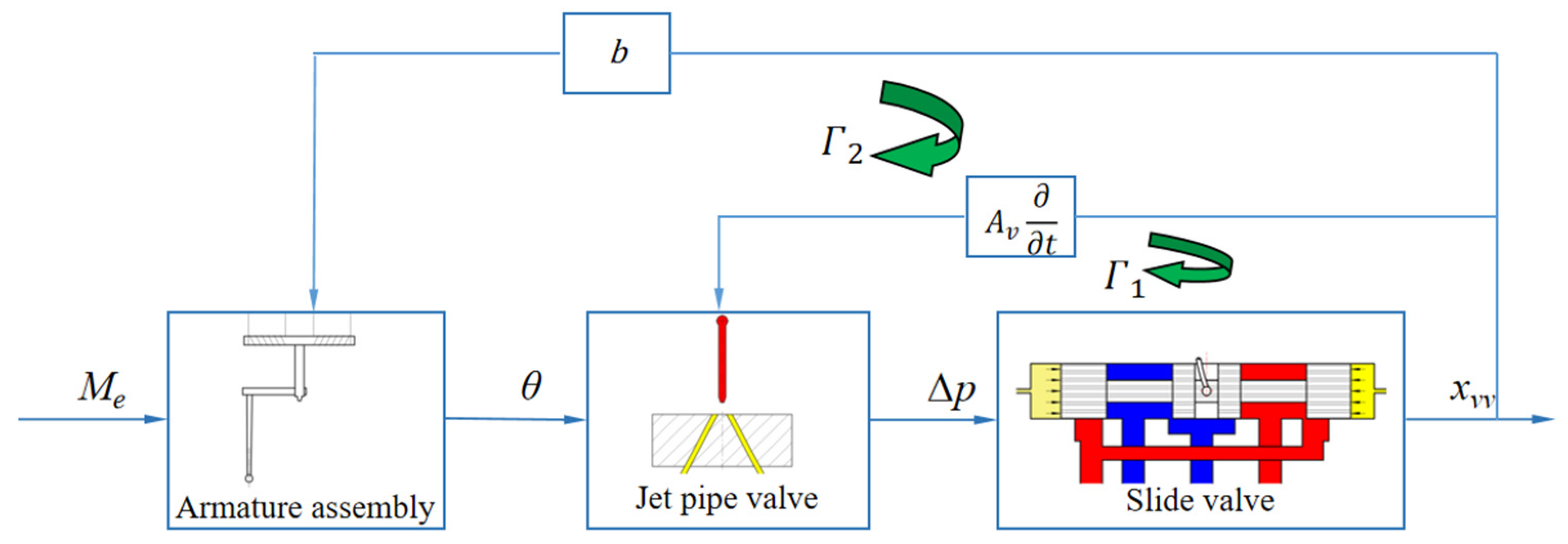
2.1.1. Kinematic Analysis of Armature Assembly
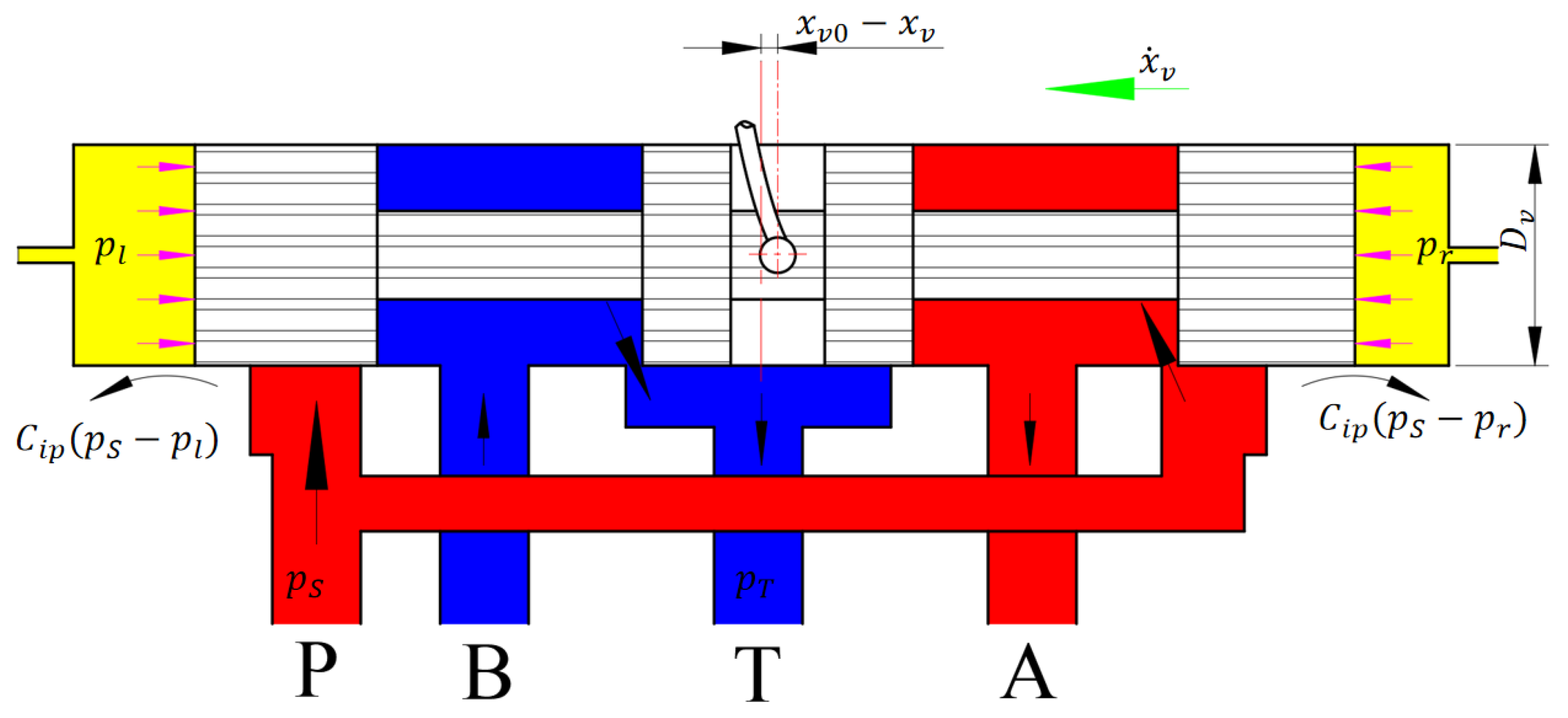
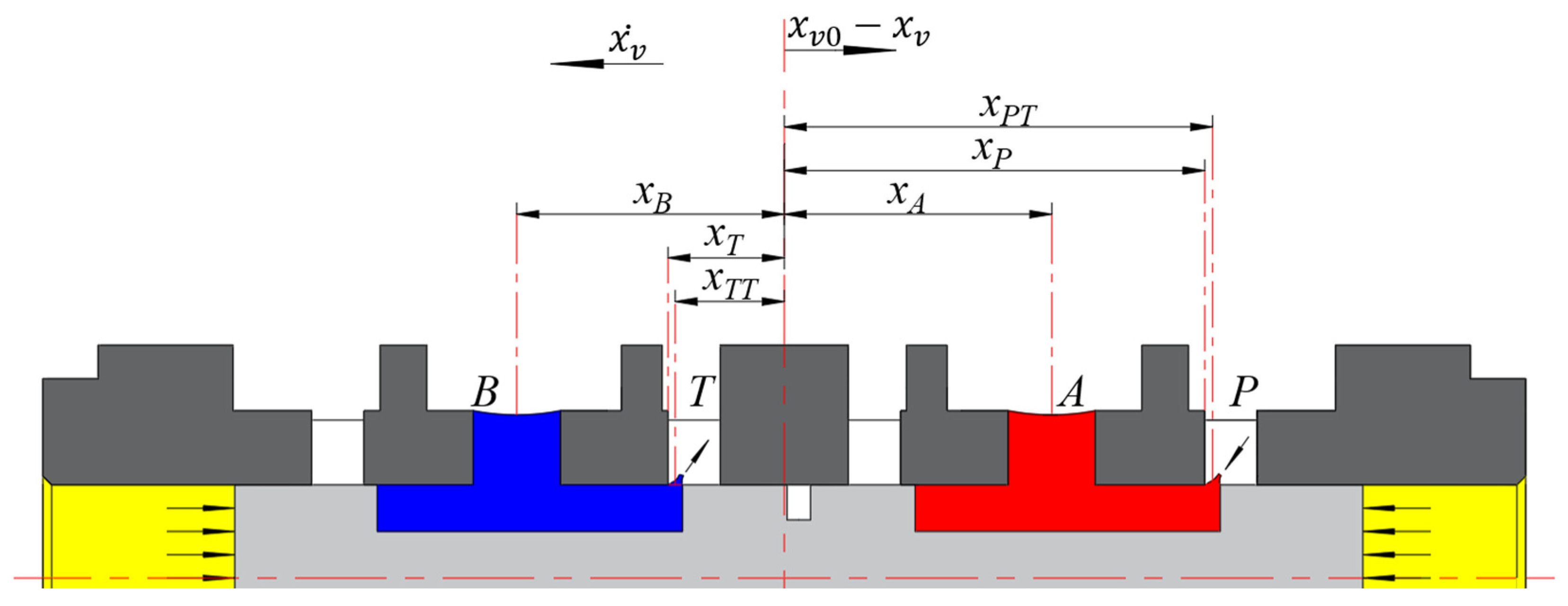
2.1.2. Flow Equations for the Control Chamber
2.2. Nonlinear Dynamic Analysis of Spool
2.3. Mathematical Modeling of Closed-Loop Systems
3. Numerical Analysis
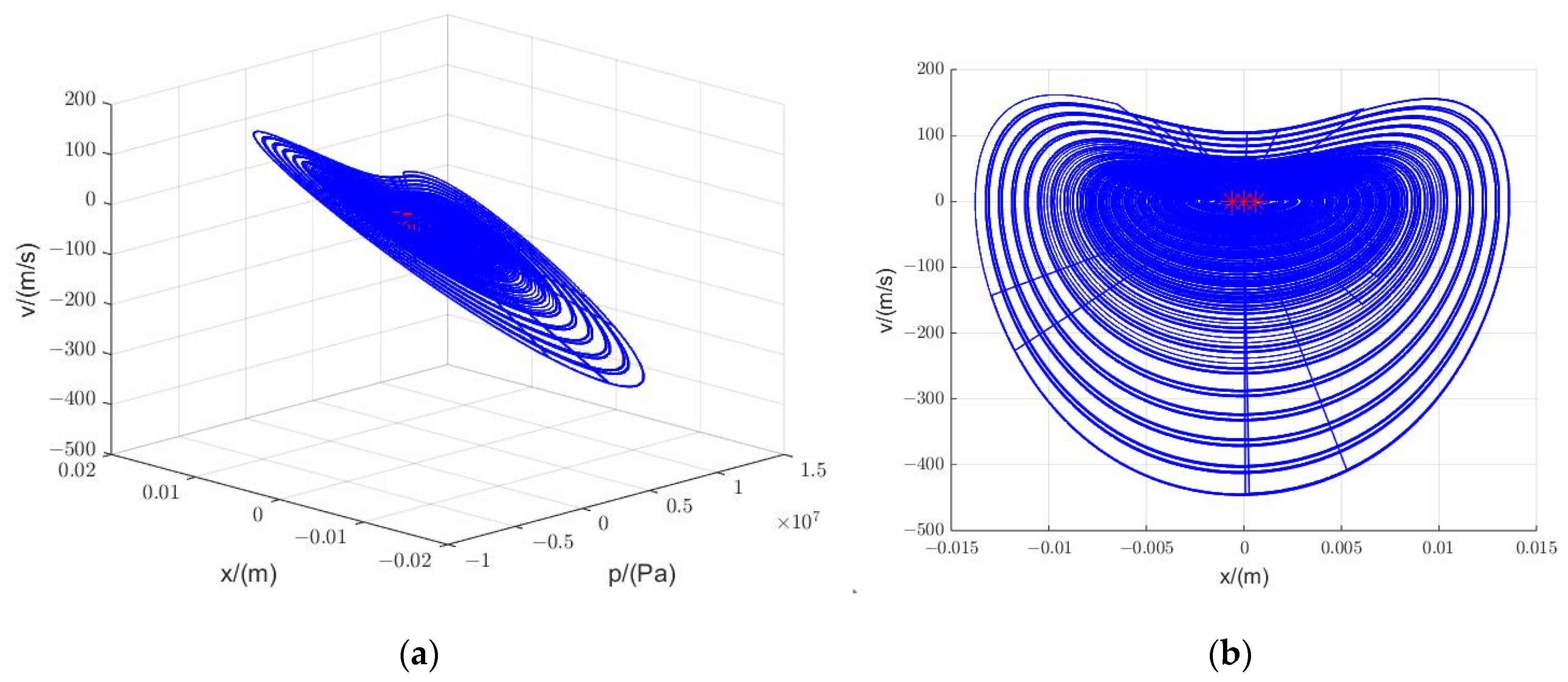
3.1. Nonlinear Analysis of the Third-Order Closed-Loop Systems
3.1.1. The Calculation of Equilibrium Points
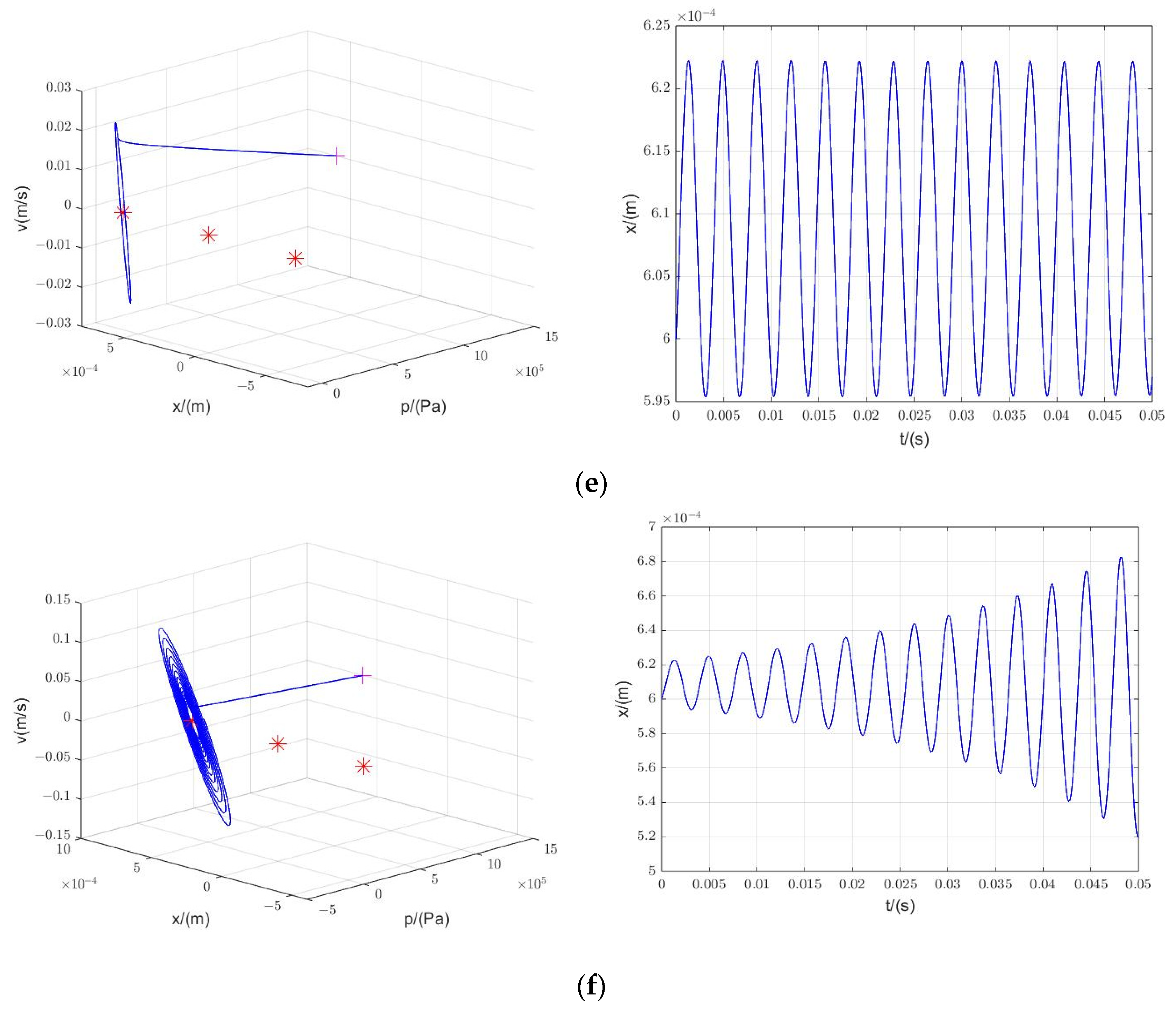
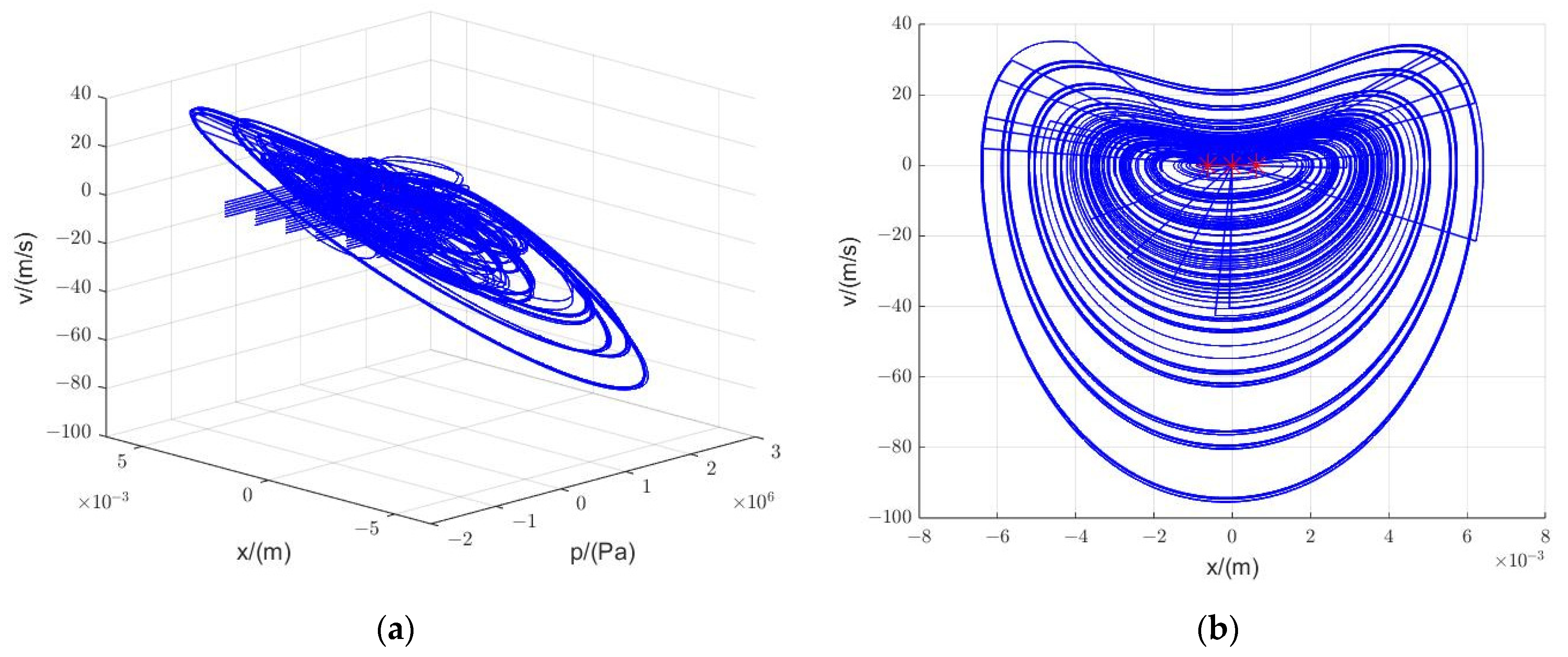
3.1.2. Phase Portrait
3.1.3. Bifurcation Characteristics
- Hopf bifurcation
- Period-doubling bifurcations
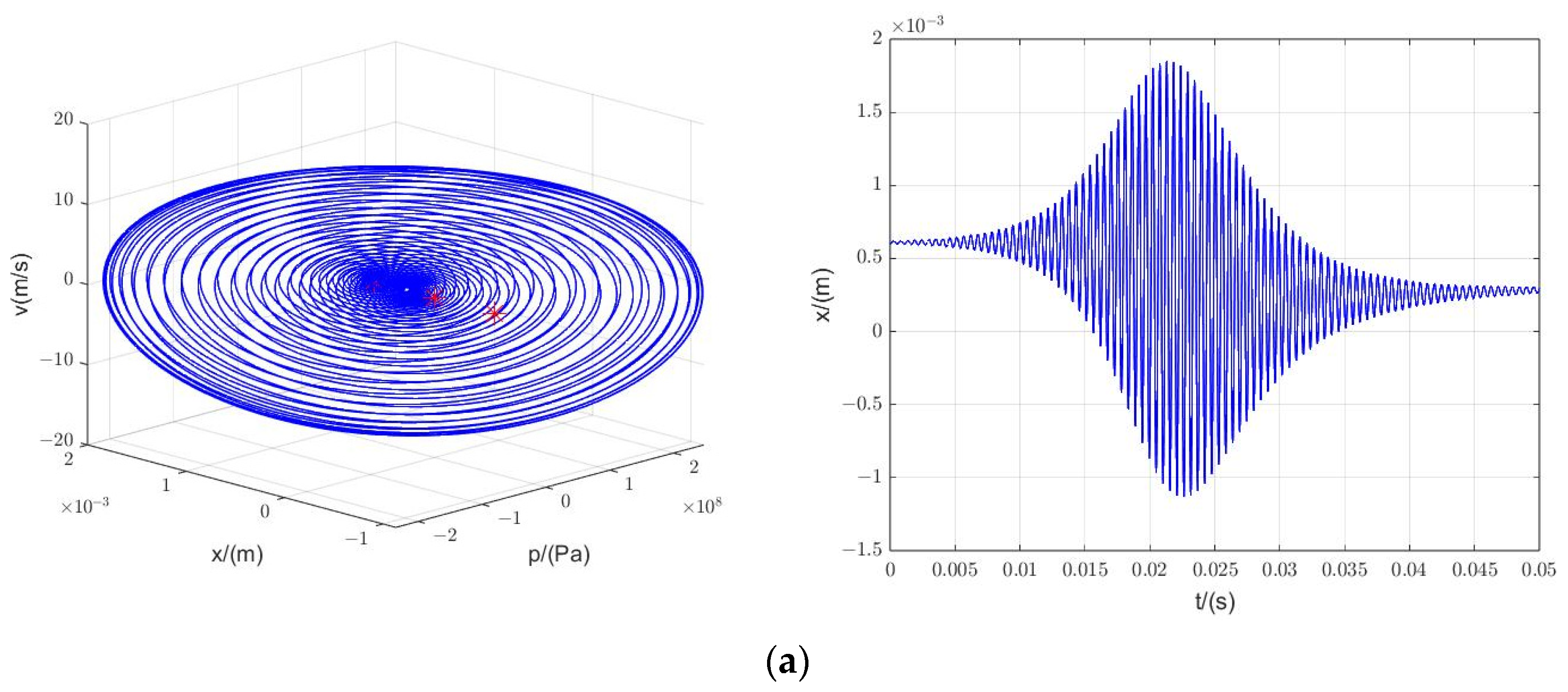
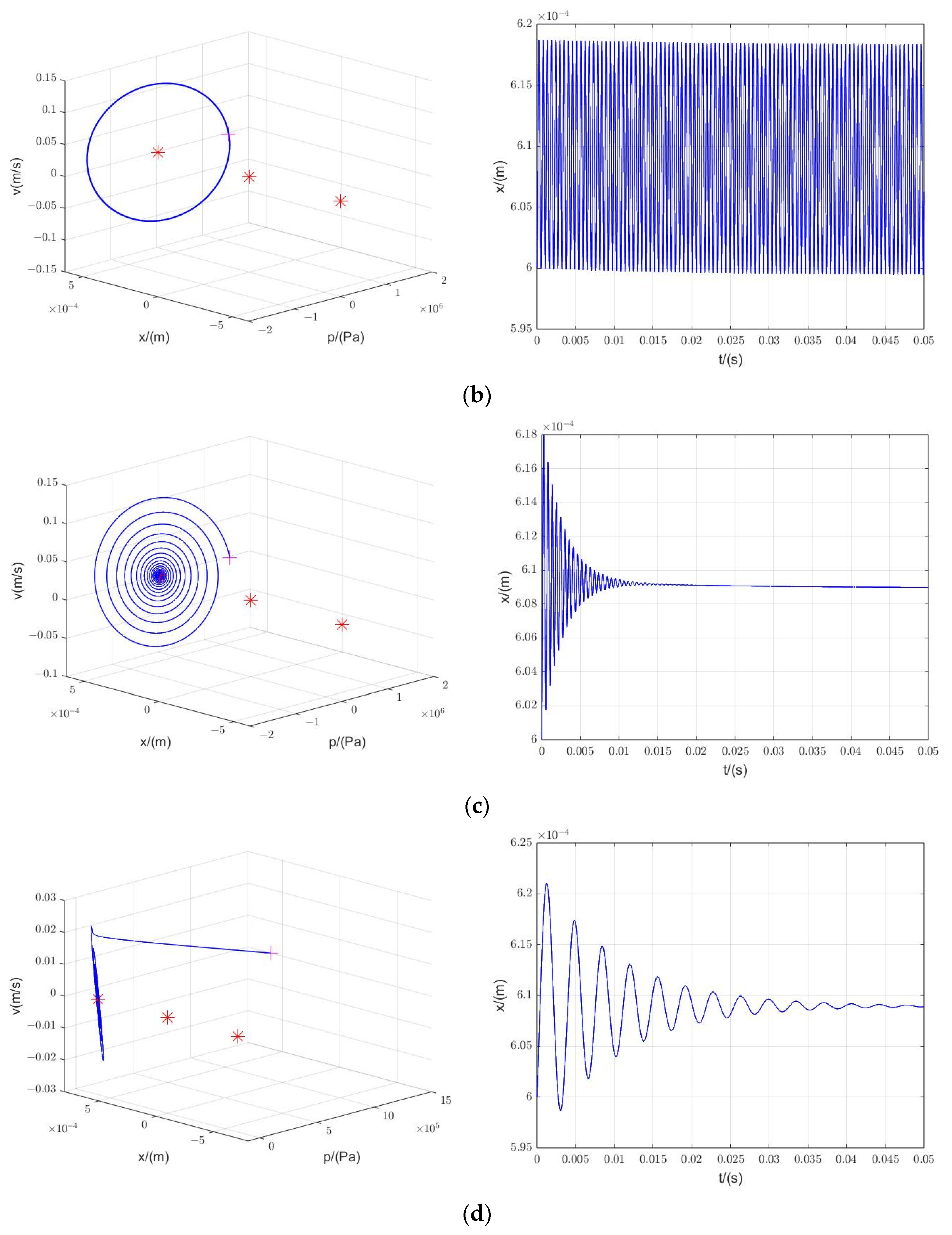
3.2. Nonlinear Analysis of the Fifth-Order Closed-Loop System
3.2.1. The Calculation of Equilibrium Points
3.2.2. Phase Portrait
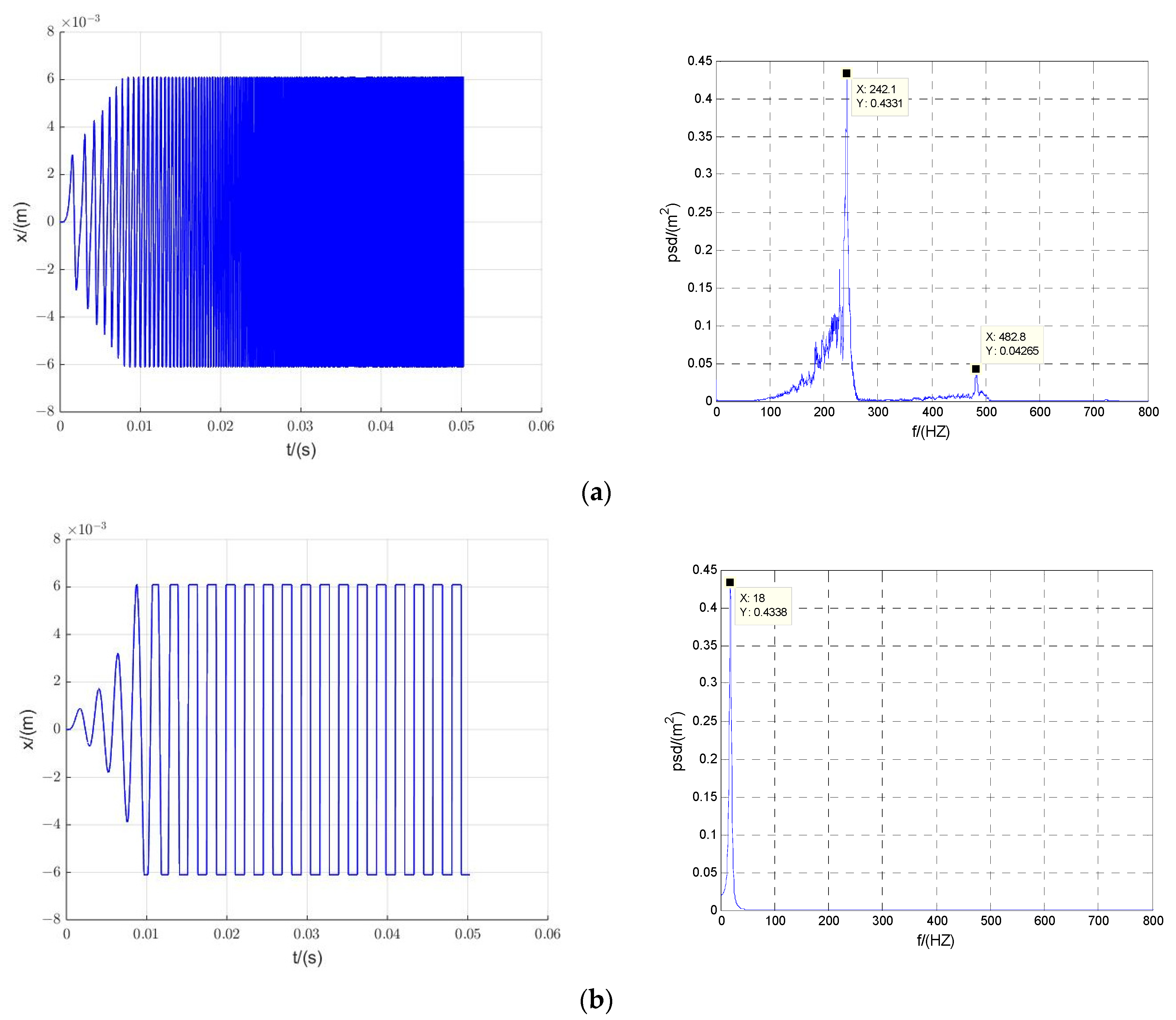
3.2.3. Simulation
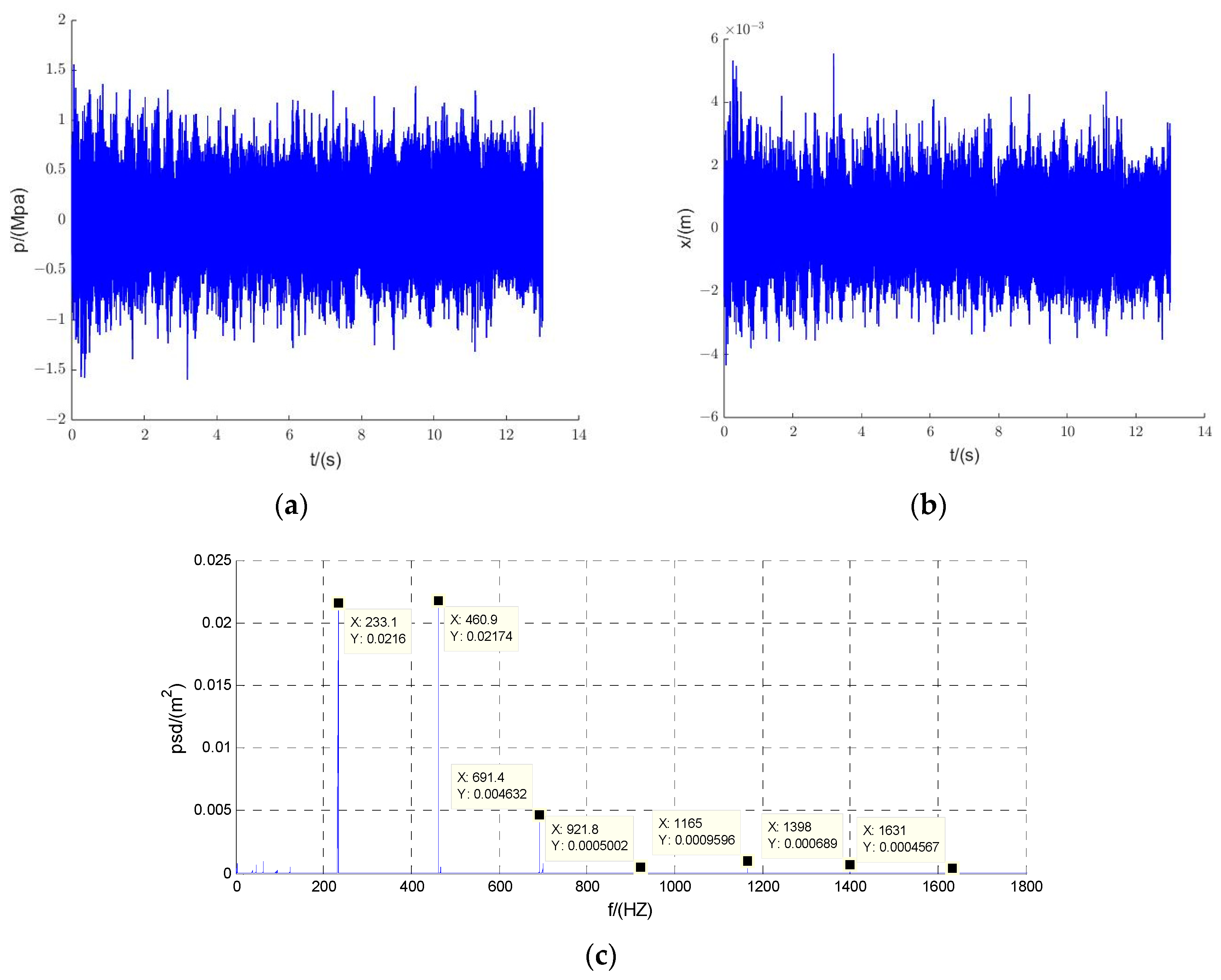
4. Experiment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Paolo, T.; Andrew, R.P.; Elia, D.; Riccardo, A. A review of electro-hydraulic servovalve research and development. Int. J. Fluid Power 2018, 20, 53–98. [Google Scholar]
- G77XK Doc. Jet Pipe Servovalve Installation and Operation Instruction. Available online: https://www.moog.com/content/dam/moog/literature/ICD/CDS33551_JetPipe.pdf (accessed on 9 February 2022).
- John, F.B.; Gerhard, R.; Shearer, J.L. Fluid Power Control, 1st ed.; The Technology Press of M.I.T.: Boston, MA, USA, 1960; pp. 235–245. [Google Scholar]
- Guo, S.R.; Yin, Y.B. Advanced Fluid Power Control, 1st ed.; Shanghai Science and Technology Press: Shanghai, China, 2017; pp. 266–272. [Google Scholar]
- Wu, L.; Chen, K.S.; Gao, Y. Research on cavitation phenomena in pilot stage of jet pipe servo-valve with a rectangular nozzle based on large-eddy simulations. AIP Adv. 2019, 9, 025109. [Google Scholar] [CrossRef]
- Fan, C.H.S.; Chen, T.F. Mathematical Model of Steady State Operation in Jet Pipe Electro-Hydraulic Servo Valve. J. Donghua Univ. 2013, 30, 269–275. [Google Scholar]
- Li, Y.S. Mathematical modelling and characteristics of the pilot valve applied to a jet-pipe/deflector-jet servovalve. Sens. Actuators A 2016, 245, 150–159. [Google Scholar] [CrossRef]
- Zhang, Y. Research on the Modeling and Simulation of Jet Pipe Servovalve. Ph.D. Thesis, Northwestern Ploytechnical University, Xi’an, China, 2015; pp. 39–58. [Google Scholar]
- Zhang, Y.; Xia, Y. Analysis and optimization of the pilot stage of jet pipe servo valve. Alex. Eng. J. 2022, 61, 41–50. [Google Scholar] [CrossRef]
- Kang, S.Q.; Kong, X.D.; Zhang, J.; Du, R.H. Research on Pressure-Flow Characteristics of Pilot Stage in Jet Pipe Servo-Valve. Sensors 2023, 23, 216. [Google Scholar] [CrossRef] [PubMed]
- Somashekhar, S.H.; Singaperumal, M.; Kuma, R.K. Mathematical modelling and simulation of a jet pipe electrohydraulic flow control servo valve. IMechE 2007, 221, 365–382. [Google Scholar] [CrossRef]
- Somashekhar, S.H. Modeling and simulation of fluid structure interaction in jet pipe electrohydraulic servovalve. Int. J. Recent Adv. Mech. Eng. (IJMECH) 2013, 2, 1–14. [Google Scholar]
- Li, R.; Nie, S.; Yi, M.; Ruan, J. Flow Characteristics Simulation of Jet Pipe Servo Valve Working in Different Medium Base on CFD. Mach. Tool Hydraul. 2011, 3, 10–12, 29. [Google Scholar]
- Zhao, K.Y.; Wu, Q.X.; Zhang, L.J.; Yuan, Z.H.; Yang, J.Q. Analysis of the Jet Pipe Electro-Hydraulic Servo Valve with Finite Element Methods; ICMME: Kuala Lumpur, Malaysia, 2017. [Google Scholar]
- Li, S.G.; Hu, L.M.; Cao, K.Q.; Xie, Z.G.; Cao, W. Modling and Simulation of Dynamic Characteristics of the Force Feedback Jet-pipe Servo Valve. Fire Control Command Control 2017, 42, 91–96. [Google Scholar]
- Yin, Y.B.; Gou, W.K.; Hu, Y.T.; Li, R.H. Modeling and frequency characteristics of jet-pipe servo valve considering eddy current effect. J. Aerosp. Power 2020, 35, 1777–1785. [Google Scholar]
- Chen, J.; Li, F.; Yang, Y.; Gao, Y. Mathematical Modelling and Hierarchical Encourage Particle Swarm Optimization Genetic Algorithm for Jet Pipe Servo Valve. Comput. Intell. Neurosci. 2022, 7, 9155248. [Google Scholar] [CrossRef]
- Gordić, D.; Babić, M.; Jovičić, N. Modelling of Spool Position Feedback Servovalves. Int. J. Fluid Power 2004, 5, 37–50. [Google Scholar] [CrossRef]
- Chen, J. Dynamic Simulation and Optimal Design and Control Method of Jet Pipe Servo Valve. Ph.D. Thesis, Northwestern Ploytechnical University, Xi’an, China, June 2017; pp. 11–40. [Google Scholar]
- Jelali, M.; Kroo, A. Hydraulic Servo-Systems Modelling, Identification and Control, 2nd ed.; Springer Ltd.: London, UK, 2003; pp. 58–59. [Google Scholar]
- Hayashi, S. Instability of poppet valve circuit. JSME Int. J. 1995, 38, 357–366. [Google Scholar] [CrossRef]
- Hayashi, S.; Hayase, T.; Kurahashi, T. Chaos in a Hydraulic Control Valve. J. Fluids Struct. 1997, 11, 693–716. [Google Scholar] [CrossRef]
- Licskó, G.; Champneys, A.; Hős, C. Nonlinear Analysis of a Single Stage Pressure Relief Valve. Int. J. Appl. Math. 2009, 11, 286–299. [Google Scholar]
- Hős, C.; Champneys, A.R. Grazing bifurcations and chatter in a pressure relief valve model. Phys. D 2012, 241, 2068–2076. [Google Scholar] [CrossRef]
- Bazsó, C.; Hős, C. An experimental study on the stability of a direct spring loaded poppet relief valve. J. Fluids Struct. 2013, 42, 456–465. [Google Scholar] [CrossRef]
- Hős, C.; Champneys, A.R.; Paul, K.; McNeely, M. Dynamic behaviour of direct spring loaded pressure relief valves connected to inlet piping: IV review and recommendations. J. Loss Prev. Process Ind. 2017, 48, 270–288. [Google Scholar] [CrossRef][Green Version]
- Bouzidi, S.E.; Hassan, M.; Ziada, S. Self-excited vibrations of spring-loaded valves operating at small pressure drops. J. Fluids Struct. 2018, 83, 72–90. [Google Scholar] [CrossRef]
- Bouzidi, S.E.; Hassan, M.; Ziada, S. Experimental characterisation of the self-excited vibrations of spring-loaded valves. J. Fluids Struct. 2018, 76, 558–572. [Google Scholar] [CrossRef]
- Awad, H.; Parrondo, J. Hydrodynamic self-excited vibrations in leaking spherical valves with annular seal. Alex. Eng. J. 2020, 59, 1515–1524. [Google Scholar] [CrossRef]
- Merritt, H.E. Hydraulic Control Systems, 1st ed.; John Wiley &Sons, Inc.: New York, NY, USA, 1967; pp. 104–105. [Google Scholar]
- Yuan, Q.; Li, P.Y. Using Steady Flow Force for Unstable Valve Design: Modeling and Experiments. J. Dyn. Syst. Meas. Control 2005, 127, 451–462. [Google Scholar] [CrossRef]
- Manring, N.D.; Zhang, S. Pressure Transient Flow Forces for Hydraulic Spool Valves. J. Dyn. Syst. Meas. Control 2012, 134, 034501. [Google Scholar] [CrossRef]
- Frosina, E.; Senatore, A.; Buono, D.; Stelson, K.A. A modeling approach to study the fluid-dynamic forces acting on the spool of a flow control valve. J. Fluids Eng. 2017, 139, 011103. [Google Scholar] [CrossRef]
- Wang, C.H. Hydraulic Control System; China Machine Press: Beijing, China, 2004; pp. 40–42. [Google Scholar]
- Li, L.; Xu, W.X.; Tan, Y.F.; Yang, Y.S.; Yang, J.G.; Tan, D.P. Fluid-induced vibration evolution mechanism of multiphase free sink vortex and the multi-source vibration sensing method. Mech. Syst. Signal Process. 2023, 189, 110058. [Google Scholar] [CrossRef]
- Beltaos, S.; Rajaratnam, N. Impinging Circular Turbulent Jets. J. Hydraul. Eng. 1974, 100, 1313–1328. [Google Scholar] [CrossRef]
- Galal Rabli, M. Fluid Power Engineering, 1st ed.; The McGraw-Hill Companies, Inc.: New York, NY, USA, 2009; pp. 333–348. [Google Scholar]
- Amirante, R.; Catalano, L.A.; Tamburrano, P. The importance of a full 3D fluid dynamic analysis to evaluate the flow forces in a hydraulic directional proportional valve. Eng. Comput. Int. J. Comput.-Aided Eng. Softw. 2014, 31, 898–922. [Google Scholar] [CrossRef]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Publishing House of Electronics Industry: Beijing, China, 2017; pp. 5–7. [Google Scholar]
- Yan, Q.; Fan, X.H.; Li, L.; Zheng, G.A. Investigations of the Mass Transfer and Flow Field Disturbance Regulation of the Gas-Liquid-Solid Flow of Hydropower Stations. J. Mar. Sci. Eng. 2024, 12, 84. [Google Scholar] [CrossRef]
- Lee, S.Y.; Blackburn, J.F. Contributions to hydraulic control 2 Transient-flow forces and valve instability. Trans. ASME 1952, 74, 1013–1016. [Google Scholar] [CrossRef]
- Karris, S.T. Numerical Analysis Using MATLAB and Spreadsheets, 2nd ed.; Orchard Publications: Fremont, CA, USA, 2004. [Google Scholar]
- Hahn, B.D.; Valentine, D.T. Essential MATLAB for Engineers and Scientists, 7th ed.; Elsevier Ltd.: Oxfird, MI, USA, 2019. [Google Scholar]
- Lynch, S. Dynamical Systems with Applications Using MATLAB, 2nd ed.; Springer International Publishing: Cham, Switzerland, 2010; pp. 151–282. [Google Scholar]
- Ding, W.J. Self-Excited Vibration, 1st ed.; Tsinghua Press: Beijing, China, 2009; pp. 34–39. [Google Scholar]
- Kuznetsov, Y.A. Elements of Applied Bifurcation Theory, 1st ed.; Harbin Institute of Technology Press: Harbin, China, 2021; pp. 1–92. [Google Scholar]
- Strogatz, S.H. Nonlinear Dynamics and Choas, 2nd ed.; China Machine Press: Beijing, China, 2018; pp. 146–291. [Google Scholar]



| Symbol | Value | Unit | Symbol | Value | Unit |
|---|---|---|---|---|---|
| 1.5 | Pa | −9.1245 | - | ||
| 1.97 | m3 | 1.788 | - | ||
| 3.217 | m2 | 2.232 | - | ||
| 3.92 | kg | 9.8065 | - | ||
| 2.0 | N/m | 2.1 | Pa | ||
| 2 | m | 5 | Pa | ||
| 1.4 | m | 2.865 | m | ||
| 6 | m | 5.32 | kg m2 | ||
| 5.6713 | - | 8.938 | Nms/rad | ||
| 1.5833 | - | 1.5 | m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, S.; Kong, X.; Zhang, J.; Du, R. Modeling of a Jet Pipe Servovalve Considering Nonlinear Flow Forces Acting on the Spool. Water 2024, 16, 683. https://doi.org/10.3390/w16050683
Kang S, Kong X, Zhang J, Du R. Modeling of a Jet Pipe Servovalve Considering Nonlinear Flow Forces Acting on the Spool. Water. 2024; 16(5):683. https://doi.org/10.3390/w16050683
Chicago/Turabian StyleKang, Shuangqi, Xiangdong Kong, Jin Zhang, and Ranheng Du. 2024. "Modeling of a Jet Pipe Servovalve Considering Nonlinear Flow Forces Acting on the Spool" Water 16, no. 5: 683. https://doi.org/10.3390/w16050683
APA StyleKang, S., Kong, X., Zhang, J., & Du, R. (2024). Modeling of a Jet Pipe Servovalve Considering Nonlinear Flow Forces Acting on the Spool. Water, 16(5), 683. https://doi.org/10.3390/w16050683







