Risk Assessment of Water Inrush from Coal Seam Roof Based on the Combined Weighting of the Geographic Information System and Game Theory: A Case Study of Dananhu Coal Mine No. 7, China
Abstract
1. Introduction
2. Study Area and Mining Conditions
3. Materials and Methods
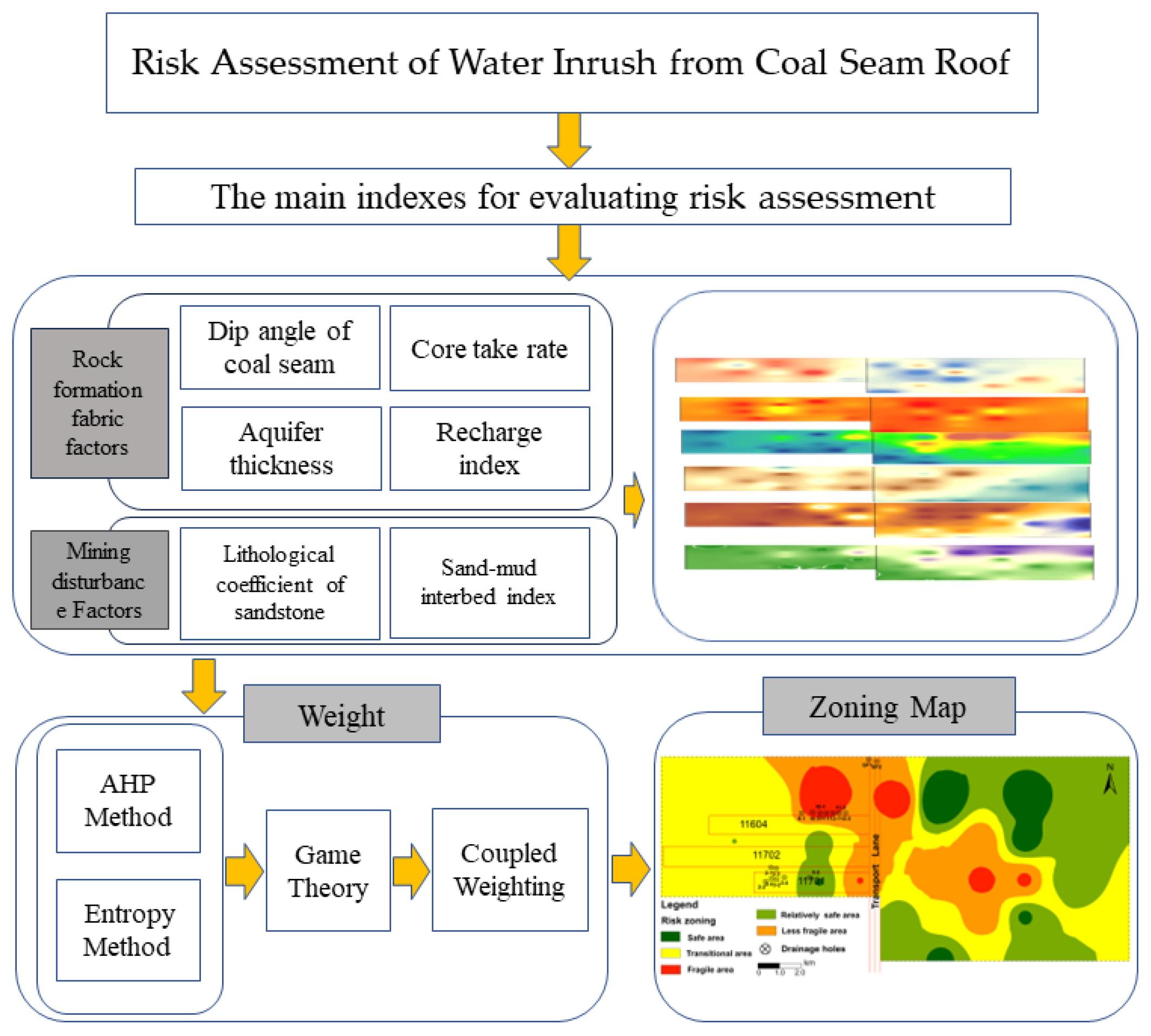
3.1. Selection of Main Control Factors and Creation of Thematic Maps
3.1.1. Rock Fabric Formation Factors
- (1)
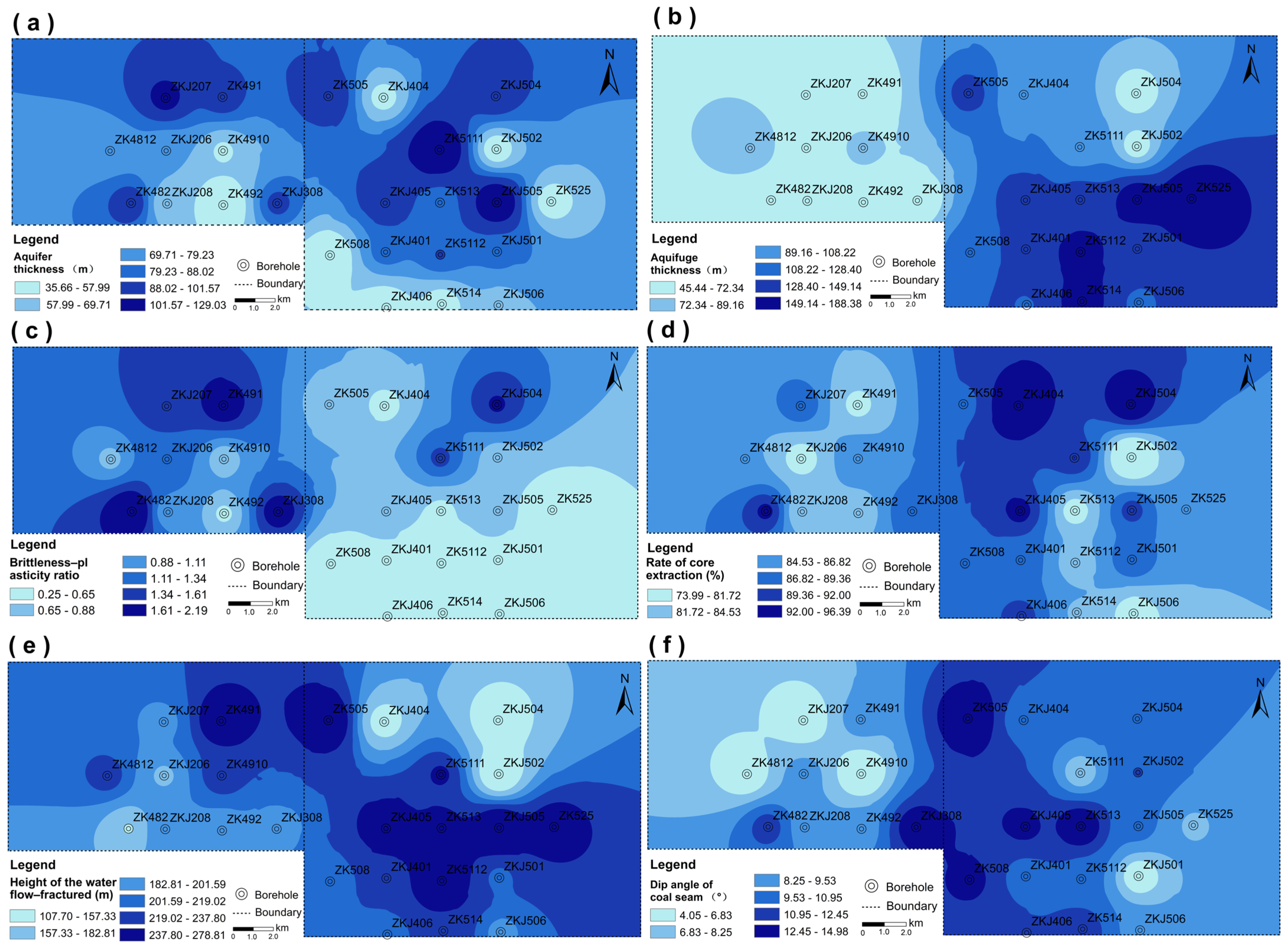
- Aquifer thickness. The arenaceous rock layer’s thickness is a critical factor affecting an aquifer’s water richness. Sandstone has a good permeability and a high porosity: the greater its thickness, the greater its water–holding capacity, and the greater the water richness of the aquifer [22]. Therefore, the thickness of sandstone in the fracture zone indicates the aquifer’s water richness. From Figure 4a, it can be observed that the aquifer’s thickness is greater in Area I and in the upper section of Area II.
- (2)
- Aquifuge thickness. Mudstone and sandy mudstone, which are plastic rocks, typically exhibit low levels of strength and hardness but possess excellent plasticity and sealing properties [23]. Therefore, the cumulative thickness of plastic rocks in the caving zone indicates their water barrier strength. From Figure 4b, it can be seen that the thickness of the confining bed is greater in the middle of Area II.
- (3)
- Brittleness–plasticity ratio. The brittleness–plasticity ratio can reflect the mechanical properties and stability of the entire rock formation. Generally speaking, brittle rocks are more prone to breakage and fracture, while plastic rocks are more likely to deform and slide. Therefore, a roof with a sizeable brittleness–plasticity ratio is more likely to crack and fracture during mining, resulting in an increased risk of roof water inrush [24]. From Figure 4c, it can be seen that the western part of Area I exhibits a higher brittleness–plasticity ratio, while Area II has a relatively consistent brittleness–plasticity ratio.
- (4)
- Rate of core extraction. The rate of core extraction refers to the ratio of the actual core length to the drilling length during the drilling process. Through core observation, we can evaluate the stability of the top slab by analyzing its integrity, lithological changes, and fracture development. A higher core sampling rate typically indicates a more complex and less stable top slab structure, which increases the likelihood of water inrush. Conversely, a lower rate indicates a reduced chance of this phenomenon [25]. Figure 4d shows that the high core extraction rate is mainly concentrated in the central parts of Area I and Area II.
3.1.2. Mining Disturbance Factors
- (1)
- Height of the water flow–fractured zone. As the thickness of the mined coal seam increases, so does the height of the water flow–fractured zone. This increases the likelihood of intersecting with the overlying aquifer and causing severe water inrush [26].
- (2)
- Dip angle of the coal seam. Generally, a larger coal seam inclination results in stronger sliding pressure and tension during mining. This increases the disturbance to the roof and the rated stresses on the overlying coal seam, making the roof’s rock more prone to misalignment and fragmentation, leading to water inrush [28]. Figure 4f shows that the upper–left coal seam dip angle of Area II is relatively large.
3.2. Determination of the Influence Weight of Each Main Control Factor
3.2.1. Analytic Hierarchy Process
3.2.2. Entropy Method
3.2.3. Game Theory Combination Weighting
3.3. Compatibility Test
4. Results
4.1. Normalization of Index Data
4.2. Risk Zoning and Evaluation
5. Discussion
6. Conclusions
- (1)
- According to the complex mining geological conditions of Dananhu Coal Mine No. 7, the height of the water flow–fractured zone, the aquifer thickness, the aquifuge thickness, the brittleness–plasticity ratio, the rate of core extraction, and the dip angle of the coal seam were selected as the leading causes of water inrush against the roof control factors of Coal Seam No. 7th.
- (2)
- The AHP and entropy methods were used to determine the subjective and objective weights. Game theory analysis was used to coordinate the competitive yet consistent relationship between the two evaluation methods, obtaining the combined weights of each influencing factor and compensating for the shortcomings of a single weighting method, and the final prediction results were more realistic. According to the final results, the dangerous zone is mainly located in the Area I of the mine, while Area II mostly consists of safe and safer zones; therefore, there is a greater possibility of roof water inrush occurring during the mining of Coal Seam No. 7 in Area I, which requires greater attention.
- (3)
- The roof water inrush hazard zoning obtained by overlaying the above–discussed six evaluation indices with weights suitable for the conditions of this mine area is consistent with the actual situation. The accuracy of the evaluation results is high, which means that this method can be used for hydrological assessment of coal mines with similar geological conditions.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bukowski, P. Water Hazard Assessment in Active Shafts in Upper Silesian Coal Basin Mines. Mine Water Environ. 2011, 30, 302–311. [Google Scholar] [CrossRef]
- Zhang, P.; Dong, Y.; Zhang, X.; Xu, D. Statistical law analysis and forecast of coal mine water disaster accidents in China from 2008 to 2021. Coal Eng. 2022, 54, 131–137. [Google Scholar]
- Jin, D.; Liu, Y.; Liu, Z.; Cheng, J. New Progress of Study on Major Water Inrush Disaster Prevention and Control Technology in Coal Mine. Coal Sci. Technol. 2013, 41, 25–29. [Google Scholar] [CrossRef]
- Zhang, R.; Jiang, Z.; Zhou, H.; Yao, C.; Xiao, S. Groundwater outbursts from faults above a confined aquifer in the coal mining. Nat. Hazards 2014, 71, 1861–1872. [Google Scholar] [CrossRef]
- Yin, S.; Zhang, J.; Liu, D. A study of mine water inrushes by measurements of in situ stress and rock failures. Nat. Hazards 2015, 79, 1961–1979. [Google Scholar] [CrossRef]
- Liu, X.; Wang, S. Mine Water Inrush Forecasting during the Mining under Waters. Disaster Adv. 2012, 5, 876–881. [Google Scholar]
- Mao, H.; Liu, Z.; Deng, C.; Wang, D. Discussion of forecasting methods for coal mining water–inrush. Hebei J. Ind. Sci. Technol. 2008, 25, 4. [Google Scholar]
- Wang, G.; Wang, X.; Li, j.; Huang, B.; Cheng, S.; Zhao, C.; Liu, G. Identification model of gushing water sources in Pingdingshsn coal mines. Coal Geol. Explor. 1998, 26, 48–51. [Google Scholar]
- Liu, Y.; Qiu, H.; Kamp, U.; Wang, N.; Wang, J.; Huang, C.; Tang, B. Higher temperature sensitivity of retrogressive thaw slump activity in the Arctic compared to the Third Pole. Sci. Total Environ. 2024, 914, 170007. [Google Scholar] [CrossRef]
- Wu, Q.; Huang, X.; Dong, D.; Yin, Z.; Li, J.; Hong, Y.; Zhang, H. “Three maps–two predictions” method to evaluate water bursting conditions on roof coal. J. China Coal Soc. 2000, 2000, 62–67. [Google Scholar] [CrossRef]
- Wu, Q.; Liu, Y.; Zhou, W.; Li, B.; Zhao, B.; Liu, S.; Sun, W.; Zeng, Y. Evaluation of water inrush vulnerability from aquifers overlying coal seams in the menkeqing coal mine, China. Mine Water Environ. 2015, 34, 258–269. [Google Scholar] [CrossRef]
- Zeng, Y.; Wu, Q.; Liu, S.; Zhai, Y.; Lian, H.; Zhang, W. Evaluation of a coal seam roof water inrush: Case study in the Wangjialing coal mine, China. Mine Water Environ. 2018, 37, 174–184. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, T. Study of a roof water inrush prediction model in shallow seam mining based on an analytic hierarchy process using a grey relational analysis method. Arab. J. Geosci. 2018, 11, 153. [Google Scholar] [CrossRef]
- Fan, G.; Zhang, S.; Zhang, D.; Zhang, C.; Chen, M.; Li, Q. An Index of Aquiclude Destabilization for Mining–Induced Roof Water Inrush Forecasting: A Case Study. Water 2019, 11, 2170. [Google Scholar] [CrossRef]
- Ruan, Z.; Li, C.; Wu, A.; Wang, Y. A New Risk Assessment Model for Underground Mine Water Inrush Based on AHP and D–S Evidence Theory. Mine Water Environ. 2019, 38, 488–496. [Google Scholar] [CrossRef]
- Sun, Z.; Bao, W.; Li, M. Comprehensive Water Inrush Risk Assessment Method for Coal Seam Roof. Sustainability 2022, 14, 10475. [Google Scholar] [CrossRef]
- Yu, W.; Qian, J.; Ma, L.; Zhao, W.; Zhou, X. The water inrush risk assessment of roof of seam 13–1 in Xieqiao mine based on GIS and AHP. Coal Geol. Explor. 2016, 44, 69–73. [Google Scholar]
- Yin, H.; Shi, Y.; Niu, H.; Xie, D.; Wei, J.; Lefticariu, L.; Xu, S. A GIS based model of potential groundwater yield zonation for a sandstone aquifer in the Juye Coalfeld, Shandong, China. J. Hydrol. 2018, 557, 434–447. [Google Scholar] [CrossRef]
- Lu, Q.; Li, X.; Li, W.; Chen, W.; Li, L.; Liu, S. Risk Evaluation of Bed–Separation Water Inrush: A Case Study in the Yangliu Coal Mine, China. Mine Water Environ. 2018, 37, 288–299. [Google Scholar] [CrossRef]
- Li, B.; Wei, T.; Liu, Z. Construction of evaluation index system for water abundance of karst aquifers and risk assessment of water inrush on coal seam roof in Southwest China. J. China Coal Soc. 2022, 47, 152–159. [Google Scholar] [CrossRef]
- Xu, Z.; Gao, S.; Cui, S.; Sun, Y.; Chen, Z.; Wu, J. Hydro–geological basic and practice for water–preserved mining in ecologically vulnerable area: A case study in Hami coalfield. J. China Coal Soc. 2017, 42, 80–87. [Google Scholar] [CrossRef]
- Ding, H.; Zhan, R.; Li, H.; Sun, G.; Chen, X.; Gu, C. Risk assessment of water inrush from roof of 11–2 coal seam in Xinji Mining Area based on AHP and GIS. Coal Sci. Technol. Mag. 2022, 43, 87–93. [Google Scholar]
- Xie, D.; Han, J.; Zhang, H.; Wang, K.; Du, Z.; Miao, T. Risk Assessment of Water Inrush from Coal Seam Roof Based on Combination Weighting–Set Pair Analysis. Sustainability 2022, 14, 11978. [Google Scholar] [CrossRef]
- Wang, Y.; Jiang, J. The application of the ratio on brittle and tenacity terrane in the analysis of causes of fault formation. J. Henan Polytech. Univ. 2001, 2001, 342–346. [Google Scholar]
- Feng, S.; Wu, Q. Research on water—Richness of aquifer using comprehensive weight method based on AHP and variation coefficient. Coal Eng. 2016, 48, 138–140. [Google Scholar]
- Zhang, S.; Tang, S.; Zhang, D.; Fan, G.; Wang, Z. Determination of the Height of the Water–Conducting Fractured Zone in Difficult Geological Structures: A Case Study in Zhao Gu No. 1 Coal Seam. Sustainability 2017, 9, 1077. [Google Scholar] [CrossRef]
- Liu, S.; Li, W.; Wang, Q. Height of the Water–Flowing Fractured Zone of the Jurassic Coal Seam in Northwestern China. Mine Water Environ. 2018, 37, 312–321. [Google Scholar] [CrossRef]
- Qu, W.; Li, B.; Li, H.; Niu, L. Study on Risk Assessment Methods for Coal Seam Roof Water Disaster in Southwestern Karst Area Based on Fuzzy Analytical Hierarchy Process. Min. Saf. Environ. Prot. 2014, 41, 59–62. [Google Scholar]
- Rezaei, J. Best–worst multi–criteria decision–making method. Omega–Int. J. Manag. Sci. 2015, 53, 49–57. [Google Scholar] [CrossRef]
- Xiao, L.; Fan, L.; Chao, N.; Dai, L.; Qian, Q.; Lin, C. Evaluation of Water Inrush Hazard in Coal Seam Roof Based on the AHP–CRITIC Composite Weighted Method. Energies 2023, 16, 114. [Google Scholar] [CrossRef]
- Liu, W.; Sun, Q.; Xu, B. Risk Evaluation of Water Inrush from Coal Seam Floor Based on GIS and Principal Component Analysis Entropy Weight Method. Min. Res. Dev. 2020, 40, 83–88. [Google Scholar] [CrossRef]
- Xue, J.; Shi, L.; Wang, H.; Ji, Z.; Shang, H.; Xu, F.; Zhao, C.; Huang, H.; Luo, A. Water abundance evaluation of a burnt rock aquifer using the AHP and entropy weight method: A case study in the Yongxin coal mine, China. Environ. Earth Sci. 2021, 80, 417. [Google Scholar] [CrossRef]
- Omrani, H.; Shafaat, K.; Emrouznejad, A. An integrated fuzzy clustering cooperative game data envelopment analysis model with application in hospital efficiency. Expert Syst. Appl. 2018, 114, 615–628. [Google Scholar] [CrossRef]
- Peng, J.; Zhang, J. Urban flooding risk assessment based on GIS– game theory combination weight: A case study of Zhengzhou City. Int. J. Disaster Risk Reduct. 2022, 77, 103080. [Google Scholar] [CrossRef]
- Yu, X.; Wang, D.; Shi, L.; Meng, M. Water–richness Evaluation Method of Water–filled Aquifer Characteristics Analysis Based on Evaluation Method. Coal Technol. 2016, 35, 152–154. [Google Scholar] [CrossRef]



| A | B1 | B2 | Eigenvector | Weight | CI | CR |
|---|---|---|---|---|---|---|
| B1 | 1 | 1/2 | 0.667 | 0.3333 | 0 | none |
| B2 | 2 | 1 | 1.333 | 0.6667 |
| B1 | C1 | C2 | C3 | C4 | Eigenvector | Weight | CI | CR |
|---|---|---|---|---|---|---|---|---|
| C1 | 1 | 2 | 3 | 1/3 | 1.088 | 0.2721 | 0.087 | 0.097 |
| C2 | 1/2 | 1 | 2 | 1/2 | 0.750 | 0.1874 | ||
| C3 | 1/3 | 1/2 | 1 | 1/2 | 0.499 | 0.1248 | ||
| C4 | 3 | 2 | 2 | 1 | 1.663 | 0.4157 |
| B2 | C5 | C6 | Eigenvector | Weight | CI | CR |
|---|---|---|---|---|---|---|
| C5 | 1 | 3 | 1.5 | 0.75 | 0 | none |
| C6 | 1/3 | 1 | 0.5 | 0.25 |
| Main Controlling Factors | Aquifer Thickness | Aquifuge Thickness | Brittleness–Plasticity Ratio | Rate of Core Extraction | Height of Water Flow–Fractured Zone | Dip Angle of Coal Seam |
|---|---|---|---|---|---|---|
| AHP Weight | 0.0907 | 0.0625 | 0.0416 | 0.1386 | 0.5000 | 0.1667 |
| Entropy Weight | 0.1870 | 0.0904 | 0.4060 | 0.1567 | 0.0518 | 0.1081 |
| Main Control Factors | Aquifer Thickness | Aquifuge Thickness | Brittleness–Plasticity Ratio | Rate of Core Extraction | Height of Diversion Fissure Zone | Dip Angle of Coal Seam |
|---|---|---|---|---|---|---|
| Comprehensive weight | 0.1354 | 0.0754 | 0.2109 | 0.1470 | 0.2918 | 0.1395 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Q.; Xu, J.; Wang, Q.; Li, W. Risk Assessment of Water Inrush from Coal Seam Roof Based on the Combined Weighting of the Geographic Information System and Game Theory: A Case Study of Dananhu Coal Mine No. 7, China. Water 2024, 16, 710. https://doi.org/10.3390/w16050710
Liu Q, Xu J, Wang Q, Li W. Risk Assessment of Water Inrush from Coal Seam Roof Based on the Combined Weighting of the Geographic Information System and Game Theory: A Case Study of Dananhu Coal Mine No. 7, China. Water. 2024; 16(5):710. https://doi.org/10.3390/w16050710
Chicago/Turabian StyleLiu, Qingtao, Jie Xu, Qiqing Wang, and Wenping Li. 2024. "Risk Assessment of Water Inrush from Coal Seam Roof Based on the Combined Weighting of the Geographic Information System and Game Theory: A Case Study of Dananhu Coal Mine No. 7, China" Water 16, no. 5: 710. https://doi.org/10.3390/w16050710
APA StyleLiu, Q., Xu, J., Wang, Q., & Li, W. (2024). Risk Assessment of Water Inrush from Coal Seam Roof Based on the Combined Weighting of the Geographic Information System and Game Theory: A Case Study of Dananhu Coal Mine No. 7, China. Water, 16(5), 710. https://doi.org/10.3390/w16050710






