Abstract
Contextualizing historic hydroclimate variability in the southeastern USA has relied significantly on proxy indicators such as tree-ring data, and while previous studies have reconstructed total precipitation, less is known about the historic variability of intense rainfall events, which are climatologically and ecologically important and distinct from non-intense rainfall events. Here, a combined longleaf pine and shortleaf pine adjusted latewood chronology spanning 1770–2020 was used to reconstruct July–September total precipitation and intense rainfall event precipitation in central North Carolina, USA. The adjusted latewood chronology explains 46% of the variance in July–September total precipitation and 37% of the variance in July–September intense rainfall event precipitation during the 1940–2020 instrumental period with intense rainfall event precipitation amounts comprising 52% of total precipitation amounts. The models provide context about historic hydroclimate variability at this location and suggest overall stability in both total and intense rainfall event precipitation amounts during the instrumental and reconstruction periods with three identical significant regime shifts during 1770–2020: 1770–1935, 1936–1959 (above-average moisture), 1960–2020 (below-average moisture). To compare model strength, the models were split into early (1940–1980) and late (1981–2020) analysis periods with the intense rainfall event precipitation model exhibiting greater skill during the early analysis period. The early analysis period has a greater frequency and magnitude of intense rainfall events, and these results suggest the influence of intense rainfall event precipitation on latewood growth and the potential susceptibility of reconstruction models to decreased skill and/or error with differing frequencies of extreme events, a finding of particular importance to future dendroclimatic research.
1. Introduction
Tree-ring data have contextualized historic hydroclimate variability in the southeastern USA by reconstructing precipitation and precipitation-related variables (e.g., [1,2,3,4,5,6,7,8,9], but none of these studies have examined the variability of intense rainfall events, which may be ecologically important for native tree species (e.g., longleaf pine (Pinus palustris) [10]). Specifically, a multi-century May precipitation reconstruction was inferred from eastern redcedar (Juniperus virginiana) tree-ring data in eastern West Virginia during 1200–1997 [1], a multi-species reconstruction analyzed drought variability in the Apalachicola–Chattahoochee–Flint river basin during 1665–2010 [2], and a longleaf pine tree-ring chronology reconstructed tropical cyclone precipitation during 1 June–15 October during 1771–2014 in coastal North Carolina [4]. Similarly, chestnut oak (Quercus prinus) tree-ring data reconstructed May–June precipitation during 1750–1981 in southwestern Virginia [3], a multi-species chronology reconstructed the Flint River May–September streamflow in Georgia during 1675–2000 [6], and mean March–October Suwanee River discharge was reconstructed during 1550–2005 [5]. Recently, a multi-species chronology reconstructed May–July Tennessee Valley streamflow during various periods from the late 1600s to the present [11], and longleaf pine chronologies reconstructed July–September quasi-stationary precipitation in central North Carolina during 1790–2018 [7], tropical cyclone precipitation in the North Carolina coastal plain during 1750–2015 [8], and Gulf coastal plain tropical cyclone precipitation during 1540–2012 [9]. These studies [1,2,3,4,5,6,7,8,9,11] indicate a nuanced contextualization of historic hydroclimate variability in the region such that some reconstructions indicate that the twentieth century (1900–2000) included the most extreme pluvials (e.g., [1,3]), while other reconstructions indicate that twentieth century pluvials were not unique when viewed over the longer-term reconstructed timescales [5].
Despite the recent focus on dendroclimatic research on specific precipitation event types (e.g., convective, frontal, tropical cyclone), few studies have isolated the relative contributions to radial growth by precipitation type in the southeastern USA (e.g., [4,7,8,9,12]). Absent this information, understanding of the interannual variability of radial growth can be confounded. For example, if the radial growth of a species is principally influenced by intense, ground-soaking precipitation events, the climate response could differ between two years with the same amount of precipitation, but delivered differently (i.e., one year with fewer intense events, one year with more events, but less-intense events). Absent making these distinctions, it is not possible to confirm if inferred reconstructed periods of either dry or wet conditions are accurate or are an artifact of changes in precipitation types that promote, for example, soil-soaking events. For example, in central North Carolina, USA, several “drought” years, inferred by narrow ring-widths of longleaf pine, were years with reduced intense precipitation, but not overall precipitation [10].
Intense or extreme rainfall events can occur throughout the year in the southeastern USA, but the type of event exhibits seasonality. The primary event types comprising extreme rainfall are produced via tropical cyclones (summer, early fall), extratropical waves and mid-latitude cyclones (fall through spring), and convective systems (spring through early fall) [13]. During 2002–2011, tropical extreme precipitation events had larger spatial distributions, produced more rainfall, and had greater longevity when compared to the more frequent non-tropical extreme precipitation events in the southeastern USA [13]. Non-tropical extreme precipitation events were better associated with thermodynamic conditions during summer rather than broad-scale dynamical patterns, suggesting the importance of convectively derived rainfall in summer [13]. Much of the southeastern USA experienced decreased annual precipitation during 1901–2015, while the frequency and intensity of extreme events have increased [14]. Further reductions in annual precipitation are projected, with increases in extreme event intensity and frequency through the 21st century under all emission scenarios [14]. However, some models project no changes in annual precipitation, with significant increases in summer (July–August) precipitation and a maximum 1-day precipitation amount [15], while other models suggest no changes to slight decreases in summer total precipitation amounts in the southeastern USA [16]. As some projections indicate decreases in total precipitation and increases in extreme precipitation events (e.g., [14]), it is possible that although overall precipitation has decreased, radial growth may increase as the modality of precipitation which most influences radial growth will be increasing (e.g., [10]). The inconclusiveness of future extreme-rainfall model projections suggests that a better understanding of inherent variability in the hydroclimate system can be gained from backward modeling using tree-ring data, which could lead to better data inputs into future projections. Improvements in tree-ring precipitation reconstructions coupled with an improved understanding of the physical dynamics of precipitation variability could lead to increased model performance, particularly as it relates to intense rainfall events.
Here, to develop a better understanding of summer rainfall variability based on type (i.e., intense vs total precipitation), we reconstruct IRE and total precipitation from 1770–2020 using a combined longleaf pine and shortleaf pine adjusted latewood chronology. We then compare the reconstructions and contextualize the phases during this time using regime shift analysis to determine the frequency of IRE phases and long-term variability in total summer precipitation over a 250-year period.
2. Methods
2.1. Tree-Ring Data
We combined longleaf pine and shortleaf pine (Pinus echinata Mill.) chronologies from previous work in the Uwharrie Mountains (35.411, −80.061) [12] to produce a multi-species chronology following standard dendroclimatological field methods. We selected co-occurring longleaf pine and shortleaf pine trees for use in analyses as both species have significant radial growth sensitivity to intense rainfall events and respond best to the same months of precipitation at this location in the Uwharrie Mountains [12]. We used COFECHA [17] to assess crossdating accuracy. The combined pine chronology contains 98 cores from 47 longleaf pine and 25 shortleaf pine trees, with a series intercorrelation of 0.574, a mean sensitivity of 0.477, and a mean series length of 116.8 years. The chronology spans 1740–2020, with an EPS > 0.80 during 1770–2020 [18,19]. We used ARSTAN [17] and dplR [19] to create a standardized chronology after testing multiple detrending options (i.e., spline, mean-value, autoregressive, Friedman, Hugershoff). We found that negative exponential detrending produces the best climate signal with latewood growth, similar to other work in this region and with this species (e.g., [20]). We adjusted the negative exponential latewood chronology to control for the potential influence of earlywood on latewood variance [21].
2.2. Climate Data
We collected July–September daily precipitation data from 1940–2020 from weather stations that are near (i.e., <70 km) the Uwharrie Mountains that have a high degree of data completeness (i.e., >95%). We selected July–September data, as previous research suggests that longleaf pine and shortleaf pine radial growth best correlate with July–September precipitation at this location (e.g., [12]). The selected weather stations were Albemarle, North Carolina (ID: USC00310090), Randleman, North Carolina (USC00317097), and Siler City, North Carolina (USC00317924) [22]. We calculated July–September intense rainfall event (IRE) frequency and IRE rainfall amount by selecting a subset of total July–September precipitation data where the daily (i.e., 24-h) precipitation amount was >2.0 standard deviations over the long-term, 1940–2020, mean (cf. [10,12]).
2.3. Statistical Analyses and Climate Reconstruction
We calculated simple linear regression models for reconstruction using the base ‘lm’ function in R version 4.2.0 with the combined pine adjusted latewood and (1) July–September total precipitation, (2) July–September IRE precipitation, and (3) non-IRE precipitation. We assessed the validity of the regression models with Cook’s distance values using the ‘cooks.distance’ function in R version 4.2.0 and leave-one-out cross-validation root-mean-square error (RMSE) values using the ‘train’ function in the ‘caret’ R package [23], a Durbin–Watson test to assess the degree of autocorrelation using the ‘dwtest’ function in the ‘lmtest’ R package [24], a Nash–Sutcliffe model efficiency statistic using the ‘vnse’ function in the ‘ie2misc’ R package [25], and a 30-year moving correlation analysis using the ‘dcc’ function in the ‘dplR’ R package [26]. To further assess the reconstructed values, we compared the distribution of observed and reconstructed total precipitation and IRE precipitation values using the ‘descdist’ function in the ‘fitdistrplus’ R package [27] with the ‘boot’ parameter set to 100 to produce 100 bootstrapped distribution estimates.
We used regime shift analysis with a 10-year cutoff length and an α = 0.05 using the ‘Rodionov’ function in the ‘rshift’ R package [28] to examine and compare long-term phases of the reconstructed IRE and total precipitation values. Additionally, we correlated each precipitation variable with time (year) to examine precipitation stability. Further, we split the analysis periods into an early period (1940–1980) and late period (1981–2020) to examine the IRE and total precipitation—latewood models. Specifically, we examined the mean values of IRE precipitation, total precipitation, adjusted latewood, and the correlations between these variables during the early and late periods.
3. Results
The combined pine adjusted latewood chronology is significantly associated with July–September (JAS) total precipitation (r = 0.678, 95% CI: 0.540–0.781, p < 0.0001), JAS IRE precipitation (r = 0.608, 95% CI: 0.450–0.730, p < 0.0001), and JAS non-IRE precipitation (r = 0.271, 95% CI: 0.056–0.462, p < 0.05) during 1940–2020. The JAS non-IRE precipitation model was not robust enough for reconstruction, while the other two variables were reconstructed during 1770–2020.
The JAS total precipitation reconstruction was calculated by:
where y is JAS total precipitation and x is combined pine adjusted latewood. The model explains 46% of the variance in JAS total precipitation during the 1940–2020 instrumental period, has an RMSE value of 82.18 (fit) and 84.46 (LOOCV) and a Durbin–Watson value of 2.03 suggesting little to no significant autocorrelation [29] and an overall skilled fit. The maximum Cook’s distance value was 0.141, suggesting no undue influence of any individual observation on the overall model. The Nash–Sutcliffe model efficiency statistic for the JAS total precipitation model is 0.460 suggesting sufficient predictive skill (i.e., a value > 0). The 100 bootstrapped distribution test suggests that the observed precipitation values best approximate a normal distribution with an estimated skewness value of 0.64 and an estimated kurtosis value of 3.06. Similarly, the bootstrapped reconstructed precipitation values best approximate a normal distribution with an estimated skewness value of 0.74 and an estimated kurtosis value of 3.07. The observed mean JAS total precipitation was 346.9 mm during 1940–2020 and the reconstructed mean JAS total precipitation was 349.4 during 1770–2020 (Table 1, Figure 1) suggesting long-term stability in mean precipitation at this location.
y = 263.31(x) + 85.44

Table 1.
Mean observed precipitation, mean reconstructed precipitation, coefficient of determination (R2), RMSE for the model fit and RMSE for the LOOCV model fit, and Durbin–Watson values for the IRE precipitation- and total precipitation-adjusted latewood regression models.
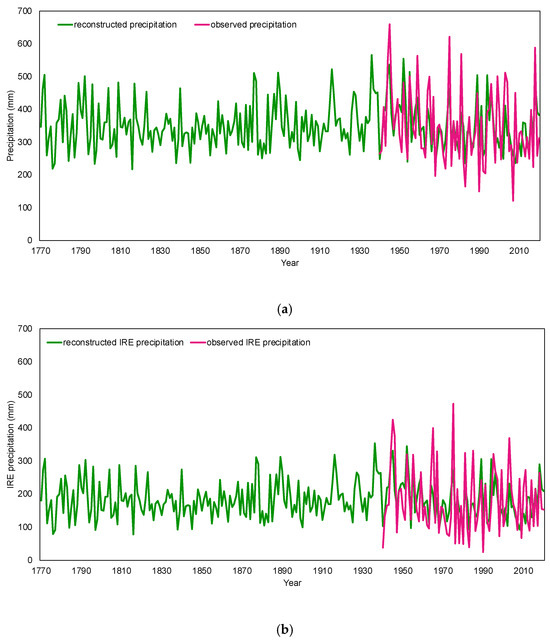
Figure 1.
Total precipitation (a) and IRE precipitation (b) during 1940–2020 (observed, purple lines) and 1770–2020 (reconstructed, green lines). IRE Precipitation accounts for 52% of the total precipitation during the observed instrumental period and 52% during the reconstruction period.
The JAS IRE precipitation reconstruction was calculated by:
where y is JAS IRE precipitation and x is combined pine adjusted latewood. The model explains 37% of the variance in IRE precipitation and has an RMSE value of 78.26 (fit) and 80.25 (LOOCV) with a Durbin–Watson value of 2.11 (Table 1), suggesting little to no autocorrelation [29] and an overall skilled fit, similar to the JAS total precipitation model. The maximum Cook’s distance value for the model was 0.142, again suggesting no undue influence of any individual observation on the overall model. The Nash–Sutcliffe model efficiency statistic for the JAS IRE precipitation model is 0.370 suggesting sufficient predictive skill (i.e., a value > 0) and a slight decrease when compared to the model efficiency statistic for the total precipitation model (0.460). The bootstrapped distribution test suggests that observed IRE precipitation values best approximate a normal distribution with an estimated skewness value of 0.77 and an estimated kurtosis value of 3.08. Similar to reconstructed total precipitation values, the bootstrapped reconstructed IRE precipitation values best approximate a normal distribution with an estimated skewness value of 0.74 and an estimated kurtosis value of 3.07. During 1940–2020, observed mean JAS IRE precipitation was 180.8 mm, while the reconstructed mean JAS IRE precipitation was 182.8 mm during 1770–2020, again suggesting long-term stability in mean IRE precipitation at this location. IRE Precipitation comprises 52% of the total precipitation during the observed instrumental period (1940–2020) and comprises 52% of total precipitation during the reconstruction period (1770–2020).
y = 208.31(x) − 26.08
Despite interannual variability, IRE precipitation and total precipitation have no significant (p < 0.05) trend with time (year) during the observed study period of 1940–2020. Further, the correlation between total precipitation and IRE precipitation remains significant (p < 0.05) with the combined pine adjusted latewood chronology during each of the evolving 30-year windows of 1940–2020 except for the most recent 1991–2020 window for IRE precipitation (Figure 2). The mean correlation of the 52 30-year moving windows between adjusted latewood and total precipitation is 0.620, while the mean correlation between IRE precipitation and adjusted latewood is 0.577 (Table 2, Figure 2).
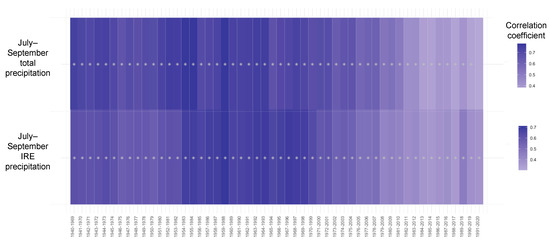
Figure 2.
Thirty-year moving window correlations between the adjusted latewood chronology and JAS total and IRE precipitation. The correlation between total precipitation and IRE precipitation remains significant (p < 0.05, asterisk) with the combined pine adjusted latewood chronology for all windows except the most recent 1991–2020 window for IRE precipitation.

Table 2.
Minimum, maximum, mean, and median values for the 52 30-year moving window correlations (r) between the adjusted latewood chronology and JAS IRE and total precipitation during 1940–2020.
Similarly, over the longer-term reconstructed time-period (i.e., 1770–2020), the reconstructed values of total precipitation and IRE precipitation have remained stable with no significant correlation with time (year). The total precipitation and IRE precipitation reconstructions have the same significant regime shifts during the reconstruction period (Figure 3): 1770–1935, 1936–1959 (above-average moisture), and 1960–2020 (below-average moisture). The mean total precipitation values for each regime are 347.45 mm (1770–1935), 409.70 mm (1936–1959), and 331.11 mm (1960–2020) while the mean IRE precipitation values for each regime are 181.20 mm (1770–1935), 230.45 mm (1936–1959), and 168.27 mm (1960–2020), suggesting that IRE and total precipitation has been mostly stable since 1770 with the exception of the 1936–1959 regime period. The IRE:Total precipitation ratio varies over time with the observed regimes and each regime is significantly different from each other (ANOVA F = 8.252, p < 0.001), with values of 52.2% (1770–1935), 56.2% (1936–1959), and 50.8% (1960–2020). Variability in the IRE:Total precipitation ratio was influenced by below-mean IRE precipitation (181.20 mm) and below-mean total precipitation (347.45 mm, Table 3) during the 1770–1935 regime period, above-mean IRE precipitation (230.45 mm) and above-mean total precipitation (409.70 mm, Table 3) during the 1936–1959 regime period, and by below-mean IRE precipitation (168.27 mm) and below-mean total precipitation (331.11 mm, Table 3) during the 1960–2020 regime period.
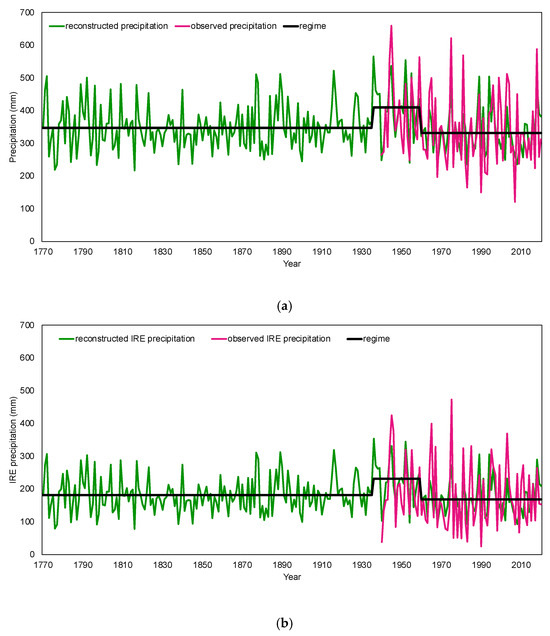
Figure 3.
Total precipitation (a) and IRE precipitation (b) reconstructions with significant regime shifts (black line, 1770–1935, 1936–1959 (above-average moisture), 1960–2020 (below-average moisture)) during 1770–2020. The IRE:Total precipitation ratio varies over time with the regime shifts, with values of 52.2% (1770–1935), 56.2% (1936–1959), and 50.8% (1960–2020).

Table 3.
Mean IRE precipitation, total precipitation, and the ratio of IRE:Total precipitation during the three regimes identified by regime shift analysis during 1770–2020: 1770–1935, 1936–1959, 1960–2020.
4. Discussion
Despite no significant relationship with time (year) in either the reconstruction models during 1770–2020 or with the observational models of 1940–2020, split-sample analyses give finer-scale insight into the total precipitation and IRE precipitation models. During the early analysis period (1940–1980), the total precipitation and IRE precipitation models have similar explanatory power such that the IRE precipitation model explains 53.6% (r = 0.732) of the adjusted latewood variance, while the total precipitation model explains 57.5% (r = 0.758, Table 4). The ratio of variance explained between the two models (i.e., IRE precipitation correlation coefficient divided by the total precipitation correlation coefficient) is 96.6% during the early period suggesting the IRE model has similar explanatory power despite IRE precipitation accounting for 50.7% of the total precipitation amounts during 1940–1980.

Table 4.
Correlation between adjusted latewood and IRE precipitation and total precipitation, the explanatory ratio (IRE precipitation model correlation/Total precipitation model correlation), and mean latewood values during the early (1940–1980) and late (1981–2020) split-sample analysis periods.
The late analysis period of 1981–2020 has greater differences between the adjusted latewood models such that the IRE precipitation model explains 18.5% (r = 0.430) of variance while the total precipitation model explains 31.0% (r = 0.556, Table 4). The explanatory ratio during the late period is 77.3%, a marked decrease from the 96.6% ratio during the early analysis period. We suggest the difference between the early and late analysis period relates to a threshold reported in earlier research at this study location [10], with the late period characterized by fewer years with high (>5 IREs/summer) IRE occurrence (Figure 4). During the early analysis period of 1940–1980, IRE frequency exceeded the 5 IREs/summer threshold on 10 occurrences, whereas during the late period of 1981–2020, IRE frequency exceeds the threshold on 9 occurrences, with smaller maximum values. The mean IRE frequency per summer during high (>5 IREs/summer) IRE years is 7.23 IREs/summer during the early period (n = 10) and 5.89 IREs/summer during the late period (n = 9, Figure 4). Further, the amount of IRE precipitation during high (>5 IREs/summer) IRE years differs between the early and late analysis periods such that the mean precipitation value is 115.18 mm during the early period and 89.11 mm during the late period, suggesting the early period had more intense, ground-soaking rainfall events that are influential for tree radial growth [10]. These results suggest that model explanatory power, and latewood sensitivity, to extreme precipitation events is dependent on the frequency and magnitude of intense rainfall events.
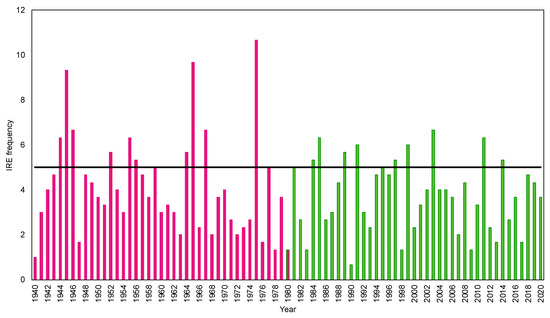
Figure 4.
IRE frequency (Y-axis) per year (X-axis) during 1940–2020. During the early analysis period of 1940–1980 (purple bars), IRE frequency exceeded the 5 IREs/summer threshold (black line) 10 times, whereas during the late period of 1981–2020 (green bars), IRE frequency exceeded the threshold (black line) 9 times, with smaller maximum values.
In addition to the high (>5 IREs/summer) IRE threshold, we analyzed thresholds in IRE frequency defined by +/−1.00 and +/−2.00 standard deviation thresholds during the early and late analysis periods. During the early period (1940–1980), IRE frequency exceeded +1.00 standard deviation on seven occasions while IRE frequency exceeded the +1.00 standard deviation threshold on five occasions during the late analysis period (Figure 5). IRE frequency exceeds the +2.00 standard deviation threshold on three occasions during the early period and on no occurrences during the late period, again suggesting the influence of high-frequency IRE years on overall adjusted latewood model strength (i.e., early period r = 0.732, late period r = 0.430). Similarly, IRE frequency is less than the −1.00 standard deviation threshold on five occasions during the early period and on six occurrences during the late analysis period. There are no values of IRE frequency below the −2.00 standard deviation threshold (Figure 5), likely because the IRE frequency distribution is skewed due to a fixed minimum value of IREs/summer (i.e., 1) and no theoretic maximum value.
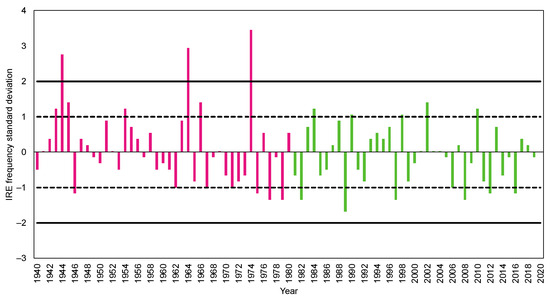
Figure 5.
IRE frequency standard deviation (Y-axis) per year (X-axis) during 1940–2020 and standard deviation thresholds of +/−2.00 (solid black lines) and +/−1.00 (dashed black lines). During the early analysis period (1940–1980, purple bars), IRE frequency exceeded +1.00 standard deviation on 7 occasions and IRE frequency exceeded +1.00 standard deviation threshold on 5 occurrences during the late analysis period (green bars). IRE frequency exceeds the +2.00 standard deviation threshold on 3 occasions during the early period and on no occurrences during the late period.
The differences in IRE precipitation model strength between the early and late analysis periods, particularly the greater occurrence of +1.00 and +2.00 standard deviation IRE frequency years during the early period, are supported by other research at this location in the Uwharrie Mountains [30]. When latewood–precipitation models were compared between models that include all precipitation years and reduced models that include only above-average (i.e., >+1.00 standard deviations) and below-average (i.e., <−1.00 standard deviations) precipitation years, the correlation between longleaf pine latewood and precipitation is significantly greater during above-average and below-average years when compared to the model that includes all years [30] suggesting the importance of non-average precipitation years on overall model strength. Conversely, the shortleaf pine latewood–precipitation models had no significant differences when comparing different precipitation combinations [30], suggesting that IRE precipitation–latewood growth responses are species dependent [12]. Here, our results suggest that IRE precipitation–latewood models perform better when the magnitude and frequency of intense rainfall events are greater.
The combined longleaf pine and shortleaf pine adjusted latewood chronology is a viable proxy of historic hydroclimate variability in the Uwharrie Mountains of central North Carolina, USA during the 1770–2020 study period for both intense and total precipitation amounts. To analyze the spatial extent that the proxy represents, we correlated the adjusted latewood chronology with the Climatic Research Unit gridded (i.e., 0.5° × 0.5°) JAS precipitation Time Series (CRU TS) version 4.07 [31] field during 1901–2020 using KNMI Climate Explorer [32]. The chronology has significant correlations (i.e., p < 0.05) with gridded JAS precipitation throughout much of the southeastern US with maximum correlation coefficient values found nearby the study location in the Uwharrie Mountains with significant correlations extending from southern Pennsylvania to northern Florida and from western Tennessee to New York (Figure 6). These results suggest that although the proxy data were collected at one location, the data represent a larger hydroclimate spatial distribution and suggest that future work can incorporate proxy data from other locations (e.g., the northeastern US [33,34]) to produce more robust reconstruction models.
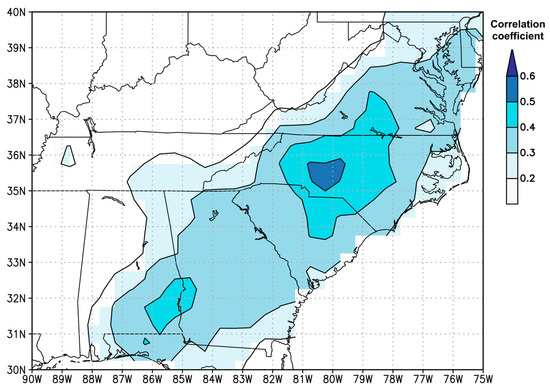
Figure 6.
Correlation coefficient between the Climatic Research Unit gridded (i.e., 0.5° × 0.5°) July–September precipitation Time Series field and the adjusted latewood longleaf pine and shortleaf pine chronology collected in the Uwharrie Mountains of central North Carolina, US. Significant correlations (i.e., p < 0.05) extend from southern Pennsylvania to northern Florida and from western Tennessee to New York. Image generated by KNMI Climate Explorer.
Here we presented the first extreme precipitation reconstruction in the region and contextualized long-term changes in moisture during 1770–2020. Previous work has indicated the importance of intense and extreme precipitation on tree radial growth (e.g., [10,35]) and other measures of plant growth (e.g., [36,37,38]) during a period of increased intense rainfall events for most of the US (e.g., [14]), a trend that is projected to increase over time [39,40]. These results suggest that increases in precipitation could become more important for plant growth in future climate change scenarios, particularly as some studies find no negative threshold for increased growth with increasing intense rainfall event size [37]. However, these positive extreme precipitation–growth relationships may be regulated and reduced by future increases in temperature [41] and by the particular climate classification of different study areas [42]. For example, Callitris columellaris radial growth best responded to extreme precipitation measures in semi-arid regions of Australia, while total precipitation measures best explained radial growth in tropical regions [42]. Here, our results suggest that positive extreme precipitation–growth relationships are regulated by the frequency and magnitude of intense rainfall events.
These results suggest overall stability in IRE precipitation and total precipitation in the Uwharrie Mountains during both the reconstructed period of 1770–2020 and the observational period of 1940–2020. However, IRE and total precipitation vary in unison over time with three significant regime shifts during the reconstruction period (1770–1935, 1936–1959 (above-average moisture), 1960–2020 (below-average moisture)). These results indicate the influence of extreme precipitation on latewood growth and model strength, particularly highlighting the susceptibility of reconstruction models to less skill and/or error with differing frequencies of extreme events.
Author Contributions
Conceptualization, T.J.M. and P.A.K.; methodology, T.J.M. and P.A.K.; software, T.J.M. and P.A.K.; validation, T.J.M. and P.A.K.; formal analysis, T.J.M. and P.A.K.; investigation, T.J.M. and P.A.K.; resources, T.J.M. and P.A.K.; data curation, T.J.M. and P.A.K.; writing—original draft preparation, T.J.M. and P.A.K.; writing—review and editing, T.J.M. and P.A.K.; visualization, T.J.M. and P.A.K.; supervision, T.J.M. and P.A.K.; project administration, T.J.M. and P.A.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to other manuscripts in preparation.
Acknowledgments
We thank Marley Allen, Avery Catherwood, John Cline, Hunter Lewis, Thomas Patterson, and Jeffy Summers for assistance in field data collection. We thank the Water Editorial Team and the five reviewers for their thoughtful and constructive comments that significantly improved the manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Maxwell, R.S.; Hessl, A.E.; Cook, E.R.; Buckley, B.M. A Multicentury Reconstruction of May Precipitation for the Mid-Atlantic Region Using Juniperus Virginiana Tree Rings. J. Clim. 2012, 25, 1045–1056. [Google Scholar] [CrossRef]
- Pederson, N.; Bell, A.R.; Knight, T.A.; Leland, C.; Malcomb, N.; Anchukaitis, K.J.; Tackett, K.; Scheff, J.; Brice, A.; Catron, B.; et al. A Long-Term Perspective on a Modern Drought in the American Southeast. Environ. Res. Lett. 2012, 7, 014034. [Google Scholar] [CrossRef]
- Dawson, A.; Austin, D.; Walker, D.; Appleton, S.; Gillanders, B.M.; Griffin, S.M.; Sakata, C.; Trouet, V. A Tree-Ring Based Reconstruction of Early Summer Precipitation in Southwestern Virginia (1750 1981). Clim. Res. 2015, 64, 243–256. [Google Scholar] [CrossRef]
- Knapp, P.A.; Maxwell, J.T.; Soulé, P.T. Tropical Cyclone Rainfall Variability in Coastal North Carolina Derived from Longleaf Pine (Pinus Palustris Mill.): AD 1771–2014. Clim. Chang. 2016, 135, 311–323. [Google Scholar] [CrossRef]
- Harley, G.L.; Maxwell, J.T.; Larson, E.; Grissino-Mayer, H.D.; Henderson, J.; Huffman, J. Suwannee River Flow Variability 1550–2005 CE Reconstructed from a Multispecies Tree-Ring Network. J. Hydrol. 2017, 544, 438–451. [Google Scholar] [CrossRef]
- Maxwell, R.S.; Harley, G.L.; Maxwell, J.T.; Rayback, S.A.; Pederson, N.; Cook, E.R.; Barclay, D.J.; Li, W.; Rayburn, J.A. An Interbasin Comparison of Tree-Ring Reconstructed Streamflow in the Eastern United States. Hydrol. Process. 2017, 31, 2381–2394. [Google Scholar] [CrossRef]
- Mitchell, T.; Knapp, P.; Patterson, T. Changes in Southeastern USA Summer Precipitation Event Types Using Instrumental (1940–2018) and Tree-Ring (1790–2018) Data. Environ. Res. Commun. 2019, 1, 111005. [Google Scholar] [CrossRef]
- Knapp, P.A.; Soulé, P.T.; Maxwell, J.T.; Ortegren, J.T.; Mitchell, T.J. Tropical Cyclone Precipitation Regimes since 1750 and the Great Suppression of 1843–1876 along Coastal North Carolina, USA. Int. J. Climatol. 2021, 41, 200–210. [Google Scholar] [CrossRef]
- Bregy, J.C.; Maxwell, J.T.; Robeson, S.M.; Harley, G.L.; Elliott, E.A.; Heeter, K.J. US Gulf Coast Tropical Cyclone Precipitation Influenced by Volcanism and the North Atlantic Subtropical High. Commun. Earth Environ. 2022, 3, 164. [Google Scholar] [CrossRef]
- Mitchell, T.J.; Knapp, P.A.; Patterson, T.W. The Importance of Infrequent, High-Intensity Rainfall Events for Longleaf Pine (Pinus Palustris Mill.) Radial Growth and Implications for Dendroclimatic Research. Trees For. People 2020, 1, 100009. [Google Scholar] [CrossRef]
- Anderson, S.; Ogle, R.; Tootle, G.; Oubeidillah, A. Tree-Ring Reconstructions of Streamflow for the Tennessee Valley. Hydrology 2019, 6, 34. [Google Scholar] [CrossRef]
- Mitchell, T.J.; Knapp, P.A. Radial Growth Responses of Four Southeastern USA Pine Species to Summertime Precipitation Event Types and Intense Rainfall Events. Atmosphere 2022, 13, 1731. [Google Scholar] [CrossRef]
- Moore, B.J.; Mahoney, K.M.; Sukovich, E.M.; Cifelli, R.; Hamill, T.M. Climatology and Environmental Characteristics of Extreme Precipitation Events in the Southeastern United States. Mon. Weather Rev. 2015, 143, 718–741. [Google Scholar] [CrossRef]
- Easterling, D.R.; Kunkel, K.; Arnold, J. Precipitation Change in the United States. 2017. Available online: https://repository.library.noaa.gov/view/noaa/32288 (accessed on 10 September 2022).
- Schoof, J.T. High-Resolution Projections of 21st Century Daily Precipitation for the Contiguous US. J. Geophys. Res. Atmos. 2015, 120, 3029–3042. [Google Scholar] [CrossRef]
- Shields, C.A.; Kiehl, J.T.; Meehl, G.A. Future Changes in Regional Precipitation Simulated by a Half-Degree Coupled Climate Model: Sensitivity to Horizontal Resolution. J. Adv. Model. Earth Syst. 2016, 8, 863–884. [Google Scholar] [CrossRef]
- Holmes, R.L. Quality Control of Crossdating and Measuring. Users Manual for Computer Program COFECHA. Tree-Ring Chronologies of Western North America: California, Eastern Oregon and Northern Great Basin 1986. Available online: http://hdl.handle.net/10150/304672 (accessed on 10 September 2022).
- Wigley, T.M.; Briffa, K.R.; Jones, P.D. On the Average Value of Correlated Time Series, with Applications in Dendroclimatology and Hydrometeorology. J. Appl. Meteorol. Climatol. 1984, 23, 201–213. [Google Scholar] [CrossRef]
- Bunn, A.G. A Dendrochronology Program Library in R (DplR). Dendrochronologia 2008, 26, 115–124. [Google Scholar] [CrossRef]
- Soulé, P.T.; Knapp, P.A.; Maxwell, J.T.; Mitchell, T.J. A Comparison of the Climate Response of Longleaf Pine (Pinus Palustris Mill.) Trees among Standardized Measures of Earlywood, Latewood, Adjusted Latewood, and Totalwood Radial Growth. Trees 2021, 35, 1065–1074. [Google Scholar] [CrossRef]
- Meko, D.M.; Baisan, C.H. Pilot Study of Latewood-Width of Conifers as an Indicator of Variability of Summer Rainfall in the North American Monsoon Region. Int. J. Climatol. A J. R. Meteorol. Soc. 2001, 21, 697–708. [Google Scholar] [CrossRef]
- NOAA National Centers for Environmental Information. Climate Data Online. Available online: https://www.ncei.noaa.gov/cdo-web/ (accessed on 10 September 2022).
- The Comprehensive R Archive Network. Caret: Classification and Regression Training. Available online: https://cran.r-project.org/package=caret (accessed on 10 September 2022).
- The Comprehensive R Archive Network. lmtest: Testing Linear Regression Models. Available online: https://cran.r-project.org/package=lmtest (accessed on 10 September 2022).
- The Comprehensive R Archive Network. ie2misc: Irucka Embry’s Miscellaneous USGS Functions. Available online: https://cran.r-project.org/package=ie2misc (accessed on 27 January 2024).
- The Comprehensive R Archive Network. dplR: Dendrochronology Program Library in R. Available online: https://cran.r-project.org/package=dplR (accessed on 10 September 2022).
- The Comprehensive R Archive Network. itdistrplus: Help to Fit of a Parametric Distribution to Non-Censored or Censored Data. Available online: https://cran.r-project.org/package=fitdistrplus (accessed on 28 January 2024).
- The Comprehensive R Archive Network. rshift: Paleoecology Functions for Regime Shift Analysis. Available online: https://cran.r-project.org/package=rshift (accessed on 10 September 2022).
- Durbin, J.; Watson, G.S. Testing for Serial Correlation in Least Squares Regression. III. Biometrika 1971, 58, 1–19. [Google Scholar] [CrossRef]
- Catherwood, A.A.; Knapp, P.A. Increasing Precipitation Variability and Climate-Growth Responses of Five Tree Species in North Carolina, USA. Environ. Res. Clim. 2023, 3, 015001. [Google Scholar] [CrossRef]
- Harris, I.; Osborn, T.J.; Jones, P.; Lister, D. Version 4 of the CRU TS Monthly High-Resolution Gridded Multivariate Climate Dataset. Sci. Data 2020, 7, 109. [Google Scholar] [CrossRef] [PubMed]
- Trouet, V.; Van Oldenborgh, G.J. KNMI Climate Explorer: A Web-Based Research Tool for High-Resolution Paleoclimatology. Tree-Ring Res. 2013, 69, 3–13. [Google Scholar] [CrossRef]
- Picard, C.J.; Winter, J.M.; Cockburn, C.; Hanrahan, J.; Teale, N.G.; Clemins, P.J.; Beckage, B. Twenty-First Century Increases in Total and Extreme Precipitation across the Northeastern USA. Clim. Chang. 2023, 176, 72. [Google Scholar] [CrossRef]
- Agel, L.; Barlow, M. How Well Do CMIP6 Historical Runs Match Observed Northeast US Precipitation and Extreme Precipitation–Related Circulation? J. Clim. 2020, 33, 9835–9848. [Google Scholar] [CrossRef]
- Howard, I.M.; Stahle, D.W. Tree-Ring Reconstruction of Single-Day Precipitation Totals over Eastern Colorado. Mon. Weather Rev. 2020, 148, 597–612. [Google Scholar] [CrossRef]
- Post, A.K.; Knapp, A.K. The Importance of Extreme Rainfall Events and Their Timing in a Semi-Arid Grassland. J. Ecol. 2020, 108, 2431–2443. [Google Scholar] [CrossRef]
- Post, A.K.; Knapp, A.K. How Big Is Big Enough? Surprising Responses of a Semiarid Grassland to Increasing Deluge Size. Glob. Chang. Biol. 2021, 27, 1157–1169. [Google Scholar] [CrossRef]
- Griffin-Nolan, R.J.; Slette, I.J.; Knapp, A.K. Deconstructing Precipitation Variability: Rainfall Event Size and Timing Uniquely Alter Ecosystem Dynamics. J. Ecol. 2021, 109, 3356–3369. [Google Scholar] [CrossRef]
- Stevenson, S.; Coats, S.; Touma, D.; Cole, J.; Lehner, F.; Fasullo, J.; Otto-Bliesner, B. Twenty-First Century Hydroclimate: A Continually Changing Baseline, with More Frequent Extremes. Proc. Natl. Acad. Sci. USA 2022, 119, e2108124119. [Google Scholar] [CrossRef]
- Emmanouil, S.; Langousis, A.; Nikolopoulos, E.I.; Anagnostou, E.N. Exploring the Future of Rainfall Extremes over CONUS: The Effects of High Emission Climate Change Trajectories on the Intensity and Frequency of Rare Precipitation Events. Earth’s Future 2023, 11, e2022EF003039. [Google Scholar] [CrossRef]
- Wise, E.K.; Dannenberg, M.P. Simulating the Impacts of Changes in Precipitation Timing and Intensity on Tree Growth. Geophys. Res. Lett. 2022, 49, e2022GL100863. [Google Scholar] [CrossRef]
- O’Donnell, A.J.; Renton, M.; Allen, K.J.; Grierson, P.F. The Role of Extreme Rain Events in Driving Tree Growth across a Continental-Scale Climatic Range in Australia. Ecography 2021, 44, 1086–1097. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).