Scour Pit Characteristics and Safety Operation Index of Riprap Spur Dikes under Runoff and Tidal Current
Abstract
1. Introduction
2. Materials and Methods
2.1. Flow and Sediment Characteristics of Tidal Reach in the Lower Reaches of the Yangtze River
2.2. Model Similarity Scale
2.3. Apparatuses for Measurements
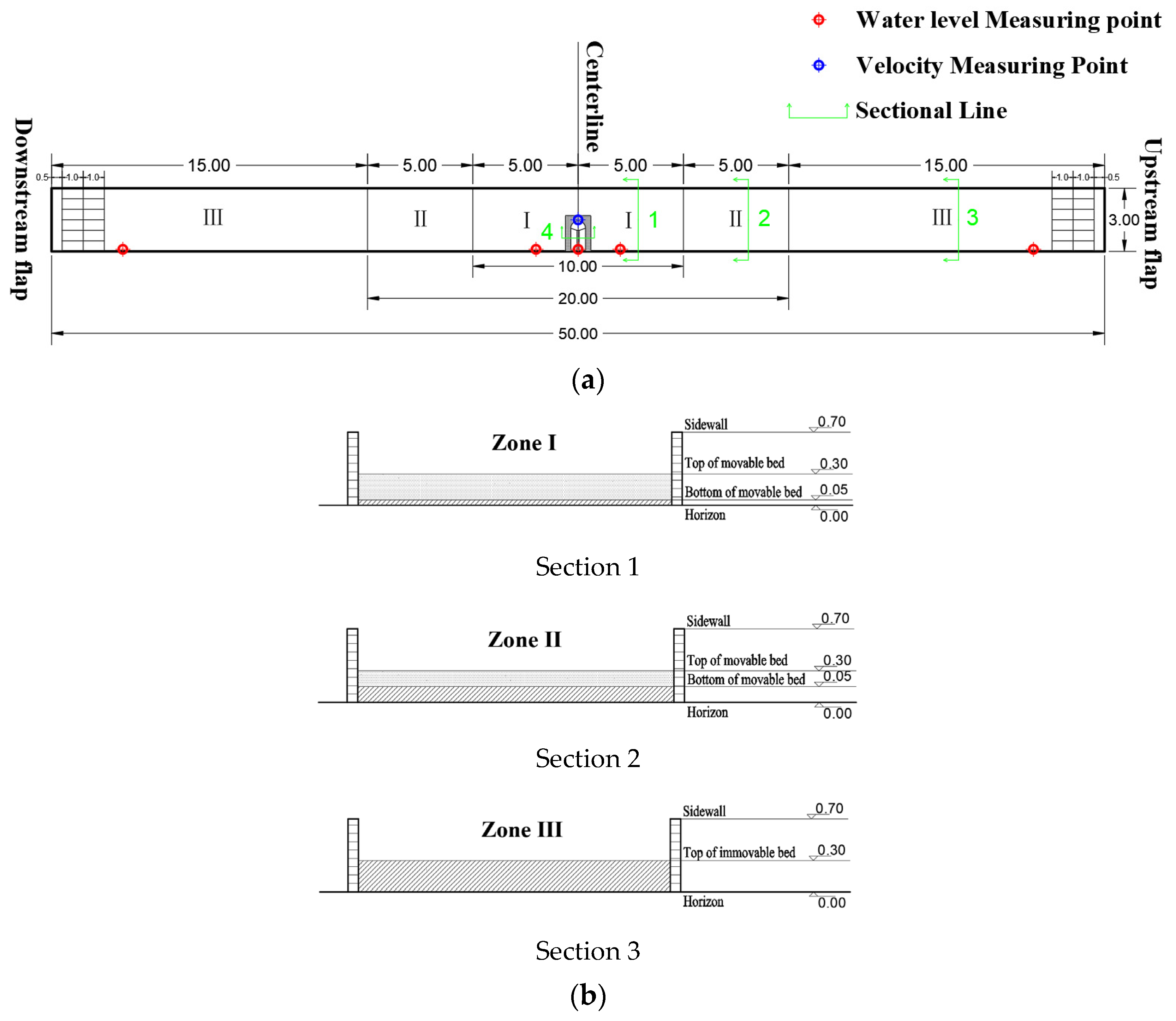
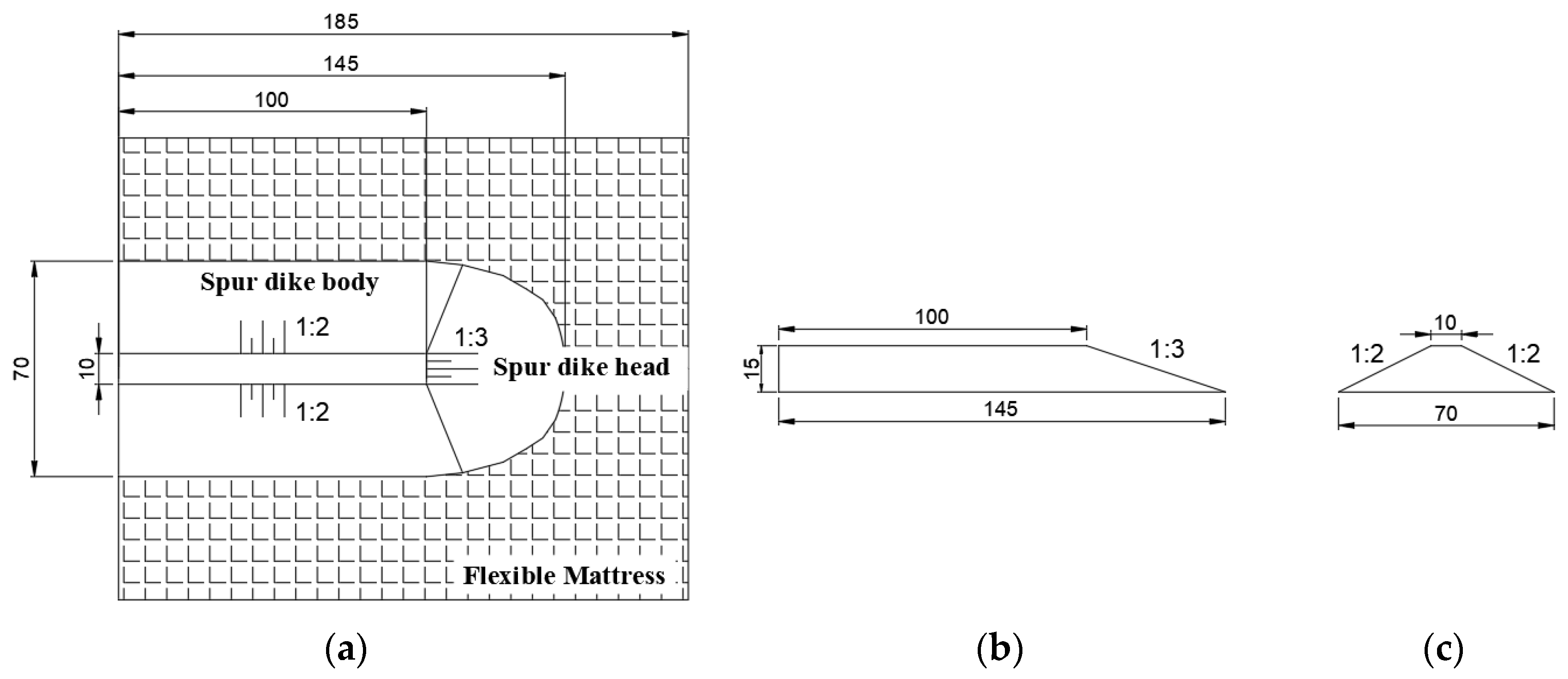
2.4. Model Layout
2.5. Test Protocol
3. Results
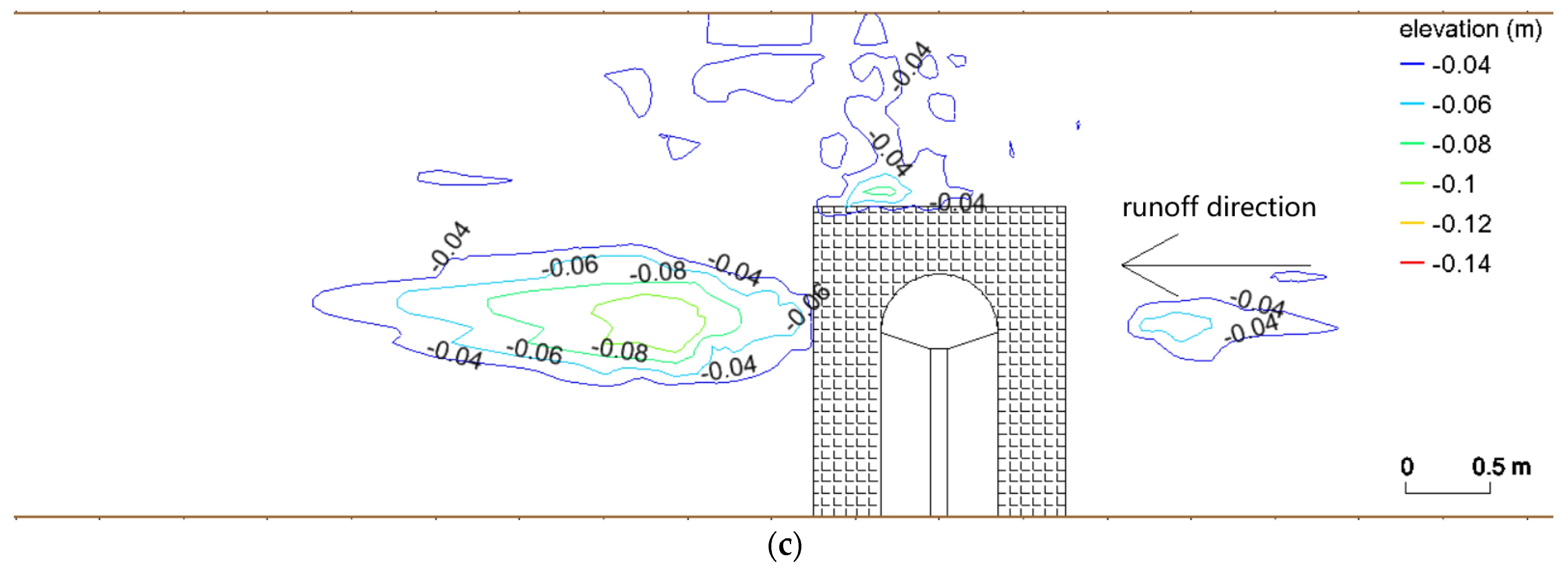
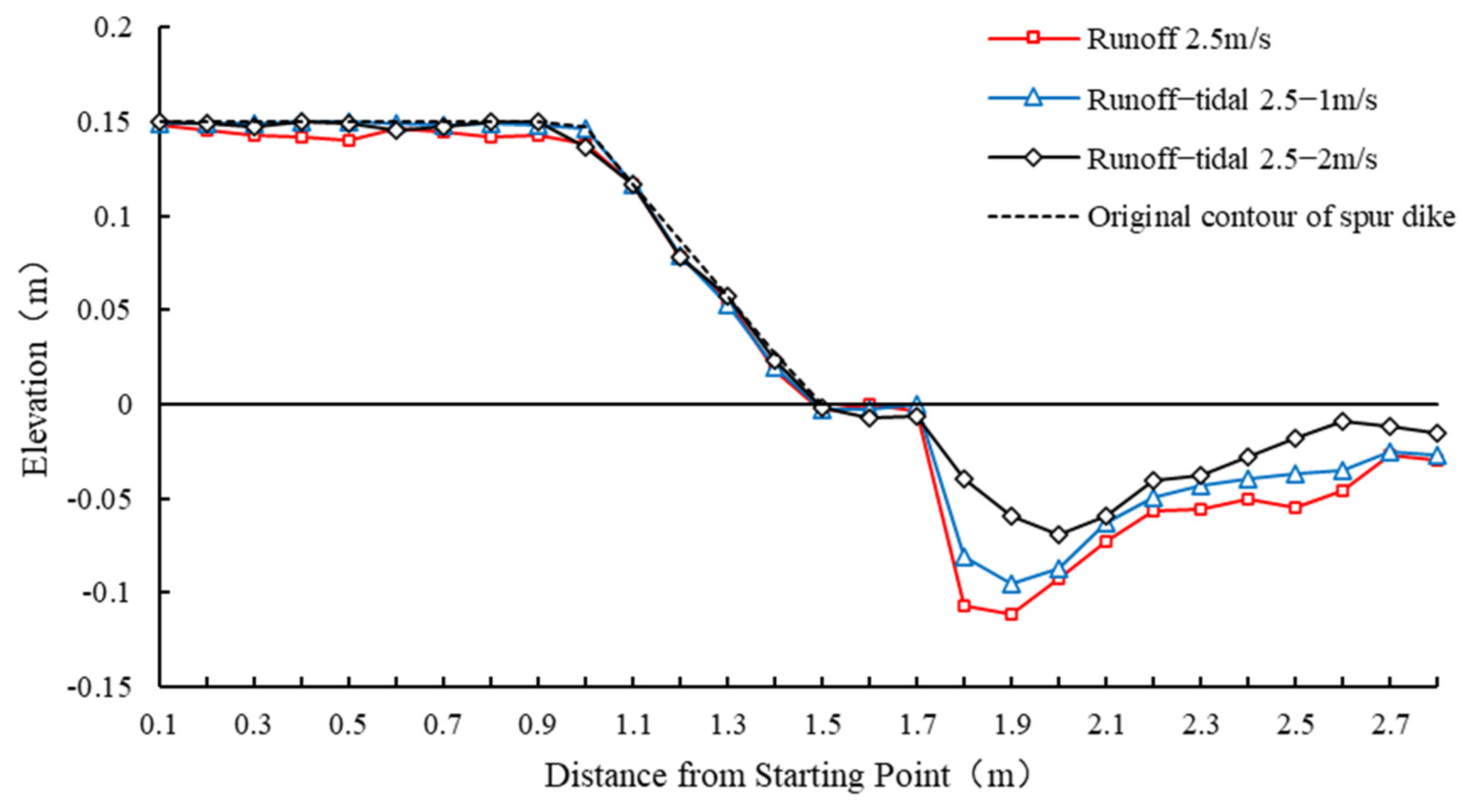
3.1. Scouring Pit Shape
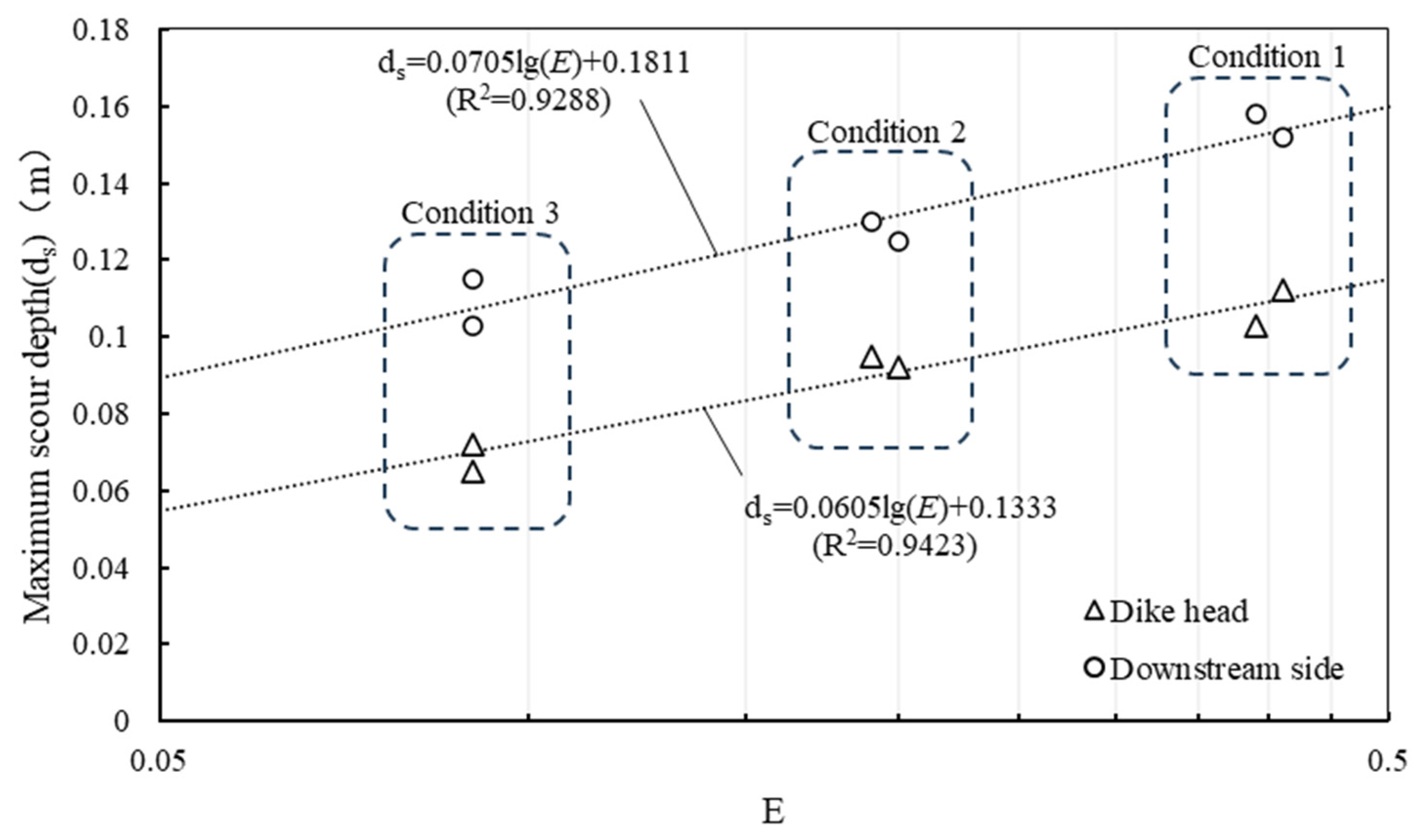
3.2. Scouring Pit Depth
4. Discussion
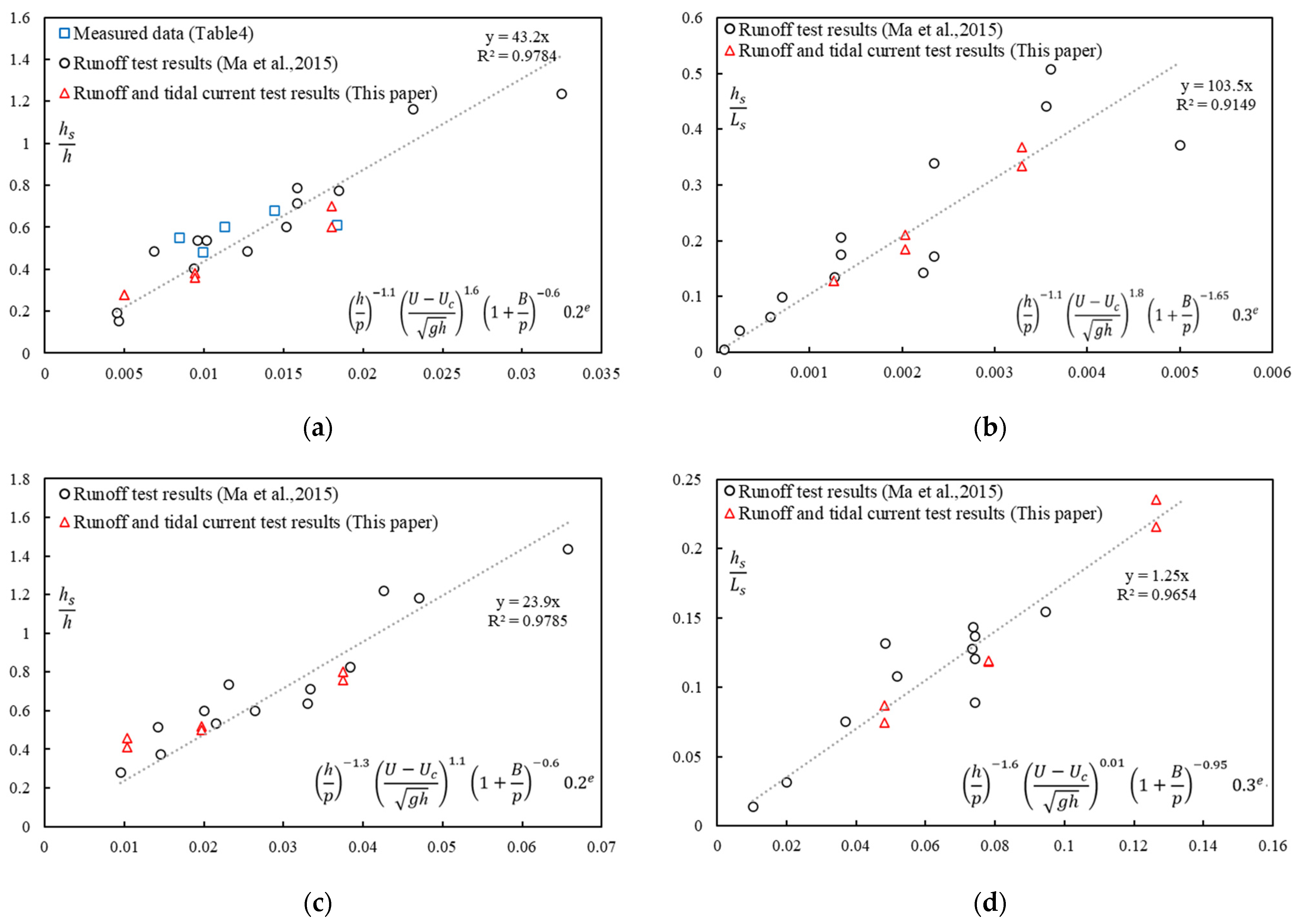
4.1. Scouring Pit Calculation Formula
- (1)
- Dike head:
- (2)
- Dike downstream side:
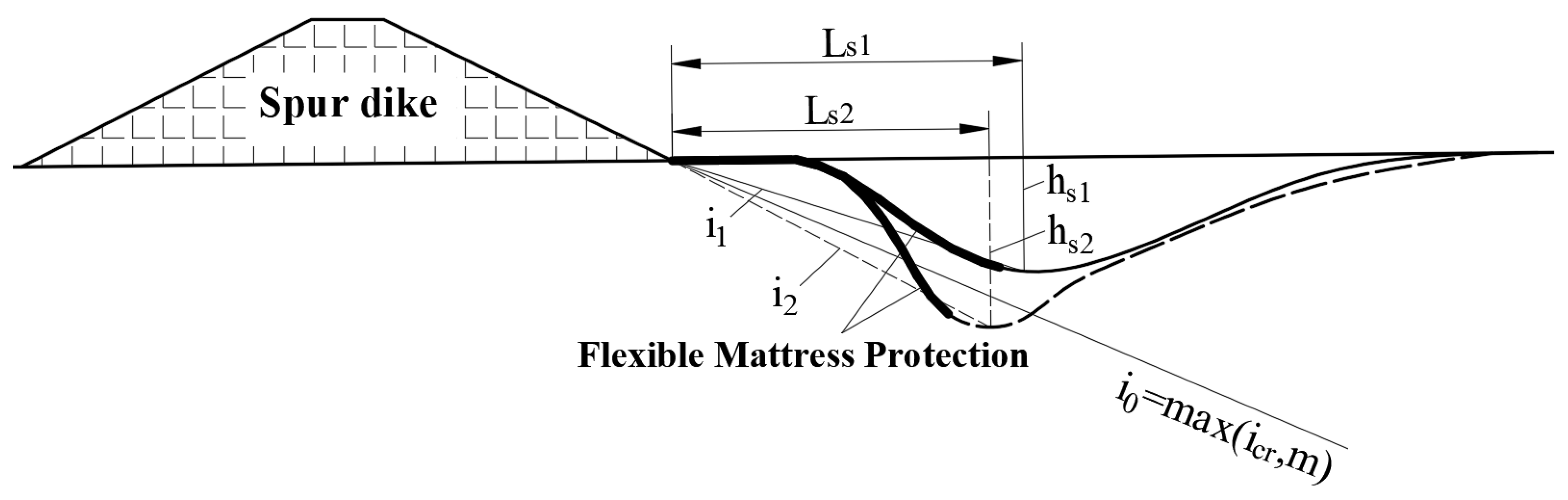
4.2. Safety Operation Index
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, Y.; Zheng, J.; Zhang, W.; Zhu, Y.; Chai, Y.; Wang, J.; Wen, Y. Quantitative relationship between channels and bars in a tidal reach of the lower Yangtze River: Implications for river management. J. Geogr. Sci. 2021, 31, 1837–1851. [Google Scholar] [CrossRef]
- Przedwojski, B. Bed topography and local scour in rivers with banks protected by groynes. J. Hydraul. Res. 1995, 33, 257–273. [Google Scholar] [CrossRef]
- Yu, T.; Duan, Q.; Wang, P.; Han, L. Experimental research of turbulence kinetic and water force acting on spur dike. Desalination Water Treat. 2022, 267, 89–97. [Google Scholar] [CrossRef]
- Zhang, W.; Qu, L.; Xu, J. Stability Analysis of Enrockment Dams in Mountain Streams. Port Waterw. Eng. 2003, 351, 10–12. (In Chinese) [Google Scholar] [CrossRef]
- Xia, Y.; Cai, Z.; Xu, H.; Yan, J. Interaction between new submerged spur dike and water flow in deepwater channel regulation. Port Waterw. Eng. 2018, 137–142. (In Chinese) [Google Scholar] [CrossRef]
- Elawady, E.; Michiue, M.; Hinokidani, O. Experimental Study of Flow Behavior around Submerged Spur-Dike on Rigid Bed. Proc. Hydraul. Eng. 2000, 44, 539–544. [Google Scholar] [CrossRef][Green Version]
- Cao, M.; Ying, H.; Qian, M. Main technical problems and research achievement of 12.5 m deep-water channel construction phase Ⅰ of the Yangtze River below Nanjing city. Port Waterw. Eng. 2015, 2, 26–35. (In Chinese) [Google Scholar] [CrossRef]
- Cao, M.; Ying, H.; Shen, X. Evolution features and regulation thinking about four reaches of deep-water channel phase Ⅱ project in the Yangtze River below Nanjing. Port Waterw. Eng. 2018, 1–12. (In Chinese) [Google Scholar] [CrossRef]
- Dou, X.; Wang, X.; Lou, B. General scouring model test of dike’s head under tidal currents and waves. Hydro-Sci. Eng. 2005, 28–33. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, X.; Dou, X.; Wang, X.; Wang, H.; Zhao, X.; Xu, X. 3D numerical modeling of local scour processes around spur dikes in tidal rivers. Adv. Water Sci. 2012, 23, 222–228. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, X. Experimental Study on the Failures of Spur Dike under Unsteady Flow. Ph.D. Thesis, Chongqing Jiaotong University, Chongqing, China, 2012. (In Chinese). [Google Scholar]
- Huang, Z.; Wu, G.; Cheng, Z. Formula of Local Scour Depth around Spur Dikes. J. Water Resour. Archit. Eng. 2004, 13–15+23. (In Chinese) [Google Scholar]
- Pandey, M.; Jamei, M.; Ahmadianfar, I.; Karbasi, M.; Lodhi, A.S.; Chu, X. Assessment of scouring around spur dike in cohesive sediment mixtures: A comparative study on three rigorous machine learning models. J. Hydrol. 2022, 606, 127330. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, P.; Yang, W.; Zuo, W.; Gu, X.; Yang, X. Geometric Characteristics of Spur Dike Scour under Clear-Water Scour Conditions. Water 2018, 10, 680. [Google Scholar] [CrossRef]
- She, J.; Xia, Y.; Xu, H.; Du, D.; Hao, S. Experimental study on local scouring of submerged spur dike head under bottom protection condition. Adv. Water Sci. 2016, 27, 579–585. (In Chinese) [Google Scholar] [CrossRef]
- Huang, W.; Creed, M.; Chen, F.; Liu, H.; Ma, A. Scour around Submerged Spur Dikes with Flexible Mattress Protection. J. Waterw. Port Coast. Ocean Eng. 2018, 144, 04018013. [Google Scholar] [CrossRef]
- Li, G.; Sui, J.; Sediqi, S.; Dziedzic, M. Local scour around submerged angled spur dikes under ice cover. Int. J. Sediment Res. 2023, 38, 781–793. [Google Scholar] [CrossRef]
- Fei, X.; Zhang, X.; Ying, Q.; Niu, C.; Chen, C. Experimental study on flow characteristics and damage of rock riprap used in river bend. Port Waterw. Eng. 2017, 7. (In Chinese) [Google Scholar] [CrossRef]
- Han, L.; Wang, P.; Liu, H.; He, Q. Discriminatory analysis of rockfill groin’s safety based on water-destruction volumetric ratio. Eng. J. Wuhan Univ. 2014, 47, 201–206. (In Chinese) [Google Scholar]
- Yu, T.; Shi, H.; Wang, P.; Kong, D. Value-at-risk analysis of spur dikes based on range analysis. Eng. J. Wuhan Univ. 2020, 53, 7. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, W.; Fang, Z.; Cai, Y. Safety reliability analysis for groyne erosion. Ocean Eng. 2005, 23, 8. (In Chinese) [Google Scholar] [CrossRef]
- Ma, A.; Wang, X.; Cai, G. Experimental Study on Structural Stability and Width Calculation of Flexible Mattress for Bottom Protection in Tidal Reach; Nanjing Hydraulic Research Institute: Nanjing, China, 2015. (In Chinese) [Google Scholar]
- Wang, W.; Li, Y.; Du, W.; Zeng, W.; Xu, Y. Tidal variation features of tidal reach of Changjiang River. Water Resour. Prot. 2017, 33, 121–124+132. (In Chinese) [Google Scholar]
- Shi, J.Z. Tidal resuspension and transport processes of fine sediment within the river plume in the partially-mixed Changjiang River estuary, China: A personal perspective. Geomorphology 2010, 121, 133–151. [Google Scholar] [CrossRef]
- USDA, Soil Survey Manual, USDA Agricultural Handbook No.18; U.S. Government Printing Office: Washington, WA, USA, 2017.
- Ettema, R.; Melville, B.W.; Barkdoll, B. Scale Effect in Pier-Scour Experiments. J. Hydraul. Eng. 1998, 124, 639–642. [Google Scholar] [CrossRef]
- Li, C.; Jin, D. River Model Test; China Communication Press: Beijing, China, 1981. (In Chinese) [Google Scholar]
- Dey, S. Turbulence in Open-Channel Flows. In Fluvial Hydrodynamics: Hydrodynamic and Sediment Transport Phenomena; Dey, S., Ed.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 95–187. [Google Scholar]
- Tominaga, A.; Nezu, I.; Ezaki, K.; Nakagawa, H. Three-dimensional turbulent structure in straight open channel flows. J. Hydraul. Res. 1989, 27, 149–173. [Google Scholar] [CrossRef]
- Cao, M.; Wang, L.; Shen, X.; Ying, H.; Zhang, L. Analysis on features and difficulties during the construction process of deep water navigation channel project in the Yangtze River below Nanjing. Port Waterw. Eng. 2019, 1–8. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, L.; Yang, Z.; Zhang, F.; Li, Z.; Wang, Y.; Gao, S. Longitudinal residual circulation in the South Passage of Yangtze Estuary: Combined influences from runoff, tide and bathymetry. Sci. China Earth Sci. 2021, 64, 2129–2143. [Google Scholar] [CrossRef]
- Kong, Y.; He, S.; Ding, P.; Hu, K. Characteristics of temporal and spatial variation of salinity and their indicating significance in the Changjiang Estuary. Acta Oceanol. Sin. 2004, 9–18. (In Chinese) [Google Scholar]
- Zhao, M.; Zhu, X.; Cheng, L.; Teng, B. Experimental study of local scour around subsea caissons in steady currents. Coast. Eng. 2012, 60, 30–40. [Google Scholar] [CrossRef]
- Valela, C.; Rennie, C.D.; Nistor, I. Improved bridge pier collar for reducing scour. Int. J. Sediment Res. 2022, 37, 37–46. [Google Scholar] [CrossRef]




| Scale Name | Symbol | Value | Scale Name | Symbol | Value |
|---|---|---|---|---|---|
| Horizontal scale | 40 | Flow movement time scale | 6.325 | ||
| Vertical scale | 40 | Weight scale | 64,000 | ||
| Velocity scale | 6.325 | Incipient velocity scale | 6.28 | ||
| Flow scale | 10,119 | Sediment transport rate scale | 11.08 | ||
| Roughness scale | 1.849 | Scouring and silting time scale | 335 |
| Conditions | Maximum Ebb Velocity (m/s) | Maximum Flood Tide Velocity (m/s) | Highest Tide Level (m) | Lowest Tidal Level (m) | Duration of Flood Tide (h) | Duration of Ebb Tide (h) | Test Duration (h) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P 1 | M | P | M | P | M | P | M | P | M | P | M | ||
| 1 | 2.5 | 0.4 | 0 | 0 | 10 | 0.25 | 10 | 0.25 | / | / | / | / | 3.5 |
| 2 | 2.5 | 0.4 | 1 | 0.16 | 11 | 0.275 | 9 | 0.225 | 4 | 0.63 | 8 | 1.26 | 6 |
| 3 | 2.5 | 0.4 | 2 | 0.32 | 12 | 0.3 | 8 | 0.2 | 4 | 0.63 | 8 | 1.26 | 6 |
| Conditions | E | Maximum Scour Depth ds (m) | ||||||
|---|---|---|---|---|---|---|---|---|
| Test1 | Test2 | Proportion in Condition 1 | Spur Dike Head | Downstream Side | Proportion in Condition 1 | |||
| Test1 | Test2 | Test1 | Test2 | |||||
| Condition 1 | 0.41 | 0.39 | / | 0.112 | 0.103 | 0.152 | 0.158 | / |
| Condition 2 | 0.19 | 0.2 | 46–51% | 0.095 | 0.092 | 0.130 | 0.125 | 79–89% |
| Condition 3 | 0.09 | 0.09 | 22–23% | 0.072 | 0.065 | 0.115 | 0.103 | 63–76% |
| Project | Spur Dike D2# | Spur Dike D3# | Spur Dike F1# | Spur Dike F2# | Spur Dike F3# |
|---|---|---|---|---|---|
| Spur dike head water depth (m) | 9 | 9 | 10 | 10 | 10 |
| Spur dike head height (m) | 7.59 | 8.79 | 5.89 | 5.35 | 6.37 |
| Spur dike head velocity (m/s) | 2.5 | 2.5 | 3 | 3 | 3 |
| Median grain size of bed sediment (mm) | 0.14 | 0.14 | 0.14 | 0.14 | 0.14 |
| Design width of flexible mattress (m) | 80 | 80 | 100 | 100 | 100 |
| Actual scour pit depth (m) | 6.1 | 5.5 | 4.8 | 5.5 | 6 |
| Calculated scour pit depth (m) | 5.61 | 7.15 | 4.3 | 3.66 | 4.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Y.; Ma, A.; Deng, Y.; Hu, Y.; Liu, M.; Cao, M. Scour Pit Characteristics and Safety Operation Index of Riprap Spur Dikes under Runoff and Tidal Current. Water 2024, 16, 438. https://doi.org/10.3390/w16030438
Wei Y, Ma A, Deng Y, Hu Y, Liu M, Cao M. Scour Pit Characteristics and Safety Operation Index of Riprap Spur Dikes under Runoff and Tidal Current. Water. 2024; 16(3):438. https://doi.org/10.3390/w16030438
Chicago/Turabian StyleWei, Yuchong, Aixing Ma, Ya Deng, Ying Hu, Manhong Liu, and Minxiong Cao. 2024. "Scour Pit Characteristics and Safety Operation Index of Riprap Spur Dikes under Runoff and Tidal Current" Water 16, no. 3: 438. https://doi.org/10.3390/w16030438
APA StyleWei, Y., Ma, A., Deng, Y., Hu, Y., Liu, M., & Cao, M. (2024). Scour Pit Characteristics and Safety Operation Index of Riprap Spur Dikes under Runoff and Tidal Current. Water, 16(3), 438. https://doi.org/10.3390/w16030438





