Wasserstein-Enabled Leaks Localization in Water Distribution Networks

Abstract

Leaks in water distribution networks are estimated to account for up to 30% of the total distributed water; moreover, the increasing demand and the skyrocketing energy cost have made leak localization and adoption ever more important to water utilities. Each leak scenario is run on a simulation model to compute the resulting values of pressure and flows over the whole network. The values recorded by the sensors are seen as features of one leak scenario and can be considered as the signature of the leak. The key distinguishing element in this paper is to consider the entire distribution of data, representing a leak as a probability distribution. In this representation, the similarity between leaks can be captured by the Wasserstein distance. This choice matches the physics of the system as follows: the equations modeling the generation of flow and pressure data are non-linear. The signatures obtained through the simulation of a set of leak scenarios are non-linearly clustered in the Wasserstein space using Wasserstein barycenters as centroids. As a new set of measurements arrives, its signature is associated with the cluster with the closest barycenter. The location of the simulated leaks belonging to that cluster are the possible locations of the observed leak. This new framework allows a richer representation of pressure and flow data embedding both the modeling and the computational modules in a space whose elements are discrete probability distribution endowed with the Wasserstein distance. Experiments on benchmark and real-world networks confirm the feasibility of the proposed approach.

1. Introduction

Leaks in water distribution networks are estimated to comprise up to 30% of the total distributed water, underscoring the substantial positive impact of even a relatively small percentage improvement in leak reduction. The escalating demand, driven by the burgeoning urban population and soaring energy costs, has heightened the importance of early leak detection, rapid localization, and the implementation of remedial actions for water utilities. Significant challenges arise from the scarcity of measurements and the uncertainty in demand, making leakage localization a particularly daunting problem. This scenario has not only significantly influenced operational practices but has also prompted the water research community to recognize the potential of artificial intelligence and the importance of synergy with the machine learning community. These advances have been facilitated by both new computational techniques and the increasing availability of pressure and flow sensors deployed throughout the water distribution network.

A key concept in this paper is the “leak scenario”, characterized by the location and severity of the leak. Each scenario undergoes a hydraulic simulation using EPANET (versione 2.2) to compute pressure and flow values. When a potential leak is detected via traditional methods such as minimum night flow analysis, the actual pressure and flow values recorded by the sensors are compared with those of the faultless network and those obtained through the simulations of various leak scenarios. The values recorded by the sensors are regarded as the features of a specific leak scenario, effectively serving as the signature of the leak in a feature space. These signatures, obtained through simulating all possible leak scenarios, are subjected to clustering. As a new set of sensor measurements arrives, its features are compared with cluster centroids to identify the most similar one. The signature is then assigned to that cluster, revealing the simulated leaky pipes associated with the scenarios of that cluster as potential leak locations. The overall workflow is depicted in Figure 1.

The distinctive feature of this paper lies in the representation of a leak signature over the simulation horizon as a discrete probability distribution. In this representation, the similarity between different leaks and between a faulty signature and a faultless one can be effectively captured by assessing the distance between their respective associated probability distributions. This transformation shifts the problem of leak detection from the Euclidean physical space to a space where the elements are discrete probability distributions. This space is organized by a distance metric between probability distributions, specifically the Wasserstein distance.

This new theoretical and computational framework allows a richer representation of pressure and flow data by embedding both the modeling and the computational modules in the Wasserstein space. A key feature of the Wasserstein distance is the ability to define the mean of a set of probability distributions, known as the Wasserstein barycenter. Leveraging the Wasserstein distance and barycenters, a clustering algorithm on probability distributions, grounded in the k-means framework, can be readily formulated. It is crucial to emphasize that discrete probability distributions can be represented in various ways, such as histograms or point clouds, while histograms provide the flexibility to control the dimension of the space by adjusting the number of bins, point clouds enable the consideration of the entire data sample. Computational results from three water distribution networks highlight the advantages of considering the complete data distribution over traditional statistics like mean or standard deviation. The findings underscore the superior efficacy of employing a point cloud representation instead of histograms.

2. Related Works

The current paper draws inspiration from a previous work [1], wherein the graph is encoded into a feature space. This feature space comprises leak signatures corresponding to various scenarios. Through a clustering procedure in the signature space, potential leaky nodes can be identified at different confidence levels. Other methodologies, such as that in [2], employ time-series of pressure data for classification and imputation, treating leaks at specific network nodes. Additionally, [3] propose an ensemble approach, combining a convolutional neural network and support vector machine, for graph-based localization in water distribution systems.

A distinct perspective is rooted in the concept of dictionary learning, as suggested by [4]. They advocate for a dictionary learning strategy applicable to both sensor placement and leakage isolation. The proposed strategy involves constructing a dictionary of atoms onto which the measured pressure residuals are projected, incorporating a sparsity constraint. Each measured residual can be expressed as a combination of a specific number of atoms. This dictionary learning approach is further advanced in a subsequent work [5]. Building upon the dictionary representation of algorithms for sensor placement, leak detection, and localization, this work introduces an additional layer of graph interpolation as input to dictionary classification.

A machine learning-based analysis of flow and pressure observations has become prevalent in the leak localization literature, giving rise to several different approaches. In [6], it is demonstrated that two distinct classifiers and a neural network can assess, for each node, the probability of a leak occurrence. In [7], a convolutional network is used to learn the pressure map characterizing each leak localization. In [8], probabilistic leak localization is performed in a water distribution network using a hybrid data-driven and model-based approach. The approach proposed in [9] is based on search space reduction driven by minimizing the difference between simulated and observed field pressures. A combination of a multilayer perceptron (MLP) and a convolutional neural network (CNN) is used in [10], trained and tested to localize leaks and estimate their sizes. A model-based approach is proposed in [11] that provides a closed-form expression for leak localization in the case of a single leak and a single pipe. The authors in [12] conduct leak detection using a multi-label classification task and leak localization using a regression algorithm while in [13] the authors use acoustic signals analyzed through support vector machines and k-NN regression.

Other machine learning-based strategies are proposed by [14], utilizing pressure sensors and spatial interpolation. Graph interpolation is used in [15] to estimate the hydraulic states of the complete WDN from real measurements at certain nodes. The authors in [16] aim to estimate the complete network state using a graph neural network approach, leveraging the topology of the physical network to estimate pressures where measurements are not available. Pressure prediction errors are transformed into residual signals on the edges. A similar approach has been proposed in [17], where nodal pressures are also estimated using graph neural networks. A related approach [18] encodes data from measured nodes as images, followed by clustering to split the network into subnetworks, and a deep neural network for binary classification.

The authors in [19] propose simulated annealing with hyperparameter optimization for leak localization. In [20], sensor placement and leak localization are jointly solved, considering mutual information, relevance, and redundancy measures. Similar, Ref. [21] simultaneously address leak detection and localization problems, with leaks detected and validated by statistically analyzing the inlet flow. Localization is formulated as a classification problem, and computational complexity is mitigated through a clustering scheme.

The Wasserstein distance, central to the present paper, is also considered in [22] for the data-driven detection and localization of leaks in industrial fluids (specifically, naphtha). The size of the network and its hydraulics are quite different from water distribution networks, and the method proposed is not directly relevant to the leak localization problem in water distribution networks. The use of Wasserstein distance in analyzing water distribution networks has been previously suggested for optimal sensor placement [23] and resilience analysis [24].

3. The Wasserstein Space

A discrete measure $\alpha$ is defined by a set of $\eta$-dimensional vector $\mathbf{a}$, whose elements are the weights, and a set of locations $x_1,\dots ,x_{\eta }\in \mathcal{X}$, also called support:

$$\alpha =\sum _{i=1}^{\eta }{\mathbf{a}}_i{\delta }_{x_i}$$

(1)

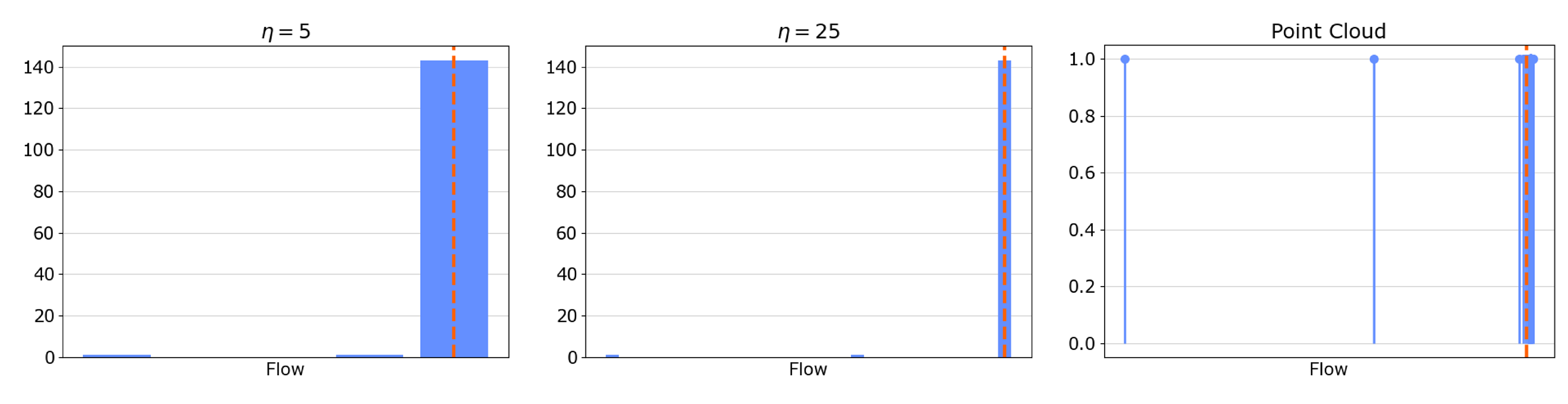
where ${\delta }_{x_i}$ is the Dirac function centered at $x_i$. The discrete measure $\alpha$ also describes a discrete probability measure if the weight vector $\mathbf{a}$ belongs to the probability simplex ${\Sigma }_{\eta }$. When each component of the weight vector a is equal to $1/\eta$, the discrete probability measure is called a point cloud and the definition becomes:

$$\alpha =\frac{1}{\eta }\sum _{i=1}^{\eta }{\delta }_{x_i}$$

(2)

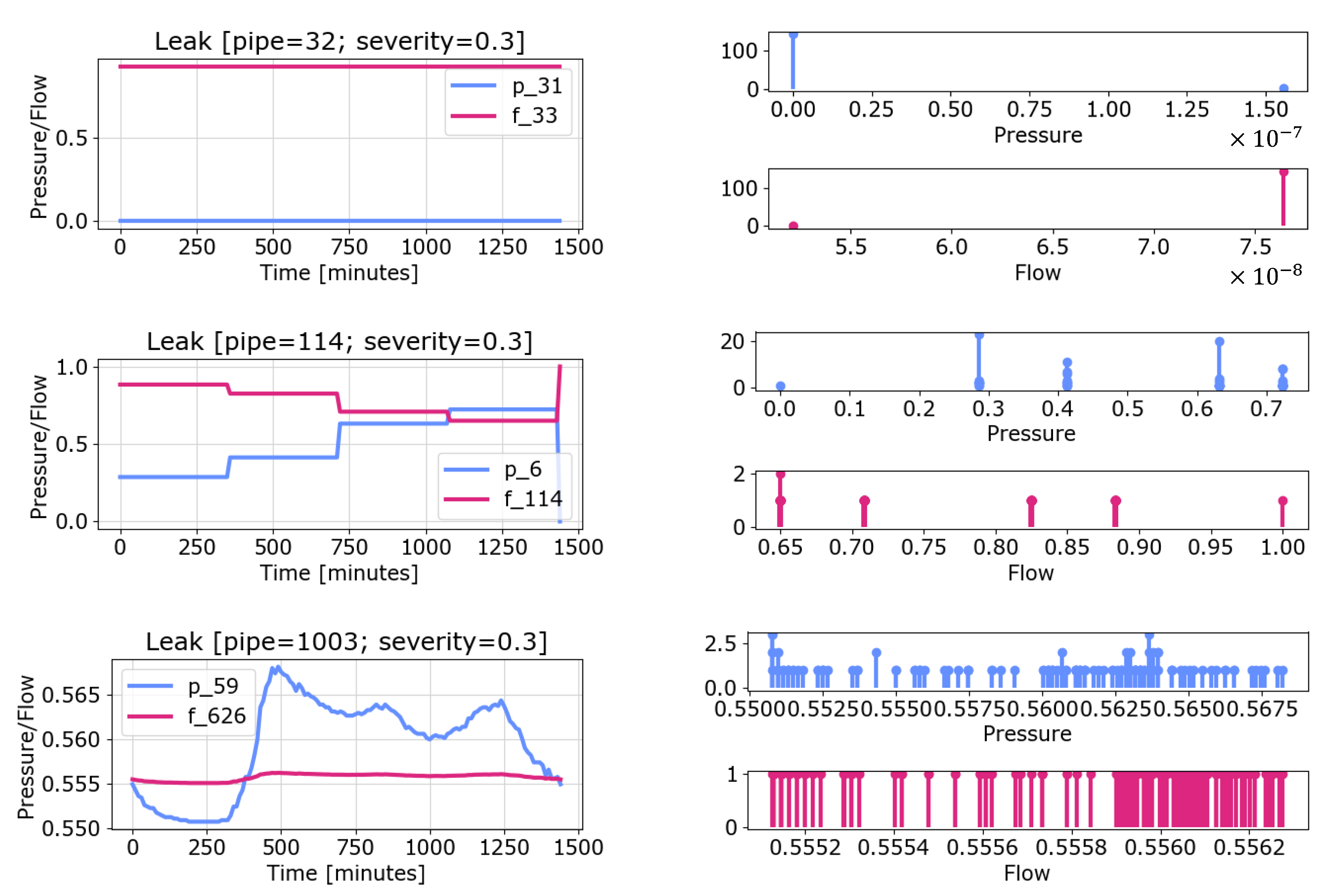
Figure 2 shows the different between a generic discrete probability distributions, also known as a histogram, and a point cloud.

Consider two discrete probability measure $\alpha$ and $\beta$ with weight vectors $\mathbf{a}$ and $\mathbf{b}$, and support $x_1,\dots ,x_{\eta }$ and $y_1,\dots ,y_{\nu }$, respectively. The Wasserstein distance, according to the Kantorovich formulation, can be formulated as follows:

$${\mathcal{W}}_p(\alpha ,\beta )=\underset{\mathcal{P}\in U(\mathbf{a},\mathbf{b})}{min}\sum _{ij}{\mathbf{C}}_{ij}^p{\mathcal{P}}_{ij}$$

(3)

where ${\mathbf{C}}_{ij}^p$ is the cost to move a single unit of mass from the i-th element to the j-th and U is the set of all possible coupling matrix between the probability vectors $\mathbf{a}$ and $\mathbf{b}$. The coupling matrix $\mathcal{P}\in {\mathbf{R}}_{+}^{\eta \times \nu }$ represents the amount of mass moved from each location $x_i$ toward each location $y_j$.

Solving the problem in Equation (3) can be computationally expensive, since, in general, it scales cubically with the sizes of the measures. In the case of a discrete probability measure whose support is one-dimensional, the computation of the Wasserstein distance can be performed by a simple sorting of the measures’ locations and the application of the following equation:

$${\mathcal{W}}_p(\alpha ,\beta )={\left(\frac{1}{n}\sum _{i=1}^n{|x_i^{*}-y_i^{*}|}^p\right)}^{\frac{1}{p}}$$

(4)

where $x^{*}$ and $y^{*}$ are the sorted samples.

One of the main advantages of the Wasserstein distance, over other probabilistic distances (as the Kullback–Leibler or the Jensen–Shannon divergence), is that it is a weak distance, i.e., it allows the comparison of discrete probability distributions whose supports are not aligned, quantifying the spacial shift between the supports.

Under the Wasserstein metric, it is possible to define the average of a set of probability measures. This mean is known as the Wasserstein barycenter and it is the measure that minimizes the sum of its Wasserstein distance to each element in the set. Consider N discrete probability measures ${\alpha }_1,\dots ,{\alpha }_N$, the associated barycenter is computed as follows:

$$\overline{\alpha }=\underset{\alpha }{\mathrm{argmin}}\frac{1}{N}\sum _{i=1}^N{\lambda }_i\mathcal{W}(\alpha ,{\alpha }_i)$$

(5)

where ${\lambda }_i$ are used to weight the different contributions of each distribution. Without a loss of generality, they can all be set to ${\lambda }_i=1/N$. The computation of Wasserstein barycenters requires one to solve a complex optimization problem. For this reason, a regularization term is usually added to the Wasserstein distance as the entropy of the coupling matrix. Then, the Sinkhorn–Knopp matrix scaling algorithm is used to compute the barycenters.

4. Wasserstein Enabled Leaks Localization

4.1. Generation of Leak Scenarios

First, a dataset of different leak scenarios is built by simulating a leak on each pipe of the network. Leaks are simulated by splitting a pipe into two sections and adding an emitter node. The demand at that node (i.e., the leaks) is computed as $q=C{p}^{\gamma }$, where p is the pressure, C is the discharge coefficient (severity), and $\gamma$ is the pressure exponent. As explained in [25], $\gamma =0.5$ has been used to simulate a circular hole, and different values of C ranging between $0.05$ and $0.5$ have been considered. The results of each simulation are the pressure and flow values at each junction and pipe, respectively. Only values in correspondence with the monitoring devices are considered. The pressure and flow variations due to each simulated leak are compared to the corresponding values obtained by simulating the faultless network. Each simulated leak is then represented by the pressure and flow variations together with the information related to the affected pipe and the damage severity. The registered values of pressure and flow can be represented as a discrete probability measure, and, in particular, as point clouds. The locations $x_1,\dots ,x_{\eta }$ are the pressure or flow values registered during the simulation. Figure 3 shows some examples of pressure and flow variation during the simulation horizon and their representation as point clouds.

In the experiments, the simulation is performed over a 24 h horizon, registering pressure and flow values every 10 min. Leaks are placed at the start of the simulation and persist for the entire duration. This results in $\eta =144$ observations for each monitoring point. The signature of a leak scenario is then a set of m point clouds, one for each monitoring point. This allows the comparison of different leaks using the Wasserstein distance.

4.2. Clustering in the Wasserstein Space

The concept of a barycenter enables clustering among probability distributions in a space whose metric is the Wasserstein distance. More simply, the barycenter in a space of distributions is analogous of the centroid in a Euclidean space. The most common and well-known algorithm for clustering data in Euclidean space is k-means. Since it is an iterative distance-based algorithm, it is easy to propose variants of k-means by simply changing the distance adopted to create clusters. The crucial point is that only the distance is changed, and the overall iterative two-step clustering algorithm is maintained.

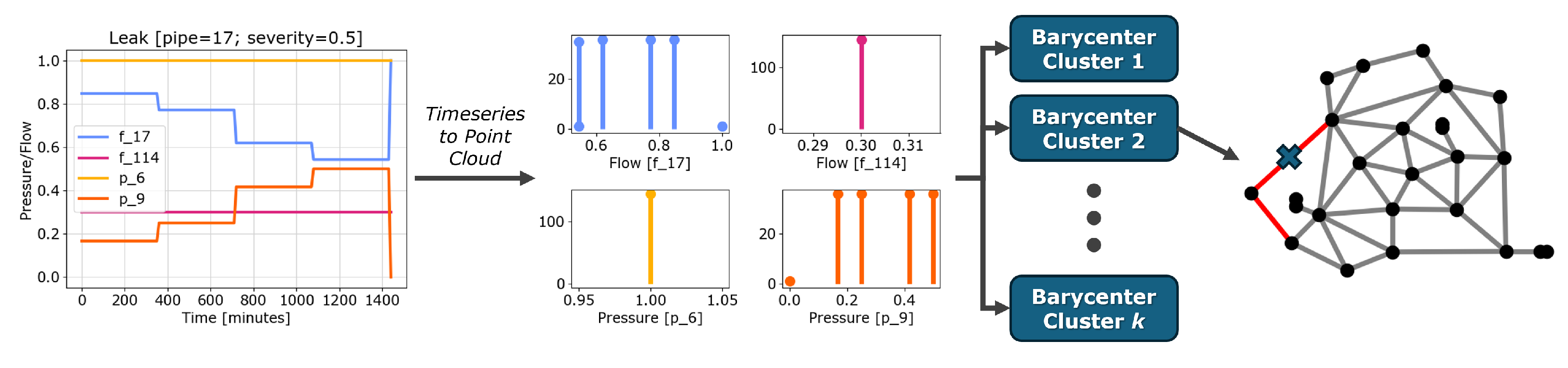
In the present paper, the Wasserstein k-means is used, where the Euclidean distance is replaced by the Wasserstein distance and where centroids are replaced by the barycenters of the distributions belonging to that cluster. As previously seen, each leak scenario can be represented as a set of m point clouds that represent the flow and pressure distributions at the monitoring points. This enables the usage of a Wasserstein-enabled k-means, in which the distance between two leakages is computed as the average Wasserstein distance over the m point clouds associated with different sensors. This approach, namely, Wasserstein-enabled leak localization (WELL), enables the usage of the entire sample of pressures and flows detected during the simulation horizon instead of just considering the average values, as in standard clustering approaches.

To locate a leakage, the detected pressures and flows can be compared to the barycenters resulting from the clustering procedure. The set of pipes potentially damaged is the set of pipes belonging to the clusters associated with the closest barycenter. Figure 4 shows an example of the prediction flow on the Anytown water distribution network.

5. Experiments and Results

5.1. Data Resources

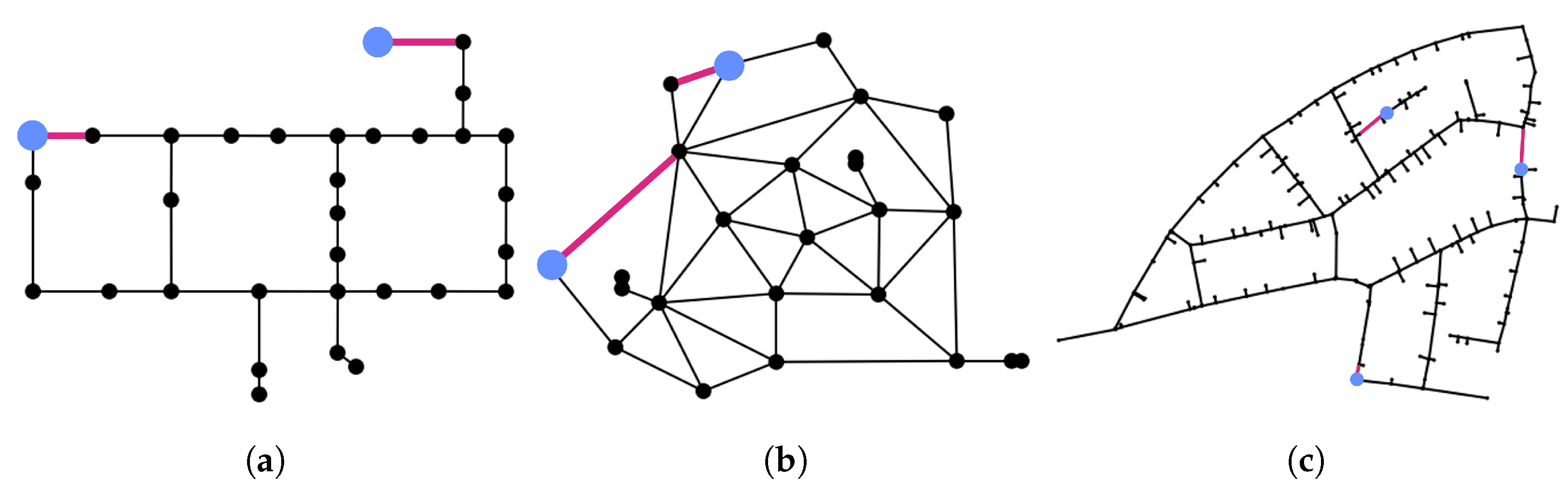
Three different networks have been used to test the proposed algorithm (Figure 5). Hanoi [26] and Anytown [27] are two benchmarks used in the literature. Hanoi is composed of 31 junctions, 1 reservoir, and 34 pipes, while Anytown has 22 junctions, 1 reservoir, 2 tanks, 43 pipes, and 3 pumps. Neptun [28] is the water distribution network of Timisoara, Romania, more specifically, it is a district metered area of a large network, and it was a pilot area of the European project ICeWater. Neptun is composed of 332 junctions, 1 reservoir, 312 pipes, and 27 valves.

For each of these networks, five different leaks have been simulated for each pipe, with different severity values (discharge coefficients), ranging from 0.1 to 0.3 with a step of 0.05. A total of 170 scenarios have been simulated for Hanoi, 215 scenarios for Anytown, and 1560 scenarios for Neptun. In addition, four sensors have been considered for the networks of Hanoi and Anytown and six sensors for the network of Neptun.

5.2. Computational Results

Two distinct versions of the proposed WELL algorithm have undergone testing against the standard k-means clustering algorithm. The first version involves a histogram representation of pressure and flow values, thereby reducing the dimensionality of the feature space. The second version employs a point cloud representation, considering the entire data sample.

The test set is constructed by simulating leaks in each pipe of the networks, but with different severity values compared to those used in the training phase. Specifically, three severity values—0.05, 0.22, and 0.5—have been employed.

Table 1. Number of leakage scenarios used as the training and test set for each network.

Network	Training Set	Test Set
Hanoi	170	102
Anytown	215	129
Neptun	1560	936

provides details regarding the size of the training and test datasets. In addition, different numbers of bins have been considered for the WELL algorithm.

To assess the performance of the three algorithms, the predictive accuracy on the test set was considered.

Table 2. Computational results in terms of prediction accuracy on three water distribution networks. The WELL-point cloud (PC) algorithm is tested against the WELL-histogram algorithm and the standard k-means. Different number of bins $\eta$ have been tested for the WELL-histogram algorithm. For each experiment, the best accuracy is highlighted in bold.

			WELL
Network	k	k-means	5	15	25	35	45	55	PC
Hanoi	5	1.000	0.941	0.971	1.000	0.971	0.971	1.000	1.000
	15	1.000	-	0.941	0.941	0.971	0.941	0.971	1.000
	25	1.000	-	-	0.971	1.000	1.000	1.000	1.000
	35	1.000	-	-	-	0.971	0.971	0.941	1.000
	45	1.000	-	-	-	-	0.941	0.941	1.000
	55	1.000	-	-	-	-	-	0.941	1.000
Anytown	5	1.000	0.791	0.907	1.000	1.000	1.000	1.000	1.000
	15	1.000	-	0.488	0.581	0.837	0.721	0.884	1.000
	25	1.000	-	-	1.000	0.860	1.000	1.000	1.000
	35	1.000	-	-	-	0.860	0.860	1.000	1.000
	45	1.000	-	-	-	-	1.000	1.000	1.000
	55	1.000	-	-	-	-	-	1.000	1.000
Neptun	5	0.996	0.877	0.972	0.985	0.991	0.984	0.986	0.997
	15	0.993	-	0.954	0.973	0.980	0.976	0.989	0.989
	25	0.981	-	-	0.917	0.929	0.929	0.933	0.988
	35	0.940	-	-	-	0.950	0.959	0.969	0.997
	45	0.944	-	-	-	-	0.946	0.954	0.996
	55	0.939	-	-	-	-	-	0.928	0.997

presents the results for the three water distribution networks. The findings underscore that for smaller networks, such as Hanoi and Anytown, employing a straightforward approach like k-means proves effective. This might be attributed to the limited variability in the flow and pressure values recorded at the monitoring points. In the case of larger, real-world networks like Neptun, the WELL algorithm demonstrates significantly superior performance compared to k-means. Within the WELL algorithm, the results indicate that increasing the number of bins leads to improved accuracy, and considering the entire data sample with a point cloud representation, yields the highest accuracy.

Real-world networks, such as Neptun (Figure 6), typically exhibit a greater variability in terms of the pressure and flow values throughout the day when compared to smaller benchmark networks like Anytown (Figure 7). In instances where the variance of observed data is high, adopting an approach that leverages the entire data distribution, such as WELL, results in superior performance. Conversely, in situations where the variance of observed data is low, utilizing a conventional method like k-means, which considers statistics rather than the entire distribution, remains an effective and more efficient approach.

6. Conclusions

The present paper introduces a novel approach, Wasserstein-enabled leaks localization (WELL), for addressing the critical issue of leak localization in water distribution networks. By considering the entire distribution of data and representing leaks as discrete probability distributions, the proposed framework leverages the Wasserstein distance to measure the similarity between different leaks. This approach captures the non-linear nature of the hydraulic simulation, providing a richer representation of pressure and flow data.

The Wasserstein space proves to be a valuable domain for modeling and clustering discrete probability distributions, allowing for the definition of Wasserstein barycenters and the implementation of a Wasserstein-enabled k-means clustering algorithm. The experiments conducted on benchmark and real-world water distribution networks showcase the effectiveness of the WELL algorithm in leak localization. Particularly, in real-world networks with a higher variability, WELL outperforms the standard k-means algorithm. On the two benchmark networks, Hanoi and Anytown, the average accuracy of k-means and WELL-PC is the same (1.00), while the histogram version of WELL reaches a lower accuracy, 0.97 on Hanoi and 0.98 on Anytown. With the real-world network, Neptun, the average accuracy of WELL-PC is 0.99, while k-means reaches 0.97; moreover, in this case, the histogram version of WELL performs worse than the other two, with an average accuracy of 0.96.

The flexibility of representing discrete probability distributions as histograms or point clouds is highlighted, with computational results emphasizing the advantages of considering the entire data distribution over traditional statistical measures, such as mean or standard deviation. The Wasserstein distance and barycenters play a crucial role in achieving better performances in leak localization.

The primary drawback lies in the increased computational complexity introduced by the computation of Wasserstein distances, particularly when determining Wasserstein barycenters, while the Wasserstein distance for discrete distributions with one-dimensional supports has a closed form, making it relatively straightforward to compute, the computation of Wasserstein barycenters still necessitates the resolution of a complex optimization problem. To mitigate this challenge, an entropic regularization has been used for the Wasserstein barycenters.

It is important to note that the proposed methodology has been tested on simulated leaks. Real-world leaks are usually affected by multiple unknown parameters and interactions, which could negatively influence the performance.