Methodology for Exploring Water and Hydropower Operating Criteria That Simultaneously Improve Economic and Environmental Considerations
Abstract
1. Introduction
2. Materials and Methods
2.1. General Methodology
- To the best of our knowledge, the proposed methodology is the first one that considers operating rules, instead of hourly water release schedules, as decision variables when exploring hydropower operations that simultaneously improve economic and environmental values. There are two advantages to this:
- ○
- First, because of the curse of dimensionality, the decision space to explore in the Monte Carlo simulation explodes when considering hourly water releases as decision variables. Conversely, our method considers less than a dozen operating rules.
- ○
- Second, the Pareto-efficient solutions identified this way would result in detailed water release scheduling patterns that hydropower operators might find too inflexible. Instead, providing hydropower operators with more general operating rulesets gives them more flexibility in their decision about real-time operations.
- We pre-process functions (or curves) that describe the link between aggregated release volumes and economic/environmental metric values. This simplification significantly accelerates the computation of the MILP problems in the MOO approach.
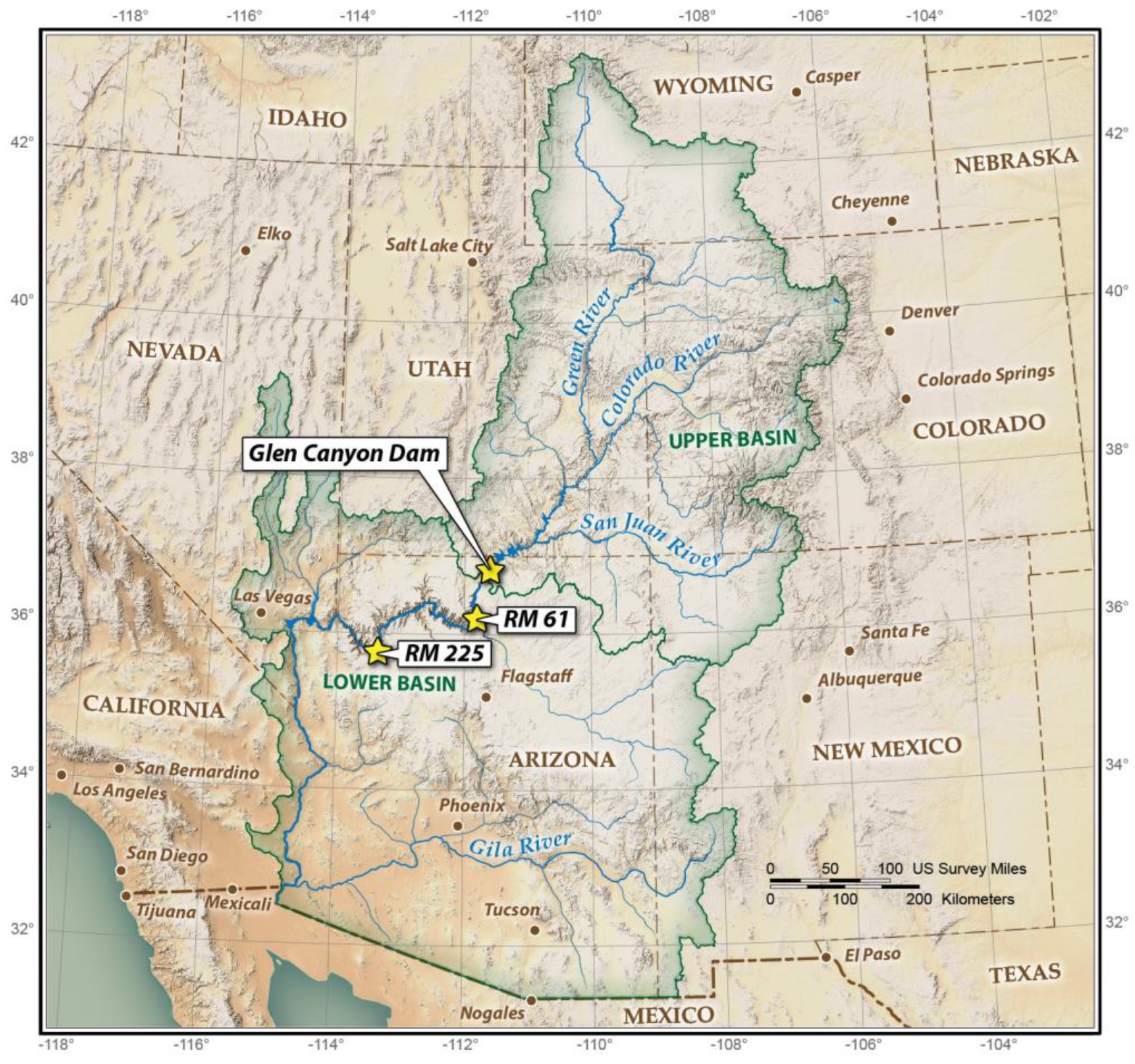
2.2. Colorado River and Glen Canyon Dam
2.3. Glen Canyon Dam Operating Rules
2.4. Economic Metric
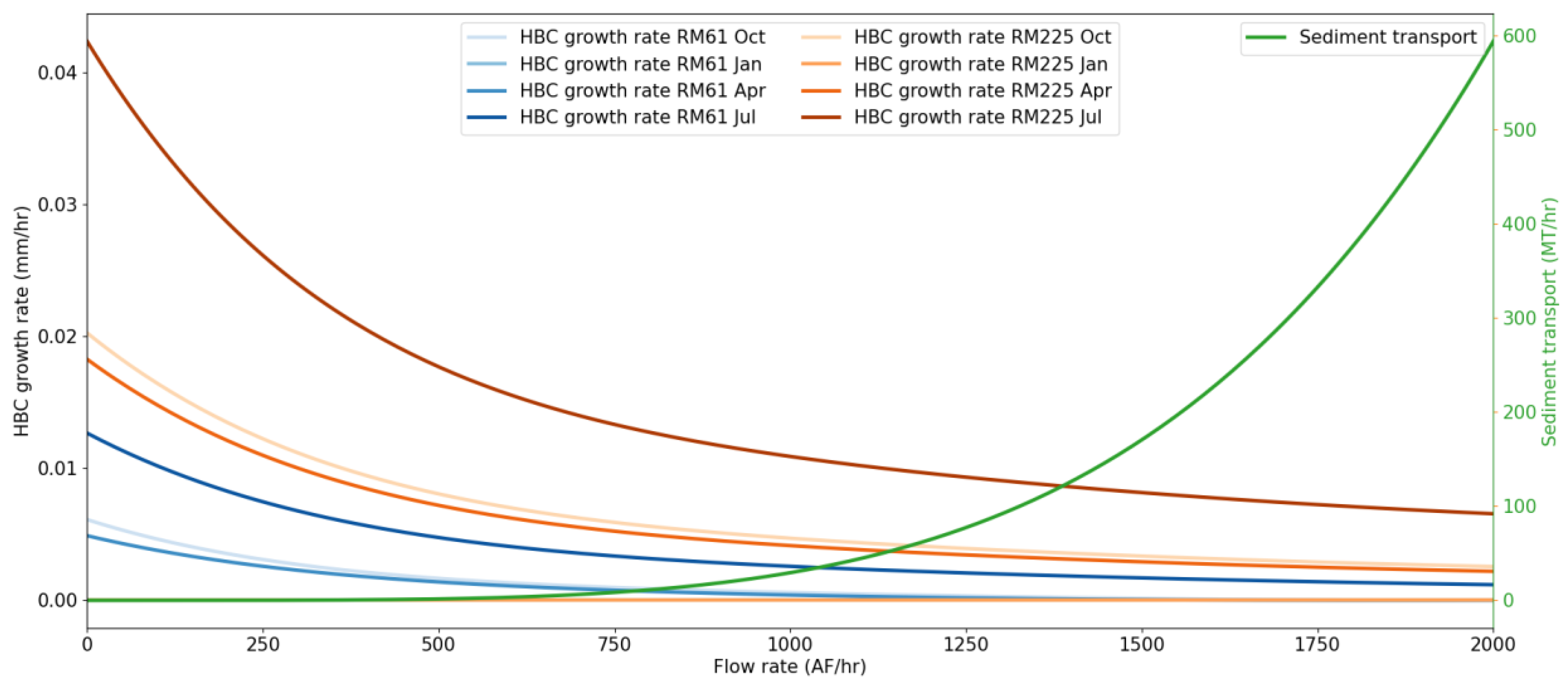
2.5. Environmental Metrics
2.6. Multiple-Criteria Decision Analysis and Pareto Front
2.7. Monte Carlo Approach
2.8. Mathematical Optimization and Weighted Sum Approach
3. Results
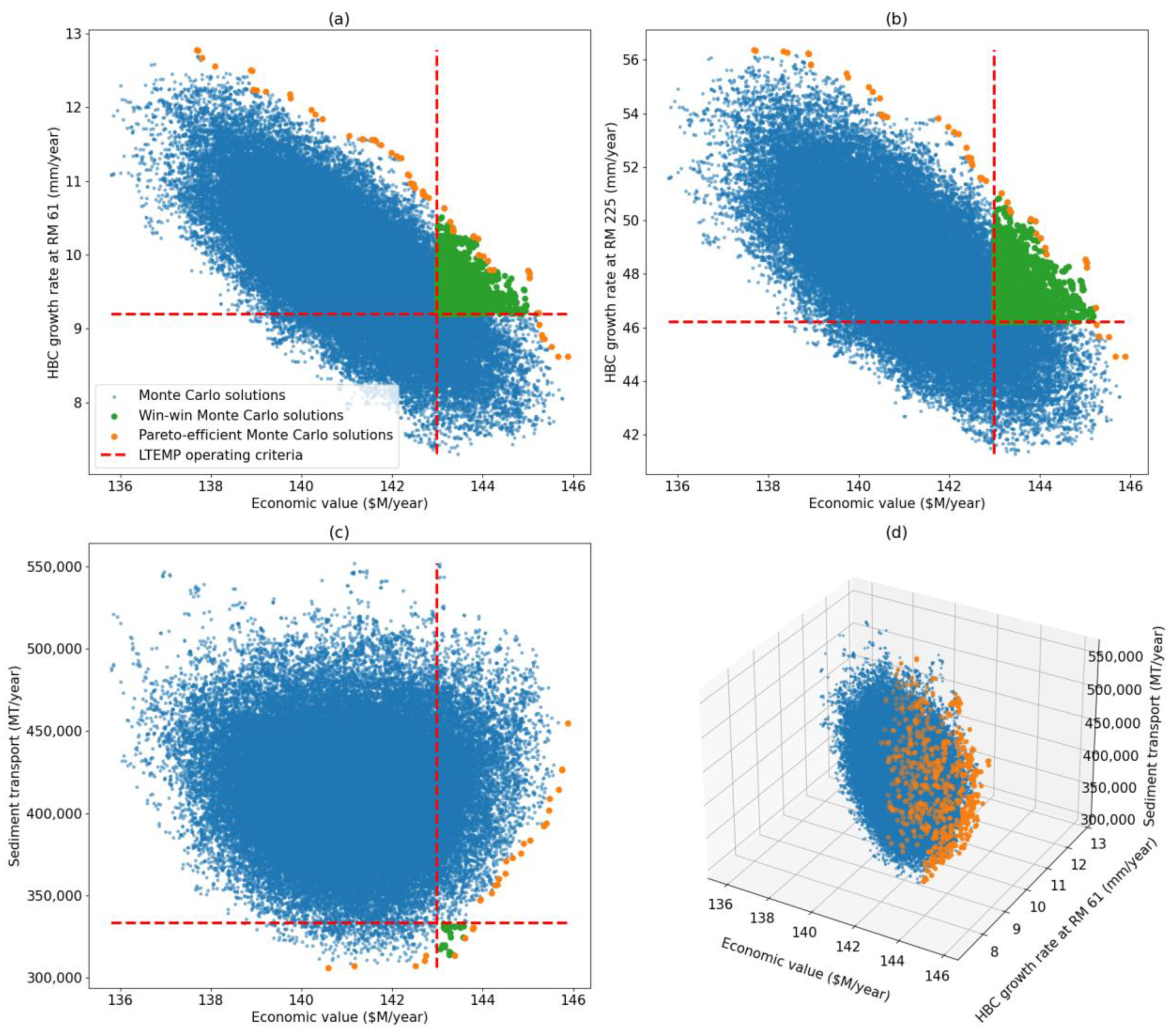
3.1. Results of the Monte Carlo Simulation
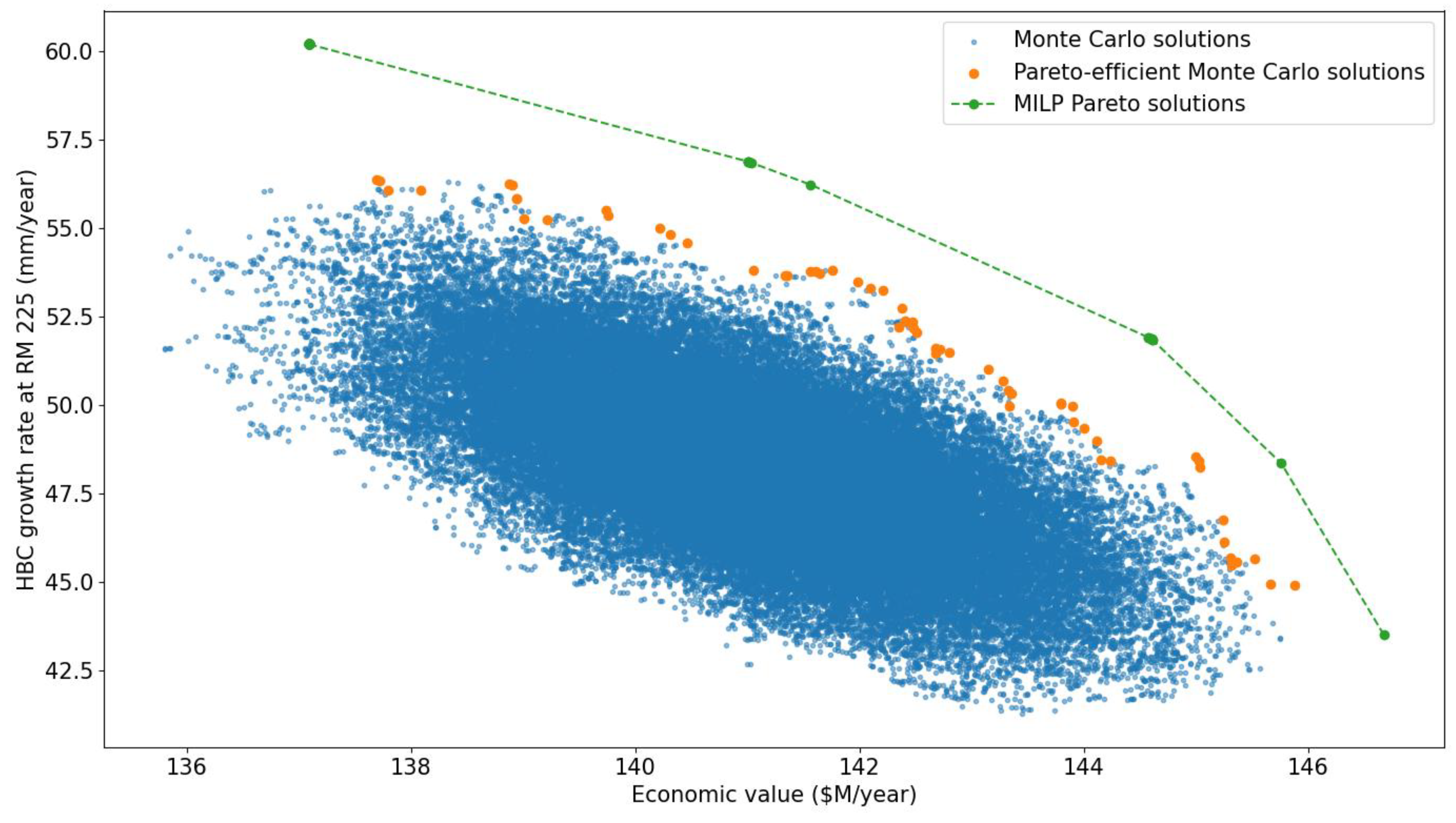
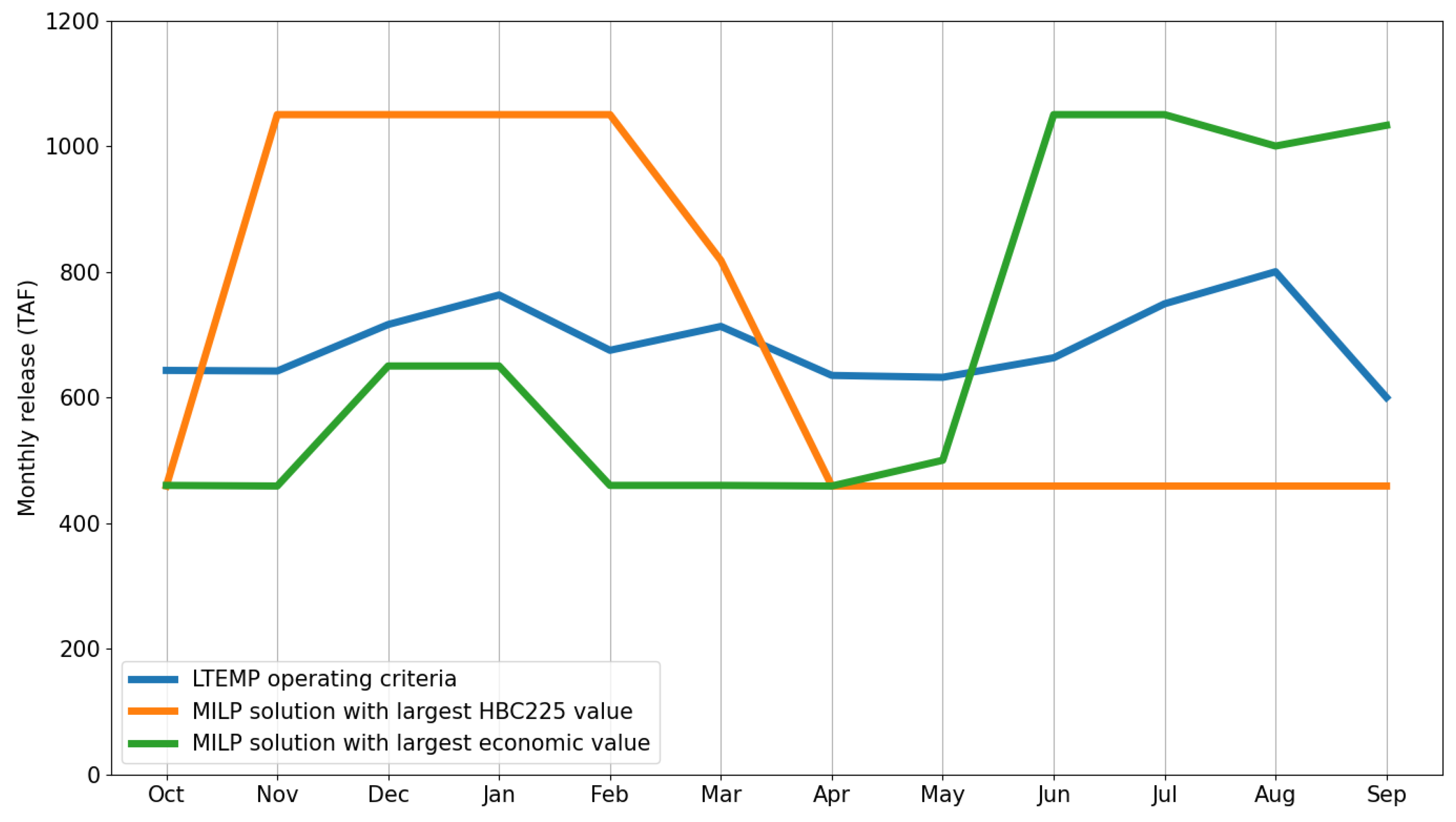
3.2. Results of the MILP MOO Problem
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Frans, H. Koch Hydropower—The Politics of Water and Energy: Introduction and Overview. Energy Policy 2002, 30, 1207–1213. [Google Scholar] [CrossRef]
- Han, S.-Y.; Kwak, S.-J.; Yoo, S.-H. Valuing Environmental Impacts of Large Dam Construction in Korea: An Application of Choice Experiments. Environ. Impact Assess. Rev. 2008, 28, 256–266. [Google Scholar] [CrossRef]
- Ge, Z.; Geng, Y.; Wei, W.; Jiang, M.; Chen, B.; Li, J. Embodied Carbon Emissions Induced by the Construction of Hydropower Infrastructure in China. Energy Policy 2023, 173, 113404. [Google Scholar] [CrossRef]
- Lu, S.; Dai, W.; Tang, Y.; Guo, M. A Review of the Impact of Hydropower Reservoirs on Global Climate Change. Sci. Total Environ. 2020, 711, 134996. [Google Scholar] [CrossRef]
- Collier, M.; Webb, R.H.; Schmidt, J.C. Dams and Rivers: A Primer on the Downstream Effects of Dams; U.S. Department of the Interior, U.S. Geological Survey: Reston, VA, USA, 1996; ISBN 978-0-607-86100-6.
- Botelho, A.; Ferreira, P.; Lima, F.; Pinto, L.M.C.; Sousa, S. Assessment of the Environmental Impacts Associated with Hydropower. Renew. Sustain. Energy Rev. 2017, 70, 896–904. [Google Scholar] [CrossRef]
- Kuriqi, A.; Pinheiro, A.N.; Sordo-Ward, A.; Bejarano, M.D.; Garrote, L. Ecological Impacts of Run-of-River Hydropower Plants—Current Status and Future Prospects on the Brink of Energy Transition. Renew. Sustain. Energy Rev. 2021, 142, 110833. [Google Scholar] [CrossRef]
- Soukhaphon, A.; Baird, I.G.; Hogan, Z.S. The Impacts of Hydropower Dams in the Mekong River Basin: A Review. Water 2021, 13, 265. [Google Scholar] [CrossRef]
- Richter, B.D.; Baumgartner, J.V.; Powell, J.; Braun, D.P. A Method for Assessing Hydrologic Alteration within Ecosystems. Conserv. Biol. 1996, 10, 11634174. [Google Scholar] [CrossRef]
- Poff, N.L.; Allan, J.D.; Bain, M.B.; Karr, J.R.; Prestegaard, K.L.; Richter, B.D.; Sparks, R.E.; Stromberg, J.C. The Natural Flow Regime. BioScience 1997, 47, 769–784. [Google Scholar] [CrossRef]
- Poff, L.N.; Richter, B.D.; Arthington, A.H.; Bunn, S.E.; Naiman, R.J.; Kendy, E.; Acreman, M.; Apse, C.; Bledsoe, B.P. The Ecological Limits of Hydrologic Alteration (ELOHA): A New Framework for Developing Regional Environmental Flow Standards. Freshw. Biol. 2010, 55, 147–170. [Google Scholar] [CrossRef]
- Moeller, K.L.; Malinowski, L.M.; Hoffecker, J.F. Analysis of Potential Impacts of Flaming Gorge Dam Hydropower Operations on Archaeological Sites; Argonne National Lab. (ANL): Argonne, IL, USA, 1955. [Google Scholar]
- Bodi, F.L. Protecting Columbia River Salmon Under the Endangered Species Act. Environ. Law 1980, 10, 349–387. [Google Scholar]
- Pontius, D. Colorado River Basin Study. Report to the Western Water Policy Review Advisory Committee. Federal Documents. 1997. Available online: https://digitalcommons.law.ggu.edu/cgi/viewcontent.cgi?article=1006&context=federal_documents (accessed on 19 January 2024).
- Renöfält, B.M.; Jansson, R.; Nilsson, C. Effects of Hydropower Generation and Opportunities for Environmental Flow Management in Swedish Riverine Ecosystems. Freshw. Biol. 2010, 55, 49–67. [Google Scholar] [CrossRef]
- U.S. Fish and Wildlife Service. Final Biological Opinion on the Operation of Flaming Gorge Dam. 1992. Available online: http://www.riversimulator.org/Resources/LawOfTheRiver/HooverDamDocs/Supplements/1992FinalBOFlamingGorgeDam.pdf (accessed on 19 January 2024).
- U.S. Forest Service. Biological Opinion for the Effects to Bull Trout from Continued Implementation of Land and Resource Management Plans and Resource Management Plans as Amended by the Interim Strategy for Managing Fish-Producing Watersheds in Eastern Oregon and Washington, Idaho, Western Montana, and Portions of Nevada (INFISH), and the Interim Strategy for Managing Anadromous Fish-Producing Watersheds in Eastern Oregon and Washington, Idaho, and Portions of California (PACFISH). 1998. Available online: https://www.fs.usda.gov/Internet/FSE_DOCUMENTS/stelprdb5427694.pdf (accessed on 19 January 2024).
- U.S. Department of the Interior. Operation of Flaming Gorge Dam Draft Environmental Impact Statement Executive Summary. Reclamation Managing Water in the West. 2004. Available online: https://www.uintahwater.org/sites/g/files/vyhlif1341/f/uploads/eis_executive_summary_september_2005.pdf (accessed on 19 January 2024).
- U.S. Department of the Interior. Record of Decision for the Glen Canyon Dam Long-Term Experimental and Management Plan Final Environmental Impact Statement; U.S. Department of the Interior: Washington, DC, USA, 2016.
- Ploussard, Q.; Veselka, T.D.; Palmer, C.S. Economic Analysis of Changes in Hydropower Operations at the Flaming Gorge Dam and the Aspinall Unit Due to the Upper Colorado River Endangered Fish Recovery Program; Argonne National Lab. (ANL): Argonne, IL, USA, 2022. [Google Scholar]
- U.S. Department of the Interior. Glen Canyon Dam Long-Term Experimental and Management Plan Draft Environmental Impact Statement. Available online: https://parkplanning.nps.gov/document.cfm?parkID=442&projectID=39292&documentID=70123 (accessed on 24 May 2023).
- Manikkuwahandi, T.D.S.; Hornberger, G.M.; Baroud, H. Decision Analysis for Expansion of Mahaweli Multipurpose Reservoir System in Sri Lanka. Water Resour. Plan. Res. 2019, 145, 05019013. [Google Scholar] [CrossRef]
- Ploussard, Q.; Veselka, T.D. Financial Analysis of the 2018 Glen Canyon Dam Bug Flow Experiment; Argonne National Lab. (ANL): Argonne, IL, USA, 2019. [Google Scholar]
- Ploussard, Q.; Veselka, T.D. Financial Analysis of Experimental Releases Conducted at Glen Canyon Dam during Water Year 2021; Argonne National Lab. (ANL): Argonne, IL, USA, 2022. [Google Scholar]
- Giupponi, C.; Sgobbi, A. Decision Support Systems for Water Resources Management in Developing Countries: Learning from Experiences in Africa. Water 2013, 5, 798–818. [Google Scholar] [CrossRef]
- Chinchuluun, A.; Pardalos, P.M.; Migdalas, A.; Pitsoulis, L. (Eds.) Pareto Optimality, Game Theory and Equilibria; Springer Optimization and Its Applications; Springer: New York, NY, USA, 2008; Volume 17, ISBN 978-0-387-77246-2. [Google Scholar]
- Dhaubanjar, S.; Davidsen, C.; Bauer-Gottwein, P. Multi-Objective Optimization for Analysis of Changing Trade-Offs in the Nepalese Water–Energy–Food Nexus with Hydropower Development. Water 2017, 9, 162. [Google Scholar] [CrossRef]
- De Silva Manikkuwahandi, T.; Hornberger, G.M. Deriving Reservoir Cascade Operation Rules for Variable Streamflows by Optimizing Hydropower Generation and Irrigation Water Delivery. J. Water Resour. Plan. Manag. 2021, 147, 05021007. [Google Scholar] [CrossRef]
- Giuliani, M.; Quinn, J.D.; Herman, J.D.; Castelletti, A.; Reed, P.M. Scalable Multiobjective Control for Large-Scale Water Resources Systems Under Uncertainty. IEEE Trans. Control. Syst. Technol. 2018, 26, 1492–1499. [Google Scholar] [CrossRef]
- Giuliani, M.; Castelletti, A.; Pianosi, F.; Mason, E.; Reed, P.M. Curses, Tradeoffs, and Scalable Management: Advancing Evolutionary Multiobjective Direct Policy Search to Improve Water Reservoir Operations. J. Water Resour. Plan. Manag. 2016, 142, 04015050. [Google Scholar] [CrossRef]
- Zhou, Y.; Guo, S.; Chang, F.-J.; Liu, P.; Chen, A.B. Methodology That Improves Water Utilization and Hydropower Generation without Increasing Flood Risk in Mega Cascade Reservoirs. Energy 2018, 143, 785–796. [Google Scholar] [CrossRef]
- Feng, Z.K.; Niu, W.J.; Cheng, C.T. Optimization of Hydropower Reservoirs Operation Balancing Generation Benefit and Ecological Requirement with Parallel Multi-Objective Genetic Algorithm. Energy 2018, 153, 706–718. [Google Scholar] [CrossRef]
- Yang, T.; Gao, X.; Sellars, S.L.; Sorooshian, S. Improving the Multi-Objective Evolutionary Optimization Algorithm for Hydropower Reservoir Operations in the California Oroville–Thermalito Complex. Environ. Model. Softw. 2015, 69, 262–279. [Google Scholar] [CrossRef]
- Mooney, C.Z. Monte Carlo Simulation; SAGE: Thousand Oaks, CA, USA, 1997; ISBN 978-0-8039-5943-9. [Google Scholar]
- PLEXOS Energy Modeling Software. Available online: https://www.energyexemplar.com/plexos (accessed on 9 January 2024).
- Reliability Modeling Anchor Data Set (ADS). Available online: https://www.wecc.org:443/ReliabilityModeling/Pages/AnchorDataSet.aspx (accessed on 9 January 2024).
- U.S. Fish & Wildlife Service. Humpback Chub Reclassified from Endangered to Threatened: Collaboration by Partners Has Improved Conservation Status. Available online: https://www.fws.gov/press-release/2021-10/humpback-chub-reclassified-endangered-threatened-collaboration-partners-has (accessed on 8 November 2023).
- Robinson, A.T.; Childs, M.R. Juvenile Growth of Native Fishes in the Little Colorado River and in a Thermally Modified Portion of the Colorado River. N. Am. J. Fish. Manag. 2001, 21, 809–815. [Google Scholar] [CrossRef]
- Kim, I.Y.; de Weck, O.L. Adaptive Weighted Sum Method for Multiobjective Optimization: A New Method for Pareto Front Generation. Struct. Multidisc. Optim. 2006, 31, 105–116. [Google Scholar] [CrossRef]
- He, H.; Daume, H., III; Eisner, J.M. Learning to Search in Branch and Bound Algorithms. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; Curran Associates, Inc.: Red Hook, NY, USA, 2014; Volume 27. [Google Scholar]
- Ploussard, Q. Piecewise Linear Approximation with Minimum Number of Linear Segments and Minimum Error: A Fast Approach to Tighten and Warm Start the Hierarchical Mixed Integer Formulation. Eur. J. Oper. Res. 2023. [Google Scholar] [CrossRef]
| Operating Rule | LTEMP Preferred Alternative |
|---|---|
| Monthly release volumes | As prescribed by [19] |
| Minimum release rate during the day (cfs) | 8000 |
| Minimum release rate at night (cfs) | 5000 |
| Maximum release rate (cfs) | 25,000 |
| Daily change limit (cfs/24-h) | Depends on the monthly release 1 |
| Up-ramp rate limit (cfs/h) | 4000 |
| Down-ramp rate limit (cfs/h) | 2500 |
| Metric Considered | Proportion of Monte Carlo Samples | ||||
|---|---|---|---|---|---|
| Economic Value | HBC Growth Rate at RM 61 | HBC Growth Rate at RM 225 | Sediment Transport | Win–Win Samples (%) | Pareto-Efficient Samples (%) |
| X | X | 2.8 | 0.075 | ||
| X | X | 3.7 | 0.065 | ||
| X | X | 0.036 | 0.036 | ||
| X | X | X | 2.7 | 0.087 | |
| X | X | X | 0 | 0.99 | |
| X | X | X | 0 | 0.90 | |
| X | X | X | X | 0 | 1.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ploussard, Q.; Veselka, T.; De Silva, T. Methodology for Exploring Water and Hydropower Operating Criteria That Simultaneously Improve Economic and Environmental Considerations. Water 2024, 16, 371. https://doi.org/10.3390/w16030371
Ploussard Q, Veselka T, De Silva T. Methodology for Exploring Water and Hydropower Operating Criteria That Simultaneously Improve Economic and Environmental Considerations. Water. 2024; 16(3):371. https://doi.org/10.3390/w16030371
Chicago/Turabian StylePloussard, Quentin, Thomas Veselka, and Thushara De Silva. 2024. "Methodology for Exploring Water and Hydropower Operating Criteria That Simultaneously Improve Economic and Environmental Considerations" Water 16, no. 3: 371. https://doi.org/10.3390/w16030371
APA StylePloussard, Q., Veselka, T., & De Silva, T. (2024). Methodology for Exploring Water and Hydropower Operating Criteria That Simultaneously Improve Economic and Environmental Considerations. Water, 16(3), 371. https://doi.org/10.3390/w16030371






