Integrating Convolutional Attention and Encoder–Decoder Long Short-Term Memory for Enhanced Soil Moisture Prediction
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Description
2.2. CAEDLSTM
2.2.1. Long Short-Term Memory Network (LSTM)
2.2.2. Convolutional Neural Network (CNN)
2.2.3. Encoder–Decoder Structure and Attention Mechanism
2.2.4. CAEDLSTM Model
- Convolutional Layer for Feature Extraction: The first stage of the CAEDLSTM model involves a convolutional layer that processes the input sequence. Unlike standard LSTMs, which tend to focus more on capturing long-term dependencies, the CNN component allows the model to capture localized patterns in the data. The 1D convolutional layer applies filters over the input sequence to extract high-level features, while max-pooling layers reduce the dimensionality of the input, retaining essential information. This step improves the model’s efficiency and enhances its ability to detect complex, localized patterns in multi-dimensional input data.
- Encoder–Decoder LSTM Structure: Once the CNN has extracted features, the data are passed through the LSTM encoder–decoder structure, which is enhanced by a multi-head attention mechanism. The encoder captures the long-term dependencies within the data, while the decoder uses these features to generate predictions based on both the encoded information and the original input. The attention mechanism dynamically assigns weights to different time steps and features, allowing the model to focus on the most relevant information for each prediction. By doing so, the CAEDLSTM model avoids treating all inputs equally and instead emphasizes the most influential aspects of the data, which is particularly crucial in capturing nonlinear and non-stationary behaviors, such as those found in soil moisture dynamics.
- Multi-Head Attention Mechanism: In the CAEDLSTM model, the multi-head attention mechanism is essential for enhancing predictive performance. Unlike traditional LSTM models, the attention layer dynamically weighs different time steps and features, enabling the model to capture crucial temporal and spatial correlations. This mechanism ensures that significant events or trends in the data receive appropriate focus while less critical information is down-weighted, resulting in more accurate and context-aware predictions.
- Output Layer: The final prediction is generated through a fully connected output layer that processes the combined information from the attention-enhanced LSTM decoder. This layer outputs predictions for future sequences based on both historical and current inputs, ensuring that the model captures the cumulative impact of all past and present data points. The CAEDLSTM model’s output is highly adaptable, making it well-suited for tasks such as soil moisture prediction and other environmental monitoring applications.
- Capture both long-term and short-term temporal patterns in multi-dimensional data with greater efficiency than traditional LSTMs.
- Prioritize important features and time steps using the attention mechanism, improving the overall accuracy and robustness of the model.
- Handle nonlinear relationships in the data by combining the strengths of CNNs and LSTMs, making them suitable for dynamic environmental conditions.
- Streamlining the Model: Investigating methods such as model pruning or weight quantization to reduce computational overhead, allowing the model to be applied in environments with constrained resources.
- Improving Data Utilization: Leveraging data-efficient strategies like data augmentation, transfer learning, or semi-supervised learning to lessen the dependency on large, high-quality datasets, improving performance where data are limited or noisy.
- Boosting Resilience: Introducing more adaptive frameworks or integrating alternative models, like graph neural networks, to better cope with extreme or unexpected events, enhancing the model’s reliability.
- Widening Application Scope: Extending the use of CAEDLSTM beyond soil moisture prediction to areas such as water resource management, ecosystem monitoring, or climate modeling, enhancing the model’s versatility and practical impact.
2.3. Model Setting and Training
2.4. Model Evaluation
3. Results
3.1. Box Plot Analysis of Predictive Performance in Soil Moisture Models
3.2. Comparative Analysis of CAEDLSTM Performance Through Cumulative Distribution Functions
3.3. Global Soil Moisture Prediction and Performance Enhancements
3.4. Evaluating the Temporal Generalization Capability of CAEDLSTM Models
3.5. Spectral Analysis of Model Performance in Soil Moisture Prediction
3.6. Comparative Analysis of CAEDLSTM and Random Forest Models
4. Discussion
5. Conclusions
- The CAEDLSTM model achieved an average increase of 5.01% in R2, a 12.89% reduction in RMSE, a 16.67% decrease in bias, and a 4.35% increase in KGE relative to the traditional LSTM model.
- It effectively addresses the limitations of traditional deep learning methods in challenging climates, including tropical Africa, the Tibetan Plateau, and Southeast Asia, resulting in significant enhancements in predictive accuracy within these regions, with R2 values improving by as much as 20%.
- The model effectively captures complex spatiotemporal dependencies in soil moisture dynamics, resulting in enhanced predictive accuracy.
- Its accurate predictions can inform optimized irrigation strategies, thereby supporting sustainable water resource management and contributing to conservation efforts in diverse agricultural and environmental contexts.
- One primary concern is the model’s susceptibility to varying environmental conditions, which may lead to performance fluctuations. This variability necessitates localized adaptations for effective practical application in different regions.
- The study’s assumption of broad applicability may not fully account for the intricate realities present in real-world scenarios. The complexities of these environments highlight the need for extensive empirical testing to ascertain the model’s robustness and versatility in diverse contexts.
- Validating the CAEDLSTM model across a range of geographical and climatic settings to thoroughly assess its robustness and adaptability. This will ensure that the model can perform effectively under different environmental conditions.
- Exploring the integration of the CAEDLSTM model with established physical and hydrological frameworks, which could further enhance its predictive capabilities and broaden its applicability in hydrological studies.
- Conducting an in-depth analysis of temporal dependencies and lag phenomena within the model to optimize its performance in dynamic environments. This exploration will contribute to a deeper understanding of how temporal factors influence soil moisture dynamics.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mimeau, L.; Tramblay, Y.; Brocca, L.; Massari, C.; Camici, S.; Finaud-Guyot, P. Modeling the response of soil moisture to climate variability in the Mediterranean region. Hydrol. Earth Syst. Sci. 2021, 25, 653–669. [Google Scholar] [CrossRef]
- Wang, C.; Fu, B.; Zhang, L.; Xu, Z. Soil moisture–plant interactions: An ecohydrological review. J. Soils Sediments 2019, 19, 1–9. [Google Scholar] [CrossRef]
- Deng, Y.; Wang, S.; Bai, X.; Luo, G.; Wu, L.; Cao, Y.; Li, H.; Li, C.; Yang, Y.; Hu, Z.; et al. Variation trend of global soil moisture and its cause analysis. Ecol. Indic. 2020, 110, 105939. [Google Scholar] [CrossRef]
- Giles, J.A.; Menéndez, C.G.; Ruscica, R.C. Nonlocal impacts of soil moisture variability in South America: Linking two land–atmosphere coupling hot spots. J. Clim. 2023, 36, 227–242. [Google Scholar] [CrossRef]
- Meza, F.J.; Montes, C.; Bravo-Martínez, F.; Serrano-Ortiz, P.; Kowalski, A.S. Soil water content effects on net ecosystem CO2 exchange and actual evapotranspiration in a Mediterranean semiarid savanna of Central Chile. Sci. Rep. 2018, 8, 8570. [Google Scholar] [CrossRef]
- Wasko, C.; Nathan, R. Influence of changes in rainfall and soil moisture on trends in flooding. J. Hydrol. 2019, 575, 432–441. [Google Scholar] [CrossRef]
- Sahoo, S.; Sahoo, B. Assessing Spatially-Distributed Soil Moisture Under Changing Land Uses and Climate. In Climate Change Impacts on Soil-Plant-Atmosphere Continuum; Springer Nature: Singapore, 2024; pp. 209–228. [Google Scholar] [CrossRef]
- Deng, L.; Wang, K.; Li, J.; Zhao, G.; Shangguan, Z. Effect of soil moisture and atmospheric humidity on both plant productivity and diversity of native grasslands across the Loess Plateau, China. Ecol. Eng. 2016, 94, 525–531. [Google Scholar] [CrossRef]
- Ray, S.; Majumder, S. Water management in agriculture: Innovations for efficient irrigation. In Modern Agronomy; International Books & Periodical Supply Service: New Delhi, India, 2024; pp. 169–185. Available online: https://www.researchgate.net/publication/381867727_Water_Management_in_Agriculture_Innovations_for_Efficient_Irrigation (accessed on 15 September 2024).
- Schweppe, R.; Thober, S.; Müller, S.; Kelbling, M.; Kumar, R.; Attinger, S.; Samaniego, L. MPR 1.0: A stand-alone multiscale parameter regionalization tool for improved parameter estimation of land surface models. Geosci. Model Dev. 2022, 15, 859–882. [Google Scholar] [CrossRef]
- Akoko, G.; Le, T.H.; Gomi, T.; Kato, T. A review of SWAT model application in Africa. Water 2021, 13, 1313. [Google Scholar] [CrossRef]
- Šimunek, J.; Van Genuchten, M.T.; Šejna, M. HYDRUS: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1263–1274. [Google Scholar] [CrossRef]
- Bakker, M.; Post, V.; Langevin, C.D.; Hughes, J.D.; White, J.T.; Starn, J.J.; Fienen, M.N. Scripting MODFLOW model development using Python and FloPy. Groundwater 2016, 54, 733–739. [Google Scholar] [CrossRef] [PubMed]
- Sabzipour, B.; Arsenault, R.; Troin, M.; Martel, J.-L.; Brissette, F.; Brunet, F.; Mai, J. Comparing a long short-term memory (LSTM) neural network with a physically-based hydrological model for streamflow forecasting over a Canadian catchment. J. Hydrol. 2023, 627, 130380. [Google Scholar] [CrossRef]
- Hong, Z.; Kalbarczyk, Z.; Iyer, R.K. A data-driven approach to soil moisture collection and prediction. In Proceedings of the 2016 IEEE International Conference on Smart Computing (SMARTCOMP), St. Louis, MO, USA, 18–20 May 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Zhao, W.; Li, A.; Huang, P.; He, J.; Ma, X. Surface soil moisture relationship model construction based on random forest method. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 2019–2022. [Google Scholar] [CrossRef]
- Qiu, Y.; Fu, B.; Wang, J.; Chen, L.; Meng, Q.; Zhang, Y. Spatial prediction of soil moisture content using multiple-linear regressions in a gully catchment of the Loess Plateau, China. J. Arid Environ. 2010, 74, 208–220. [Google Scholar] [CrossRef]
- Mabunga, Z.P.; Cruz, J.C.D. An optimized soil moisture prediction model for smart agriculture using Gaussian process regression. In Proceedings of the 2022 IEEE 18th International Colloquium on Signal Processing & Applications (CSPA), Selangor, Malaysia, 12–12 May 2022; pp. 243–247. [Google Scholar] [CrossRef]
- Elshorbagy, A.; Parasuraman, K. On the relevance of using artificial neural networks for estimating soil moisture content. J. Hydrol. 2008, 362, 1–18. [Google Scholar] [CrossRef]
- Saxe, A.M.; Bansal, Y.; Dapello, J.; Advani, M.; Kolchinsky, A.; Tracey, B.D.; Cox, D.D. On the information bottleneck theory of deep learning. J. Stat. Mech. Theory Exp. 2019, 2019, 124020. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Filipović, N.; Brdar, S.; Mimić, G.; Marko, O.; Crnojević, V. Regional soil moisture prediction system based on Long Short-Term Memory network. Biosyst. Eng. 2022, 213, 30–38. [Google Scholar] [CrossRef]
- Arsenault, R.; Martel, J.-L.; Brunet, F.; Brissette, F.; Mai, J. Continuous streamflow prediction in ungauged basins: Long short-term memory neural networks clearly outperform traditional hydrological models. Hydrol. Earth Syst. Sci. 2023, 27, 139–157. [Google Scholar] [CrossRef]
- Fang, K.; Shen, C. Near-real-time forecast of satellite-based soil moisture using long short-term memory with an adaptive data integration kernel. J. Hydrometeorol. 2020, 21, 399–413. [Google Scholar] [CrossRef]
- Datta, P.; Faroughi, S.A. A multihead LSTM technique for prognostic prediction of soil moisture. Geoderma 2023, 433, 116452. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, J.; Wang, J. High-resolution load forecasting on multiple time scales using Long Short-Term Memory and Support Vector Machine. Energies 2023, 16, 1806. [Google Scholar] [CrossRef]
- Zargar, S. Introduction to Sequence Learning Models: RNN, LSTM, GRU. Ph.D. Thesis, Department of Mechanical and Aerospace Engineering, North Carolina State University, Raleigh, NC, USA, 2021. [Google Scholar] [CrossRef]
- Hnamte, V.; Nhung-Nguyen, H.; Hussain, J.; Hwa-Kim, Y. A novel two-stage deep learning model for network intrusion detection: LSTM-AE. IEEE Access 2023, 11, 37131–37148. [Google Scholar] [CrossRef]
- Zhu, Q.; Liao, K.; Xu, Y.; Yang, G.; Wu, S.; Zhou, S. Monitoring and prediction of soil moisture spatial–temporal variations from a hydropedological perspective: A review. Soil Res. 2013, 50, 625–637. [Google Scholar] [CrossRef]
- Sagheer, A.; Kotb, M. Unsupervised pre-training of a deep LSTM-based stacked autoencoder for multivariate time series forecasting problems. Sci. Rep. 2019, 9, 19038. [Google Scholar] [CrossRef]
- Du, S.; Li, T.; Yang, Y.; Horng, S.-J. Multivariate time series forecasting via attention-based encoder–decoder framework. Neurocomputing 2020, 388, 269–279. [Google Scholar] [CrossRef]
- Li, Q.; Li, Z.; Shangguan, W.; Wang, X.; Li, L.; Yu, F. Improving soil moisture prediction using a novel encoder-decoder model with residual learning. Comput. Electron. Agric. 2022, 195, 106816. [Google Scholar] [CrossRef]
- Han, D.; Liu, P.; Xie, K.; Li, H.; Xia, Q.; Cheng, Q.; Wang, Y.; Yang, Z.; Zhang, Y.; Xia, J. An attention-based LSTM model for long-term runoff forecasting and factor recognition. Environ. Res. Lett. 2023, 18, 024004. [Google Scholar] [CrossRef]
- Li, P.; Zhang, J.; Krebs, P. Prediction of flow based on a CNN-LSTM combined deep learning approach. Water 2022, 14, 993. [Google Scholar] [CrossRef]
- Fan, H.; Jiang, M.; Xu, L.; Zhu, H.; Cheng, J.; Jiang, J. Comparison of long short term memory networks and the hydrological model in runoff simulation. Water 2020, 12, 175. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, C.; Shangguan, W.; Wei, Z.; Yuan, H.; Zhu, J.; Li, X.; Li, L.; Li, G.; Liu, P.; et al. LandBench 1.0: A benchmark dataset and evaluation metrics for data-driven land surface variables prediction. Expert Syst. Appl. 2024, 243, 122917. [Google Scholar] [CrossRef]
- Yan, Y.; Li, G.; Li, Q.; Zhu, J. Enhancing hydrological variable prediction through multitask LSTM models. Water 2024, 16, 2156. [Google Scholar] [CrossRef]
- Li, Q.; Xiao, Q.; Zhang, C.; Zhu, J.; Chen, X.; Yan, Y.; Liu, P.; Shangguan, W.; Wei, Z.; Li, L.; et al. Improving global soil moisture prediction through cluster-averaged sampling strategy. Geoderma 2024, 449, 116999. [Google Scholar] [CrossRef]
- Xie, K.; Liu, P.; Xia, Q.; Li, X.; Liu, W.; Zhang, X.; Cheng, L.; Wang, G.; Zhang, J. Global soil moisture storage capacity at 0.5° resolution for geoscientific modelling. Earth Syst. Sci. Data Discuss. 2022, 14, 4473–4488. [Google Scholar] [CrossRef]
- Friedl, M.A.; Sulla-Menashe, D.; Tan, B.; Schneider, A.; Ramankutty, N.; Sibley, A.; Huang, X. MODIS Collection 5 global land cover: Algorithm refinements and characterization of new datasets. Remote Sens. Environ. 2010, 114, 168–182. [Google Scholar] [CrossRef]
- Tarek, M.; Brissette, F.P.; Arsenault, R. Evaluation of the ERA5 reanalysis as a potential reference dataset for hydrological modelling over North America. Hydrol. Earth Syst. Sci. 2020, 24, 2527–2544. [Google Scholar] [CrossRef]
- Valipour, M.; Dietrich, J. Developing ensemble mean models of satellite remote sensing, climate reanalysis, and land surface models. Theor. Appl. Climatol. 2022, 150, 909–926. [Google Scholar] [CrossRef]
- Poggio, L.; de Sousa, L.M.; Batjes, N.H.; Heuvelink, G.B.M.; Kempen, B.; Ribeiro, E.; Rossiter, D. SoilGrids 2.0: Producing soil information for the globe with quantified spatial uncertainty. Soil 2021, 7, 217–240. [Google Scholar] [CrossRef]
- Jiang, Q.; Li, W.; Fan, Z.; He, X.; Sun, W.; Chen, S.; Wen, J.; Gao, J.; Wang, J. Evaluation of the ERA5 reanalysis precipitation dataset over Chinese Mainland. J. Hydrol. 2021, 595, 125660. [Google Scholar] [CrossRef]
- Gomis-Cebolla, J.; Rattayova, V.; Salazar-Galán, S.; Francés, F. Evaluation of ERA5 and ERA5-Land reanalysis precipitation datasets over Spain (1951–2020). Atmos. Res. 2023, 284, 106606. [Google Scholar] [CrossRef]
- McColl, K.A.; Alemohammad, S.H.; Akbar, R.; Konings, A.G.; Yueh, S.; Entekhabi, D. The global distribution and dynamics of surface soil moisture. Nat. Geosci. 2017, 10, 100–104. [Google Scholar] [CrossRef]
- Gelati, E.; Decharme, B.; Calvet, J.-C.; Minvielle, M.; Polcher, J.; Fairbairn, D.; Weedon, G.P. Hydrological assessment of atmospheric forcing uncertainty in the Euro-Mediterranean area using a land surface model. Hydrol. Earth Syst. Sci. 2018, 22, 2091–2115. [Google Scholar] [CrossRef]
- Guan, X.; Huang, J.; Guo, N.; Bi, J.; Wang, G. Variability of soil moisture and its relationship with surface albedo and soil thermal parameters over the Loess Plateau. Adv. Atmos. Sci. 2009, 26, 692–700. [Google Scholar] [CrossRef]
- Small, E.E.; Kurc, S.A. Tight coupling between soil moisture and the surface radiation budget in semiarid environments: Implications for land-atmosphere interactions. Water Resour. Res. 2003, 39, 1278. [Google Scholar] [CrossRef]
- Wetzel, P.J.; Chang, J.T. Concerning the relationship between evapotranspiration and soil moisture. J. Appl. Meteorol. Climatol. 1987, 26, 18–27. [Google Scholar] [CrossRef]
- Yamazaki, D.; Ikeshima, D.; Tawatari, R.; Yamaguchi, T.; O’Loughlin, F.; Neal, J.C.; Sampson, C.C.; Kanae, S.; Bates, P.B. A high-accuracy map of global terrain elevations. Geophys. Res. Lett. 2017, 44, 5844–5853. [Google Scholar] [CrossRef]
- Sherstinsky, A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. Adv. Neural Inf. Process. Syst. 2019, 32, 8024–8035. [Google Scholar] [CrossRef]
- Namatēvs, I. Deep convolutional neural networks: Structure, feature extraction and training. Inf. Technol. Manag. Sci. 2017, 20, 40–47. [Google Scholar] [CrossRef]
- Wang, S.; Mu, L.; Liu, D. A hybrid approach for El Niño prediction based on Empirical Mode Decomposition and convolutional LSTM Encoder-Decoder. Comput. Geosci. 2021, 149, 104695. [Google Scholar] [CrossRef]
- Zheng, S.; Lu, J.; Zhao, H.; Zhu, X.; Luo, Z.; Wang, Y.; Fu, Y.; Feng, J.; Xiang, T.; Torr, P.H.; et al. Rethinking semantic segmentation from a sequence-to-sequence perspective with transformers. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 6881–6890. [Google Scholar] [CrossRef]
- Reza, S.; Ferreira, M.C.; Machado, J.; Tavares, J.M.R. A multi-head attention-based transformer model for traffic flow forecasting with a comparative analysis to recurrent neural networks. Expert Syst. Appl. 2022, 202, 117275. [Google Scholar] [CrossRef]
- Vaswani, A. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. Available online: https://user.phil.hhu.de/~cwurm/wp-content/uploads/2020/01/7181-attention-is-all-you-need.pdf (accessed on 15 September 2024).
- Ratner, B. The correlation coefficient: Its values range between+1/−1, or do they? J. Target. Meas. Anal. Mark. 2009, 17, 139–142. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. Peerj Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef] [PubMed]
- Knoben WJ, M.; Freer, J.E.; Woods, R.A. Inherent benchmark or not? Comparing Nash–Sutcliffe and Kling–Gupta efficiency scores. Hydrol. Earth Syst. Sci. 2019, 23, 4323–4331. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE). Geosci. Model Dev. Discuss. 2014, 7, 1525–1534. [Google Scholar] [CrossRef]
- Alan, A.R.; Bayındır, C.; Ozaydin, F.; Altintas, A.A. The Predictability of the 30 October 2020 İzmir-Samos Tsunami Hydrodynamics and Enhancement of Its Early Warning Time by LSTM Deep Learning Network. Water 2023, 15, 4195. [Google Scholar] [CrossRef]
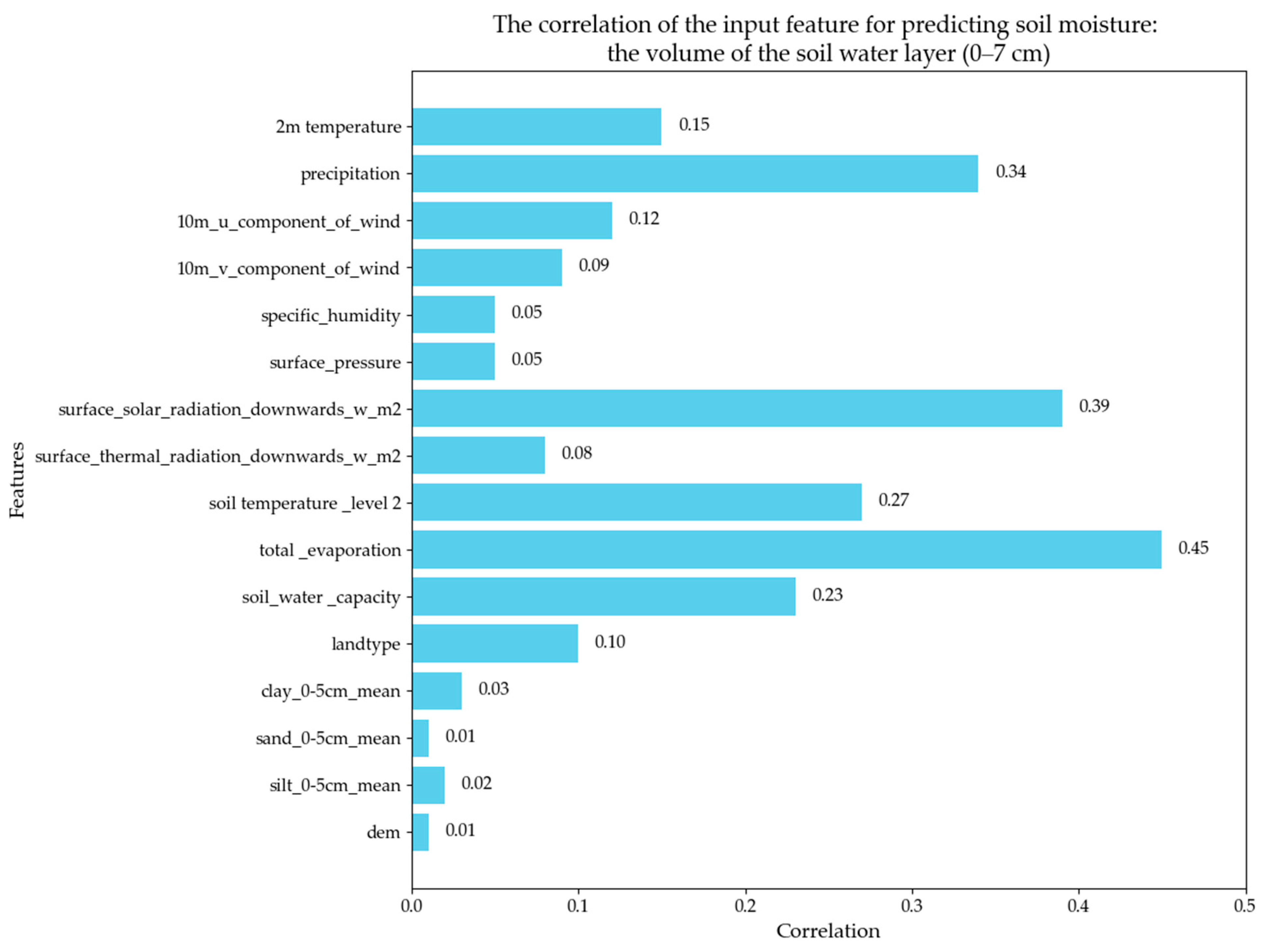









| Long Name | Description | Unit |
|---|---|---|
| Land surface variables from ERA5-Land | ||
| Volumetric soil water layer 1 | Volume of water in soil layer 1 (0–7 cm) | m3/m3 |
| Surface solar radiation downwards | Amount of surface solar radiation | J/m2 |
| Surface thermal radiation downwards | Amount of surface thermal radiation | J/m2 |
| Soil temperature level 1 | Temperature of the soil in layer 1 (0–7 cm) | K |
| Evaporation | Accumulated amount of water vapor | m |
| Atmospheric variables from ERA5 | ||
| Precipitation | Daily precipitation | m |
| 2m_Temperature | Temperature of air at 2 m above the surface of land or inland waters | K |
| U component of wind | Wind in x/longitude direction | m/s |
| V component of wind | Wind in y/latitude direction | m/s |
| Surface_pressure | Surface pressure | Pa |
| Specific_humidity | Mixing ratio of water vapor | kg/kg |
| Static variables | ||
| Clay (from SoilGrid) | Clay content | g/kg |
| Sand (from SoilGrid) | Sand content | g/kg |
| Silt (from SoilGrid) | Silt content | g/kg |
| Soil water capacity | Reconstructed soil moisture storage capacity | mm |
| Vegetation type | Physical and biological material that covers the Earth’s surface | none |
| DEM | Ground elevation | m |
| Learning Rate | Hidden Size | Batch Size | Epoch | Niter | R |
|---|---|---|---|---|---|
| 0.01 | 128 | 64 | 1000 | 400 | 0.8564 |
| 0.001 | 128 | 64 | 1000 | 400 | 0.9543 |
| 0.0001 | 128 | 64 | 1000 | 400 | 0.9391 |
| 0.001 | 64 | 64 | 1000 | 400 | 0.9437 |
| 0.001 | 256 | 64 | 1000 | 400 | 0.9455 |
| 0.001 | 128 | 32 | 1000 | 400 | 0.9359 |
| 0.001 | 128 | 128 | 1000 | 400 | 0.9524 |
| 0.001 | 128 | 64 | 500 | 400 | 0.9420 |
| 0.001 | 128 | 64 | 1500 | 400 | 0.9543 |
| 0.001 | 128 | 64 | 1000 | 200 | 0.9361 |
| 0.001 | 128 | 64 | 1000 | 600 | 0.9463 |
| Model | Frequency-Domain RMSE | Frequency-Domain R2 |
|---|---|---|
| CAEDLSTM | 0.0011 | 0.9995 |
| AEDLSTM | 0.0014 | 0.9992 |
| AttLSTM | 0.0018 | 0.9986 |
| EDLSTM | 0.0017 | 0.9988 |
| CNNLSTM | 0.0019 | 0.9986 |
| LSTM | 0.0017 | 0.9989 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, J.; Hong, J.; Chen, X.; Wang, J.; Zhu, J.; Li, X.; Yan, Y.; Li, Q. Integrating Convolutional Attention and Encoder–Decoder Long Short-Term Memory for Enhanced Soil Moisture Prediction. Water 2024, 16, 3481. https://doi.org/10.3390/w16233481
Han J, Hong J, Chen X, Wang J, Zhu J, Li X, Yan Y, Li Q. Integrating Convolutional Attention and Encoder–Decoder Long Short-Term Memory for Enhanced Soil Moisture Prediction. Water. 2024; 16(23):3481. https://doi.org/10.3390/w16233481
Chicago/Turabian StyleHan, Jingfeng, Jian Hong, Xiao Chen, Jing Wang, Jinlong Zhu, Xiaoning Li, Yuguang Yan, and Qingliang Li. 2024. "Integrating Convolutional Attention and Encoder–Decoder Long Short-Term Memory for Enhanced Soil Moisture Prediction" Water 16, no. 23: 3481. https://doi.org/10.3390/w16233481
APA StyleHan, J., Hong, J., Chen, X., Wang, J., Zhu, J., Li, X., Yan, Y., & Li, Q. (2024). Integrating Convolutional Attention and Encoder–Decoder Long Short-Term Memory for Enhanced Soil Moisture Prediction. Water, 16(23), 3481. https://doi.org/10.3390/w16233481






