Evaluating Hydrologic Model Performance for Characterizing Streamflow Drought in the Conterminous United States
Abstract
1. Introduction
- Error Components: How well the models simulate the timing, magnitude, and variability of streamflow during periods of drought according to Spearman’s r [46], percent bias, and the ratio of standard deviations, respectively. This approach examines how errors in streamflow are split across these three components [47].
- Drought Signatures: How well the models simulate drought duration, intensity, and severity according to the normalized mean absolute errors of annualized data. These three drought characteristics are widely used by the research community and play a large role in the impact of droughts.
2. Materials and Methods
2.1. Modeling Applications and Observed Data
2.1.1. Modeling Applications
2.1.2. Observed Data
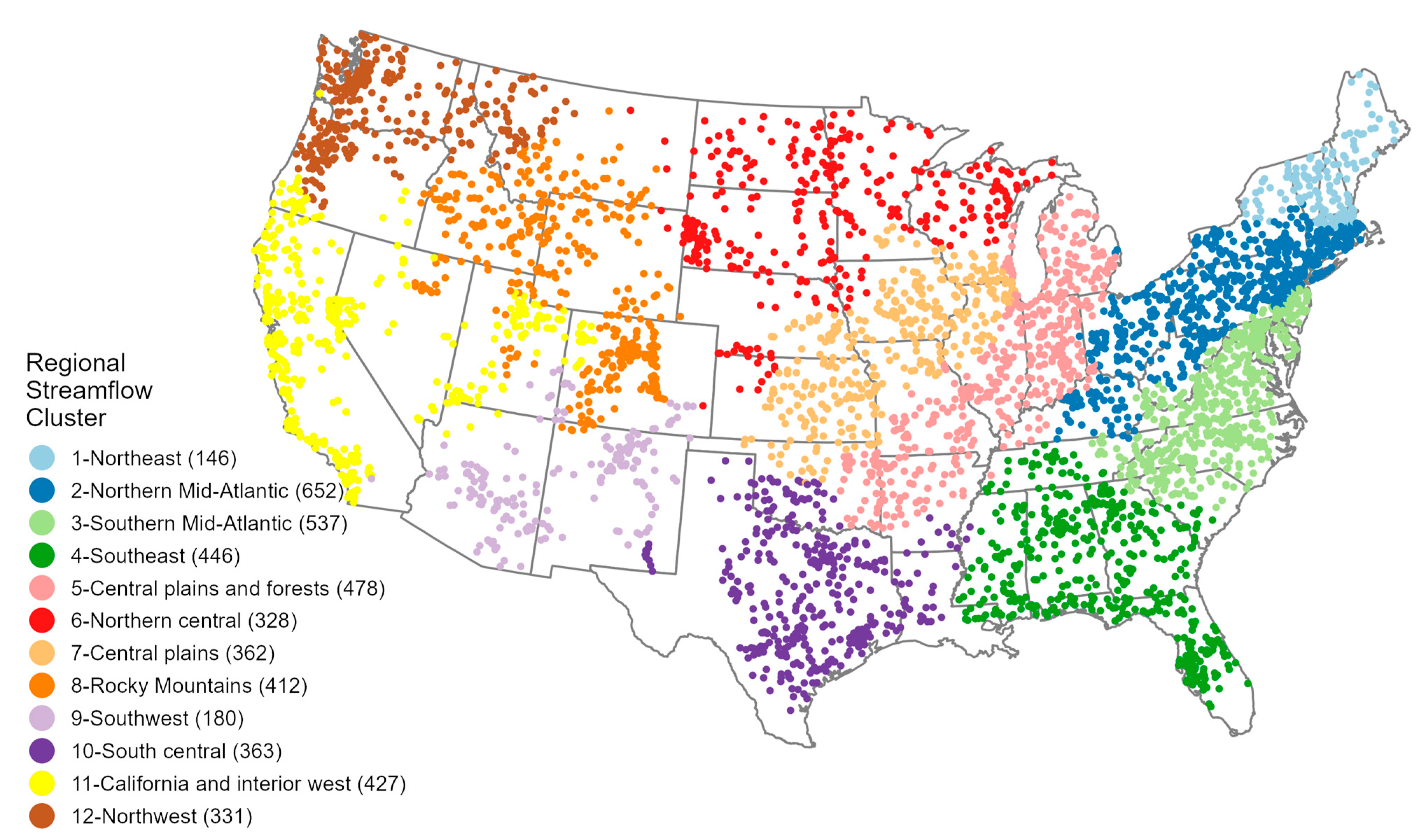
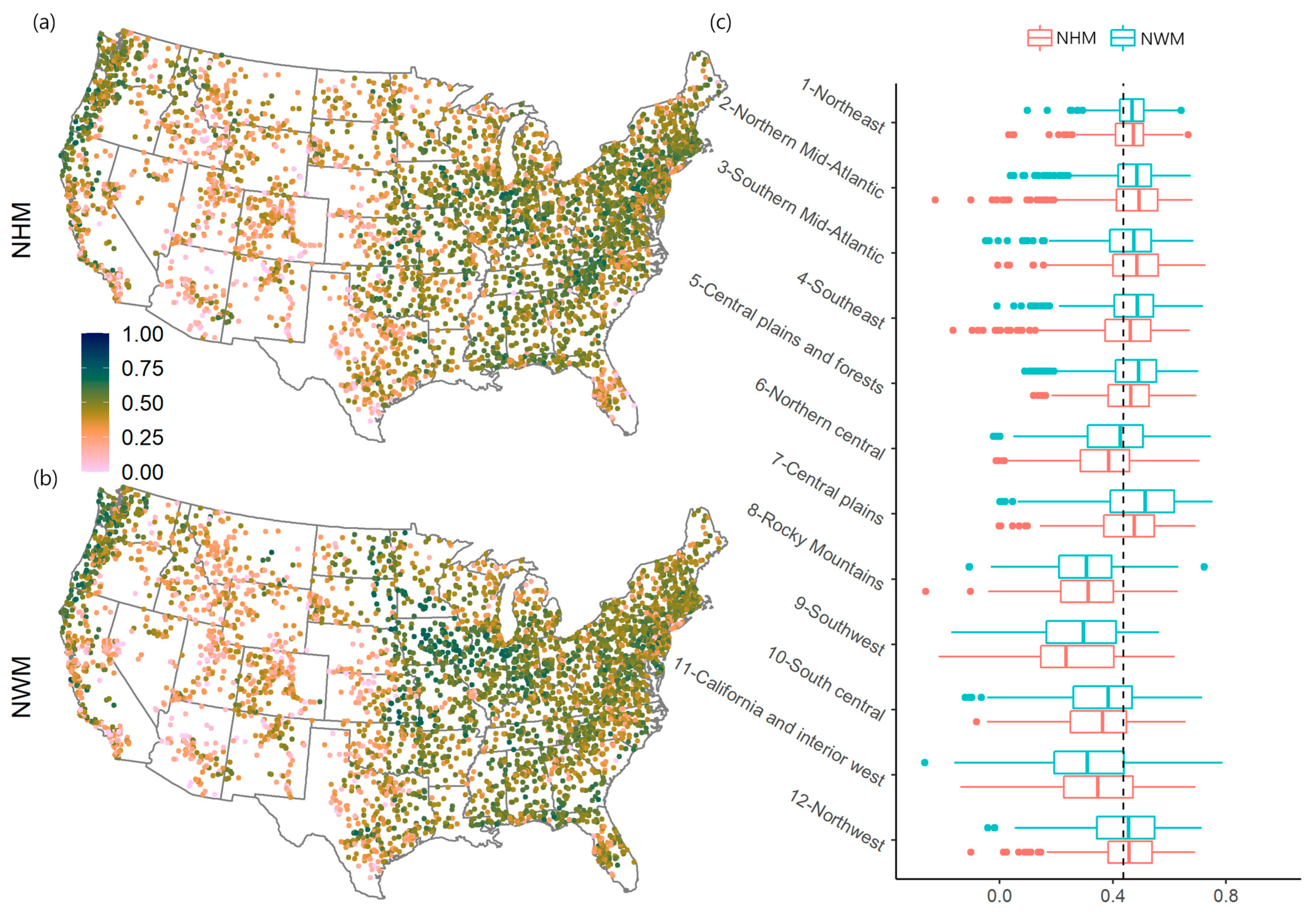
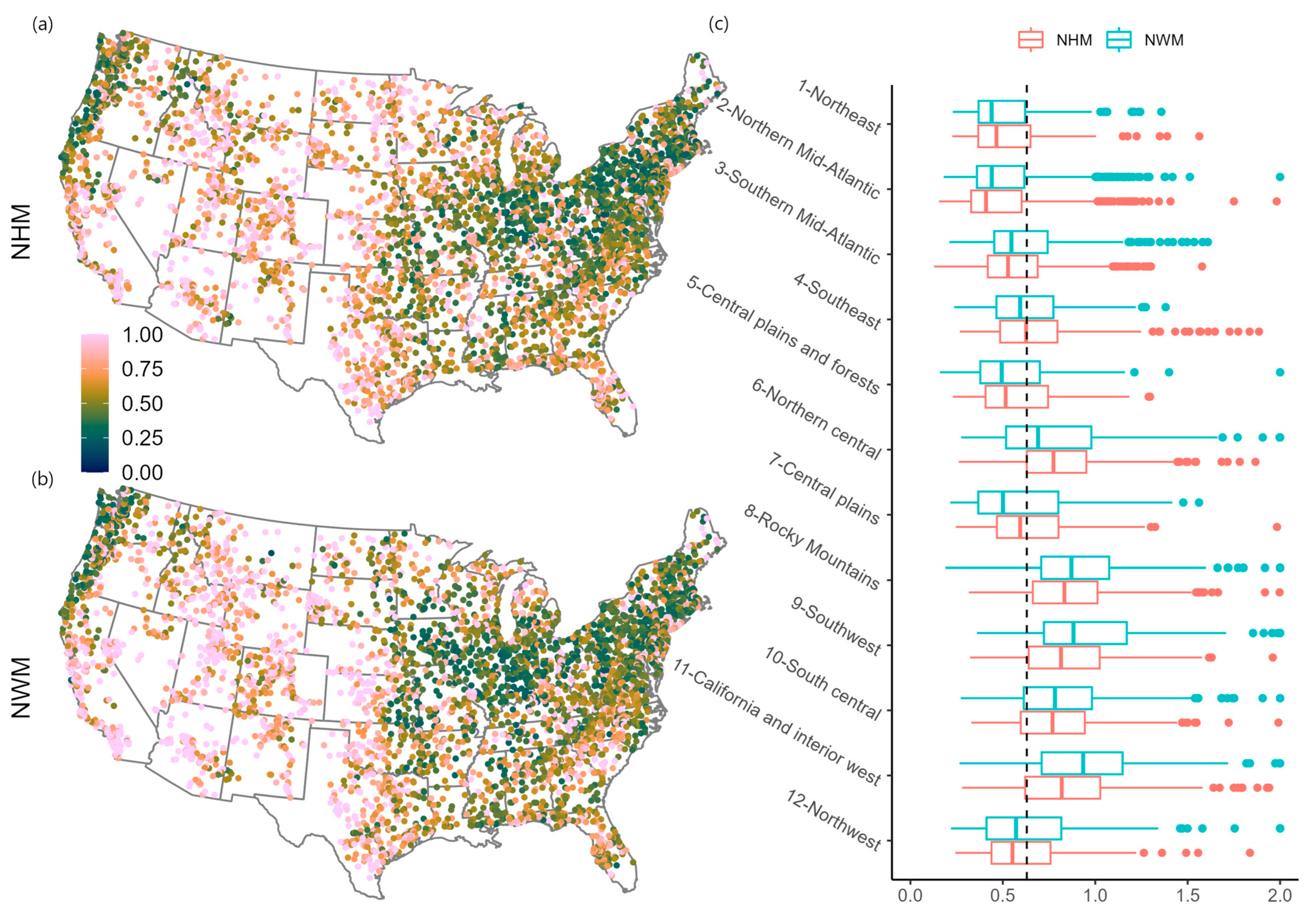
2.1.3. Evaluating Regional Performance
2.2. Identification of Drought
- Drought duration: the total number of days below the threshold (days);
- Drought severity: the sum of flow departures or deficit below the threshold (cms-days);
- Drought intensity: the maximum drought intensity (minimum percentiles).
2.3. Evaluation for Drought Performance
2.3.1. Event Classification Evaluation
2.3.2. Error Components Evaluation
2.3.3. Drought Signatures Evaluation
3. Results
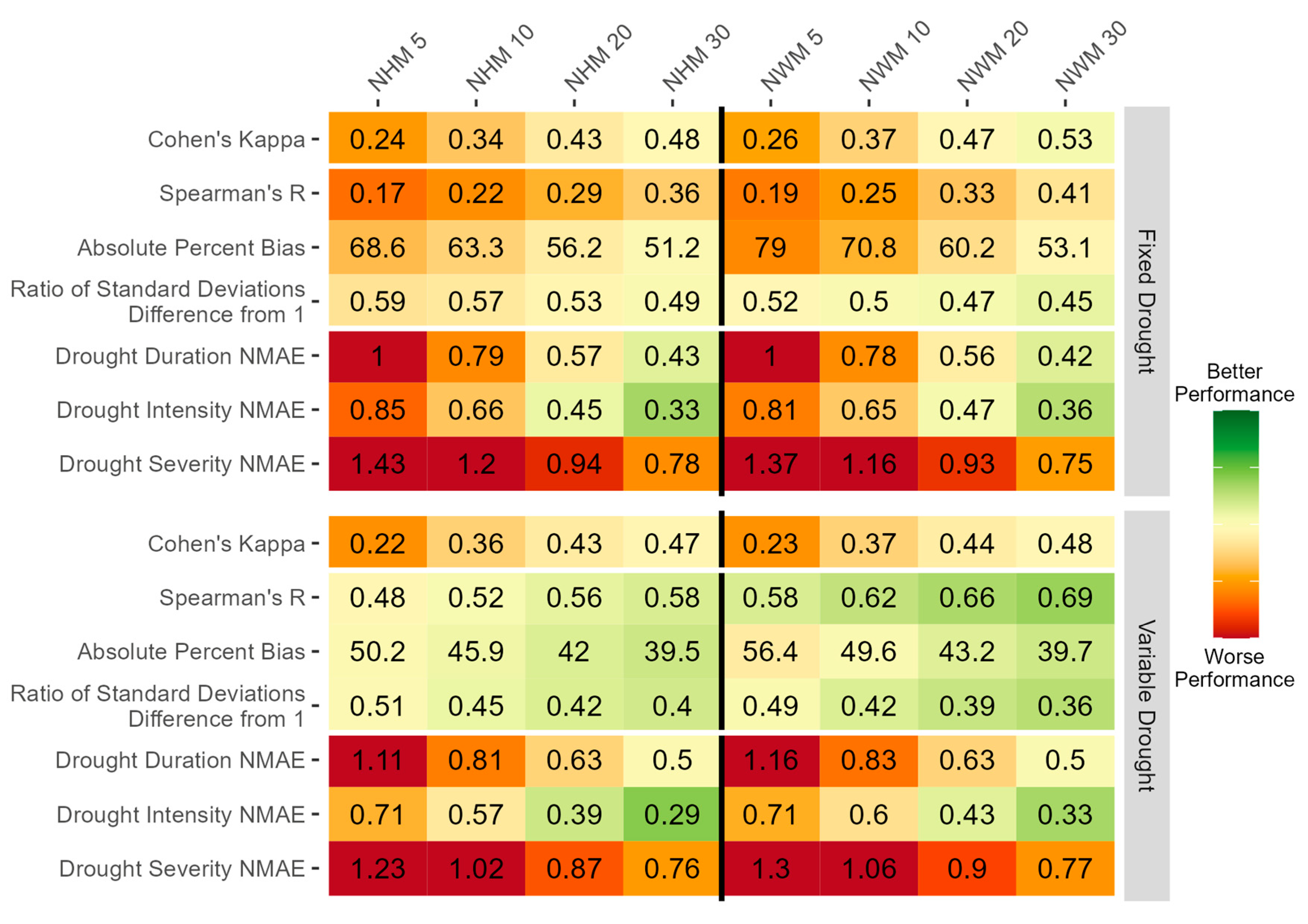
3.1. Event Classification
3.2. Error Components
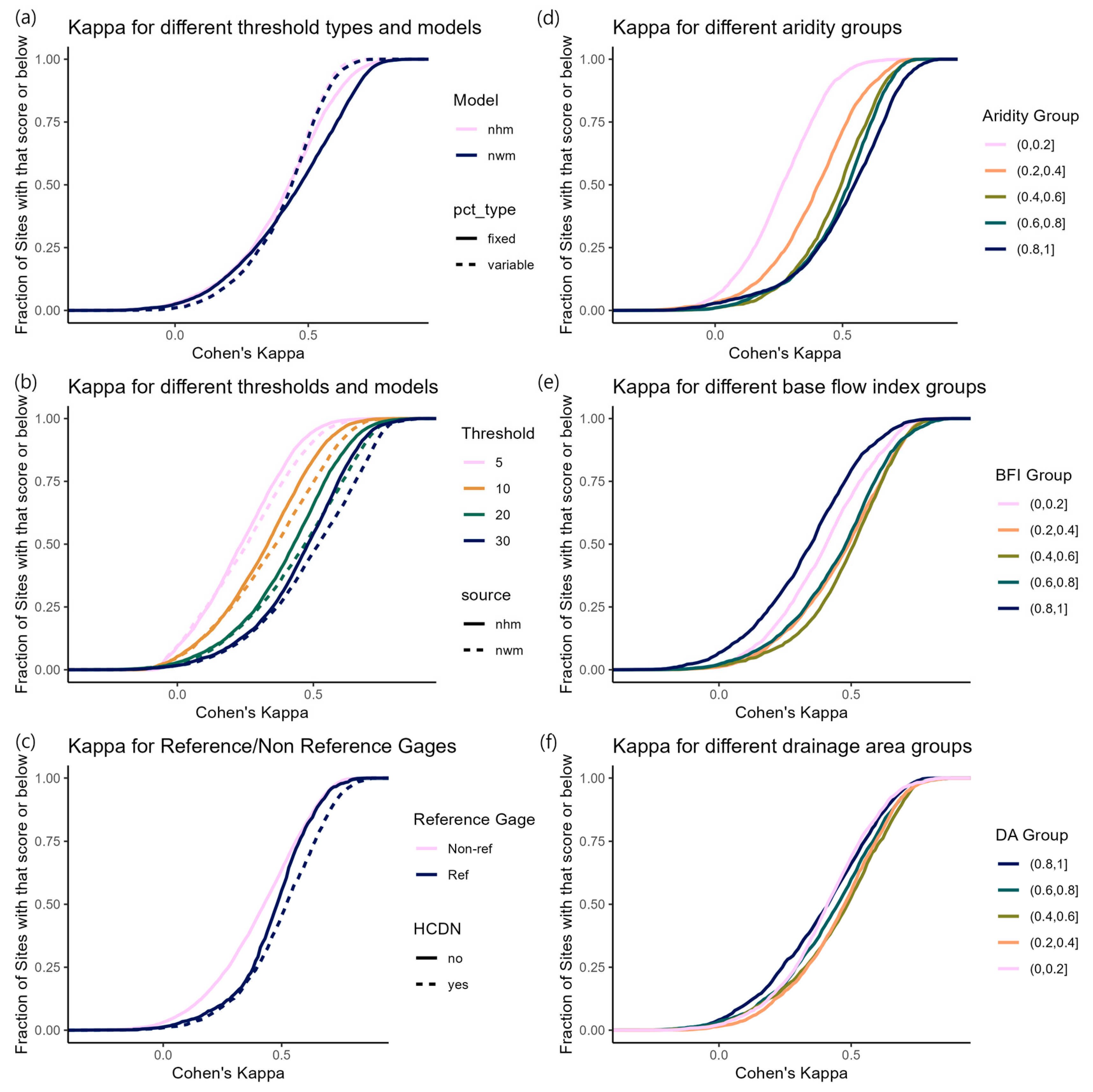
3.3. Drought Signatures
4. Discussion
4.1. Tradeoffs in Specific Model Performance
4.2. Model Performance Exhibits Regional Variation with Better Performance in Wetter Eastern Regions than in Drier Western Regions
4.3. Larger Differences in Performance Between Thresholds than Between Models Highlights the Importance of Using Consistent Benchmarking Methods
4.4. Summary
4.5. Limitations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wlostowski, A.N.; Jennings, K.S.; Bash, R.E.; Burkhardt, J.; Wobus, C.W.; Aggett, G. Dry landscapes and parched economies: A review of how drought impacts nonagricultural socioeconomic sectors in the US Intermountain West. Wiley Interdiscip. Rev. Water 2022, 9, e1571. [Google Scholar] [CrossRef]
- Smith, A.B.; Matthews, J.L. Quantifying uncertainty and variable sensitivity within the US billion-dollar weather and climate disaster cost estimates. Nat. Hazards 2015, 77, 1829–1851. [Google Scholar] [CrossRef]
- NOAA. National Centers for Environmental Information (NCEI) U.S. Billion-Dollar Weather and Climate Disasters. Retrieved from Billion-Dollar Weather and Climate Disasters|National Centers for Environmental Information (NCEI); 2022. Available online: https://www.ncei.noaa.gov/access/billions/ (accessed on 1 October 2021).
- Hasan, H.H.; Razali, S.F.M.; Muhammad, N.S.; Ahmad, A. Research trends of hydrological drought: A systematic review. Water 2019, 11, 2252. [Google Scholar] [CrossRef]
- Van Huijgevoort, M.H.J.; Hazenberg, P.; Van Lanen, H.A.J.; Teuling, A.J.; Clark, D.B.; Folwell, S.; Gosling, S.N.; Hanasaki, N.; Heinke, J.; Koirala, S.; et al. Global multimodel analysis of drought in runoff for the second half of the twentieth century. J. Hydrometeorol. 2013, 14, 1535–1552. [Google Scholar] [CrossRef]
- Quintana-Seguí, P.; Barella-Ortiz, A.; Regueiro-Sanfiz, S.; Míguez-Macho, G. The Utility of Land-Surface Model Simulations to Provide Drought Information in a Water Management Context Using Global and Local Forcing Datasets. Water Resour. Manag. 2020, 34, 2135–2156. [Google Scholar] [CrossRef]
- Stahl, K.; Vidal, J.P.; Hannaford, J.; Tijdeman, E.; Laaha, G.; Gauster, T.; Tallaksen, L.M. The challenges of hydrological drought definition, quantification and communication: An interdisciplinary perspective. Proc. Int. Assoc. Hydrol. Sci. 2020, 383, 291–295. [Google Scholar] [CrossRef]
- Brunner, M.I.; Slater, L.; Tallaksen, L.M.; Clark, M. Challenges in modeling and predicting floods and droughts: A review. WIREs Water 2021, 8, e1520. [Google Scholar] [CrossRef]
- Rivera, J.A.; Infanti, J.M.; Kumar, R.; Mutemi, J.N. Challenges of Hydrological Drought Monitoring and Prediction. Front. Water 2021, 3, 750311. [Google Scholar] [CrossRef]
- Tallaksen, L.M.; Van Lanen, H.A. (Eds.) Hydrological Drought: Processes and Estimation Methods for Streamflow and Groundwater. 2004. Available online: https://hdl.handle.net/11311/1256137 (accessed on 1 October 2021).
- Van Loon, A.F. Hydrological drought explained. WIREs Water 2015, 2, 359–392. [Google Scholar] [CrossRef]
- Wilhite, D.A.; Glantz, M.H. Understanding the drought phenomenon: The role of definitions. Water Int. 1985, 10, 111–120. [Google Scholar] [CrossRef]
- Guo, Y.; Huang, S.; Huang, Q.; Wang, H.; Fang, W.; Yang, Y.; Wang, L. Assessing socioeconomic drought based on an improved multivariate standardized reliability and resilience index. J. Hydrol. 2019, 568, 904–918. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. Drought modeling—A review. J. Hydrol. 2011, 403, 157–175. [Google Scholar] [CrossRef]
- Hao, Z.; Singh, V.P.; Xia, Y. Seasonal drought prediction: Advances, challenges, and future prospects. Rev. Geophys. 2018, 56, 108–141. [Google Scholar] [CrossRef]
- Smith, K.A.; Barker, L.J.; Tanguy, M.; Parry, S.; Harrigan, S.; Legg, T.P.; Prudhomme, C.; Hannaford, J. A multi-objective ensemble approach to hydrological modelling in the UK: An application to historic drought reconstruction. Hydrol. Earth Syst. Sci. 2019, 23, 3247–3268. [Google Scholar] [CrossRef]
- Fung, K.F.; Huang, Y.F.; Koo, C.H.; Soh, Y.W. Drought forecasting: A review of modelling approaches 2007–2017. J. Water Clim. Change 2020, 11, 771–799. [Google Scholar] [CrossRef]
- Sutanto, S.J.; Van Lanen, H.A. Streamflow drought: Implication of drought definitions and its application for drought forecasting. Hydrol. Earth Syst. Sci. 2021, 25, 3991–4023. [Google Scholar] [CrossRef]
- Dyer, J.; Mercer, A.; Raczyński, K. Identifying Spatial Patterns of Hydrologic Drought over the Southeast US Using Retrospective National Water Model Simulations. Water 2022, 14, 1525. [Google Scholar] [CrossRef]
- Yihdego, Y.; Vaheddoost, B.; Al-Weshah, R.A. Drought indices and indicators revisited. Arab. J. Geosci. 2019, 12, 69. [Google Scholar] [CrossRef]
- Faiz, M.A.; Zhang, Y.; Ma, N.; Baig, F.; Naz, F.; Niaz, Y. Drought indices: Aggregation is necessary or is it only the researcher’s choice? Water Supply 2021, 21, 3987–4002. [Google Scholar] [CrossRef]
- Alawsi, M.A.; Zubaidi, S.L.; Al-Bdairi, N.S.S.; Al-Ansari, N.; Hashim, K. Drought Forecasting: A Review and Assessment of the Hybrid Techniques and Data Pre-Processing. Hydrology 2022, 9, 115. [Google Scholar] [CrossRef]
- Archfield, S.A.; Clark, M.; Arheimer, B.; Hay, L.E.; McMillan, H.; Kiang, J.E.; Seibert, J.; Hakala, K.; Bock, A.; Wagener, T.; et al. Accelerating advances in continental domain hydrologic modeling. Water Resour. Res. 2015, 51, 10078–10091. [Google Scholar] [CrossRef]
- Towler, E.; Foks, S.S.; Dugger, A.L.; Dickinson, J.E.; Essaid, H.I.; Gochis, D.; Viger, R.J.; Zhang, Y. Benchmarking high-resolution hydrologic model performance of long-term retrospective streamflow simulations in the contiguous United States. Hydrol. Earth Syst. Sci. 2023, 27, 1809–1825. [Google Scholar] [CrossRef]
- Smakhtin, V.U. Low flow hydrology: A review. J. Hydrol. 2001, 240, 147–186. [Google Scholar] [CrossRef]
- Nicolle, P.; Pushpalatha, R.; Perrin, C.; François, D.; Thiéry, D.; Mathevet, T.; Le Lay, M.; Besson, F.; Soubeyroux, J.-M.; Viel, C.; et al. Benchmarking hydrological models for low-flow simulation and forecasting on French catchments. Hydrol. Earth Syst. Sci. 2014, 18, 2829–2857. [Google Scholar] [CrossRef]
- Hodgkins, G.A.; Dudley, R.W.; Russell, A.M.; LaFontaine, J.H. Comparing trends in modeled and observed streamflows at minimally altered basins in the United States. Water 2020, 12, 1728. [Google Scholar] [CrossRef]
- Mubialiwo, A.; Abebe, A.; Onyutha, C. Performance of rainfall–runoff models in reproducing hydrological extremes: A case of the River Malaba sub-catchment. SN Appl. Sci. 2021, 3, 515. [Google Scholar] [CrossRef]
- Worland, S.C.; Farmer, W.H.; Kiang, J.E. Improving predictions of hydrological low-flow indices in ungaged basins using machine learning. Environ. Model. Softw. 2018, 101, 169–182. [Google Scholar] [CrossRef]
- Pfannerstill, M.; Guse, B.; Fohrer, N. Smart low flow signature metrics for an improved overall performance evaluation of hydrological models. J. Hydrol. 2014, 510, 447–458. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Pushpalatha, R.; Perrin, C.; Le Moine, N.; Andreassian, V. A review of efficiency criteria suitable for evaluating low-flow simulations. J. Hydrol. 2012, 420, 171–182. [Google Scholar] [CrossRef]
- Dehghani, M.; Saghafian, B.; Rivaz, F.; Khodadadi, A. Evaluation of dynamic regression and artificial neural networks models for real-time hydrological drought forecasting. Arab. J. Geosci. 2017, 10, 266. [Google Scholar] [CrossRef]
- Barella-Ortiz, A.; Quintana-Seguí, P. Evaluation of drought representation and propagation in regional climate model simulations across Spain. Hydrol. Earth Syst. Sci. 2019, 23, 5111–5131. [Google Scholar] [CrossRef]
- Hammond, J.C.; Simeone, C.; Hecht, J.S.; Hodgkins, G.A.; Lombard, M.; McCabe, G.; Wolock, D.; Wieczorek, M.; Olson, C.; Caldwell, T.; et al. Going Beyond Low Flows: Streamflow Drought Deficit and Duration Illuminate Distinct Spatiotemporal Drought Patterns and Trends in the U.S. During the Last Century. Water Resour. Res. 2022, 58, e2022WR031930. [Google Scholar] [CrossRef]
- Heudorfer, B.; Stahl, K. Comparison of different threshold level methods for drought propagation analysis in Germany. Hydrol. Res. 2017, 48, 1311–1326. [Google Scholar] [CrossRef]
- Sarailidis, G.; Vasiliades, L.; Loukas, A. Analysis of streamflow droughts using fixed and variable thresholds. Hydrol. Process. 2019, 33, 414–431. [Google Scholar] [CrossRef]
- Jehanzaib, M.; Bilal Idrees, M.; Kim, D.; Kim, T.W. Comprehensive evaluation of machine learning techniques for hydrological drought forecasting. J. Irrig. Drain. Eng. 2021, 147, 04021022. [Google Scholar] [CrossRef]
- Collier, N.; Hoffman, F.M.; Lawrence, D.M.; Keppel-Aleks, G.; Koven, C.D.; Riley, W.J.; Mu, M.; Randerson, J.T. The International Land Model Benchmarking (ILAMB) System: Design, Theory, and Implementation. J. Adv. Model. Earth Syst. 2018, 10, 2731–2754. [Google Scholar] [CrossRef]
- Gochis, D.J.; Barlage, M.; Cabell, R.; Casali, M.; Dugger, A.; FitzGerald, K.; McAllister, M.; McCreight, J.; RafieeiNasab, A.; Read, L.; et al. The WRF-Hydro® Modeling System Technical Description, (Version 5.1.1). NCAR Technical Note. 2020. 107p. Available online: https://ral.ucar.edu/sites/default/files/public/projects/wrf-hydro/technical-description-user-guide/wrf-hydrov5.2technicaldescription.pdf (accessed on 1 October 2021).
- Regan, R.S.; Markstrom, S.L.; Hay, L.E.; Viger, R.J.; Norton, P.A.; Driscoll, J.M.; LaFontaine, J.H. Description of the national hydrologic model for use with the precipitation-runoff modeling system (prms) (No. 6-B9). In US Geological Survey Techniques and Methods; U.S. Geological Survey: Reston, VA, USA, 2018. [Google Scholar] [CrossRef]
- Hay, L.E.; LaFontaine, J.H. Application of the National Hydrologic Model Infrastructure with the Precipitation-Runoff Modeling System (NHM-PRMS), 1980–2016, Daymet Version 3 Calibration [Data Set]; U.S. Geological Survey: Reston, VA, USA, 2020. [CrossRef]
- Hay, L.E.; LaFontaine, J.H.; Van Beusekom, A.E.; Norton, P.A.; Farmer, W.H.; Regan, R.S.; Markstrom, S.L.; Dickinson, J.E. Parameter estimation at the conterminous United States scale and streamflow routing enhancements for the National Hydrologic Model infrastructure application of the Precipitation-Runoff Modeling System (NHM-PRMS). In U.S. Geological Survey Techniques and Methods; U.S. Geological Survey: Reston, VA, USA, 2023; Chapter B10; 50p. [Google Scholar] [CrossRef]
- Zhao, L. Event prediction in the big data era: A systematic survey. ACM Comput. Surv. (CSUR) 2021, 54, 1–37. [Google Scholar] [CrossRef]
- Cohen, J. A coefficient of agreement for nominal scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
- Spearman, C. The Proof and Measurement of Association Between Two Things. In Studies in Individual Differences: The Search for Intelligence; Jenkins, J.J., Paterson, D.G., Eds.; Appleton-Century-Crofts: New York, NY, USA, 1961; pp. 45–58. [Google Scholar]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Hughes, M.; Jackson, D.L.; Unruh, D.; Wang, H.; Hobbins, M.; Ogden, F.L.; Cifelli, R.; Cosgrove, B.; DeWitt, D.; Dugger, A.; et al. Evaluation of retrospective National Water Model Soil moisture and streamflow for drought-monitoring applications. J. Geophys. Res. Atmos. 2024, 129, e2023JD038522. [Google Scholar] [CrossRef]
- Addor, N.; Do, H.X.; Alvarez-Garreton, C.; Coxon, G.; Fowler, K.; Mendoza, P.A. Large-sample hydrology: Recent progress, guidelines for new datasets and grand challenges. Hydrol. Sci. J. 2020, 65, 712–725. [Google Scholar] [CrossRef]
- Bales, R.C.; Goulden, M.L.; Hunsaker, C.T.; Conklin, M.H.; Hartsough, P.C.; O’Geen, A.T.; Hopmans, J.W.; Safeeq, M. Mechanisms controlling the impact of multi-year drought on mountain hydrology. Sci. Rep. 2018, 8, 690. [Google Scholar] [CrossRef] [PubMed]
- Gupta, H.V.; Perrin, C.; Blöschl, G.; Montanari, A.; Kumar, R.; Clark, M.; Andréassian, V. Large-sample hydrology: A need to balance depth with breadth. Hydrol. Earth Syst. Sci. 2014, 18, 463–477. [Google Scholar] [CrossRef]
- Thornton, P.E.; Thornton, M.M.; Mayer, B.W.; Wei, Y.; Devarakonda, R.; Vose, R.S.; Cook, R.B. Daymet: Daily Surface Weather Data on a 1-km Grid for North America, Version 3; ORNL DAAC: Oak Ridge, TN, USA, 2017. [Google Scholar] [CrossRef]
- Fall, G.; Kitzmiller, D.; Pavlovic, S.; Zhang, Z.; Patrick, N.; St. Laurent, M.; Trypaluk, C.; Wu, W.; Miller, D. The Office of Water Prediction’s Analysis of Record for Calibration, version 1.1: Dataset description and precipitation evaluation. JAWRA J. Am. Water Resour. Assoc. 2023, 59, 1246–1272. [Google Scholar] [CrossRef]
- Krause, P.; Boyle, D.P.; Base, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Gochis, D.J.; Cosgrove, B.; Dugger, A.L.; Karsten, L.; Sampson, K.M.; McCreight, J.L.; Flowers, T.; Clark, E.P.; Vukicevic, T.; Salas, F.R.; et al. Multi-variate evaluation of the NOAA National Water Model. In AGU Fall Meeting; NSF National Center for Atmospheric Research: Boulder, CO, USA, 2018. [Google Scholar]
- Lahmers, T.M.; Hazenberg, P.; Gupta, H.; Castro, C.; Gochis, D.; Dugger, A.; Yates, D.; Read, L.; Karsten, L.; Wang, Y.-H. Evaluation of NOAA National Water Model Parameter Calibration in Semiarid Environments Prone to Channel Infiltration. J. Hydrometeorol. 2021, 22, 2939–2969. [Google Scholar]
- Hodgkins, G.A.; Over, T.M.; Dudley, R.W.; Russell, A.M.; LaFontaine, J.H. The consequences of neglecting reservoir storage in national-scale hydrologic models: An appraisal of key streamflow statistics. J. Am. Water Resour. Assoc. 2023, 60, 110–131. [Google Scholar] [CrossRef]
- Johnson, J.M.; Fang, S.; Sankarasubramanian, A.; Rad, A.M.; da Cunha, L.K.; Jennings, K.S.; Clarke, K.C.; Mazrooei, A.; Yeghiazarian, L. Comprehensive analysis of the NOAA National Water Model: A call for heterogeneous formulations and diagnostic model selection. J. Geophys. Res. Atmos. 2023, 128, e2023JD038534. [Google Scholar] [CrossRef]
- Foks, S.S.; Towler, E.; Hodson, T.O.; Bock, A.R.; Dickinson, J.E.; Dugger, A.L.; Dunne, K.A.; Essaid, H.I.; Miles, K.A.; Over, T.M.; et al. Streamflow benchmark locations for conterminous United States (cobalt gages). In U.S. Geological Survey Data Release; U.S. Geological Survey: Reston, VA, USA, 2022. [Google Scholar] [CrossRef]
- Carpenter, D.H.; Hayes, D.C. Low-flow characteristics of streams in Maryland and Delaware. Water-Resour. Investig. Rep. 1996, 94, 4020. [Google Scholar]
- Feaster, T.D.; Lee, K.G. Low-flow frequency and flow-duration characteristics of selected streams in Alabama through March 2014. In U.S. Geological Survey Scientific Investigations Report 2017–5083; U.S. Geological Survey: Reston, VA, USA, 2017; 371p. [Google Scholar] [CrossRef]
- Lins, H.F. USGS hydro-climatic data network 2009 (HCDN-2009). In US Geological Survey Fact; U.S. Geological Survey: Reston, VA, USA, 2012; Sheet 2012-3047. [Google Scholar]
- McCabe, G.J.; Wolock, D.M. Clusters of monthly streamflow values with similar temporal patterns at 555 HCDN (Hydro-Climatic Data Network) sites for the period 1981 to 2019. In U.S. Geological Survey Data Release; U.S. Geological Survey: Reston, VA, USA, 2022. [Google Scholar] [CrossRef]
- Laaha, G.; Gauster, T.; Tallaksen, L.M.; Vidal, J.P.; Stahl, K.; Prudhomme, C.; Heudorfer, B.; Vlnas, R.; Ionita, M.; Van Lanen, H.A.J.; et al. The European 2015 drought from a hydrological perspective. Hydrol. Earth Syst. Sci. 2017, 21, 3001–3024. [Google Scholar] [CrossRef]
- Simeone, C.E. Streamflow Drought Metrics for select GAGES-II streamgages for three different time periods from 1921–2020. In U.S. Geological Survey Data Release; U.S. Geological Survey: Reston, VA, USA, 2022. [Google Scholar] [CrossRef]
- Van Huijgevoort, M.H.J.; Hazenberg, P.; Van Lanen, H.A.J.; Uijlenhoet, R. A generic method for hydrological drought identification across different climate regions. Hydrol. Earth Syst. Sci. 2012, 16, 2437–2451. [Google Scholar] [CrossRef]
- Landis, J.R.; Koch, G.G. The measurement of observer agreement for categorical data. Biometrics 1977, 33, 159–174. [Google Scholar] [CrossRef] [PubMed]
- Clark, M.P.; Vogel, R.M.; Lamontagne, J.R.; Mizukami, N.; Knoben, W.J.; Tang, G.; Gharari, S.; Freer, J.E.; Whitfield, P.H.; Shook, K.R.; et al. The abuse of popular performance metrics in hydrologic modeling. Water Resour. Res. 2021, 57, e2020WR029001. [Google Scholar] [CrossRef]
- Hodson, T.O.; Over, T.M.; Foks, S.S. Mean squared error, deconstructed. J. Adv. Model. Earth Syst. 2021, 13, e2021MS002681. [Google Scholar] [CrossRef]
- Helsel, D.R.; Hirsch, R.M.; Ryberg, K.R.; Archfield, S.A.; Gilroy, E.J. Statistical methods in water resources. In U.S. Geological Survey Techniques and Methods; [Supersedes USGS Techniques of Water-Resources Investigations, Book 4, Chapter A3, version 1.1.]; U.S. Geological Survey: Reston, VA, USA, 2020; Book 4, Chapter A3; 458p. [Google Scholar] [CrossRef]
- Yue, S.; Pilon, P.; Cavadias, G. Power of the Mann-Kendall and Spearman’s rho tests for detecting monotonic trends in hydrological series. J. Hydrol. 2002, 259, 254–271. [Google Scholar] [CrossRef]
- Barber, C.; Lamontagne, J.R.; Vogel, R.M. Improved estimators of correlation and R2 for skewed hydrologic data. Hydrol. Sci. J. 2020, 65, 87–101. [Google Scholar] [CrossRef]
- Tijerina-Kreuzer, D.; Condon, L.; FitzGerald, K.; Dugger, A.; O’neill, M.M.; Sampson, K.; Gochis, D.; Maxwell, R. Continental hydrologic intercomparison project, phase 1: A large-scale hydrologic model comparison over the continental United States. Water Resour. Res. 2021, 57, e2020WR028931. [Google Scholar] [CrossRef]
- Yilmaz, K.K.; Gupta, H.V.; Wagener, T. A process-based diagnostic approach to model evaluation: Application to the NWS distributed hydrologic model. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Newman, A.J.; Mizukami, N.; Clark, M.P.; Wood, A.W.; Nijssen, B. Benchmarking of a physically based hydrologic model. J. Hydrometeorol. 2017, 18, 2215–2225. [Google Scholar] [CrossRef]
- Yevjevich, V.M. An Objective Approach to Definitions and Investigations of Continental Hydrologic Droughts; Colorado State University: Fort Collins, CO, USA, 1967; Volume 23, p. 25. [Google Scholar]
- Dracup, J.A.; Lee, K.S.; Paulson, E.G., Jr. On the statistical characteristics of drought events. Water Resour. Res. 1980, 16, 289–296. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Noel, M.; Bathke, D.; Fuchs, B.; Gutzmer, D.; Haigh, T.; Hayes, M.; Poděbradská, M.; Shield, C.; Smith, K.; Svoboda, M. Linking drought impacts to drought severity at the state level. Bull. Am. Meteorol. Soc. 2020, 101, E1312–E1321. [Google Scholar] [CrossRef]
- Addor, N.; Nearing, G.; Prieto, C.; Newman, A.J.; Le Vine, N.; Clark, M.P. A ranking of hydrological signatures based on their predictability in space. Water Resour. Res. 2018, 54, 8792–8812. [Google Scholar] [CrossRef]
- McMillan, H.K. A review of hydrologic signatures and their applications. WIREs Water 2021, 8, e1499. [Google Scholar] [CrossRef]
- Pournasiri Poshtiri, M.; Towler, E.; Pal, I. Characterizing and understanding the variability of streamflow drought indicators within the USA. Hydrol. Sci. J. 2018, 63, 1791–1803. [Google Scholar] [CrossRef]
- Simeone, C.; Leah, S.; Katharine, K. Results of benchmarking National Water Model v2.1 simulations of streamflow drought duration, severity, deficit, and occurrence in the conterminous United States. In U.S. Geological Survey Data Release; U.S. Geological Survey: Reston, VA, USA, 2024. [Google Scholar]
- Simeone, C.; Leah, S.; Katharine, K. Results of benchmarking National Hydrologic Model application of the Precipitation-Runoff Modeling System (v1.0 byObsMuskingum) simulations of streamflow drought duration, severity, deficit, and occurrence in the conterminous United States. In U.S. Geological Survey Data Release; U.S. Geological Survey: Reston, VA, USA, 2024; Chapter B10; 50p. [Google Scholar]
- Rudd, A.C.; Bell, V.A.; Kay, A.L. National-scale analysis of simulated hydrological droughts (1891–2015). J. Hydrol. 2017, 550, 368–385. [Google Scholar] [CrossRef]
- Massmann, C. Identification of factors influencing hydrologic model performance using a top-down approach in a large number of US catchments. Hydrol. Process. 2020, 34, 4–20. [Google Scholar] [CrossRef]
- Overholser, B.R.; Sowinski, K.M. Biostatistics primer: Part 2. Nutr. Clin. Pract. 2008, 23, 76–84. [Google Scholar] [CrossRef]
- Farmer, W.H.; Vogel, R.M. On the deterministic and stochastic use of hydrologic models. Water Resour. Res. 2016, 52, 5619–5633. [Google Scholar] [CrossRef]
- Moges, E.; Ruddell, B.L.; Zhang, L.; Driscoll, J.M.; Norton, P.; Perez, F.; Larsen, L.G. HydroBench: Jupyter supported reproducible hydrological model benchmarking and diagnostic tool. Front. Earth Sci. 2022, 10, 884766. [Google Scholar] [CrossRef]
- Wan, T.; Covert, B.H.; Kroll, C.N.; Ferguson, C.R. An Assessment of the National Water Model’s Ability to Reproduce Drought Series in the Northeastern United States. J. Hydrometeorol. 2022, 23, 1929–1943. [Google Scholar] [CrossRef]
- Falcone, J.A. GAGES-II: Geospatial Attributes of Gages for Evaluating Streamflow; U.S. Geological Survey: Reston, VA, USA, 2011. [CrossRef]
- Gudmundsson, L.; Wagener, T.; Tallaksen, L.M.; Engeland, K. Evaluation of nine large-scale hydrological models with respect to the seasonal runoff climatology in Europe: Land Surface Models Evaluation. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Maidment, D.R. Conceptual Framework for the National Flood Interoperability Experiment. J. Am. Water Resour. Assoc. 2016, 53, 245–257. [Google Scholar] [CrossRef]
- NOAA. National Water Model CONUS Retrospective Dataset. Available online: https://registry.opendata.aws/nwm-archive (accessed on 1 October 2021).
- UCAR. Supporting the NOAA National Water Model. 2019. Available online: https://ral.ucar.edu/projects/supporting-the-noaa-national-water-model (accessed on 1 October 2021).
- Regan, R.S.; Juracek, K.E.; Hay, L.E.; Markstrom, S.L.; Viger, R.J.; Driscoll, J.M.; LaFontaine, J.H.; Norton, P.A. The US Geological Survey National Hydrologic Model infrastructure: Rationale, description, and application of a watershed-scale model for the conterminous United States. Environ. Model. Softw. 2019, 111, 192–203. [Google Scholar] [CrossRef]
- Hansen, C.; Shiva, J.S.; McDonald, S.; Nabors, A. Assessing retrospective National Water Model streamflow with respect to droughts and low flows in the Colorado River basin. JAWRA J. Am. Water Resour. Assoc. 2019, 55, 964–975. [Google Scholar] [CrossRef]
- Carlisle, D.; Wolock, D.M.; Konrad, C.P.; McCabe, G.J.; Eng, K.; Grantham, T.E.; Mahler, B. Flow Modification in the Nation’s Streams and Rivers; US Department of the Interior, US Geological Survey: Reston, VA, USA, 2019.
- Friedrich, K.; Grossman, R.L.; Huntington, J.; Blanken, P.D.; Lenters, J.; Holman, K.D.; Gochis, D.; Livneh, B.; Prairie, J.; Skeie, E.; et al. Reservoir evaporation in the Western United States: Current science, challenges, and future needs. Bull. Am. Meteorol. Soc. 2018, 99, 167–187. [Google Scholar] [CrossRef]
- Hare, D.K.; Helton, A.M.; Johnson, Z.C.; Lane, J.W.; Briggs, M.A. Continental-scale analysis of shallow and deep groundwater contributions to streams. Nat. Commun. 2021, 12, 1450. [Google Scholar] [CrossRef]
- Lane, R.A.; Coxon, G.; Freer, J.E.; Wagener, T.; Johnes, P.J.; Bloomfield, J.P.; Greene, S.; Macleod, C.J.A.; Reaney, S.M. Benchmarking the predictive capability of hydrological models for river flow and flood peak predictions across over 1000 catchments in Great Britain. Hydrol. Earth Syst. Sci. 2019, 23, 4011–4032. [Google Scholar] [CrossRef]
- Vogel, R.M. Editorial: Stochastic and deterministic world views. J. Water Resour. Plan. Manag. 1999, 125, 311–313. [Google Scholar] [CrossRef]
- Ahmadalipour, A.; Moradkhani, H.; Svoboda, M. Centennial drought outlook over the CONUS using NASA-NEX downscaled climate ensemble. Int. J. Climatol. 2017, 37, 2477–2491. [Google Scholar] [CrossRef]
- Salehabadi, H.; Tarboton, D.G.; Udall, B.; Wheeler, K.G.; Schmidt, J.C. An Assessment of Potential Severe Droughts in the Colorado River Basin. J. Am. Water Resour. Assoc. 2022, 58, 1053–1075. [Google Scholar] [CrossRef]
- Williams, A.P.; Cook, B.I.; Smerdon, J.E. Rapid intensification of the emerging southwestern North American megadrought in 2020–2021. Nat. Clim. Chang. 2022, 12, 232–234. [Google Scholar] [CrossRef]
- Xia, Y.; Mitchell, K.; Ek, M.; Cosgrove, B.; Sheffield, J.; Luo, L.; Alonge, C.; Wei, H.; Meng, J.; Livneh, B.; et al. Continental-scale water and energy flux analysis and validation for North American Land Data Assimilation System project phase 2 (NLDAS-2): 2. Validation of model-simulated streamflow. J. Geophys. Res. Atmos. 2012, 117, D03110. [Google Scholar] [CrossRef]
- Simeone, C.E.; Foks, S.S. HyMED—Hydrologic Model Evaluation for Drought: R package version 1.0.0. In U.S. Geological Survey Software Release; U.S. Geological Survey: Reston, VA, USA, 2024. [Google Scholar]

| Category | Statistic | Description | Range (Perfect) | Comments |
|---|---|---|---|---|
| Event Classification | Cohen’s kappa | Cohen’s kappa statistic for inter-rater reliability [45] | −1 to 1 (1) | A measure of agreement relative to the probability of achieving results by chance. |
| Error Components | Spearman’s r | Spearman’s rank correlation coefficient | −1 to 1 (1) | A nonparametric estimator of correlation for flow timing. |
| Ratio of standard deviations | Ratio of simulated to observed standard deviations (for the scorecard this is presented as the absolute deviation from the target of 1) | 0 to Inf (1) | Indicates if the flow variability is being over or underestimated. | |
| Percent bias | Percent bias (simulated minus observed) (for the scorecard this is presented as the absolute percent bias) | −100 to Inf (0) | Indicates if total streamflow volume is being over or underestimated. | |
| Drought Signatures | Drought Duration | Normalized mean absolute error (NMAE) in the annual time series of drought duration, i.e., the sum of days of drought each year for a given threshold. | 0 to Inf (0) | Indicates how well the model simulates annual drought durations. |
| Drought Intensity | NMAE in the annual time series of the distance the minimum percentile is below the drought threshold, i.e., the overall maximum distance below the threshold for any drought during the year. | 0 to Inf (0) | Indicates how well the model simulates annual minimum flow. | |
| Drought Severity (Flow Deficit Volume) | NMAE in the annual time series of drought deficit volume in cubic meters per second-days (cms-days), i.e., the sum of drought deficits for all droughts during the year. | 0 to Inf (0) | Indicates how well the model simulates annual flow deficit. This is a measure of drought severity. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Simeone, C.; Foks, S.; Towler, E.; Hodson, T.; Over, T. Evaluating Hydrologic Model Performance for Characterizing Streamflow Drought in the Conterminous United States. Water 2024, 16, 2996. https://doi.org/10.3390/w16202996
Simeone C, Foks S, Towler E, Hodson T, Over T. Evaluating Hydrologic Model Performance for Characterizing Streamflow Drought in the Conterminous United States. Water. 2024; 16(20):2996. https://doi.org/10.3390/w16202996
Chicago/Turabian StyleSimeone, Caelan, Sydney Foks, Erin Towler, Timothy Hodson, and Thomas Over. 2024. "Evaluating Hydrologic Model Performance for Characterizing Streamflow Drought in the Conterminous United States" Water 16, no. 20: 2996. https://doi.org/10.3390/w16202996
APA StyleSimeone, C., Foks, S., Towler, E., Hodson, T., & Over, T. (2024). Evaluating Hydrologic Model Performance for Characterizing Streamflow Drought in the Conterminous United States. Water, 16(20), 2996. https://doi.org/10.3390/w16202996






