Sensitivity and Uncertainty Analysis of the GeeSEBAL Model Using High-Resolution Remote-Sensing Data and Global Flux Site Data
Abstract
1. Introduction
2. Methods
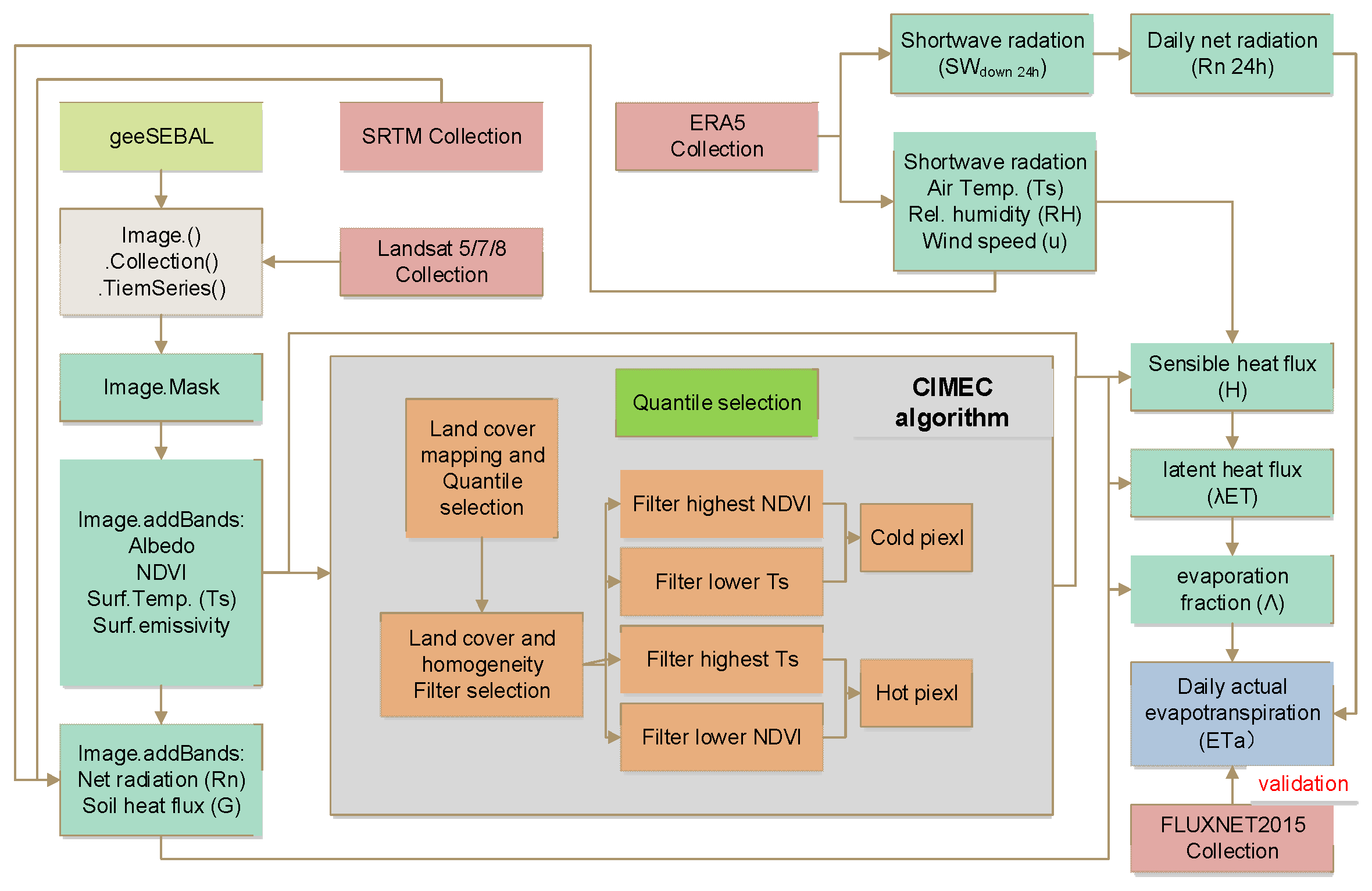
2.1. SEBAL Model
2.2. Automatic Calibration of Cold and Hot End Element Component Selection for the geeSEBAL Model
2.3. Sobol’s Sensitivity Analysis Method
2.4. Parameter Optimization Model
2.5. Model Validation
3. Data
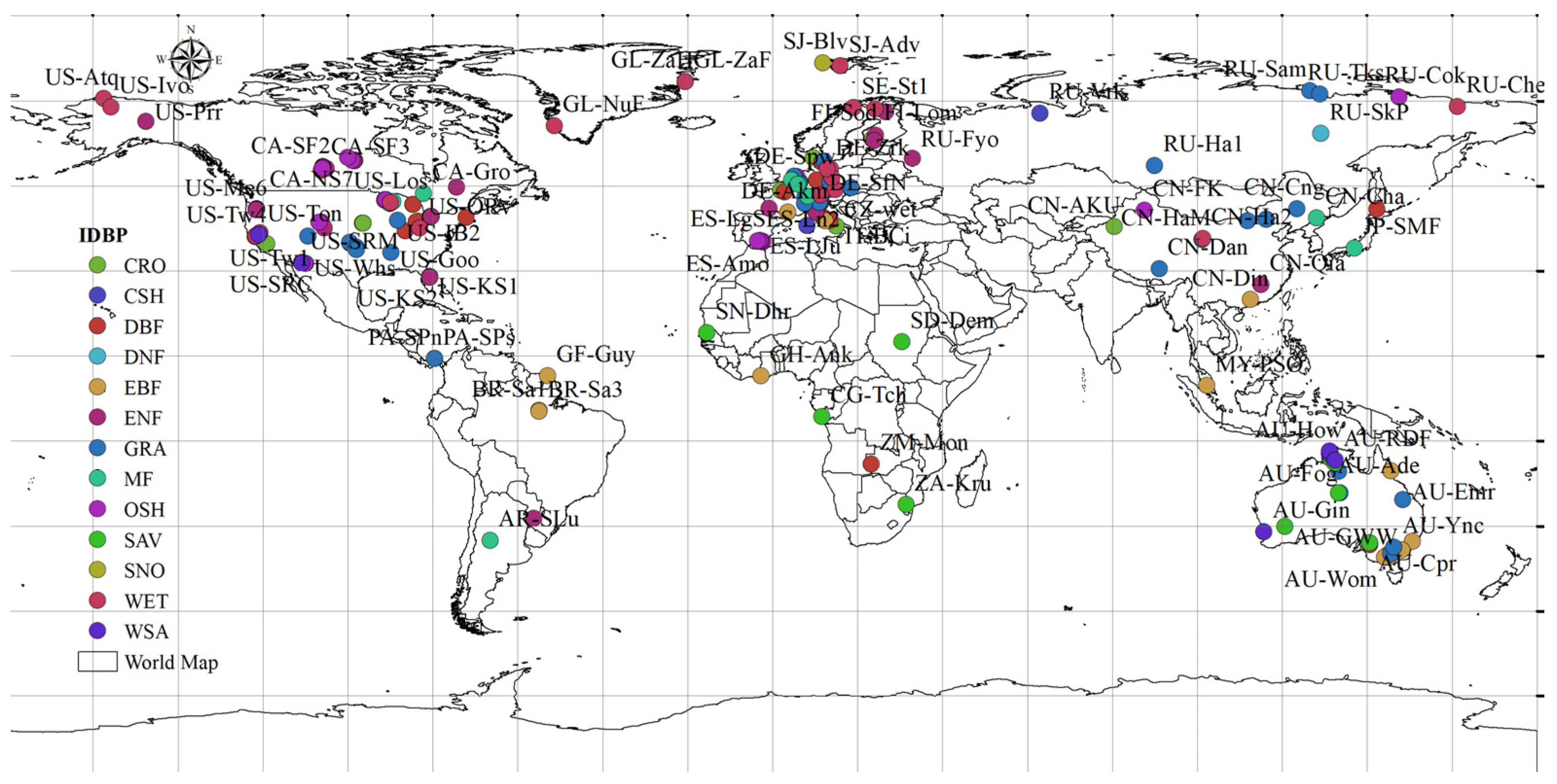
3.1. Remote-Sensing Data
3.2. Model Validation Data
4. Results and Analysis
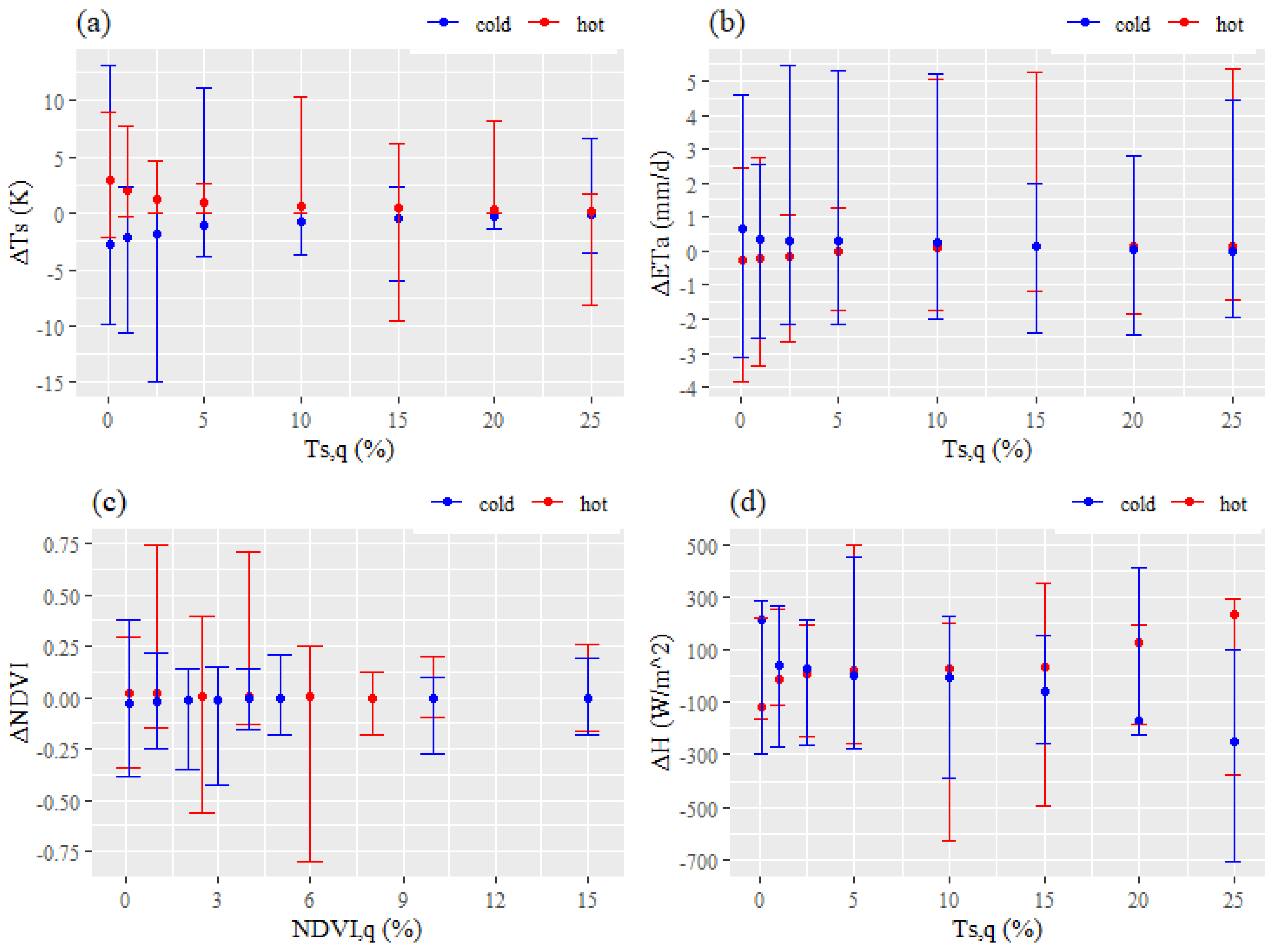
4.1. Sensitivity Analysis of Numerical Calibration for End-Element Component Quantiles
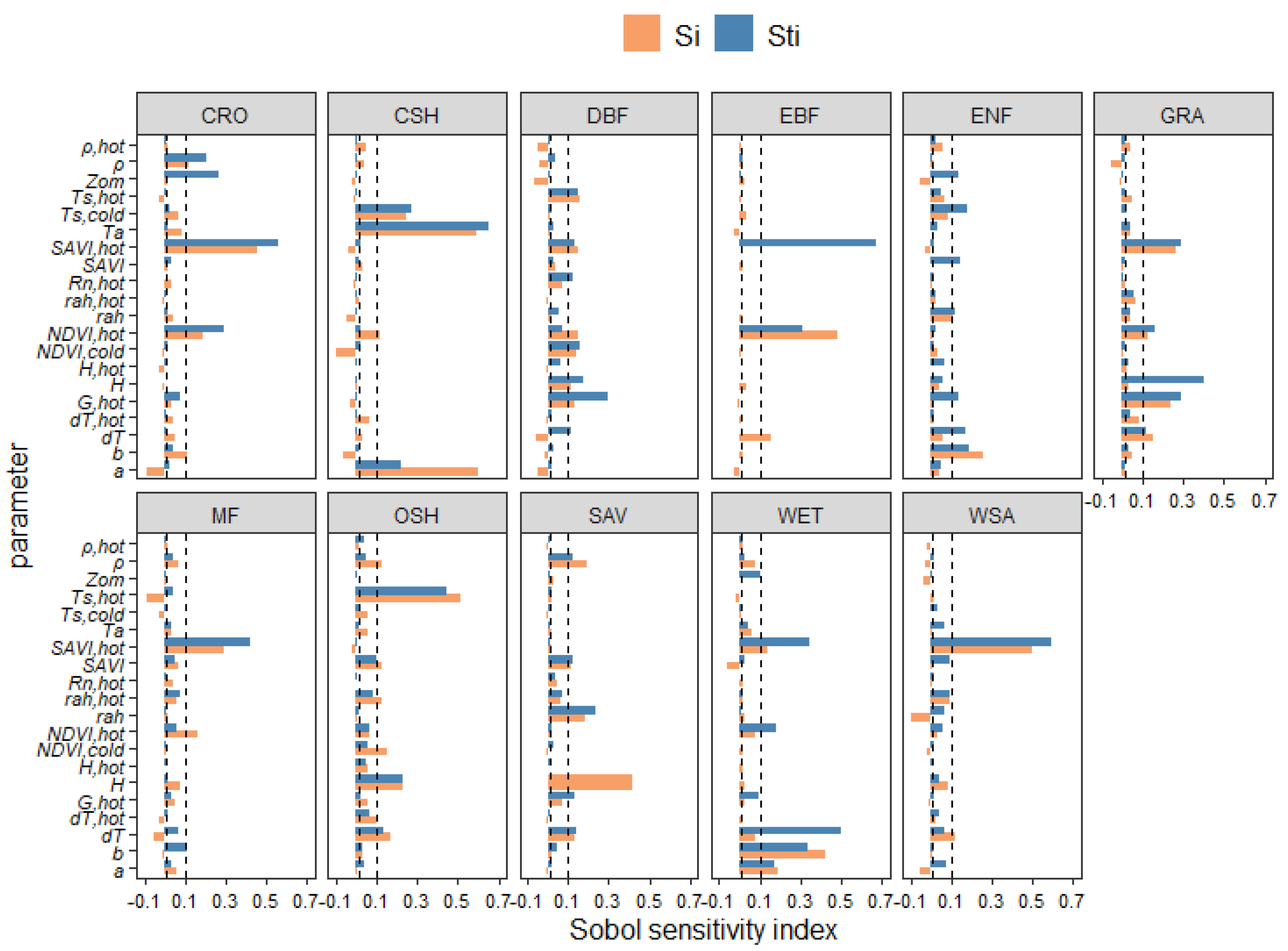
4.2. Sensitivity Analysis of Model Parameters
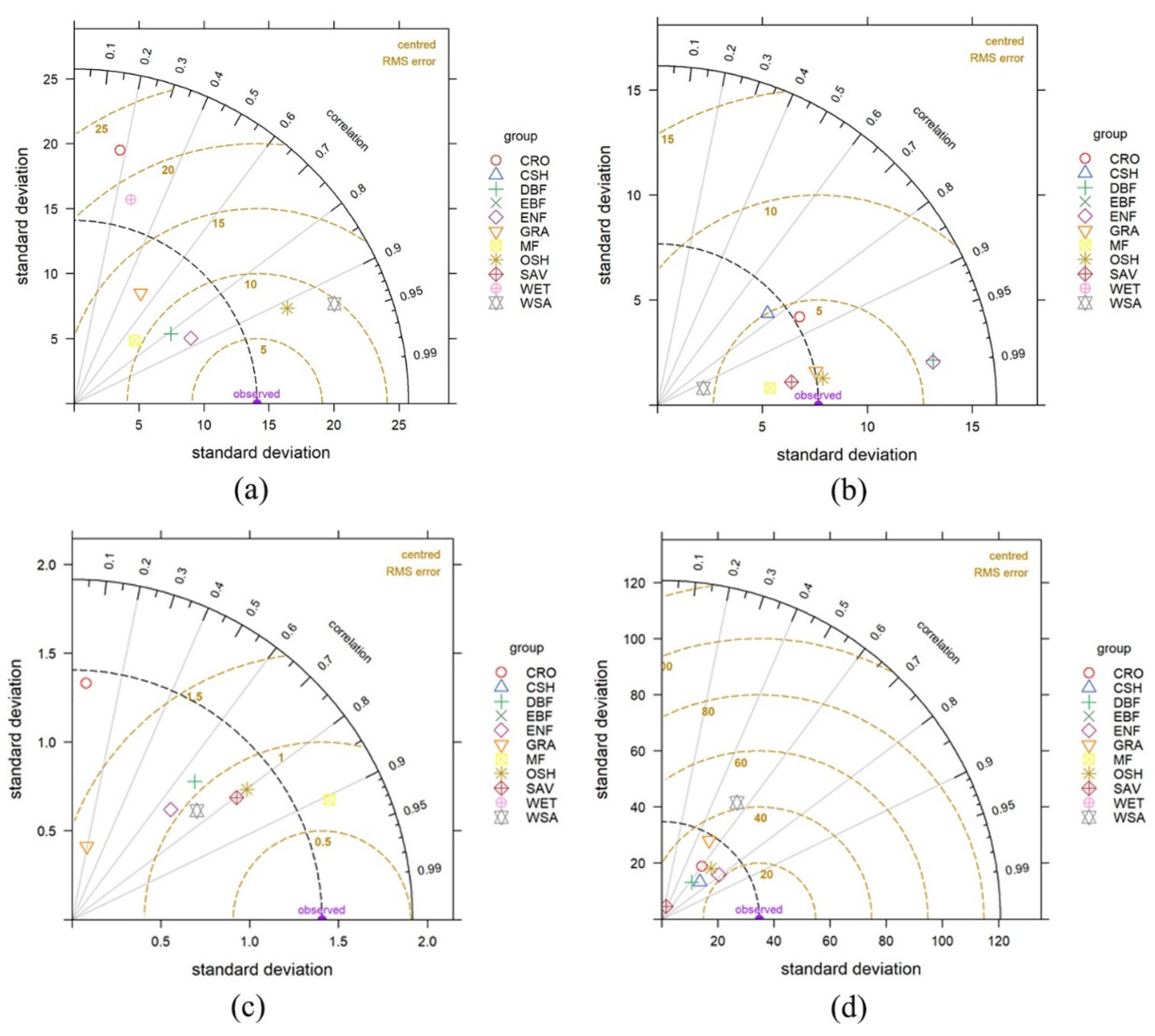
4.3. Optimization of the SEBAL Model Based on Measured ETa Data from Flux Stations
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Maroufpoor, S.; Bozorg-Haddad, O.; Maroufpoor, E. Reference evapotranspiration estimating based on optimal input combination and hybrid artificial intelligent model: Hybridization of artificial neural network with grey wolf optimizer algorithm. J. Hydrol. 2020, 588, 125060. [Google Scholar] [CrossRef]
- Vinukollu, R.K.; Wood, E.F.; Ferguson, C.R.; Fisher, J.B. Global estimates of evapotranspiration for climate studies using multi-sensor remote sensing data: Evaluation of three process-based approaches. Remote Sens. Environ. 2011, 115, 801–823. [Google Scholar] [CrossRef]
- Chao, L.; Zhang, K.; Wang, J.; Feng, J.; Zhang, M. A comprehensive evaluation of five evapotranspiration datasets based on ground and GRACE satellite observations: Implications for improvement of evapotranspiration retrieval algorithm. Remote Sens. 2021, 13, 2414. [Google Scholar] [CrossRef]
- Novick, K.A.; Ficklin, D.L.; Stoy, P.C.; Williams, C.A.; Bohrer, G.; Oishi, A.C.; Papuga, S.A.; Blanken, P.D.; Noormets, A.; Sulman, B.N.; et al. The increasing importance of atmospheric demand for ecosystem water and carbon fluxes. Nat. Clim. Chang. 2016, 6, 1023–1027. [Google Scholar] [CrossRef]
- Talebmorad, H.; Abedi-Koupai, J.; Eslamian, S.; Mousavi, S.F.; Akhavan, S.; Ostad-Ali-Askari, K.; Singh, V.P. Evaluation of the impact of climate change on reference crop evapotranspiration in Hamedan-Bahar plain. Int. J. Hydrol. Sci. Technol. 2021, 11, 333–347. [Google Scholar] [CrossRef]
- Anderson, M.C.; Hain, C.; Otkin, J.; Zhan, X.; Mo, K.; Svoboda, M.; Wardlow, B.; Pimstein, A. An intercomparison of drought indicators based on thermal remote sensing and NLDAS-2 simulations with U.S. drought monitor classifications. J. Hydrometeorol. 2013, 14, 1035–1056. [Google Scholar] [CrossRef]
- Schwalm, C.R.; Huntinzger, D.N.; Michalak, A.M.; Fisher, J.B.; Kimball, J.S.; Mueller, B.; Zhang, K.; Zhang, Y. Sensitivity of inferred climate model skill to evaluation decisions: A case study using CMIP5 evapotranspiration. Environ. Res. Lett. 2013, 8, 024028. [Google Scholar] [CrossRef]
- Wang, S.; Pan, M.; Mu, Q.; Shi, X.; Mao, J.; Brümmer, C.; Jassal, R.S.; Krishnan, P.; Li, J.; Black, T.A. Comparing evapotranspiration from eddy covariance measurements, water budgets, remote sensing, and land surface models over Canada. J. Hydrometeorol. 2015, 16, 1540–1560. [Google Scholar] [CrossRef]
- Kim, Y.; Kimball, J.S.; Zhang, K.; Didan, K.; Velicogna, I.; McDonald, K.C. Attribution of divergent northern vegetation growth responses to lengthening nonfrozen seasons using satellite optical-NIR and microwave remote sensing. Int. J. Remote Sens. 2014, 35, 3700–3721. [Google Scholar] [CrossRef]
- Zhao, L.; Xia, J.; Xu, C.Y.; Wang, Z.; Sobkowiak, L.; Long, C. Evapotranspiration estimation methods in hydrological models. J. Geog. Sci. 2013, 23, 359–369. [Google Scholar] [CrossRef]
- Huntingford, C.; Verhoef, A.; Stewart, H. Dual versus single source models for estimating surface temperature of African savannah. Hydrol. Earth Syst. Sci. 2000, 4, 185–191. [Google Scholar] [CrossRef]
- Lhomme, J.P.; Monteney, B.; Amadou, M. Estimating sensible heat flux from radiometric temperature over sparse millet. Agric. Water Manag. 1994, 68, 77–91. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M. SEBAL-based sensible and latent heat fluxes in the irrigated Gediz Basin. Turkey J. Hydrol. 2000, 229, 87–100. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Morse, A. Satellite-based evapotranspiration by METRIC and Landsat for western states water management. In Proceedings of the U.S. Bureau of Reclamation Evapotranspiration Workshop, Ft. Collins, CO, USA, 8–10 February 2005. [Google Scholar]
- Allen, R.G.; Tasumi, M.; Trezza, R. Satellite-based energy balance for mapping evapotranspiration with internalized calibration (METRIC)—Model. J. Irrig. Drain. Eng. 2007, 133, 380–394. [Google Scholar] [CrossRef]
- Su, Z.; Schmugge, T.; Kustas, W.P.; Massman, W.J. An evaluation of two models for estimation of the roughness height for heat transfer between the land surface and the atmosphere. J. Appl. Meteorol. 2001, 40, 1933–1951. [Google Scholar] [CrossRef]
- Su, Z.B. The surface energy balance system (SEBS) for estimation of turbulent heat fluxes. Hydrol. Earth Syst. Sci. 2002, 6, 85–99. [Google Scholar] [CrossRef]
- Jaafar, H.; Mourad, R.; Schull, M. A global 30-m ET model (HSEB) using harmonized Landsat and Sentinel-2, MODIS and VIIRS: Comparison to ECOSTRESS ET and LST. Remote Sens. Environ. 2022, 274, 112995. [Google Scholar] [CrossRef]
- Senay, G.B.; Budde, M.; Verdin, J.P.; Melesse, A.M. A coupled remote sensing and simplified surface energy balance approach to estimate actual evapotranspiration from irrigated fields. Sensors 2007, 7, 979–1000. [Google Scholar] [CrossRef]
- Anderson, M.C.; Kustas, W.P.; Norman, J.M.; Hain, C.R.; Mecikalski, J.R.; Schultz, L.; Gonzalez-Dugo, M.P.; Cammalleri, C.; d’Urso, G.; Pimstein, A.; et al. Mapping daily evapotranspiration at field to continental scales using geostationary and polar orbiting satellite imagery. Hydrol. Earth Syst. Sci. 2011, 15, 223–239. [Google Scholar] [CrossRef]
- Marshall, M.; Tu, K.; Andreo, V. On parameterizing soil evaporation in a direct remote sensing model of ET: PT—JPL. Water Resour. Res. 2020, 56, e2019WR026290. [Google Scholar] [CrossRef]
- Mu, Q.; Heinsch, F.A.; Zhao, M.; Running, S.W. Development of a global evapotranspiration algorithm based on modis and global meteorology data. Remote Sens. Environ. 2007, 111, 519–536. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Running, S.W. Running. Improvements to a modis global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Kimball, J.S.; McDowell, N.G.; Running, S.W. A remotely sensed global terrestrial drought severity index. Am. Meteorol. Soc. 2013, 94, 83–98. [Google Scholar] [CrossRef]
- Zhao, F.; Ma, S.; Wu, Y.; Qiu, L.; Wang, W.; Lian, Y.; Chen, J.; Sivakumar, B. The role of climate change and vegetation greening on evapotranspiration variation in the Yellow River Basin, China. Agric. For. Meteorol. 2022, 316, 108842. [Google Scholar] [CrossRef]
- Veloso, G.A.; Ferreira, M.E.; Júnior, L.G.F.; da Silva, B.B. Modelling gross primary productivity in tropical savanna pasturelands for livestock intensification in Brazil. Remote Sens. Appl. Soc. Environ. 2020, 17, 100288. [Google Scholar] [CrossRef]
- Long, D.; Singh, V.P. Assessing the impact of end-member selection on the accuracy of satellite-based spatial variability models for actual evapotranspiration estimation. Water Resour. Res. 2013, 49, 2601–2618. [Google Scholar] [CrossRef]
- Hong, S.; Hendrickx, J.M.H.; Borchers, B. Up-scaling of SEBAL derived evapotranspiration maps from Landsat (30 m) to MODIS (250 m) scale. J. Hydrol. 2009, 370, 122–138. [Google Scholar] [CrossRef]
- Bhattarai, N.; Liu, T. LandMOD ET mapper: A new matlab-based graphical user interface (GUI) for automated implementation of SEBAL and METRIC models in thermal imagery. Environ. Model. Softw. 2019, 118, 76–82. [Google Scholar] [CrossRef]
- Morton, C.G.; Huntington, J.L.; Pohll, G.M.; Allen, R.G.; McGwire, K.C.; Bassett, S.D. Assessing calibration uncertainty and automation for estimating evapotranspiration from agricultural areas using METRIC. J. Am. Water Resour. Assoc. 2013, 49, 549–562. [Google Scholar] [CrossRef]
- Long, D.; Singh, V.P.; Li, Z.L. How sensitive is SEBAL to changes in input variables, domain size and satellite sensor? J. Geophys. Res. 2011, 116, 1–20. [Google Scholar] [CrossRef]
- Marx, A.; Kunstmann, H.; Schüttemeyer, D.; Moene, A.F. Uncertainty analysis for satellite derived sensible heat fluxes and scintillometer measurements over Savannah environment and comparison to mesoscale meteorological simulation results. Agric. For. Meteorol. 2008, 148, 656–667. [Google Scholar] [CrossRef]
- Allen, R.G.; Burnett, B.; Kramber, W.; Huntington, J.; Kjaersgaard, J.; Kilic, A.; Kelly, C.; Trezza, R. Automated calibraton of the METRIC-Landsat evapotranspiration process. J. Am. Water Resour. Assoc. 2013, 49, 563–576. [Google Scholar] [CrossRef]
- Wang, J.; Sammis, T.W.; Gutschick, V.P.; Gebremichael, M.; Miller, D.R. Sensitivity Analysis of the Surface Energy Balance Algorithm for Land (SEBAL). Trans. ASABE 2009, 52, 801–811. [Google Scholar] [CrossRef]
- Sobol’, I.M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math. Comput. Simul 2001, 55, 271–280. [Google Scholar] [CrossRef]
- Brust, C.; Kimball, J.S.; Maneta, M.P.; Jencso, K.; He, M.; Reichle, R.H. Using SMAP Level-4 soil moisture to constrain MOD16 evapotranspiration over the contiguous USA. Remote Sens. Environ. 2021, 255, 112277. [Google Scholar] [CrossRef]
- Clark, J.S.; Gelfand, A.E. A future for models and data in environmental science. Trends Ecol. Evol. 2006, 21, 375–380. [Google Scholar] [CrossRef]
- Vrugt, J.A.; ter Braak, C.J.; Diks, C.G.; Robinson, B.A.; Hyman, J.M.; Higdon, D. Accelerating Markov chain Monte Carlo simulation by differential evolution with self-adaptive randomized subspace sampling. Int. J. Nonlinear Sci. Numer. Simul. 2009, 10, 273–290. [Google Scholar] [CrossRef]
- Ter Braak, C.J.; Vrugt, J.A. Differential evolution Markov chain with snooker updater and fewer chains. Stat. Comput. 2008, 18, 435–446. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. The surface energy balance algorithm for land (SEBAL): Part 1 formulation. J. Hydrol. 1998, 212–213, 198–212. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. A remote sensing surface energy balance algorithm for land (SEBAL) 1. formulation. J. Hydrol. 1998, 212–213, 213–229. [Google Scholar] [CrossRef]
- Laipelt, L.; Kayser, R.H.B.; Fleischmann, A.S.; Ruhoff, A.; Bastiaanssen, W.; Erickson, T.A.; Melton, F. Long-term monitoring of evapotranspiration using the SEBAL algorithm and Google Earth Engine cloud computing. ISPRS J. Photogramm. Remote Sens. 2021, 178, 81–96. [Google Scholar] [CrossRef]
- Laipelt, L.; Ruhoff, A.L.; Fleischmann, A.S.; Kayser, R.H.B.; Kich, E.D.M.; da Rocha, H.R.; Neale, C.M.U. Assessment of an automated calibration of the SEBAL algorithm to estimate dry-season surface-energy partitioning in a Forest—Savanna transition in Brazil. Remote Sens. 2020, 12, 1108. [Google Scholar] [CrossRef]
- Kayser, R.H.; Ruhoff, A.; Laipelt, L.; de Mello Kich, E.; Roberti, D.R.; de Arruda Souza, V.; Rubert, G.C.D.; Collischonn, W.; Neale, C.M.U. Assessing geeSEBAL automated calibration and meteorological reanalysis uncertainties to estimate evapotranspiration in subtropical humid climates. Agric. For. Meteorol. 2022, 314, 108775. [Google Scholar] [CrossRef]
- Nishida, K.; Nemani, R.R.; Running, S.W.; Glassy, J.M. An operational remote sensing algorithm of land surface evaporation. J. Geophys. Res. 2003, 108, D94270. [Google Scholar] [CrossRef]

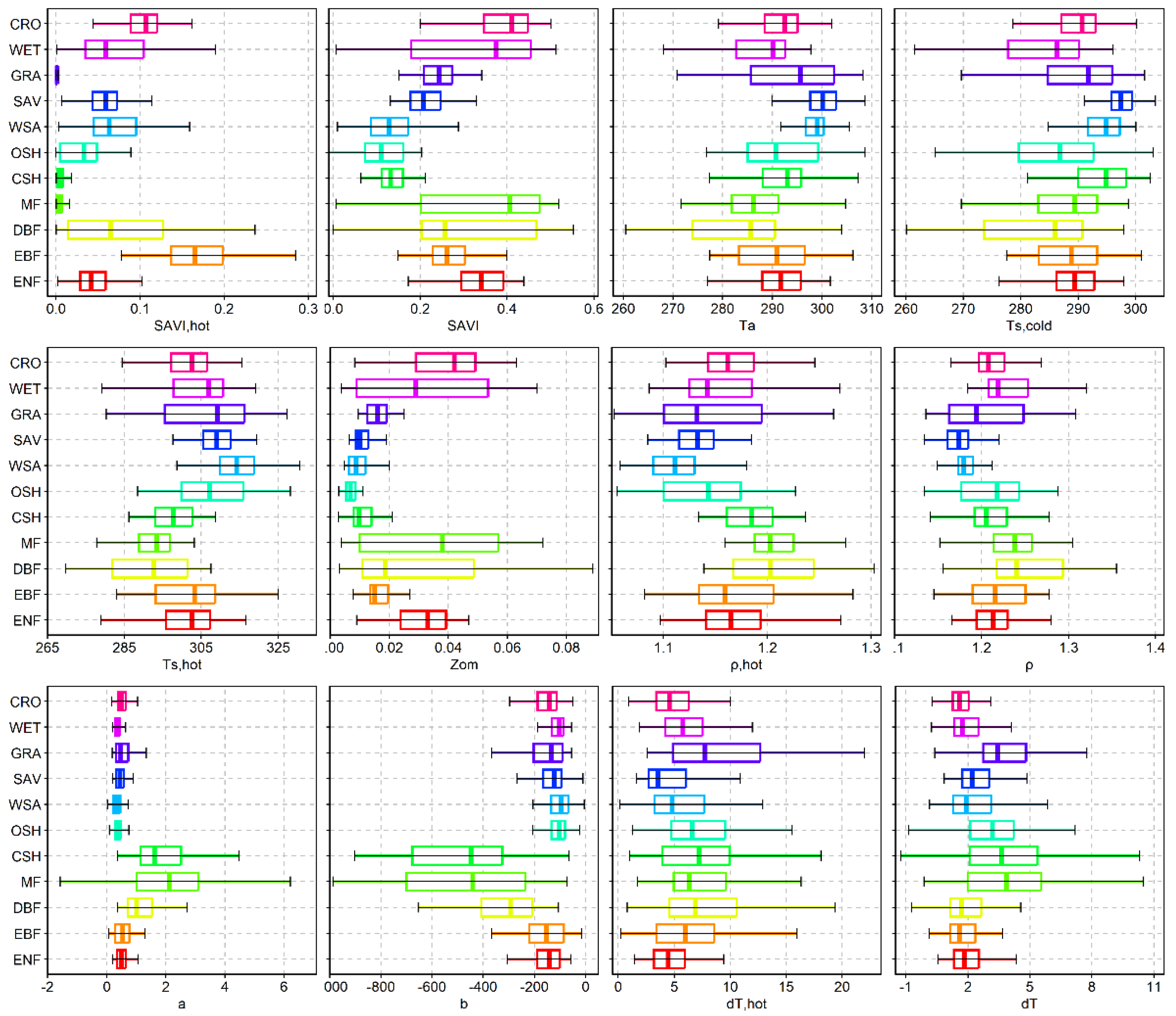

| Parameters | Describe | Intermediate Variable | Prior Distribution | Unit |
|---|---|---|---|---|
| Ts,hot | Maximum surface temperature Ts in pixels | [280.16, 320.84] | K | |
| Ts,cold | Minimum value of surface temperature Ts in pixels | [267.50, 302.44] | K | |
| NDVI,hot | Completely exposed surface NDVI value | [0.12, 0.28] | - | |
| NDVI,cold | Surface NDVI values completely covered by vegetation | [0.79, 0.81] | - | |
| SAVI | Adjusting the vegetation index for soil brightness | [−1, 1] | - | |
| SAVI,hot | Vegetation index for adjusting soil brightness limited by maximum surface temperature Ts | [0, 0.285] | - | |
| ρ | air density | [1.134, 1.356] | kg/m3 | |
| ρ,hot | Thermal pixel air density | [1.061, 1.179] | kg/m3 | |
| Rn,hot | Thermal pixel net radiation | [0, 250] | W/m2 | |
| G,hot | Thermal image element soil heat flux | [125.1, 188.5] | W/m2 | |
| H | Sensible heat flux | [101, 239.9] | W/m2 | |
| H,hot | Thermal pixel sensible heat flux | [48.089, 716.254] | W/m2 | |
| Zom | Surface roughness | [0.015, 0.1] | m | |
| rah | Aerodynamic impedance between different heights of land surface | [5.168, 136.415] | - | |
| rah,hot | Aerodynamic impedance between land surface at different heights limited by maximum surface temperature Ts | [0.0117, 103.761] | - | |
| Ta | Surface temperature per pixel | ; | [260.536, 308.668] | K |
| dT | Temperature difference between different heights of land surface | [−1.26, 10.431] | K | |
| dT,hot | Temperature difference between different heights of land surface limited by maximum surface temperature Ts | [0.119, 22.014] | K | |
| a | Regression coefficient of cold and hot pixels | [0.22, 1.22] | - | |
| b | Regression coefficient of cold and hot pixels | [−367.3, −63.6] | - |
| Pixel | End Element Components | Quantiles |
|---|---|---|
| Cold (wet) | NDVI | 0.01%, 0.1%, 1%, 2%, 3%, 4%, 5%,10%,15%. |
| Ts | 0.01%, 0.1%, 1%, 2.5%, 5%, 10%, 15%, 20%, 25%. | |
| Hot (dry) | NDVI | 0.01%, 0.1%, 1%, 2.5%, 4%, 6%, 8%, 10%,15%. |
| Ts | 0.01%, 0.1%, 1%, 2.5%, 5%, 10%, 15%, 20%, 25%. |
| Product | GEE ID | Band | Time Frame | Resolution Ratio |
|---|---|---|---|---|
| LANDSAT 5 TM | LANDSAT/LT05/C01/T1_SR LANDSAT/LT05/C01/T1 | Surface reflectance, brightness temperature, pixel QA (quality attributes) | 1984–2012 | 30 m |
| LANDSAT 7 ETM+ | LANDSAT/LE07/C01/T1_SRLANDSAT/LE07/C01/T1 | Surface reflectance, brightness temperature, pixel QA (quality attributes) | 1999–Now | 30 m |
| LANDSAT 8 OLI/TIRS | ANDSAT/LC08/C01/T1_SRLANDSAT/ LC08/C01/T1 | Surface reflectance, brightness temperature, pixel QA (quality attributes) | 2013–Now | 30 m |
| ERA5-Land hourly | ECMWF/ERA5_LAND/HOURLY | Air temperature at 2 m, dew point temperature at 2 m, eastward wind speed at 10 m, northward wind speed at 10 m, surface solar radiation. | 1981–Now | 0.1° |
| SRTM | USGS/SRTMGL1_003 | Elevation | 2000 | 30 m |
| Type | End Element Component Quantiles | Effects | ||||||
|---|---|---|---|---|---|---|---|---|
| Ts,cold (K) | Ts,hot (K) | NDVI,cold | NDVI,hot | RMSE (mm/d) | Bias (mm/d) | NSE | R2 | |
| ENF | 1 | 10 | 1 | 6 | 2.31 | −0.38 | −0.93 | 0.64 |
| EBF | 25 | 25 | 15 | 15 | 2.11 | −0.31 | −0.78 | 0.52 |
| DBF | 5 | 25 | 3 | 15 | 1.89 | 0.05 | 0.67 | 0.76 |
| MF | 0.1 | 10 | 0.1 | 6 | 2.67 | 0.09 | 0.34 | 0.61 |
| CSH | 2.5 | 25 | 2 | 15 | 2.45 | −1.34 | −0.57 | 0.51 |
| OSH | 10 | 0.1 | 4 | 0.1 | 4.89 | −1.09 | −1.89 | 0.47 |
| WSA | 25 | 0.01 | 15 | 0.01 | 0.99 | −0.89 | −2.16 | 0.53 |
| SAV | 0.1 | 25 | 0.1 | 15 | 2.11 | 0.56 | −0.04 | 0.54 |
| GRA | 0.01 | 10 | 0.01 | 6 | 3.67 | 0.79 | −0.45 | 0.53 |
| WET | 15 | 0.01 | 5 | 0.01 | 2.76 | −0.89 | 0.13 | 0.66 |
| CRO | 20 | 20 | 5 | 10 | 1.25 | −0.06 | −0.89 | 0.77 |
| Type | RMSE (mm/d) | Bias (mm/d) | NSE | R2 | |
|---|---|---|---|---|---|
| ENF | Ori | 7.67 | −3.14 | −0.45 | 0.55 |
| Opt | 2.16 | −1.78 | 0.53 | 0.65 | |
| EBF | Ori | 5.34 | −2.11 | −0.73 | 0.57 |
| Opt | 1.42 | −0.75 | 0.35 | 0.63 | |
| DBF | Ori | 8.18 | 0.19 | 0.34 | 0.49 |
| Opt | 0.66 | −0.11 | 0.52 | 0.6 | |
| MF | Ori | 4.59 | 1.55 | 0.54 | 0.52 |
| Opt | 1.36 | 1.01 | 0.65 | 0.63 | |
| CSH | Ori | 2.88 | −3.51 | −0.17 | 0.6 |
| Opt | 0.08 | −1.35 | 0.12 | 0.67 | |
| OSH | Ori | 3.23 | −2.57 | −1.04 | 0.47 |
| Opt | 1.02 | −1.76 | 0.15 | 0.53 | |
| WSA | Ori | 6.45 | −1.76 | 0.34 | 0.53 |
| Opt | 2.32 | 1.13 | 0.55 | 0.59 | |
| SAV | Ori | 4.19 | 4.1 | −4.67 | 0.41 |
| Opt | 1.67 | 2.59 | −0.27 | 0.45 | |
| GRA | Ori | 2.11 | −1.05 | −1.4 | 0.51 |
| Opt | 0.45 | 0.98 | 0.11 | 0.59 | |
| WET | Ori | 7.98 | 1.8 | 0.13 | 0.55 |
| Opt | 2.05 | 1.43 | 0.47 | 0.69 | |
| CRO | Ori | 6.12 | 1.8 | 0.06 | 0.62 |
| Opt | 1.24 | 1.02 | 0.57 | 0.73 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, S.; Tian, C.; Jiao, P. Sensitivity and Uncertainty Analysis of the GeeSEBAL Model Using High-Resolution Remote-Sensing Data and Global Flux Site Data. Water 2024, 16, 2978. https://doi.org/10.3390/w16202978
Hu S, Tian C, Jiao P. Sensitivity and Uncertainty Analysis of the GeeSEBAL Model Using High-Resolution Remote-Sensing Data and Global Flux Site Data. Water. 2024; 16(20):2978. https://doi.org/10.3390/w16202978
Chicago/Turabian StyleHu, Shunjun, Changyan Tian, and Ping Jiao. 2024. "Sensitivity and Uncertainty Analysis of the GeeSEBAL Model Using High-Resolution Remote-Sensing Data and Global Flux Site Data" Water 16, no. 20: 2978. https://doi.org/10.3390/w16202978
APA StyleHu, S., Tian, C., & Jiao, P. (2024). Sensitivity and Uncertainty Analysis of the GeeSEBAL Model Using High-Resolution Remote-Sensing Data and Global Flux Site Data. Water, 16(20), 2978. https://doi.org/10.3390/w16202978






