Abstract
In regions with abundant groundwater resources, pre-excavation dewatering on deep foundation pits often leads to the deformation of the enclosure wall and settlement of the surrounding ground. Based on a series of engineering measurements, we conducted a series of numerical simulations to investigate the behaviors of wall and soil during pre-excavation dewatering with and without the existing pile foundations and under different distances between the existing pile foundations and foundation pits (D). Numerical results indicated that when the foundation pit is adjacent to existing building pile foundations, the soil was restricted by the pile foundations (i.e., soil-blocking effect). When D ≤ 40 m, the soil-blocking effect grows stronger as D gets smaller; while when D > 40 m, the soil-blocking effect is significantly weakened and the water-blocking effect (i.e., the blockage of groundwater seepage by the building pile foundation) gradually appears, which intensifies the ground surface settlement. The maximum settlement position of the soil behind the pile foundation of the existing building is farther away from the foundation pit as the soil-blocking effect becomes stronger. The coupling effect of soil-blocking and water-blocking on the ground deformation should be considered in the design of the foundation pit project to get a more reasonable support and dewatering scheme.
1. Introduction
With the accelerating urbanization in China, numerous deep excavation projects are emerging in densely populated urban areas [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]; foundation pits located adjacent to existing underground building structures have become very common; the interaction between adjacent structures and excavation pits has become a focal point of research [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41].
Currently, soil excavation and dewatering are two major factors causing the deformation of the foundation pit and ground environment during the pit construction process [42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65]. The environmental disturbance caused by excavation has drawn extensive attention from scholars [59,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87]. Zhang et al. [88] conducted numerical analysis and experiments to study the damage to existing buildings caused by an adjacent foundation pit during excavation. Zhu et al. [89] introduced a safety monitoring and warning system used to analyze the influence of excavation pits on adjacent buildings. Zhang et al. [90] studied the time-domain analysis of viscoelastic mechanisms during the excavation of foundation pits on adjacent building deformations; Wei et al. [91] researched the effect of foundation pit excavation and dewatering on adjacent buildings in detail.
Regarding the impact of dewatering from a foundation pit on the surrounding environment, several scholars have conducted relevant studies as follows. Zeng et al. [51] used ABAQUS 6.14-4 to establish a three-dimensional fluid–solid coupling element model to study the enclosure wall deflection induced by pre-excavation dewatering under different construction conditions. Zhang et al. [92] studied effective control of ground settlement during dewatering in a Double-Layered Foundation pit based on the Seepage Control–Recharge Coupling Model.
The research mentioned above focuses on the impact of foundation pit excavation and dewatering on the surrounding environment. However, existing underground buildings around the foundation pit also affect the deformation of the foundation pit [64,93,94]. For example Liao et al. [95], through numerical parametric studies and case studies, have demonstrated that the presence of existing building piles creates a soil-blocking effect (i.e., hindering the soil settlement). This results in different ground deformations outside the foundation pit when there are existing building piles compared to when there are none. However, they did not consider how the foundation pit dewatering process with existing building piles might affect the ground strata.
Therefore, this study establishes a numerical model for deep foundation pit dewatering based on a subway station in Nankai District, Tianjin, China. Using the ABAQUS finite element analysis software, a numerical model of deep foundation pit dewatering was established to study the blocking effects of existing building pile foundations on water and soil and how these influence the deformation characteristics of the enclosure walls and surrounding soil layers during pre-excavation dewatering. The findings aim to provide technical references for related engineering designs.
2. Engineering Background
2.1. Project Description
Figure 1 presents an excavation project for a subway station site located in Nankai District, Tianjin, China. The pit was approximately 153.6 m long, 37.6 m wide, and with an excavation depth of about 16.9 m. The enclosure wall of the foundation pit adopts an underground diaphragm wall that was constructed using reinforced concrete, with a thickness of 0.8 m and a length of 32.5 m (the hydraulic connection between the inside and outside of the foundation pit was not cut off).
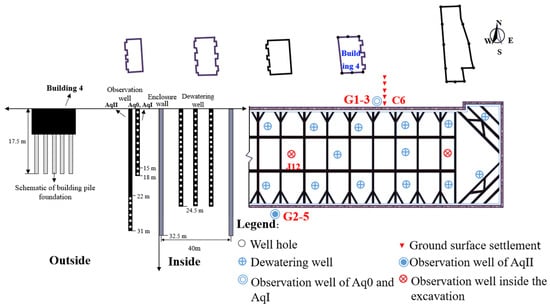
Figure 1.
Plans and sections of an excavation and layout of instrumentation.
The horizontal support of the subway station’s main structure excavation adopts three layers of C30 concrete supports. To minimize construction disturbances to the enclosure wall, the first support was installed in advance. There were 25 pumping wells installed inside the foundation pit to lower the water level. Among these, 22 pumping wells were opened to withdraw groundwater, while the remaining 3 pumping wells were unoperated and functioned as observation wells to monitor the variations in groundwater level within the foundation pit. Simultaneously, several groundwater observation wells were arranged outside the foundation pit to monitor the variations in water levels in different aquifers.
2.2. Geological Conditions
As depicted in Figure 1, the south of the pit site is an open area without buildings, while on the north, there is a row of residential community buildings with foundations supported by pipe piles. The buildings in the community are approximately 36 m away from the foundation pit, with the pile foundation buried at a depth of 17.5 m. Within the 50 m depth range of the ground surface in the construction site, the foundation pit site mainly consisted of silty clays, clayey or sandy silts, and silty sands. There are five aquifers (designated as Aq0, AqI, AqII, AqIII, and AqIV, respectively), separated by aquitards (designated as AdI, AdII, AdIII, and AdIV). Figure 2 shows the distribution of soil layers and the main soil parameters (the data were obtained from site investigation and laboratory soil tests), where γ represents the unit weight; K0 denotes the coefficient of earth pressure at rest; ω indicates the water content; e represents the initial void ratio; ES is the constrained modulus; Vs is the shear wave velocity.
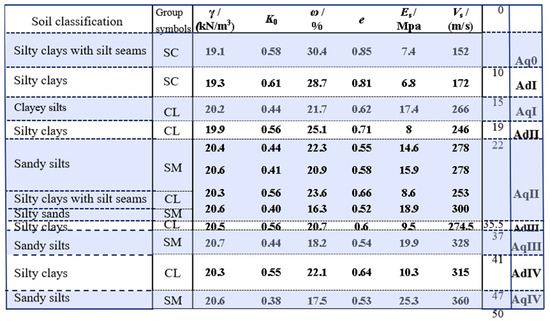
Figure 2.
Strata distribution and the main soil mechanical parameters.
2.3. Pumping Test
Figure 2 shows the positions and relationships among various enclosure walls, pumping wells, and observation wells. The enclosure wall does not completely cut off AqII, and the dewatering wells inside the pit are inserted into AqII. Therefore, dewatering inside the foundation pit would also cause groundwater drawdown outside the foundation pit, which further induces ground surface settlement.
To assess the effectiveness of the retaining structure’s water resistance and the pumping wells’ pumping capacity, seven pumping tests were conducted by engineers before soil excavation of the foundation pit, with a total test duration of 21 days. Therein taking a typical group well pumping test as an example, it lasted for 3.2 days. Through observation wells inside the foundation pit and settlement monitoring points outside the pit, it was observed that the water level inside the pit dropped by approximately 15 m. The water levels have dropped by approximately 8 m on the south side and 3 m on the north side outside the foundation pit, respectively. The reason is that the dewatering on the south side occurs in AqII, which is different from the dewatering on the north side that occurs in AqI, and there are building piles on the north side that obstruct the flow of water. Furthermore, the maximum ground surface settlement has reached up to 12 mm [11]. This indicates that the impact of the pumping tests on the surrounding environment of the foundation pit cannot be ignored. In addition, the only difference in the above experimental results is whether or not there are pile-supported buildings between the north and south sides. This implies that the presence of piled foundation structures affects groundwater seepage and stratum deformation.
Therefore, the following section investigates the influence mechanism of the adjacent pile foundation’s seepage barrier effect on groundwater and stratum deformation during the excavation dewatering process. The development mechanism is revealed through a series of numerical simulation studies.
3. Numerical Analysis
3.1. Modeling Scheme
This section utilized ABAQUS to establish two types of models based on the engineering background described in Section 2. The first type of model simulated the pumping test from the previous section (i.e., without a building pile foundation on the north side of the foundation pit, because of the uncertainty and complexity of the real conditions of the pile foundation) and was validated against actual measured data from the engineering. The second type of model is based on the first type, with the premise of incorporating the existing adjacent building pile foundation on the north side outside the foundation pit. It varies the parameters of the distance (D) between the piled foundation and the foundation pit and the depth of pit dewatering (Hd) (where D is set to 5, 10, 15, 20, 40, and 60 m, and Hd is set to 10, 15, 19, and 22 m), to investigate the influence of existing pile foundation seepage barrier effects on strata deformation induced by pit dewatering. Since the processes for establishing the two types of models are similar, the following only shows the modeling process specifically for the second type of model in detail.
3.2. Model Setup
Considering the complexity of modeling for the entire project and the deformations that often occur in the middle section of the foundation pit, this section models the middle section of the elongated foundation pit (as shown in Figure 1), with the three-dimensional model depicted in Figure 3. The dimensions of the enclosure wall and the plan and vertical view of the dewatering wells in the model are roughly like the engineering conditions described in Section 2. The model is constructed based on a common group pile foundation, with a 10 m deep underground building basement and 36 piles, each 31 m long and 0.85 m in diameter (spaced at 3.06 m intervals).
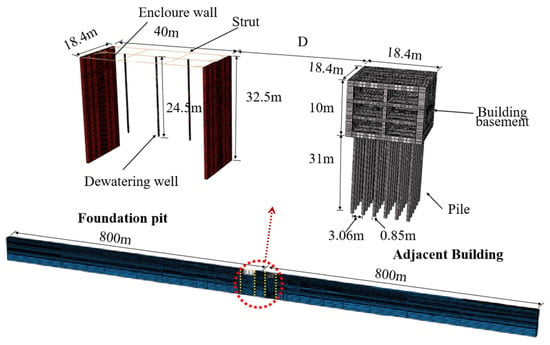
Figure 3.
Finite element material diagram of the model (adapted from Reference [8]).
The over-exploitation of groundwater in coastal areas of China and recent restrictions on groundwater extraction, as a result, led to fluctuating groundwater levels in Tianjin, causing the soil to exhibit elastic deformation under typical groundwater drawdown conditions [96,97]. Hence, the soil model utilizes the Mohr–Coulomb (MC) model [49,98,99]. Based on the actual site conditions described in Section 2 of the project, the soil layers in the model are divided into 12 layers, simulated using pore-pressure solid elements (C3D8P). Consideration of fluid–structure interaction is included in the calculations. The Poisson ratio for silty clays and clay is 0.33, while for silt, silty sands, and fine sand, it is 0.30. Detailed model parameters are provided in Table 1. The effective cohesion (c′) and the effective internal friction angle (φ′) of the soil are determined based on on-site investigation and laboratory soil tests. The elastic modulus (E) and the horizontal and vertical permeability coefficient (KH and KV) are obtained through inverse calculation, comparing the model computation results with the measurements from pumping tests described in Section 2. For detailed procedures of the inverse calculation, please refer to the article by Wang et al. [100]. The enclosure wall and building piles are simulated using solid incompatible elements C3D8I, the dewatering wells are simulated using shell elements S4, and the first line supports are simulated using linear beam elements B31. According to previous studies and experience from scholars [27], the modeling process neglects the gap between the dewatering well casing and the wellbore. The (μ) between the dewatering wells, building pile foundations, and enclosure wall with the soil is taken as 0.30. Assuming linear elastic behavior for the stress–strain relationship of retaining structures, dewatering wells, and building pile foundations, their respective elastic moduli are 30 MPa, 210 MPa, and 30 MPa.

Table 1.
Soil distribution and parameters used in the model (adapted from Reference [8]).
Due to the hydraulic connection between the inside and outside of the pit, to avoid the settlement of soil affecting areas beyond the model boundary during dewatering inside the pit, the influence range (R) of dewatering, assuming a maximum drawdown of 35.5 m for AqII, using the Sichardt Formula (1) [101], is defined as follows:
where SW and Kh are the groundwater drawdown and horizontal permeability of the pumped aquifer, and R is influencing a range of dewatering.
The calculation yields R = 615 m (Kh = 3 m/d). To prevent the influence of water level changes during pit dewatering from extending beyond the model boundary, the distance between the model soil boundary and the pit is set to 800 m, which is 40 times the maximum drawdown depth.
Apart from the top surface of the model, horizontal constraints are applied to the entire model boundary. Additionally, vertical constraints are applied to the bottom surface of the soil, and the water level is also set at the constant head hydraulic supply position at the model’s ground surface boundary. To simulate dewatering, a constant head boundary is established on the soil surface in contact with the dewatering wells. For example, for the model where the water level inside the pit drops by 22 m (with a model well bottom depth of 24.5 m), the zero-pore pressure boundary condition can be set within the range of 0 to 22 m, and a fixed head boundary condition based on hydrostatic pressure can be sit in the range of 22 to 24.5 m. Therefore, the simulation of different dewatering depths only requires adjusting the ranges of the zero-pore pressure and fixed head boundary conditions accordingly.
3.3. Model Validation
Following the numerical simulation based on the pumping test process, the variations in water levels inside and outside the pit and ground surface settlement caused by pumping are obtained. By comparing these with the measured values, we found that the simulated values have a good level of consistency with the measured values. However, due to the existence of differences in actual geological conditions, such as uneven soil layer thickness or variations in soil properties, the measured values and simulated values cannot be completely consistent. In summary, this study’s numerical simulation broadly reflects the development of practical water level change and soil deformation caused by pumping. The detailed comparison results can be referred to in the article by Zeng et al. [8]. Therefore, the second type of model established based on this model is considered relatively reliable.
4. Simulation Results and Analysis
4.1. Distribution of Groundwater Drawdown
Figure 4 shows the distribution pattern of groundwater drawdown outside the foundation pit as a function of depth, using a dewatering depth Hd = 22 m as an example. The three main points that can be observed are as follows:
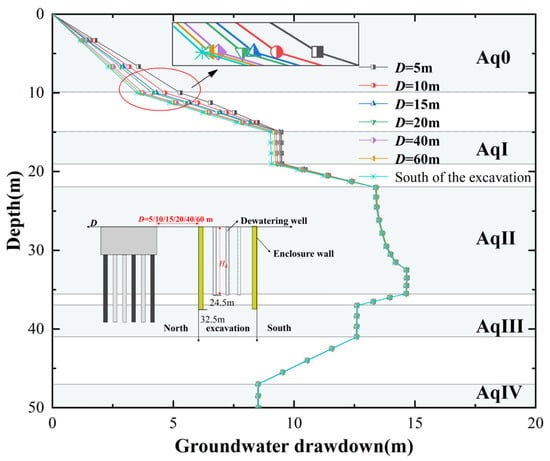
Figure 4.
Groundwater drawdown outside the pit along the depth.
- Compared to the side without building pile foundations, the side with building pile foundations has a greater depth of groundwater drawdown. This is because groundwater flow toward the foundation pit is hindered by the presence of building piles, causing some groundwater to circumvent the underground structures, thereby elongating its seepage pathway;
- As D increases, the drawdown of water level outside the foundation pit decreases, approaching the drawdown observed without building piles. This indicates that the farther the pile foundations are from the foundation pit, the weaker their barrier effect on water;
- In Aq0, the variation in water levels outside the foundation pit is significantly influenced by D on the sides with pile foundations. However, below Aq0, the differences in water level variations between sides with and without pile foundations gradually diminish. This is because within the depth range of the Aq0, there are underground structures such as building basements, which create a strong barrier effect on groundwater. Below this depth range are pile foundations, where the soil between the piles allows groundwater to seep through, thus significantly reducing their barrier effect on water.
Figure 5 shows the horizontal variation curve of drawdown in the water level of the first confined aquifer AqI under the condition of Hd = 22 m. From the figure, it can be observed that along the horizontal distribution, as the distance from the foundation pit increases, the drawdown in water level decreases; as D increases, the barrier effect of the pile foundation on water gradually diminishes. Furthermore, comparing the groundwater drawdown on the side of the foundation pit with and without pile foundations, it is evident that regardless of D, the side with pile foundations consistently shows greater water level variations than the side without pile foundations. This corresponds with the vertical distribution of groundwater drawdown shown in Figure 4.
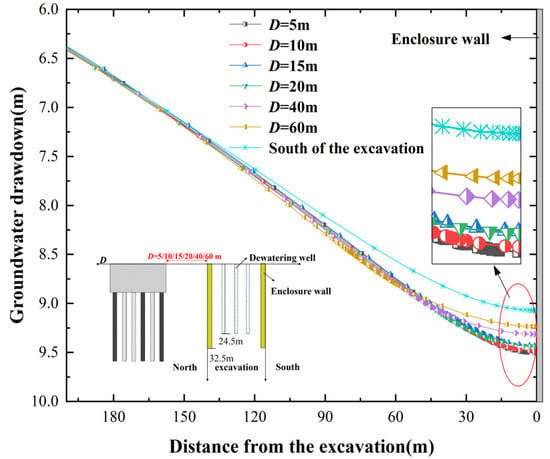
Figure 5.
Distribution curves of groundwater drawdown outside along level in AqI.
To assess the water-barrier effect of building pile foundations during pre-watering excavation, the water resistance intensity factor η = S2/S1. (S2 is the maximum groundwater drawdown on the northern side of the foundation pit, while S1 is the maximum groundwater drawdown on the southern side without a building pile foundation). Figure 6 shows the trend of η as D varies when Hd = 22 m. As shown in Figure 6, regardless of D, the η is always greater than one. This indicates that the existing building pile foundations obstruct the water flow into the foundation pit, resulting in a greater groundwater drawdown compared to the condition without buildings. In addition, the fitted curve of η shows a decreasing trend. This indicates that as D increases, η gradually decreases, which means the obstructive effect of building pile foundations on water becomes weaker gradually.
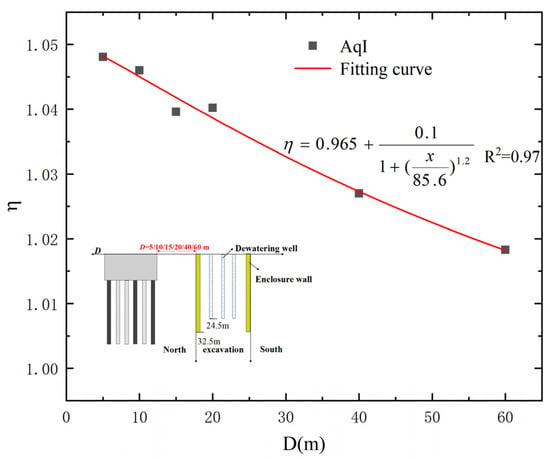
Figure 6.
Variation of η = S2/S1 with D.
4.2. Distribution of Enclosure Wall Deflection and Ground Surface Settlement
Figure 7, taking a dewatering depth of Hd = 22 m as an example, demonstrates the pattern of ground surface settlement and enclosure wall deflection outside the foundation pit induced by dewatering, under different distances (D) between building pile foundations and the foundation pit. From the enclosure wall deflection pattern the following is observed:
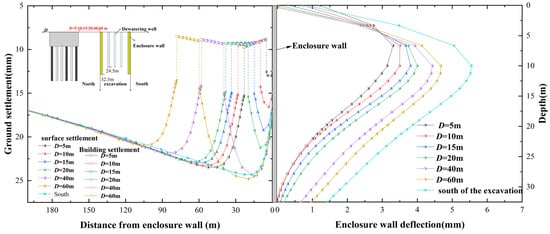
Figure 7.
Settlement of the ground outside the pit and adjacent structures and lateral displacement curve.
- Regardless of whether there are pile foundations outside the foundation pit or not, dewatering inside the foundation pit causes the enclosure wall to undergo an inward ‘bulging’ type of deflection. This is because the initial support provided by the first construction stage before dewatering causes minimal lateral movement at the head on the enclosure wall. At the same time, the deeper soil exerts a constraining effect on the bottom of the enclosure wall, resulting in less lateral movement at deeper positions of the enclosure wall. Therefore, the deformation of the enclosure wall mainly occurs in the near-middle section;
- When there are foundation piles outside the foundation pit, as D increases, the lateral movement of the enclosure wall caused by dewatering also increases but overall remains smaller than when there are not pile foundations (i.e., at the south side of the foundation pit).
From the ground surface settlement pattern outside the foundation pit the following is observed:
- Dewatering causes a dual settlement groove pattern in the ground surface on the north side of the foundation pit (i.e., the settlement groove behind the existing pile foundations and the settlement groove between the enclosure wall and the existing pile foundations). While on the south side without pile foundations, the ground settlement outside the foundation pit exhibits a single settlement groove pattern;
- For the scenarios with ground surface settlement involving existing pile foundations, when D < 40 m (i.e., D = 5 m, 10 m, 15 m, and 20 m), the ground settlement between the enclosure wall and the existing pile foundations is less than without pile foundations (i.e., the ground settlement corresponding to the south side of the pit); when D ≥ 40 (i.e., D = 40 m and 60 m), the ground settlement between the enclosure wall and the existing pile foundations is greater than without pile foundations. This indicates that during the pre-excavation dewatering process, as D increases, both the soil-blocking effect and the water-blocking effect gradually diminish. Moreover, when D < 40 m, the barrier effect of the soil plays a predominant role, thereby hindering the settlement of the soil between the existing pile foundations and the enclosure wall. When D > 40 m, the water-blocking effect plays a predominant role, thereby lengthening the flow path, resulting in a more significant decrease in groundwater level between the existing pile foundations and the enclosure wall, consequently leading to greater settlement.
From the settlement pattern of the existing pile foundations the following is observed:
- When existing pile foundations hinder the movement of soil, they themselves deform with the movement of the soil, resulting in uneven settlement. This is particularly evident when they are close to the foundation pit, but the settlement of the pile foundations is always less than the settlement of the nearby ground surface;
- As D increases, the settlement of the building transitions from a greater settlement at the front side compared to the back side to gradually less settlement at the front side compared to the backside. It is important to consider this pattern and its impact on the structural integrity during the project.
4.3. Distribution of Maximum Ground Settlement and Maximum Enclosure Wall Deflection
Figure 8 shows the relationship between the maximum ground settlement (δvm) in front and behind existing pile foundations outside the foundation pit, as well as the maximum lateral displacement of the enclosure wall (δhm) at different dewatering depths and D. The following can be observed:
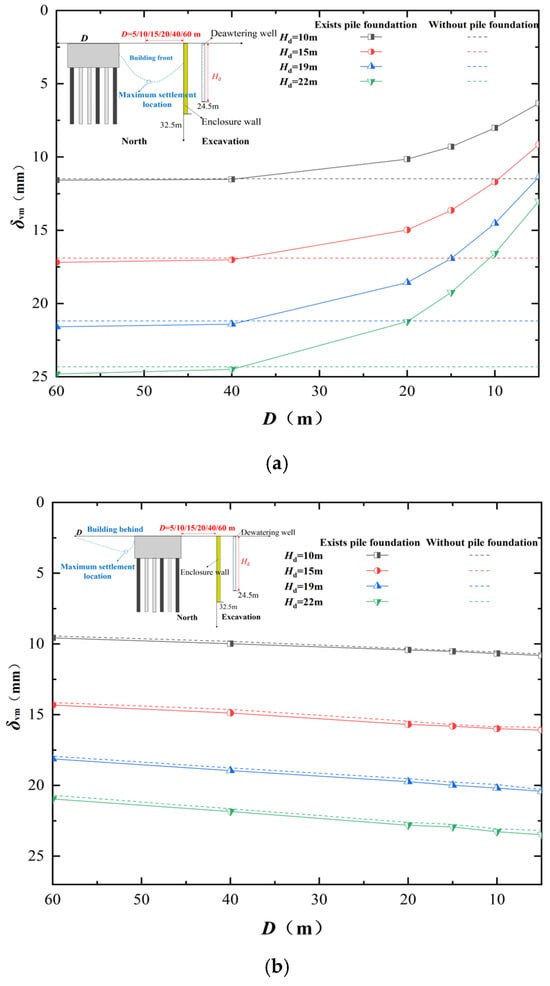
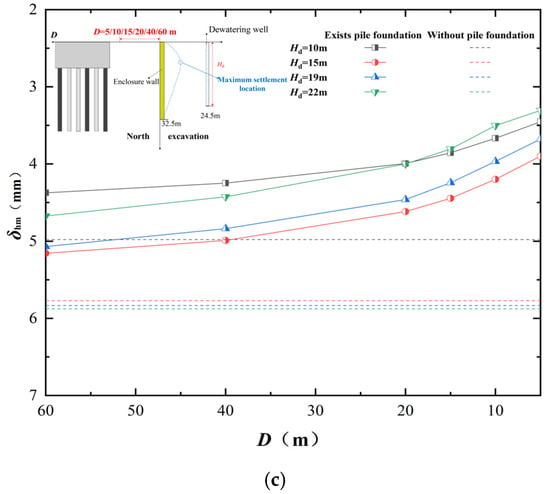
Figure 8.
Relation between δhm and D under different dewatering depths: (a) relation between pile foundation and foundation pit δvm and D; (b) relation between behind the pile foundation δvm and D; (c) relation between δhm and D.
- Overall, the pumping causes both the front δvm and δhm of the existing pile foundations outside the pit to increase with the increase in D. This trend becomes more pronounced under deeper dewatering depths. This reflects the impact of the continuous weakening effect of existing pile foundations outside the foundation pit on restraining soil movement;
- As in Figure 8a, in the front of the existing pile foundations, when D ≤ 40 m, the δvm on the side with existing pile foundations is significantly smaller than the δvm under the same conditions when there are not pile foundations. This is because the barrier effect of the building has a positive influence. Furthermore, it primarily relies on the water-blocking effect. However, when (D > 40 m), the δvm on the side with existing pile foundations is slightly larger than the δvm under the same conditions without pile foundations. This is because the barrier effect of the building has a negative impact, primarily relying on the soil-blocking effect. It can be considered that under the same dewatering depth, there exists a critical value for D in terms of the influence of dewatering-induced δvm. As D changes, the coupled effects of barrier pile foundations on the soil and pile foundations on the water gradually become apparent;
- As in Figure 8b, At the same dewatering depth, the δvm behind the existing pile foundations gradually decreases with increasing D. The δvm on the side with/without existing pile foundations is roughly the same. This is because water can permeate between the pile foundations; Thus, the extent of water level decline behind the pile foundations is similar to that on the side without pile foundations (see Figure 5), resulting in similar consolidation settlement of the soil mass;
- From Figure 8c, it can be observed that with increasing dewatering depth, δhm shows a pattern of initially increasing and then decreasing, reaching its maximum at Hd = 15 m. This is because when the dewatering depth is shallow (Hd ≤ 15 m), there is less groundwater replenishment from outside the foundation pit to the inside, resulting in smaller maximum lateral displacement under corresponding conditions. However, when the dewatering depth is greater (Hd > 15 m), the water level inside the foundation pit decreases significantly, while groundwater from outside the foundation pit promptly replenishes into it. This results in a significant decrease in water levels both inside and outside the foundation pit, causing the enclosure wall to exhibit lateral displacement tendencies in both directions—towards the inside and outside of the foundation pit. Due to these two trends counteracting each other, the maximum lateral displacement under these conditions is smaller compared to when the dewatering depth Hd = 15 m. Because the barrier effect plays a positive role in restraining the lateral deformation of the enclosure wall, δhm is consistently less than the maximum lateral displacement of the enclosure wall without pile foundations.
Figure 9 shows the relationship between maximum ground surface settlement (δvm) and maximum lateral displacement of the enclosing wall (δhm) under different dewatering depths (Hd). To facilitate comparison with previous studies, this paper calculates non-dimensionless δvm and δhm by dividing them by Hd, resulting in δvm/Hd and δhm/Hd. Among them, the horizontal data points in Figure 9, from top to bottom, represent the variation in D from 60 m to 5 m, respectively. The following can be observed:
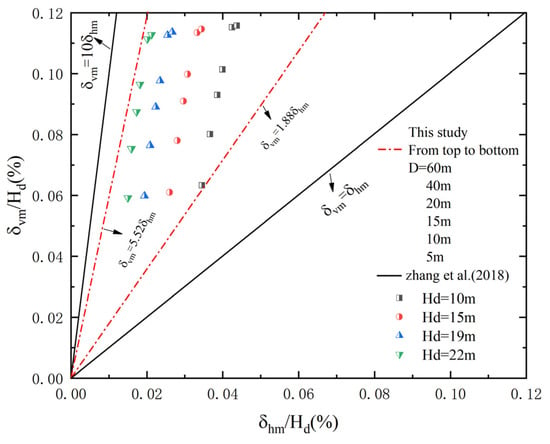
Figure 9.
Relationship between δvm/Hd and δhm/Hd [102].
- δvm mostly lies between δvm = 1.88 δhm and δvm = 5.52 δhm, caused by pre-watering excavation, with δvm ranging from 0.051% Hd to 0.114% Hd, and δhm changes from 0.015 Hd to 0.044 Hd. The ratio relationship between δvm and δhm in this study is generally within the range of the measurement data from Zhang et al. [102] (i.e., from δvm = δhm to δvm = 10 δhm). Zhang et al. and this study both investigate the relationship between the changes in δvm and δhm caused by foundation pit dewatering when there is hydraulic connectivity between the inside and outside of the foundation pit (i.e., dewatering inside the pit leads to a rapid decline in the water level outside the pit);
- As D continues to increase, the slope of the relationship between δvm and δhm also increases correspondingly. This is because, as D increases, the barrier effect of the building gradually weakens, which aggravates surface ground settlement while also restraining the lateral displacement of the enclosure wall. In addition, as the depth of dewatering (Hd) increases, it will also lead to an increase in the slope of the relationship between δvm and δhm.
4.4. Maximum Settlement Increment and Maximum Lateral Displacement Increment
Figure 10 illustrates the relationship between the maximum settlement increment of the ground surface between existing pile foundations and the foundation pit (Δδvm), as well as the maximum lateral displacement increment of the enclosure wall (Δδhm), concerning the distance between existing pile foundations and the enclosure wall (D) and the dewatering depth (Hd).
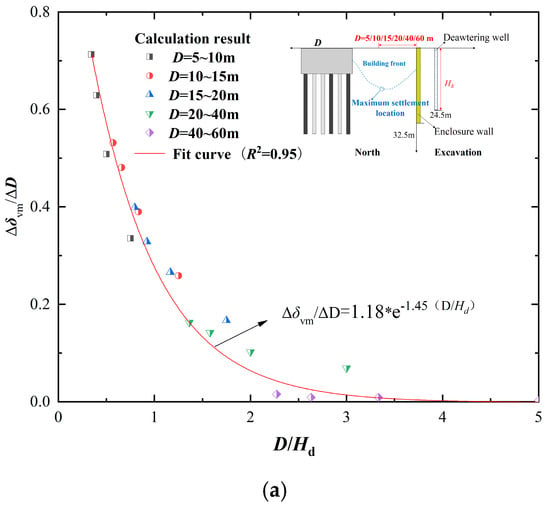
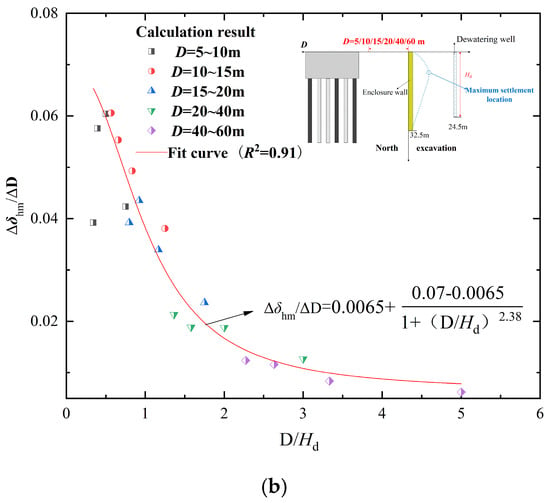
Figure 10.
Relation between D and Hd of maximum ground settlement increment and maximum lateral displacement increment of enclosure structure between adjacent structure and foundation pit: (a) Δδvm/ΔD relative to D/Hd; (b) Δδhm/ΔD relative to D/Hd.
From Figure 10, it can be observed that as D increases, both Δδvm and Δδhm decrease nonlinearly, when D ranges from 5 to 40 m, the variations in Δδvm and Δδhm are significant, indicating that Δδvm and Δδhm are highly sensitive to changes in both D and Hd. To simplify the calculation of maximum surface settlement outside the foundation pit (δvm) and maximum lateral displacement of the enclosure wall (δhm) caused by dewatering, Origin software (OriginPro 2018C) is used to fit the scatter data points into two types of mathematical functions, respectively, describing the trends of Δδvm and Δδhm changes. Therefore, based on the deformation observation results of the existing foundation pit, preliminary estimates can be made for the maximum lateral displacement of the enclosure wall and maximum settlement caused by dewatering in the new construction foundation pit under similar geological conditions at different distances (D). This can provide initial references for the dewatering design of the foundation pit.
5. Discussion
In summary, the factors affecting the seepage barrier effect are mainly the differences in the barrier structures and the distance (D) between the building pile foundations and the foundation pit. When the barrier structure is a basement, its water-barrier effect is significantly stronger than that of building pile foundations (like the third conclusion in Section 4.1). Due to the coupling effects of the water-barriers effect and soil-barriers effect from existing nearby buildings, when the distance D between the building pile foundations and the pit is less than 40 m, the soil-barrier effect dominates; when D is greater than 40 m, the water-barrier effect dominates. This paper considers pre-excavation dewatering without building pile foundations and does not discuss dewatering during the excavation process. Due to the current lack of measured data, this will be a focus of future research, comparing it with the actual excavation process.
6. Conclusions
This article investigates the influence of the seepage barrier effect of existing building pile foundations on the deformation of strata induced by foundation pit dewatering using three-dimensional finite element numerical simulation. Based on this study, the following conclusions can be obtained:
- From the perspective of the depth distribution of water level drawdown outside the pit, the water level drawdown on the side with a building pile foundation is greater than that on the side without any buildings. It is noteworthy that in the aquifer layer Aq0, the changes in water level outside the foundation pit on both sides with and without building pile foundations are significantly influenced by distance (D), while below the aquifer layer Aq0, the differences in water level changes between both sides gradually diminish. From the perspective of the horizontal distribution of water level drawdown outside the foundation pit, the further away from the foundation pit, the smaller the water level drawdown. As the distance (D) increases, the barrier effect of the building pile foundation on the water gradually weakens;
- From the perspective of enclosure wall deformation patterns, due to the presence of the first support at the top of the diaphragm wall of the foundation pit, the maximum lateral displacement generated by the enclosure wall occurs primarily around a depth of 10 m, regardless of the presence or absence of building pile foundations. Under the same dewatering depth conditions, the lateral displacement of the enclosure wall increases gradually with the distance between existing building pile foundations and the foundation pit. Additionally, the lateral displacement of the enclosure wall on the north side of the foundation pit is consistently smaller than that on the south side at corresponding positions. This indicates that both the barrier effect of the existing building pile foundation soil and the barrier effect of the existing building pile foundation water positively influence the lateral displacement pattern of the enclosure wall;
- From the perspective of ground surface settlement patterns between the existing building pile foundation and the pit, when there are not building pile foundations, the settlement outside the pit caused by pre-excavation dewatering exhibits a single settlement groove. If there are building pile foundations, it manifests as a double settlement groove pattern. Under the same dewatering conditions, the distance (D) between the building pile foundation and the pit increases, and the settlement of the soil outside the pit also increases. When D < 40 m, the soil-blocking effect gradually diminishes with increasing D, resulting in the settlement of the soil being less than that at the corresponding position on the south side of the pit. However, when D > 40 m, the soil-barrier effect significantly weakens, while the pile foundations enhance their obstruction to groundwater flow, leading to settlement being greater than that at the corresponding position on the south side of the foundation pit. From the perspective of ground surface settlement patterns behind the building pile foundation outside the foundation pit, the settlement of the soil behind the building pile foundation is greater compared to the settlement at corresponding positions without building pile foundations. Moreover, the settlement of the soil behind the existing building pile foundations gradually approaches the settlement at corresponding positions on the south side of the foundation pit as D increases;
- Regarding the maximum settlement of the soil outside the foundation pit and the maximum lateral movement of the enclosure wall, as well as their increments, δvm mostly lies between δvm = 1.88 δhm and δvm = 5.52, with δhm caused by pre-watering excavation. It is largely consistent with the measurement data from Zhang et al., ranging from δvm = δhm to δvm = 10 δhm. There exists a critical value for the influence of different D values on δvm of the soil between the building pile foundation and the foundation pit (i.e., D = 40 m). The settlement of the soil behind the building pile foundation decreases linearly with increasing D. The greater the depth of dewatering, the more pronounced that the influence of the building pile foundation on deformation induced by pumping becomes.
Author Contributions
Conceptualization, C.Z.; Methodology, C.Z.; Software, D.H.; Formal analysis, D.H.; Investigation, H.S.; Resources, Y.Z. and L.H.; Data curation, Y.Z. and L.H.; Writing—original draft, D.H. and X.X.; Writing—review & editing, C.Z. and C.X. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China [grant numbers 52478342, 51978261 and 52238009], the Science and Technology Innovation Program of Hunan Province [grant number 2022RC1172], and the Natural Science Foundation of Jiangxi Province [grant number 20223BBG71018]. Finally, we deeply appreciate the warm and efficient work of editors and reviewers.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to confidentiality requirement.
Acknowledgments
The authors are grateful for the warm and efficient work by editors and reviewers.
Conflicts of Interest
Author Youwu Zhao was employed by the company China Construction Fifth Engineering Division Corp., Ltd. Author Lei Han was employed by the company China Construction Eighth Engineering Division Corp., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Zhang, D.; Shen, Y.; Huang, Z.; Xie, X. Auto machine learning-based modelling and prediction of excavation-induced tunnel displacement. J. Rock Mech. Geotech. Eng. 2022, 14, 1100–1114. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, R.; Wang, W.; Zhang, F.; Goh, A.T.C. A Multivariate Adaptive Regression Splines model for determining horizontal wall deflection envelope for braced excavations in clays. Tunn. Undergr. Space Technol. 2019, 84, 461–471. [Google Scholar] [CrossRef]
- Waichita, S.; Jongpradist, P.; Jamsawang, P. Characterization of deep cement mixing wall behavior using wall-to-excavation shape factor. Tunn. Undergr. Space Technol. 2019, 83, 243–253. [Google Scholar] [CrossRef]
- Soomro, M.A.; Mangnejo, D.A.; Bhanbhro, R.; Memon, N.A.; Memon, M.A. 3D finite element analysis of pile responses to adjacent excavation in soft clay: Effects of different excavation depths systems relative to a floating pile. Tunn. Undergr. Space Technol. 2019, 86, 138–155. [Google Scholar] [CrossRef]
- Jamsawang, P.; Voottipruex, P.; Tanseng, P.; Jongpradist, P.; Bergado, D.T. Effectiveness of deep cement mixing walls with top-down construction for deep excavations in soft clay: Case study and 3D simulation. Acta Geotech. 2019, 14, 225–246. [Google Scholar] [CrossRef]
- Goh, A.T.C.; Zhang, F.; Zhang, W.; Zhang, Y.; Liu, H. A simple estimation model for 3D braced excavation wall deflection. Comput. Geotech. 2017, 83, 106–113. [Google Scholar] [CrossRef]
- Zeng, C.-F.; Powrie, W.; Chen, H.-B.; Wang, S.; Diao, Y.; Xue, X.-L. Ground Behavior due to Dewatering Inside a Foundation Pit Considering the Barrier Effect of Preexisting Building Piles on Aquifer Flow. J. Geotech. Geoenviron. Eng. 2024, 150, 05024004. [Google Scholar] [CrossRef]
- Xue, X.-L.; Sun, H.-Y.; Zeng, C.-F.; Chen, H.-B.; Zheng, G.; Xu, C.-J.; Han, L. Why pile-supported building settled continuously after water level was stabilized during dewatering: Clues from interaction between pile and multi aquifers. J. Hydrol. 2024, 638, 131539. [Google Scholar] [CrossRef]
- Zeng, C.-F.; Chen, H.-B.; Liao, H.; Xue, X.-L.; Chen, Q.-N.; Diao, Y. Behaviours of groundwater and strata during dewatering of large-scale excavations with a nearby underground barrier. J. Hydrol. 2023, 620, 129400. [Google Scholar] [CrossRef]
- Xue, T.; Xue, X.; Long, S.; Chen, Q.; Lu, S.; Zeng, C. Effect of Pre-Existing Underground Structures on Groundwater Flow and Strata Movement Induced by Dewatering and Excavation. Water 2023, 15, 814. [Google Scholar] [CrossRef]
- Zeng, C.-F.; Liao, H.; Xue, X.-L.; Long, S.-C.; Luo, G.-J.; Diao, Y.; Li, M.G. Responses of groundwater and soil to dewatering considering the barrier effect of adjacent metro station on multi-aquifers. J. Hydrol. 2022, 612, 128117. [Google Scholar] [CrossRef]
- Liu, H.; Li, P.; Liu, J. Numerical investigation of underlying tunnel heave during a new tunnel construction. Tunn. Undergr. Space Technol. 2011, 26, 276–283. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Shi, J.; Hong, Y. Three-dimensional centrifuge modelling of basement excavation effects on an existing tunnel in dry sand. Can. Geotech. J. 2013, 50, 874–888. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, M.; Wang, W. Evaluation of deformation response for adjacent tunnels due to soil unloading in excavation engineering. Tunn. Undergr. Space Technol. 2013, 38 (Suppl. C), 244–253. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Sun, H.S.; Lei, G.H.; Shi, J.W.; Mašín, D. Ability of three different soil constitutive models to predict a tunnel’s response to basement excavation. Can. Geotech. J. 2015, 52, 1685–1698. [Google Scholar] [CrossRef]
- Shi, J.; Ng, C.W.W.; Chen, Y. Three-dimensional numerical parametric study of the influence of basement excavation on existing tunnel. Comput. Geotech. 2015, 63, 146–158. [Google Scholar] [CrossRef]
- Chen, R.; Meng, F.; Li, Z.; Ye, Y.; Ye, J. Investigation of response of metro tunnels due to adjacent large excavation and protective measures in soft soils. Tunn. Undergr. Space Technol. 2016, 58 (Suppl. C), 224–235. [Google Scholar] [CrossRef]
- Liu, G.B.; Huang, P.; Shi, J.W.; Ng, C.W.W. Performance of a Deep Excavation and Its Effect on Adjacent Tunnels in Shanghai Soft Clay. J. Perform. Constr. Facil. 2016, 30, 04016041. [Google Scholar] [CrossRef]
- Shi, J.; Ng, C.W.W.; Chen, Y. A simplified method to estimate three-dimensional tunnel responses to basement excavation. Tunn. Undergr. Space Technol. 2017, 62 (Suppl. C), 53–63. [Google Scholar] [CrossRef]
- Liang, R.; Wu, W.; Yu, F.; Jiang, G.; Liu, J. Simplified method for evaluating shield tunnel deformation due to adjacent excavation. Tunn. Undergr. Space Technol. 2018, 71 (Suppl. C), 94–105. [Google Scholar] [CrossRef]
- Whittle, A.J.; Corral, G.; Jen, L.C.; Rawnsley, R.P. Prediction and Performance of Deep Excavations for Courthouse Station, Boston. J. Geotech. Geoenviron. Eng. 2015, 141, 04014123. [Google Scholar] [CrossRef]
- Orazalin, Z.Y.; Whittle, A.J.; Olsen, M.B. Three-dimensional analyses of excavation support system for the Stata Center basement on the MIT campus. J. Geotech. Geoenviron. Eng. 2015, 141, 05015001. [Google Scholar] [CrossRef]
- Bryson, L.; Zapata-Medina, D. Method for estimating system stiffness for excavation support walls. J. Geotech. Geoenviron. Eng. 2012, 138, 1104–1115. [Google Scholar] [CrossRef]
- Finno, R.J.; Roboski, J.F. Three-dimensional responses of a tied-back excavation through clay. J. Geotech. Geoenviron. Eng. 2005, 131, 273–282. [Google Scholar] [CrossRef]
- Moormann, C. Analysis of wall and ground movements due to deep excavations in soft soil based on a new worldwide database. Soils Found. 2004, 44, 87–98. [Google Scholar] [CrossRef]
- Zeng, C.-F.; Xue, X.-L.; Li, M.-K. Use of cross wall to restrict enclosure movement during dewatering inside a metro pit before soil excavation. Tunn. Undergr. Space Technol. 2021, 112, 103909. [Google Scholar] [CrossRef]
- Zeng, C.-F.; Wang, S.; Xue, X.-L.; Zheng, G.; Mei, G.-X. Evolution of deep ground settlement subject to groundwater drawdown during dewatering in a multi-layered aquifer-aquitard system: Insights from numerical modelling. J. Hydrol. 2021, 603, 127078. [Google Scholar] [CrossRef]
- Zeng, C.-F.; Song, W.-W.; Xue, X.-L.; Li, M.-K.; Bai, N.; Mei, G.-X. Construction dewatering in a metro station incorporating buttress retaining wall to limit ground settlement: Insights from experimental modelling. Tunn. Undergr. Space Technol. 2021, 116, 104124. [Google Scholar] [CrossRef]
- Zeng, C.F.; Powrie, W.; Xue, X.L.; Li, M.K.; Mei, G.X. Effectiveness of a buttress wall in reducing retaining wall movement during dewatering before bulk excavation. Acta Geotech. 2021, 16, 3253–3267. [Google Scholar] [CrossRef]
- De Caro, M.; Crosta, G.B.; Previati, A. Modelling the interference of underground structures with groundwater flow and remedial solutions in Milan. Eng. Geol. 2020, 272, 105652. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Wang, J.H.; Li, M.G. Effect of Dewatering in a Confined Aquifer on Ground Settlement in Deep Excavations. Int. J. Geomech. 2018, 18, 04018120. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, J.; Gong, X.; Wu, J.; Wang, Z. Pumping-induced stress and strain in aquifer systems in Wuxi, China. Hydrogeol. J. 2018, 26, 771–787. [Google Scholar] [CrossRef]
- Gu, K.; Shi, B.; Liu, C.; Jiang, H.; Li, T.; Wu, J. Investigation of land subsidence with the combination of distributed fiber optic sensing techniques and microstructure analysis of soils. Eng. Geol. 2018, 240, 34–47. [Google Scholar] [CrossRef]
- Figueroa-Miranda, S.; Tuxpan-Vargas, J.; Ramos-Leal, J.A.; Hernández-Madrigal, V.M.; Villaseñor-Reyes, C.I. Land subsidence by groundwater over-exploitation from aquifers in tectonic valleys of Central Mexico: A review. Eng. Geol. 2018, 246, 91–106. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Li, M.G.; Wang, J.H.; Chen, J.J.; Zhu, Y.F. Field tests of pumping-recharge technology for deep confined aquifers and its application to a deep excavation. Eng. Geol. 2017, 228, 249–259. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, J.; Xue, Y.; Wang, Z. Fully coupled three-dimensional nonlinear numerical simulation of pumping-induced land movement. Environ. Earth Sci. 2017, 76, 552. [Google Scholar] [CrossRef]
- Pedro, A.M.G.; Zdravković, L.; Potts, D.; Almeida e Sousa, J. Derivation of model parameters for numerical analysis of the Ivens shaft excavation. Eng. Geol. 2017, 217, 49–60. [Google Scholar] [CrossRef]
- Motagh, M.; Shamshiri, R.; Haghighi, M.H.; Wetzel, H.U.; Akbari, B.; Nahavandchi, H.; Roessner, S.; Arabi, S. Quantifying groundwater exploitation induced subsidence in the Rafsanjan plain, southeastern Iran, using InSAR time-series and in situ measurements. Eng. Geol. 2017, 218, 134–151. [Google Scholar] [CrossRef]
- Wang, J.; Wu, Y.; Liu, X. Areal subsidence under pumping well–curtain interaction in subway foundation pit dewatering: Conceptual model and numerical simulations. Environ. Earth Sci. 2016, 75, 1–13. [Google Scholar] [CrossRef]
- Pujades, E.; Jurado, A.; Carrera, J.; Vázquez-Suñé, E.; Dassargues, A. Hydrogeological assessment of non-linear underground enclosures. Eng. Geol. 2016, 207, 91–102. [Google Scholar] [CrossRef]
- Zhu, L.; Gong, H.; Li, X.; Wang, R.; Chen, B.; Dai, Z.; Teatini, P. Land subsidence due to groundwater withdrawal in the northern Beijing plain, China. Eng. Geol. 2015, 193, 243–255. [Google Scholar] [CrossRef]
- Nejjar, K.; Dias, D.; Cuira, F.; Chapron, G.; Lebissonnais, H. Experimental study of the performance of a 32 m deep excavation in the suburbs of Paris. Géotechnique 2021, 73, 469–479. [Google Scholar] [CrossRef]
- Sailer, E.; Taborda, D.M.G.; Zdravković, L.; Potts, D.M. Fundamentals of the coupled thermo-hydro-mechanical behaviour of thermo-active retaining walls. Comput. Geotech. 2019, 109, 189–203. [Google Scholar] [CrossRef]
- Finno, R.J.; Kim, S.; Lewis, J.; Winkle, N.V. Observed Performance of a Sheetpile-Supported Excavation in Chicago Clays. J. Geotech. Geoenviron. Eng. 2019, 145, 05018005. [Google Scholar] [CrossRef]
- Faustin, N.E.; Elshafie, M.Z.E.B.; Mair, R.J. Case studies of circular shaft construction in London. Proc. Inst. Civ. Eng.-Geotech. Eng. 2018, 171, 391–404. [Google Scholar] [CrossRef]
- Schwamb, T.; Elshafie, M.Z.E.B.; Soga, K.; Mair, R.J. Considerations for monitoring of deep circular excavations. Proc. Inst. Civ. Eng.-Geotech. Eng. 2016, 169, 477–493. [Google Scholar] [CrossRef]
- Dong, Y.P.; Burd, H.J.; Houlsby, G.T. Finite-element analysis of a deep excavation case history. Géotechnique 2016, 66, 1–15. [Google Scholar] [CrossRef]
- Zeng, C.-F.; Zheng, G.; Zhou, X.-F.; Xue, X.-L.; Zhou, H.-Z. Behaviours of wall and soil during pre-excavation dewatering under different foundation pit widths. Comput. Geotech. 2019, 115, 103169. [Google Scholar] [CrossRef]
- Zeng, C.-F.; Zheng, G.; Xue, X.-L. Responses of deep soil layers to combined recharge in a leaky aquifer. Eng. Geol. 2019, 260, 105263. [Google Scholar] [CrossRef]
- Zeng, C.F.; Zheng, G.; Xue, X.L.; Mei, G.X. Combined recharge: A method to prevent ground settlement induced by redevelopment of recharge wells. J. Hydrol. 2019, 568, 1–11. [Google Scholar] [CrossRef]
- Zeng, C.F.; Xue, X.L.; Zheng, G.; Xue, T.Y.; Mei, G.X. Responses of retaining wall and surrounding ground to pre-excavation dewatering in an alternated multi-aquifer-aquitard system. J. Hydrol. 2018, 559, 609–626. [Google Scholar] [CrossRef]
- Zeng, C.-F.; Wang, S.; Xue, X.-L.; Zheng, G.; Mei, G.-X. Characteristics of ground settlement due to combined actions of groundwater drawdown and enclosure wall movement. Acta Geotech. 2022, 17, 4095–4112. [Google Scholar] [CrossRef]
- Chang, C.-T.; Sun, C.-W.; Duann, S.W.; Hwang, R.N. Response of a Taipei Rapid Transit System (TRTS) tunnel to adjacent excavation. Tunn. Undergr. Space Technol. 2001, 16, 151–158. [Google Scholar] [CrossRef]
- Doležalová, M. Tunnel complex unloaded by a deep excavation. Comput. Geotech. 2001, 28, 469–493. [Google Scholar] [CrossRef]
- Sharma, J.S.; Hefny, A.M.; Zhao, J.; Chan, C.W. Effect of large excavation on deformation of adjacent MRT tunnels. Tunn. Undergr. Space Technol. 2001, 16, 93–98. [Google Scholar] [CrossRef]
- Hu, Z.F.; Yue, Z.Q.; Zhou, J.; Tham, L.G. Design and construction of a deep excavation in soft soils adjacent to the Shanghai Metro tunnels. Can. Geotech. J. 2003, 40, 933–948. [Google Scholar] [CrossRef]
- Ou, C.-Y.; Liao, J.-T.; Cheng, W.-L. Building response and ground movements induced by a deep excavation. Géotechnique 2000, 50, 209–220. [Google Scholar] [CrossRef]
- Ong, D.E.L.; Leung, C.F.; Chow, Y.K. Time-Dependent Pile Behaviour Due to Excavation-Induced Soil Movement in Clay. In Proceedings of the 12th Pan-American Conference on Soil Mechanics and Geotechnical Engineering, Cambridge, MA, USA, 22–26 June 2003; pp. 2035–2040. [Google Scholar]
- Finno, R.J.; Voss, F.T.; Rossow, E.; Blackburn, J.T. Evaluating Damage Potential in Buildings Affected by Excavations. J. Geotech. Geoenviron. Eng. 2005, 131, 1199–1210. [Google Scholar] [CrossRef]
- Leung, C.F.; Ong, D.E.L.; Chow, Y.K. Pile behavior due to excavation-induced soil movement in clay. II: Collapsed wall. J. Geotech. Geoenviron. Eng. 2006, 132, 45–53. [Google Scholar] [CrossRef]
- Ong, D.E.L.; Leung, C.E.; Chow, Y.K. Pile behavior due to excavation-induced soil movement in clay. I: Stable wall. J. Geotech. Geoenviron. Eng. 2006, 132, 36–44. [Google Scholar] [CrossRef]
- Ong, D.E.L.; Leung, C.F.; Chow, Y.K. Behavior of pile groups subject to excavation-induced soil movement in very soft clay. J. Geotech. Geoenviron. Eng. 2009, 135, 1462–1474. [Google Scholar] [CrossRef]
- Chai, J.; Shen, S.; Ding, W.; Zhu, H.; Carter, J. Numerical investigation of the failure of a building in Shanghai, China. Comput. Geotech. 2014, 55, 482–493. [Google Scholar] [CrossRef]
- Shi, J.; Liu, G.; Huang, P.; Ng, C.W.W. Interaction between a large-scale triangular excavation and adjacent structures in Shanghai soft clay. Tunn. Undergr. Space Technol. 2015, 50, 282–295. [Google Scholar] [CrossRef]
- Tan, Y.; Huang, R.; Kang, Z.; Bin, W. Covered Semi-Top-Down Excavation of Subway Station Surrounded by Closely Spaced Buildings in Downtown Shanghai: Building Response. J. Perform. Constr. Facil. 2016, 30, 04016040. [Google Scholar] [CrossRef]
- Lim, A.; Ou, C.-Y. Performance and Three-Dimensional Analyses of a Wide Excavation in Soft Soil with Strut-Free Retaining System. Int. J. Geomech. 2018, 18, 05018007. [Google Scholar] [CrossRef]
- Lim, A.; Ou, C.-Y.; Hsieh, P.-G. An innovative earth retaining supported system for deep excavation. Comput. Geotech. 2019, 114, 103135. [Google Scholar] [CrossRef]
- Lim, A.; Ou, C.-Y.; Hsieh, P.-G. A novel strut-free retaining wall system for deep excavation in soft clay: Numerical study. Acta Geotech. 2019, 15, 1557–1576. [Google Scholar] [CrossRef]
- Li, M.-G.; Demeijer, O.; Chen, J.-J. Effectiveness of servo struts in controlling excavation-induced wall deflection and ground settlement. Acta Geotech. 2020, 15, 2575–2590. [Google Scholar] [CrossRef]
- Li, M.-G.; Chen, J.-J.; Xu, Y.-S.; Tong, D.-G.; Cao, W.-W.; Shi, Y.-J. Effects of groundwater exploitation and recharge on land subsidence and infrastructure settlement patterns in Shanghai. Eng. Geol. 2021, 282, 105995. [Google Scholar] [CrossRef]
- Zhou, H.Z.; Zheng, G.; He, X.P.; Wang, E.Y.; Guo, Z.Y.; Nie, D.Q.; Ma, S.K. Numerical modelling of retaining structure displacements in multi-bench retained excavations. Acta Geotech. 2020, 15, 2691–2703. [Google Scholar] [CrossRef]
- Feng, S.-J.; Lu, S.-F. Failure of a Retaining Structure in a Metro Station Excavation in Nanchang City, China. J. Perform. Constr. Facil. 2016, 30, 04015097. [Google Scholar] [CrossRef]
- Tan, Y.; Li, M. Measured performance of a 26 m deep top-down excavation in downtown Shanghai. Can. Geotech. J. 2011, 48, 704–719. [Google Scholar] [CrossRef]
- Tan, Y.; Wei, B. Observed Behaviors of a Long and Deep Excavation Constructed by Cut-and-Cover Technique in Shanghai Soft Clay. J. Geotech. Geoenviron. Eng. 2012, 138, 69–88. [Google Scholar] [CrossRef]
- Tan, Y.; Wei, B. Performance of an Overexcavated Metro Station and Facilities Nearby. J. Perform. Constr. Facil. 2012, 26, 241–254. [Google Scholar] [CrossRef]
- Tan, Y.; Wang, D. Characteristics of a large-scale deep foundation pit excavated by the central-island technique in Shanghai soft clay. I: Bottom-up construction of the central cylindrical shaft. J. Geotech. Geoenviron. Eng. 2013, 139, 1875–1893. [Google Scholar] [CrossRef]
- Hashash, Y.M.A.; Osouli, A.; Marulanda, C. Central Artery/Tunnel Project Excavation Induced Ground Deformations. J. Geotech. Geoenviron. Eng. 2008, 134, 1399–1406. [Google Scholar] [CrossRef]
- Lee, F.H.; Juneja, A.; Tan, T.S. Stress and pore pressure changes due to sand compaction pile installation in soft clay. Géotechnique 2004, 54, 1–16. [Google Scholar] [CrossRef]
- Hashash, Y.M.A.; Whittle, A.J. Mechanisms of Load Transfer and Arching for Braced Excavations in Clay. J. Geotech. Geoenviron. Eng. 2002, 128, 187–197. [Google Scholar] [CrossRef]
- Bolton, M.D.; Stewart, D.I. The effect on propped diaphragm walls of rising groundwater in stiff clay. Géotechnique 1994, 44, 111–127. [Google Scholar] [CrossRef]
- Mair, R.J. Developments in geotechnical engineering research: Application to tunnels and deep excavations. Unwin Memorial Lecture 1992. Proc. Inst. Civ. Eng. 1993, 93, 27–41. [Google Scholar]
- Gunn, M.J.; Clayton, C.R.I. Installation effects and their importance in the design of earth-retaining structures. Géotechnique 1992, 42, 137–141. [Google Scholar] [CrossRef]
- Fourie, A.B.; Potts, D.M. Comparison of finite element and limiting equilibrium analyses for an embedded cantilever retaining wall. Géotechnique 1989, 39, 175–188. [Google Scholar] [CrossRef]
- Potts, D.M.; Fourie, A.B. A numerical study of the effects of wall deformation on earth pressures. Int. J. Numer. Anal. Methods Geomech. 1986, 10, 383–405. [Google Scholar] [CrossRef]
- Wood, L.A.; Perrin, A.J. Observations of a strutted diaphragm wall in London clay: A preliminary assessment. Géotechnique 1984, 34, 563–579. [Google Scholar] [CrossRef]
- Hubbard, H.W.; Potts, D.M.; Miller, D.; Burland, J.B. Design of the retaining walls for the M25 cut and cover tunnel at Bell Common. Géotechnique 1984, 34, 495–512. [Google Scholar] [CrossRef]
- Burland, J.B.; Longworth, T.I.; Moore, J.F.A. A study of ground movement and progressive failure caused by a deep excavation in Oxford Clay. Géotechnique 1977, 27, 557–591. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, J.; Zhang, Y.; Gao, Y. Cause investigation of damages in existing building adjacent to foundation pit in construction. Eng. Fail. Anal. 2018, 83, 117–124. [Google Scholar] [CrossRef]
- Zhu, C.; Yan, Z.; Lin, Y.; Xiong, F.; Tao, Z. Design and application of a monitoring system for a deep railway foundation pit project. IEEE Access 2019, 7, 107591–107601. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, M.; Zhang, C.; Jiang, K.; Lu, M. Time-domain analyses for pile deformation induced by adjacent excavation considering influences of viscoelastic mechanism. Tunn. Undergr. Space Technol. 2019, 85, 392–405. [Google Scholar] [CrossRef]
- Wei, H. Influence of foundation pit excavation and precipitation on settlement of surrounding buildings. Adv. Civ. Eng. 2021, 2021, 6638868. [Google Scholar] [CrossRef]
- Zhang, C.-H.; Wang, B.-T.; Liu, Y. Research on the Effective Control of Ground Settlement during Double-Layered Foundation Pit Dewatering Based on Seepage Control-Recharge Coupling Model. Adv. Civ. Eng. 2022, 2022, 9669176. [Google Scholar] [CrossRef]
- Shen, S.L.; Wu, Y.X.; Misra, A. Calculation of head difference at two sides of a cut-off barrier during excavation dewatering. Comput. Geotech. 2017, 91, 192–202. [Google Scholar] [CrossRef]
- Zhang, Q.; Hu, J.; Wang, J.; He, P.; Hou, L.L.; Lin, P.; Song, S. Study on the mechanical behavior of a foundation pit retaining structure adjacent to the pile foundation of a subway station. Environ. Earth Sci. 2021, 80, 704. [Google Scholar] [CrossRef]
- Liao, S.-M.; Wei, S.-F.; Shen, S.-L. Structural responses of existing metro stations to adjacent deep excavations in Suzhou, China. J. Perform. Constr. Facil. 2016, 30, 04015089. [Google Scholar] [CrossRef]
- Zheng, G.; Ha, D.; Loaiciga, H.; Zhou, H.; Zeng, C.; Zhang, H. Estimation of the hydraulic parameters of leaky aquifers based on pumping tests and coupled simulation/optimization: Verification using a layered aquifer in Tianjin, China. Hydrogeol. J. 2019, 27, 3081–3095. [Google Scholar] [CrossRef]
- Wu, Y.X.; Lyu, H.M.; Han, J.; Shen, S.L. Dewatering-Induced Building Settlement around a Deep Excavation in Soft Deposit in Tianjin, China. J. Geotech. Geoenviron. Eng. 2019, 145, 05019003. [Google Scholar] [CrossRef]
- Zhang, Y.-Q.; Wang, J.-H.; Chen, J.-J.; Li, M.-G. Numerical study on the responses of groundwater and strata to pumping and recharge in a deep confined aquifer. J. Hydrol. 2017, 548, 342–352. [Google Scholar] [CrossRef]
- Li, M.G.; Chen, J.J.; Xia, X.H.; Zhang, Y.Q.; Wang, D.F. Statistical and hydro-mechanical coupling analyses on groundwater drawdown and soil deformation caused by dewatering in a multi-aquifer-aquitard system. J. Hydrol. 2020, 589, 125365. [Google Scholar] [CrossRef]
- Wang, X.-W.; Yang, T.-L.; Xu, Y.-S.; Shen, S.-L. Evaluation of optimized depth of waterproof curtain to mitigate negative impacts during dewatering. J. Hydrol. 2019, 577, 123969. [Google Scholar] [CrossRef]
- Bear, J. Hydraulics of Groundwater: Courier Corporation; Dover Publications: New York, NY, USA, 2012. [Google Scholar]
- Zhang, W.; Goh, A.; Goh, K.; Chew, O.; Zhou, D.; Zhang, R. Performance of braced excavation in residual soil with groundwater drawdown. Undergr. Space 2018, 3, 150–165. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).