Inversion Method for Material Parameters of Concrete Dams Using Intelligent Algorithm-Based Displacement Separation
Abstract
1. Introduction
2. Numerical Model
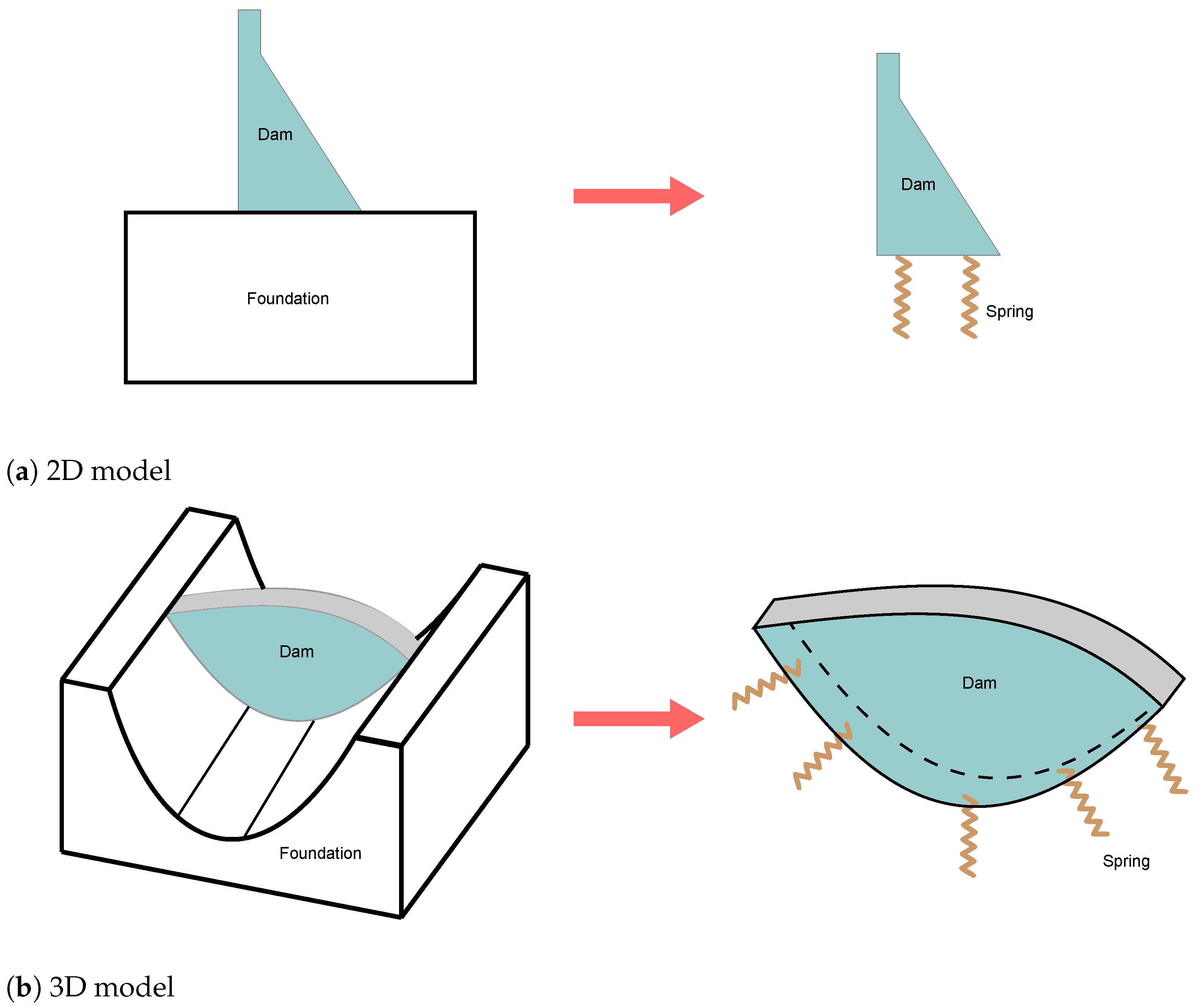
2.1. A Finite Element Method for Separation of Constrained Displacement Based on Equivalent Spring
2.2. Interpolation of Measurement Point Displacements
3. Optimisation Method
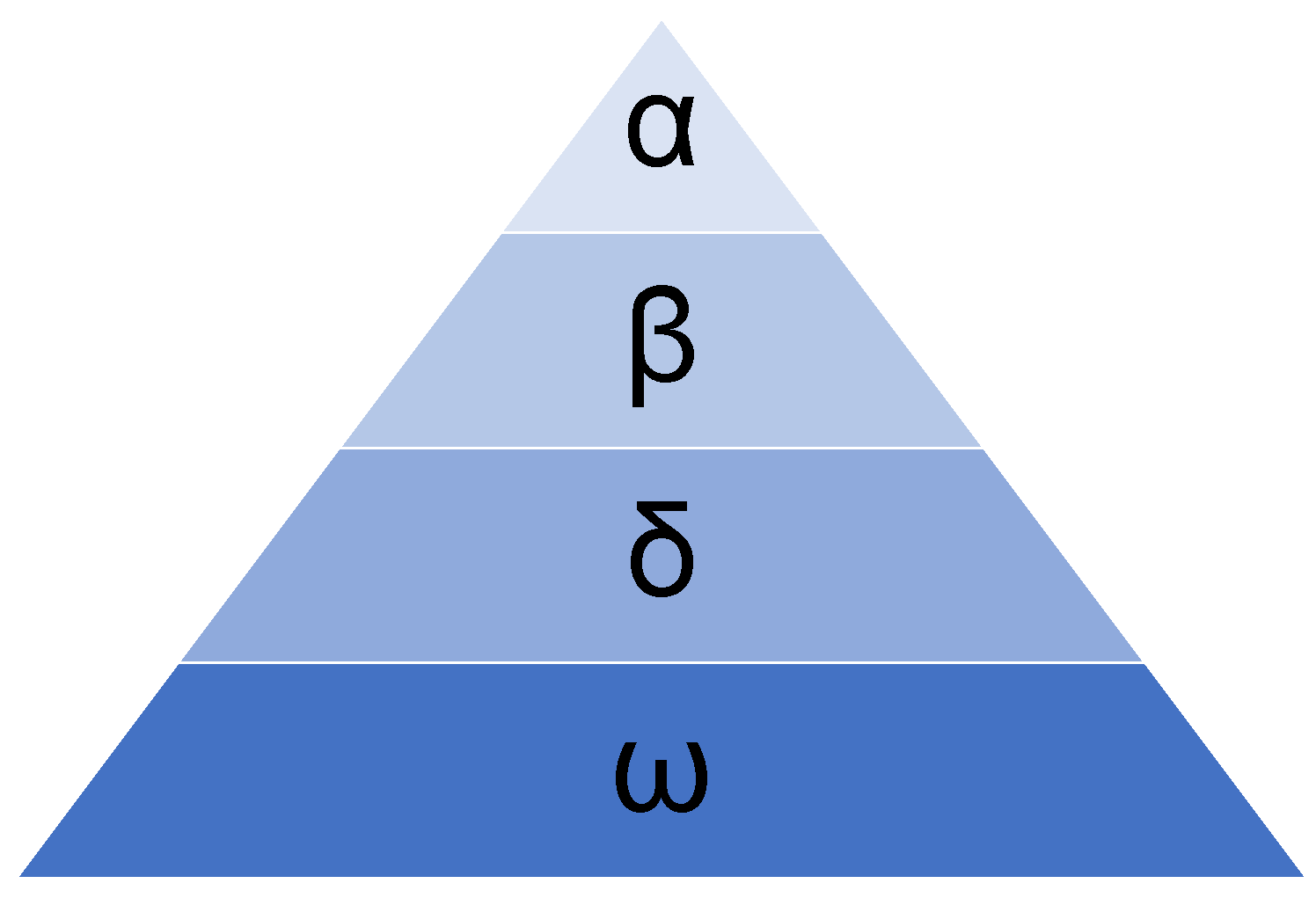
3.1. Grey Wolf Optimiser
3.2. Multi-Threaded Strategy
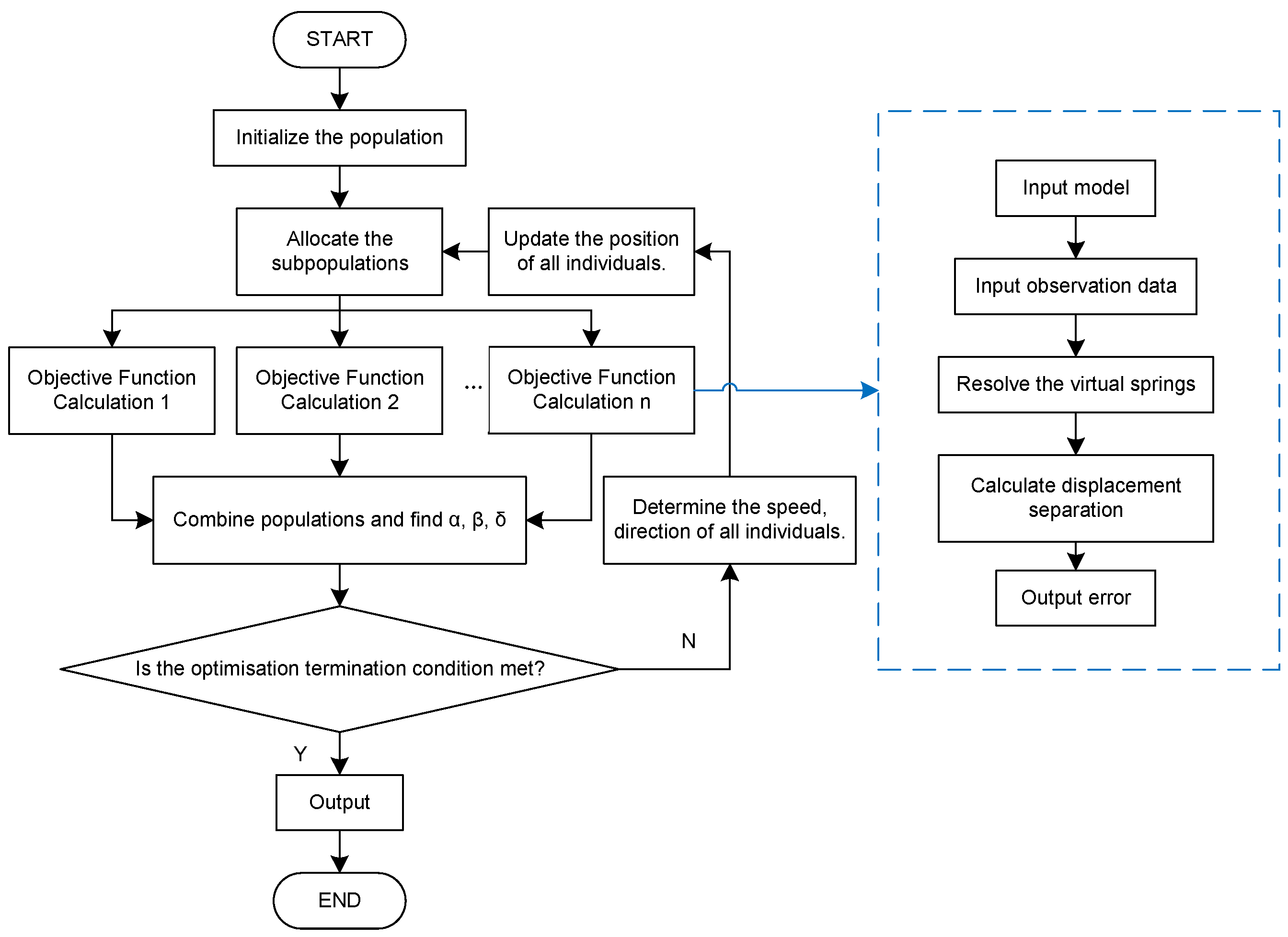
3.3. Intelligent Models for Parameter Inversion
- (1) Initialize populations.
- (2) Assign sub-populations according to computer hardware.
- (3) Start multi-threaded execution of objective function content.
- (3.1) Input finite element model and observations.
- (3.2) Solve the virtual springs.
- (3.3) Calculate displacement field separation and output RRMSE.
- (4) Combine populations, and then determine , , and .
- (5) Determine if the optimisation termination conditions are met. If so, the calculation is terminated. If not, perform a position update calculation for each individual and repeat steps 2–5.
- (6) Output the result.
4. Validation
4.1. 2D Gravity Dam Case
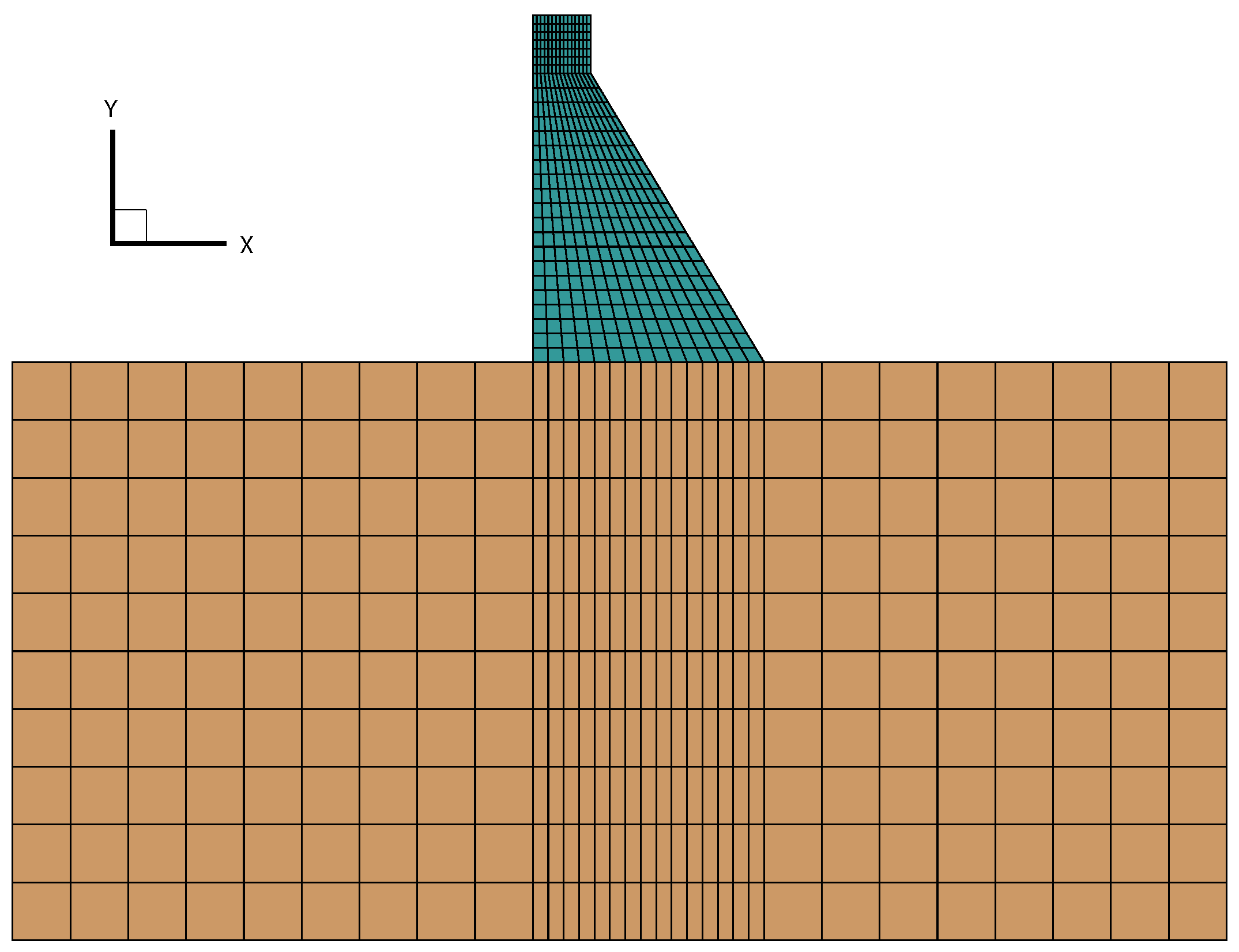
4.1.1. Model
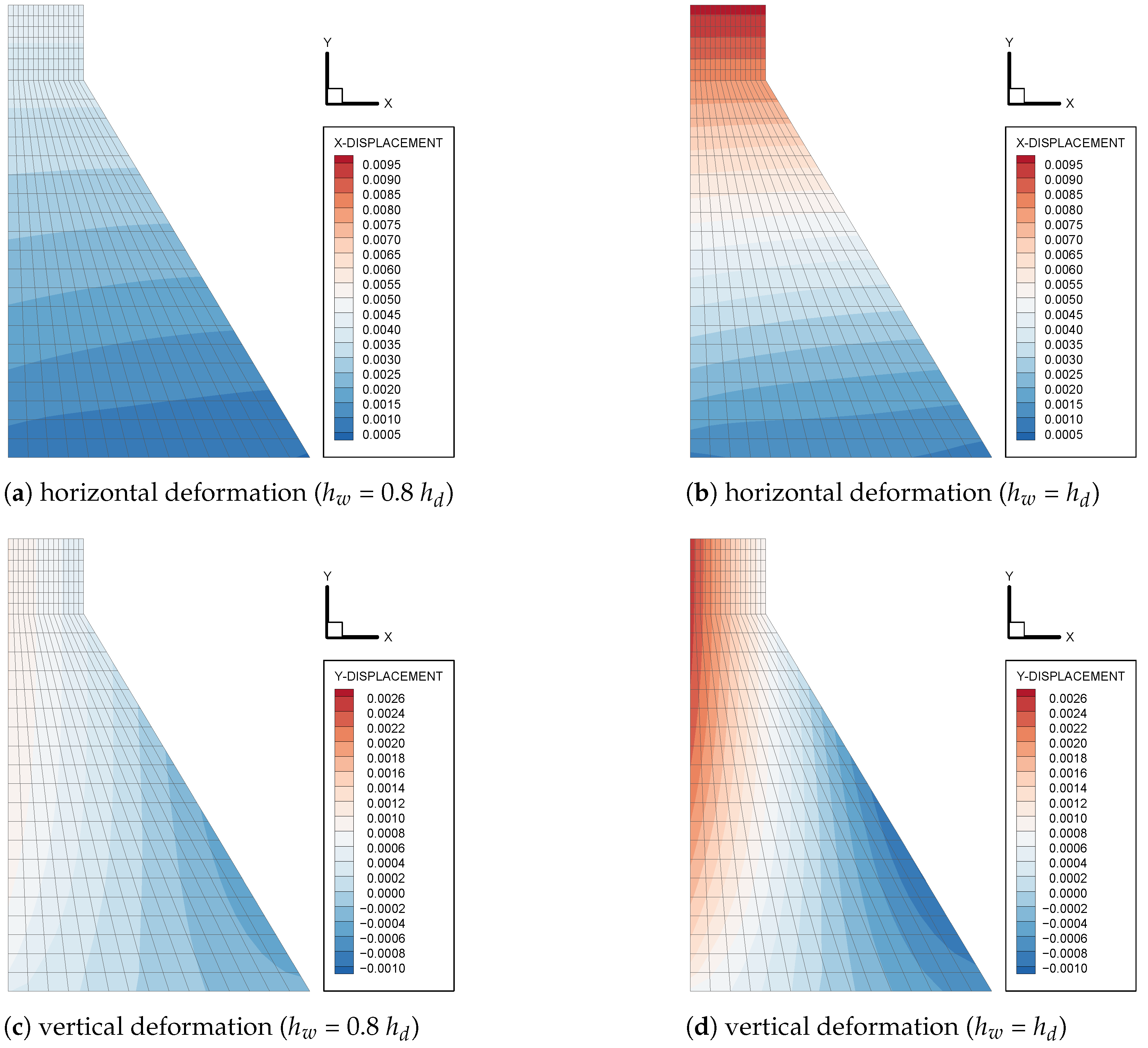
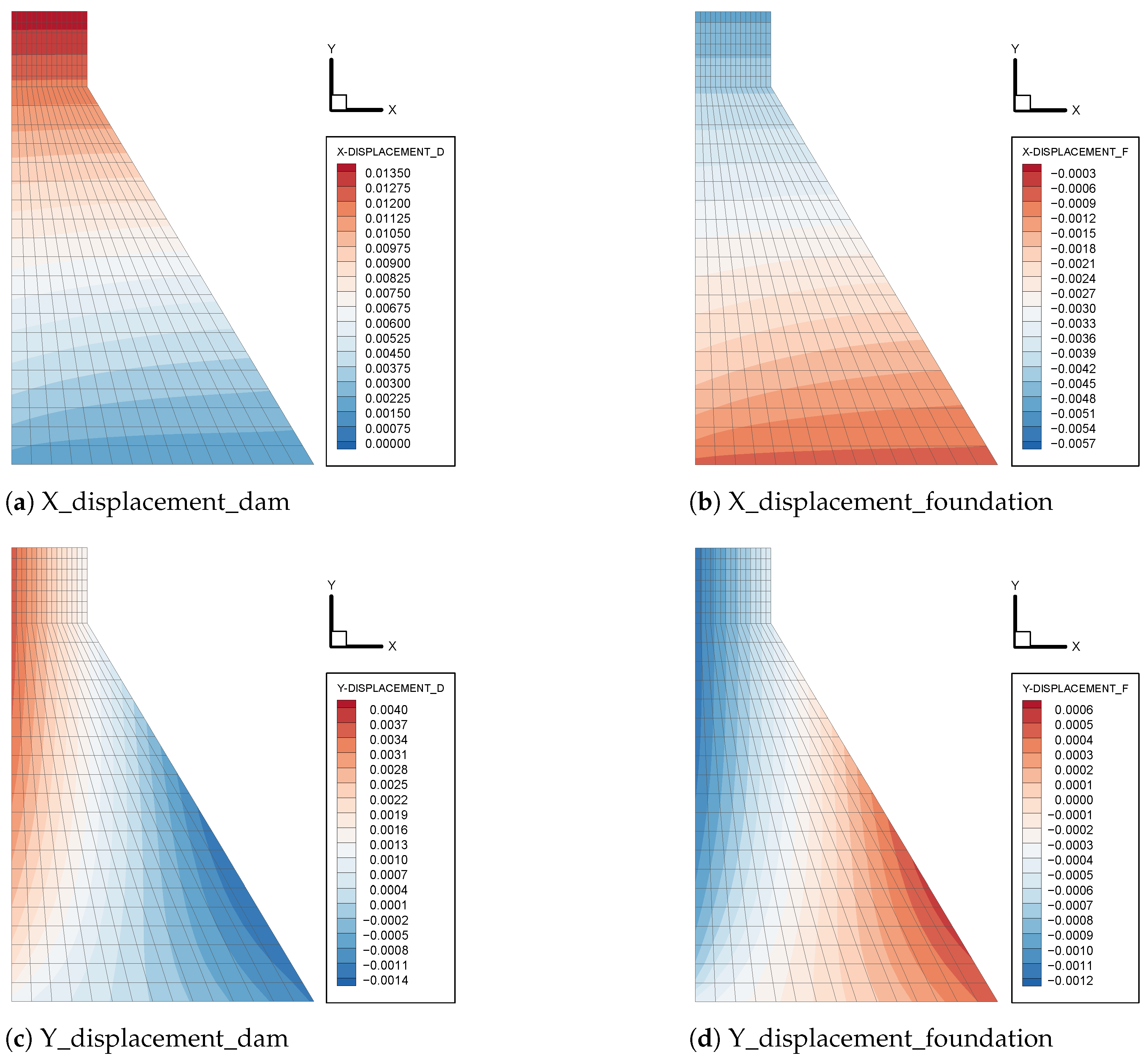
4.1.2. Numerical Simulation
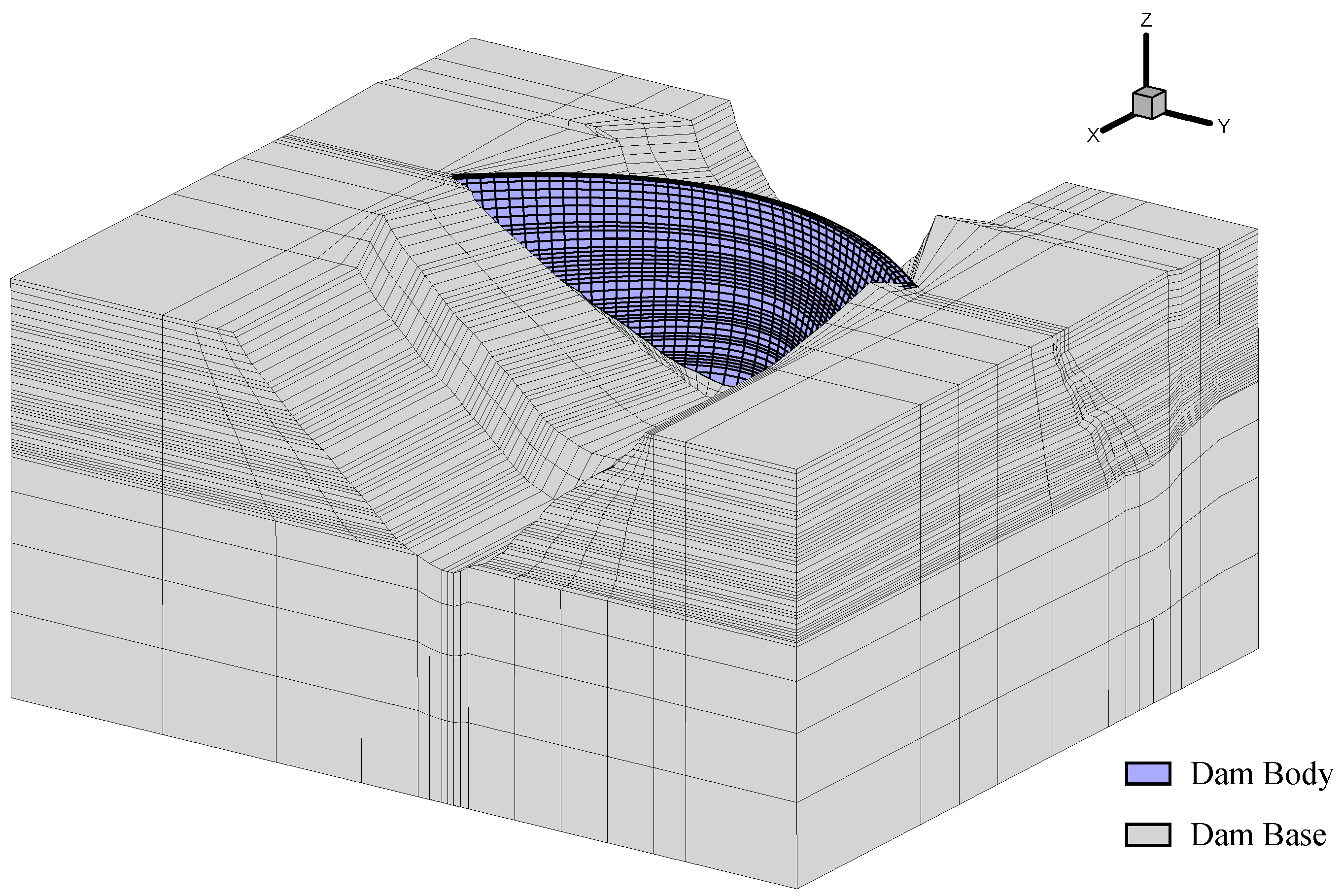
4.2. 3D Arch Dam Case
4.2.1. Model
4.2.2. Numerical Simulation
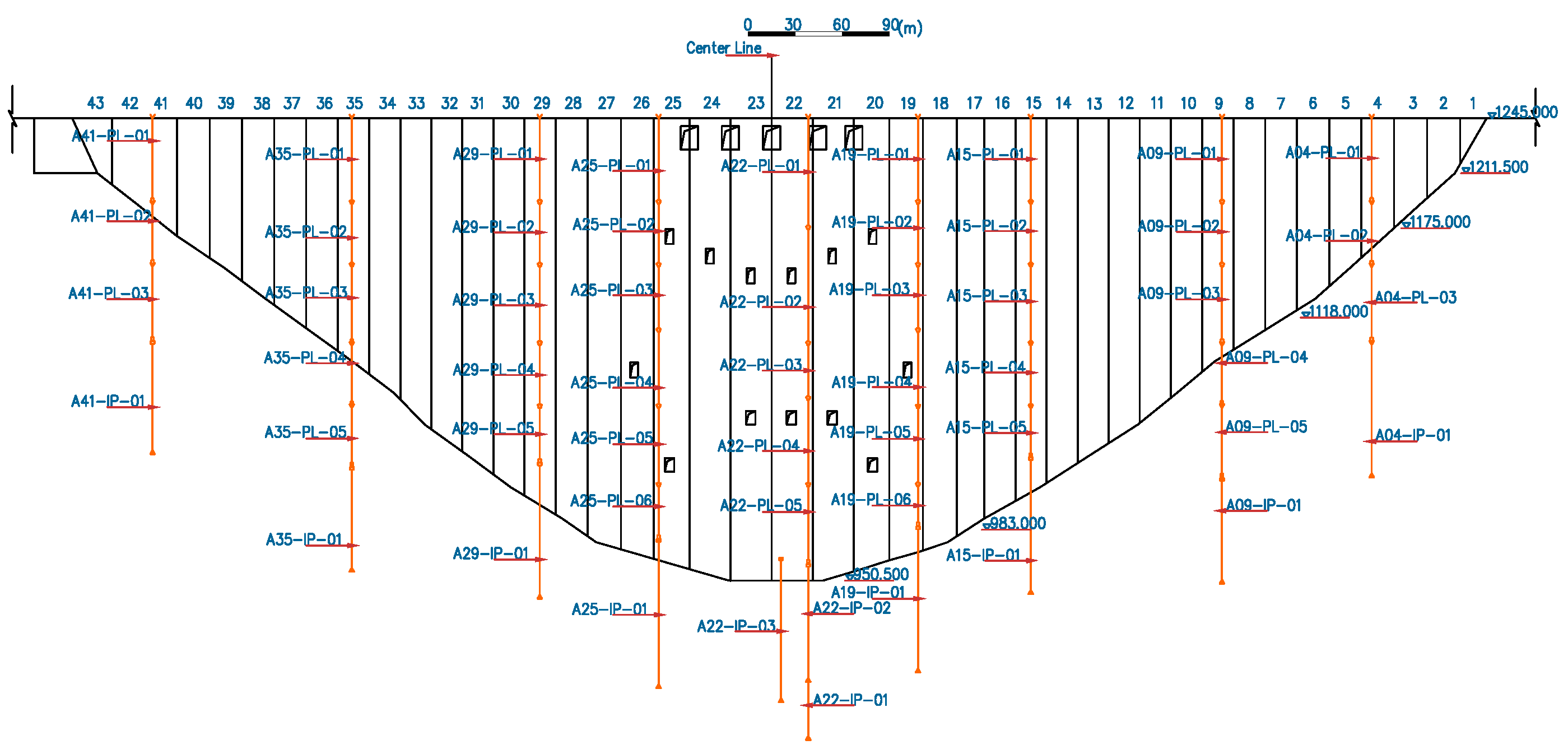
5. An Application in the Health Diagnosis of a High Arch Dam in China
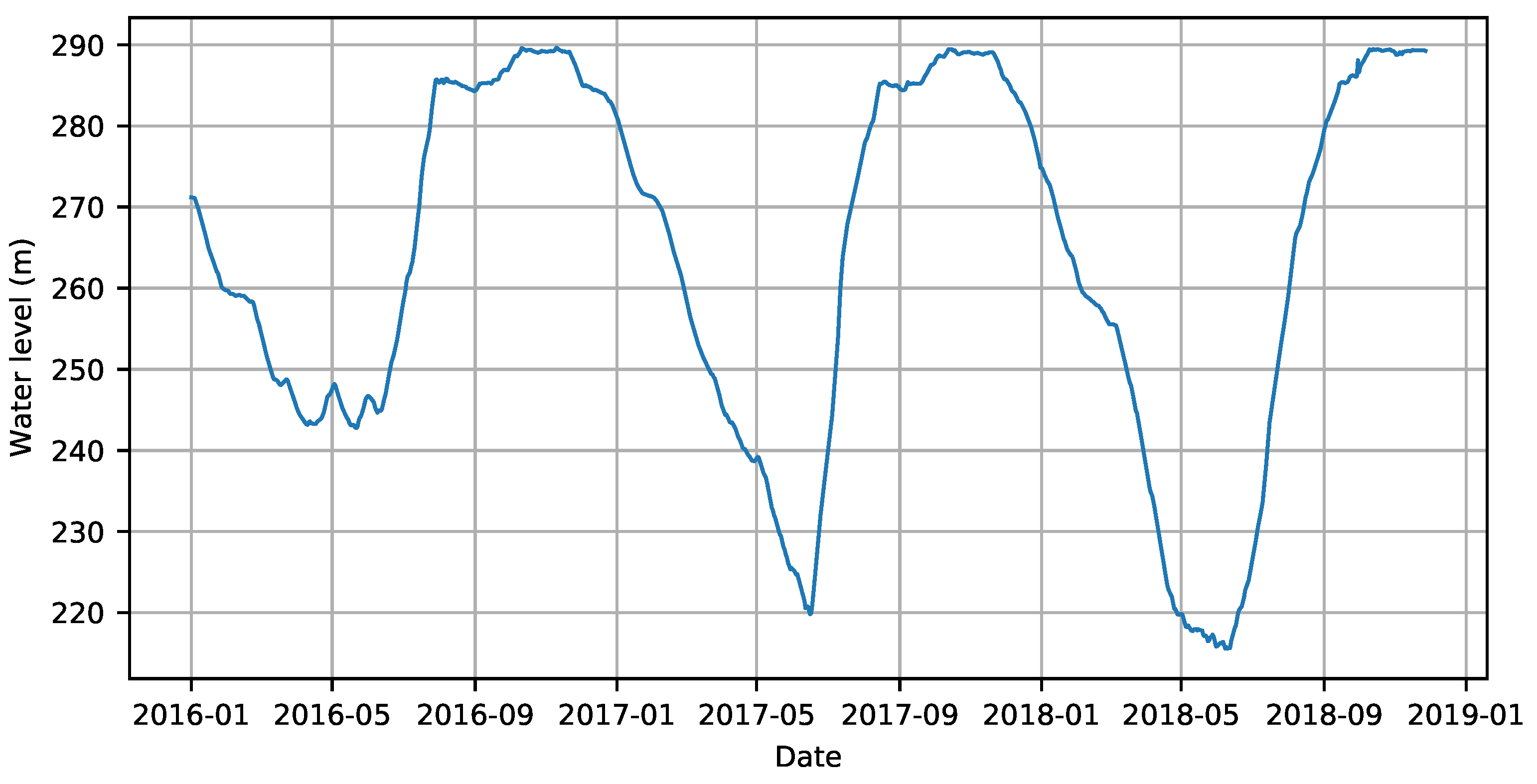
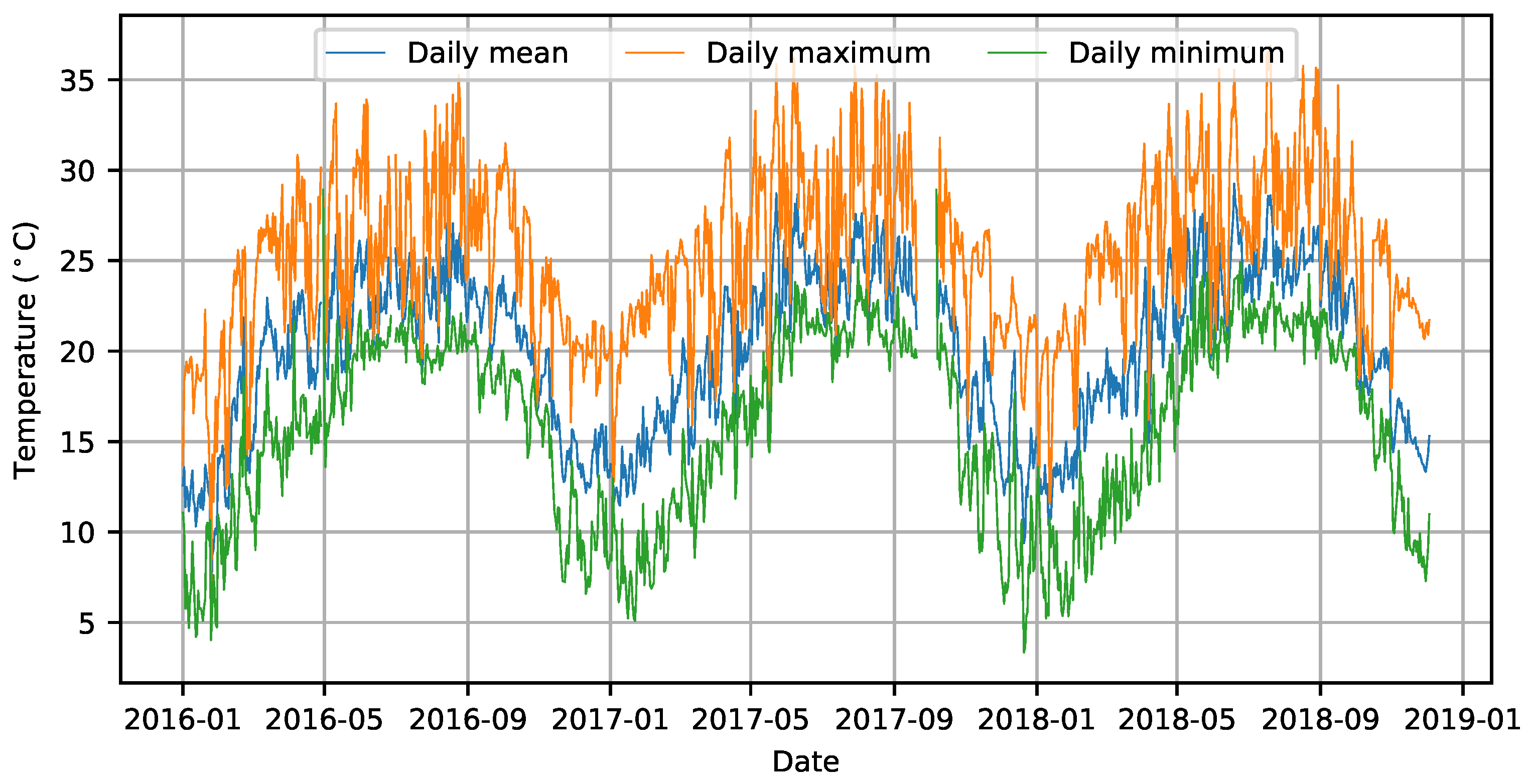
5.1. Model
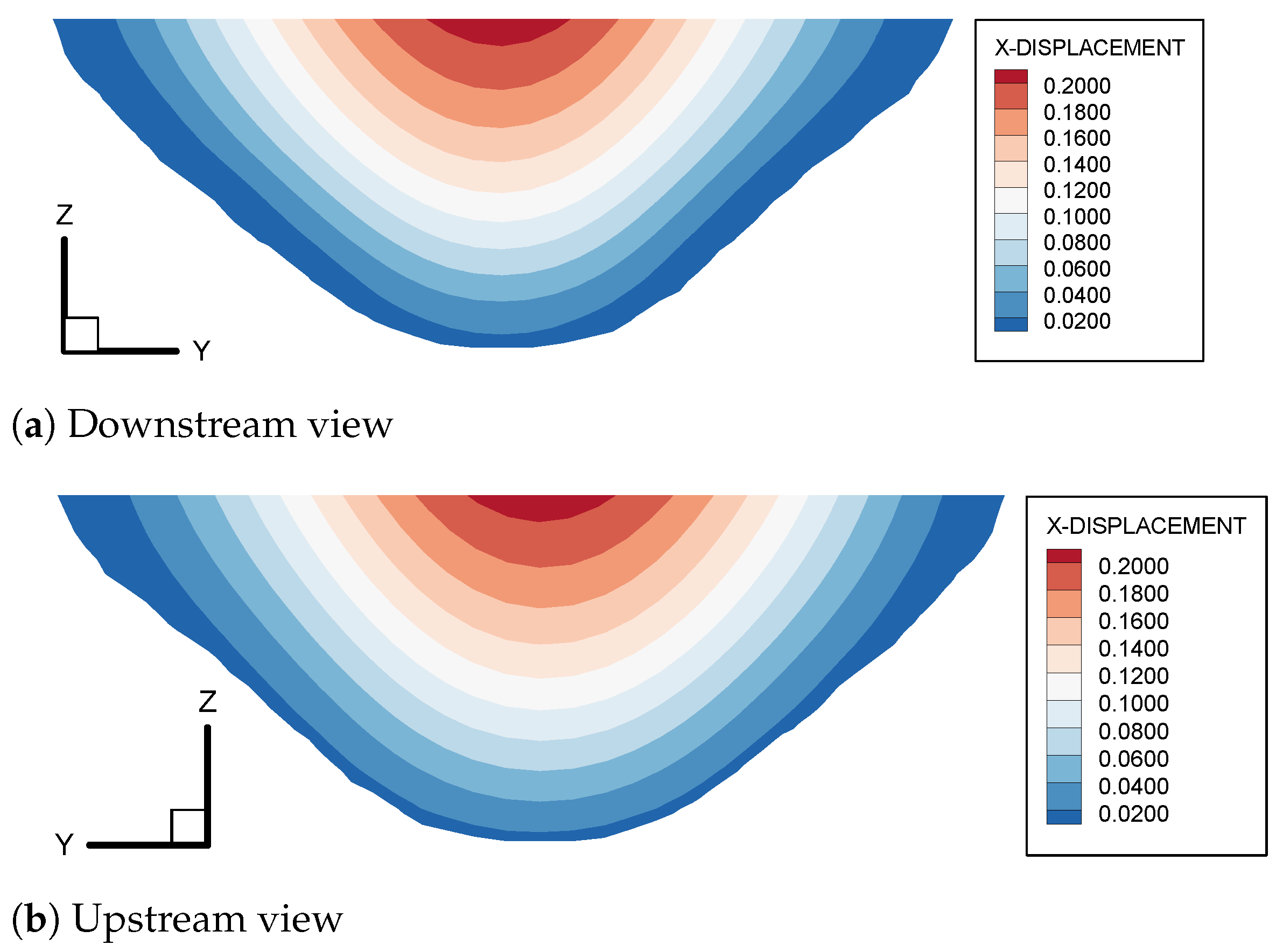
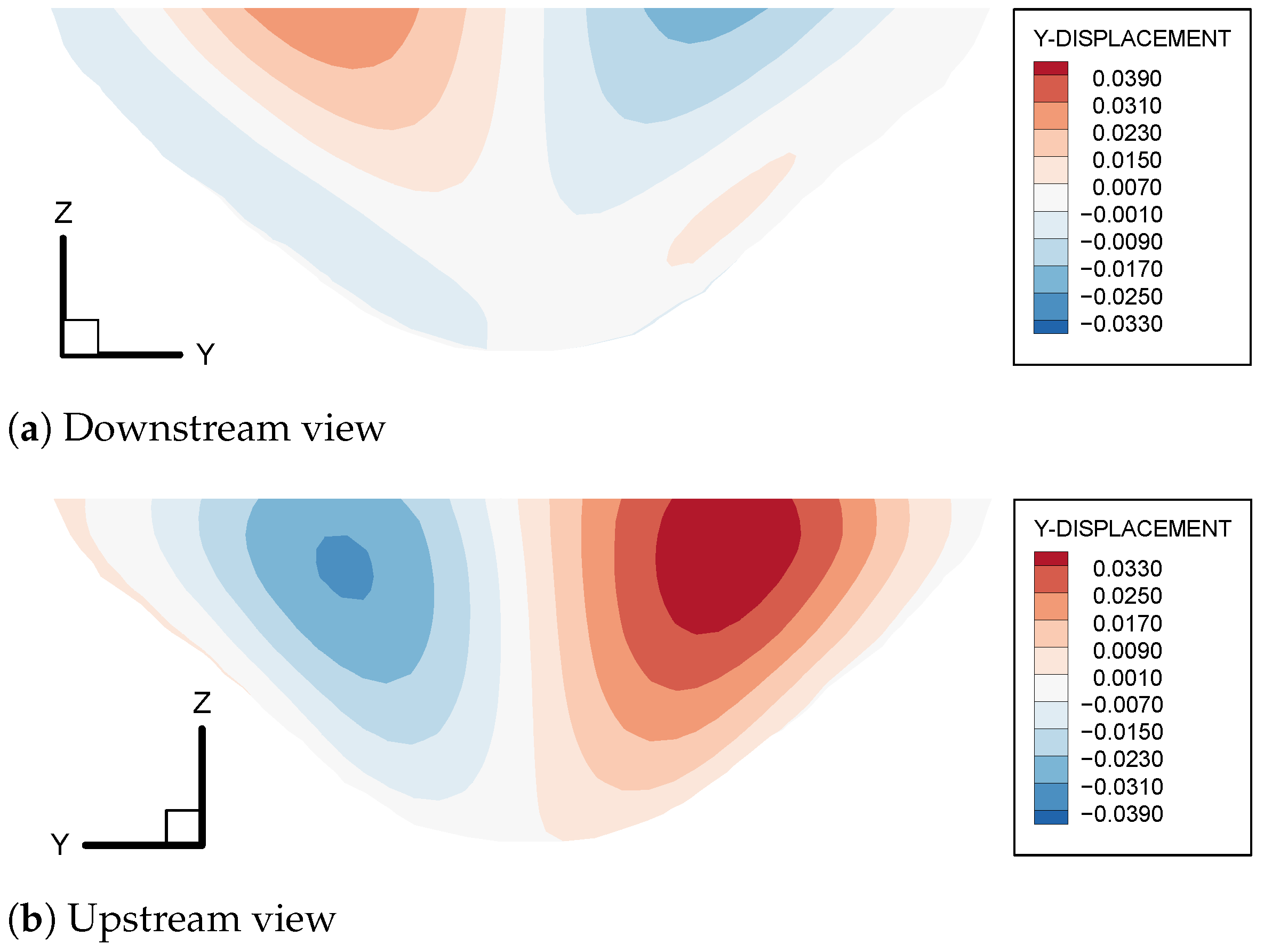
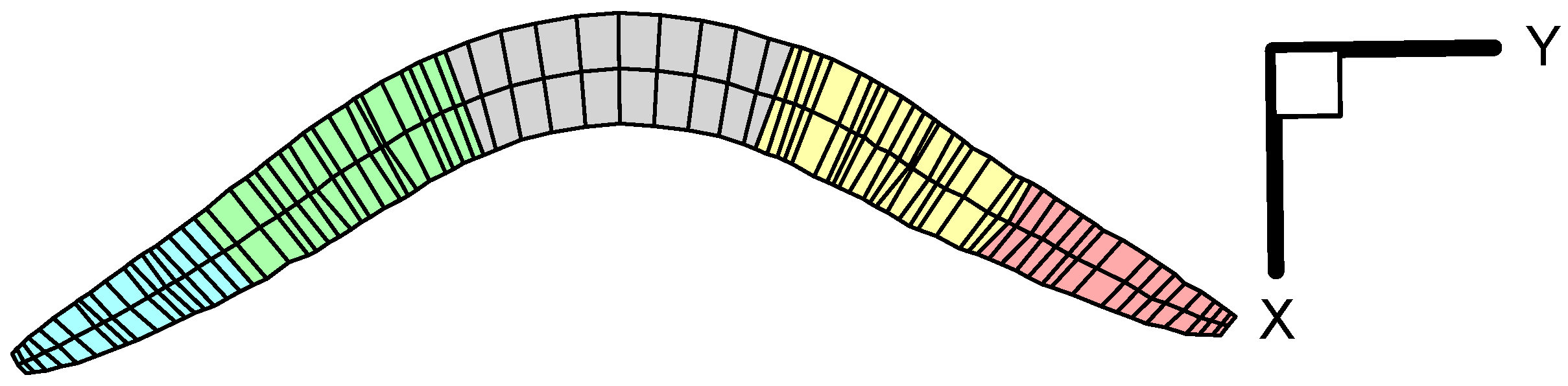
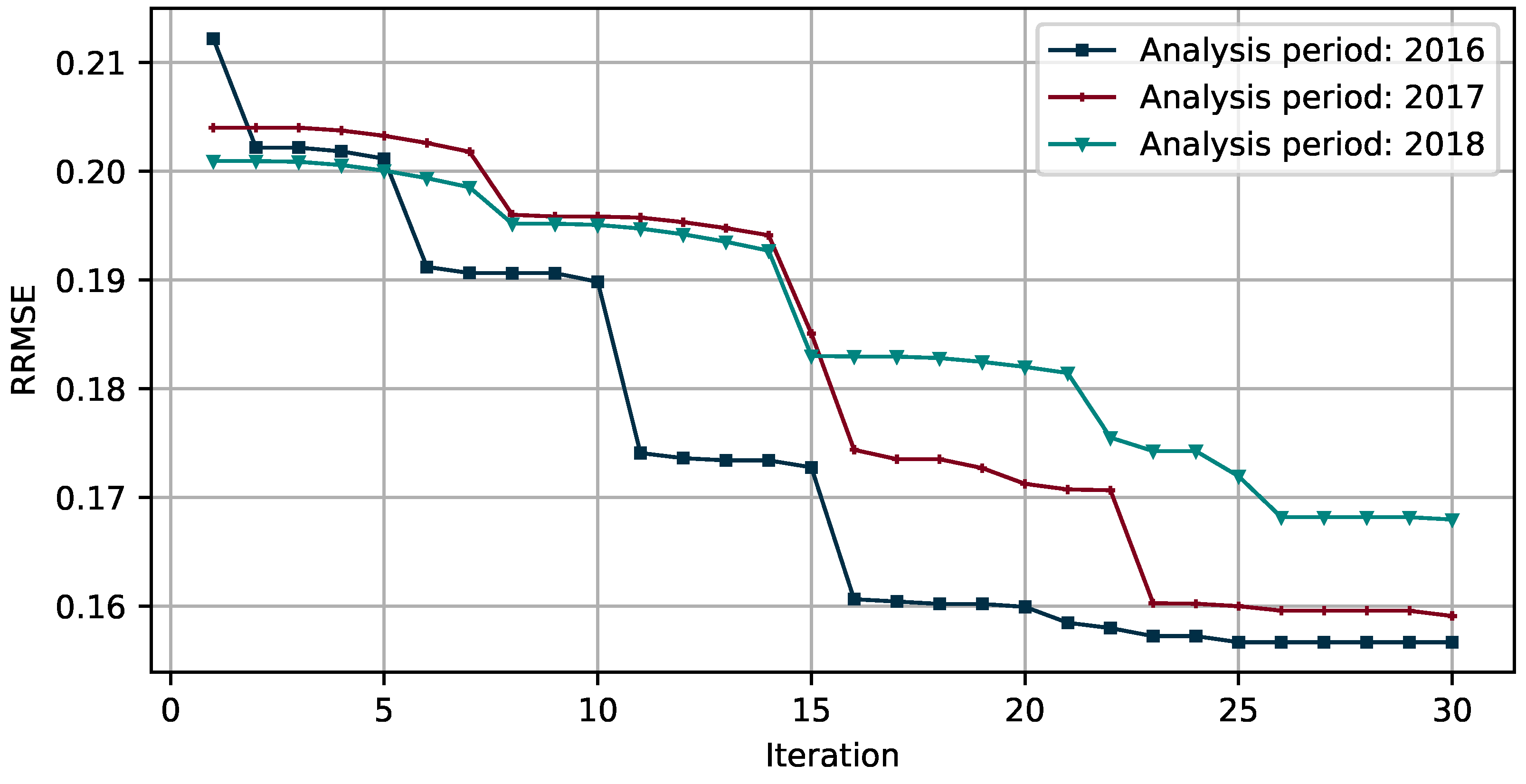
5.2. Parameter Inverted and Discussion
6. Conclusions
- (1)
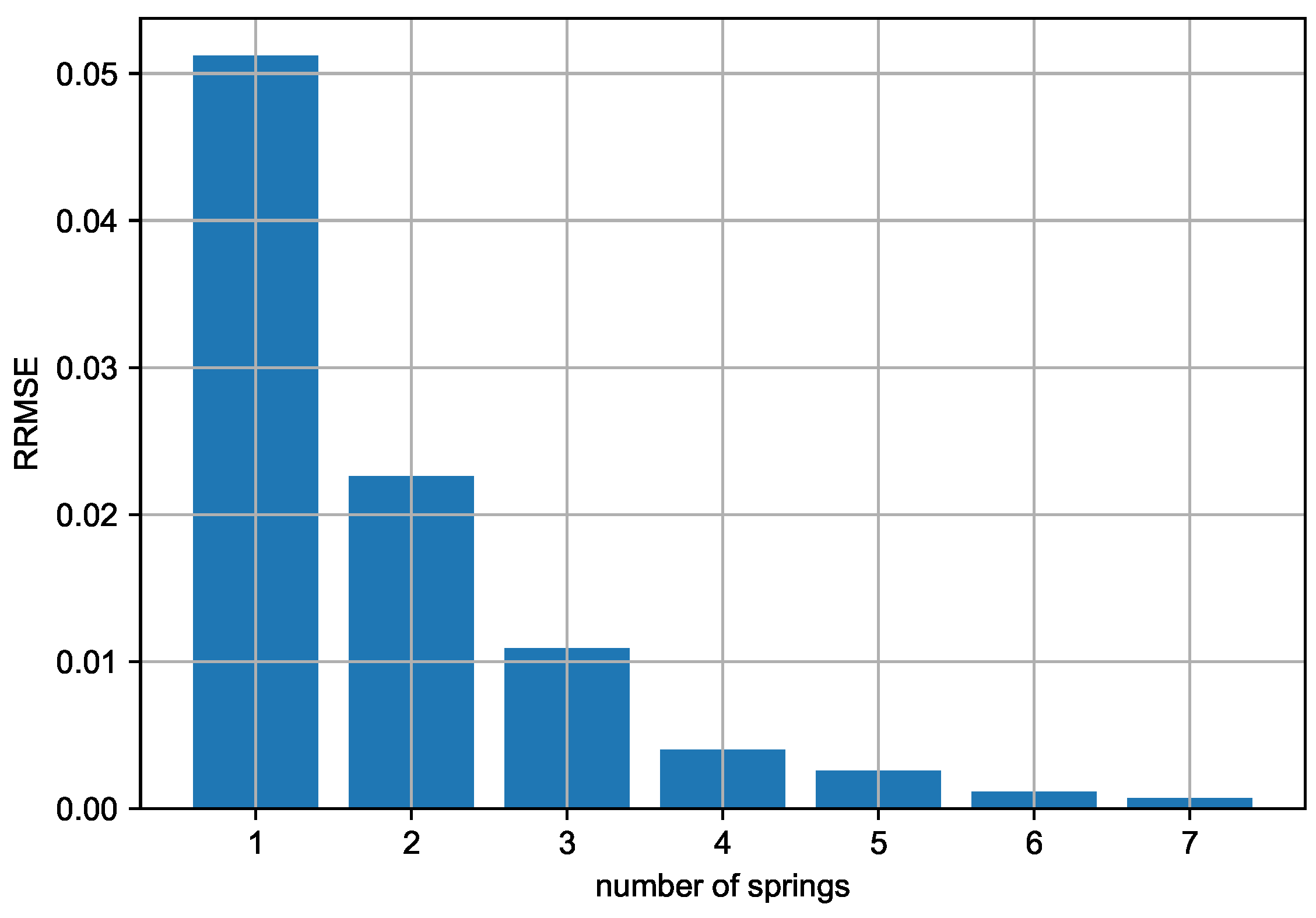
- The displacement separation model proposed in this paper can be applied to the solution of multiple degrees of freedom, including two-dimensional gravity dam sections, three-dimensional arch dams, or gravity dams, as verified by calculation cases. In the case of sufficient measurement data, as the number of virtual springs increases, the model accuracy will increase, but the trend of improvement will slow down.
- (2)
- In combination with the interpolation of displacement fields, it is no longer necessary to make element nodes coincide with measurement points when modelling the dam, improving the simplicity of modelling the separation model.
- (3)
- Applying multi-threaded strategies to swarm intelligence optimisation methods can improve computational efficiency. When the method is executed on a computer with a multi-core processor, results can be obtained quickly. Using the error in displacement separation as an objective function, combined with an optimisation method, it is possible to achieve a rapid inverse analysis of the deformation parameters of a concrete dam without the need to determine physical mechanical parameters of the foundation.
- (4)
- The model proposed in this paper was successfully applied to the structural health diagnosis of a very high concrete arch dam in southern China. Rapid identification of concrete deformation parameters in three zones of the dam body was achieved with reasonable results. As an accurate and efficient structural diagnosis model for concrete dams that does not require assumptions about foundation parameters, it can provide a reference for structural health diagnosis of concrete dams during operation.
- (1)
- Advanced sensing and data integration: Incorporate data from emerging technologies like distributed fiber optic sensors and wireless sensor networks to provide more comprehensive information about dam behavior. This would enable more accurate parameter inversion and health diagnosis, potentially revealing subtle changes in dam performance that current methods might miss.
- (2)
- Machine learning enhancement: Explore the application of deep learning algorithms, such as convolutional neural networks or recurrent neural networks, to improve the accuracy and efficiency of parameter inversion. These techniques could be particularly effective in handling large datasets and capturing complex, non-linear relationships in dam behavior, potentially leading to more robust and adaptive health monitoring systems.
- (3)
- Multi-physics modeling and long-term monitoring: Extend the approach to include coupled thermal-structural analysis or even hydro-mechanical-thermal coupling for a more comprehensive understanding of dam behavior. Develop a framework for continuous monitoring and analysis using the proposed method, enabling predictive maintenance strategies and early warning systems based on detected changes in inverted parameters over time.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jia, J. A Technical Review of Hydro-Project Development in China. Engineering 2016, 2, 302–312. [Google Scholar] [CrossRef]
- Ren, Q.; Li, M.; Song, L.; Liu, H. An optimized combination prediction model for concrete dam deformation considering quantitative evaluation and hysteresis correction. Adv. Eng. Inform. 2020, 46, 101154. [Google Scholar] [CrossRef]
- Shao, C.; Gu, C.; Yang, M.; Xu, Y.; Su, H. A novel model of dam displacement based on panel data. Struct. Control Health Monit. 2018, 25, e2037. [Google Scholar] [CrossRef]
- Feng, X.T.; Zhang, Z.; Sheng, Q. Estimating mechanical rock mass parameters relating to the Three Gorges Project permanent shiplock using an intelligent displacement back analysis method. Int. J. Rock Mech. Min. Sci. 2000, 37, 1039–1054. [Google Scholar] [CrossRef]
- Stojanovic, B.; Milivojevic, M.; Milivojevic, N.; Antonijevic, D. A self-tuning system for dam behavior modeling based on evolving artificial neural networks. Adv. Eng. Softw. 2016, 97, 85–95. [Google Scholar] [CrossRef]
- Kang, F.; Liu, X.; Li, J.; Li, H. Multi-parameter inverse analysis of concrete dams using kernel extreme learning machines-based response surface model. Eng. Struct. 2022, 256, 113999. [Google Scholar] [CrossRef]
- Azmi, M.; Paultre, P. Three-dimensional analysis of concrete dams including contraction joint non-linearity. Eng. Struct. 2002, 24, 757–771. [Google Scholar] [CrossRef]
- Kao, C.Y.; Loh, C.H. Monitoring of long-term static deformation data of Fei-Tsui arch dam using artificial neural network-based approaches. Struct. Control Health Monit. 2013, 20, 282–303. [Google Scholar] [CrossRef]
- Habib, P. The Malpasset Dam failure. Eng. Geol. 1987, 24, 331–338. [Google Scholar] [CrossRef]
- Roth, S.N.; Léger, P.; Soulaïmani, A. Strongly coupled XFEM formulation for non-planar three-dimensional simulation of hydraulic fracturing with emphasis on concrete dams. Comput. Methods Appl. Mech. Eng. 2020, 363, 112899. [Google Scholar] [CrossRef]
- Ardito, R.; Maier, G.; Massalongo, G. Diagnostic analysis of concrete dams based on seasonal hydrostatic loading. Eng. Struct. 2008, 30, 3176–3185. [Google Scholar] [CrossRef]
- Szostak-Chrzanowski, A.; Chrzanowski, A.; Massiéra, M. Use of deformation monitoring results in solving geomechanical problems - Case studies. Eng. Geol. 2005, 79, 3–12. [Google Scholar] [CrossRef]
- Sharifzadeh, M.; Tarifard, A.; Moridi, M.A. Time-dependent behavior of tunnel lining in weak rock mass based on displacement back analysis method. Tunn. Undergr. Space Technol. 2013, 38, 348–356. [Google Scholar] [CrossRef]
- De Sortis, A.; Paoliani, P. Statistical analysis and structural identification in concrete dam monitoring. Eng. Struct. 2007, 29, 110–120. [Google Scholar] [CrossRef]
- Agullo, L.; Mirambell, E.; Aguado, A. A model for the analysis of concrete dams due to environmental thermal effects. Int. J. Numer. Methods Heat Fluid Flow 1996, 6, 25–36. [Google Scholar] [CrossRef]
- Stojanovic, B.; Milivojevic, M.; Ivanovic, M.; Milivojevic, N.; Divac, D. Adaptive system for dam behavior modeling based on linear regression and genetic algorithms. Adv. Eng. Softw. 2013, 65, 182–190. [Google Scholar] [CrossRef]
- Wei, B.; Chen, L.; Li, H.; Yuan, D.; Wang, G. Optimized prediction model for concrete dam displacement based on signal residual amendment. Appl. Math. Model. 2020, 78, 20–36. [Google Scholar] [CrossRef]
- Mata, J.; Tavares De Castro, A.; Sá Da Costa, J. Constructing statistical models for arch dam deformation. Struct. Control Health Monit. 2014, 21, 423–437. [Google Scholar] [CrossRef]
- Salazar, F.; Toledo, M.T.; Oñate, E.; Suárez, B. Interpretation of dam deformation and leakage with boosted regression trees. Eng. Struct. 2016, 119, 230–251. [Google Scholar] [CrossRef]
- Kang, F.; Liu, J.; Li, J.; Li, S. Concrete dam deformation prediction model for health monitoring based on extreme learning machine. Struct. Control Health Monit. 2017, 24, 1997. [Google Scholar] [CrossRef]
- Dai, B.; Gu, C.; Zhao, E.; Qin, X. Statistical model optimized random forest regression model for concrete dam deformation monitoring. Struct. Control Health Monit. 2018, 25, e2170. [Google Scholar] [CrossRef]
- Kang, F.; Li, J.; Zhao, S.; Wang, Y. Structural health monitoring of concrete dams using long-term air temperature for thermal effect simulation. Eng. Struct. 2019, 180, 642–653. [Google Scholar] [CrossRef]
- Fedele, R.; Maier, G.; Miller, B. Health assessment of concrete dams by overall inverse analyses and neural networks. Int. J. Fract. 2006, 137, 151–172. [Google Scholar] [CrossRef]
- Bonaldi, P.; Fanelli, M.; Giuseppetti, G. Displacement Forecasting for Concrete Dams. Int. Water Power Dam Constr. 1977, 29, 42–50. [Google Scholar] [CrossRef]
- Zienkiewicz, O.; Taylor, R.; Zhu, J. The Finite Element Method for Solid and Structural Mechanics; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Li, H.; Wang, G.; Wei, B.; Zhong, Y.; Zhan, L. Dynamic inversion method for the material parameters of a high arch dam and its foundation. Appl. Math. Model. 2019, 71, 60–76. [Google Scholar] [CrossRef]
- Bocciarelli, M.; Ranzi, G. An inverse analysis approach for the identification of the hygro-thermo-chemical model parameters of concrete. Int. J. Mech. Sci. 2018, 138–139, 368–382. [Google Scholar] [CrossRef]
- Zhou, W.; Li, S.L.; Ma, G.; Chang, X.L.; Ma, X.; Zhang, C. Parameters inversion of high central core rockfill dams based on a novel genetic algorithm. Sci. China Technol. Sci. 2016, 59, 783–794. [Google Scholar] [CrossRef]
- Yazdani, M.; Sharifzadeh, M.; Kamrani, K.; Ghorbani, M. Displacement-based numerical back analysis for estimation of rock mass parameters in Siah Bisheh powerhouse cavern using continuum and discontinuum approach. Tunn. Undergr. Space Technol. 2012, 28, 41–48. [Google Scholar] [CrossRef]
- Oreste, P. Back-analysis techniques for the improvement of the understanding of rock in underground constructions. Tunn. Undergr. Space Technol. 2005, 20, 7–21. [Google Scholar] [CrossRef]
- Guo, Q.; Pei, L.; Zhou, Z.; Chen, J.; Yao, F. Response surface and genetic method of deformation back analysis for high core rockfill dams. Comput. Geotech. 2016, 74, 132–140. [Google Scholar] [CrossRef]
- Yang, L.; Su, H.; Wen, Z. Improved PLS and PSO methods-based back analysis for elastic modulus of dam. Adv. Eng. Softw. 2019, 131, 205–216. [Google Scholar] [CrossRef]
- Lin, C.; Li, T.; Chen, S.; Lin, C.; Liu, X.; Gao, L.; Sheng, T. Structural identification in long-term deformation characteristic of dam foundation using meta-heuristic optimization techniques. Adv. Eng. Softw. 2020, 148, 102870. [Google Scholar] [CrossRef]
- Yang, L.; Wen, Z.; Yan, X.; Hua, Q.; Su, H. Structural inverse analysis of concrete dams: Considering residual hydration heat effect on dam displacements. Eng. Comput. 2023, 39, 2829–2849. [Google Scholar] [CrossRef]
- Wang, S.; Xu, C.; Liu, Y.; Xu, B. Zonal intelligent inversion of viscoelastic parameters of high arch dams using an HEST statistical model. J. Civ. Struct. Health Monit. 2022, 12, 207–223. [Google Scholar] [CrossRef]
- Zhang, W.; Xu, L.; Shen, Z.; Ma, B. A new approach for mechanical parameter inversion analysis of roller compacted concrete dams using modified PSO and RBFNN. Clust. Comput. 2022, 25, 4633–4652. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C. Achievements and some unsolved problems of the finite element method. Int. J. Numer. Methods Eng. 2000, 47, 9–28. [Google Scholar] [CrossRef]
- Uriarte, C.; Pardo, D.; Omella, Á.J. A Finite Element based Deep Learning solver for parametric PDEs. Comput. Methods Appl. Mech. Eng. 2022, 391, 114562. [Google Scholar] [CrossRef]
- Lin, C.; Li, T.; Liu, X.; Zhao, L.; Chen, S.; Qi, H. A deformation separation method for gravity dam body and foundation based on the observed displacements. Struct. Control Health Monit. 2019, 26, 1–18. [Google Scholar] [CrossRef]
- Li, T.; He, J.; Zhao, L.; Li, X.; Niu, Z. Strength reduction method for stability analysis of local discontinuous rock mass with iterative method of partitioned finite element and interface boundary element. Math. Probl. Eng. 2015, 2015, 872834. [Google Scholar] [CrossRef]
- Fan, S.; Li, T.; Liu, X.; Zhao, L.; Niu, Z.; Qi, H. A hybrid algorithm of partitioned finite element and interface element for dynamic contact problems with discontinuous deformation. Comput. Geotech. 2018, 101, 130–140. [Google Scholar] [CrossRef]
- Gao, L.; Li, T.; Liu, X.; Qi, H.; Fan, S.; Lin, C.; Zhou, M. A novel dynamic stability analysis method for jointed rock slopes based on block-interface interaction. Comput. Geotech. 2021, 134, 104113. [Google Scholar] [CrossRef]
- Qi, H.; Li, T.; Liu, X.; Zhao, L.; He, J.; Li, X. A fast local nonlinear solution technique based on the partitioned finite element and interface element method. Int. J. Numer. Methods Eng. 2022, 123, 2214–2236. [Google Scholar] [CrossRef]
- Salazar, F.; Vicente, D.J.; Irazábal, J.; De-Pouplana, I.; San Mauro, J. A Review on Thermo-mechanical Modelling of Arch Dams During Construction and Operation: Effect of the Reference Temperature on the Stress Field. Arch. Comput. Methods Eng. 2020, 27, 1681–1707. [Google Scholar] [CrossRef]
- Soltani, N.; Alembagheri, M.; Khaneghahi, M.H. Risk-based probabilistic thermal-stress analysis of concrete arch dams. Front. Struct. Civ. Eng. 2019, 13, 1007–1019. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Emary, E.; Zawbaa, H.M.; Hassanien, A.E. Binary grey wolf optimization approaches for feature selection. Neurocomputing 2016, 172, 371–381. [Google Scholar] [CrossRef]
- Li, E.; Yang, F.; Ren, M.; Zhang, X.; Zhou, J.; Khandelwal, M. Prediction of blasting mean fragment size using support vector regression combined with five optimization algorithms. J. Rock Mech. Geotech. Eng. 2021, 13, 1380–1397. [Google Scholar] [CrossRef]
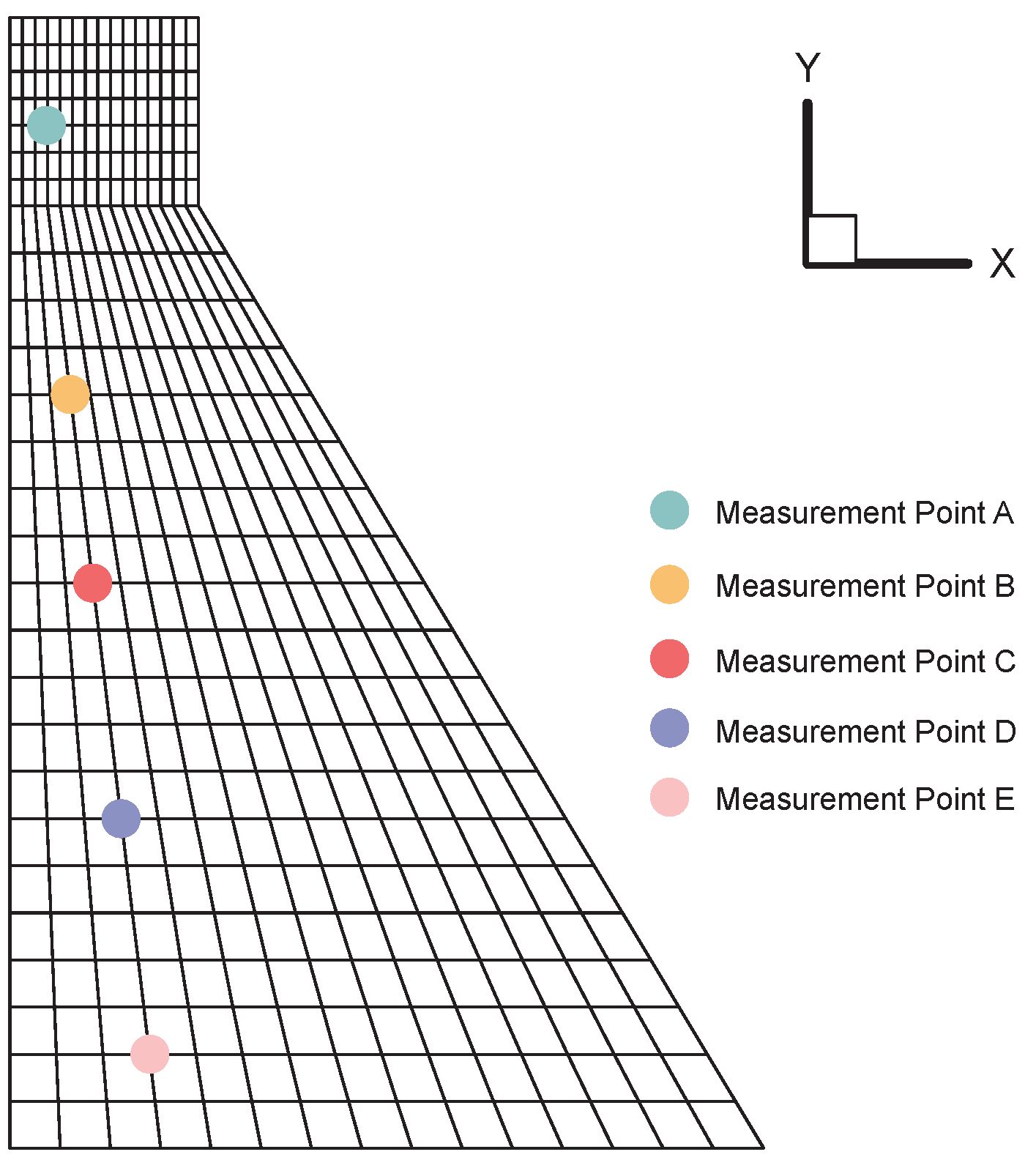


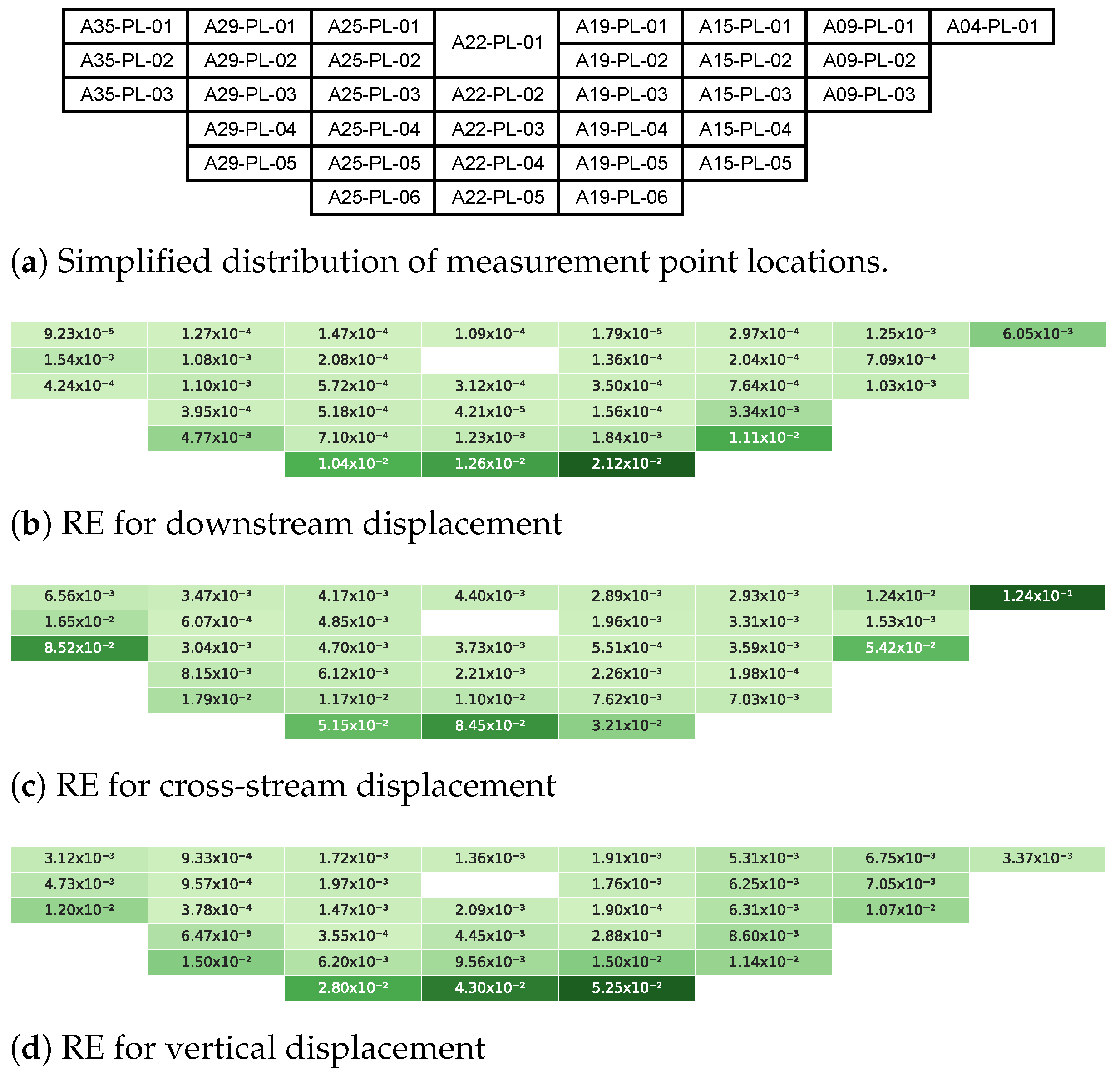


| Point | Direction | (m) | (m) | RE |
|---|---|---|---|---|
| A | X | |||
| Y | ||||
| B | X | |||
| Y | ||||
| C | X | |||
| Y | ||||
| D | X | |||
| Y | ||||
| E | X | |||
| Y |
| Division | E/GPa | |||
|---|---|---|---|---|
| A | 2500 | 1.047 | 8.479 | 32.1 |
| B | 2500 | 1.056 | 8.227 | 31.1 |
| C | 2500 | 1.072 | 8.016 | 30.1 |
| Period | A | B | C |
|---|---|---|---|
| 2016 | 39.56 | 39.73 | 37.95 |
| 2017 | 39.72 | 40.02 | 38.10 |
| 2018 | 39.65 | 39.96 | 38.10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Gao, L.; Li, T.; Guo, J.; Qi, H.; Peng, Y.; Wang, J. Inversion Method for Material Parameters of Concrete Dams Using Intelligent Algorithm-Based Displacement Separation. Water 2024, 16, 2979. https://doi.org/10.3390/w16202979
Xu J, Gao L, Li T, Guo J, Qi H, Peng Y, Wang J. Inversion Method for Material Parameters of Concrete Dams Using Intelligent Algorithm-Based Displacement Separation. Water. 2024; 16(20):2979. https://doi.org/10.3390/w16202979
Chicago/Turabian StyleXu, Jianrong, Lingang Gao, Tongchun Li, Jinhua Guo, Huijun Qi, Yu Peng, and Jianxin Wang. 2024. "Inversion Method for Material Parameters of Concrete Dams Using Intelligent Algorithm-Based Displacement Separation" Water 16, no. 20: 2979. https://doi.org/10.3390/w16202979
APA StyleXu, J., Gao, L., Li, T., Guo, J., Qi, H., Peng, Y., & Wang, J. (2024). Inversion Method for Material Parameters of Concrete Dams Using Intelligent Algorithm-Based Displacement Separation. Water, 16(20), 2979. https://doi.org/10.3390/w16202979







