Influence of Rainfall Patterns on Rainfall–Runoff Processes: Indices for the Quantification of Temporal Distribution of Rainfall
Abstract
1. Introduction
2. Quantification Indices for the Temporal Distribution of Rainfall
3. Quantification of Temporal Distribution by Rainfall Scenario
3.1. Generation of Rainfall Scenario
3.2. Distribution of Skewp and NRMSEp by Rainfall Scenario
3.3. Comparison of Quantification Index with Conventional Huff Distribution
4. Change in Peak Flood Discharge of the Rainfall–Runoff Processes According to the Temporal Distribution of Rainfall
4.1. Selection of Target Areas and Rainfall–Runoff Simulation Method
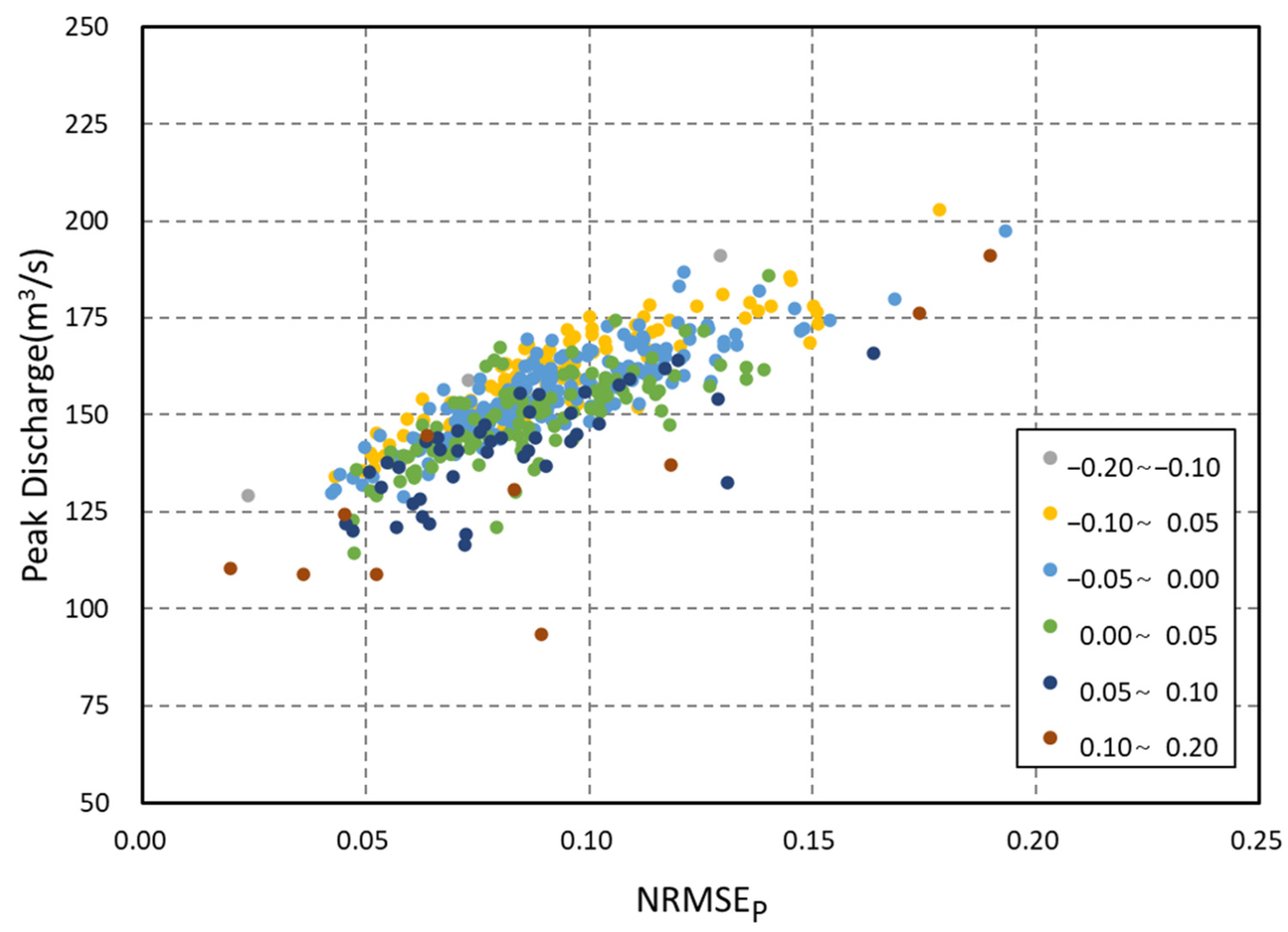
4.2. Relationship among skewP, NRMSEP, and Peak Flood Discharge
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill: New York, NY, USA, 1988. [Google Scholar]
- Bras, R.L. Hydrology: An Introduction to Hydrologic Science; Addison-Wesley: Boston, MA, USA, 1990. [Google Scholar]
- Tarboton, D.G. Rainfall-Runoff Processes; Utah State University: Logan, UT, USA, 2003. [Google Scholar]
- Obled, C.; Wendling, J.; Beven, K. The sensitivity of hydrological models to spatial rainfall patterns: An evaluation using observed data. J. Hydrol. 1994, 159, 305–333. [Google Scholar] [CrossRef]
- Segond, M.L.; Wheater, H.S.; Onof, C. The significance of spatial rainfall representation for flood runoff estimation: A numerical evaluation based on the Lee chatchment, UK. J. Hydrol. 2007, 347, 116–131. [Google Scholar] [CrossRef]
- Máca, P.; Torfs, P. The influence of temporal rainfall distribution in the flood runoff modelling. Soil Water Res. 2009, 4, S102–S110. [Google Scholar] [CrossRef]
- Oh, T.; Kim, M.; Moon, Y.; Ahn, J. An analysis of the characteristics in design rainfall according to the data periods. J. Korean Soc. Hazard. Mitigat. 2009, 9, 115–127. (In Korean) [Google Scholar]
- Kim, S.U.; Lee, Y.S. Flood frequency analysis considering probability distribution and return period under non-stationary condition. J. Korea Water Resour. Assoc. 2015, 48, 567–579. (In Korean) [Google Scholar] [CrossRef]
- Ministry of the Interior and Safety (MOIS). Establishment Disaster Prev. Perform. Targets Reg. Considering Clim. Change Eff.; MOIS: Sejong-si, Republic of Korea, 2017. (In Korean)
- Ministry of the Interior and Safety (MOIS). Establishment Disaster Prev. Perform. Targets Reg.; MOIS: Sejong-si, Republic of Korea, 2022. (In Korean)
- Lenderink, G.; Buishand, A.; van Deursen, W.P.A. Estimates of future discharges of the river Rhine using two scenario methodologies: Direct versus delta approach. Hydrol. Earth Syst. Sci. 2007, 11, 1145–1159. [Google Scholar] [CrossRef]
- Korea Water and Wastewater Works Association (KWWA). Drainage Sewer Design Guideline; KWWA: Seoul, Republic of Korea, 2022. (In Korean) [Google Scholar]
- Ministry of the Interior and Safety (MOIS). Small Stream Design Guideline; MOIS: Sejong-si, Republic of Korea, 2024. (In Korean)
- Jeong, J.; Kim, J. Improved practical methods for considering climate change in design flood estimation. J. Korean Soc. Hazard Mitig. 2022, 22, 301–309. (In Korean) [Google Scholar] [CrossRef]
- Wang, F. Temporal pattern analysis of local rainstorm events in China during the flood season based on time series clustering. Water 2020, 12, 725. [Google Scholar] [CrossRef]
- Dunkerley, D. The importance of incorporating rain intensity profiles in rainfall simulation studies of infiltration, runoff production, soil erosion, and related land surface processes. J. Hydrol. 2021, 603, 126834. [Google Scholar] [CrossRef]
- Bell, V.A.; Moore, R.J. The sensitivity of catchment runoff models to rainfall data at different spatial scales. Hydrol. Earth Syst. Sci. 2000, 4, 653–667. [Google Scholar] [CrossRef]
- Gires, A.; Onof, C.; Maksimovic, C.; Schertzer, D.; Tchiguirinskaia, I.; Simoes, N. Quantifying the impact of small scale unmeasured rainfall variability on urban runoff through multifractal downscaling: A case study. J. Hydrol. 2012, 442–443, 117–128. [Google Scholar] [CrossRef]
- Bruni, G.; Reinoso, R.; van de Giesen, N.C.; Clemens, F.H.L.R.; ten Veldhuis, J.A.E. On the sensitivity of urban hydrodynamic modelling to rainfall spatial and temporal resolution. Hydrol. Earth Syst. Sci. 2015, 19, 691–709. [Google Scholar] [CrossRef]
- Yuan, W.; Liu, M.; Wan, F. Study on the impact of rainfall pattern in small watersheds on rainfall warning index of flash flood event. Nat. Hazards 2019, 97, 665–682. [Google Scholar] [CrossRef]
- Huff, F.A. Time distribution of rainfall in heavy storms. Water Resour. Res. 1967, 3, 1007–1019. [Google Scholar] [CrossRef]
- Jeong, J.; Yoon, Y. Design Practices for Water Resources, 2nd ed.; Goomi Press: Seoul, Republic of Korea, 2007. [Google Scholar]
- Yen, B.C.; Chow, V.T. Design hyetographs for small drainage structures. J. Hydr. Div. 1980, 106, 1055–1076. [Google Scholar] [CrossRef]
- Oliver, J.E. Monthly precipitation distribution: A comparative index. Prof. Geogr. 1980, 32, 300–309. [Google Scholar] [CrossRef]
- Michiels, P.; Gabriels, D.; Hartmann, R. Using the seasonal and temporal precipitation concentration index for characterizing the monthly rainfall distribution in Spain. Catena 1992, 19, 43–58. [Google Scholar] [CrossRef]
- Wartalska, K.; Kaźmierczak, B.; Nowakowska, M.; Kotowski, A. Analysis of hyetographs for drainage system modeling. Water 2020, 12, 149. [Google Scholar] [CrossRef]
- Kim, C.; Kim, D.H. Effects of rainfall spatial distribution on the relationship between rainfall spatiotemporal resolution and runoff prediction accuracy. Water 2020, 12, 846. [Google Scholar] [CrossRef]
- Ministry of Land, Transport and Maritime Affairs (MLTMA). Improvement and Supplement of Probability Rainfall in South Korea; MLTMA: Sejong City, Republic of Korea, 2011. (In Korean) [Google Scholar]
- Ministry of Environment. Standard Guideline for Design Flood; Ministry of Environment: Sejong, Republic of Korea, 2019. (In Korean)
- Ministry of Land, Infrastructure and Transport (MOLIT). Development of Advanced Technology for Hydrologic Analysis in Korea; MOLIT: Sejong, Republic of Korea, 2017. (In Korean)
- Korea Water Resources Association (KWRA). River Design Guideline and Commentary; KWRA: Daejeon, Republic of Korea, 2019. (In Korean) [Google Scholar]
- Clark, C.O. Storage and the unit hydrograph. Trans. Am. Soc. Civ. Eng. 1945, 110, 1419–1446. [Google Scholar] [CrossRef]
- Ministry of Land, Transport and Maritime Affairs (MLTMA). Design Flood Estimation Guide; MLTMA: Sejong City, Republic of Korea, 2012. (In Korean) [Google Scholar]
- Sabol, G.V.; Unit, C. Clark Unit Hydrograph and R-parameter estimation. J. Hydraul. Eng. 1988, 114, 103–111. [Google Scholar] [CrossRef]
- Yoo, C.S. A theoretical review of basin storage coefficient and concentration time using the Nash model. J. Korea Water Resour. Assoc. 2009, 42, 235–246. (In Korean) [Google Scholar] [CrossRef][Green Version]
- Soil Conservation Service (SCS), Chapter 10; Soil Conservation Service. Hydrology. In National Engineering Handbook; United States Department of Agriculture: Washington, DC, USA, 1956; Section 4, Supplement A.


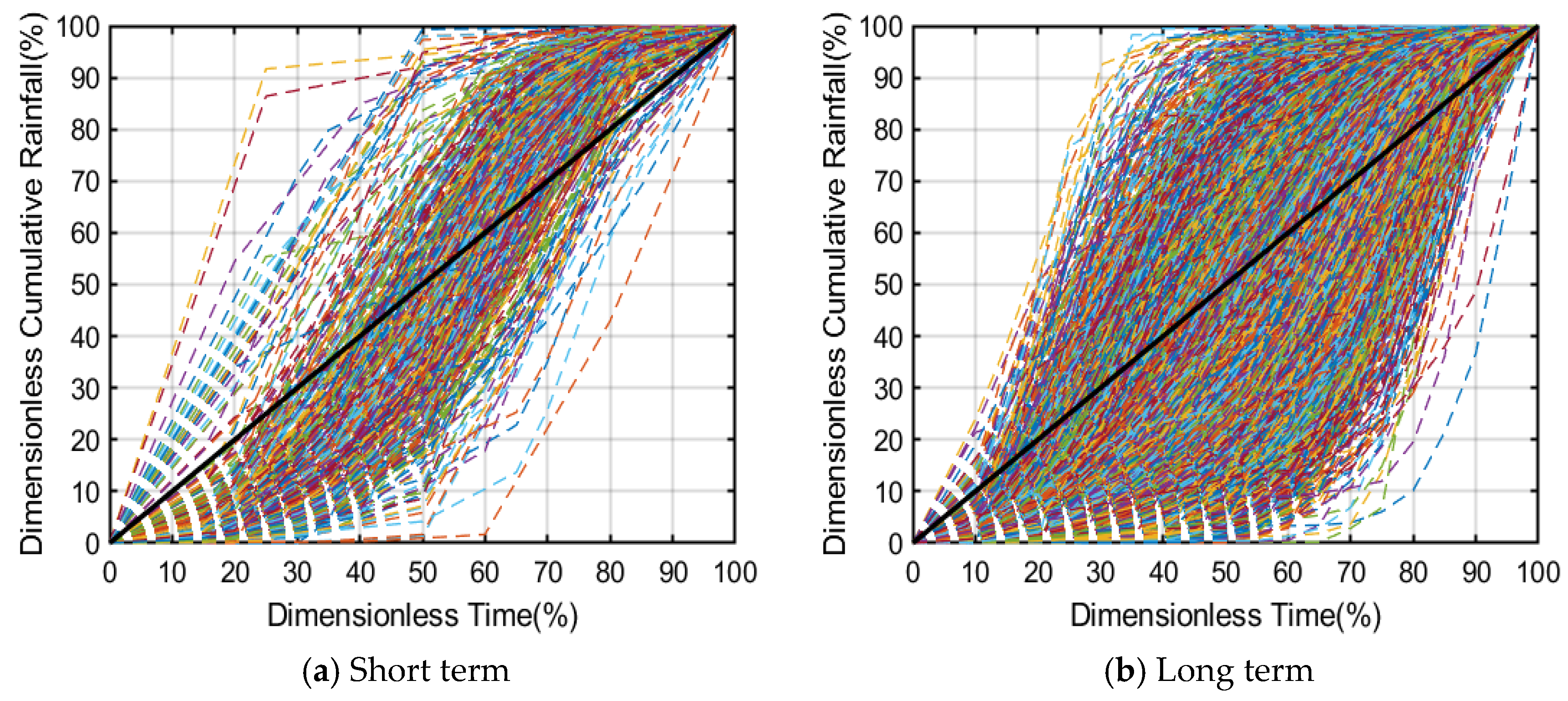






| Rainfall Duration | Short Term (<6 h) | Long Term (≥6 h) | ||
|---|---|---|---|---|
| Data source | OBS | CCS | OBS | CCS |
| Number of scenarios | 34 | 415 | 42 | 5747 |
| Note | Primarily used in streams or medium-sized rivers | Primarily used in regional/large-sized rivers or national rivers | ||
| Range of Skewp | Linear Regression | Correlation Coefficient |
|---|---|---|
| −0.20 to −0.10 | Y = 584.06X + 115.82 | 1.00 |
| −0.10 to −0.05 | Y = 423.78X + 121.21 | 0.89 |
| −0.05 to 0.00 | Y = 408.25X + 118.29 | 0.87 |
| 0.00 to 0.05 | Y = 398.51X + 114.94 | 0.74 |
| 0.05 to 0.10 | Y = 368.41X + 110.98 | 0.71 |
| 0.10 to 0.20 | Y = 452.45X + 93.12 | 0.84 |
| Range of NRMSEp | Linear Regression | Correlation Coefficient |
|---|---|---|
| 0.00 to 0.06 | Y = −101.03X + 132.95 | −0.70 |
| 0.06 to 0.08 | Y = −94.53X + 145.12 | −0.50 |
| 0.08 to 0.10 | Y = −103.87X + 152.92 | −0.52 |
| 0.10 to 0.12 | Y = −102.45X + 161.07 | −0.56 |
| 0.12 to 0.14 | Y = −176.56X + 165.08 | −0.77 |
| 0.14 to 0.20 | Y = −11.10X + 179.77 | −0.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oh, B.; Kim, J.; Hwang, S. Influence of Rainfall Patterns on Rainfall–Runoff Processes: Indices for the Quantification of Temporal Distribution of Rainfall. Water 2024, 16, 2904. https://doi.org/10.3390/w16202904
Oh B, Kim J, Hwang S. Influence of Rainfall Patterns on Rainfall–Runoff Processes: Indices for the Quantification of Temporal Distribution of Rainfall. Water. 2024; 16(20):2904. https://doi.org/10.3390/w16202904
Chicago/Turabian StyleOh, Byunghwa, JongChun Kim, and Seokhwan Hwang. 2024. "Influence of Rainfall Patterns on Rainfall–Runoff Processes: Indices for the Quantification of Temporal Distribution of Rainfall" Water 16, no. 20: 2904. https://doi.org/10.3390/w16202904
APA StyleOh, B., Kim, J., & Hwang, S. (2024). Influence of Rainfall Patterns on Rainfall–Runoff Processes: Indices for the Quantification of Temporal Distribution of Rainfall. Water, 16(20), 2904. https://doi.org/10.3390/w16202904






