Coal-Mine Water-Hazard Risk Evaluation Based on the Combination of Extension Theory, Game Theory, and Dempster–Shafer Evidence Theory

Abstract

Due to the complex hydrogeological conditions and water hazards in coal mines, there are multiple indexes, complexities, incompatibilities, and uncertainty issues in the risk evaluation process of coal-mine water hazards. To accurately evaluate the risk of coal-mine water hazards, a comprehensive evaluation method based on extension theory, game theory, and Dempster–Shafer (DS) evidence theory is proposed. Firstly, a hierarchical water-hazard risk-evaluation index system is established, and then matter-element theory in extension theory is used to establish a matter-element model for coal-mine water-hazard risk. The membership relationship between various evaluation indexes and risk grades of coal-mine water-hazard risk is quantified using correlation functions of extension set theory, and the quantitative results are normalized to obtain basic belief assignments (BBAs) of risk grades for each index. Then, the subjective weights of evaluation indexes are calculated using the order relation analysis (G1) method, and the objective weights of evaluation indexes are calculated using the entropy weight (EW) method. The improved combination weighting method of game theory (ICWMGT) is introduced to determine the combination weight of each evaluation index, which is used to correct the BBAs of risk grades for each index. Finally, the fusion of DS evidence theory based on matrix analysis is used to fuse BBAs, and the rating with the highest belief fusion result is taken as the final evaluation result. The evaluation model was applied to the water-hazard risk evaluation of Sangbei Coal Mine, the evaluation result was of II grade water-hazard risk, and it was in line with the actual engineering situation. The evaluation result was compared with the evaluation results of three methods, namely the expert scoring method, the fuzzy comprehensive evaluation method, and the extension method. The scientificity and reliability of the method adopted in this paper were verified through this method. At the same time, based on the evaluation results, in-depth data mining was conducted on the risk indexes of coal-mine water hazards, and it was mainly found that 11 secondary indexes are the focus of coal-mine water-hazard risk prevention and control, among which seven indexes are the primary starting point for coal-mine water-hazard risk prevention and control. The groundwater index in particular has the most prominent impact. These results can provide a theoretical basis and scientific guidance for the specific water-hazard prevention and control work of coal mines.

1. Introduction

Chinese coal production accounts for about 50% of the world’s total, and its raw coal production has been ranked first in the world for many consecutive years. The distribution of coal in China is extensive, and China’s land is composed of multiple tectonic plates that have undergone multiple geological tectonic movements. As a result, the water filling conditions for coal mines in China are extremely complex [1,2]. In recent years, with the extension of mining levels and the expansion of mining scope, the mining of coal seams has faced the presence of water accumulation in the goaf above the roof and high-pressure water near the bottom plate, which increases the control factors for water inrush. The mechanism and types of water inrush are also complex and varied, and the threat of water hazards to mines has become increasingly severe [3,4]. Mine water hazards seriously threaten the safety production of coal mines and the life safety of underground workers, which has caused great losses to workers and coal mines [5]. According to incomplete statistics, there were a total of 1103 water accidents in China from 2001 to 2022; these accidents resulted in 4667 deaths [6], which seriously threatens the efficient development process of China’s coal resources. How to prevent and control coal-mine water hazards is one of the key issues that urgently needs to be addressed. The sixteen-character principle of “prediction and forecasting, investigation if suspected, exploration before excavation, and treatment before mining” and the comprehensive water control measures of “prevention, blocking, dredging, drainage, and interception” have been proposed for the prevention and control of water hazards in coal mines [7]. It can be seen that prediction and forecasting are the primary link and foundation of coal-mine water-hazard prevention and control. The scientific and reasonable prediction and forecasting of coal-mine water hazards, as well as the evaluation of the risk grade of coal-mine water hazards, have practical guiding significance for guiding water-hazard prevention and control work in coal mines.

The occurrence of coal-mine water accidents is a result of the comprehensive influence and control of multiple factors based on hydrogeological conditions. The factors causing coal-mine water hazards can generally be divided into two categories: water filling sources and water diversion channels. Different combinations of water filling sources and water diversion channels will constitute different mine water-filling intensities and water-hazard threat grades [8,9,10]. Based on the main causes of water hazards, coal technology workers have conducted extensive research on the prediction, forecasting, and risk evaluation of coal-mine water hazards from different perspectives and directions. The impact of mine water sources on the occurrence of mine water inrush is reflected in their provision of water sources for mining space, which is the fundamental prerequisite for the occurrence of water inrush. Water filling sources mainly include atmospheric precipitation, surface water, groundwater, and old goaf water, and the methods for identifying water filling sources mainly include geological and hydrogeological analysis, water temperature and level analysis, hydrochemical analysis, mathematical theory analysis, etc. [11]. The hydrochemical characteristics of groundwater are strictly controlled by factors such as recharge sources, transport conditions, and the lithological characteristics of the storage space. Therefore, groundwater chemistry can reflect the most essential characteristics of groundwater. If the hydrochemical characteristics of a target aquifer that may become a water filling source are analyzed, the risk grade of water filling in the mine can be accurately evaluated, and water-hazard prevention measures can be proposed based on it [12,13,14,15]. Mine water-diversion channels are another prerequisite for the occurrence of mine water accidents. As an important channel for communicating the water filling source and mining space, it is an important factor affecting the evolution of the original aquifer structure under mining conditions. The water diversion channels in mines can be roughly divided into two types: natural channels and artificial channels [10]. Natural channels include fault zones, water-conducting collapse columns, hidden outcrops, etc. Based on the analysis of a large number of water inrush accidents, more than 80% of them are related to the faults [16,17]. Many engineering examples also show that the existence of faults reduces the strength of rocks, and the vast majority of non-water-conducting faults are activated during coal seam mining, which results in the continuous expansion of fractures and provides conditions for the formation of water diversion channels. Studying the activation law of faults provides a theoretical basis for predicting and forecasting mine water inrush risk and scientific management [3,18,19,20,21]. Artificial channels include mining induced fractures, ground karst collapse zones, and poorly sealed boreholes. During the process of coal seam mining, rock layers around the goaf lose their support, which causes changes in the original stress state and results in the destruction of the roof, floor, and coal walls. This forms mining-induced fractures around the mining area, and if mining-induced fractures develop into aquifers, they can cause water inrush in mines. Studying the development law of mining-induced fractures has important guiding significance for predicting and forecasting mine water-hazard risk [22,23,24,25,26].

The above is mainly based on one of the two major types of disaster-causing factors for mine water-hazard prediction and risk evaluation. Some scholars have also combined different theories and methods based on the two types of disaster-causing factors to predict and evaluate water hazards locally or globally in mines. Bai et al. [5] used analytic hierarchy process and criteria importance though intercriteria correlation to determine the comprehensive weights of seven factors; they established a risk index model for mine water inrush and identified a risk area of roof water inrush in the No.1 coal seam of Liuzhuang Coal Mine. Chen et al. [27] selected six main influencing factors as discriminant indexes and established a Fisher discriminant model based on multiple training samples, which accurately predicted water inrush risk areas of three main coal seams in the southern mining area of Qidong Coal Mine. Huang et al. [28] used analytic hierarchy process and the entropy weight method to calculate the weights of six indexes; they established a vulnerability index model for bottom-plate water inrush and successfully predicted the potential water risk area of the 182,602 working face. Ruan et al. [29] used an improved analytic hierarchy process method to calculate the weights of thirty evaluation indexes, and a decision model for underground water inrush in mines was established combining DS evidence theory. They also predicted the probability of water inrush in the 20,101 ventilation roadway of Wangjialing Coal Mine. Wang et al. [30] conducted a special evaluation of water inrush risk in six coal mines around Yangzhuang Coal Mine using the safety checklist method. Wang et al. [31] evaluated the risk of mine water inrush accidents using analytic hierarchy process and an expert scoring method. Zhao [32] evaluated the degree of water damage threat to a mine in Ningdong Mining Area using the analytic hierarchy process method and fuzzy comprehensive evaluation method. Xu et al. [33] evaluated the water-hazard risk of Zhaojiazhai Coal Mine based on the combination weighting method and fuzzy comprehensive evaluation method; they proposed suggestions for water-hazard prevention and control. Li et al. [34] used an evaluation model combining the analytic network hierarchy process method and a cloud model to conduct a water inrush risk warning evaluation of Y Coal Mine, and the evaluation model is now available and reliable. Chen et al. [35] constructed an evaluation model for coal-mine water inrush risk based on the fuzzy network analysis method.

Conducting mine water-hazard risk evaluation and understanding the water-hazard risk grade of mines in a timely manner can provide decision-making support for coal-mine water-hazard prevention and control work and promote the improvement of management level and efficiency of coal mines. It also serves as a favorable tool for higher-level supervisory departments to grasp the safety production status of coal mines and strengthen safety supervision. Although many scholars have used various evaluation methods to analyze mine water-hazard risk, which have played an important guiding role in preventing and reducing water accidents, there are more or less the following problems: firstly, the selection of evaluation indexes is not representative, and the establishment of evaluation index system is not scientific and perfect, which may introduce certain difficulties to the promotion of this method. Secondly, the weight calculation method of evaluation indexes is unreasonable, and the imbalance of weight calculation is caused by a single weighting method, which leads to a great increase in uncertainty in the evaluation process. Thirdly, there is a lack of scientific rigor in the selection of comprehensive evaluation methods, as well as a lack of consideration for inherent connections between evaluation indexes—these may also lead to deviations between evaluation results and engineering reality. Therefore, it is particularly necessary to establish a scientific and reasonable risk-evaluation method for mine water hazards. Based on the above reasons, this paper proposes a coal-mine water-hazard risk-evaluation method based on the combination of extension theory, game theory and DS evidence theory, in order to accurately evaluate water-hazard risk.

2. Basic Theories and Evaluation Methods

2.1. Extension Theory

Extension theory is a theoretical framework based on matter-element theory and extension set theory. It cannot only use the extensibility of matter elements to determine qualitative methods, but it also uses extension set theory to perform quantitative calculations through correlation functions. Based on the extensibility of matter elements, many problems described as contradictions can be solved under the matter-element model [36,37,38]. The specific analysis steps are as follows:

2.1.1. Establishing Matter-Element Model

Firstly, the evaluation matter-element $R$ is determined, where $R$ is the ordered ternary group composed of “matter, characteristic, value”, $R=\left(\begin{array}{ccc}N& C& V\end{array}\right)$. Among them, $N$ represents the matter of matter elements, $C$ represents the characteristic of matter elements, and $V$ represents the value of matter elements; it is a basic element matter to describe an object. Then, the classical domain matter-element $R_j$, node domain matter-element $R_p$ and matter-element to be evaluated $R_0$ are determined, respectively.

$$R_j=\left(\begin{array}{ccc}{N}_j& c_i& v_{ji}\end{array}\right)=\left[\begin{array}{ccc}{N}_j& c_1& v_{j1}\\ & c_2& v_{j2}\\ & ⋮& ⋮\\ & c_n& v_{jn}\end{array}\right]=\left[\begin{array}{ccc}{N}_j& c_1& \left[a_{j1},b_{j1}\right]\\ & c_2& \left[a_{j2},b_{j2}\right]\\ & ⋮& ⋮\\ & c_n& \left[a_{jn},b_{jn}\right]\end{array}\right]$$

(1)

where $R_j$ represents the classical domain matter-element model of the $j$th evaluation grade of evaluation object, ($j=1,2,\cdots ,m$). $N_j$ represents the $j$th evaluation level of the evaluation object; $c_i$ represents the $i$th evaluation index ($i=1,2,\cdots ,n$); and $v_{ji}=\left[a_{ji},b_{ji}\right]$ represents the range of the value taken by the $j$th evaluation level with respect to the $i$th evaluation index.

$$R_p=\left(\begin{array}{ccc}{N}_p& c_i& v_{pi}\end{array}\right)=\left[\begin{array}{ccc}{N}_p& c_1& v_{p1}\\ & c_2& v_{p2}\\ & ⋮& ⋮\\ & c_n& v_{pn}\end{array}\right]=\left[\begin{array}{ccc}{N}_j& c_1& \left[a_{p1},b_{p1}\right]\\ & c_2& \left[a_{p2},b_{p2}\right]\\ & ⋮& ⋮\\ & c_n& \left[a_{pn},b_{pn}\right]\end{array}\right]$$

(2)

where $R_p$ represents a characteristic range of the joint domain matter-element model for all evaluation grades of the evaluation object. $N_p$ represents all the evaluation grades of the evaluation object. $v_{pi}$ represents the value range of evaluation index $c_i$ with respect to all grades, $v_{pi}=\left[a_{pi},b_{pi}\right]$.

$$R_0=\left(\begin{array}{ccc}{N}_0& c_i& v_i\end{array}\right)=\left[\begin{array}{ccc}{N}_0& c_1& v_1\\ & c_2& v_2\\ & ⋮& ⋮\\ & c_n& v_n\end{array}\right]$$

(3)

where $R_0$ represents the matter-element model determined according to the evaluation object. $N_0$ represents the evaluation object, and $v_i$ represents that evaluation object. $N_0$ corresponds to the assignment of evaluation index $c_i$.

2.1.2. Calculating Correlation Functions

After determining the above three matter-element models, in order to express the variation range of an index with respect to each evaluation grade—that is, to describe the quantitative and qualitative change of matter elements—the concept of a correlation function is introduced, and its calculation equation is defined as

$$K_j\left(v_i\right)=\left\{\begin{array}{cc}{\displaystyle \frac{-\rho \left(v_i,v_{ji}\right)}{\left|v_{ji}\right|}}& v_i\in v_{ji}\\ {\displaystyle \frac{\rho \left(v_i,v_{ji}\right)}{\rho \left(v_i,v_{pi}\right)-\rho \left(v_i,v_{ji}\right)}}& v_i\notin v_{ji}\end{array}\right.$$

(4)

where $\rho \left(v_i,v_{ji}\right)=\left|v_i-{\displaystyle \frac{a_{ji}+b_{ji}}{2}}\right|-{\displaystyle \frac{b_{ji}-a_{ji}}{2}}$, $\rho \left(v_i,v_{pi}\right)=\left|v_i-{\displaystyle \frac{a_{pi}+b_{pi}}{2}}\right|-{\displaystyle \frac{b_{pi}-a_{pi}}{2}}$, $K_j\left(v_i\right)$ represents the correlation degree between the $i$th index and the $j$th grade of evaluation object $N_0$, $\rho \left(v_i,v_{ji}\right)$ represents the distance between the evaluation index value of matter-element $R_0$ and the classical domain matter-element $R_j$, and $\rho \left(v_i,v_{pi}\right)$ represents the distance between the evaluation index value of matter-element $R_0$ and the joint domain matter-element $R_p$.

2.2. Improved Combination Weighting Method of Game Theory

At present, the main weighting methods are divided into the subjective weighting method, the objective weighting method and the combination weighting method [5,39]. The subjective weighting method mainly depends on the experience of experts and cannot well reflect objective reality; the objective weighting method has strong objectivity and calculation accuracy, but it ignores the positive subjective initiative of experts. The combination weighting method can overcome the shortcomings of the single weighting method and obtain the optimal weight combination, taking into account the characteristics of the different weighting methods. It can improve the scientific rationality of the evaluation. The subjective and objective combination weighting method based on improved game theory is used to determine combination weights of evaluation indexes, where the subjective weighting method chooses the G1 method and the objective weighting method chooses the EW method.

2.2.1. Order Relation Analysis Method

The G1 method is a subjective weighting method proposed by Chinese scholar Professor Guo Yajun [40]. This method determines the subjective weight of the index according to the importance relationship between the adjacent evaluation indexes. Compared with the traditional analytic hierarchy process, its evaluation process is clear and does not need to build a judgment matrix and consistency test, which avoids the large amount of calculation and tedious calculation process. The calculation steps are as follows:

(1)

Determining the order relation.

Relative to a certain evaluation object, the set of each evaluation index is $\left\{c_i\right\}$, and $c_i$ is the $i$th evaluation index, ($i=1,2,\cdots ,n$). According to the subjective experience, the expert selects the largest value in evaluation index set, which is marked as $c_1^{\ast }$, and the second-most-important evaluation index is selected among the remaining $n-1$ evaluation indexes, which is recorded as $c_2^{\ast }$. If the last evaluation index is recorded as $c_n^{\ast }$, the order relation of evaluation indexes is established as

$$c_1^{\ast }\ge c_2^{\ast }\ge \cdots \ge c_n^{\ast }$$

(5)

(2)

Giving the ratio of the relative importance.

If the ratio of the importance degree of evaluation indexes $c_{k-1}^{\ast }$ and $c_k^{\ast }$ in the order relation is ${\displaystyle \frac{w_{k-1}^{(1)\ast }}{w_k^{(1)\ast }}}$, $w_k^{(1)\ast }$ is the weight of the $k$th evaluation index of the subjective weighting method, the weight ratio of the adjacent evaluation index can be expressed as

$${\displaystyle \frac{w_{k-1}^{(1)\ast }}{w_k^{(1)\ast }}}=r_k(k=n,n-1,\cdots ,2)$$

(6)

where $r_k$ is the assignment of the importance of the order relation regarding evaluation indexes $c_{k-1}^{\ast }$ and $c_k^{\ast }$, and the $r_k$ assignment is shown in

Table 1. Assignment table.

${\mathit{r}}_{\mathit{k}}$	$\mathbf{Importance} \mathbf{of} \mathbf{Evaluation} \mathbf{Index} {\mathit{c}}_{\mathit{k}-1}^{\ast }$$\mathbf{to} {\mathit{c}}_{\mathit{k}}^{\ast }$
1	Equally Important
1.2	Slightly Important
1.4	Obviously Important
1.6	Strongly Important
1.8	Extremely Important
1.1, 1.3, 1.5, 1.7	The median of the above two adjacent judgments

.

(3)

Determining the subjective weights.

The weight equation of evaluation index $c_n^{\ast }$ is defined as

$$w_n^{(1)\ast }={\left(1+{\displaystyle \sum _{k=2}^n{\displaystyle \prod _{i=k}^n{r}_k}}\right)}^{-1}$$

(7)

According to the recursive equation, the weights of other indexes can be determined as

$$w_{k-1}^{(1)\ast }=r_k{w}_k^{(1)\ast }$$

(8)

Because $w_k^{(1)\ast }$ is the weight corresponding to the order relation, it needs to adjust the weight according to the corresponding order of the original evaluation indexes $c_1$, $c_2$,$\cdots$, $c_n$, and the adjustment result is $w_k^{(1)}$.

2.2.2. Entropy Weight Method

The EW method is an objective weighting method [41]. Its core idea is to determine the weight of each index datapoint based on the discretization degree of each index datapoint. If the discretization degree of index data is greater, it means that the index contains more information and has a great influence on the decision-making results. Therefore, it will be given a greater weight, and vice versa. The calculation steps are as follows:

(1)

Constructing an evaluation index matrix.

There are $m$ evaluation objects and $n$ evaluation indexes, and the evaluation index data are $b_{ji}$, ($j=1,2,\cdots ,m$; $i=1,2,\cdots ,n$). The index matrix is defined as

$$B={\left[b_{ji}\right]}_{m\times n}$$

(9)

Matrix $B$ is standardized by Equations (10) and (11), and the standardized matrix $B^{\prime }$ is obtained, $B^{\prime }={\left[b_{ji}^{\prime }\right]}_{m\times n}$, $b_{ji}^{\prime }$ is the standardization result of $b_{ji}$.

For the index of the bigger the better (income-type attribute), the standardized equation is defined as

$$b_{ji}^{\prime }={\displaystyle \frac{b_{ji}-\min \left(b_{ji}\right)}{\max \left(b_{ji}\right)-\min \left(b_{ji}\right)}}$$

(10)

For the index of the smaller the better (cost-type attribute), the standardized equation is defined as

$$b_{ji}^{\prime }={\displaystyle \frac{\max \left(b_{ji}\right)-b_{ji}}{\max \left(b_{ji}\right)-\min \left(b_{ji}\right)}}$$

(11)

(2)

Calculating entropy value $E_i$ of the $i$th evaluation index.

$$E_i=-{\displaystyle \frac{1}{\ln n}}{\displaystyle \sum _{j=1}^m{P}_{ji}}\ln P_{ji}$$

(12)

where $P_{ji}={\displaystyle \frac{b_{ji}^{\prime }}{{\displaystyle \sum _{j=1}^m{b}_{ji}^{\prime }}}}$, $P_{ji}$ is the characteristic proportion of $b_{ji}^{\prime }$ in matrix $B^{\prime }$.

(3)

Determining the objective weights.

The entropy weight $w_i^{(2)}$of the evaluation index is obtained by normalizing entropy value $E_i$.

$$w_i^{(2)}={\displaystyle \frac{1-E_i}{{\displaystyle \sum _{i=1}^n\left(1-E_i\right)}}}$$

(13)

2.2.3. Combination Weighting

The combination weighting method of game theory aims at the Nash equilibrium. It is a coordinated and integrated process to achieve consistency and compromise among different weighting methods, which maximizes the common interests of different weighting methods [42,43]. However, the combination coefficient obtained may be negative, so the constraint condition is introduced to improve the combination weighting method of game theory [44]. The specific steps of the ICWMGT are as follows:

(1)

Suppose $W^{\left(1\right)}={\left[w_1^{\left(1\right)},w_2^{\left(1\right)},\cdots w_n^{\left(1\right)}\right]}^T$, which represents a weight vector weighted by the G1 method, and $w_i^{(1)}$ represents the $i$th weight of the G1 method, ($i=1,2,\cdots ,n$).

Suppose $W^{\left(2\right)}={\left[w_1^{\left(2\right)},w_2^{\left(2\right)},\cdots w_n^{\left(2\right)}\right]}^T$, which represents a weight vector weighted by the EW method, and $w_i^{(2)}$ represents the $i$th weight of the EW method, ($i=1,2,\cdots ,n$). Then, any linear combination of $W^{\left(1\right)}$ and $W^{\left(2\right)}$ weight vectors can be expressed as

$$W={\displaystyle \sum _{s=1}^2{\alpha }_s{W}^{\left(s\right)}}$$

(14)

where $W$ is all the possible combination weight vectors, $W={\left[w_1,w_2,\cdots w_n\right]}^T$, ${\alpha }_s$ is a linear combination coefficient, and ${\alpha }_s>0$, $W^{\left(s\right)}$ is the weight calculated by the single weighting method, ($s=1,2$).

(2)

To find the optimal $W$ based on game theory—that is, to find a set of coefficients that minimizes the deviation between the combination weight vector and each single weight vector—the optimal weight coefficient is solved according to the equation as

$$\underset{{\alpha }_s}{\min }\hspace{1em}{‖{\displaystyle \sum _{s=1}^2{\alpha }_s{W}^{\left(s\right)}}-W^{\left(l\right)}‖}_2,\hspace{1em}(l=1,2)$$

(15)

(3)

The optimal first-derivative condition of Equation (15) is expressed as

$${\displaystyle \sum _{s=1}^2{\alpha }_s{(W^{\left(l\right)})}^T{W}^{\left(s\right)}}={\left(W^{\left(l\right)}\right)}^T{W}^{\left(l\right)}$$

(16)

It can be seen that the traditional game theory cannot guarantee that the linear combination coefficient ${\alpha }_s$ is greater than 0. If it is negative, it cannot satisfy Equation (14). Combining Equation (15) and optimizing the game model, a new objective function is established as

$$\underset{{\alpha }_s}{\min }\hspace{1em}{\displaystyle \sum _{l=1}^2{‖{\displaystyle \sum _{s=1}^2{\alpha }_s{(W^{\left(l\right)})}^T{W}^{\left(s\right)}}-{(W^{\left(l\right)})}^T{W}^{\left(l\right)}‖}_2}\hspace{1em}$$

(17)

(4)

In order to ensure that the combination coefficient is non-negative, the ICWMGT optimization model is established by adding constraints.

$$\left\{\begin{array}{ll}\underset{{\alpha }_s}{\min }& {\displaystyle \sum _{l=1}^2{‖{\displaystyle \sum _{s=1}^2{\alpha }_s{(W^{\left(l\right)})}^T{W}^{\left(s\right)}}-{(W^{\left(l\right)})}^T{W}^{\left(l\right)}‖}_2}\\ s.t.& \hspace{1em}\hspace{1em}\hspace{1em}{\displaystyle \sum _{s=1}^2{\alpha }_s^2=1,{\alpha }_s>0}\end{array}\right.$$

(18)

(5)

In order to solve the model, the optimization model of the Lagrange function is established, the linear combination coefficient ${\alpha }_s$ is obtained by partial derivative, and the combined weight coefficient ${\alpha }_s^{\ast }$ is obtained after normalization.

$${\alpha }_s^{\ast }={\displaystyle \frac{{\displaystyle \sum _{s=1}^2{(W^{\left(l\right)})}^T{W}^{\left(s\right)}}}{{\displaystyle \sum _{l=1}^2{\displaystyle \sum _{s=1}^2{(W^{\left(l\right)})}^T{W}^{\left(s\right)}}}}}$$

(19)

(6)

The combination weight $W^{\ast }$ can be expressed as

$$W^{\ast }={\displaystyle \sum _{s=1}^2{\alpha }_s^{\ast }{W}^{\left(s\right)}}$$

(20)

2.3. Fusion of DS Evidence Theory

2.3.1. DS Evidence Theory

DS evidence theory belongs to the reasoning method of uncertainty, which was put forward by A. P. Dempster in 1967 and was further developed by G. Shafer in 1976, so it is called DS evidence theory [45,46]. Compared with the traditional probability theory, DS evidence theory can better grasp the unknown and uncertainty of the problem.

Let $\Theta$ be the recognition framework of evidence theory, which represents the set composed of mutually exclusive and exhaustive propositions [47]. The ghost set of recognition frame $\Theta$ is marked as $2^{\Theta }$, corresponding to a set function $m$: $2^{\Theta }\to [0,1]$ on the identification framework, and it satisfies the following equation as

$$\left\{\begin{array}{c}m(\mathrm{\Phi })=0\\ {\displaystyle \sum _{A\subseteq \Theta }m(A)=1}\end{array}\right.$$

(21)

where $m(A)$ is the BBA of the corresponding proposition $A$. If $m(A)>0$, $A$ is called the focal element of $m$, where $A$ is any subset of $\Theta$.

The Dempster fusion rule is the core of DS evidence theory. Let $m_1$ and $m_2$ be two BBA functions on the same recognition frame, and the focal elements are $B$ and $C$, where $A=B\cap C$. If the fusion result of $m_1$ and $m_2$ is $m=m_1\oplus m_2$, $\oplus$ represents the orthogonal sum, and the Dempster fusion rule is defined as

$$m(A)=\left(m_1\oplus m_2\right)(A)=\left\{\begin{array}{cc}0& D=\mathrm{\Phi }\\ {\displaystyle \frac{{\displaystyle \sum _{B\cap C=A}{m}_1(B)m_2(C)}}{1-K}}& D\ne \mathrm{\Phi }\end{array}\right.$$

(22)

where $K={\displaystyle \sum _{B\cap C=\mathrm{\Phi }}{m}_1(B)m_2(C)}$, and $K$ represents the degree of conflict between $m_1$ and $m_2$.

2.3.2. Fusion Algorithm Based on Matrix Analysis

Suppose $n$ evaluation indexes evaluate an object together, the evaluation result has $\overline{m}$ kinds of results. If the fusion result is calculated by using the Dempster fusion rule, it will cause the problem of too much calculation, which leads to the difficulty of applying evidence theory to multi-information fusion. In this paper, the fusion algorithm based on matrix analysis is adopted, which can reduce the amount of calculation [48]. The BBAs can be expressed by the matrix of $n\times \overline{m}$.

$$M=\left[\begin{array}{cccc}{m}_{11}& m_{12}& \cdots & m_{1\overline{m}}\\ m_{21}& m_{22}& \cdots & m_{2\overline{m}}\\ ⋮& ⋮& ⋮& ⋮\\ m_{n1}& m_{n2}& \cdots & m_{n\overline{m}}\end{array}\right]$$

(23)

where any element $m_{ij}$ in the matrix $M$ represents the BBA of the $i$th evaluation index for the $j$th evaluation result, ($i=1,2,\cdots ,n$, $j=1,2,\cdots ,\overline{m}$).

Since the evaluation index of DS evidence theory is assigned to $\overline{m}$ possible evaluation results, the sum of beliefs is 1. In this matrix, the sum of the elements of each row should satisfy the normalization condition.

$$m_{i1}+m_{i2}+\cdots +m_{i\overline{m}}=1$$

(24)

The transposition of the $i$th row of matrix $M$ is multiplied by the $k$th row.

$$M_i^T\times M_k={\left[\begin{array}{cccc}{m}_{i1}& m_{i2}& \cdots & m_{i\overline{m}}\end{array}\right]}^T\left[\begin{array}{cccc}{m}_{k1}& m_{k2}& \cdots & m_{k\overline{m}}\end{array}\right]$$

(25)

Then, a new matrix $B$ of $\overline{m}\times \overline{m}$ is obtained.

$$B=\left[\begin{array}{cccc}{m}_{i1}\times m_{k1}& m_{i1}\times m_{k2}& \cdots & m_{i1}\times m_{k\overline{m}}\\ m_{i2}\times m_{k1}& m_{i2}\times m_{k2}& \cdots & m_{i2}\times m_{k\overline{m}}\\ ⋮& ⋮& ⋮& ⋮\\ m_{i\overline{m}}\times m_{k1}& m_{i\overline{m}}\times m_{k2}& \cdots & m_{i\overline{m}}\times m_{k\overline{m}}\end{array}\right]$$

(26)

The elements of the diagonal of matrix $B$ represent the accumulation of beliefs of two evaluation indexes, and the sum of other elements except the main diagonal elements is the degree of conflict of BBA functions.

$$K={\displaystyle \sum _{p\ne q}{m}_{ip}\times }{m}_{kp}(p,q=1,2,\cdots ,\overline{m})$$

(27)

2.3.3. Acquisition of the BBA Function Based on Correlation Degree

In the matter-element theory, the correlation degree represents the degree to which an element belongs to a certain property, and it is necessary to transform the correlation degree of matter-element theory into the BBA of DS evidence theory. In order to maintain consistency between them, $e^x$ function can be used for equivalent transfer transformation. Since the range of the BBA function of DS evidence theory is [0,1], the correlation degree needs to be normalized in order to establish a recognition framework that meets the requirements of DS evidence theory due to the BBA function. $K_{ji}$ represents the correlation degree between the $i$th index and the $j$th grade of the evaluation object $N_0$, ($i=1,2,\cdots ,n$, $j=1,2,\cdots ,\overline{m}$). Through Equation (28), it is transformed into the BBA on the identification frame $\Theta$.

$$m_i\left({\theta }_j\right)={\displaystyle \frac{e^{K_{ji}}}{{\displaystyle \sum _{1\le i\le n}{e}^{K_{ji}}}}}$$

(28)

Because the exponential function $e^x$ is monotonously increasing, the greater the value of $K_{ji}$, the greater the $m_i\left({\theta }_j\right)$, and the smaller the $K_{ji}$, the smaller the $m_i\left({\theta }_j\right)$, and $0\le m_i\left({\theta }_j\right)\le 1$.

2.3.4. Fusion Algorithm Based on Combination Weights

Suppose there are $n$ evaluation indexes for a certain object to be evaluated. Among them, the weight of the $i$th evaluation index is $w_i^{\ast }$, ($i=1,2,\cdots ,n$). Then, the weight vector of the BBAs provided by all evaluation indexes is $W^{\ast }=\left[w_1^{\ast },w_2^{\ast },\cdots w_n^{\ast }\right]$, and if $w_g^{\ast }=\max \left\{w_1^{\ast },w_2^{\ast },\cdots w_n^{\ast }\right\}$, $W^l=\left[w_1^{\ast },w_2^{\ast },\cdots w_n^{\ast }\right]/w_g^{\ast }$. Thus, it is determined that the relative importance of a BBA in all BBAs is defined as

$${\beta }_i={\displaystyle \frac{w_i^{\ast }}{w_g^{\ast }}}$$

(29)

${\beta }_i$ is called the quantity weight, and as a discount coefficient to adjust the BBA of each evaluation index, the adjusted equation is defined as

$$m_i^{\ast }({\theta }_j)=\left\{\begin{array}{cc}{\beta }_i{m}_i({\theta }_j)& {\theta }_j\ne \Theta \\ 1-{\displaystyle \sum _{1\le j\le \overline{m}}{m}_i^{\ast }({\theta }_j)}& {\theta }_j=\Theta \end{array}\right.$$

(30)

The modified BBA $m_i^{\ast }({\theta }_j)$ is used to form the BBA matrix, and the fusion algorithm based on matrix analysis is applied to obtain the evidence fusion result. The evaluation results of the object to be evaluated are judged according to the maximum membership degree principle.

3. Preparation Work for Water-Hazard Risk Evaluation

3.1. Constructing Evaluation Index System

The construction of a coal-mine water-hazard risk-evaluation index system should be comprehensive and scientific in order to ensure the reliability and accuracy of the evaluation results. Referring to the relevant data [31,32,33,34,49,50,51], the overall structure of the coal-mine water-hazard risk-evaluation index system is established. The mine hazard risk-evaluation index system is divided into a target layer, a first-level index and a second-level index. Taking coal-mine water-hazard risk evaluation as the target layer, according to the accident cause theory, the factors causing accidents can be summarized into four kinds of factors: human, machine, environment and management. That is, personnel factors, equipment factors, environmental factors and management factors are the necessary causes of accidents. According to the energy convergence theory, these four kinds of factors appearing at the same time will eventually lead to the occurrence of the accident. Combined with the characteristics of water hazards in coal mine, five aspects of these four types of factors are taken as first-level indexes, including personnel factors, drainage factors, water filling-source factors, water diversion-channel factors and management factors. Then, 21 coal-mine water-hazard influencing factors supporting first-level indexes are selected as second-level indexes to evaluate the grade of coal-mine water-hazard risk. The specific contents of the evaluation index system are shown in

Table 2. Index system of coal-mine water-hazard risk evaluation.

Target Layer	First-Level Indexes	Second-Level Indexes
Coal-mine water-hazard risk evaluation	Personnel factors B1	Professional skill level of personnel c1
		Personnel training and education c2
		Personnel “three violations” rate c3
		Physical and psychological status of personnel c4
	Drainage factors B2	Surface waterproofing and drainage engineering c5
		Waterproof coal pillar and waterproof gate c6
		Water silos, pumps and drainage pipes c7
		Power supply lines and equipment c8
	Water filling-source factors B3	Atmospheric precipitation c9
		Surface water c10
		Ground water c11
		Old goaf water c12
	Water diversion-channel factors B4	Structural fault zone channel c13
		Mining fracture zone passage c14
		Artificial engineering passageway c15
		Other types of water diversion channels c16
	Management factors B5	Standard degree of basic hydrogeological data c17
		Perfection and implementation of rules and regulations c18
		Inspection and maintenance management of equipment c19
		Flood rectification and improvement c20
		Accident emergency rescue capability c21

.

3.2. Grading Standard for Evaluation Indexes

Using the relevant standard of coal-mine hazard risk classification [31,32,33,34], the coal-mine hazard risk is divided into five evaluation grades, namely, I, II, III, IV, and V, corresponding to lower risk, low risk, medium risk, high risk and higher risk, respectively. Different risk grades are assigned different characteristics, and at the same time, the scoring range of risk grades is provided as a reference for evaluation. The evaluation standard of each index is shown in

Table 3. Evaluation standard.

Risk Grades	Risk Evaluation	Grade Characteristics	Score Range
I	lower risk	Safety, normal production	[90,100]
II	low risk	Improving risk defense	[80,89]
III	medium risk	Strictly monitoring the risk to avoid rising	[70,79]
IV	high risk	Suggesting carrying out rectification and reform	[60,69]
V	higher risk	Stop production immediately and take measures to reduce risk	[0,59]

.

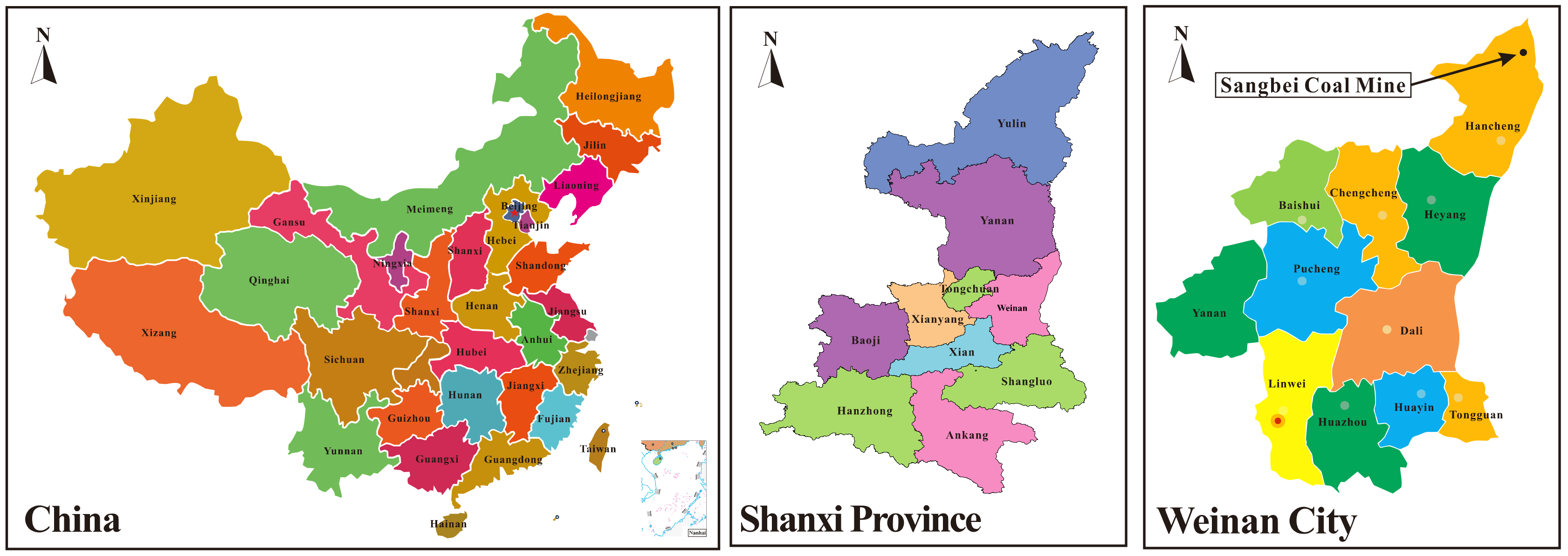
3.3. Project Overview

Sangbei Coal Mine is located in the northeast of Hancheng City, Shaanxi Province, China, and the location is shown in Figure 1. The designed production capacity of the mine is 1.8 million t/a, and the hydrogeological type of the mine is complex. Groundwater aquifer rock groups in the mining area can be divided into nine aquifer rock groups according to burial conditions; these constitute the main water filling source of the mine. At present, the normal water inflow of the mine is 150 m³/h, and the maximum water inflow is 270 m³/h. Three-dimensional seismic interpretation of the mine displays a total of 89 fault lines and 12 collapsed columns, which constitute a natural water diversion channel. At present, the No. 3 coal seam is mined in this mine, and the average thickness is 5.47 m. The mining of the thick coal seam has caused damage to the roof and floor, forming a mining fracture, which constitutes an artificial water diversion channel. Because the floor elevation of the No. 3 coal seam is lower than that of the Ordovician limestone karst water level, it belongs to pressure mining under the Ordovician limestone karst water level. When it is located in the area of structural development and the waterproof layer of the floor is damaged by structure, or there is a vertical water diversion channel, coal seam mining may cause Ordovician limestone water outburst and the hidden danger of mine water inrush. According to the investigation, there have been water inrush accidents in adjacent mines. In 1975, Xiangshan Coal Mine experienced a water inrush of 414 m³/h; in 1976, Sangshuping Coal Mine experienced a water inrush of 1530 m³/h; and in 1976, Magouqu Coal Mine experienced a water inrush with a maximum water inrush of 12,000 m³/h and an average water inflow of 5956 m³/h. This resulted in a water inrush accident in the well.

3.4. Determining the Value of Evaluation Indexes

Five experts from universities, design institutes and coal mines were invited to form a safety diagnosis expert group to conduct a field investigation in Sangbei Coal Mine. According to their own understanding of the actual situation of coal-mine water-hazard prevention and control, experts gave scores of 21 water-hazard evaluation indexes according to Table 3. The same weight was given to each expert, and the final scores are shown in

Table 4. Scores of evaluation indexes.

Evaluation Indexes	c1	c2	c3	c4	c5	c6	c7	c8	c9	c10	c11
Scores	81.8	82.8	86.8	87.8	87	88.6	87.4	86.6	85.4	84	82.6
Evaluation indexes	c12	c13	c14	c15	c16	c17	c18	c19	c20	c21	——
Scores	91.2	81.6	80.8	81	85.2	84.2	79.6	82.4	84.4	83.6	——

.

4. Application of Evaluation Methods

4.1. Establishing Extension Model

(1)

Determining the classical domain, node domain and matter element to be evaluated.

According to Table 3 and Equation (1), the classical domains matter-element $R_j$ related to water-hazard risk evaluation is determined, ($j=1,2,\cdots 5$).

$$\begin{array}{ccc}{R}_1=\left[\begin{array}{ccc}{N}_1& c_1& \left[90,100\right]\\ & c_2& \left[90,100\right]\\ & ⋮& ⋮\\ & c_{21}& \left[90,100\right]\end{array}\right],& R_2=\left[\begin{array}{ccc}{N}_2& c_1& \left[80,89\right]\\ & c_2& \left[80,89\right]\\ & ⋮& ⋮\\ & c_{21}& \left[80,89\right]\end{array}\right],& R_3=\left[\begin{array}{ccc}{N}_3& c_1& \left[70,79\right]\\ & c_2& \left[70,79\right]\\ & ⋮& ⋮\\ & c_{21}& \left[70,79\right]\end{array}\right],\\ R_4=\left[\begin{array}{ccc}{N}_4& c_1& \left[60,69\right]\\ & c_2& \left[60,69\right]\\ & ⋮& ⋮\\ & c_{21}& \left[60,69\right]\end{array}\right],& R_5=\left[\begin{array}{ccc}{N}_5& c_1& \left[0,59\right]\\ & c_2& \left[0,59\right]\\ & ⋮& ⋮\\ & c_{21}& \left[0,59\right]\end{array}\right],& \end{array}$$

The nodal domain matter-element $R_p$ of water-hazard risk evaluation is determined by Equation (2).

$$R_p=\left[\begin{array}{ccc}{N}_p& c_1& \left[0,100\right]\\ & c_2& \left[0,100\right]\\ & ⋮& ⋮\\ & c_{21}& \left[0,100\right]\end{array}\right]$$

The matter-element $R_0$ to be evaluated for water-hazard risk evaluation is determined by Equation (3).

$$R_0=\left[\begin{array}{ccc}{N}_0& c_1& 81.8\\ & c_2& 82.8\\ & ⋮& ⋮\\ & c_{21}& 83.6\end{array}\right]$$

(2)

Calculating correlation degrees.

According to Equation (4), correlation degrees of 21 evaluation indexes with respect to five hazard risk grades are calculated, and the results are shown in

Table 5. Evaluation index grades’ correlation degrees.

Evaluation Indexes	I Grade Risk	II Grade Risk	III Grade Risk	IV Grade Risk	V Grade Risk
c1	−0.3106	0.2000	−0.1333	−0.4129	−0.5561
c2	−0.2951	0.3111	−0.1810	−0.4452	−0.5805
c3	−0.1951	0.2444	−0.3714	−0.5742	−0.6780
c4	−0.1528	0.1333	−0.4190	−0.6065	−0.7024
c5	−0.1875	0.2222	−0.3810	−0.5806	−0.6829
c6	−0.1094	0.0444	−0.4571	−0.6323	−0.7220
c7	−0.1711	0.1778	−0.4000	−0.5935	−0.6927
c8	−0.2024	0.2667	−0.3619	−0.5677	−0.6732
c9	−0.2396	0.4000	−0.3048	−0.5290	−0.6439
c10	−0.2727	0.4444	−0.2381	−0.4839	−0.6098
c11	−0.2984	0.2889	−0.1714	−0.4387	−0.5756
c12	0.1200	−0.2000	−0.5810	−0.7161	−0.7854
c13	−0.3134	0.1778	−0.1238	−0.4065	−0.5512
c14	−0.3239	0.0889	−0.0857	−0.3806	−0.5317
c15	−0.3214	0.1111	−0.0952	−0.3871	−0.5366
c16	−0.2449	0.4222	−0.2952	−0.5226	−0.6390
c17	−0.2685	0.4667	−0.2476	−0.4903	−0.6146
c18	−0.3377	−0.0192	−0.0286	−0.3419	−0.5024
c19	−0.3016	0.2667	−0.1619	−0.4323	−0.5707
c20	−0.2642	0.4889	−0.2571	−0.4968	−0.6195
c21	−0.2807	0.4000	−0.2190	−0.4710	−0.6000

.

4.2. Calculating Combination Weights

The subjective weight is calculated by the G1 method. The order relation and importance ratio between indexes are obtained by the expert group’s rational judgment of evaluation indexes, and the subjective weight $W^{\left(1\right)}$ is obtained by Equations (5)~(8). $w_i^{(1)}$ is shown in

Table 6. Weights and ranking of evaluation indexes.

Evaluation Indexes	${\mathit{W}}^{\left(1\right)}$	${\mathit{W}}^{\left(2\right)}$	${\mathit{W}}^{\ast }$	${\mathit{W}}^{\mathit{l}}$	Ranking of Importance
c1	0.0357	0.0558	0.0449	0.4369	9
c2	0.0297	0.0318	0.0307	0.2984	18
c3	0.0815	0.0326	0.0591	0.5745	6
c4	0.0153	0.0514	0.0318	0.3095	15
c5	0.0203	0.0378	0.0283	0.2755	19
c6	0.0270	0.0365	0.0314	0.3051	16
c7	0.0570	0.0347	0.0468	0.4547	7
c8	0.0518	0.0313	0.0424	0.4123	10
c9	0.0139	0.0591	0.0346	0.3367	12
c10	0.0224	0.0463	0.0333	0.3242	14
c11	0.1194	0.0834	0.1028	1.0000	1
c12	0.0126	0.0386	0.0245	0.2387	21
c13	0.1085	0.0843	0.0974	0.9470	2
c14	0.0987	0.0498	0.0762	0.7414	3
c15	0.0185	0.0345	0.0259	0.2514	20
c16	0.0246	0.0463	0.0346	0.3360	13
c17	0.0168	0.0475	0.0309	0.3004	17
c18	0.0741	0.0595	0.0674	0.6554	5
c19	0.0432	0.0378	0.0407	0.3959	11
c20	0.0897	0.0466	0.0699	0.6798	4
c21	0.0393	0.0545	0.0463	0.4499	8

. Based on the scores of experts, the objective weight is calculated by the EW method, and characteristic proportion and entropy value of each index are calculated by Equations (9)~(13). The objective weight $W^{\left(2\right)}$ is obtained, and $w_i^{(2)}$ is shown in Table 6. The subjective weight $W^{\left(1\right)}$ and the objective weight $W^{\left(2\right)}$ are calculated by Equation (19) to obtain ${\alpha }_1^{\ast }$ = 0.5410 and ${\alpha }_2^{\ast }$ = 0.4590, and the combination weight $W^{\ast }$ is calculated by Equation (20). The results based on ICWMGT are shown in Table 6. We can obtain $w_g^{\ast }$ = 0.1028, $W^l$ is obtained by Equation (29), and ${\beta }_i$ is shown in Table 6.

The results of ICWMGT weighting, subjective weighting and objective weighting are compared in Figure 2, and it can be seen that the fluctuation of weights obtained by the G1 weighting method is relatively large, while the fluctuation of weights obtained by the EWD weighting method is relatively small. The fluctuation of weights obtained by ICWMGT is between the two. So, ICWMGT weighting is more practical and can better reflect the impact of various indexes on coal-mine hazard risk at the same time. If the cumulative percentage of evaluation indexes is 0~80%, these are called the controlling factors [33]. Then, 14 evaluation indexes, $c_1$, $c_3$, $c_7$, $c_8$, $c_9$, $c_{10}$, $c_{11}$, $c_{13}$, $c_{14}$, $c_{16}$, $c_{18}$, $c_{19}$, $c_{20}$ and $c_{21}$, account for 79.64% of the total weight. Therefore, these 14 evaluation indexes are the main controlling factors of the water-hazard risk grade of the mine, which is also the basis and starting point for the mine to carry out water-hazard prevention and control and reduce the water-hazard risk grade.

4.3. Determining Risk Grade

According to the risk classification in Table 3, coal-mine hazard-risk grade recognition framework $\Theta =\left\{{\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4,{\theta }_5\right\}$ based on DS evidence theory is established. In the recognition framework, ${\theta }_j$ indicates the coal-mine water-hazard risk-evaluation grade, ($j=1,2,\cdots ,5$). Then, BBA functions based on $\Theta$ are $m_1$~$m_{21}$. Based on Table 5, using Equation (28), we can realize the transformation between the correlation degree and the BBA. Taking the quantity weight as the discount coefficient, BBAs are modified by Equation (30) based on Table 6, and then the modified BBAs of water-disaster risk evaluation are calculated as shown in

Table 7. The modified BBAs.

Evaluation Indexes	${\mathit{m}}_{\mathit{i}}^{\ast }({\mathit{\theta }}_1)$	${\mathit{m}}_{\mathit{i}}^{\ast }({\mathit{\theta }}_2)$	${\mathit{m}}_{\mathit{i}}^{\ast }({\mathit{\theta }}_3)$	${\mathit{m}}_{\mathit{i}}^{\ast }({\mathit{\theta }}_4)$	${\mathit{m}}_{\mathit{i}}^{\ast }({\mathit{\theta }}_5)$	${\mathit{m}}_{\mathit{i}}^{\ast }(\mathbf{\Theta })$
c1	0.0788	0.1313	0.0941	0.0711	0.0616	0.5631
c2	0.0536	0.0983	0.0601	0.0461	0.0403	0.7016
c3	0.1224	0.1900	0.1027	0.0838	0.0755	0.4255
c4	0.0718	0.0956	0.0550	0.0456	0.0414	0.6905
c5	0.0597	0.0899	0.0492	0.0403	0.0364	0.7245
c6	0.0761	0.0888	0.0538	0.0451	0.0413	0.6949
c7	0.1019	0.1445	0.0811	0.0668	0.0605	0.5453
c8	0.0864	0.1382	0.0737	0.0600	0.0540	0.5877
c9	0.0641	0.1216	0.0601	0.0480	0.0428	0.6633
c10	0.0578	0.1184	0.0599	0.0468	0.0413	0.6758
c11	0.1798	0.3235	0.2042	0.1563	0.1363	0.0000
c12	0.0780	0.0566	0.0387	0.0338	0.0315	0.7613
c13	0.1709	0.2792	0.2065	0.1557	0.1347	0.0530
c14	0.1339	0.2023	0.1699	0.1265	0.1088	0.2586
c15	0.0454	0.0700	0.0569	0.0425	0.0366	0.7486
c16	0.0630	0.1228	0.0599	0.0477	0.0425	0.6640
c17	0.0535	0.1116	0.0546	0.0429	0.0378	0.6996
c18	0.1174	0.1615	0.1600	0.1169	0.0996	0.3446
c19	0.0712	0.1258	0.0819	0.0625	0.0544	0.6041
c20	0.1209	0.2567	0.1217	0.0958	0.0847	0.3202
c21	0.0805	0.1589	0.0856	0.0665	0.0585	0.5501

Note: $i=1,2,\cdots ,21$, $m_i^{\ast }({\theta }_1)$ represents the BBA between the index $c_i$ and I grade risk.

.

As a result, the risk grade of each evaluation index can be determined, as shown in Figure 3. It can be seen that except the index $c_{12}$ being of the I grade risk, all the indexes are the II grade risk. It can be seen that the distribution of risk BBAs of indexes $c_{11}$, $c_{13}$, $c_{20}$, $c_{14}$, $c_3$, $c_{18}$, $c_{21}$, $c_7$, $c_8$, $c_1$, $c_{19}$, $c_{16}$, $c_9$, $c_{10}$, $c_{17}$, $c_2$, $c_4$, $c_5$, $c_6$, and $c_{15}$ gradually decreased. That is, the II grade risk of $c_{11}$ is the most prominent, which is the key index of water-hazard prevention and control, followed by other indexes.

Suppose $M_1^{\ast }$ is defined as $m_1^{\ast }\oplus m_2^{\ast }\oplus m_3^{\ast }\oplus m_4^{\ast }$, $M_2^{\ast }$ is defined as $m_5^{\ast }\oplus m_6^{\ast }\oplus m_7^{\ast }\oplus m_8^{\ast }$, $M_3^{\ast }$ is defined as $m_9^{\ast }\oplus m_{10}^{\ast }\oplus m_{11}^{\ast }\oplus m_{12}^{\ast }$, $M_4^{\ast }$ is defined as $m_{13}^{\ast }\oplus m_{14}^{\ast }\oplus m_{15}^{\ast }\oplus m_{16}^{\ast }$, and $M_5^{\ast }$ is defined as $m_{17}^{\ast }\oplus m_{18}^{\ast }\oplus m_{19}^{\ast }\oplus m_{20}^{\ast }\oplus m_{21}^{\ast }$, the BBA fusion results of the indexes of second-level are shown in

Table 8. Fusion results of second-level indexes.

Evaluation Indexes	${\mathit{M}}_{\mathit{k}}^{\ast }({\mathit{\theta }}_1)$	${\mathit{M}}_{\mathit{k}}^{\ast }({\mathit{\theta }}_2)$	${\mathit{M}}_{\mathit{k}}^{\ast }({\mathit{\theta }}_3)$	${\mathit{M}}_{\mathit{k}}^{\ast }({\mathit{\theta }}_4)$	${\mathit{M}}_{\mathit{k}}^{\ast }({\mathit{\theta }}_5)$	${\mathit{M}}_{\mathit{k}}^{\ast }(\mathbf{\Theta })$
B1	0.1566	0.2767	0.1468	0.1119	0.0977	0.2104
B2	0.1653	0.2552	0.1268	0.1017	0.0909	0.2602
B3	0.1786	0.3658	0.1927	0.1416	0.1213	0.0000
B4	0.1623	0.3395	0.2146	0.1421	0.1163	0.0252
B5	0.1468	0.3584	0.1764	0.1218	0.1017	0.0949

Note: $k=1,2,\cdots ,5$, $M_k^{\ast }({\theta }_1)$ represents the BBA between the index $B_k$ and I grade risk.

.

The risk grades of first-level indexes can be determined as shown in Figure 4. It can be seen that the BBAs of first-level indexes are obtained from the BBA fusion of second-level indexes, and the maximum value of the BBAs is obviously improved, so it is easier to judge the risk grades of first-level indexes, all of which are II grade risk. The II grade risk of indexes $B_3$, $B_4$ and $B_5$ is relatively certain, but it can also be seen that these three first-level indexes also have potential safety risks, and there is a tendency towards the III grade risk. In particular, the hidden danger of the index $B_4$ is more prominent. Combined with Figure 3, we can note that among four indexes, $c_{13}$, $c_{14}$ and $c_{15}$ are supporting index $B_4$ and are all of II grade risk. Combined with Table 6 for further analysis, we can see that the ranking of the impact weights of indexes $c_{13}$ and $c_{14}$ is second and third, respectively. Both of them are the main controlling factors of water-hazard risk. This is the main starting point and basis for improving the risk grade of the index $B_4$. The indexes $c_{11}$ and $c_{10}$, supporting the index $B_3$, are also classified as II grade risk and have a tendency towards III grade risk. The impact weights of these two indexes are ranked first and fourteenth, and both belong to the main controlling factors of water-hazard risk. The impact of the index $c_{11}$ is particularly prominent. Five indexes, $c_{17}$, $c_{18}$, $c_{19}$, $c_{20}$ and $c_{21}$, supporting the index $B_5$ are all the II grade risk. Due to the ranking of the impact weights of indexes $c_{20}$, $c_{18}$ and $c_{21}$ as fourth, fifth, and eighth, respectively, these three indexes are also the main controlling factors of water-hazard risk. Therefore, in order to reduce the risk grade of indexes $B_3$, $B_4$, and $B_5$, further water-hazard risk-control work should be carried out on the above seven indexes first, in order to achieve significant water-hazard prevention and control effects. Although the II grade risk of indexes $B_1$ and $B_2$ are relatively certain, they have a tendency towards the I grade risk. The reason for this is that the coal mine has performed well in these two aspects and has received unanimous recognition from experts. As the index $c_1$ is the II grade risk and also a major control factor, the mining company should further improve the technical level of personnel, while the other three major control factors of $c_3$, $c_7$ and $c_8$ should continue to be maintained and continuously improved to achieve the I grade risk. Although the index $c_2$ is not the main controlling factor, it should also be noted by the mining company, and personnel training and education should be further improved.

Suppose $M_1^{\ast \ast }$ is defined as $M_1^{\ast }\oplus M_2^{\ast }$, $M_2^{\ast \ast }$ is defined as $M_1^{\ast \ast }\oplus M_3^{\ast }$, $M_3^{\ast \ast }$ is defined as $M_2^{\ast \ast }\oplus M_4^{\ast }$, and $M_4^{\ast \ast }$ is defined as $M_3^{\ast \ast }\oplus M_5^{\ast }$. Furthermore, the BBA fusion results of first-level indexes are shown in

Table 9. Fusion results of first-level indexes.

Fusion Frequency	${\mathit{M}}_{\mathit{k}}^{\ast \ast }({\mathit{\theta }}_1)$	${\mathit{M}}_{\mathit{k}}^{\ast \ast }({\mathit{\theta }}_2)$	${\mathit{M}}_{\mathit{k}}^{\ast \ast }({\mathit{\theta }}_3)$	${\mathit{M}}_{\mathit{k}}^{\ast \ast }({\mathit{\theta }}_4)$	${\mathit{M}}_{\mathit{k}}^{\ast \ast }({\mathit{\theta }}_5)$	${\mathit{M}}_{\mathit{k}}^{\ast \ast }\left(\mathbf{\Theta }\right)$
1	0.1839	0.3561	0.1515	0.1122	0.0969	0.0993
2	0.1584	0.5217	0.1514	0.0938	0.0746	0.0000
3	0.1052	0.6734	0.1285	0.0556	0.0373	0.0000
4	0.0660	0.7930	0.0906	0.0313	0.0191	0.0000

Note: $k=1,2,\cdots ,4$, $M_k^{\ast \ast }({\theta }_1)$ represents the BBA for I grade risk after the $k$th fusion.

.

The maximum BBA of the fusion results is 0.7930; it can be determined that the water hazard of Sangbei Coal Mine is the II grade risk, corresponding to low risk. The investigation is in line with the current situation of water-hazard prevention and control in the mine. Although the hydrogeological conditions of Sangbei Coal Mine are complex, the current working face has not yet entered the mining area with pressure, so the risk of safety production being affected by highly confined water is low. Due to the good performance of water prevention equipment, water control management and water prevention staff in the mine, this is also one of the main reasons why Sangbei Coal Mine is the II grade water-hazard risk. Because the water diversion channel is one of the main hazard factors causing water inrush in coal mines, Sangbei Coal Mine should strengthen the detailed exploration of underground structures, accurately locate and control fault structures, study the failure law of roofs and floors, and master the development of the roof fracture zones and floor failure depths of mining faces. For water filling sources, Sangbei Coal Mine should establish and improve the water source database and strengthen the prediction of water filling sources. The prediction of water filling sources is economical and reasonable, which is also the basic premise of waterproofing work.

5. Discussion

(1)

The traditional combinatorial weighting method of game theory cannot ensure that the linear combination coefficient is greater than 0. Here, the traditional game theory is used for combination weighting by Equation (16), and the coefficient calculation result is ${\alpha }_1$ = 1.0537, ${\alpha }_2$ = −0.0718. It can be seen that coefficient ${\alpha }_2$ is negative, so it is contradictory to the hypothesis. This also greatly limits the application scope of game theory, and according to the ICWMGT, we cannot only ensure that the parameter is non-negative; rather, we must also achieve the goal of game theory. Therefore, the ICWMGT has more scientific and extensive application prospects.

(2)

The BBA fusion is directly carried out by Equation (22), and the time required for calculation is T(6²¹). If there is an increase in the number of indexes, the time required will increase exponentially—it can cause “focal element explosion”. In order to solve this problem, a fusion algorithm based on matrix analysis can greatly improve the computational efficiency, and the whole calculation time is T(20 × 6²). As a result, the complexity of time is reduced from the original exponential level to the polynomial level, and there is an obvious difference between them in the number of operations and amount of operation time.

(3)

The extension theory can solve the problem of the incompatibility of various features of things, DS evidence theory can better deal with the combination of fuzzy and uncertain information, and the description of uncertain problems is closer to people’s habits of thinking. The organic combination of extension theory and DS evidence theory can improve the accuracy of risk evaluation. Based on the combination weights obtained in this paper, the expert scoring method [31], fuzzy comprehensive evaluation method [33], and extension evaluation method [52] were used to evaluate the coal-mine hazard risk, respectively, to further verify the accuracy of the evaluation results in this paper. The expert scoring method was used to obtain an evaluation score of 83.8, which is a II grade risk. The fuzzy comprehensive evaluation method was used to obtain an evaluation score of 85.48, which is a II grade risk. The comprehensive correlation degrees of each risk grade obtained using the extension method are −0.2566, 0.2362, −0.2319, −0.4797, and −0.6066, respectively. Therefore, the highest correlation degree with a II grade risk is 0.2362. All of these results are consistent with the evaluation result obtained in this paper, but it can be seen that the method used in this paper is more scientifically reasonable. The expert scoring method calculates the sum of the product of each index’ score and its weight to obtain the evaluation result; although it is simple and practical, it cannot reflect the unknown uncertainty and incompatibility in the evaluation process, and it is also unable to further explore the potential intrinsic information, such as the degree of membership between various indexes and risk grades. The membership degree calculation process of the fuzzy evaluation method fails to fully utilize expert scoring results, which makes it difficult to comprehensively reflect the risk membership degree of each index, and the synthesized algorithm needs further exploration. The extension method can only solve the problem of incompatible features of things, but it cannot effectively handle uncertain information. Therefore, the reasoning process of the three methods mentioned above is not as rigorous as the method proposed in this paper.

6. Conclusions

In response to the shortcomings of current coal-mine water-hazard risk-evaluation models and methods, a risk evaluation method based on extension theory, game theory and DS evidence theory is put forward. Based on the accident cause theory, the evaluation index system and risk-evaluation grade of coal-mine water-hazard risk are established. Based on the concepts of matter elements and correlation function, the relationship between the evaluation index of coal-mine water-hazard risk and each risk-evaluation grade is quantified and normalized, so as to obtain the BBA of the evaluation index. The objectivity of obtaining the BBA is improved. This paper improves the game theory and puts forward the ICWMGT, and it can avoid the weight deviation that may be caused by the single weighting method in the process of weight calculation. Based on the combination weights, the BBAs of evaluation indexes are modified, and a fusion algorithm based on combination weights is used to fuse the modified BBAs, which can reduce the uncertainty in the evaluation process and obtain results from coal-mine hazard risk evaluation. The grade of coal-mine water-hazard risk is consistent with the actual situation of coal mines, and the evaluation results are verified by another three methods at the same time. The main conclusions in this paper are as follows:

(1)

The ICWMGT was used to optimize the combination of the G1 method weighting results and the EW method weighting results, with Nash equilibrium as the coordination objective. This can balance the conflicts between them and obtain the optimal weighting combination that takes into account the characteristics of different weighting methods. This overcomes the uncertainty and one-sidedness of the single weighting method in the decision-making process and improves the scientific rationality of index weighting. According to the calculation results of ICWMGT, the importance ranking of 21 evaluation indexes had been determined, and 14 evaluation indexes could be identified as the control factors for coal-mine water-hazard risk. This was the basis and starting point for the mine to carry out water-hazard prevention and control and reduce the water-hazard risk grade.

(2)

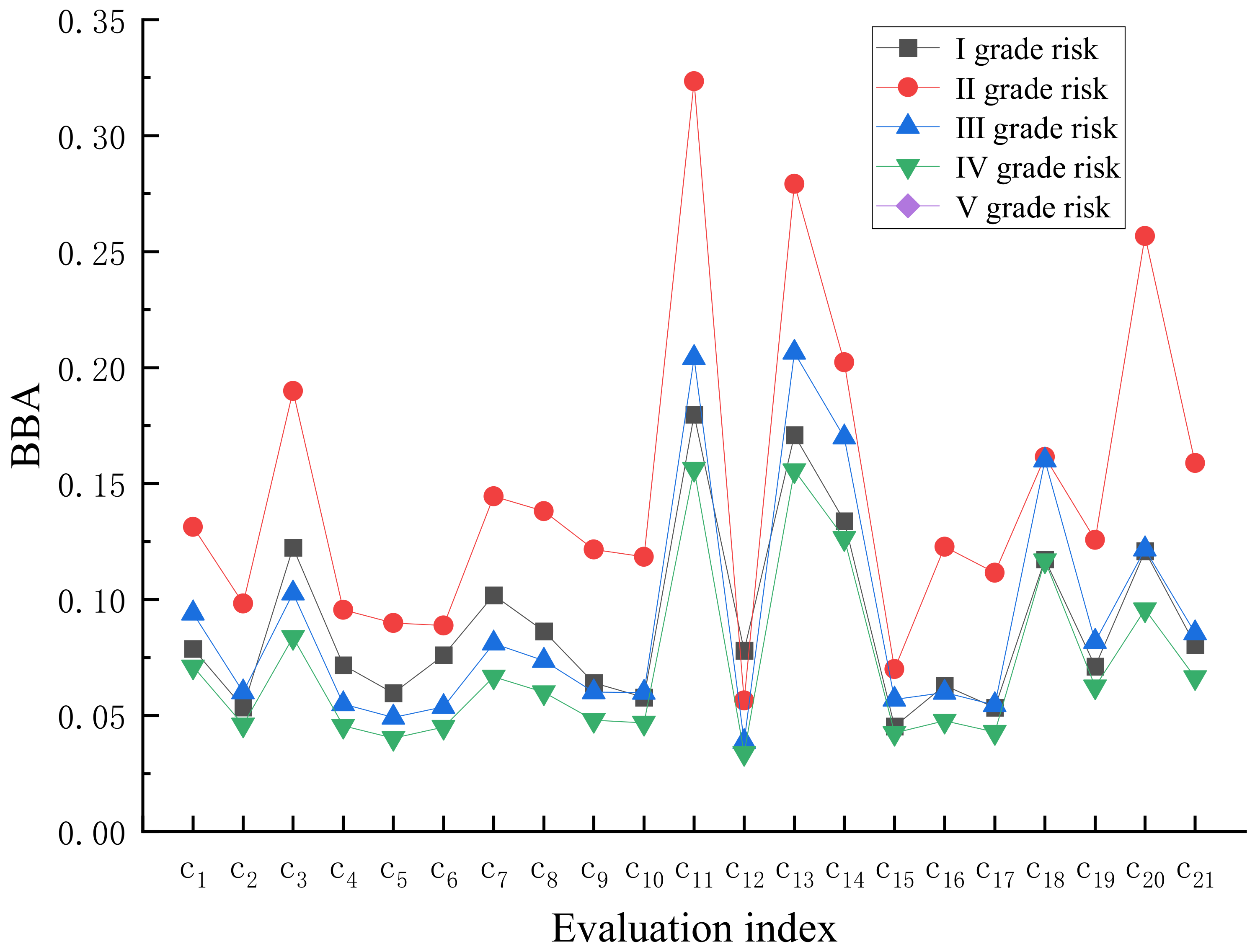
Based on extension theory, the classical domain, section domain, and evaluated object elements of coal-mine water-hazard risk evaluation were determined. The correlation degree of 21 evaluation indexes for coal-mine water-hazard risk evaluation with respect to five water-hazard risk grades was calculated according to the correlation function. The obtained comprehensive correlation degree was equivalently transformed and normalized using the $e^x$ function to obtain the BBA on the evidence theory recognition framework. The BBA was modified by ICWMGT weighting results. Based on the fusion of DS evidence theory, the risk grades of various primary indicators were determined. Based on the weighting results of ICWMGT and the BBAs results of secondary indexes, it was found that 11 secondary indexes were the focus of coal-mine water-hazard risk prevention and control, among which seven indexes were the primary starting point for coal-mine water-hazard risk prevention and control—especially the groundwater index, which had the most prominent impact.

(3)

The water-hazard risk of Sangbei Coal Mine was the II grade, and the results were consistent with the hydrogeological conditions of the mine. Based on this result, the expert scoring method, fuzzy comprehensive evaluation method, and extension evaluation method were used to evaluate the risk of coal-mine water hazard, respectively, to further verify the accuracy of the evaluation results in this paper. Through comparison, it was found that the method used in this paper is scientifically reasonable. At the same time, the ICWMGT proposed in this paper can overcome the disadvantage of the traditional game theory weighting method that may obtain negative coefficients. The fusion algorithm based on matrix analysis can reduce the complexity of computation time from the exponential level to the polynomial level, greatly improving computational efficiency, and the description of uncertain problems is closer to human thinking habits. Thus, the method proposed in this paper has certain promotion and application value, and it can also be evaluated and applied in other fields.