Abstract
The use of green roofs, a low-impact development practice, can be an effective means of reducing direct runoff in urban centers. Green roof modeling can enable efficient design by preliminarily grasping the behavior of the green roof system according to specific configurations. In this study, we aimed to find appropriate evapotranspiration and parameter optimization schemes for HYDRUS-1D, a commonly used modeling tool for green roofs. Comparative studies of this sort in the context of green roof runoff modeling have not been conducted previously and are important in guiding users to overcome the difficulties of choosing the right numerical schemes for an accurate prediction of runoff from a green roof. As a study site, the Portland Building Ecoroof in Portland, Oregon, USA, was chosen, as green roof configurations and observed data for climate and runoff were available. From the simulation results of the runoff volume, the Blaney–Criddle method, which was considered an alternative, was found to be appropriate for calculating evapotranspiration from a green roof (R2 = 0.82) relative to the Hargreaves method built in HYDRUS-1D (R2 = 0.46). In addition, this study showed that the optimization method using the harmony search algorithm, which was proposed as an alternative optimizer, was better (R2 = 0.95) than that of the HYDRUS-1D’s own optimization module (R2 = 0.82) in calibrating HYDRUS-1D for green roof runoff. The findings are thought to be useful in guiding modelers who are considering using HYDRUS-1D for green roof runoff simulations.
1. Introduction
The increase in the impervious area of the watershed due to urbanization causes a decrease in soil infiltration, an increase in direct runoff and flood peak, and an increase in nonpoint source pollution, thereby distorting the water circulation system. As an alternative measure to this, low-impact development (LID) practices, eco-friendly plans to efficiently manage urban stormwater by infiltrating and storing rainwater, have been proposed. As technical measures of the LID practices, vegetation reservoirs, water permeable pavement, retention ponds, grassed swales, rainwater tanks, constructed wetlands, and green roofs have been developed and applied. Among them, the term green roof refers to the greening of buildings so that plants can grow on the roof of a building.
It is often difficult to secure green spaces in a city center that has already been developed, but utilizing green roofs is a practice that makes it possible to create green spaces in the urban core. Green roofs are generally divided into the following four layers: the drainage layer, a filter that prevents the soil losses, the substrate layer, and vegetation [1]. Green roofs have various application effects such as mitigating stormwater and heat island phenomena, saving energy for cooling and heating in buildings, and improving urban landscapes. Thanks to the advantages of green roofs, interest in the application of green roofs has been increasing domestically and internationally. Studies on monitoring changes in the quantity and quality of runoff water according to the installation of a green roof [2,3] and modeling studies to predict and evaluate the stormwater reduction efficiency [4,5,6] have also been widely carried out.
Models commonly employed to simulate green roofs are EPA’s SWMM, SWMS-2D SWAP and HYDRUS [7]. Among them, HYDRUS is a soil physics model for simulating the movement of water, heat, and solutes in porous media with various dimensions and shapes [8]. Several studies have been conducted on the modeling of the runoff response of green roofs using HYDRUS [4,8,9,10,11,12].
Hilten [4] carried out pioneering work in the USA that used HYDRUS-1D for green roof runoff simulations and showcased its capability for the first time. Similar efforts were continued in Hawaii, USA, by Li and Babcock [8] to derive practical regression equations that predict the hydrologic performance of green roofs to be used for design purposes. More recently, Yang and Davidson [11] have studied the aging effect of green roofs in the USA and found improvements in retention and detention performance with aging, showing that HYDRUS-1D can replicate the conditions.
In other parts of the world, Fietosa and Wilkinson [9] studied stormwater response regarding green roofs in New Zealand for different depths using HYDRUS-1D. Peczkowski et al. [10] investigated the efficiency of runoff reduction by green roofs in Poland for variable substrate thicknesses using HYDRUS-1D. Wang et al. [12] explored the hydrological response of green roofs in the USA with different capacities in regard to water storage layers and water storage on the soil surface through simulated rainfall experiments and HYDRUS-1D. Research around the world was seen to be maturing, accounting for various aspects of green roofs in mitigating stormwater runoff.
Many factors influence the capacity of green roofs to reduce urban runoff, such as evaporation and transpiration, initial moisture conditions, rainfall intensity, and the hydraulic properties of the soils. Of these factors, evapotranspiration is an important mechanism for soil moisture removal in regard to restoring its retention capacity [13]. HYDRUS-1D allows users to input evapotranspiration estimates that have been pre-determined outside [9]. Therefore, users are faced with the difficulty of choosing a particular evapotranspiration method. However, there is no study on the comparison of possible estimation methods for evapotranspiration from green roofs.
Estimating the parameters of the model is another essential task in accurately simulating the effectiveness of green roofs prior to installation [4]. Since the HYDRUS-1D model itself includes an optimization module for hydraulic parameters (, many studies using this module [14,15,16] have been performed. However, its performance was not compared against other competitive optimization schemes for alternative considerations. According to the foregoing discussions, major difficulties and challenges for the modeler’s considering HYDRUS include finding a way to account for the important loss mechanisms of evapotranspiration from green roofs and, also, establishing how model parameters can be fitted. In this study, we aimed to find appropriate evapotranspiration and parameter optimization schemes for HYDRUS-1D, a commonly used modeling tool for green roofs. A comparative study of this sort in the context of modeling green roof runoff has not been conducted previously and is important in regard to guiding modelers who may be interested in using HYDRUS-1D for an accurate prediction of runoff from a green roof, thus improving knowledge over the cases discussed in the literature.
For evapotranspiration methods, two simple evapotranspiration schemes are considered. They are the Hargreaves method and Blaney–Criddle method, which have been applied many times in the literature [17,18]. As for optimizations, HYDRUS’ own inverse solution module is compared against the harmony search algorithm, the excellence of which in regard to optimization has also been recognized in various engineering fields [19] as a possible alternative.
2. Materials and Methods
2.1. Field Study Site
In this study, the Portland Building Ecoroof was chosen as the study site by identifying a green roof that can facilitate model construction and where necessary data were available thanks to prior research [20,21,22] (Figure 1a). The Portland Building Ecoroof was retrofitted in November of 2006 on top of a 15-story building located in downtown Portland, OR, USA.
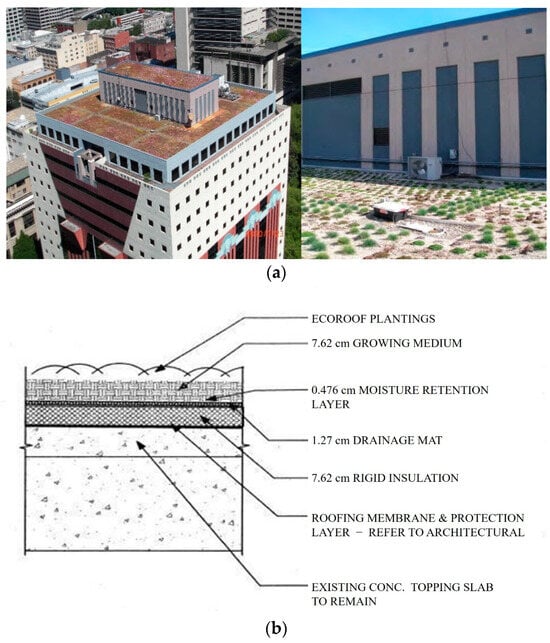
Figure 1.
Portland Building Ecoroof [21,22]. (a) Portland Building Ecoroof. (b) Cross-sectional view of the Portland Building Ecoroof.
Monitoring for the data was performed on the southwest corner of the roof (348 m2) belonging to the third quadrant and half of the green-roofed penthouse (139 m2) that drains to the quadrant since March 2007. Blue oat grass and sedum species were used as green roof vegetation. The soil layer depth was 7.6 cm and consisted of a mixture of sandy loam, compost, pumice, and Sockosorb polymer. In addition, the roof consists of a soil-moisture retention layer and a drainage mat. Figure 1b is the cross-sectional view of the study site.
The rainfall data for calibration and validation are from the Rain Gage at the Portland Fire Bureau, located 55 SW Ash St. [23], which is the closest station to the Portland Building Ecoroof. Also, the total rainfall data from the International BMP Database [24] were used. As for the runoff monitoring data, the data from the same database were used. In particular, the data from October 2007 to December 2009, the period which the water quality monitoring data cover, were used partly for calibration (2007–2008) and for validation (2009). It was conducted in such a way that water quality simulation can be carried out later as a future work. The roof runoff was directed to a V-notch flume attached to the drain, where water depths were measured with a flow meter (Sigma 950, Hach, Loveland, CO, USA) and related to flow rates [21].
2.2. HYDRUS-1D
In general, there are four ways to model a green roof: curve methods, single reservoir models, linear/non-linear storage reservoirs, and physical models [25]. In this study, a physical model, HYDURS-1D, was selected to simulate water movement on the green roof.
HYDRUS version 4 is a Microsoft Windows-based modeling suite for analyzing water flow and solute transport in variably saturated porous media [26,27]. The software package includes a computational finite element model for the simulation of the one-, two-, and three-dimensional movement of water, heat, and multiple solutes in variably saturated media. The model has a parameter optimization algorithm for inverse estimation of soil hydraulic and/or solute transport parameters. The model comes with an interactive graphics-based interface for data-preprocessing, generation of structured and unstructured finite element meshes, and a graphic presentation of the results.
HYDRUS-1D is capable of most of the features also sound in HYDRUS-2D/3D; however, soil dimension is limited to a single dimension [7]. The one-dimensional water flow in a partially saturated porous media is described using a modified version of the Richards equation:
where θ is the volumetric water content [–], h is the water pressure head [L], t is time [T], z is the vertical coordinate [L], K is the unsaturated hydraulic conductivity [LT−1], α is the angle between the vertical axis and the flow direction (for the horizontal flow, α = 90°), and S is the sink term [L3L−3T−1] that accounts for root water uptake.
The Van Genuchten equation and the Mualem model can be combined to describe hydraulic properties:
where θs and θr are the saturated and residual water content [–], αs is the parameter used in the soil retention function [L−1], m and n are empirical parameters that depend on soil type [–], Ks is the saturated hydraulic conductivity [L T−1], Se is the effective water saturation [–] where 0 ≤ Se ≤ 1, and l denotes the tortuosity parameter in the conductivity function [–], for which the analyses of various soils revealed a value of 0.5 [14].
The model had been set up for simulations as follows. For the calculation domain, a growing medium was considered to define the upper and lower boundaries of the green roof layer. The initial condition was set to be an initially dry condition. As for the boundary conditions, the upper boundary condition was chosen to be the atmospheric condition, with the surface layer using precipitations and evapotranspiration, and the lower boundary condition was set to be free drainage.
2.3. Evapotranspiration
It is often important to consider potential evapotranspiration when modeling green roof runoff. There are several methods of evaluating evapotranspiration that can be used by HYDRUS-1D: the Penman–Montheith equation, the Hargreaves formula, and energy balance boundary conditions. Although the Penman–Montheith method was recommended by the authors of HYDRUS for the potential evapotranspiration, the potential evapotranspiration estimated monthly using the simpler Hargreaves method was found to be not statistically different (p > 0.05) from the evapotranspiration derived from the Penman–Montheith method by ANOV at a significance level of 0.05 [4]. More recently, Wadzuk et al. [28] and Limos et al. [29] reported that the simpler Blaney–Criddle method also provided satisfactory estimates in regard to evapotranspiration.
In this study, the Hargreaves formula (Equation (6)) and the Blaney–Criddle method (Equation (7)), two simple but reliable methods for evapotranspiration estimates, were compared and analyzed for green roof modeling by HYDRUS-1D:
where Ra is extraterrestrial radiation (LT−1), Tm is the daily mean air temperature, TR is the range of temperature between the mean daily maximum and minimum air temperature, and p is the mean daily percentage of annual daytime hours depending on the latitude and month. Since the Blaney–Criddle method is not included in HYDRUS, it was used from outside to calculate evapotranspiration as an input to HYDRUS.
The extraterrestrial radiation (Ra) is calculated by HYDRUS itself when latitude is substituted and the temperature references the Portland international airport station data closest to the Portland Building Ecoroof [30]. Tm is obtained using Equation (8),
where Tmax is the daily maximum temperature and Tmin is the daily minimum temperature. The mean daily percentage of annual daytime hours, p, can be found in Table 1 [31].

Table 1.
Mean daily percentage (p) of annual day time hours for different latitudes [31].
2.4. Parameter Estimation
The substrate for green roofs is an artificial medium with improved performance compared to natural soil [32]. The measurement of the hydraulic parameters (θr, θs, α, n and Ks) of the HYDRUS-1D model for green roofs is relatively expensive and time-consuming [33]. The HYDRUS model contains its own optimization module for these parameters. This study compared HYDRUS-1D’s own module with a harmony search algorithm, another well-known optimization scheme [19], for the assessment of their performances in parameter optimization in the context of green roof runoff modeling.
2.4.1. Inverse Solution
The HYDRUS-1D model itself includes an optimization module for hydraulic parameters (, and many studies have been carried out using this module [14,15,16]. The inverse method is used on the basis of the minimization on an objective function representing the difference between the observed and predicted values [26]. Minimization of the objective function (Equation (9)) proceeds using the Levenberg–Marquardt optimization,
where, for the first term, the is the number of measurement sets; is the number of measurements for a specific measurement set; represents particular measurements at time for the -th measurement set at location ; are the corresponding model predictions for the optimized parameter set, ; and and are weights associated with a specific measurement set or point [26]. As for the second term, , , , and have similar meanings as the first term but this time for the hydraulic properties. Finally, for the last term, are prior knowledge on the soil hydraulic properties, are their final estimated values, with being the number of parameters given prior knowledge, and represents preassigned weights.
The range of parameters was referenced in previous studies [32], and the middle value of the range was used as the initial parameter value. Table 2 shows the range of variables. In addition, according to a previous study that modeled a green roof using HYDRUS-1D [15], a maximum of 20 iterations were used without any weighting for the parameter estimation process.

Table 2.
HYDRUS-1D Parameter range [32].
2.4.2. Harmony Search
A harmony search was devised by Geem et al. [34] and is an algorithm that mimics the process of finding a harmony that produces a beautiful sound when composing music. Variables considered for harmony searches include harmony memory (HM), harmony memory size (HMS), harmony memory considering rate (HMCR), and pitch adjusting rate (PAR). The process of executing the harmony search algorithm consists of 5 steps, as follows, and a detailed flowchart is shown in Figure 2 [34].
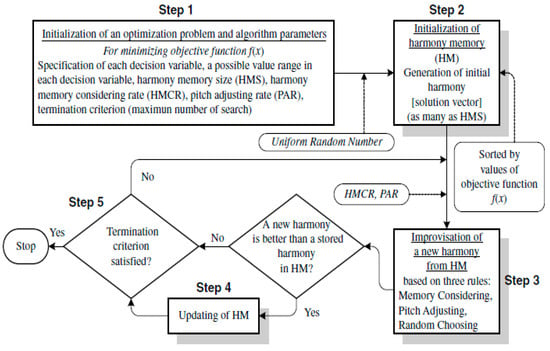
Figure 2.
Harmony search algorithm optimization procedure [34].
Step 1: Setting-up of the optimization problem and algorithm parameters.
Step 2: Initialization of the HM.
Step 3: Generation of a new harmony from the HM.
Step 4: Updating of the HM.
Step 5: Repeat steps 3 and 4 until the termination condition is satisfied.
In this study, we used MATLAB Release 2021a to implement the harmony search algorithm, and, among the many commercial codes available, the code written by Sajjad [35] was used. As for the optimization parameters, the values used in the previous study [29] on the same study site were utilized (HMS = 10, HMCR = 0.8, PAR = 0.3, bandwidth = 0.001, maximum number of iterations = 5000). The range of parameters was the same as the range used in the inverse solution.
2.4.3. Applicability Evaluation
The applicability evaluation index used when modeling the runoff volume from a green roof was the Nash–Sutcliffe model efficiency coefficient (NSE), which is widely used as an indicator of water quantity and quality model evaluation [36]. The equation for calculating the NSE value is shown in Equation (10) [37]. Additionally, the coefficient of determination (R2) was used for statistical verification of runoff volume, and the corresponding equation is given as Equation (11) [38].
where Oi is the measured value, Pi is the model predicted value, and and are the averages of the measured and predicted values, respectively. The range of NSE values is from 1 to −∞, and the range of R2 is from 0 to 1. The closer the NSE and R2 are to 1, the closer the predicted results of the model are to the measured values [38]. The evaluation criteria by NSE and R2 in the hydrology simulation are shown in Table 3.

Table 3.
Evaluation criteria for simulation of water quantity using NSE and R2 [38].
2.5. Sensitivity Analysis
A sensitivity analysis for the model parameter set was performed to understand model behavior [33] (Baek et al., 2020). In this study, the influence of an input parameter on the simulated values of the output variable was calculated using condition number (CN) [39],
where k is the initial value of the parameter, c is the simulation result when k is used, Δk is the changed amount of the parameter relative to the initial value, and Δc is the changed amount of simulated value relative to the initial simulation result by using the k. A parameter with a large CN value is a parameter that has a large influence on the simulated values. If the CN value is positive, it means that the simulation values increase as the parameter increases, and, if it is negative, the simulated values decrease.
3. Results and Discussion
3.1. Inverse Solution
3.1.1. Parameter Estimation
A runoff volume test based on HYDRUS’ own optimization module was performed using five parameters for the green roof runoff volume, and, based on this, the test statistics and the values of related parameters were estimated. Table 4 shows the estimated values of the parameters after model optimization using the Hargreaves formula for the evapotranspiration calculation method. Table 5 shows the estimated values of the parameters after model optimization using the Blaney–Criddle method for the evapotranspiration calculation method.

Table 4.
HYDRUS-1D parameter calibration by HYDRUS module (Hargreaves formula).

Table 5.
HYDRUS-1D parameter calibration by HYDRUS module (Blaney–Criddle method).
Here, has converged to the maximum value of 0.757 for the range constrained for both the Hargreaves and Blaney–Criddle methods. This is interpreted as an effort by optimization scheme to maximize the pore space in the substrate to withhold rainwater so that a good model prediction for the observed runoff volume is achieved. Calibrated saturation porosity is considered large but is in the possible range reported in Sandoval et al. [32].
In a similar context, Ks was calibrated lower than expected in an effort to control the speed at which runoff from the green roof matches the observed runoff volume. This is partly due to HYDRUS’ inability to model moisture retention layers which can retard runoff from green roofs. To account for this delay indirectly, the optimization scheme had to reduce Ks further. Another mechanism not accounted for was the root water uptake, which would have contributed to the reduction in runoff volume. Since this is not accounted for in our simulation, this also can be factored into the reduction in Ks.
3.1.2. Applicability Evaluations
In the case of modeling the total runoff volume using the Hargreaves formula as an evapotranspiration calculation method, the NSE was −0.45 and the R2 was 0.46, indicating the statistical evaluation of “not satisfactory” (NSE 0.5 and R2 0.6). The validation results showed an NSE of 0.22 and an R2 of 0.69, indicating the statistics of “not satisfactory” (NSE 0.5) and “satisfactory” (R2 < 0.7), respectively.
As for the results using the Blaney–Criddle method as an evapotranspiration calculation method, the NSE was 0.73 and the R2 was 0.82, indicating a statistical evaluation of “good” (NSE > 0.7) and “very good” (R2 > 0.75), respectively. The validation results showed an NSE of 0.46 and an R2 of 0.85, indicating the statistical evaluation of “not satisfactory” (NSE 0.5) and “very good” (R2 > 0.75), respectively. Figure 3 shows sample scatter plots of measured vs. calibrated results that employed the two evapotranspiration models for the total runoff volume. From the results of the applicability evaluation, it was found that the Blaney–Criddle method has much better applicability than the Hargreaves formula for the prediction of the total runoff volume.
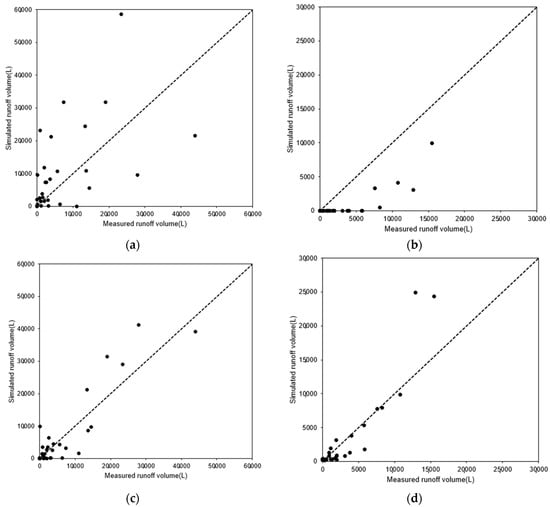
Figure 3.
HYDRUS-1D model scatter plots of measured vs. simulated results of employing the two evapotranspiration methods for total runoff volume (calibration performed by HYDRUS’ own optimization module). (a) Calibration—Hargreaves formula. (b) Validation—Hargreaves formula. (c) Calibration—Blaney–Criddle method. (d) Validation—Blaney–Criddle method.
3.2. Harmony Search
3.2.1. Parameter Estimation
Runoff volume prediction on the basis of the harmony search algorithm was performed using five parameters for the green roof, and, based on this, performance statistics and the values of related parameters were estimated. Table 6 shows the estimates of the parameter values after model optimization using the Hargreaves formula for the evapotranspiration calculation method. Table 7 shows the estimated values of the parameters after the model optimization using the Blaney–Criddle method for the evapotranspiration calculation method.

Table 6.
HYDRUS-1D parameter calibration by harmony search algorithm (Hargreaves formula).

Table 7.
HYDRUS-1D parameter calibration by harmony search algorithm (Blaney–Criddle method).
As was the case with the inverse solution, the harmony search solution also showed that has converged to the maximum value of 0.757 for the range constrained for both the Hargreaves and Blaney–Criddle methods. This is also interpreted as an effort by optimization scheme in maximizing the pore space in the substrate to withhold rainwater so that a good model prediction for the observed runoff volume is achieved. Calibrated saturation porosity is considered large but is in the possible range reported in Sandoval et al. [32].
In a similar context, Ks was calibrated lower than usual for the green roof substrate in an effort to control the speed at which runoff from the green roof again matched the observed runoff volume. This is partly due to HYDRUS’ inability to model moisture retention layers, which can retard runoff from green roofs. To account for this delay indirectly, the optimization scheme seemed to have reduced Ks further. Another mechanism not accounted for was root water uptake, which would have contributed to the reduction in runoff volume. Since this is not accounted for in our simulation, this also can be factored into the reduction in Ks. It is noted that the Ks values calibrated by the harmony search algorithm are greater than the ones calibrated by the inverse solution, which is seen as more desirable.
3.2.2. Applicability Evaluation
In the case of modeling total runoff volume using the Hargreaves formula as an evapotranspiration calculation method, the NSE was 0.86 and the R2 was 0.95, indicating the statistical evaluation of “very good” (NSE > 0.8; R2 > 0.75), respectively, based on the same evaluation criteria. The validation results showed an NSE of 0.59 and an R2 of 0.78, indicating a statistical evaluation of “satisfactory” (NSE > 0.5) and “very good” (R2 > 0.75), respectively.
As for the results using the Blaney–Criddle method as an evapotranspiration calculation method, the NSE was 0.90 and the R2 was 0.95, indicating a statistical evaluation of “very good” (NSE > 0.8; R2 > 0.75) based on the same evaluation criteria. The validation results showed an NSE of 0.60 and an R2 of 0.77, indicating a statistical evaluation of “satisfactory” (NSE > 0.5) and “very good” (R2 > 0.75), respectively. Figure 4 shows sample scatter plots of measured vs. calibrated results of the two models for the total runoff volume.
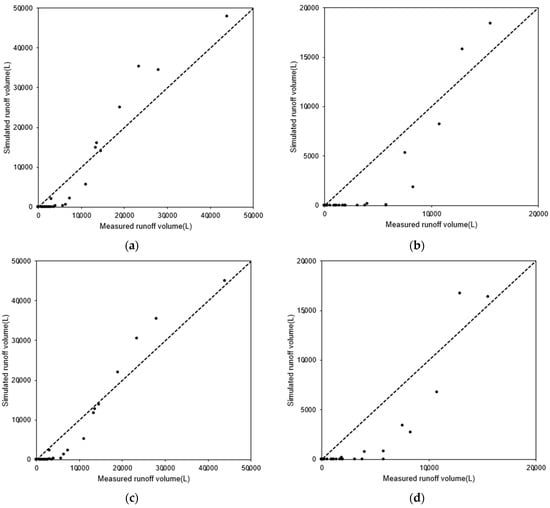
Figure 4.
HYDRUS-1D model scatter plots of measured vs. simulated results of employing the two evapotranspiration methods for total runoff volume (calibration performed by the harmony search algorithm). (a) Calibration—Hargreaves formula (b) Validation—Hargreaves formula. (c) Calibration—Blaney–Criddle method. (d) Validation—Blaney–Criddle method.
From the results of the applicability evaluation, it was found that there were no significant differences between the results by the Hargreaves formula and the Blaney–Criddle method, and both methods were found to properly simulate measured values.
3.3. Sensitivity Analysis
Figure 5 shows the parameter sensitivity analysis of HYDRUS-1D for runoff volume from the green roof subject to +/−10, 20 and a 30% change in parameter values relative to baseline values. It was found that the runoff volumes calculated by the model were found to be sensitive to the following parameters in the order of n, alpha, saturated water content, saturated hydraulic conductivity, and residual water content based on the magnitude of the condition number, which is the measure of model sensitivity relative to the change in parameter values.
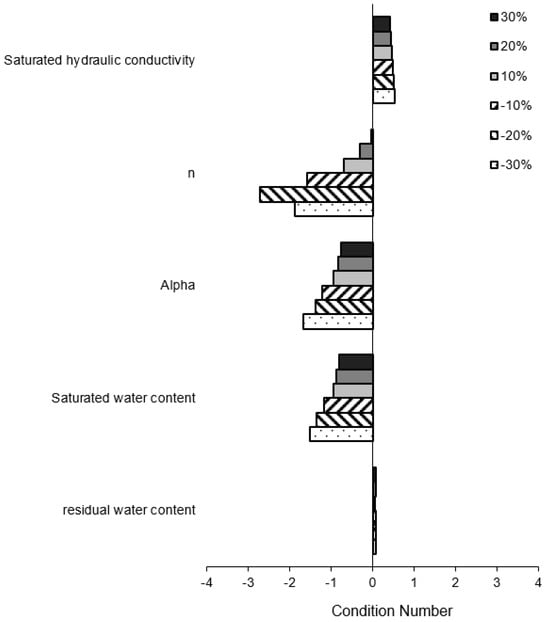
Figure 5.
HYDRUS-1D model parameter sensitivity analysis in terms of runoff volume for +/−10, 20 and 30% change in parameter values.
The condition numbers of n, alpha and saturation water content were noticeably larger than other parameters. This means that these parameters have a great influence on the runoff volume predicted by the HYDRUS-1D model, so the user should consider these parameters to be more important [33]. The parameters n and alpha present in Equation (2) are for calculating the water retention and unsaturated hydraulic conductivity; therefore, they have a significant influence on runoff volume. Since saturated water content represents available pore spaces that can be filled with water, it also has an important effect on runoff volume [32].
The parameters with a negative CN value are n, alpha, and saturated water content. This means that runoff volume is negatively correlated with these parameters. In the case of n and alpha, as shown in Equation (2), volumetric water content decreases with the increase in n and alpha, thus leading to less runoff by making more pore space available for retention. In the case of saturation water content, as the value of saturated water content increases, the runoff volume decreases due to the available soil moisture storage increasing. The parameters where the CN value features as a positive value are residual water content and saturated hydraulic conductivity. In the case of residual water content, as the value decreases, the runoff volume decreases since the amount of volume of water that the soil can retain increases. In the case of saturated hydraulic conductivity, as the value increases, water transport through soil becomes faster so that the runoff volume increases.
4. Conclusions
In this study, not only were the Hargreaves formula and the Blaney–Criddle method compared, but the HYDRUS’ own optimization module (inverse solution) and the optimization method using the harmony search algorithm were compared and analyzed to find evapotranspiration and optimization schemes that have better applicability for green roof runoff modeling.
From the results of the applicability evaluation, it was found that the applicability when using the Blaney–Criddle method was better than the one using the Hargreaves method for both optimization methods—HYDRUS’ own optimization module and the harmony search algorithm. In particular, the applicability results when using the Blaney–Criddle method in HYDRUS’ own optimization module were much better (R2 = 0.82) than the applicability results when using the Hargreaves formula (R2 = 0.46). This is in resemblance to the findings in Limos et al. [29], where the Blaney–Criddle evapotranspiration calculation method was found to be the most applicable in green roof runoff modeling. HYDRUS’ own optimization module had shown a good applicability evaluation index; however, except for the objective function specified by itself, it is limited by the aspect that other useful performance statistics are unable to be designated as objective functions.
In the case of using the harmony search algorithm, both the NSE (0.9) and R2 (0.95) values were higher compared to the ones (NSE = 0.73; R2 = 0.82) obtained by HYDRUS-1D’s own optimization module. This seems to be due to a limitation of HYDRUS-1D’s optimization module, as other useful objective functions, such as NSE and R2, which may improve its performance, cannot be specified. In contrast, the harmony search algorithm gives the flexibility to the users to choose the applicability evaluation indices so that the parameters can be optimized for the best possible performance. The harmony search algorithm has been successfully applied in green infrastructure modeling [40,41]. Therefore, in this study, the harmony search algorithm was proposed as an alternative parameter optimization method for predicting green roof runoff when using HYDRUS-1D, which is expected to be useful for future studies experimenting with various evaluation indices as objective functions.
Lastly, the sensitivity analysis in the form of condition numbers showed that the parameters of n, alpha, and saturation water content were noticeably larger than other parameters, emphasizing the importance of these parameters in obtaining the good fit of the runoff volume predicted by the HYDRUS-1D model. This was similarly found in other studies [32,33].
Overall, the findings in this study should help potential users considering using HYDRUS-1D to model green roof performance for stormwater mitigation in selecting evapotranspiration and optimization es, which are important for accurately predicting green roof runoff responses to various rainfall conditions.
Author Contributions
Conceptualization, H.K. and J.Y.; methodology, H.K. and H.S.; software, H.S.; validation, H.S.; formal analysis, H.S.; investigation, H.K. and J.Y.; data curation, H.S. and S.H.; writing—original draft, H.S.; writing—review and editing, H.K., S.H., Z.W.G., H.A., Y.H. and J.Y.; visualization, H.S.; supervision, H.K., Z.W.G., H.A., Y.H. and J.Y.; project administration, H.K.; funding acquisition, J.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by grants (2018R1D1A3B07042576; 2020R1I1A3064269) from the Basic Science Research Program through the National Research Foundatioin (NRF), funded by the Ministry of Education, Republic of Korea. This work was also supported in part by a grant from Korea University.
Data Availability Statement
The data used to support the findings of this study are available from the International Stormwater BMP Database at www.bmpdatabase.org.
Conflicts of Interest
The authors have no relevant financial or non-financial interests to disclose.
Glossary/Nomenclature/Abbreviations
| α | Parameter used in the soil retention function |
| θ | Volumetric water content |
| θs | Saturated water content |
| θr | Residual water content |
| h | Water pressure head |
| K | Unsaturated hydraulic conductivity |
| Ks | Saturated hydraulic conductivity |
| Ra | Extraterrestrial radiation |
| S | Sink term that accounts for root water uptake. |
| Se | Effective water saturation |
| Tm | Daily mean air temperature |
| TR | Temperature range between the mean daily maximum and minimum air temperature |
| p | Mean daily percentage of annual daytime hours depending on the latitude and month. |
| CN | Condition number |
| HM | harmony memory |
| HMCR | harmony memory considering rate |
| PAR | pitch adjusting rate |
References
- Berndtsson, J.C. Green roof performance towards management of runoff water quantity and quality: A review. Ecol. Eng. 2010, 36, 351–360. [Google Scholar] [CrossRef]
- Gregoire, B.G.; Clausen, J.C. Effect of a modular extensive green roof on stormwater runoff and water quality. Ecol. Eng. 2011, 37, 963–969. [Google Scholar] [CrossRef]
- Toland, D.C.; Haggard, B.E.; Boyer, M.E. Evaluation of Nutrient Concentrations in Runoff Water from Green Roofs, Conventional Roofs, and Urban Streams. Trans. ASABE 2012, 55, 99–106. [Google Scholar] [CrossRef]
- Hilten, R.N.; Lawrence, T.M.; Tollner, E.W. Modeling stormwater runoff from green roofs with HYDRUS-1D. J. Hydrol. 2008, 358, 288–293. [Google Scholar] [CrossRef]
- Krebs, G.; Kuoppamaki, K.; Kokkonen, T.; Koivusalo, H. Simulation of green roof test bed runoff. Hydrol. Process 2016, 30, 250–262. [Google Scholar] [CrossRef]
- Mobilia, M.; Longobardi, A. Impact of rainfall properties on the performance of hydrological models for green roofs simulation. Water Sci. Technol. 2020, 81, 1375–1387. [Google Scholar] [CrossRef]
- Li, Y.L.; Babcock, R.W. Green roof hydrologic performance and modeling: A review. Water Sci. Technol. 2014, 69, 727–738. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.L.; Babcock, R.W. Modeling Hydrologic Performance of a Green Roof System with HYDRUS-2D. J. Environ. Eng. 2015, 141, 04015036. [Google Scholar] [CrossRef]
- Feitosa, R.C.; Wilkinson, S. Modelling green roof stormwater response for different soil depths. Landsc. Urban Plan 2016, 153, 170–179. [Google Scholar] [CrossRef]
- Peczkowski, G.; Kowalczyk, T.; Szawernoga, K.; Orzepowski, W.; Zumda, R.; Pokladek, R. Hydrological performance and runoff water quality of experimental green roofs. Water 2018, 10, 1185. [Google Scholar] [CrossRef]
- Yang, G.; Davidson, C.I. Green roof aging effect on physical properties and hydrologic performance. J. Sustain. Water Buil. 2022, 7, 0402007. [Google Scholar] [CrossRef]
- Wang, J.; Garg, A.; Liu, N.; Chen, D.Q.; Mei, G.X. Experimental and numerical investigation on hydrological characteristics of extensive green roofs under the influence of rainstorms. Environ. Sci. Pollut. Res. 2022, 29, 53121–53136. [Google Scholar] [CrossRef] [PubMed]
- Palla, A.; Gnecco, I.; La Barbera, P. Assessing the Hydrologic Performance of a Green Roof Retrofitting Scenario for a Small Urban Catchment. Water 2018, 10, 1052. [Google Scholar] [CrossRef]
- Turco, M.; Kodesova, R.; Brunetti, G.; Nikodem, A.; Fer, M.; Piro, P. Unsaturated hydraulic behaviour of a permeable pavement: Laboratory investigation and numerical analysis by using the HYDRUS-2D model. J. Hydrol. 2017, 554, 780–791. [Google Scholar] [CrossRef]
- Bouzouidja, R.; Sere, G.; Claverie, R.; Ouvrard, S.; Nuttens, L.; Lacroix, D. Green roof aging: Quantifying the impact of substrate evolution on hydraulic performances at the lab-scale. J. Hydrol. 2018, 564, 416–423. [Google Scholar] [CrossRef]
- Palermo, S.A.; Turco, M.; Principato, F.; Piro, P. Hydrological effectiveness of an extensive green roof in mediterranean climate. Water 2019, 11, 1738. [Google Scholar] [CrossRef]
- Ebrahimian, A.; Wadzuk, B.; Traver, R. Evapotranspiration in green stormwater infrastructure systems. Sci. Total Environ. 2019, 688, 797–810. [Google Scholar] [CrossRef]
- Hardin, M.; Wanielista, M.; Chopra, M. A Mass Balance Model for Designing Green Roof Systems that Incorporate a Cistern for Re-Use. Water 2012, 4, 914–931. [Google Scholar] [CrossRef]
- Nasir, M.; Sadollah, A.; Grzegorzewski, P.; Yoon, J.H.; Geem, Z.W. Harmony Search Algorithm and Fuzzy Logic Theory: An Extensive Review from Theory to Applications. Mathematics 2021, 9, 2665. [Google Scholar] [CrossRef]
- Kurtz, T. Flow Monitoring of Three Ecoroofs in Portland, Oregon. In Proceedings of the International Low Impact Development Conference 2008: Low Impact Development for Urban Ecosystem and Habitat Protection, Seattle, WA, USA, 16–19 November 2008. [Google Scholar]
- Kurtz, T. Ecoroof Performance Monitoring in Portland, Oregon. In Proceedings of the International Low Impact Development 2010: Redefining Water in the City, San Francisco, CA, USA, 11–14 April 2010. [Google Scholar]
- Bureau of Environmental Services. Stormwater Management Facility Monitoring Report; City of Portland: Portland, OR, USA, 2010; pp. 45–55.
- United States Geological Survey, Oregon Water Science Centre―Portland Fire Bureau Rain Gage 55 SW Ash St. Available online: https://or.water.usgs.gov/non-usgs/bes/ankeny.rain (accessed on 15 January 2024).
- International Stormwater BMP Database. Water Environment Research Foundation. Available online: http://www.bmpdatabase.org/ (accessed on 3 January 2024).
- Xie, H.W.; Wu, Y.W.; Wang, L.P.; Luo, W.L.; Zhou, W.Q.; Zhou, H.; Yan, Y.C.; Liu, J. Comparing simulations of green roof hydrological processes by SWMM and HYDRUS-1D. Water Sci. Techol. 2020, 20, 130–139. [Google Scholar]
- Simunek, J.; van Genuchten, M.T.; Sejna, M. The HYDRUS-1D Software Package for Simulating the Movement of Water, Heat, and Multiple Solutes in Variably Saturated Media, Version 3.0; HYDRUS Software Series 1; Department of Environmental Sciences, University of California Riverside: Riverside, CA, USA, 2005. [Google Scholar]
- Li, Y.; Simunek, J.; Jing, L.F.; Zhang, Z.T.; Ni, L.X. Evaluation of water movement and water losses in a direct-seeded-rice field experiment using Hydrus-1D. Agric. Water Manag. 2014, 142, 38–46. [Google Scholar] [CrossRef]
- Wadzuk, B.M.; Schneider, D.; Feller, M.; Traver, R.G. Evapotranspiration from a green-roof storm-water control measure. J. Irrig. Drain. Eng. 2013, 139, 995–1003. [Google Scholar] [CrossRef]
- Limos, A.G. Modeling of Evapotranspiration in Green Roof Using SWMM Framework. Master’s Thesis, Korea University, Seoul, Republic of Korea, December 2016. [Google Scholar]
- Weather Underground, Portland, OR Weather History―Portland International Airport Station. Available online: https://www.wunderground.com/history/weekly/us/or/portland/KPDX/date (accessed on 15 January 2024).
- Brouwer, C.; Heibloem, M. Irrigation Water Management Training Manual; No. 3; FAO Land and Water, Development Division, FAO: Rome, Italy, 2010. [Google Scholar]
- Sandoval, V.; Bonilla, C.A.; Gironas, J.; Vera, S.; Victorero, F.; Bustamante, W.; Rojas, V.; Leiva, E.; Pasten, P.; Suarez, F. Porous Media Characterization to Simulate Water and Heat Transport through Green Roof Substrates. Vadose Zone J. 2017, 16, 1–14. [Google Scholar] [CrossRef]
- Baek, S.; Ligaray, M.; Pachepsky, Y.; Chun, J.A.; Yoon, K.S.; Park, Y.; Cho, K.H. Assessment of a green roof practice using the coupled SWMM and HYDRUS models. J. Environ. Manag. 2020, 261, 109920. [Google Scholar] [CrossRef] [PubMed]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Harmony Search Algorithm by Sajjad, Y., MATLAB Central File Exchange. Available online: https://www.mathworks.com/matlabcentral/fileexchange/41158-harmony-search-algorithm (accessed on 15 January 2024).
- Palla, A.; Gnecco, I. Hydrologic modeling of Low Impact Development systems at the urban catchment scale. J. Hydrol. 2015, 528, 361–368. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and Water Quality Models: Performance Measures and Evaluation Criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar]
- Chapra, S.C. Surface Water-Quality Modeling; Waveland Press: Long Grove, IL, USA, 2008. [Google Scholar]
- Kim, H.; Hong, S.; Limos, A.G.; Geem, Z.W.; Yoon, J. Improving water quality modelling for green roof runoff using Storm Water Management Model. Urban Clim. 2023, 52, 101717. [Google Scholar] [CrossRef]
- Pugliese, F.; Gerundo, C.; De Paola, F.; Caroppi, G.; Giugni, M. Enhancing the Urban Resilience to Flood Risk Through a Decision Support Tool for the LID-BMPs Optimal Design. Water Resour. Manag. 2022, 36, 5633–5654. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).