Optimizing the Activation of WWTP Wet-Weather Operation Using Radar-Based Flow and Volume Forecasting with the Relative Economic Value (REV) Approach
Abstract
1. Introduction
2. Theory and Methods
2.1. Contingency Table and Verification Measures
2.2. Objective Functions for Associating Economic Values to Outcomes
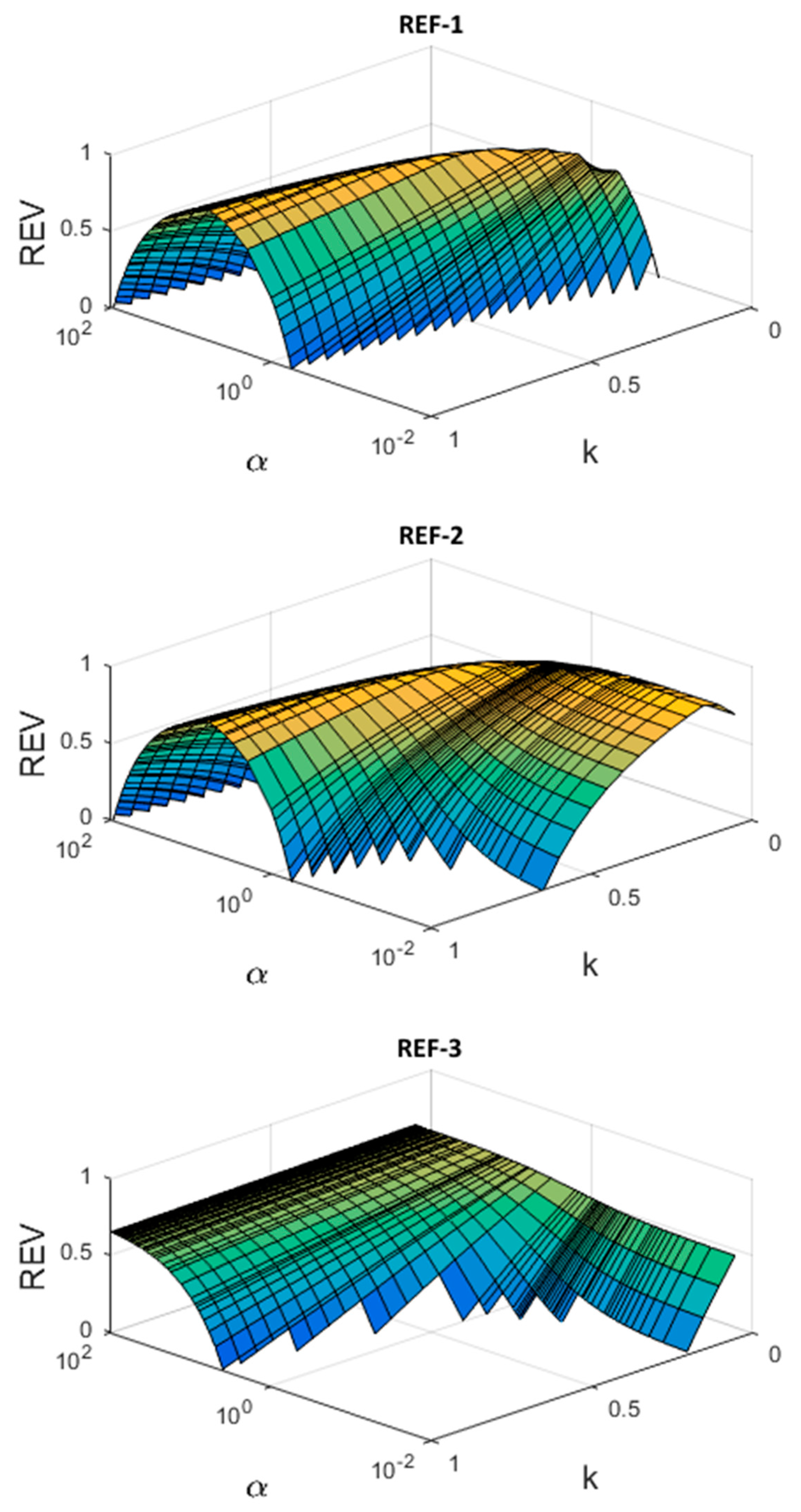
2.3. Formulating the Relative Economic Value (REV)
2.4. Closed Form Expression for REV
3. Case Study, Data and Investigated Control Strategies
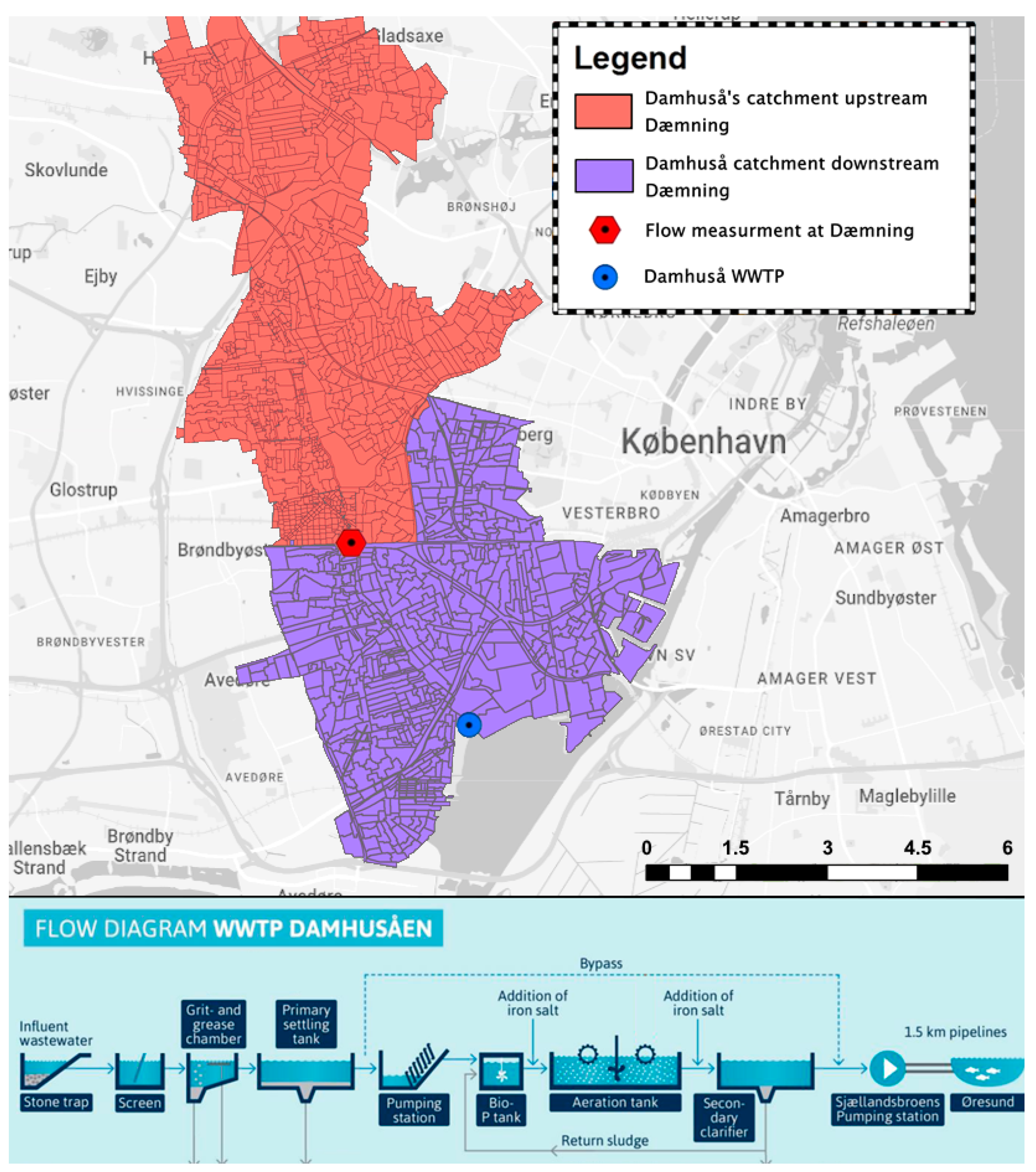
3.1. The Damhusåen Catchment and WWTP
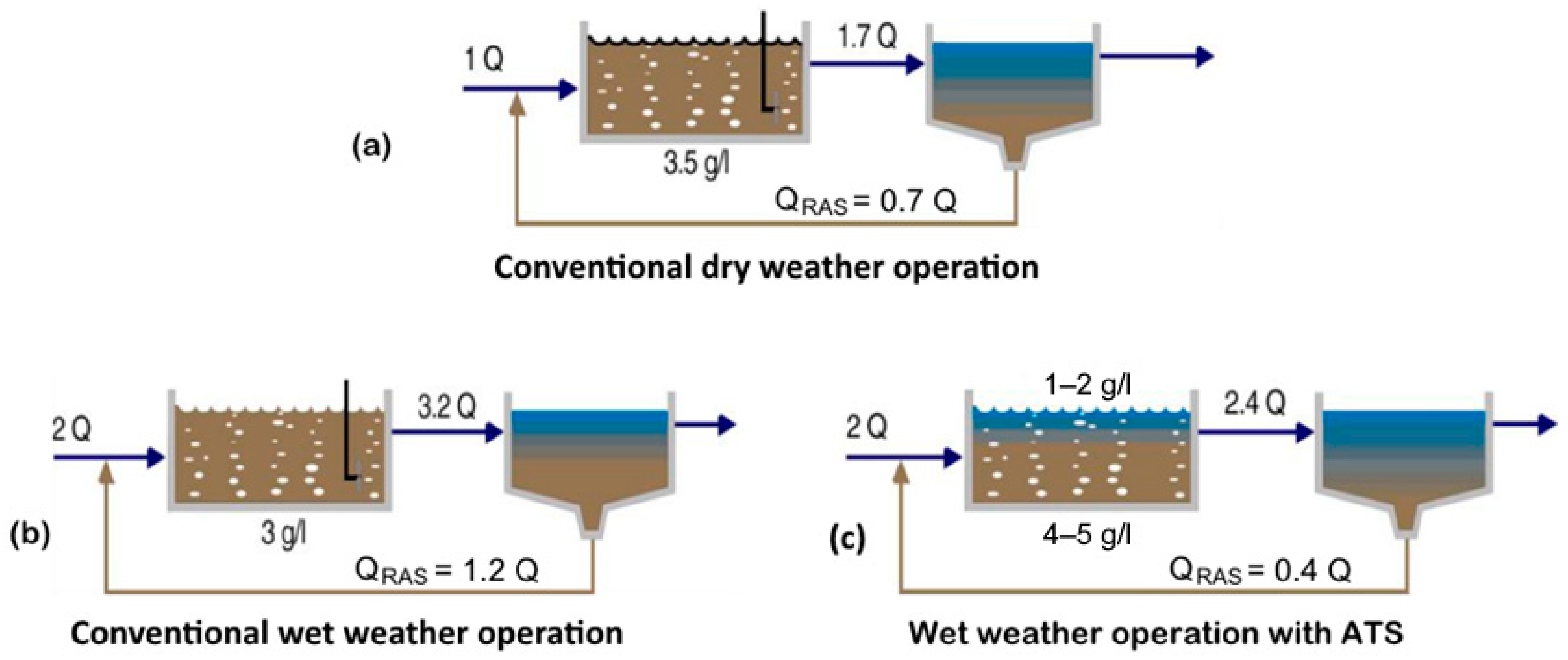
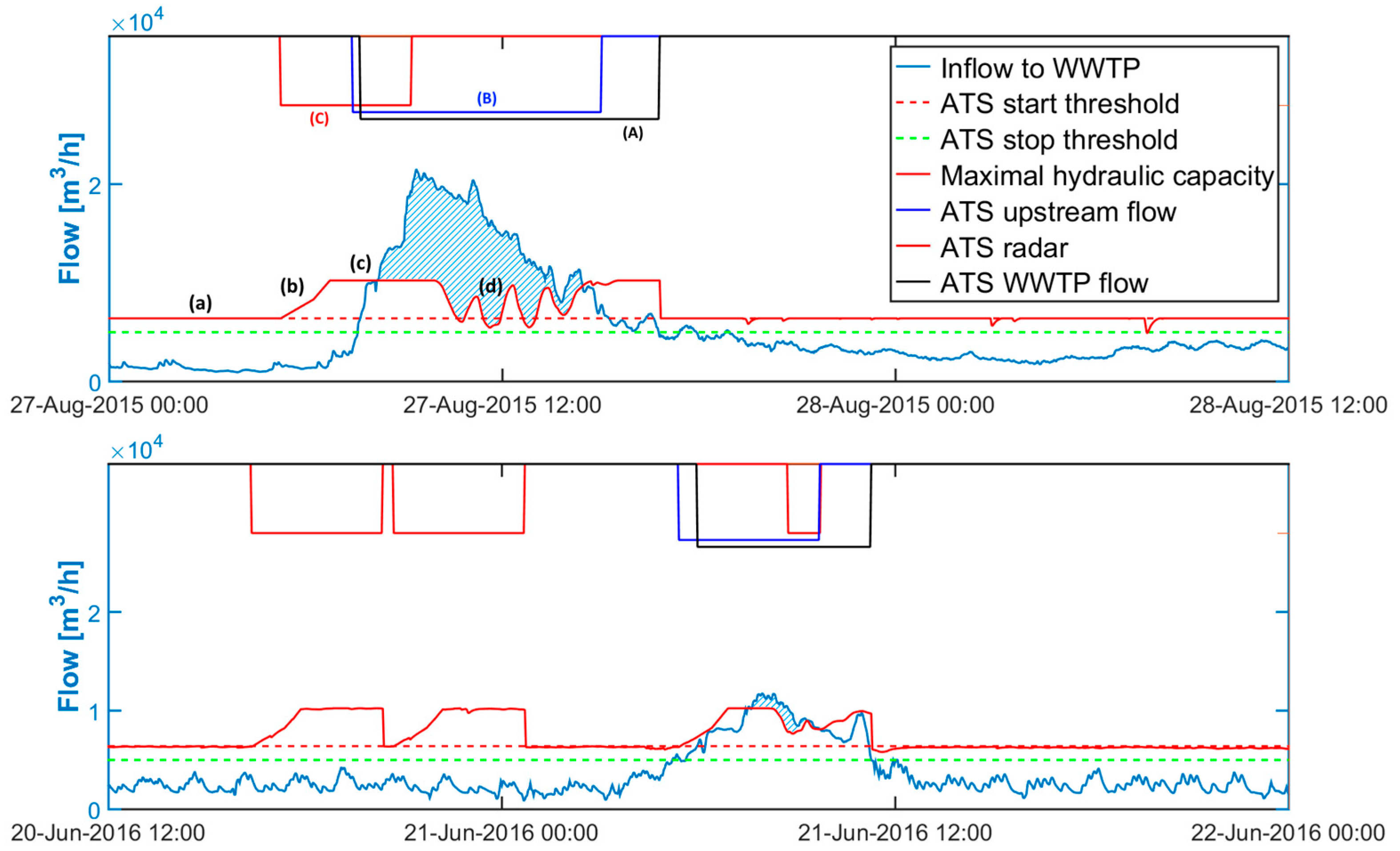
3.2. Aeration Tank Settling for Switching the WWTP into Wet-Weather Operation
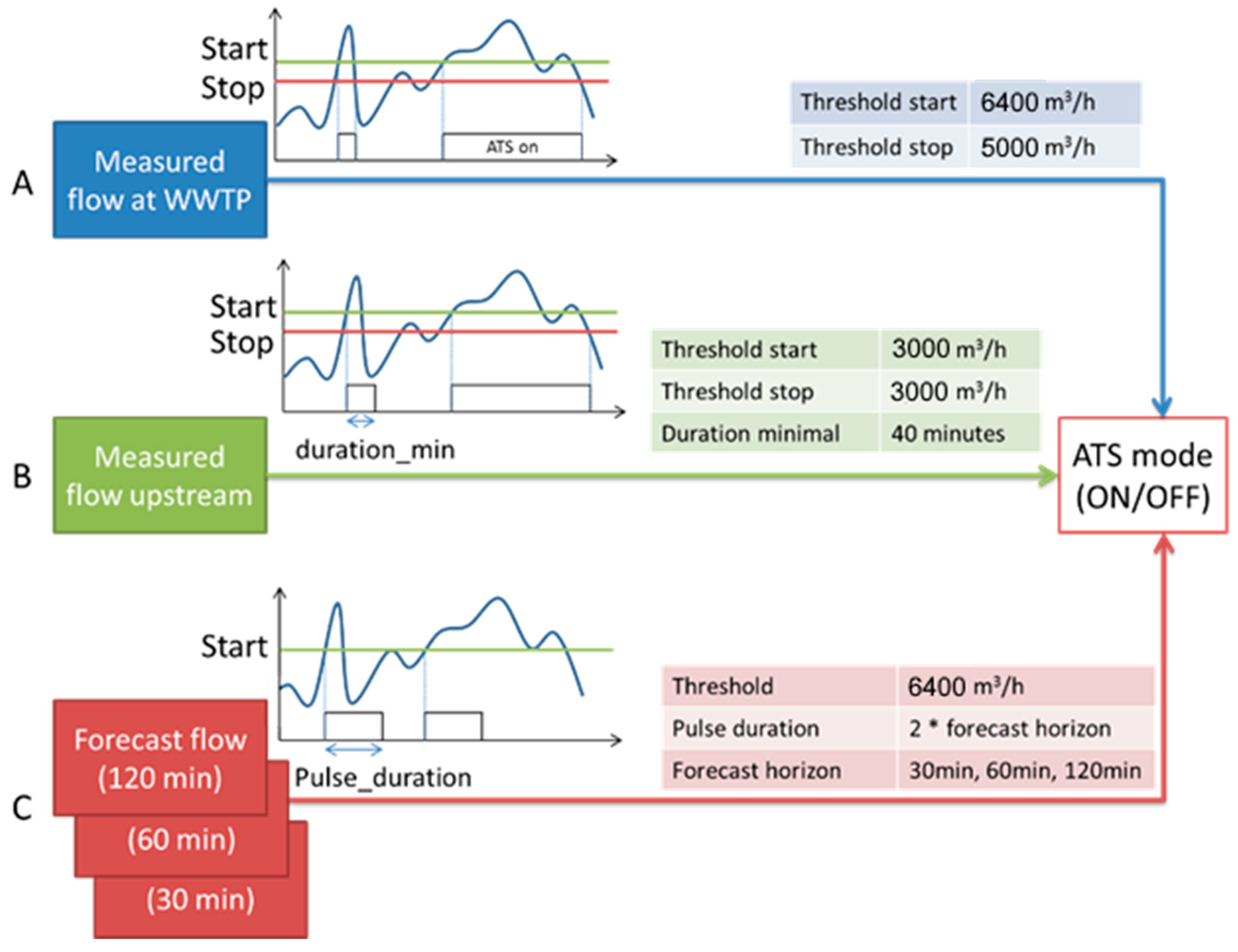
3.3. Baseline ATS Control Switch at the Damhuså WWTP
3.4. Investigated Control Strategies
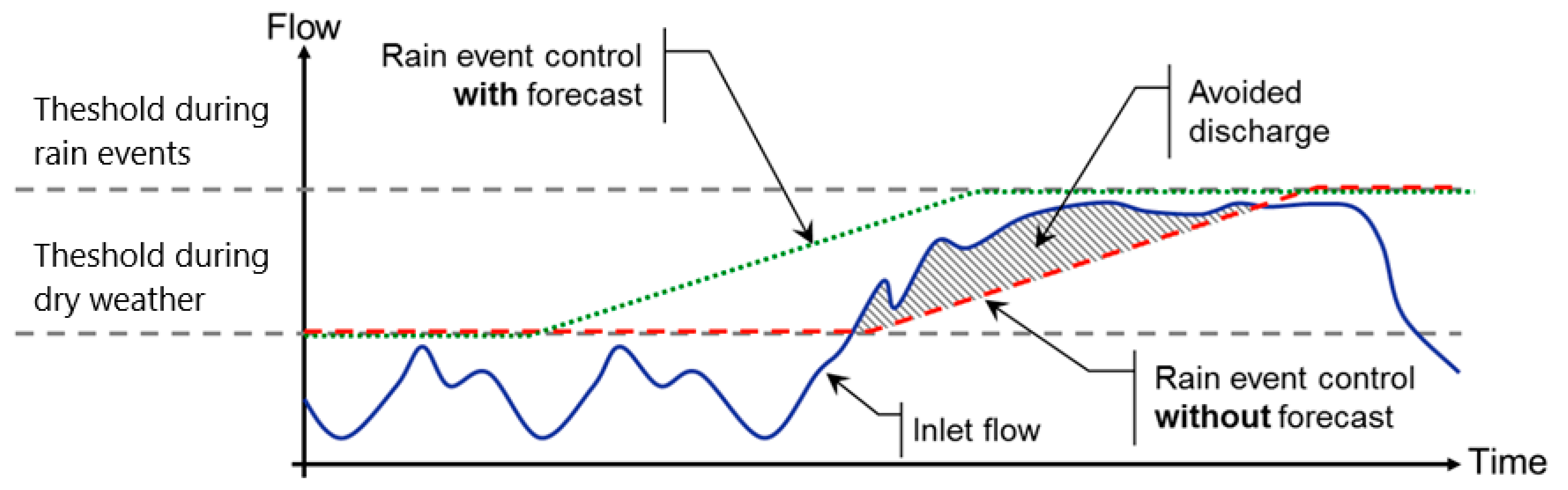
3.4.1. Perfect Control (EPerfect) and Reference Control (ERef)
3.4.2. Control Strategies Utilizing Flow and Volume Forecasts
3.5. Observation and Rainfall-Runoff Forecast Time Series Used in the Study
4. Results and Discussion
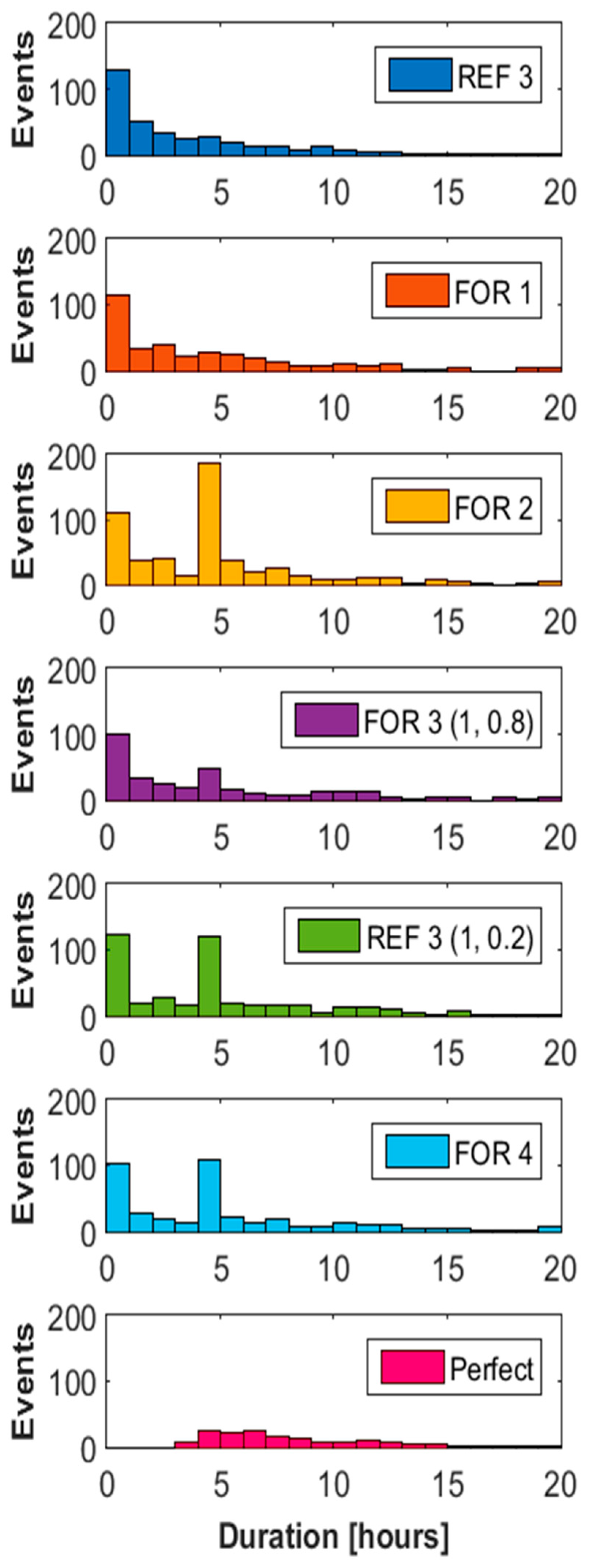
4.1. Comparing the Baseline Control (FOR-2) to the Perfect Control (PERFECT)
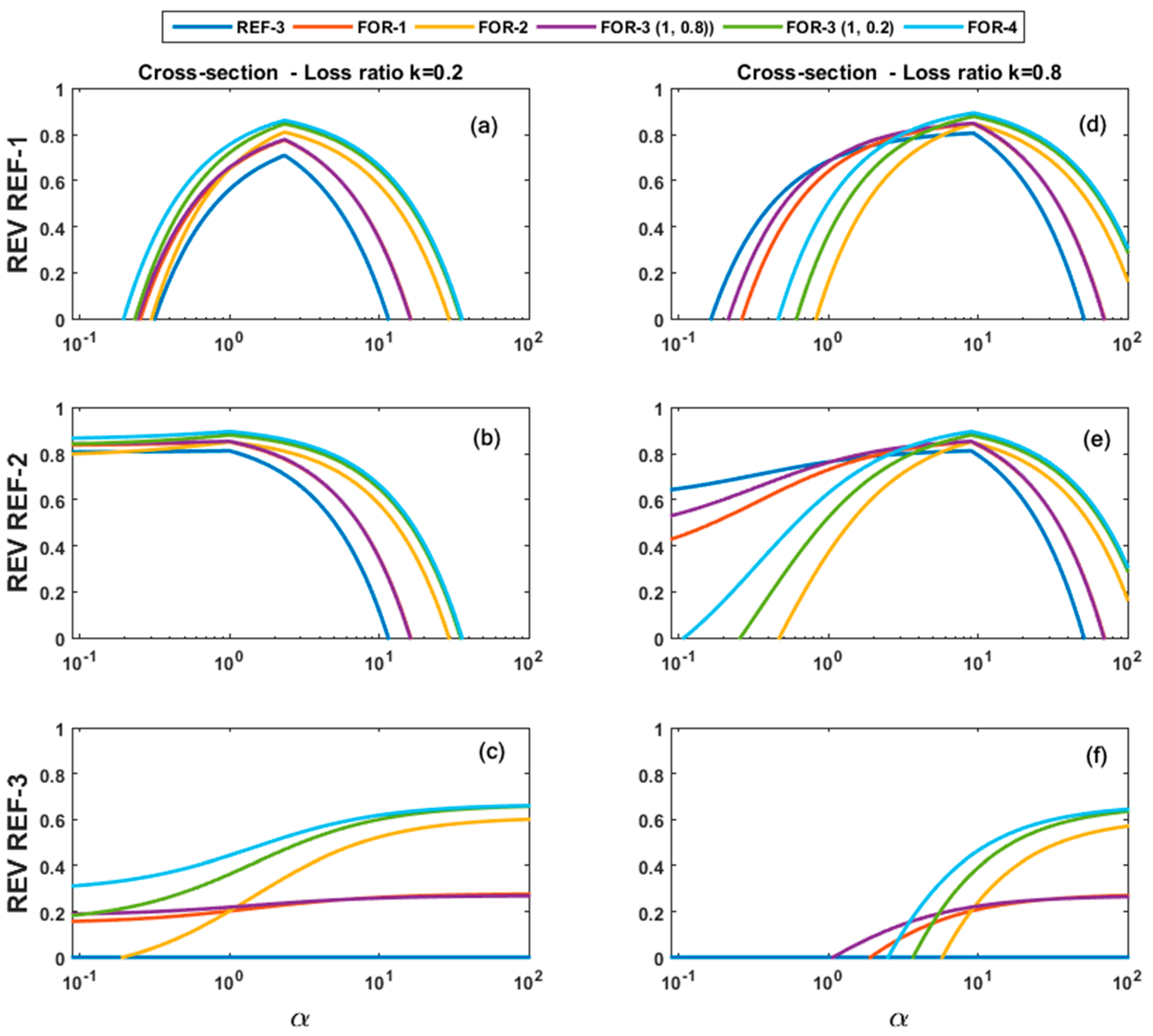
4.2. Evaluation of the Optimized Parameters (FOR-3) and the New Control Switch (FOR-4)
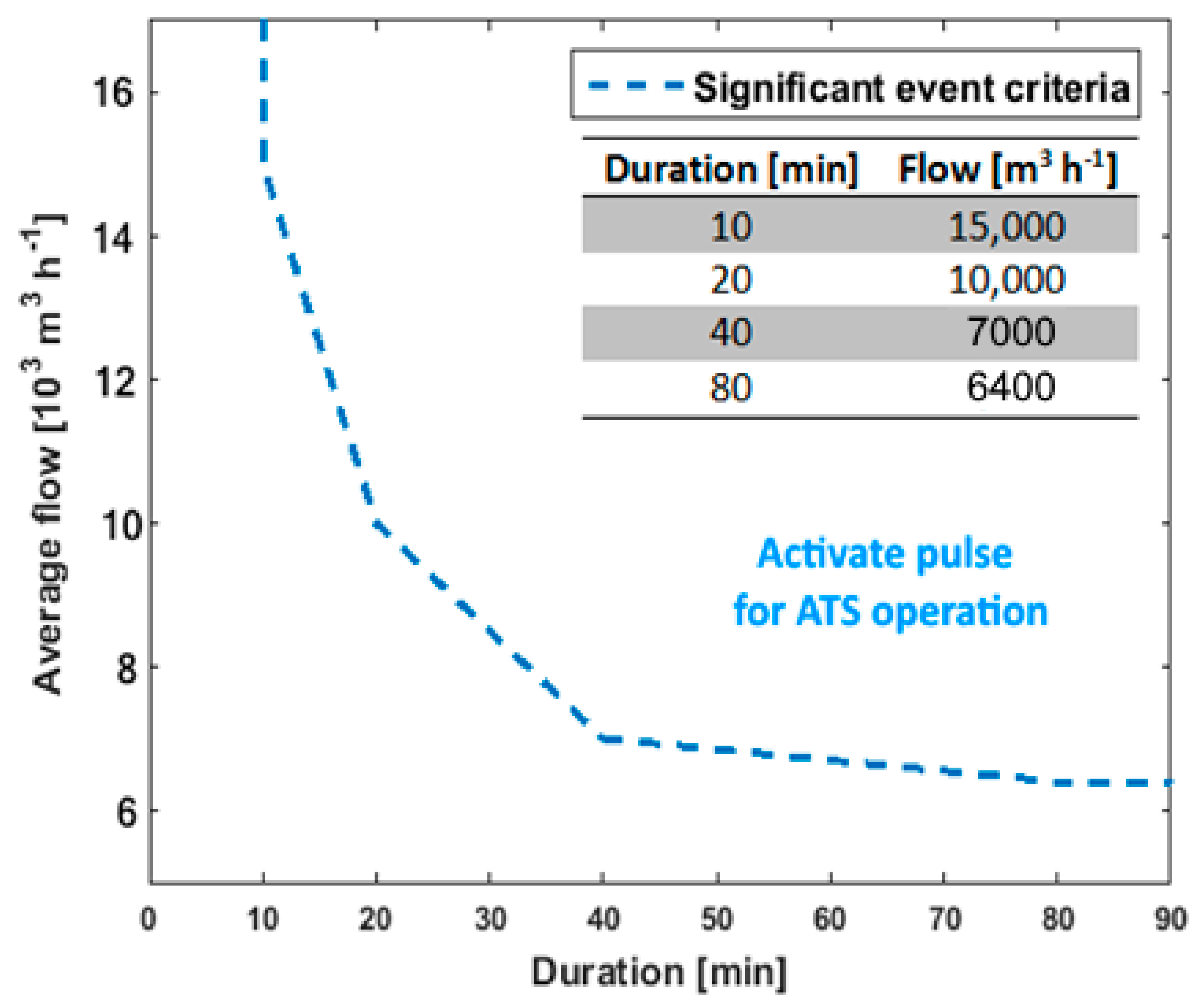
4.3. Defining and Quantifying the Objective Function
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviation | Meaning |
| ATS | Aeration tank settling |
| CSI | Critical Success Index |
| NWP | Numerical weather prediction |
| PoD | Probability of detection |
| PoFD | Probability of false detection |
| QRAS | Return activated sludge flow |
| REV | Relative economic value |
| RTC | Real time control |
| SS | Suspended solids |
| TSS | Total suspended solids |
| UDS | Urban drainage system |
| WWTP | Wastewater treatment plant |
References
- Semadeni-Davies, A.; Hernebring, C.; Svensson, G.; Gustafsson, L.-G. The impacts of climate change and urbanisation on drainage in Helsingborg, Sweden: Combined sewer system. J. Hydrol. 2008, 350, 100–113. [Google Scholar] [CrossRef]
- Lund, N.L.S.; Borup, M.; Madsen, H.; Mark, O.; Arnbjerg-Nielsen, K.; Mikkelsen, P.S. Integrated stormwater inflow control of sewers, green infrastructure and urban landscapes. Nature Sustain. 2019, 2, 1003–1010. [Google Scholar] [CrossRef]
- Lessard, P.; Beck, M.B. Operational water quality management: Control of storm sewage at a wastewater treatment plant. Res. J. Water Pollut. Control Fed. 1990, 62, 810–819. [Google Scholar]
- Ahnert, M.; Tra, J.; Gu, N.; Hoeft, S.; Krebs, P. Model-based comparison of two ways to enhance WWTP capacity under stormwater conditions. Water Sci. Technol. 2009, 60, 1875–1883. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Gao, H.; Zhao, X.; Chen, X.; Hong, S.N. Wastewater treatment: Enhanced biological treatment of storm flows. Filtr. Sep. 2010, 47, 23–27. [Google Scholar] [CrossRef]
- Rönner-Holm, S.G.E.; Alves, I.K.; Steinmetz, H.; Holm, N.C. Optimisation potential for a SBR plant based upon integrated modelling for dry and wet weather conditions. Water Sci. Technol. 2009, 60, 1953–1964. [Google Scholar] [CrossRef] [PubMed]
- Munk-Nielsen, T.; Poulsen, T.S.; Öennerth, T.B.; Thirsing, C. Real time control combined with weather radar forecast and aeration tank settling improves the hydraulic capacity and the treatment efficiency during wet weather operation. In Proceedings of the 2nd IWA New Developments in IT & Water Conference, Rotterdam, The Netherlands, 8–10 February 2015. [Google Scholar]
- Thorndahl, S.; Einfalt, T.; Willems, P.; Nielsen, J.E.; ten Veldhuis, M.-C.; Arnbjerg-Nielsen, K.; Rasmussen, M.R.; Molnar, P. Weather radar rainfall data in urban hydrology. Hydrol. Earth Syst. Sci. 2017, 21, 1359–1380. [Google Scholar] [CrossRef]
- Thorndahl, S.; Rasmussen, M.R. Short-term forecasting of urban storm water runoff in real-time using extrapolated radar rainfall data. J. Hydroinformatics 2013, 15, 897–912. [Google Scholar] [CrossRef]
- Heinonen, M.; Jokelainen, M.; Fred, T.; Koistinen, J.; Hohti, H. Improved wet weather wastewater influent modelling at Viikinmäki WWTP by on-line weather radar information. Water Sci. Technol. 2013, 68, 499–505. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Wei, X.; Kusiak, A. Short-term prediction of influent flow in wastewater treatment plant. Stoch. Environ. Res. Risk Assess. 2015, 29, 241–249. [Google Scholar] [CrossRef]
- Richardson, D.S. Skill and relative economic value of the ECMWF ensemble prediction system. Q. J. R. Meteorol. Soc. 2000, 126, 649–667. [Google Scholar] [CrossRef]
- Courdent, V.; Grum, M.; Munk-Nielsen, T.; Mikkelsen, P.S. A gain–loss framework based on ensemble flow forecasts to switch the urban drainage–wastewater system management towards energy optimization during dry periods. Hydrol. Earth Syst. Sci. 2017, 21, 2531–2544. [Google Scholar] [CrossRef]
- Einfeldt, J. The implementation of biological phosphorus and nitrogen removal with the Bio-Denipho proces on a 265,000 PE treatment plant. Water Sci. Technol. 1992, 25, 161–168. [Google Scholar] [CrossRef]
- BIOFOS: Miljøberetning, Copenhagen. Available online: http://www.biofos.dk/wp-content/uploads/2014/11/Miljoeberetning-2015.pdf (accessed on 17 June 2017).
- Bundgaard, E.; Nielsen, M.K.; Henze, M. Process development by full-scale on-line tests and documentation. Water Sci. Technol. 1996, 33, 281–287. [Google Scholar] [CrossRef]
- Nielsen, M.K.; Carstensen, J.; Harremoës, P. Combined control of sewer and treatment plant during rainstorm. Water Sci. Technol. 1996, 34, 181–187. [Google Scholar] [CrossRef]
- Nielsen, M.K.; Bechmann, H.; Henze, M. Modelling and test of aeration tank settling (ATS). Water Sci. Technol. 2000, 41, 179–184. [Google Scholar] [CrossRef]
- Sharma, A.K.; Guildal, T.; Thomsen, H.A.R.; Mikkelsen, P.S.; Jacobsen, B.N. Aeration tank settling and real time control as a tool to improve the hydraulic capacity and treatment efficiency during wet weather: Results from 7 years’ full-scale operational data. Water Sci. Technol. 2013, 67, 2169–2176. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, M.K.; Lynggaard-Jensen, A. Superior tuning and reporting (STAR)—A new concept for on-line process control of wastewater treatment plants. In Proceedings of the IAWQ ICA Workshop, Hamilton, ON, Canada, 17–25 June 1993. [Google Scholar]
- Thorndahl, S.; Rasmussen, M.R. Vejrradarbaseret Styring af Spildevandsanlæg; DCE Technical Report No. 95; Aalborg University: Aalborg, Denmark, 2010. [Google Scholar]
- Pedersen, J.W.; Lund, N.S.V.; Borup, M.; Löwe, R.; Poulsen, T.S.; Mikkelsen, P.S.; Grum, M. Evaluation of Maximum a Posteriori Estimation as Data Assimilation Method for Forecasting Infiltration-Inflow Affected Urban Runoff with Radar Rainfall Input. Water 2016, 8, 381. [Google Scholar] [CrossRef]
- Korsholm, U.S.; Petersen, C.; Sass, B.H.; Nielsen, N.W.; Jensen, D.G.; Olsen, B.T.; Gill, R.; Vedel, H. A new approach for assimilation of 2D radar precipitation in a high-resolution NWP model. Meteorol. Appl. 2015, 22, 48–59. [Google Scholar] [CrossRef]
- Olsen, B.T.; Korsholm, U.S.; Petersen, C.; Nielsen, N.W.; Sass, B.H.; Vedel, H. On the performance of the new NWP nowcasting system at the Danish Meteorological Institute during a heavy rain period. Meteorol. Atmos. Phys. 2015, 127, 519–535. [Google Scholar] [CrossRef]

| Perfect Control | ||||
|---|---|---|---|---|
| On | Off | |||
| Real/Simulated control | On | Hits (a) REV: G | False alarms (b) REV: L1 | a + b |
| Off | Misses (c) REV: L2 | Correct negatives (d) REV: 0 | c + d | |
| a + c | b + d | a + b + c + d = n | ||
| Score | Formula | Range | Perfect |
|---|---|---|---|
| PoD, Probability of detection | a/(a + c) | [0, 1] | 1 |
| PoFD, Probability of false detection | b/(b + d) | [0, 1] | 0 |
| CSI, Critical success index | a/(a + b + c) | [0, 1] | 1 |
| µ, Occurrence frequency of events | (a + c)/n | [0, 1] | n/a |
| Acronym | Explanation | WWTP Flow Meas. (A, Figure 4) | Upstream Flow Meas. (B, Figure 4) | Radar Prognosis (C) | ||
|---|---|---|---|---|---|---|
| Baseline (Flow) | Optimized (Flow) | New (Volume) | ||||
| REF-3 | Reference control strategy (Section 2.3 and Section 3.4.1) | X | ||||
| FOR-1 | ATS control switch originally installed in 2012 | X | X | |||
| FOR-2 | Baseline ATS control switch described in Section 3.3 and Figure 4 | X | X | X | ||
| FOR-3.1 | Like above, but with optimized flow-thresholds | X | X | X | ||
| FOR-3.2 | ||||||
| FOR-4 | New control-switch, based on volume-forecasting | X | X | X | ||
| PERFECT | Perfect control (Section 3.4.1) | n/a | n/a | n/a | n/a | n/a |
| Bypass Volume [106 m3 y−1] | Percentage of Reduction | Number of ATS Events per Year | Prop. of ATS Operation | PoD | PoFD | CSI | |||
|---|---|---|---|---|---|---|---|---|---|
| With/Without TSS Ctrl | With/Without TSS Ctrl | ||||||||
| Without ATS | - | 3.89 | - | - | - | - | - | - | - |
| REF-3 | - | 2.08 | - | 46.4% | 188 | 11% | 0.82 | 0.008 | 0.78 |
| FOR-1 | - | 1.97 | - | 49.4% | 183 | 12.7% | 0.87 | 0.020 | 0.76 |
| FOR-2 (Baseline) | 2.78 | 1.88 | 28.5% | 51.7% | 281 | 18.8% | 0.93 | 0.080 | 0.60 |
| FOR-3.1 (1, 0.8) | - | 1.94 | - | 51.1% | 174 | 12.1% | 0.89 | 0.020 | 0.78 |
| FOR-3.2 (1, 0.2) | - | 1.85 | - | 52.5% | 227 | 16.0% | 0.94 | 0.055 | 0.68 |
| FOR-4 | - | 1.85 | - | 52.5% | 209 | 15.6% | 0.94 | 0.045 | 0.71 |
| Perfect | - | 1.80 | - | 53.8% | 91 | 12.5% | 1 | 0 | 1 |
| Perfect ATS Control | |||
|---|---|---|---|
| On | Off | ||
| Current ATS control | On | 0.1169 | 0.0712 |
| Off | 0.0082 | 0.8036 | |
| Upstream Flow Threshold [m3 h−1] | Radar Flow Prognosis Threshold [m3 h−1] | |
|---|---|---|
| FOR-3.1 (1, 0.8) | 4000 | 16,875 |
| FOR-3.2 (1, 0.2) | 2855 | 9500 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Courdent, V.; Munk-Nielsen, T.; Mikkelsen, P.S. Optimizing the Activation of WWTP Wet-Weather Operation Using Radar-Based Flow and Volume Forecasting with the Relative Economic Value (REV) Approach. Water 2024, 16, 2806. https://doi.org/10.3390/w16192806
Courdent V, Munk-Nielsen T, Mikkelsen PS. Optimizing the Activation of WWTP Wet-Weather Operation Using Radar-Based Flow and Volume Forecasting with the Relative Economic Value (REV) Approach. Water. 2024; 16(19):2806. https://doi.org/10.3390/w16192806
Chicago/Turabian StyleCourdent, Vianney, Thomas Munk-Nielsen, and Peter Steen Mikkelsen. 2024. "Optimizing the Activation of WWTP Wet-Weather Operation Using Radar-Based Flow and Volume Forecasting with the Relative Economic Value (REV) Approach" Water 16, no. 19: 2806. https://doi.org/10.3390/w16192806
APA StyleCourdent, V., Munk-Nielsen, T., & Mikkelsen, P. S. (2024). Optimizing the Activation of WWTP Wet-Weather Operation Using Radar-Based Flow and Volume Forecasting with the Relative Economic Value (REV) Approach. Water, 16(19), 2806. https://doi.org/10.3390/w16192806






