Abstract
This study introduces a time-lag-informed Random Forest (RF) framework for streamflow time-series prediction across diverse catchments and compares its results against SWAT predictions. We found strong evidence of RF’s better performance by adding historical flows and time-lags for meteorological values over using only actual meteorological values. On a daily scale, RF demonstrated robust performance (Nash–Sutcliffe efficiency [NSE] > 0.5), whereas SWAT generally yielded unsatisfactory results (NSE < 0.5) and tended to overestimate daily streamflow by up to 27% (PBIAS). However, SWAT provided better monthly predictions, particularly in catchments with irregular flow patterns. Although both models faced challenges in predicting peak flows in snow-influenced catchments, RF outperformed SWAT in an arid catchment. RF also exhibited a notable advantage over SWAT in terms of computational efficiency. Overall, RF is a good choice for daily predictions with limited data, whereas SWAT is preferable for monthly predictions and understanding hydrological processes in depth.
1. Introduction
Accurate and timely streamflow estimation in watersheds and water resource systems is essential for efficient and effective water resource management [1,2,3]. However, the quickly changing nature of the flow, shaped by ecohydrological and climate changes coupled with human activities, poses a considerable challenge for flow prediction [2,3,4]. To mitigate this problem, several hydrological models, ranging from simple empirical models to sophisticated process-based models, have been developed and extensively employed to effectively simulate a wide range of hydrological processes, including streamflow [5,6,7,8,9,10]. The Soil and Water Assessment Tool (SWAT) is a widely utilized process-based eco-hydrological model that integrates hydrological processes based on the water-balance principle [11]. Several studies have demonstrated the reliability of SWAT for accurately depicting spatial information and efficiently modeling diverse hydrological processes across a range of watershed scales [7,9,12,13].
Despite its widespread adoption, SWAT has faced criticism for its demanding data requirements, which make hydrological modeling computationally expensive and challenging [10,14,15,16]. The inherent complexity of its process-based approach also poses difficulties for users with limited hydrologic expertise [2]. In addition, its heavy reliance on detailed soil and land use information presents a significant challenge, particularly in regions with limited data availability [14,17]. The calibration of multiple parameters in SWAT is a complex process, and introduces uncertainties in the model’s outcomes [15] and the potential for misleading conclusions due to equifinality, in which different parameter sets yield similar results [18]. SWAT also has limitations in representing groundwater systems accurately, as it lacks the ability to account for geological information and neglects inter-basin groundwater flows [18,19]. Furthermore, its shortcomings extend to an inability to capture non-linear flows [15] and to model hydrological processes in mid- and high-latitude regions and arid areas [20]. However, using physics-based models such as SWAT continues to be a crucial method for comprehending the fundamental physical mechanisms that govern hydrological fluctuations.
In recent years, the use of machine learning (ML) techniques including the Random Forest (RF) model [21,22,23,24,25], support-vector regression [21,26,27], and deep learning such as artificial neural network [28,29], long-short-term-memory (LSTM) neural networks [30,31], and extreme gradient-boosting neural networks [32,33,34], have gained significant attention among hydrologists as alternatives to traditional process-based models [15,35]. ML methods are capable of capturing non-linear processes numerically with no knowledge of the underlying physical processes involved [1,36,37,38,39]. Moreover, ML models can identify relationships between input and output variables, which lead to inherent errors in streamflow estimates [2,35]. Despite the potentially time-consuming training phases, ML predictions are faster than process-based models [35]. In addition, ML models pre-trained on data from diverse basins can be fine-tuned for specific basins through transfer learning.
Previous studies have mainly shown that LSTM models perform very well in flow prediction [30,31,37,38,39,40]. LSTM models can also store and regulate information over time [41,42], making these models particularly suitable for simulating the memory effects of different hydrological variables with short-term and long-term dependencies. However, LSTM, as a deep learning method, is computationally quite expensive and produces results that are not easily explainable. This is problematic because, in modeling natural processes, explainability is essential so that model users can understand the outputs and validate them against physical processes.
Among regression-based models, RF has gained popularity in flow prediction due to its advantages in terms of visualization and interpretation of the model structure, as well as its computational efficiency [43,44,45,46,47]. Shortridge et al. [46] showed that RF can also outperform artificial neural networks but pointed out that model predictions have too-high uncertainty under extreme weather conditions. Tongal and Booij [47] observed good performance of RF in predicting streamflow for four rivers in the United States. Similarly, Fernández-Delgado et al. [48] compared 179 learning models from 17 families using 121 classification datasets, and found that RF performed best in terms of its error magnitude.
Despite its notable strengths, RF lacks the inherent capability to consider ordered sequences or the time-dependent structure of data, which poses challenges in time-series forecasting [49,50]. Unlike other ML or deep learning models, such as LSTM, which capture long-term dependencies and complex patterns in hydrological time series [37,51], RF has a limited ability to capture temporal dependencies.
Our study aimed to overcome these limitations of RF by incorporating covariates that explicitly account for temporal dependencies into the RF model. We introduced time lags, rolling aggregates, and calendar-based variables like day and month of the year, which allow the model to capture relevant temporal patterns and seasonal variations in the data. These modifications aimed to improve the predictive power of RF in time-series-based streamflow forecasting by simulating the temporal awareness inherent in models such as LSTM. In addition, we aimed to compare the performance of RF with SWAT more rigorously. Previous comparisons have mainly centered around aspects like forecasting sediment yield and soil erosion [15,52,53], evaluating aquatic ecosystems [54], and assessing the impact of climate change on stream ecology [55]. This highlights the need for a comparison that specifically addresses streamflow prediction. Moreover, previous studies that compared SWAT and RF models for streamflow prediction were often restricted to catchments with similar climates and topographic conditions, and typically focused on daily or monthly time scales. Therefore, the second aim of this study was to compare the predictive capabilities of RF and SWAT in simulating streamflow on daily and monthly time steps across four catchments with very different climatic and topographic conditions.
Specifically, our study answered the following research questions: (1) How can RF’s limitations in handling time-series data be addressed? (2) How well does the time-lag-adjusted RF perform compared to the process-based model SWAT among different catchments? (3) Which model is more computationally efficient? The last research question is particularly relevant in light of efforts to reduce the carbon footprint of AI to achieve “green AI” [56,57].
2. Study Areas
We used four study catchments with different sizes, land use, topography, and climatic conditions as our study areas: Argos (Spain), Porijõgi (Estonia), Rib (Ethiopia), and Bald Eagle (USA) (Figure 1).
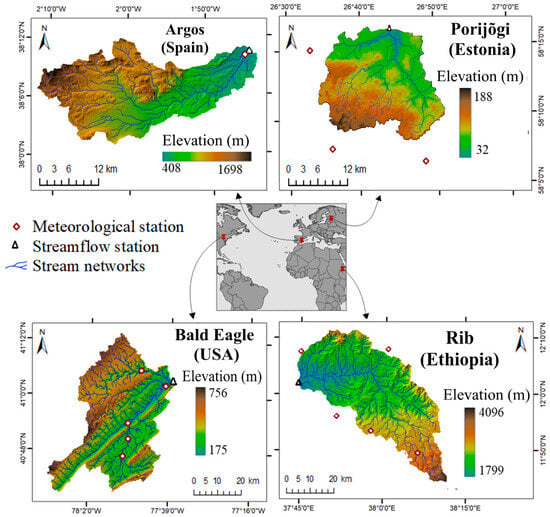
Figure 1.
Locations of the study areas.
The Argos catchment, covering an area of 448 km2, is situated in southeastern Spain at elevations ranging from 408 to 1698 m above sea level (m a.s.l.). The catchment primarily comprises calcic Xerosols, although a range of soil types can be found [58]. The catchment is characterized by a semi-arid climate with mean annual precipitation between 345 and 440 mm, and an average monthly temperature that typically ranges from 11 to 16 °C [58].
The Porijõgi catchment, situated in southern Estonia, spans an area of 235 km2 at elevations ranging from 32 to 188 m a.s.l. Agriculture and forests account for 45 and 49% of the total area, respectively [59]. The predominant upland soils are podzoluvisols, planosols, and podzols with loamy sand or fine sandy loam texture and a surface soil organic matter content of 1.6 to 1.9% (Kmoch et al., 2021). The mean annual precipitation and temperature are 678 mm and 6.4 °C, respectively [60].
The Rib catchment, spanning 1293 km2, is situated in the northwestern Ethiopian highlands, with an elevation range of 1799 to 4096 m a.s.l. The dominant land use is cropland, accounting for more than 85% of the area [61]. The catchment contains various soil types, including Luvisols, Vertisols, Leptosols, and Regosols, which cover more than 80% of the land [62]. The mean annual precipitation and temperature are 1502 mm and 15.6 °C, respectively [63].
The Bald Eagle–Spring Creek catchment (1446 km2) lies in Pennsylvania State, USA, spanning Center and Clinton counties. Its elevation ranges between 175 and 756 m a.s.l, and the physiographic province comprises valley, ridge, and Appalachian plateau topography. To simplify the modeling, we restricted the catchment boundary to the sub-basin, including the streamflow gauge location farthest downstream. Loam and fine loam soils are predominant, and the catchment experiences an average annual precipitation of around 1000 mm and a mean annual temperature of approximately 10 °C [64].
3. Materials and Methods
3.1. RF Model
RF is a supervised ensemble-learning algorithm that consists of many regression trees that together form the “forest” [65]. RF uses a set of observed input training data to predict the mean of the decision-tree ensemble for new input data [45]. The model minimizes over-fitting and statistical uncertainty by using the bootstrap aggregation (bagging) technique to build many decision trees by randomly sampling the observed dataset with replacement [47,66]. As a result, the trees have low bias and high variance, which leads to a more robust overall model after averaging the predictions of the individual regression trees [67,68].
We developed six RF models for each watershed (three for daily and three for monthly flow prediction) using different combinations of predictors. The predictor variables (features) we utilized were derived from datasets containing daily precipitation, streamflow, maximum temperature, and minimum temperature (Table 1). Unlike deep learning methods such as LSTM, RF generally has no internal concept to model or to explain ordered data sequences, such as time steps. One way to model temporal dependencies in time series, such as the sequence of streamflow days and weeks before a focal time, is to create these explicitly as individual covariates. Here, we employed various time lags, rolling aggregates of previous observations, and numeric representations of the day or month of the year alongside the actual measurement value at each time step to let RF learn the time sequences and improve its predictive capabilities. In the context of our RF model, a time lag refers to using past measurements of predictor variables (precipitation, temperature, and streamflow) from previous days or months to predict future streamflow. Rolling aggregates refer to using summary statistics (mean, maximum, and minimum) of variables over a certain period of time (e.g., 7 days or 3 months) as additional predictors. Day and month of the year represent the calendar time at which a particular measurement was recorded.
For daily prediction, we focused on time lags of 1 to 7 days, with a 1-day lead time, following Rasouli et al.’s [69] recommendation that shorter lead times are more effective for local observation-based predictors. For monthly prediction, we extended the time lag window to 12 months with a 1-month lead time to capture longer-term patterns and dependencies (Figure 2). We also used rolling aggregates as predictor variables, encompassing the previous 7 to 28 days with a 7-day gap for daily steps, and 3 to 12 months with a 3-month gap for monthly steps. Consequently, we created different feature sets (predictor combinations), which resulted in three daily models (DM1, DM2, and DM3) and three monthly models (MM1, MM2, and MM3). Streamflow was not used as a predictor in DM1 and MM1. The precipitation and temperature were excluded from DM2 and MM2. Finally, DM3 and MM3 used all predictors from DM1 and MM1, respectively, while also including the streamflow measurement for the corresponding day or month. We allocated the observed streamflow data into two datasets: 50% for model development (training) and 50% for model evaluation (testing). The number of trees used to train each of the RF models was set to 100. The RF models were built using the Scikit-learn Python package version 1.5.2 [70].
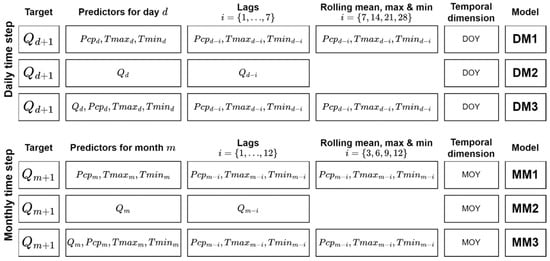
Figure 2.
Overview of the three daily and three monthly Random Forest models with different feature sets. Abbreviations: DM1, DM2, and DM3, RF models at a daily time step; DOY, numeric day of the year; i, lag days or months; MM1, MM2, and MM3, Random Forest models at a monthly time step; MOY, numeric month of the year; Pcpd, average precipitation on day d; Pcpm, average precipitation in month m; Qd, average streamflow on day d; Qd+1, streamflow prediction for the next day; Qm, average streamflow in month m; Qm+1, streamflow prediction for the next month; Tmaxd and Tmind, maximum and minimum air temperature on day d; Tmaxm and Tminm, maximum and minimum air temperature in month m.
3.2. SWAT Model
SWAT is a hydrological model that operates at different time steps and regulates the hydrological processes in a catchment to quantify their rate of change [11]. The model uses a water-balance equation that includes factors such as precipitation, surface runoff, percolation, evapotranspiration, lateral flow, and baseflow [71]. The model requires input data such as a digital elevation model (DEM), soil, land use, and hydro-climatic data. We used the same global land use, soil, and DEM data sources for all catchments (Table 1). These environmental factors greatly influence SWAT’s performance by affecting hydrological processes such as evapotranspiration, runoff, infiltration, and nutrient dynamics, which in turn enhance its simulation accuracy across different conditions (refer to [72] for detailed insights on their impact and spatial variability within the studied watershed). We obtained the daily hydro-meteorological data records (streamflow, precipitation, maximum temperature, and minimum temperature; Figure S1) from the hydro-meteorological service centers of the studied countries. We used the QSWAT3 interface [73] with QGIS 3.16 to build one model for each catchment. We simulated the models at daily and monthly time steps and calibrated and validated the models using the SUFI-2 method in the SWAT-CUP software version 5.1.3 [74]. Hereafter, we will use the terms “training” and “testing” to refer to the calibration and validation phases of SWAT to maintain consistency with the RF model nomenclature. For all catchments, we utilized the same period of 14 years, with the initial 2 years designated for model warmup and the remaining years evenly divided between training and testing phases (Tables S1 and S2).


Table 1.
Summary of the data used in this study. Abbreviations: DEM, digital elevation model; ESA, European Space Agency.
Table 1.
Summary of the data used in this study. Abbreviations: DEM, digital elevation model; ESA, European Space Agency.
| Dataset | Description | Sources |
|---|---|---|
| Elevation data | AW3D30 DEM at 30 m spatial resolution, released in 2022 | JAXA [75] |
| Landcover map | ESA land cover data for 2020 at 10 m spatial resolution | Zanaga et al. [76] |
| Soil map | Harmonized World Soil Database v1.2 for 2008 at 1 km spatial resolution | Fischer et al. [77] |
| Hydro-meteorological data | Daily streamflow, precipitation, maximum temperature, and minimum temperature | Hydro-meteorological service centers of the studied countries |
3.3. Model Evaluation Metrics
We assessed the predictive capacity of the models using three metrics: the Nash–Sutcliffe efficiency coefficient (NSE) [78], normalized root-mean-squared errors (NRMSE), and percentage of bias (PBIAS) [79] (Table 2). NSE measures the agreement between observed and predicted values, with a perfect fit indicated by a value of 1 and a value exceeding 0.5 considered acceptable [80]. NRMSE offers a standardized measure of accuracy by normalizing the error and accounting for data variability. We selected NRMSE over RMSE to facilitate comparisons across different catchments (i.e., catchments with varying ranges of parameter values). PBIAS quantifies the average tendency of simulated data to deviate from observed data, and expresses the extent of over- or underestimation as a percentage [81].

Table 2.
Statistical metrics used for performance evaluation of the Soil and Water Assessment Tool (SWAT) and Random Forest (RF) models. O and P refer to the observed and predicted (simulated) streamflow, respectively; Ō refers to the mean observed streamflow, and n is the number of observations. Abbreviations: NRMSE, normalized root-mean-squared error; NSE, Nash–Sutcliffe efficiency; PBIAS, percentage of bias.
The results were visualized using boxplots, Taylor diagrams, and hydrographs. The Taylor diagram [82] provides a visual representation that effectively illustrates the proximity between predicted values and observed data based on key metrics such as Pearson’s correlation coefficient, centered root-mean-squared errors (CRMSE), and standard deviations. Figure 3 illustrates the workflow we applied to compare and evaluate the performance of the SWAT and RF models. In addition, the most important predictors for the RF models were detected using the SHapley Additive exPlanations (SHAP) explainable AI method [83]. SHAP values indicate how much (i.e., m3 s−1) and in which direction (i.e., increase or decrease in streamflow) each predictor contributes to the model’s prediction, with more important predictors accounting for more variance in the predictions.
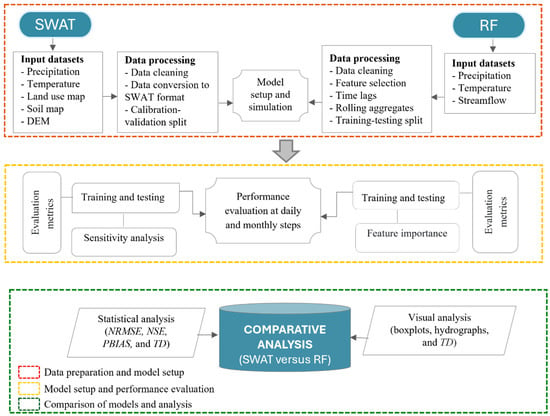
Figure 3.
Workflow used to compare the performance of SWAT and RF models. Abbreviations: DEM, digital elevation model; NRMSE, normalized root-mean-square error; NSE, Nash–Sutcliffe efficiency coefficient; PBIAS, percentage of bias; RF, Random Forest; SWAT, Soil and Water Assessment Tool; TD, Taylor diagram.
4. Results
4.1. Performance of RF
There were differences in RF performance between catchments. Of the three daily RF models, DM2 and DM3 generally achieved satisfactory performance on a daily time step (NSE > 0.5), except for the Argos catchment (NSE < 0.25; Figure 4A). However, when streamflow was excluded as a predictor (model DM1), the model failed to accurately predict daily flows in all catchments (NSE < 0), except for Rib (NSE = 0.81). For monthly predictions, all RF models exhibited poor performance during the testing period (NSE < 0.4) in all catchments, except for Rib (NSE > 0.75) (Figure 4B). All RF models generally performed well in the Rib catchment at both temporal steps. For Argos, all monthly RF models outperformed the daily models. Overall, when the streamflow is considered as a predictor (MM2 and MM3), RF exhibited better performance on a daily step than on a monthly step in most cases. Flow (Q) consistently emerged as the main predictor in all catchments for daily predictions (DM3 model; Figure S2) and, in most cases, for monthly predictions (MM3 model; Figure S3), highlighting its strong influence on the model’s predictions.
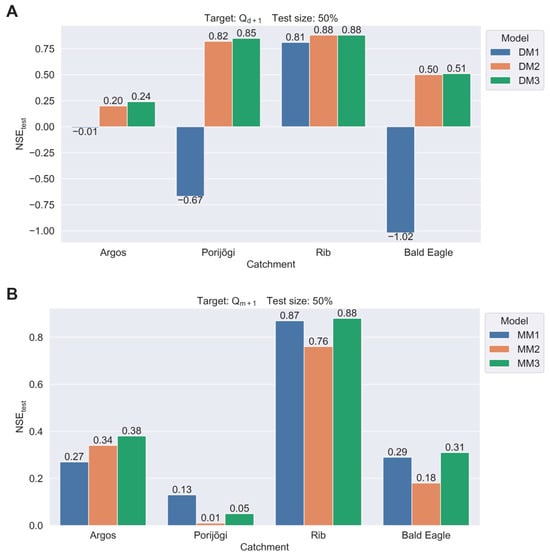
Figure 4.
Nash–Sutcliffe efficiency (NSE) for the (A) daily and (B) monthly streamflow predictions (during the testing period) for the Random Forest models.
4.2. Performance of SWAT
The global sensitivity analysis for streamflow calibrations with SWAT revealed that among the sensitive parameters identified, the Curve Number (r_CN2) exhibited the highest statistically significant sensitivity across all catchments (Table 3). In addition, the parameters associated with groundwater (v_GWQMN, v_ALPHA_BF, v_RCHRG_DP), soil properties (r_SOL_BD), and slope steepness (v_HRU_SLP) exhibited a statistically significant sensitivity in most catchments. In the Rib catchment, a substantial reduction (36%) in the fitted value of r_CN2 was observed, but there was an increase in the value of v_HRU_SLP (0.42 m/m). The forested catchments (Porijõgi and Bald Eagle) had a higher soil evaporation compensation factor (v_ESCO) than the other catchments. Furthermore, in the Argos and Rib catchments, the fitted values of v_GW_DELAY were much higher than the values in the other catchment and indicated a significant time delay (>400 days) between the water leaving the soil profile and it entering the shallow aquifer.

Table 3.
Sensitivity analysis results for parameters that were commonly sensitive across all catchments during the training period on a monthly time step. Parameters (r = relative change to the initial value (i.e., multiplication of the existing value by [1 + given value]), v = replacement of the actual value by a given value: CN2, Soil Conservation Service (SCS) runoff curve number; SOL_BD, moist soil bulk density (g/cm3); GW_DELAY, groundwater delay (days); RCHRG_DP, recharge to the deep aquifer; GWQMN, depth of water for return flow (mm); GW_REVAP, groundwater “revap” coefficient; ALPHA_BF, baseflow alpha factor for the recession constant (days); HRU_SLP, average slope steepness (m/m); ESCO, soil evaporation compensation factor; CH_N2, Manning coefficient for main channel; CH_K1, effective hydraulic conductivity in tributary channel alluvium (mm/h). *, significant at p < 0.05.
During the testing period, the performance of SWAT for daily predictions was generally unsatisfactory (NSE < 0.5), except in the Rib catchment (NSE = 0.86) (Table 4). Most catchments (except Argos) also experienced overestimation of the daily streamflow prediction (positive PBIAS values) and significant discrepancies between predicted and measured values, resulting in larger prediction errors (NRMSE > 5%). However, SWAT generally exhibited good performance for monthly predictions. Based on the criteria of Moriasi et al. (2007), the model achieved satisfactory or better performance (NSE > 0.5) in most cases, except for Argos and Bald Eagle during the testing period (NSE < 0.5) (Table 5). However, the Argos and Porijõgi catchments exhibited significant prediction errors on the monthly time step, particularly during testing (NRMSE > 18%, except for Rib). SWAT showed a general tendency to underestimate peak flows and overestimate base flows across all catchments on both daily and monthly steps.

Table 4.
Statistical summary of daily streamflow prediction performance across catchments using the Soil and Water Assessment Tool (SWAT) model and the Random Forest (RF) DM3 model. Abbreviations: NRMSE, normalized root-mean-square error; NSE, Nash–Sutcliffe efficiency; PBIAS, percentage of bias.

Table 5.
Statistical summary of monthly streamflow prediction performance across catchments using the Soil and Water Assessment Tool (SWAT) model and Random Forest (RF) MM3 model. Abbreviations: NRMSE, normalized root-mean-square error; NSE, Nash–Sutcliffe efficiency.
4.3. Comparing the Performance of RF and SWAT
To compare RF with SWAT, we focused on the daily DM3 model and the monthly MM3 model, which included all predictors and were the best-performing RF models. For daily predictions, RF outperformed SWAT, with higher correlation coefficients and lower CRMSE values between the observed and modeled values across all catchments in both the training and testing periods (Figure 5). SWAT’s predictions on a daily time step generally displayed lower correlations and larger deviations from the observed data, indicating a greater difference between actual and predicted flows. Moreover, daily RF generally demonstrated strong performance based on the other statistical metrics (NSE > 0.5, NRMSE < 7%, PBIAS ≤ ±5; Table 4). In most cases, SWAT tended to overestimate the daily streamflow, especially for Bald Eagle during testing (PBIAS = 27.4%) and Porijõgi during training (PBIAS = 22.6%). Conversely, RF provided more reasonable predictions, with only slight over- or underestimation in a few cases. This trend was further supported by visual analysis of the hydrographs (Figure 6), where the RF model demonstrated better performance in capturing both peak- and base-flow levels.
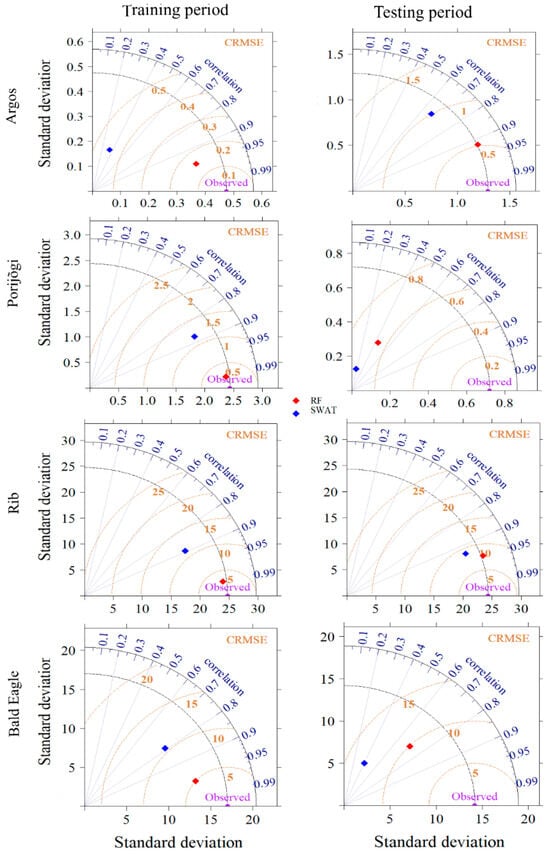
Figure 5.
Taylor diagrams for comparison of the observed daily streamflow and the predictions by the Random Forest (RF) DM3 model and the Soil and Water Assessment Tool (SWAT) model across catchments. The “observed” data points (purple) are the reference values for evaluating the model predictions. The black dashed line corresponds to the standard deviation of the observed data. The golden contour lines indicate the values of the centered root-mean-squared errors (CRMSE). Perfect alignment between the observed and predicted values at the “observed” data point suggests a strong correlation, with no error (zero CRMSE) and similar variability (a similar standard deviation).
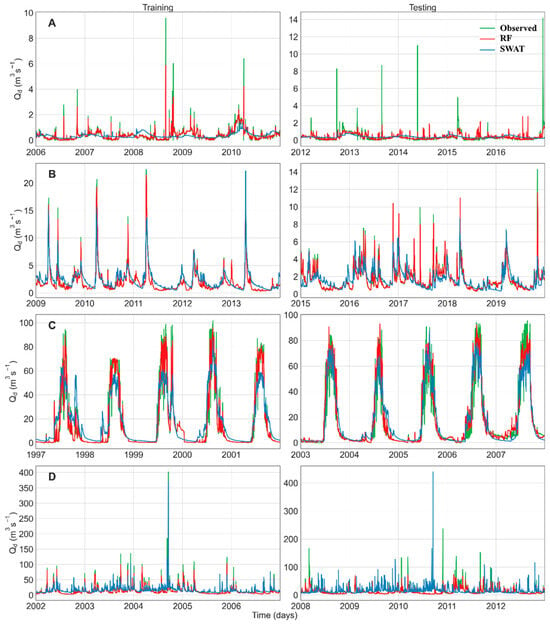
Figure 6.
Hydrographs for comparison of the observed daily streamflow to the predictions of the Random Forest (RF) DM3 model and the Soil and Water Assessment Tool (SWAT) model for the (A) Argos, (B) Porijõgi, (C) Rib, and (D) Bald Eaglecatchments.
For the monthly predictions, SWAT outperformed RF, particularly in catchments with irregular flow regimes (Figure 7). The SWAT and RF models both achieved satisfactory or better performance during training in all catchments (NSE > 0.5). However, RF struggled to maintain acceptable performance during testing, especially for Porijõgi (NSE = 0.05; Table 5). The monthly predictions showed higher NRMSE values than the daily predictions across all catchments except Rib. However, the monthly prediction for Rib exhibited the lowest NRMSE values compared to the monthly and daily predictions in other catchments. For Argos (the arid catchment), RF generally outperformed SWAT in terms of all metrics and in the visual analysis for both temporal steps.
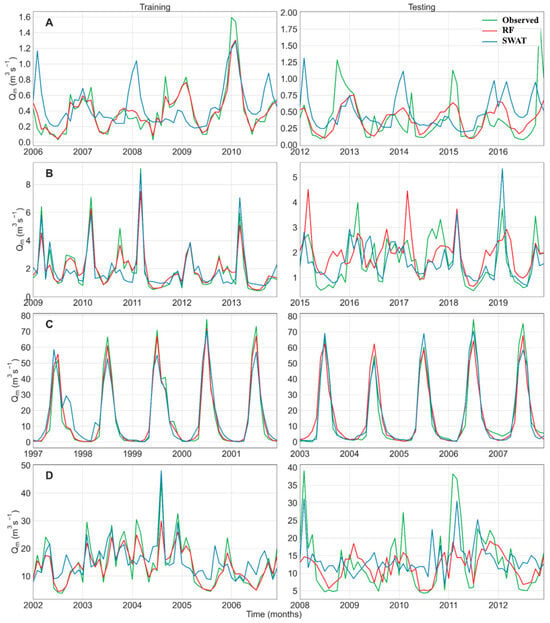
Figure 7.
Hydrographs for comparison of the observed monthly streamflow and the predictions by the Random Forest (RF) MM3 model and the Soil and Water Assessment Tool (SWAT) model in the (A) Argos, (B) Porijõgi, (C) Rib, and (D) Bald Eagle catchments.
4.4. Computational Efficiency
We evaluated the computational efficiency of SWAT and RF by measuring the total time required to complete a simulation. On a single-core Windows computer with a 3.60 GHz processor and 64 GB of RAM, the average time needed for a single simulation in SWAT ranged between 78 s (on a monthly time step) to 90 s (on a daily time step). Achieving satisfactory NSE values in SWAT demanded a considerable amount of time: 10 to 14 iterations, each requiring 1500 to 2000 simulations. The time needed for SWAT simulations, therefore, ranged from approximately 72 h for Porijõgi on a monthly time step to approximately 241 h for Bald Eagle on a daily time step (Figure S4A). In contrast, the RF models exhibited remarkable computational efficiency compared to SWAT. With a maximum training time of less than 12 s for the daily time step (Figure S4B), testing RF on both daily and monthly time steps required less than 12 s. It is essential to highlight that our comparison primarily focused on the training and testing phases of the models; nevertheless, developing a fully functional SWAT model demanded considerable overall time.
5. Discussion
5.1. Temporal Considerations and Feature Engineering for RF Models
Our investigation of the performance of RF revealed significant differences that depended on the combination of predictors employed. Sole reliance on precipitation and temperature proved insufficient for precise streamflow predictions, which is likely to be attributable to the existence of non-linear relationships and a weak correlation between meteorological variables and streamflow [47]. However, we observed a notable improvement in prediction accuracy when incorporating historical flow values as inputs. This improvement can be ascribed to the influence of prior observations, which facilitate and improve utilization of historical patterns and permit more effective management of temporal dependencies [15,45,47,84]. Moreover, our results suggest that RF models that incorporate time-lag information as inputs performed better than models without lag information. This could be associated with the complex and lagged relationship between streamflow and meteorological variables [47,85], which is influenced by factors such as variable soil types, land cover and use types, and geological characteristics [85,86]. As a result, integrating the lagged information into predictions supports a more thorough comprehension of the temporal dynamics of streamflow and a more accurate representation of the interplay between meteorological factors and streamflow processes.
The selection of optimal time lags as predictors significantly influence the accuracy of streamflow predictions [28,47,87]. Conversely, including inefficient or redundant lags may lead to the development of poor or overly complex models [28]. Our analysis indicates that time lags ranging from 1 to 7 days for daily predictions and 1 to 3 months for monthly predictions result in satisfactory model performance. This suggests that shorter time lags effectively capture relevant patterns and dependencies in the data, which agrees with previous findings that historical data with longer intervals, significantly exceeding 60 days, do not yield notable improvements [85,88]. However, it is essential to note that the ideal lag periods for hydrological variables may differ among sub-basins of a catchment [85].
5.2. Comparison of RF and SWAT
RF outperformed SWAT in daily predictions, whereas SWAT was more accurate for monthly predictions, particularly in catchments with irregular flow patterns. This observation agrees with Jimeno-Sáez et al.’s [15] findings, and highlights the better performance of ML models, including RF, over SWAT for daily hydrological predictions. RF has exhibited robust performance, even at shorter temporal scales such as hourly scales, as has been indicated in multiple studies [89,90]. This suggests that ML can effectively capture the characteristics of complex hydrological systems [8,15,91]. RF’s ensemble learning, which incorporates multiple decision trees, enhances its ability to recognize patterns under extreme flow conditions, thereby improving its accuracy in capturing both peak events and baseflow dynamics, which is critical for flood forecasting and water resource management [45,92]. Akbarian et al. [93] and Ferreira et al. [94] also confirmed RF’s better performance in high-flow basins. RF’s feature importance analysis based on SHAP values also aids in identifying key variables that influence streamflow, thereby contributing to a better understanding of hydrological processes than with process-based models [91].
SWAT encountered challenges in accurately predicting daily streamflow, particularly in capturing peak and base flows, whereas RF exhibited better performance for these characteristics. The more dispersed the data points, the worse the SWAT model’s performance [15,95]. This might be associated with the fact that SWAT was initially designed for long-term analyses and is more suitable for monthly or longer time scales [11], thereby providing weaker capability at handling event-based simulations, such as flash floods and peak flows [96]. The uncertainties introduced by daily data, including measurement errors and missing values, pose challenges to SWAT’s reliability in model calibration. Additionally, simulating hydrological processes on a daily time step demands complex parameterization and calibration, which further complicates SWAT’s performance in such scenarios. However, SWAT demonstrated better performance on a monthly time step than its own daily predictions and the monthly predictions of RF. This aligns with other findings that highlight the enhanced efficacy of SWAT at lower temporal resolutions, such as an annual time step [91]. Monthly data, which are more reliable and have fewer gaps, improves the model’s performance by reducing uncertainties associated with measurement errors. In addition, our findings indicated that SWAT demonstrated a more robust capability in catchments with irregular flow patterns, which results from SWAT’s ability to incorporate hydrological processes explicitly, monitor the catchment’s water budget, and effectively represent dynamic changes within the system [11]. Given its ability to operate without direct input from observed streamflow data, SWAT remains a valuable model, particularly in basins with limited streamflow data [15].
Hydrological modeling in arid and semi-arid regions poses a formidable challenge that can be attributed to water scarcity, irregular precipitation, and complex hydrological interactions [97,98]. In the arid (Argos) catchment that we studied, the SWAT and RF models both exhibited poorer performance than in wetter catchments, with RF consistently outperforming SWAT across metrics and temporal steps. Argos’s hydrogeological complexity, influenced by ground and surface water flows, presents challenges for effective modeling [58]; RF’s advantage lies in managing non-linear relationships and adapting to spatial and temporal variability, which is especially beneficial for predicting streamflow in conditions with extended droughts or with flash floods. With only one hydro-meteorological station, Argos highlights the challenge of limited climate data, a situation in which RF excels compared to the data-intensive SWAT [99].
Hydrological models also face challenges in catchments influenced by snow, resulting in variable performance [45,98]. Both SWAT and RF showed diminished performance in predicting peak flows in the snow-influenced Porijõgi and Bald Eagle catchments. Winter precipitation as snow introduces complexities in hydrological processes, particularly the intricate freeze–thaw dynamics, which affect soil moisture, groundwater, and overall model predictions [100]. RF’s inability to directly account for snow retention adds to its challenges in capturing snow-related hydrological processes [45]. SWAT’s poor performance in snow-dominated catchments can be attributed to difficulties in modeling snow dynamics, insufficient parameterization, and constraints in capturing spatial and temporal variations. Improving parameter tuning, representing snow-related processes, and enhancing data quality may enhance model accuracy in snow-dominated catchments.
RF greatly outperforms SWAT in computational efficiency during both training and testing. Creating a fully functional SWAT model demands substantial time due to the intricate workflow, including data preparation, model setup, and the training and testing processes [101]. SWAT’s computational intensity increases notably with larger scales and high-resolution data, and this is amplified by iterative procedures [102]. In contrast, RF’s streamlined model structure results in efficiency across feature selection, engineering, training, and testing. Overall, our findings show that with significantly less modeling effort and resources, RF still performs better than SWAT in daily streamflow prediction. Nonetheless, for monthly predictions, especially in catchments with irregular flow patterns, SWAT may be a preferred option. SWAT considers numerous parameters in its flow simulation, making it the preferred choice for studies that analyze the influence of diverse parameters on flow simulation and conduct more in-depth investigations of hydrological processes. Researchers should carefully consider the specific demands and objectives of their hydrological modeling task to review the potential trade-offs between the two models.
Accurate hydrological modeling often relies on in situ gauges, but limited distribution of such gauges in the studied catchments hinders overall model performance. Although our RF model focused on 1-day streamflow forecasting, exploring extended lag times would be helpful for strategic water resource management [1]. Separating streamflow components into peak and base flows can enhance ML models [47], though our study did not explore this aspect. Likewise, separating streamflow for dry and wet periods and then combining the optimal results into an overall simulation series can notably enhance SWAT’s performance, especially in catchments with seasonal variations [103]. Moreover, RF might perform better at a sub-daily time step, but we did not examine this possibility due to the unavailability of data for such a timeframe.
Incorporating the RF and SWAT models into water resource management and flood warning systems could offer significant potential for enhancing environmental protection and scientific research. RF is particularly advantageous due to its flexibility and rapid setup, especially in data-scarce situations, making it suitable for quick assessments and flood predictions. Together, these models can optimize water allocation and conservation strategies while improving flood preparedness and response, ultimately helping to safeguard communities and ecosystems against climate variability and change. Furthermore, their integration can facilitate advanced scientific research by providing reliable data-driven insights into hydrological processes and environmental dynamics.
6. Conclusions
In this study, we incorporated time lags into RF models to make them more efficient in predicting flow time-series and compared the performance of time-lag-adjusted RF with process-based SWAT models to predict streamflow across diverse catchments. We showed that incorporating time lags for predictor values improved RF’s ability to predict time series, and the performance of SWAT and RF differed among catchments due to catchment-specific characteristics that affected model efficacy. To address the limitations associated with ensemble learning methods such as RF in time-series predictions, we introduced time lag values for the predictors as model inputs. This greatly improved RF’s accuracy and applicability in flow prediction, which confirms our first hypothesis. RF outperformed SWAT for daily predictions, whereas SWAT showed greater accuracy for monthly predictions, albeit with a much greater computational effort. SWAT also performed better in catchments with irregular flow patterns, which can likely be attributed to its explicit integration of hydrological processes, water budget monitoring, and effective representation of dynamic system changes. SWAT is also preferable in basins with limited streamflow data since it does not require observed streamflow as a direct input. Our findings also revealed the limited efficacy of both SWAT and RF in predicting peak flows in snow-influenced catchments. However, RF demonstrated better adaptability to the arid catchment, which showcases its ability to handle spatial and temporal variability under dry environmental conditions. In terms of computational efficiency, RF greatly outperformed SWAT, requiring less data and time, especially for daily streamflow prediction. The ensemble learning approach used by RF contributed to its effectiveness under extreme flow conditions, making it a valuable tool for real-time flood forecasting with reduced computational demands. This creates another advantage for RF: it adapts more easily to changes in conditions such as climate change, since the model can be retrained and revalidated more quickly than a SWAT model. SWAT and RF generally differed in prediction accuracy and computational efficiency across catchments and time steps, which confirms our second hypothesis. Our results contribute valuable insights into the strengths and weaknesses of both models, emphasizing their suitability in different contexts and shedding light on their performance across diverse catchments.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/w16192805/s1, Table S1. The lengths of the warmup, training, and testing periods (year–month–day) for the daily SWAT and RF models, Table S2. The lengths of the warmup, training, and testing periods (year–month–day) for the monthly SWAT and RF models. Figure S1. Daily streamflow (Qd), precipitation (Pcpd), maximum temperature (Tmax,d), and minimum temperature (Tmin,d) observations in the (A) Argos, (B) Porijõgi, (C) Rib, and (D) Bald Eagle catchments during the corresponding study periods. Figure S2. SHapley Additive exPlanation (SHAP) values for the most important (top 10) features for the Random Forest (RF) DM3 model (with a daily time step) for the four catchments. Figure S3. SHapley Additive exPlanation (SHAP) values for the most important (top 10) features for the Random Forest (RF) MM3 model with a monthly time step for the four catchments. Figure S4. Total time required to train and test (A) the Soil and Water Assessment Tool (SWAT) model at both time steps and (B) the Random Forest (RF) model at a daily time step. Qd+1 represents daily flow the day after the focal date. For the SWAT model, the process considered 14 parameters and 10 to 14 iterations, each containing 1500 to 2000 runs.
Author Contributions
D.M.M.: Conceptualization, data curation, formal analysis, methodology, software, validation, visualization, writing—original draft, writing—review and editing. H.V.: Conceptualization, formal analysis, methodology, software, validation, visualization, writing—original draft, writing—review and editing. A.K.: Conceptualization, methodology, funding acquisition, writing—review and editing. R.C.: Conceptualization, data curation, writing—review and editing. R.A.N.R.: Data curation, writing—review and editing. A.M.-S.: Data curation, writing—review and editing. C.C.-G.: Data curation, writing—review and editing. E.U.: Conceptualization, investigation, methodology, supervision, resources, project administration, writing—review and editing, funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the Estonian Research Agency (grant number PRG1764, PSG841), Estonian Ministry of Education and Research, Centre of Excellence for Sustainable Land Use (TK232) and by the European Union (ERC, WaterSmartLand, 101125476). However, the views and opinions expressed are those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council Executive Agency. Neither the European Union nor the granting authority can be held responsible for them.
Data Availability Statement
The datasets utilized in this study are available on Zenodo at https://zenodo.org/doi/10.5281/zenodo.11066218, and the source code for flow modeling with RF is available in a public GitLab repository at https://github.com/LandscapeGeoinformatics/flow_swat_ml_paper (accessed on 29 September 2024).
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Cheng, M.; Fang, F.; Kinouchi, T.; Navon, I.M.; Pain, C.C. Long Lead-Time Daily and Monthly Streamflow Forecasting Using Machine Learning Methods. J. Hydrol. 2020, 590, 125376. [Google Scholar] [CrossRef]
- Fathian, F.; Mehdizadeh, S.; Kozekalani Sales, A.; Safari, M.J.S. Hybrid Models to Improve the Monthly River Flow Prediction: Integrating Artificial Intelligence and Non-Linear Time Series Models. J. Hydrol. 2019, 575, 1200–1213. [Google Scholar] [CrossRef]
- Lian, X.; Hu, X.; Bian, J.; Shi, L.; Lin, L.; Cui, Y. Enhancing Streamflow Estimation by Integrating a Data-Driven Evapotranspiration Submodel into Process-Based Hydrological Models. J. Hydrol. 2023, 621, 129603. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, P.; Cheng, L.; Xie, K.; Han, D.; Zhou, L. The Temporal Variations in Runoff-Generation Parameters of the Xinanjiang Model Due to Human Activities: A Case Study in the Upper Yangtze River Basin, China. J. Hydrol. Reg. Stud. 2021, 37, 100910. [Google Scholar] [CrossRef]
- Devia, G.K.; Ganasri, B.P.; Dwarakish, G.S. A Review on Hydrological Models. Aquat. Procedia 2015, 4, 1001–1007. [Google Scholar] [CrossRef]
- Parra, V.; Fuentes-Aguilera, P.; Muñoz, E. Identifying Advantages and Drawbacks of Two Hydrological Models Based on a Sensitivity Analysis: A Study in Two Chilean Watersheds. Hydrol. Sci. J. 2018, 63, 1831–1843. [Google Scholar] [CrossRef]
- Rahman, K.; Shang, S.; Shahid, M.; Wen, Y. Hydrological Evaluation of Merged Satellite Precipitation Datasets for Streamflow Simulation Using SWAT: A Case Study of Potohar Plateau, Pakistan. J. Hydrol. 2020, 587, 125040. [Google Scholar] [CrossRef]
- Rahman, K.U.; Pham, Q.B.; Jadoon, K.Z.; Shahid, M.; Kushwaha, D.P.; Duan, Z.; Mohammadi, B.; Khedher, K.M.; Anh, D.T. Comparison of Machine Learning and Process-Based SWAT Model in Simulating Streamflow in the Upper Indus Basin. Appl. Water Sci. 2022, 12, 178. [Google Scholar] [CrossRef]
- Singh, A.; Imtiyaz, M.; Isaac, R.K.; Denis, D.M. Comparison of Soil and Water Assessment Tool (SWAT) and Multilayer Perceptron (MLP) Artificial Neural Network for Predicting Sediment Yield in the Nagwa Agricultural Watershed in Jharkhand, India. Agric. Water Manag. 2012, 104, 113–120. [Google Scholar] [CrossRef]
- Zakizadeh, H.; Ahmadi, H.; Zehtabian, G.; Moeini, A.; Moghaddamnia, A. A Novel Study of SWAT and ANN Models for Runoff Simulation with Application on Dataset of Metrological Stations. Phys. Chem. Earth Parts A/B/C 2020, 120, 102899. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large Area Hydrologic Modeling and Assessment Part I: Model Development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Rouholahnejad, E.; Vaghefi, S.; Srinivasan, R.; Yang, H.; Kløve, B. A Continental-Scale Hydrology and Water Quality Model for Europe: Calibration and Uncertainty of a High-Resolution Large-Scale SWAT Model. J. Hydrol. 2015, 524, 733–752. [Google Scholar] [CrossRef]
- Aloui, S.; Mazzoni, A.; Elomri, A.; Aouissi, J.; Boufekane, A.; Zghibi, A. A Review of Soil and Water Assessment Tool (SWAT) Studies of Mediterranean Catchments: Applications, Feasibility, and Future Directions. J. Environ. Manag. 2023, 326, 116799. [Google Scholar] [CrossRef]
- Akoko, G.; Le, T.H.; Gomi, T.; Kato, T. A Review of SWAT Model Application in Africa. Water 2021, 13, 1313. [Google Scholar] [CrossRef]
- Jimeno-Sáez, P.; Martínez-España, R.; Casalí, J.; Pérez-Sánchez, J.; Senent-Aparicio, J. A Comparison of Performance of SWAT and Machine Learning Models for Predicting Sediment Load in a Forested Basin, Northern Spain. Catena 2021, 212, 105953. [Google Scholar] [CrossRef]
- Pradhan, P.; Tingsanchali, T.; Shrestha, S. Evaluation of Soil and Water Assessment Tool and Artificial Neural Network Models for Hydrologic Simulation in Different Climatic Regions of Asia. Sci. Total Environ. 2020, 701, 134308. [Google Scholar] [CrossRef]
- Panagopoulos, Y.; Makropoulos, C.; Baltas, E.; Mimikou, M. SWAT Parameterization for the Identification of Critical Diffuse Pollution Source Areas under Data Limitations. Ecol. Model. 2011, 222, 3500–3512. [Google Scholar] [CrossRef]
- Sánchez-Gómez, A.; Martínez-Pérez, S.; Pérez-Chavero, F.M.; Molina-Navarro, E. Optimization of a SWAT Model by Incorporating Geological Information through Calibration Strategies. Optim. Eng. 2022, 23, 2203–2233. [Google Scholar] [CrossRef]
- Senent-Aparicio, J.; Alcalá, F.J.; Liu, S.; Jimeno-Sáez, P. Coupling SWAT Model and CMB Method for Modeling of High-Permeability Bedrock Basins Receiving Interbasin Groundwater Flow. Water 2020, 12, 657. [Google Scholar] [CrossRef]
- Cai, Y.; Zhang, F.; Shi, J.; Carl Johnson, V.; Ahmed, Z.; Wang, J.; Wang, W. Enhancing SWAT Model with Modified Method to Improve Eco-Hydrological Simulation in Arid Region. J. Clean. Prod. 2023, 403, 136891. [Google Scholar] [CrossRef]
- Abbasi, M.; Farokhnia, A.; Bahreinimotlagh, M.; Roozbahani, R. A Hybrid of Random Forest and Deep Auto-Encoder with Support Vector Regression Methods for Accuracy Improvement and Uncertainty Reduction of Long-Term Streamflow Prediction. J. Hydrol. 2021, 597, 125717. [Google Scholar] [CrossRef]
- Li, X.; Sha, J.; Wang, Z.-L. Comparison of Daily Streamflow Forecasts Using Extreme Learning Machines and the Random Forest Method. Hydrol. Sci. J. 2019, 64, 1857–1866. [Google Scholar] [CrossRef]
- Peng, F.; Wen, J.; Zhang, Y.; Jin, J. Monthly Streamflow Prediction Based on Random Forest Algorithm and Phase Space Reconstruction Theory. J. Phys. Conf. Ser. 2020, 1637, 012091. [Google Scholar] [CrossRef]
- Pham, L.T.; Luo, L.; Finley, A. Evaluation of Random Forests for Short-Term Daily Streamflow Forecasting in Rainfall- and Snowmelt-Driven Watersheds. Hydrol. Earth Syst. Sci. 2021, 25, 2997–3015. [Google Scholar] [CrossRef]
- Shen, Y.; Ruijsch, J.; Lu, M.; Sutanudjaja, E.H.; Karssenberg, D. Random Forests-Based Error-Correction of Streamflow from a Large-Scale Hydrological Model: Using Model State Variables to Estimate Error Terms. Comput. Geosci. 2022, 159, 105019. [Google Scholar] [CrossRef]
- Fadhillah, M.F.; Lee, S.; Lee, C.-W.; Park, Y.-C. Application of Support Vector Regression and Metaheuristic Optimization Algorithms for Groundwater Potential Mapping in Gangneung-Si, South Korea. Remote Sens. 2021, 13, 1196. [Google Scholar] [CrossRef]
- Liu, J.; Xu, L.; Chen, N. A Spatiotemporal Deep Learning Model ST-LSTM-SA for Hourly Rainfall Forecasting Using Radar Echo Images. J. Hydrol. 2022, 609, 127748. [Google Scholar] [CrossRef]
- Danandeh, A.; Ghadimi, S.; Marttila, H.; Torabi Haghighi, A. A New Evolutionary Time Series Model for Streamflow Forecasting in Boreal Lake-River Systems. Theor. Appl. Clim. 2022, 148, 255–268. [Google Scholar] [CrossRef]
- Wei, Y.; Hashim, H.; Chong, K.L.; Huang, Y.F.; Ahmed, A.N.; El-Shafie, A. Investigation of Meta-Heuristics Algorithms in ANN Streamflow Forecasting. KSCE J. Civ. Eng. 2023, 27, 2297–2312. [Google Scholar] [CrossRef]
- Dehghani, A.; Moazam, H.M.Z.H.; Mortazavizadeh, F.; Ranjbar, V.; Mirzaei, M.; Mortezavi, S.; Ng, J.L.; Dehghani, A. Comparative Evaluation of LSTM, CNN, and ConvLSTM for Hourly Short-Term Streamflow Forecasting Using Deep Learning Approaches. Ecol. Inform. 2023, 75, 102119. [Google Scholar] [CrossRef]
- Sabzipour, B.; Arsenault, R.; Troin, M.; Martel, J.-L.; Brissette, F.; Brunet, F.; Mai, J. Comparing a Long Short-Term Memory (LSTM) Neural Network with a Physically-Based Hydrological Model for Streamflow Forecasting over a Canadian Catchment. J. Hydrol. 2023, 627, 130380. [Google Scholar] [CrossRef]
- Ni, L.; Wang, D.; Wu, J.; Wang, Y.; Tao, Y.; Zhang, J.; Liu, J. Streamflow Forecasting Using Extreme Gradient Boosting Model Coupled with Gaussian Mixture Model. J. Hydrol. 2020, 586, 124901. [Google Scholar] [CrossRef]
- Sahour, H.; Gholami, V.; Torkaman, J.; Vazifedan, M.; Saeedi, S. Random Forest and Extreme Gradient Boosting Algorithms for Streamflow Modeling Using Vessel Features and Tree-Rings. Environ. Earth Sci. 2021, 80, 747. [Google Scholar] [CrossRef]
- Yu, X.; Wang, Y.; Wu, L.; Chen, G.; Wang, L.; Qin, H. Comparison of Support Vector Regression and Extreme Gradient Boosting for Decomposition-Based Data-Driven 10-Day Streamflow Forecasting. J. Hydrol. 2020, 582, 124293. [Google Scholar] [CrossRef]
- Gurbuz, F.; Mudireddy, A.; Mantilla, R.; Xiao, S. Using a Physics-Based Hydrological Model and Storm Transposition to Investigate Machine-Learning Algorithms for Streamflow Prediction. J. Hydrol. 2024, 628, 130504. [Google Scholar] [CrossRef]
- Boo, K.B.W.; El-Shafie, A.; Othman, F.; Khan, M.M.H.; Birima, A.H.; Ahmed, A.N. Groundwater Level Forecasting with Machine Learning Models: A Review. Water Res. 2024, 252, 121249. [Google Scholar] [CrossRef]
- Liang, W.; Chen, Y.; Fang, G.; Kaldybayev, A. Machine Learning Method Is an Alternative for the Hydrological Model in an Alpine Catchment in the Tianshan Region, Central Asia. J. Hydrol. Reg. Stud. 2023, 49, 101492. [Google Scholar] [CrossRef]
- Deng, C.; Yin, X.; Zou, J.; Wang, M.; Hou, Y. Assessment of the Impact of Climate Change on Streamflow of Ganjiang River Catchment via LSTM-Based Models. J. Hydrol. Reg. Stud. 2024, 52, 101716. [Google Scholar] [CrossRef]
- Ghimire, S.; Yaseen, Z.M.; Farooque, A.A.; Deo, R.C.; Zhang, J.; Tao, X. Streamflow Prediction Using an Integrated Methodology Based on Convolutional Neural Network and Long Short-Term Memory Networks. Sci. Rep. 2021, 11, 17497. [Google Scholar] [CrossRef]
- Majeske, N.; Zhang, X.; Sabaj, M.; Gong, L.; Zhu, C.; Azad, A. Inductive Predictions of Hydrologic Events Using a Long Short-Term Memory Network and the Soil and Water Assessment Tool. Environ. Model. Softw. 2022, 152, 105400. [Google Scholar] [CrossRef]
- Gauch, M.; Kratzert, F.; Klotz, D.; Nearing, G.; Lin, J.; Hochreiter, S. Rainfall–Runoff Prediction at Multiple Timescales with a Single Long Short-Term Memory Network. Hydrol. Earth Syst. Sci. 2021, 25, 2045–2062. [Google Scholar] [CrossRef]
- Yang, M.; Yang, Q.; Shao, J.; Wang, G.; Zhang, W. A New Few-Shot Learning Model for Runoff Prediction: Demonstration in Two Data Scarce Regions. Environ. Model. Softw. 2023, 162, 105659. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random Forest in Remote Sensing: A Review of Applications and Future Directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Li, J.; Wang, Z.; Lai, C.; Zhang, Z. Tree-Ring-Width Based Streamflow Reconstruction Based on the Random Forest Algorithm for the Source Region of the Yangtze River, China. Catena 2019, 183, 104216. [Google Scholar] [CrossRef]
- Schoppa, L.; Disse, M.; Bachmair, S. Evaluating the Performance of Random Forest for Large-Scale Flood Discharge Simulation. J. Hydrol. 2020, 590, 125531. [Google Scholar] [CrossRef]
- Shortridge, J.E.; Guikema, S.D.; Zaitchik, B.F. Machine Learning Methods for Empirical Streamflow Simulation: A Comparison of Model Accuracy, Interpretability, and Uncertainty in Seasonal Watersheds. Hydrol. Earth Syst. Sci. 2016, 20, 2611–2628. [Google Scholar] [CrossRef]
- Tongal, H.; Booij, M.J. Simulation and Forecasting of Streamflows Using Machine Learning Models Coupled with Base Flow Separation. J. Hydrol. 2018, 564, 266–282. [Google Scholar] [CrossRef]
- Fernandez-Delgado, M.; Cernadas, E.; Barro, S.; Amorim, D. Do We Need Hundreds of Classifiers to Solve Real World Classification Problems? J. Mach. Learn. Res. 2014, 15, 3133–3181. [Google Scholar]
- Goehry, B.; Yan, H.; Goude, Y.; Massart, P.; Poggi, J.-M. Random Forests for Time Series 2021. REVSTAT-Stat. J. 2023, 21, 283–302. [Google Scholar]
- Qiu, X.; Zhang, L.; Nagaratnam Suganthan, P.; Amaratunga, G.A.J. Oblique Random Forest Ensemble via Least Square Estimation for Time Series Forecasting. Inf. Sci. 2017, 420, 249–262. [Google Scholar] [CrossRef]
- Hauswirth, S.M.; Bierkens, M.F.P.; Beijk, V.; Wanders, N. The Potential of Data Driven Approaches for Quantifying Hydrological Extremes. Adv. Water Resour. 2021, 155, 104017. [Google Scholar] [CrossRef]
- Ghosh, A.; Maiti, R. Application of SWAT, Random Forest and Artificial Neural Network Models for Sediment Yield Estimation and Prediction of Gully Erosion Susceptible Zones: Study on Mayurakshi River Basin of Eastern India. Geocarto Int. 2022, 37, 9663–9687. [Google Scholar] [CrossRef]
- Khosravi, K.; Golkarian, A.; Booij, M.J.; Barzegar, R.; Sun, W.; Yaseen, Z.M.; Mosavi, A. Improving Daily Stochastic Streamflow Prediction: Comparison of Novel Hybrid Data-Mining Algorithms. Hydrol. Sci. J. 2021, 66, 1457–1474. [Google Scholar] [CrossRef]
- Woo, S.Y.; Jung, C.G.; Lee, J.W.; Kim, S.J. Evaluation of Watershed Scale Aquatic Ecosystem Health by SWAT Modeling and Random Forest Technique. Sustainability 2019, 11, 3397. [Google Scholar] [CrossRef]
- Woo, S.Y.; Jung, C.G.; Kim, J.U.; Kim, S.J. Assessment of climate change impact on Aquatic ecology Health Indices in Han River basin using SWAT and random forest. J. Korea Water Resour. Assoc. 2018, 51, 863–874. [Google Scholar]
- Dhar, P. The Carbon Impact of Artificial Intelligence. Nat. Mach. Intell. 2020, 2, 423–425. [Google Scholar] [CrossRef]
- Verdecchia, R.; Sallou, J.; Cruz, L. A Systematic Review of Green AI 2023. Data Min. Knowl. Discov. 2023, 13, e1507. [Google Scholar] [CrossRef]
- Martínez-Salvador, A.; Conesa-García, C. Suitability of the SWAT Model for Simulating Water Discharge and Sediment Load in a Karst Watershed of the Semiarid Mediterranean Basin. Water Resour. Manag. 2020, 34, 785–802. [Google Scholar] [CrossRef]
- Mander, Ü.; Kull, A.; Kuusemets, V.; Tamm, T. Nutrient Runoff Dynamics in a Rural Catchment: Influence of Land-Use Changes, Climatic Fluctuations and Ecotechnological Measures. Ecol. Eng. 2000, 14, 405–417. [Google Scholar] [CrossRef]
- Moges, D.M.; Kmoch, A.; Uuemaa, E. Application of Satellite and Reanalysis Precipitation Products for Hydrological Modeling in the Data-Scarce Porijõgi Catchment, Estonia. J. Hydrol. Reg. Stud. 2022, 41, 101070. [Google Scholar] [CrossRef]
- Moges, D.M.; Bhat, H.G. An Insight into Land Use and Land Cover Changes and Their Impacts in Rib Watershed, North-Western Highland Ethiopia. Land. Degrad. Dev. 2018, 29, 3317–3330. [Google Scholar] [CrossRef]
- Moges, D.M.; Kmoch, A.; Bhat, H.G.; Uuemaa, E. Future Soil Loss in Highland Ethiopia under Changing Climate and Land Use. Reg. Environ. Chang. 2020, 20, 32. [Google Scholar] [CrossRef]
- Moges, D.M.; Bhat, H. Integration of Geospatial Technologies with RUSLE for Analysis of Land Use/Cover Change Impact on Soil Erosion: Case Study in Rib Watershed, North-Western Highland Ethiopia. Environ. Earth Sci. 2017, 76, 765. [Google Scholar] [CrossRef]
- Jayaprathiga, M.; Cibin, R.; Sudheer, K.P. Reliability of Hydrology and Water Quality Simulations Using Global Scale Datasets. J. Am. Water Resour. Assoc. 2022, 58, 453–470. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Ferreira, L.B.; da Cunha, F.F.; de Oliveira, R.A.; Fernandes Filho, E.I. Estimation of Reference Evapotranspiration in Brazil with Limited Meteorological Data Using ANN and SVM–A New Approach. J. Hydrol. 2019, 572, 556–570. [Google Scholar] [CrossRef]
- Li, J.; Heap, A.D.; Potter, A.; Daniell, J.J. Application of Machine Learning Methods to Spatial Interpolation of Environmental Variables. Environ. Model. Softw. 2011, 26, 1647–1659. [Google Scholar] [CrossRef]
- Tyralis, H.; Papacharalampous, G.; Langousis, A. A Brief Review of Random Forests for Water Scientists and Practitioners and Their Recent History in Water Resources. Water 2019, 11, 910. [Google Scholar] [CrossRef]
- Rasouli, K.; Hsieh, W.W.; Cannon, A.J. Daily Streamflow Forecasting by Machine Learning Methods with Weather and Climate Inputs. J. Hydrol. 2012, 414, 284–293. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation Version 2009; Texas Water Resources Institute: College Station, TX, USA, 2011.
- Moges, D.M.; Virro, H.; Kmoch, A.; Cibin, R.; Rohith, A.N.; Martínez-Salvador, A.; Conesa-García, C.; Uuemaa, E. How Does the Choice of DEMs Affect Catchment Hydrological Modeling? Sci. Total Environ. 2023, 892, 164627. [Google Scholar] [CrossRef]
- Dile, Y.T.; Daggupati, P.; George, C.; Srinivasan, R.; Arnold, J. Introducing a New Open Source GIS User Interface for the SWAT Model. Environ. Model. Softw. 2016, 85, 129–138. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; van Genuchten, M.T.; Schulin, R.; Schläppi, E. A Sequential Uncertainty Domain Inverse Procedure for Estimating Subsurface Flow and Transport Parameters. Water Resour. Res. 1997, 33, 1879–1892. [Google Scholar] [CrossRef]
- JAXA ALOS Global Digital Surface Model (DSM). ALOS World 3D-30m (AW3D30) Version 3.1: Product Description; Earth Obs. Res. Cent. Japan Aerosp. Explor. Agency (JAXA EORC). Available online: https://www.eorc.jaxa.jp/ALOS/ (accessed on 29 March 2022).
- Zanaga, D.; Van De Kerchove, R.; De Keersmaecker, W.; Souverijns, N.; Brockmann, C.; Quast, R.; Wevers, J.; Grosu, A.; Paccini, A.; Vergnaud, S.; et al. ESA WorldCover 10 m 2020 V100 2021. Available online: https://worldcover2020.esa.int/download (accessed on 21 March 2022).
- Fischer, G.; Nachtergaele, V.F.; Prieler, S.; van Velthuizen, H.T.; Verelst, L.; Wiberg, D. Global Agro-Ecological Zones Assessment for Agriculture (GAEZ 2008); IIASA Laxenburg Austria FAO: Rome, Italy, 2008. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River Flow Forecasting through Conceptual Models Part I—A Discussion of Principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of Automatic Calibration for Hydrologic Models: Comparison with Multilevel Expert Calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and Water Quality Models: Performance Measures and Evaluation Criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing Multiple Aspects of Model Performance in a Single Diagram. J. Geophys. Res. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.-I. From Local Explanations to Global Understanding with Explainable AI for Trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef]
- Hussain, D.; Khan, A.A. Machine Learning Techniques for Monthly River Flow Forecasting of Hunza River, Pakistan. Earth Sci. Inf. 2020, 13, 939–949. [Google Scholar] [CrossRef]
- Ma, K.; He, D.; Liu, S.; Ji, X.; Li, Y.; Jiang, H. Novel Time-Lag Informed Deep Learning Framework for Enhanced Streamflow Prediction and Flood Early Warning in Large-Scale Catchments. J. Hydrol. 2024, 631, 130841. [Google Scholar] [CrossRef]
- Kalu, I.; Ndehedehe, C.E.; Ferreira, V.G.; Kennard, M.J. Machine Learning Assessment of Hydrological Model Performance under Localized Water Storage Changes through Downscaling. J. Hydrol. 2024, 628, 130597. [Google Scholar] [CrossRef]
- Garg, V.; Sambare, R.S.; Thakur, P.K.; Dhote, P.R.; Nikam, B.R.; Aggarwal, S.P. Improving Stream Flow Estimation by Incorporating Time Delay Approach in Soft Computing Models. ISH J. Hydraul. Eng. 2022, 28, 57–68. [Google Scholar] [CrossRef]
- Feng, D.; Fang, K.; Shen, C. Enhancing Streamflow Forecast and Extracting Insights Using Long-Short Term Memory Networks With Data Integration at Continental Scales. Water Resour. Res. 2020, 56, e2019WR026793. [Google Scholar] [CrossRef]
- Besaw, L.E.; Rizzo, D.M.; Bierman, P.R.; Hackett, W.R. Advances in Ungauged Streamflow Prediction Using Artificial Neural Networks. J. Hydrol. 2010, 386, 27–37. [Google Scholar] [CrossRef]
- Saadi, M.; Oudin, L.; Ribstein, P. Random Forest Ability in Regionalizing Hourly Hydrological Model Parameters. Water 2019, 11, 1540. [Google Scholar] [CrossRef]
- Islam, K.I.; Elias, E.; Carroll, K.C.; Brown, C. Exploring Random Forest Machine Learning and Remote Sensing Data for Streamflow Prediction: An Alternative Approach to a Process-Based Hydrologic Modeling in a Snowmelt-Driven Watershed. Remote Sens. 2023, 15, 3999. [Google Scholar] [CrossRef]
- Papacharalampous, G.A.; Tyralis, H. Evaluation of Random Forests and Prophet for Daily Streamflow Forecasting. Adv. Geosci. 2018, 45, 201–208. [Google Scholar] [CrossRef]
- Akbarian, M.; Saghafian, B.; Golian, S. Monthly Streamflow Forecasting by Machine Learning Methods Using Dynamic Weather Prediction Model Outputs over Iran. J. Hydrol. 2023, 620, 129480. [Google Scholar] [CrossRef]
- Ferreira, R.G.; da Silva, D.D.; Elesbon, A.A.A.; Fernandes-Filho, E.I.; Veloso, G.V.; de Souza Fraga, M.; Ferreira, L.B. Machine Learning Models for Streamflow Regionalization in a Tropical Watershed. J. Environ. Manag. 2021, 280, 111713. [Google Scholar] [CrossRef]
- Choukri, F.; Raclot, D.; Naimi, M.; Chikhaoui, M.; Nunes, J.P.; Huard, F.; Hérivaux, C.; Sabir, M.; Pépin, Y. Distinct and Combined Impacts of Climate and Land Use Scenarios on Water Availability and Sediment Loads for a Water Supply Reservoir in Northern Morocco. Int. Soil. Water Conserv. Res. 2020, 8, 141–153. [Google Scholar] [CrossRef]
- Ahmadi, M.; Moeini, A.; Ahmadi, H.; Motamedvaziri, B.; Zehtabiyan, G.R. Comparison of the Performance of SWAT, IHACRES and Artificial Neural Networks Models in Rainfall-Runoff Simulation (Case Study: Kan Watershed, Iran). Phys. Chem. Earth Parts A/B/C 2019, 111, 65–77. [Google Scholar] [CrossRef]
- Samimi, M.; Mirchi, A.; Moriasi, D.; Ahn, S.; Alian, S.; Taghvaeian, S.; Sheng, Z. Modeling Arid/Semi-Arid Irrigated Agricultural Watersheds with SWAT: Applications, Challenges, and Solution Strategies. J. Hydrol. 2020, 590, 125418. [Google Scholar] [CrossRef]
- Wing, O.E.J.; Bates, P.D.; Sampson, C.C.; Smith, A.M.; Johnson, K.A.; Erickson, T.A. Validation of a 30 m Resolution Flood Hazard Model of the Conterminous United States. Water Resour. Res. 2017, 53, 7968–7986. [Google Scholar] [CrossRef]
- Ruiz-Aĺvarez, M.; Gomariz-Castillo, F.; Alonso-Sarría, F. Evapotranspiration Response to Climate Change in Semi-Arid Areas: Using Random Forest as Multi-Model Ensemble Method. Water 2021, 13, 222. [Google Scholar] [CrossRef]
- Sharifinejad, A.; Hassanzadeh, E. Evaluating Climate Change Effects on a Snow-Dominant Watershed: A Multi-Model Hydrological Investigation. Water 2023, 15, 3281. [Google Scholar] [CrossRef]
- Yen, H.; Ahmadi, M.; White, M.J.; Wang, X.; Arnold, J.G. C-SWAT: The Soil and Water Assessment Tool with Consolidated Input Files in Alleviating Computational Burden of Recursive Simulations. Comput. Geosci. 2014, 72, 221–232. [Google Scholar] [CrossRef]
- Ahmadi, M.; Ascough, J.C.; DeJonge, K.C.; Arabi, M. Multisite-Multivariable Sensitivity Analysis of Distributed Watershed Models: Enhancing the Perceptions from Computationally Frugal Methods. Ecol. Model. 2014, 279, 54–67. [Google Scholar] [CrossRef]
- Zhang, D.; Chen, X.; Yao, H.; Lin, B. Improved Calibration Scheme of SWAT by Separating Wet and Dry Seasons. Ecol. Model. 2015, 301, 54–61. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).