Flow Characteristics in Open Channels with Non-Submerged Rigid Vegetation Landscape
Abstract
1. Introduction
2. Materials and Methods
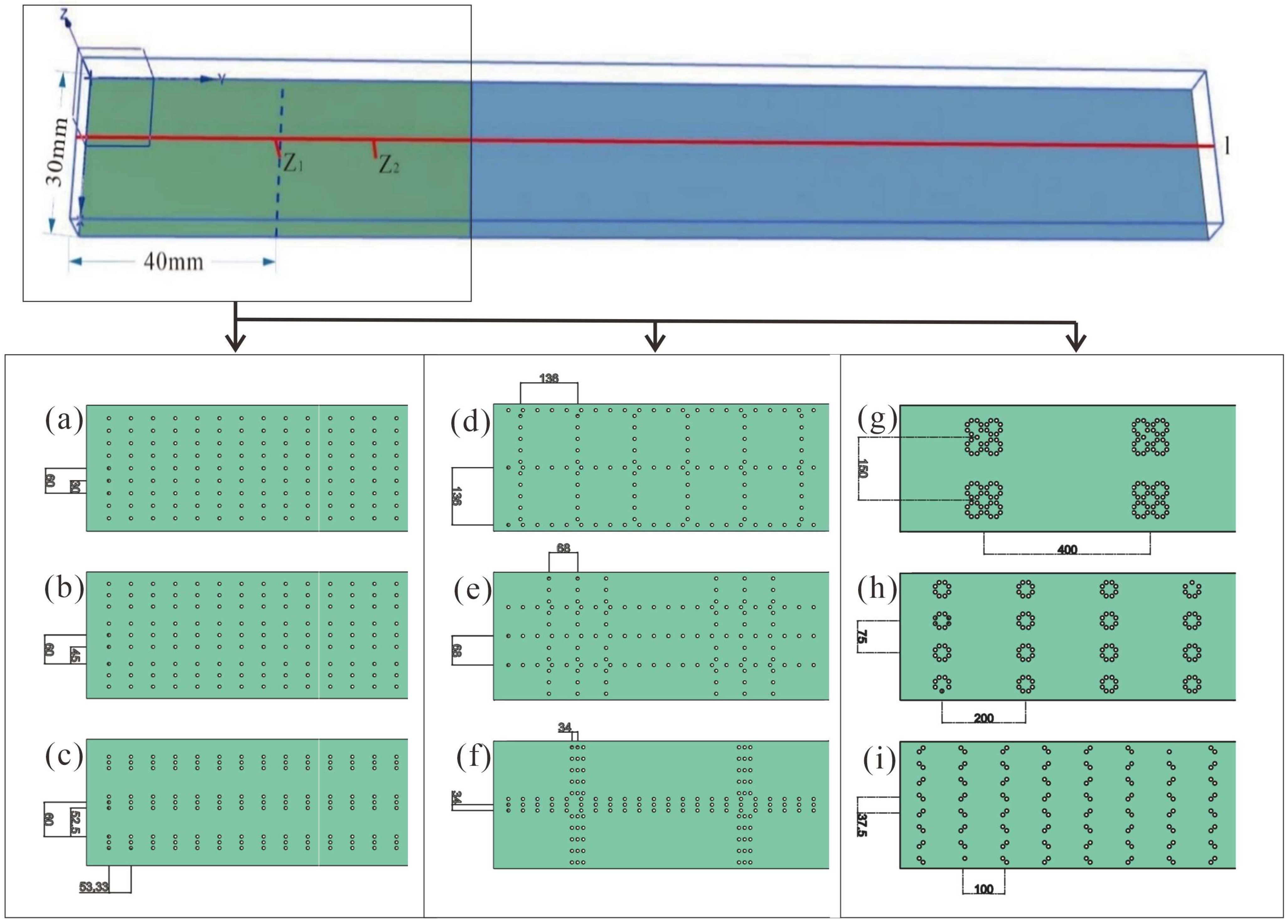
2.1. Problem Definition and Geometry
2.2. Governing Equations and Boundary Conditions
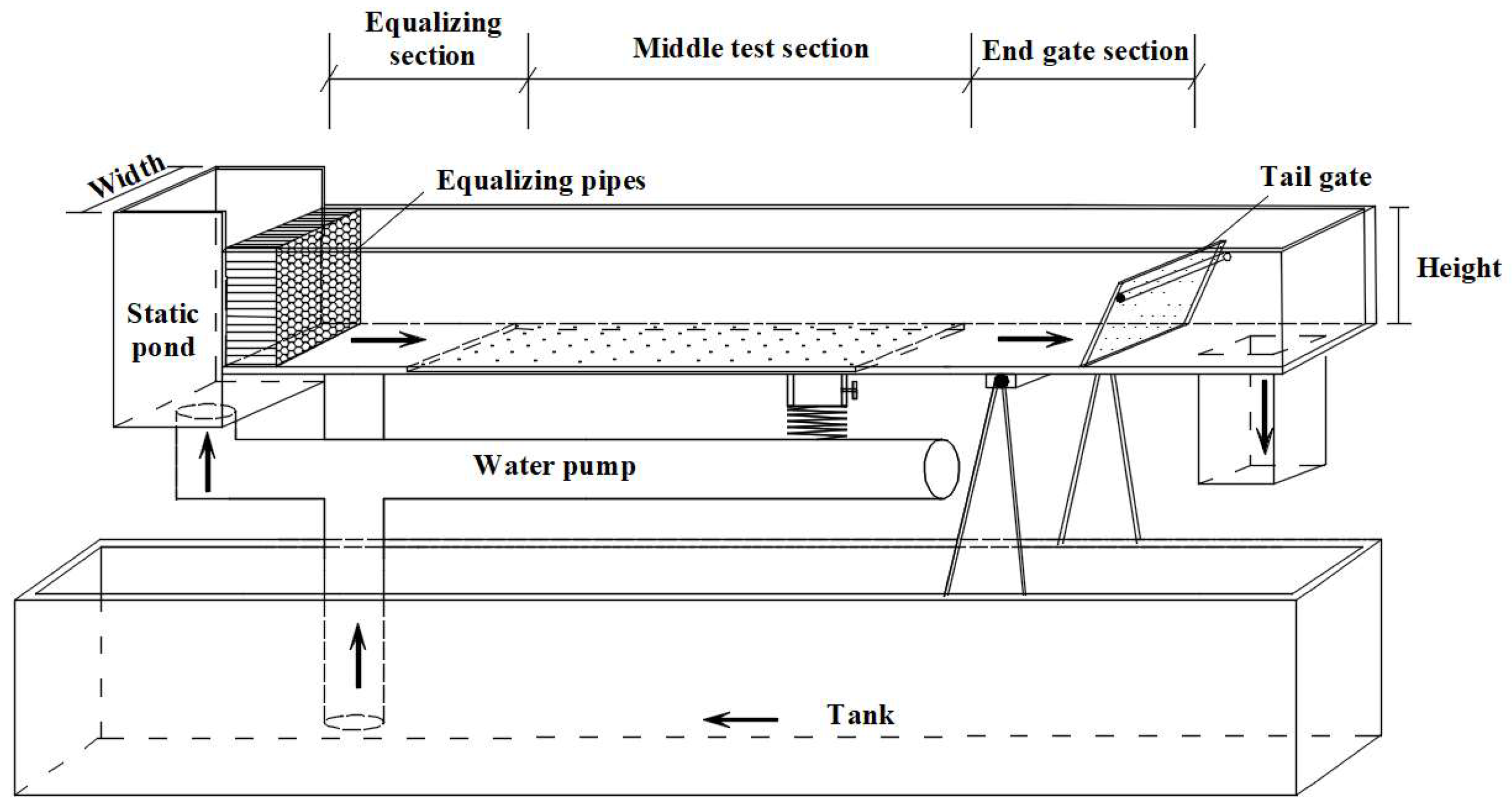
2.3. Numerical Model Verification
3. Results
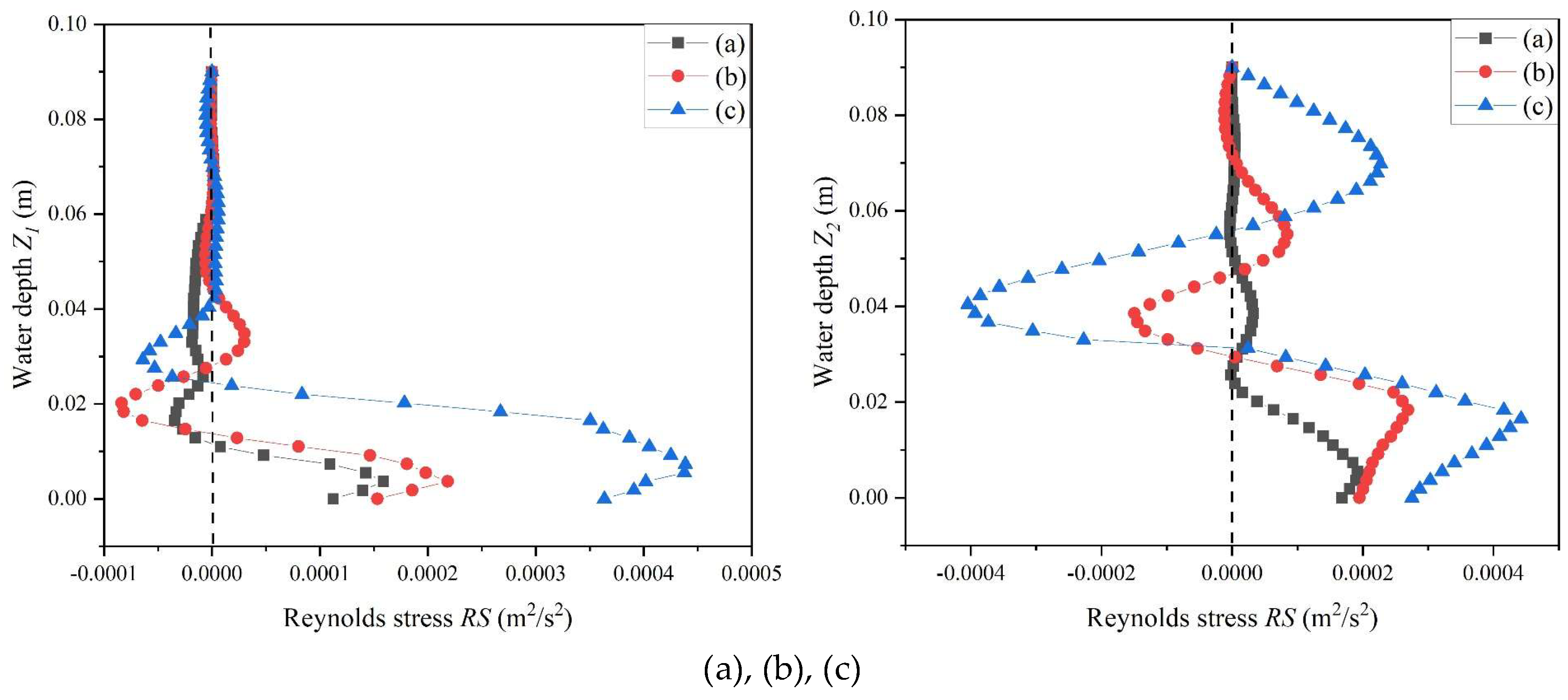
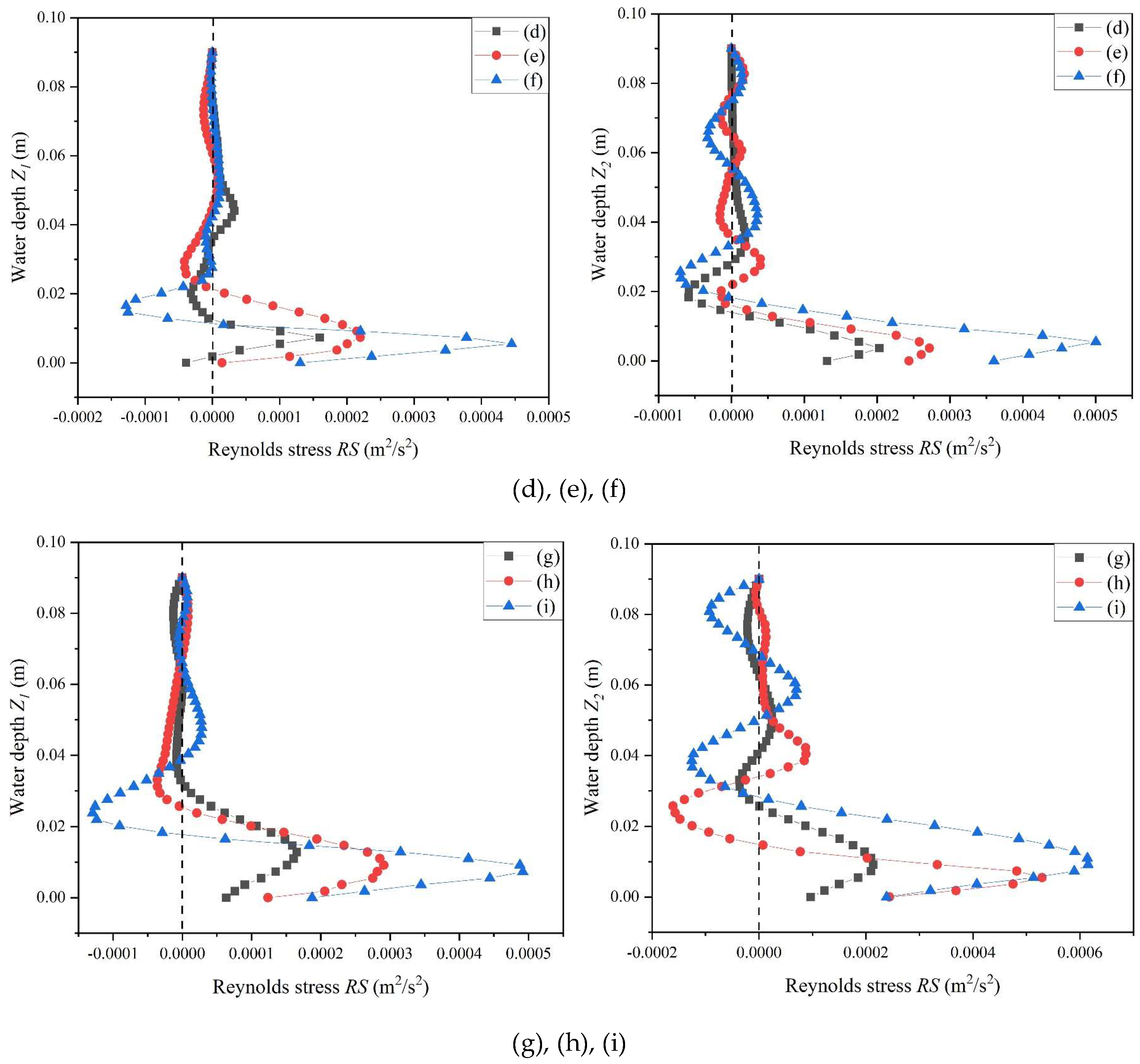
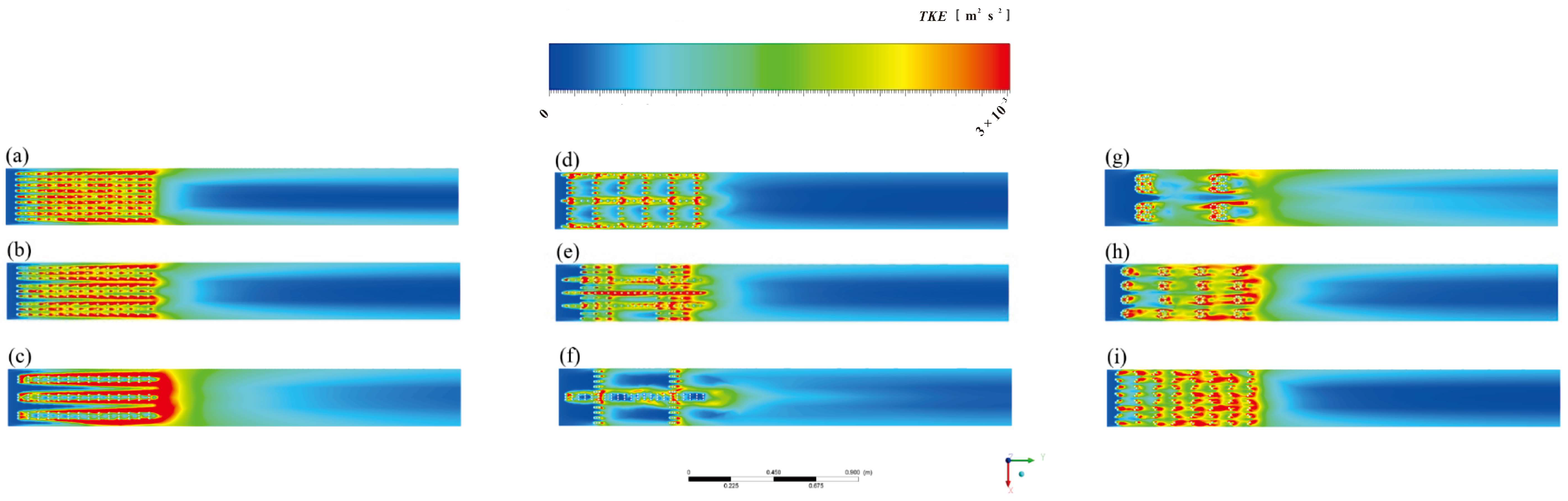
3.1. Reynolds Stress in the Gap Area and the Vegetation Area under the Influence of Water Depth
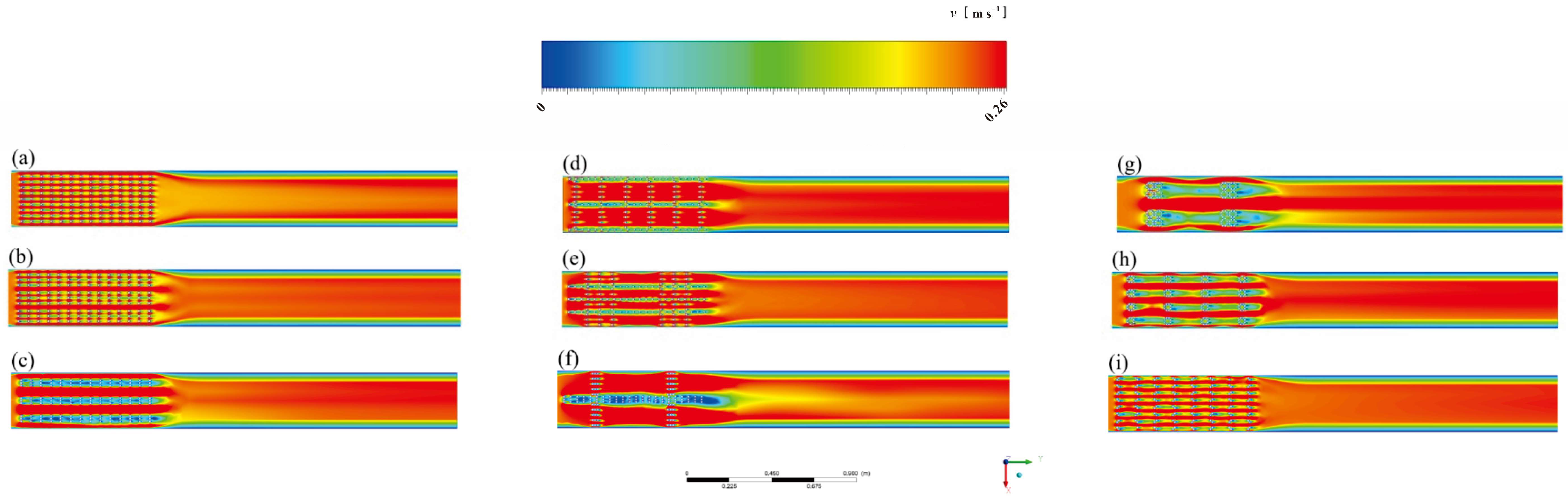
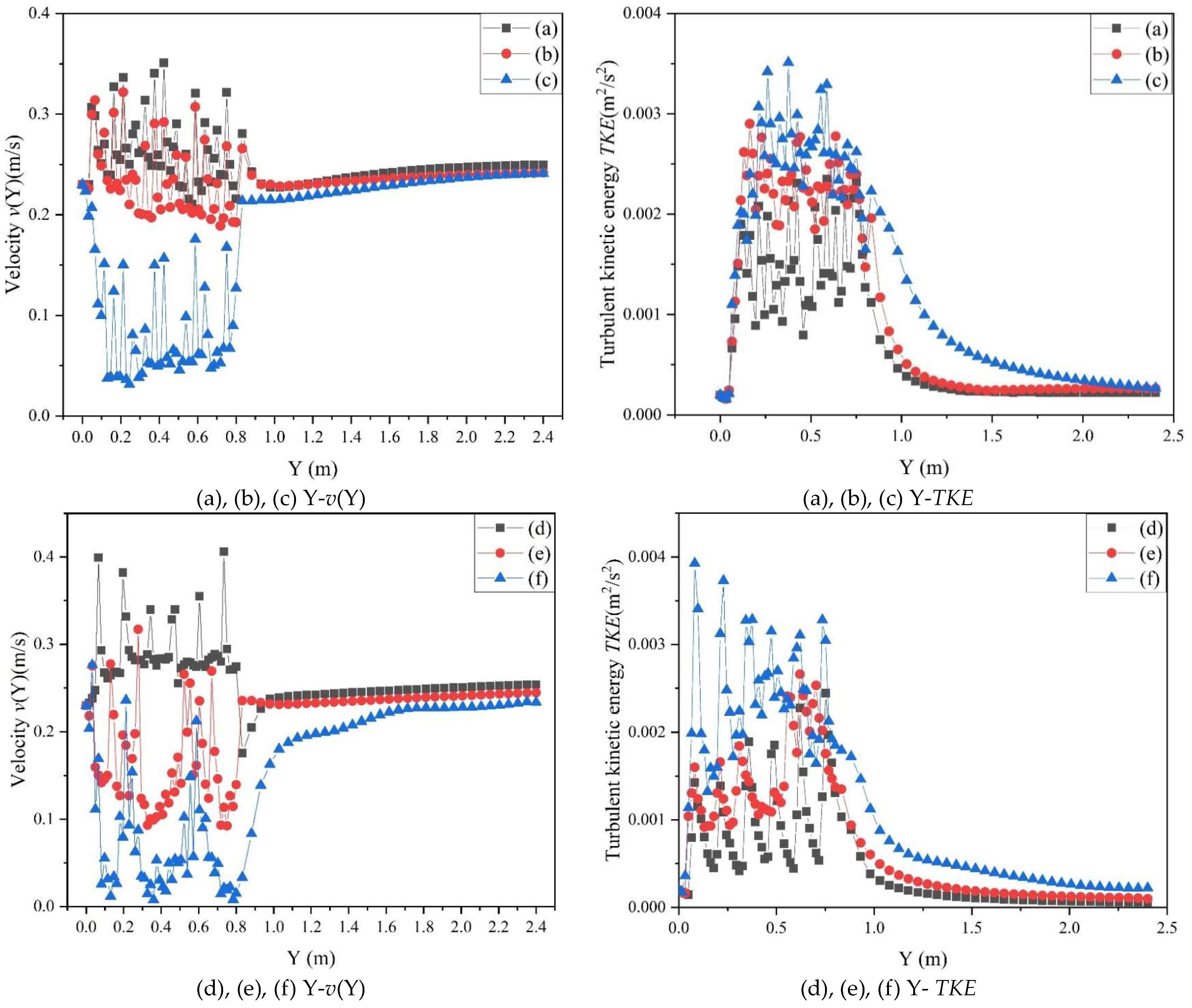
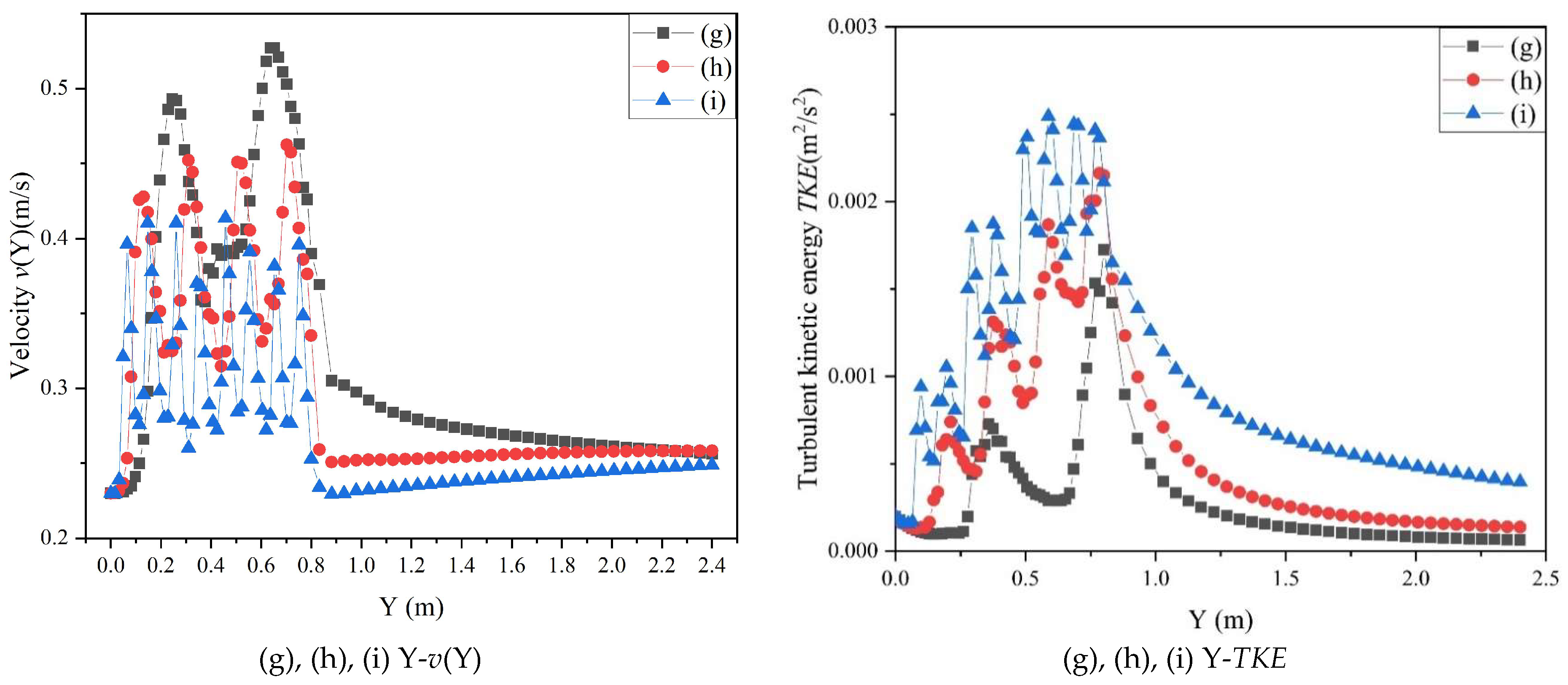
3.2. Analysis of the Surface Hydraulic Characteristics of Non-Submerged Rigid Vegetation
4. Discussion
4.1. Analysis of Flow Hydraulic Parameters under the Influence of Water Depth for Different Vegetation Arrangements
4.2. Analysis of Hydraulic Parameters of Water Flow under the Influence of Different Arrangements of Vegetation along the Way
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Curran, J.C.; Hession, W.C. Vegetative impacts on hydraulics and sediment processes across the fluvial system. J. Hydrol. 2013, 505, 364–376. [Google Scholar] [CrossRef]
- Uijttewaal, W.S.J.; Truong, S.H. Transverse momentum exchange induced by large coherent structures in a vegetated compound channel. Water Resour. Res. 2019, 55, 589–612. [Google Scholar]
- Chen, X.; Taylor, A.R.; Reich, P.B.; Hisano, M.; Chen, H.Y.H.; Chang, S.X. Tree diversity increases decadal forest soil carbon and nitrogen accrual. Nature 2023, 618, 94–101. [Google Scholar] [CrossRef] [PubMed]
- Fathi-Moghadam, M.; Kashefipour, M.; Ebrahimi, N.; Emamgholizadeh, S. Physical and numerical modeling of submerged vegetation roughness in rivers and flood plains. J. Hydrol. Eng. 2011, 16, 858–864. [Google Scholar] [CrossRef]
- Temmerman, S.; Meire, P.; Bouma, T.J.; Herman, P.M.J.; Ysebaert, T.; Vriend, H.J.D. Ecosystem-based coastal defence in the face of global change. Nature 2013, 504, 79–83. [Google Scholar] [CrossRef] [PubMed]
- Grabowski, R.C.; Surian, N.; Gurnell, A.M. Characterizing geomorphological change to support sustainable river restoration and management. WIREs Water 2014, 1, 483–512. [Google Scholar] [CrossRef]
- Zdankus, N.; Punys, P.; Martinaitis, E.; Zdankus, T. Lowland river flow control by an artificial water plant system. River Res. Appl. 2016, 32, 1382–1391. [Google Scholar] [CrossRef]
- D’Ippolito, A.; Calomino, F.; Penna, N.; Dey, S.; Gaudio, R. Simulation of accelerated subcritical flow profiles in an open channel with emergent rigid vegetation. Appl. Sci. 2022, 12, 6960. [Google Scholar] [CrossRef]
- Yang, J.Q. Solute flow and particle transport in aquatic ecosystems: A review on the effect of emergent and rigid vegetation. Env. Sci. Ecotechnol. 2024, 21, 100429. [Google Scholar] [CrossRef]
- Yang, L.F.; Fang, H.Z.; Yang, Z.H.; Huai, W.X. Longitudinal dispersive coefficient in channels with aquatic vegetation: A review. J. Hydrodyn. 2023, 35, 379–395. [Google Scholar] [CrossRef]
- Huai, W.X.; Li, S.; Katul, G.G.; Liu, M.Y.; Yang, Z.H. Flow dynamics and sediment transport in vegetated rivers: A review. J. Hydrodyn. 2021, 33, 400–420. [Google Scholar] [CrossRef]
- Nepf, H.M. Hydrodynamics of vegetated channels. J. Hydraul. Res. 2012, 50, 262–279. [Google Scholar] [CrossRef]
- Aberle, J.; Järvelä, J. Flow resistance of emergent rigid and flexible floodplain vegetation. J. Hydraul. Res. 2013, 51, 33–45. [Google Scholar] [CrossRef]
- Boothroyd, R.J.; Hardy, R.J.; Warburton, J.; Marjoribanks, T.I. Modeling complex flow structures and drag around a submerged plant of varied posture. Water Resour. Res. 2017, 53, 2877–2901. [Google Scholar] [CrossRef]
- Rominger, J.T.; Nepf, H.M. Flow adjustment and interior flow associated with a rectangular porous obstruction. J. Fluid. Mech. 2011, 680, 636–659. [Google Scholar] [CrossRef]
- Velísková, Y.; Dulovičová, R.; Schügerl, R. Impact of vegetation on flow in a lowland stream during the growing season. Biologia 2017, 72, 840–846. [Google Scholar] [CrossRef]
- Jørgensen, S.E. Application of ecological engineering principles in lake management. Lakes Reserv. Res. Manag. 2006, 11, 103–109. [Google Scholar] [CrossRef]
- Zhang, G.; Liu, G.; Zhang, P.; Yi, L. Influence of vegetation parameters on runoff and sediment characteristics in patterned artemisia capillaris plots. J. Arid. Land 2013, 6, 352–360. [Google Scholar] [CrossRef]
- Hongyang, Z.; Kuandi, Z.; Juanjuan, L.; Meng, W.; Youdong, C. Quantifying the effects of grass distribution patterns on the relative hydrodynamic parameters of overland flow. Hydrol. Process. 2022, 36, e14707. [Google Scholar]
- Sun, G.-Q.; Wang, C.-H.; Chang, L.-L.; Wu, Y.-P.; Li, L.; Jin, Z. Effects of feedback regulation on vegetation patterns in semi-arid environments. Appl. Math. Model. 2018, 61, 200–215. [Google Scholar] [CrossRef]
- Fu, S.; Mu, H.; Liu, B.; Yu, X.; Zhang, G.; Liu, Y. Effects on the plant stem arrangement onsediment transport capacity of croplands. Land Degrad. Dev. 2019, 31, 1325–1334. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, S.; Wang, C.; Wang, W.; Ma, L. Influence of combined stem vegetation distribution and discretization on the hydraulic characteristics of overland flow. J. Clean. Prod. 2022, 376, 134188. [Google Scholar] [CrossRef]
- Ding, W.; Li, M. Effects of grass coverage and distribution patterns on erosion and overland flow hydraulic characteristics. Environ. Earth Sci. 2016, 75, 477. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, J.; Liu, Y.; Liu, Y.; Wang, Z. The effects of vegetation distribution pattern on overland flow. Water Environ. J. 2018, 32, 392–403. [Google Scholar] [CrossRef]
- Liu, C.; Shan, Y.; Sun, W.; Yan, C.; Yang, K. An open channel with an emergent vegetation patch: Predicting the longitudinal profiles of velocities based on exponential decay. J. Hydrol. 2020, 582, 124429. [Google Scholar] [CrossRef]
- Anjum, N.; Tanaka, N. Study on the flow structure around discontinued vertically layered vegetation in an open channel. J. Hydrodyn. 2019, 32, 454–467. [Google Scholar] [CrossRef]
- Ruiz-Reynes, D.; Gomila, D.; Sintes, T.; Hernandez-Garcia, E.; Marba, N.; Duarte, C.M. Fairy circle landscapes under the sea. Sci. Adv. 2017, 3, e1603262. [Google Scholar] [CrossRef]
- Folkard, A.M. Hydrodynamics of model posidonia oceanica patches in shallow water. Limnol. Oceanogr. 2005, 50, 1592–1600. [Google Scholar] [CrossRef]
- Afzalimehr, H.; Maddahi, M.R.; Sui, J.; Rahimpour, M. Impacts of vegetation over bedforms on flow characteristics in gravel-bed rivers. J. Hydrodyn. 2019, 31, 986–998. [Google Scholar] [CrossRef]
- Xu, S.; Zhao, Q.; Ding, S.; Qin, M.; Ning, L.; Ji, X. Improving soil and water conservation of riparian vegetation based on landscape leakiness and optimal vegetation pattern. Sustainability 2018, 10, 1571. [Google Scholar] [CrossRef]
- Gimbun, J. Cfd simulation of aerocyclone hydrodynamics and performance at extreme temperature. Eng. Appl. Comput. Fluid. Mech. 2014, 2, 22–29. [Google Scholar] [CrossRef]
- Kazemi, E.; Nichols, A.; Tait, S.; Shao, S. Sph modelling of depth-limited turbulent open channel flows over rough boundaries. Int. J. Numer. Methods Fluids 2017, 83, 3–27. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Zhang, S.; Wang, C.; Wang, W.; Ma, L. Flow characteristics of open channels based on patch distribution of partially discontinuous rigid combined vegetation. Front. Plant. Sci. 2022, 13, 976646. [Google Scholar] [CrossRef] [PubMed]
- Jia, F.C.; Wang, W.J.; Liu, L.H.; Li, J.J.; Huang, A.P.; Zhang, J.; Fu, Y.C.; Yu, Y. Derivation of new resistance principle on flow-induced morphological response of flexible vegetation. Env. Sci. Pollut. Res. Int. 2023, 30, 31561–31582. [Google Scholar] [CrossRef] [PubMed]
- Chanson, H. Environmental Hydraulics for Open Channel Flows; Elsevier Ltd.: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Zhang, H.Y.; Wang, Z.Y.; Xu, W.G.; Dai, L.M. Effects of rigid unsubmerged vegetation on flow field structure and turbulent kinetic energy of gradually varied flow. River Res. Appl. 2015, 31, 1166–1175. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, S.; Zhang, J.; Bilal, A. Numerical study of the effects of vegetation stem thickness on the flow characteristics of curved channels. Water Supply 2024, 24, 2218–2231. [Google Scholar] [CrossRef]
- Anjum, N.; Tanaka, N. Investigating the turbulent flow behaviour through partially distributed discontinuous rigid vegetation in an open channel. River Res. Appl. 2020, 36, 1701–1716. [Google Scholar] [CrossRef]
- Nezu, I.; Rodi, W. Open-channel flow measurements with a laser doppler anemometer. J. Hydraul. Eng. 1986, 112, 335–355. [Google Scholar] [CrossRef]
- Wang, F.; Huai, W.; Guo, Y.; Liu, M. Turbulence structure and momentum exchange in compound channel flows with shore ice covered on the floodplains. Water Resour. Res. 2021, 57, e2020WR028621. [Google Scholar] [CrossRef]
- Fazeleh, K.; Reza, M.T.M.; Mohammad, S. Effect of vegetative bed on flow structure through a pool-riffle morphology. Flow. Meas. Instrum. 2022, 86, 102197. [Google Scholar]
- Suyu, J.; Fei, Y.; Jian, Z.; Bo, S. Multi-scale wake characteristics of the flow over a cylinder with different v-groove numbers. Water 2023, 15, 805. [Google Scholar] [CrossRef]
- Cai, Z.; Xie, J.; Chen, Y.; Yang, Y.; Wang, C.; Wang, J. Rigid vegetation affects slope flow velocity. Water 2024, 16, 2240. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, J.; Liu, Y.; Liu, Y.; Li, G. The resistance effect of vegetation stem diameter on overland runoff under different slope gradients. Water Sci. Technol. 2018, 78, 2383–2391. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Chen, G.; Shan, Y.; Wang, Y.; Xie, Y.; Ba, Y.; Ba, D.; Liu, K. Research on pumping laws of different-shaped roots rotors for multi-stage vacuum pump design. Mech. Syst. Signal Process. 2023, 203, 110752. [Google Scholar] [CrossRef]
- Zeng, C.; Li, C.-W. Measurements and modeling of open-channel flows with finite semi-rigid vegetation patches. Environ. Fluid. Mech. 2014, 14, 113–134. [Google Scholar] [CrossRef]
- Wang, M.; Avital, E.; Korakianitis, T.; Williams, J.; Ai, K. A numerical study on the influence of curvature ratio and vegetation density on a partially vegetated u-bend channel flow. Adv. Water Resour. 2021, 148, 103843. [Google Scholar] [CrossRef]
- Zhao, F.; Huai, W. Hydrodynamics of discontinuous rigid submerged vegetation patches in open-channel flow. J. Hydro-Environ. Res. 2016, 12, 148–160. [Google Scholar] [CrossRef]
- Zhang, S.; Li, G. Effect of partially submerged vegetation distribution directions on flood flow resistance. Environ. Eng. Sci. 2019, 36, 1147–1155. [Google Scholar] [CrossRef]
- Li, S.H.; Kuang, Q.F.; Yue, W.P.; Guo, T.T. Numerical simulation of the 1.2mw wind turbine flow-field. Adv. Mater. Res. 2011, 383–390, 2045–2050. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, S.; Wang, C.; Wang, W.; Ma, L.; Xu, X.; Zhou, J. Influence of vegetation lodging on the flow regime and resistance characteristic of overland flow. Hydrol. Process. 2023, 37, e14848. [Google Scholar] [CrossRef]

| (a) | (b) | (c) | (d) | (e) | (f) | (g) | (h) | (i) | Total Mean Error | |
|---|---|---|---|---|---|---|---|---|---|---|
| Mean error | 4.32% | 5.10% | 7.12% | 5.34% | 10.97% | 4.32% | 3.86% | 4.19% | 5.95% | 5.69% |
| Research Vertical Line | Vertical Line Z1 in the Gap Area | Vertical Line Z2 in the Vegetation Area | |
|---|---|---|---|
| Arrangements | |||
| (a) | (1.91 × 10−4 m2/s2, 5.10 × 10−3 m) | (1.59 × 10−4 m2/s2, 3.67 × 10−3 m) | |
| (b) | (2.69 × 10−4 m2/s2, 1.84 × 10−2 m) | (2.04 × 10−4 m2/s2, 3.67 × 10−3 m) | |
| (c) | (4.42 × 10−4 m2/s2, 1.65 × 10−2 m) | (4.39 × 10−4 m2/s2, 7.50 × 10−3 m) | |
| (d) | (2.03 × 10−4 m2/s2, 3.67 × 10−3 m) | (1.60 × 10−4 m2/s2, 7.35 × 10−3 m) | |
| (e) | (2.72 × 10−4 m2/s2, 3.67 × 10−3 m) | (2.20 × 10−4 m2/s2, 7.35 × 10−3 m) | |
| (f) | (5.00 × 10−4 m2/s2, 5.51 × 10−3 m) | (4.45 × 10−4 m2/s2, 2.45 × 10−4 m) | |
| (g) | (2.72 × 10−4 m2/s2, 9.18 × 10−3 m) | (1.65 × 10−4 m2/s2, 1.29 × 10−3 m) | |
| (h) | (5.29 × 10−4 m2/s2, 5.51 × 10−3 m) | (2.91 × 10−4 m2/s2, 9.18 × 10−3 m) | |
| (i) | (6.15 × 10−4 m2/s2, 9.18 × 10−3 m) | (4.92 × 10−4 m2/s2, 7.35 × 10−3 m) | |
| Test Area | The Wake Area | |||||
|---|---|---|---|---|---|---|
| v1 (m/s) | TKE1 (m2/s2) | v2 (m/s) | TKE2 (m2/s2) | v3 (m/s) | TKE3 (m2/s2) | |
| (a) | 0.3900 | 6.28 × 10−4 | 0.3785 | 1.13 × 10−3 | 0.2570 | 5.55 × 10−5 |
| (b) | 0.3480 | 1.12 × 10−3 | 0.3352 | 1.25 × 10−3 | 0.2500 | 1.04 × 10−4 |
| (c) | 0.3035 | 1.40 × 10−3 | 0.2448 | 1.54 × 10−3 | 0.2420 | 2.00 × 10−4 |
| (d) | 0.3234 | 8.97 × 10−4 | 0.2746 | 1.31 × 10−3 | 0.2535 | 5.70 × 10−5 |
| (e) | 0.3100 | 1.23 × 10−3 | 0.1797 | 1.37 × 10−3 | 0.2482 | 1.45 × 10−4 |
| (f) | 0.2490 | 1.60 × 10−3 | 0.1270 | 1.65 × 10−3 | 0.2416 | 2.24 × 10−4 |
| (g) | 0.3008 | 1.41 × 10−3 | 0.2158 | 1.54 × 10−3 | 0.2420 | 2.22 × 10−4 |
| (h) | 0.2054 | 1.47 × 10−3 | 0.1526 | 2.08 × 10−3 | 0.2416 | 2.64 × 10−4 |
| (i) | 0.1568 | 1.85 × 10−3 | 0.1132 | 2.46 × 10−3 | 0.2408 | 2.90 × 10−4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Long, A.; Lai, X.; Zhang, J.; Xu, T. Flow Characteristics in Open Channels with Non-Submerged Rigid Vegetation Landscape. Water 2024, 16, 2759. https://doi.org/10.3390/w16192759
Wang W, Long A, Lai X, Zhang J, Xu T. Flow Characteristics in Open Channels with Non-Submerged Rigid Vegetation Landscape. Water. 2024; 16(19):2759. https://doi.org/10.3390/w16192759
Chicago/Turabian StyleWang, Wenjun, Aihua Long, Xiaoying Lai, Jingzhou Zhang, and Tongxuan Xu. 2024. "Flow Characteristics in Open Channels with Non-Submerged Rigid Vegetation Landscape" Water 16, no. 19: 2759. https://doi.org/10.3390/w16192759
APA StyleWang, W., Long, A., Lai, X., Zhang, J., & Xu, T. (2024). Flow Characteristics in Open Channels with Non-Submerged Rigid Vegetation Landscape. Water, 16(19), 2759. https://doi.org/10.3390/w16192759








