Uncertainty Quantification in Rate Transient Analysis of Multi-Fractured Tight Gas Wells Exhibiting Gas–Water Two-Phase Flow

Abstract

The production performances of fractured tight gas wells are closely related to several complex and unknown factors, including the formation properties, fracture parameters, gas–water two-phase flow, and other nonlinear flow mechanisms. The rate transient analysis (RTA) results have significant uncertainties, which should be quantified to evaluate the formation and fracturing treatment better. This paper provides an efficient method for uncertainty quantification in the RTA of fractured tight gas wells with multiple unknown factors incorporated. The theoretical model for making forward predictions is based on a trilinear flow model, which incorporates the effects of two-phase flow and other nonlinear flow mechanisms. The normalized rates and material balance times of both water and gas phases are regarded as observations and matched with the theoretical model. The unknowns in the model are calibrated using the ensemble Kalman filter (EnKF), which applies an ensemble of multiple realizations to match the observations and updates the unknown parameters step by step. Finally, a comprehensive field case from Northwestern China is implemented to benchmark the proposed method. The results show that the parameters and rate transient responses have wide ranges and significant uncertainties before history matching, while all the realizations in the ensemble can have good matches to the field data after calibration. The posterior distribution of each unknown parameter in the model can be obtained after history matching, which can be used to quantify the uncertainties in the RTA of the fractured tight gas wells. The ranges and uncertainties of the parameters are significantly narrowed down, but the parameters are still with significant uncertainties. The main contribution of the paper is the provision of an efficient integrated workflow to quantify the uncertainties in RTA. It can be readily used in field applications of multi-fractured horizontal wells from tight gas reservoirs.

1. Introduction

The unconventional tight gas resources have been the main contributor to the gas industry’s gradual depletion of conventional gas reservoirs in many countries [1]. The tight formations are with low porosity and low permeability and productivity, so hydraulic fracturing treatments are often used to stimulate the tight gas well [2,3]. An important target in gas reservoir engineering is to obtain ideal development results by optimizing the development strategies and hydraulic fracturing designs. Therefore, having a better understanding of the formation properties and fracturing treatment efficiency is crucial for this purpose [4,5].

Rate transient analysis (RTA) is an efficient method to perform formation and hydraulic fracturing evaluations in gas reservoir engineering, which is based on inversing the formation properties by analyzing the dynamic production data obtained from the wellbore [6,7]. Compared to core, well-logging, and seismic data interpretation results, the formation properties obtained with RTA are regarded to better represent the average formation properties. However, the RTA of fractured tight gas wells is also with significant uncertainties, which can result in misleading formation evaluation results [8]. There are several factors influencing the production of a fractured tight gas well, including the formation properties, the fracture properties, and the nonlinear gas–water two-phase flow mechanisms [9,10,11,12], so the values of many parameters should be considered to make production predictions. However, many parameters cannot be obtained directly with present technologies, especially for regions far away from the wellbore. History matching is need in RTA to inverse the unknown parameters, and multi-solution problems will occur when there are many unknown parameters in the model.

There are mainly three history matching techniques used in RTA, including manual history matching by type curve fitting, typical line/point fitting, and the automatic matching method based on Newton’s algorithm [13,14]. For traditional vertical wells completed in conventional reservoirs, radial flow models are used in RTA and the unknown parameters include formation permeability, porosity, and thickness. The RTA methods can be further refined by using the Agarwal–Gardner and Blasingame type curve fitting [15,16]. A match point in the type curve is used to generate two equations and calculate the unknown parameters. For multi-fractured horizontal wells with single-phase flow, linear flow and trilinear flow models are commonly used in RTA [17,18]. The early linear/bilinear flow regimes are used as typical lines in history matching, and the end time (typical point) of the linear/bilinear flow regimes is used to evaluate the fracture space [19,20]. Then, automatic matching methods should be used to inverse the model parameters because the unknowns are much more prominent than with the traditional vertical wells. For tight gas wells, the production performance is further influenced by gas–water two-phase flow and nonlinear flow mechanisms [10,21,22]. Present methods for the RTA of multi-fractured tight gas wells often combine type curve fitting, typical line/point fitting, and the automatic history matching method to reduce the uncertainties in history matching [23,24,25]. However, only one realization is obtained with the present RTA method, and the uncertainties in RTA cannot be quantified.

The uncertainty quantification is not a new topic in reservoir engineering; it has been widely studied for model calibrations in numerical reservoir simulations [26]. The reservoir parameters are adjusted in history matching to make the simulation results consistent with the historical production data. The development of computer technology and optimization algorithms, gradient algorithms, artificial neural networks (ANNs), evolutionary algorithms, the ensemble Kaman filter (EnKF), and other methods have enabled their use in automatic history matching [27,28,29]. The EnKF has been attracting attention in the petroleum industry for its efficiency in history matching. Many field problems, either the formation heterogeneities’ characterization in conventional reservoirs or the complex fracture networks’ calibration in unconventional reservoirs, are handled with the EnKF [30,31,32]. The advantages of the EnKF mainly consists of three aspects. First, the unknown parameters are calibrated by using the ensemble to calculate the Kalman gain in the EnKF, so it is independent of simulators [33]. Second, the production data and other monitoring data can be absorbed sequentially with the EnKF. Third, the posterior distributions can be obtained after updating the ensemble, thus the uncertainties can be quantified after history matching [34,35]. However, the EnKF has not been used in history matching and the uncertainty quantification of RTA for multi-fractured horizontal wells in a tight gas formation.

In this paper, we are focused on proposing a method to quantify the uncertainties in the RTA of fractured tight gas wells. The production prediction model and RTA method are based on our previous work [10,23], in which gas–water two-phase flow and multiple nonlinear flow mechanisms are considered. First, the theoretical fundamentals of mathematical models, the RTA method, and the EnKF are presented. Then, an integrated workflow for the RTA and uncertainty quantification of multi-fractured tight gas wells is proposed. Finally, a comprehensive field case study from Northwestern China is provided to test the efficiency of the proposed method.

2. Methodology

In this section, a method for history matching and uncertainty quantification of the production data based on the concept of RTA is provided. First, the model description and RTA method based on our previous studies are applied [10,23]. The model parameters and the uncertainties in history matching are briefly analyzed. Then, the theory and workflow of the EnKF for history matching and uncertainty quantification in the RTA is presented.

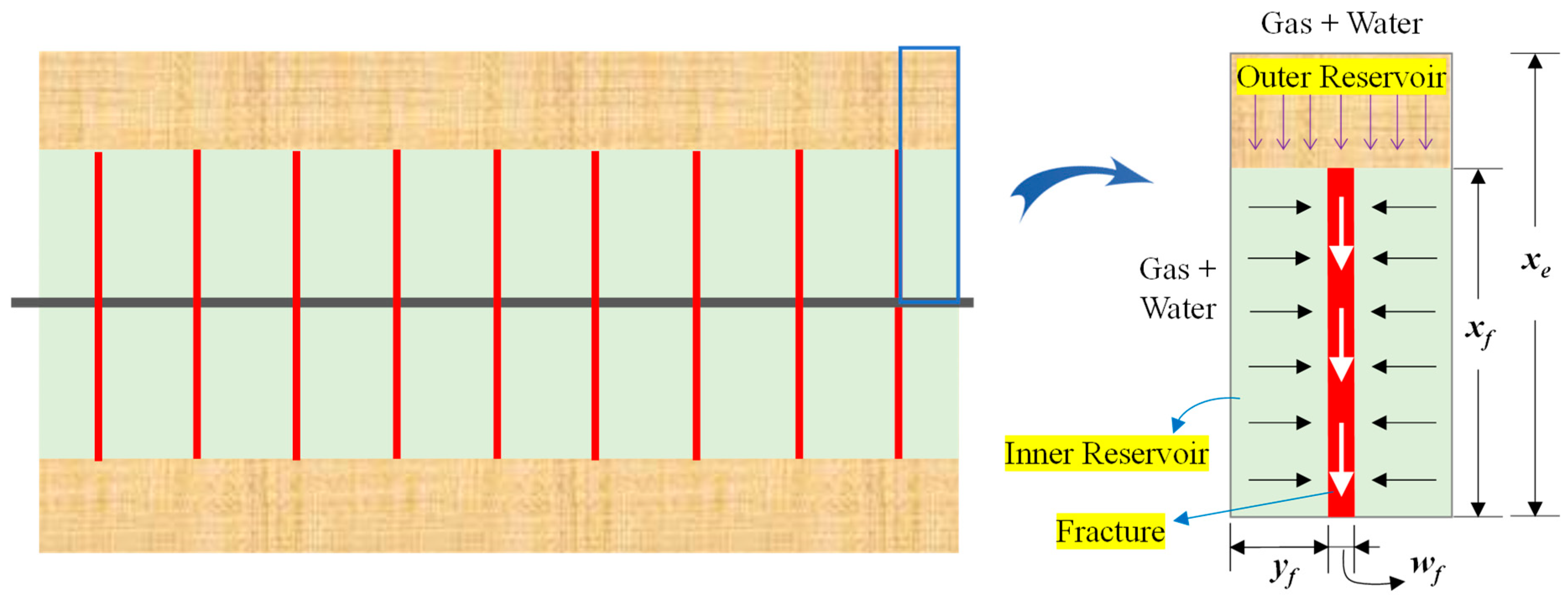
2.1. Model Description

The mathematical model in our previous study is used in this section [10]. As shown in Figure 1, the hydraulic fractures generated in the formation after hydraulic fracturing of the horizontal well are characterized using the classical trilinear flow model. In the model, the formation around the horizontal well can be discretized into three zones, including the main hydraulic fractures, the inner stimulated reservoir at two sides of the fracture, and the outer unstimulated reservoir beyond the fracture tips.

The uncertainties of the model mainly come from the unknown fracture and formation properties. The uncertain initial formation parameters include the average formation thickness, porosity, permeability, and initial water saturation. After hydraulic fracturing, hydraulic fractures are generated and the properties of the inner reservoir are enhanced, but the actual properties are unknown, including the fracture length, fracture conductivity, fracture space/number, and porosity and permeability of the inner reservoir. In addition to these parameters, the nonlinear flow mechanisms for gas and water flow in the formation also significantly influence the model uncertainties, including gas–water relative permeability, gas slippage, low-velocity non-Darcy flow, and stress-dependent permeabilities. In the following, the characterized methods of the nonlinear flow mechanisms and the unknown parameters will be analyzed.

The Brooks–Corey model is often used to match the relative permeability curves, given by

$$k_{rg}=k_{gr}{\left(S^{*}\right)}^{n_g}$$

(1)

$$k_{rwg}=k_{wr}{\left(1-S^{*}\right)}^{n_w}$$

(2)

$$S^{*}={\displaystyle \frac{S_g-S_{gc}}{1-S_{wrg}-S_{gc}}}$$

(3)

in which $S_w$ and $S_g$ are, respectively, the water and gas saturations in the formation, where $S_w+S_g=1$ in the tight gas formation; $k_{rw}$ and $k_{rg}$ are, respectively, the water and gas relative permeabilities; $S_{wc}$ is the irreducible water saturation; $S_{gc}$ is the residual gas saturation; $k_{wr}$ is the water relative permeability at residual gas saturation; $k_{gr}$ is the gas relative permeability at irreducible water saturation; and $n_w$ and $n_g$ are, respectively, the exponents of water and gas relative permeabilities.

In the Brooks–Corey model, 6 model parameters are used to match the relative permeability curves, including $S_{wc}$, $S_{gc}$, $k_{wr}$, $k_{gr}$, $n_w$, and $n_g$.

The gas slippage effect can be captured using the model proposed by Klinkenberg (1941) [36], given by

$${\displaystyle \frac{k_g}{k_{\infty }}}=1+{\displaystyle \frac{b}{\widehat{p}}}$$

(4)

in which $\widehat{p}$ is the average formation pressure, MPa; $k_g$ is the permeability considering the gas slippage effect, mD; $k_{\infty }$ is the permeability without the gas slippage, mD; and b is the slippage factor, MPa. It should be noted that the model parameter b is unknown and should be matched in the RTA.

Gas flow in the tight formation is often regarded to be with the low-velocity non-Darcy flow effect, which is often captured by adding a pseudo threshold pressure gradient (PTPG) in Darcy’s equation [37], given by

$$v_{\mathrm{g}}=-{\displaystyle \frac{k_g}{\mu }}\left({\displaystyle \frac{dp}{dx}}-\lambda \right)$$

(5)

where $v_g$ is the percolation velocity of gas, m/s; $\mu$ is the gas viscosity, Pa·s; $p$ is the formation pressure, Pa; and $\lambda$ is the PTPG, Pa/m. One should note that the PTPG $\lambda$ is often unknown and should be matched in the RTA.

The exponential model proposed by Nur and Yilmaz can be used to capture the effect of stress-dependent permeability [38], given by

$$k=k_i{e}^{-\gamma \left(p_i-p\right)}$$

(6)

where $\gamma$ is the permeability modulus, Pa⁻¹ and $p_i$ is the initial formation pressure, Pa. The permeability modulus $\gamma$ is also an unknown parameter and should be matched in the RTA.

After considering the nonlinear flow mechanisms and the fractures generated in the formation, the mathematical model can be proposed and solved semi-analytically. In this paper, since we are focused on the uncertainty quantification in the RTA of fractured tight gas wells, the derivation of the mathematical model is provided in our previous work [23].

2.2. Rate Transient Analysis Method

RTA is an efficient method to inverse the unknown fracture and formation properties, which is widely used in performing formation evaluations. There are mainly two reasons. First, analytical and semi-analytical models can be used in history matching, which are significantly cheaper in computational costs than numerical models. Second, the production data are normalized in RTA, and plenty of computational costs can be saved by avoiding matching the variable rate/BHP data.

In this paper, the RTA method provided in our previous paper is applied to generate the theoretical type curves and process the field production data [23]. To match the variable production rate and BHP data in the field, the concepts of material balance time and the normalized rate are used to process the field production data. It should be noted that the production performances of water and gas phases should be handled at the same time. The mathematical model for two-phase flow in the formation is nonlinear, and the gas and water production rates are obtained based on numerical iterations, so the type curves for gas and water phases are also obtained based on the concepts of material balance time and the normalized rate.

For the gas phase, the material balance time and normalized rate are, respectively, defined as

$$t_{c,g}={\displaystyle \frac{{\mu }_i{c}_{ti}}{q_g}}{\displaystyle \underset{0}{\overset{t}{\int }}\frac{q_g}{\mu c_t}}dt=-{\displaystyle \frac{G_i}{q_g}}{\displaystyle \frac{{\mu }_i{c}_{ti}{Z}_i}{2p_i}}({\psi }_i-\overline{\psi })$$

(7)

$$q_{N,g}={\displaystyle \frac{q_g}{{\psi }_i-{\psi }_{wf}}}$$

(8)

For the water phase, the material balance time and normalized rate are, respectively, defined as

$$t_{c,w}={\displaystyle \frac{W_p}{q_w}}$$

(9)

$$q_{N,w}={\displaystyle \frac{q_w}{p_i-p_{wf}}}$$

(10)

in which $t_{c,g}$ and $t_{c,w}$ are, respectively, the material balance time for gas and water phases, d; $q_{N,g}$ is the normalized rate for the gas phase, ${\mathrm{m}}^3/\mathrm{d}/\left({\mathrm{MPa}}^2/\mathrm{mPa}·\mathrm{s}\right)$; $q_g$ and $q_w$ are, respectively, the gas and water production rates, m³/d; $p_i$ and $p_{wf}$ are, respectively, the initial pressure and BHP, MPa; $Z_i$ is the gas compressibility factor at the initial pressure, dimensionless; $\mu$ is the gas viscosity, mPa·s; ${\mu }_i$ is the gas viscosity at the initial pressure, mPa·s; $c_t$ is the total formation compressive coefficient, MPa⁻¹; $c_{ti}$ is the total formation compressive coefficient at initial pressure, MPa⁻¹; $G_i$ is the gas reserve in place, m³; and ${\psi }_i$, ${\psi }_{wf}$, and $\overline{\psi }$ are, respectively, the pseudo-pressure at the initial, wellbore, and average formation pressure condition, MPa²/mPa·s.

By using the concept of material balance time and the normalized rate, the gas and water production performances in the field can be matched and analyzed based on the theoretical model.

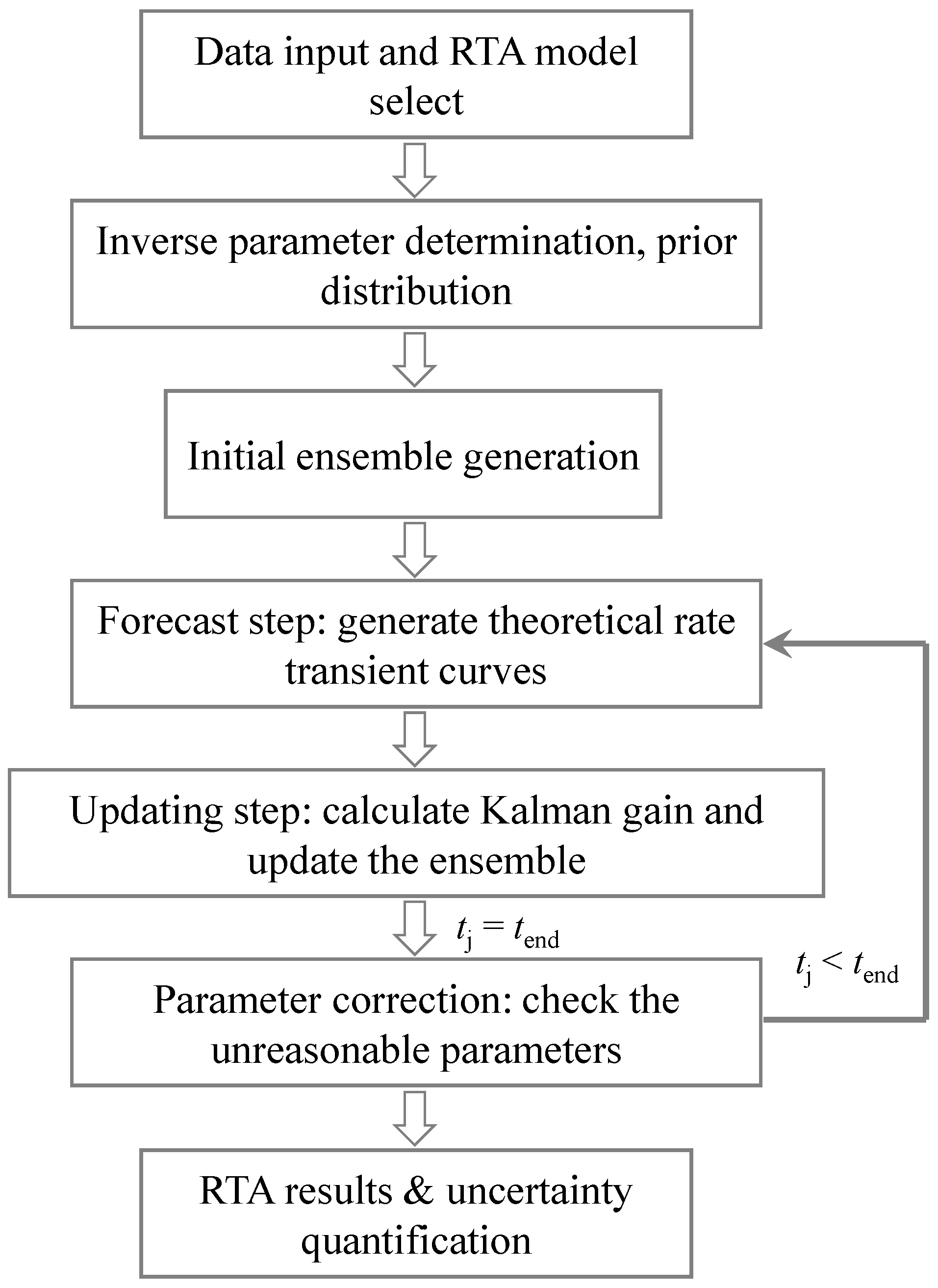
2.3. EnKF for History Matching and Uncertainty Quantification

History matching should be used in RTA to match the field data with the theoretical model. Manual fitting and least squares fitting are widely used in RTA to match the model parameters, thus providing a basis for conducting formation and hydraulic fracturing evaluations. For multi-fractured horizontal wells in a tight gas formation, there are more than 10 unknown model parameters, which makes it difficult to perform history matching using traditional methods. This problem was avoided in our previous work by directly assigning the value of some parameters and reducing the number of matching parameters. However, this will make the history matching results unreasonable when the directly given values greatly deviate from the real values. In this section, the EnKF is applied to match the field production data and quantify the uncertainties in the RTA. Three steps are included in the EnKF, including the initial ensemble generation, the forecasting step, and the updating step.

In the initial ensemble generation step, the unknown formation and fracture parameters should be sampled from the prior PDF of the parameter space. $N_e$ realizations are generated for each unknown parameter. As shown in Section 2.1, the vector of the unknown parameters is given by

$$m={\left[H, S_{wi}, {\varphi }_m, k_m, {\varphi }_I, k_I, \gamma , x_F, N_F, k_F, S_{gc}, S_{wr}, k_{rgrw}, k_{rwrg}, n_g, n_w, b, \lambda \right]}^T$$

(11)

where $H$ is the average formation thickness, m; ${\varphi }_m$ is the formation porosity, dimensionless; $k_m$ is the formation permeability, mD; ${\varphi }_I$ is porosity of the inner stimulated reservoir, dimensionless; $k_I$ is the permeability of the inner stimulated reservoir, mD; $N_F$ is the fracture number, dimensionless; and $k_F$ is the permeability of the hydraulic fractures, mD.

The state vector can be written as

$$y=\left[\begin{array}{c}m\\ g\left(m\right)\end{array}\right]$$

(12)

It should be noted that the formation pressure and saturation state are not included in the state vector since a semi-analytical model is used in the history matching. The vector of production performance comprise the normalized gas and water production rates at the present step, $g\left(m\right)=\left[q_{N,g}\left(m\right);q_{N,w}\left(m\right)\right]$, so the length of $g\left(m\right)$ $N_d=2$. The state vector is a vector with a length of $N_m+N_d$, in which $N_m$ is the number of unknown parameters in $m$.

Putting the $N_e$ realizations in the same matrix, the initial ensemble can be written as

$$Y=\left(y_1,y_2,\cdots ,y_{N_e}\right)$$

(13)

Defining $H=\left[\begin{array}{cc}{O}_{N_d\times N_m},& I_{N_d\times N_d}\end{array}\right]$, we obtain

$$\left[g\left(m_1\right),\cdots ,g\left(m_{N_e}\right)\right]=HY$$

(14)

In the forecasting step, the production performance vectors $\left[g\left(m_1\right),\cdots ,g\left(m_{N_e}\right)\right]$ can be obtained by running the semi-analytical model with the given parameter ensemble $\left[m_1,\cdots ,m_{N_e}\right]$.

In the updating step, the field production performance is used to update the unknown parameters in the ensemble.

$$Y_n^u=Y_n^f+K_{e,n}\left(d_{obs,n}-H{Y}_n^f\right)$$

(15)

in which $d_{obs,n}$ are the normalized gas and water production rates using the field production data at the present step and $K_{e,n}$ is the Kalman gain matrix at the present step, given by

$$K_{e,n}=C_{Y,n}^f{H}^T{\left(H{C}_{Y,n}^f{H}^T+C_D\right)}^{-1}$$

(16)

where $C_D$ is the covariance matrix of the observation error of the production performance data and $C_{Y,n}^f$ is a covariance matrix of the state ensemble in the present step.

$$C_{Y,n}^f={\displaystyle \frac{1}{N_e-1}}\left(Y_n^f-{\overline{Y}}_n^f\right){\left(Y_n^f-{\overline{Y}}_n^f\right)}^T$$

(17)

Figure 2 presents the workflow for the RTA and uncertainty quantification of fractured horizontal wells in a fractured tight gas formation. Seven steps are included in the workflow:

• Understanding from the geological and hydraulic fracturing data should be used to choose a proper model for the RTA.
• The uncertainties of model parameters should be primarily analyzed. The values of parameters with low uncertainties can be directly given, while other parameters can be regarded as inverse parameters and should be given the prior distributions.
• An initial ensemble with $N_e$ realizations of the $N_m$ inverse parameters is generated by sampling from the prior distributions.
• In the forecasting step, the production performance will be predicted step by step. The semi-analytical model proposed in our previous work [10] is used to predict the water and gas production performance for model parameters in the initial ensemble. The normalized rate and material balance time for both water and gas production performances are obtained, which are used to update the vectors $\left[g\left(m_1\right),\cdots ,g\left(m_{N_e}\right)\right]$ in the initial ensemble.
• In the updating step, the unknown parameters will be updated step by step. Equations (15) and (16) are used to obtain the Kalman gain and update the unknown parameters in the ensemble.
• The parameters in the ensemble may be outside the initial setting range of the inverse parameters, so a correction to the unreasonable parameters is essential.
• The model parameters in the initial ensemble are calibrated, with which the posterior distribution of each inverse parameter can be obtained. In this way, the uncertainties in the RTA can be quantified, and the uncertainties in production performance can be predicted.

3. Results and Discussion

In this section, a field case from Northwestern China is applied to show the application of the proposed history matching and uncertainty quantification method in the RTA of multi-fractured horizontal wells in tight gas reservoirs. The workflow provided in Figure 2 is used in this section. In the following, a problem description of the field case is first given. Then, the history matching and uncertainty quantification results are presented, respectively.

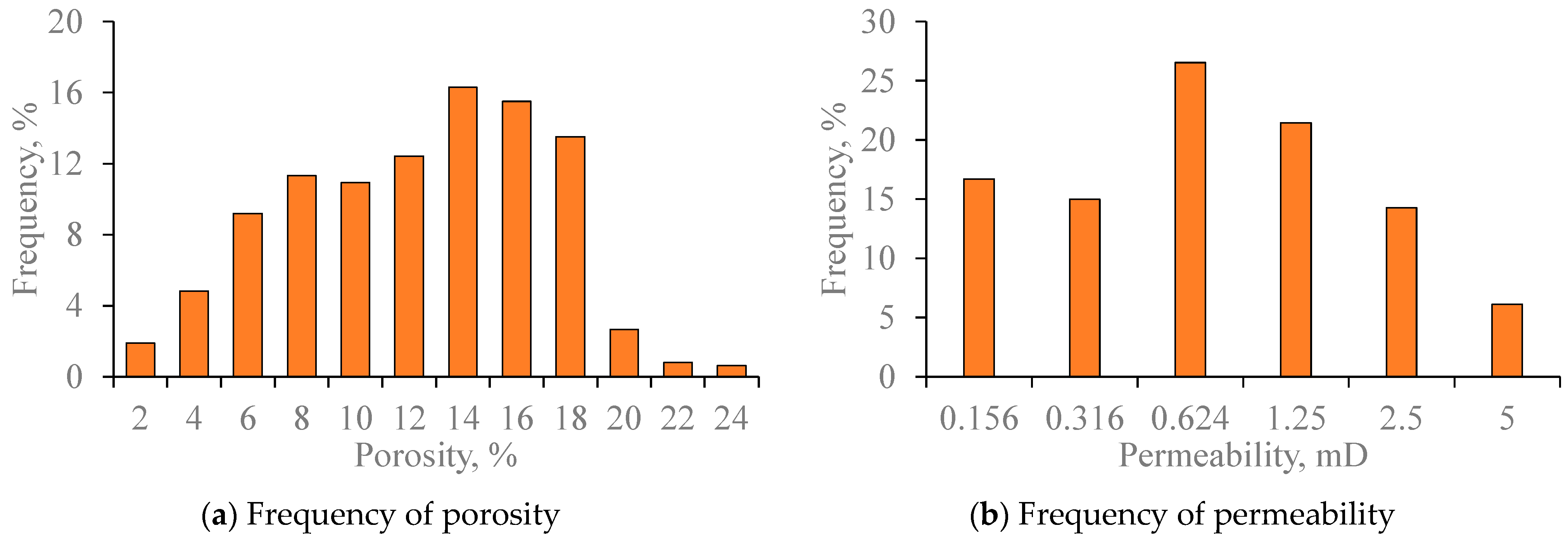
3.1. Description of the Field Case

The formation is located in the upper Paleozoic tight sandstone gas reservoir in Ordos Basin. The reservoir is a lithologic structural gas reservoir, where the middle to lower part of the reservoir is mainly a water layer and the gas layer is developed in the high part of the structure. However, due to the influence of a mudstone interlayer, the reservoir is scattered and the gas–water interface is not uniform. In addition, it is generally believed that the tight sandstone in this area has high irreducible water saturation, but the irreducible water saturation obtained by different measurement methods is different to some extent. The original water saturation obtained by closed coring and logging data is 20%~30%, while the irreducible water saturation determined by experimentation is greater than 40% [39]. In addition, the gas–water two-phase flow permeability curves in the formation conditions are unknown. Therefore, we can conclude that the formation is saturated with high water content, but the initial and irreducible water saturations and the permeability curves are with great uncertainties.

The distribution of formation porosity and permeability from geological studies in this area is provided in Figure 3. It is suggested that a wide range is exhibited for the formation heterogeneities. The pore size of the tight matrix is shown to be within the range of 20~2000 nm, concentrated in the range of 40~600 nm. The average relative pore volumes of micropores, mesopores, and macropores are 70.9%, 27.57%, and 1.53%, respectively [40]. In this case, gas flow in the tight formation has significant low-velocity non-Darcy flow and gas slippage effects. These factors add to the difficulty and uncertainty in the RTA of fractured tight gas wells.

A multi-fractured horizontal well is used to develop tight gas in the formation. However, an efficient hydraulic fracturing evaluation is difficult for many fractured wells because the hydraulic fracturing process is monitored for many wells. To inverse the fracture parameters and perform a fracturing evaluation, RTA is widely used to for this and for further predicting the eventual ultimate recovery (EUR) of the reservoir. In our previous paper, RTA is used to analyze a multi-fractured horizontal well in this tight gas field. However, only one realization is matched to the field data by using the least squares method [23], as shown in Figure 4, and only a few unknown parameters are inversed, including the fracture length, fracture number, fracture conductivity, formation permeability, and permeability modulus. In addition, we have no understanding of the uncertainties in RTA. To overcome this problem, the proposed history matching and uncertainty quantification method is used in this part. The same field case is used in this paper to make a comparison with our previous work.

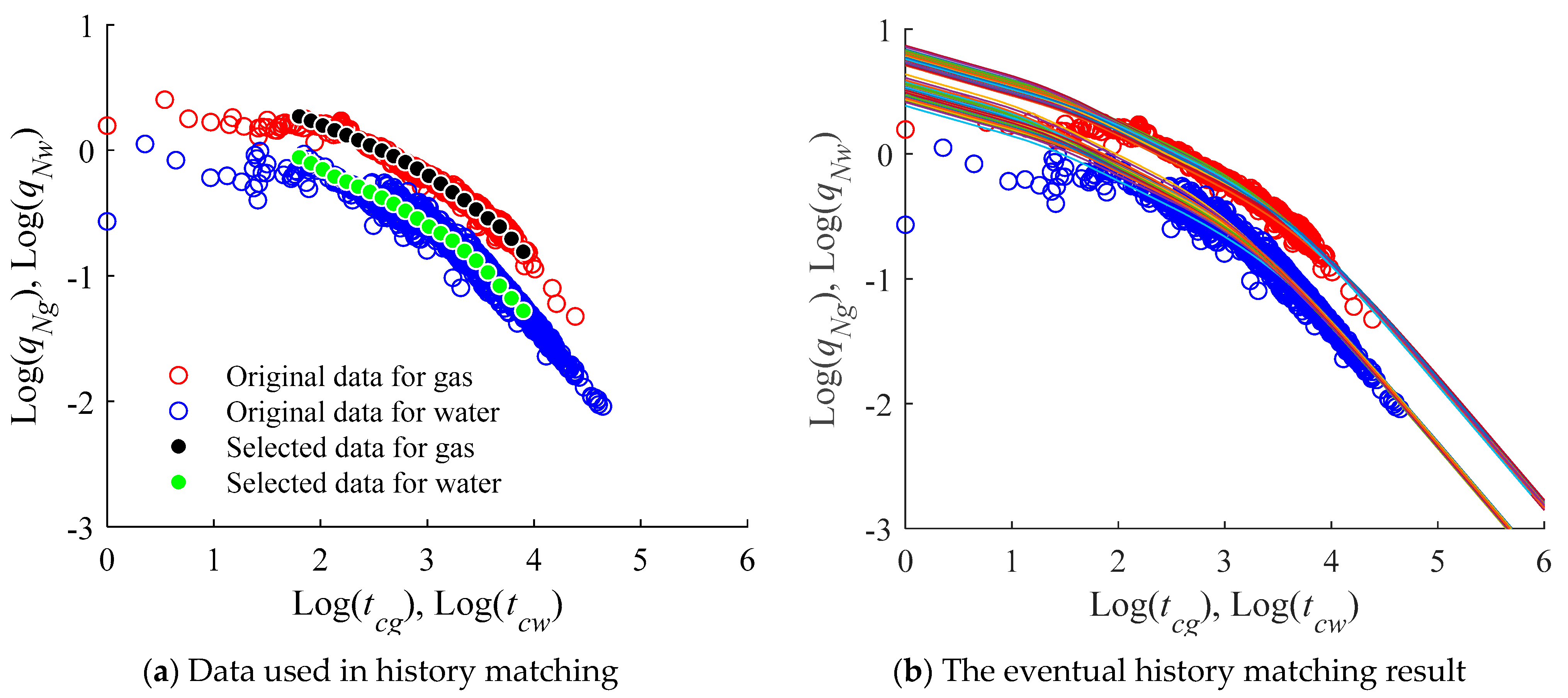
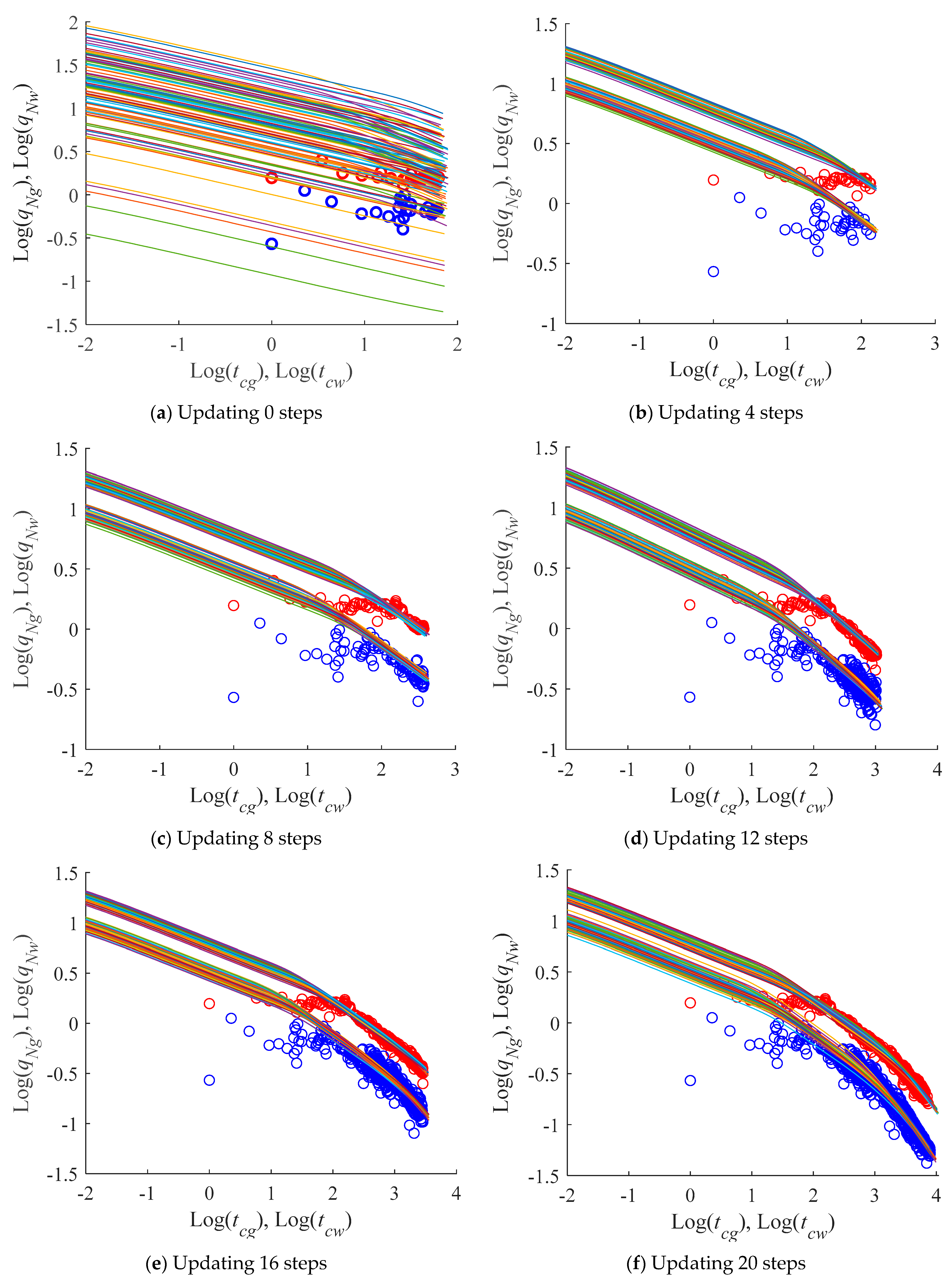
3.2. History Matching Results

For the hydraulic fractured horizontal well in a tight gas reservoir, the gas–water two-phase trilinear flow model and the proposed history matching method are used for RTA. The processed data using the concept of the normalized production rate and material balance time shown in Figure 4 are used as the observed data in history matching. The known parameters are shown in

Table 1. Given model parameters for the field case.

Model Parameter	Value	Units
Initial formation pressure	23.4	MPa
Formation temperature	345	K
Well length	1215	m
Hydraulic fracturing stages	12	Dimensionless
Well space	600	m
Rock compressibility	5 × 10−5	MPa−1
Porosity of the hydraulic fracture	0.3	Dimensionless
Viscosity of water	0.3	mPa·s
Water compressibility	5 × 10−4	MPa−1

, including the initial formation pressure, formation temperature, well length, etc. The unknown parameters are summarized in

Table 2. Prior and posterior unknown model parameters for the field case.

Model Parameter	Prior Distribution (Uniform Distribution)	Posterior Distribution (See Figure 7)
Formation thickness, m	[6, 15]	[6.5, 9.5]
Initial water saturation	[0.55, 0.75]	[0.62, 0.67]
The porosity of the outer reservoir	[0.07, 0.15]	[0.108, 0.15]
The permeability of the outer reservoir, mD	[0.1, 0.8]	[0.35, 0.6]
The porosity of the inner reservoir	[0.07, 0.2]	[1, 1.4]
The permeability of the inner reservoir, mD	[0.1, 1.6]	[1, 1.6]
Log (permeability modulus), MPa−1	[−4, −2]	[−4, −2]
Half-length of the fracture, m	[50, 130]	[60, 105]
Number of fractures	[8, 18]	[12, 16]
Log (fracture permeability), mD	[2, 4]	[2.45, 2.95]
Residual gas saturation	[0.05, 0.35]	[0.05, 0.17]
Irreducible water saturation	[0.15, 0.45]	[0.18, 0.36]
Gas relative permeability at irreducible water saturation	[0.1, 0.9]	[0.3, 0.55]
Water relative permeability at residual gas saturation	[0.1, 0.5]	[0.1, 0.25]
Exponent of gas relative permeability	[1, 3]	[1.7, 2.6]
Exponent of water relative permeability	[1, 3]	[1.6, 2.5]
Slippage factor, MPa	[0.2, 1.8]	[0.5, 1.3]
Log (PTPG), MPa/m	[−4, −2]	[−3.5, −2.7]

, including the key formation and fracture parameters, as explained in Section 3.1. The prior distributions of the model parameters are not available since the geological data are not enough, so wide ranges and uniform distributions are used as the prior distribution for the unknown parameters, as shown in Table 2.

In this case, 18 model parameters are sampled from the prior distributions to generate the initial ensemble. The number of models in the initial ensemble is given as 50. In the forecasting step, the RTA responses are obtained using the model proposed in our previous work [23]. Because the data are matched in the log–log plots in the RTA, the logarithm values of the normalized gas and water production rates are matched for each material balance time. Here, one should note that the values of material balance time for gas and water phases are not the same for the same production time. In addition, the material balance time should be used in RTA. Therefore, the normalized production rates for gas and water phases are matched at the same material balance time instead of the production time in this study. In the updating step, the EnKF method is used to calculate the Kalman gain and update the model parameters. In this case, the data are gradually assimilated with 20 steps. To obtain a good match to the field data, 20 points are used in history matching for the gas and water phases, as shown in Figure 5a.

The history matching results to the field data using the EnKF are shown in Figure 5b. It is obvious that almost all the realizations in the ensemble have good matches to the field data. This shows that the inverse problem of fractured tight gas wells is with significant uncertainties. The history matching result obtained using the traditional RTA method is just one realization, as shown in Figure 4. Therefore, the uncertainties in the RTA of fractured tight gas wells should be given great attention for the inverse problem with many unknown parameters.

To further analyze the behavior of the EnKF in the RTA, the history matching results after updating 0, 4, 8, 12, 16, and 20 steps are provided, as shown in Figure 6. The results show that the ranges of the parameters in the initial ensemble are wide enough so that the field RTA responses can be covered by the theoretical model. The uncertainties in history matching are significantly reduced after updating four steps with more field data being assimilated with the EnKF, and good matches to the field data can be obtained after eight steps of assimilation. After updating eight steps, the changes in the bands of the rate transient responses for both water and gas phases are small, but good matches are obtained for all cases. This shows that the EnKF converges quickly in the first several assimilation steps and stays stable to get closer to the actual solution. The proposed workflow also works efficiently in terms of computational time, and only 38 s is needed for history matching. When parallel computation is used in the computer, the computational time can be reduced to 8 s.

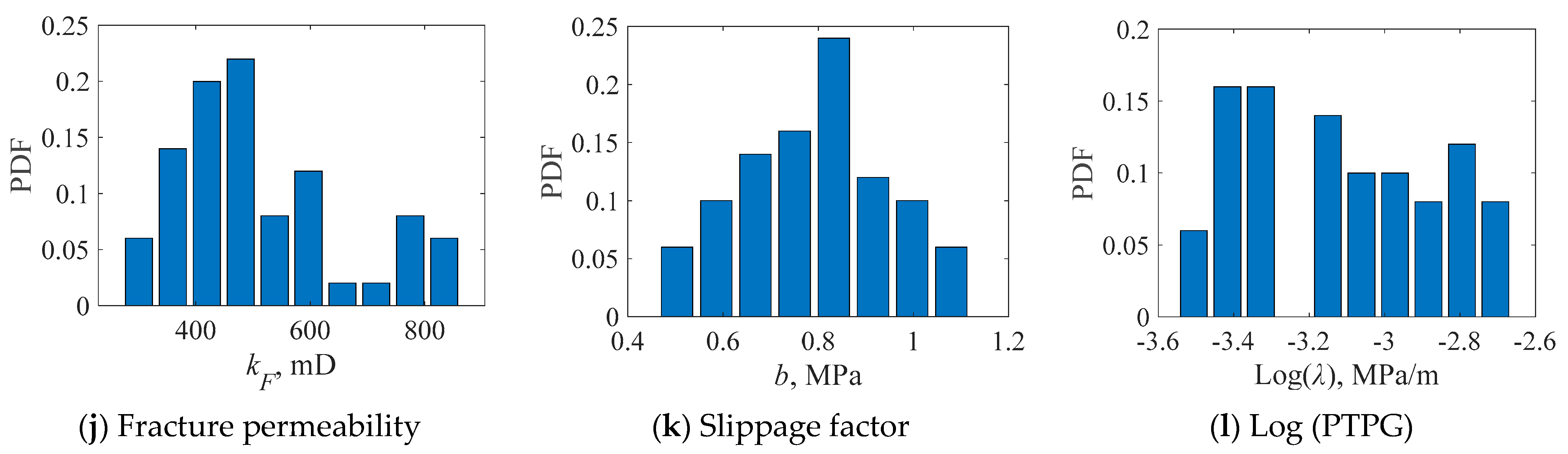
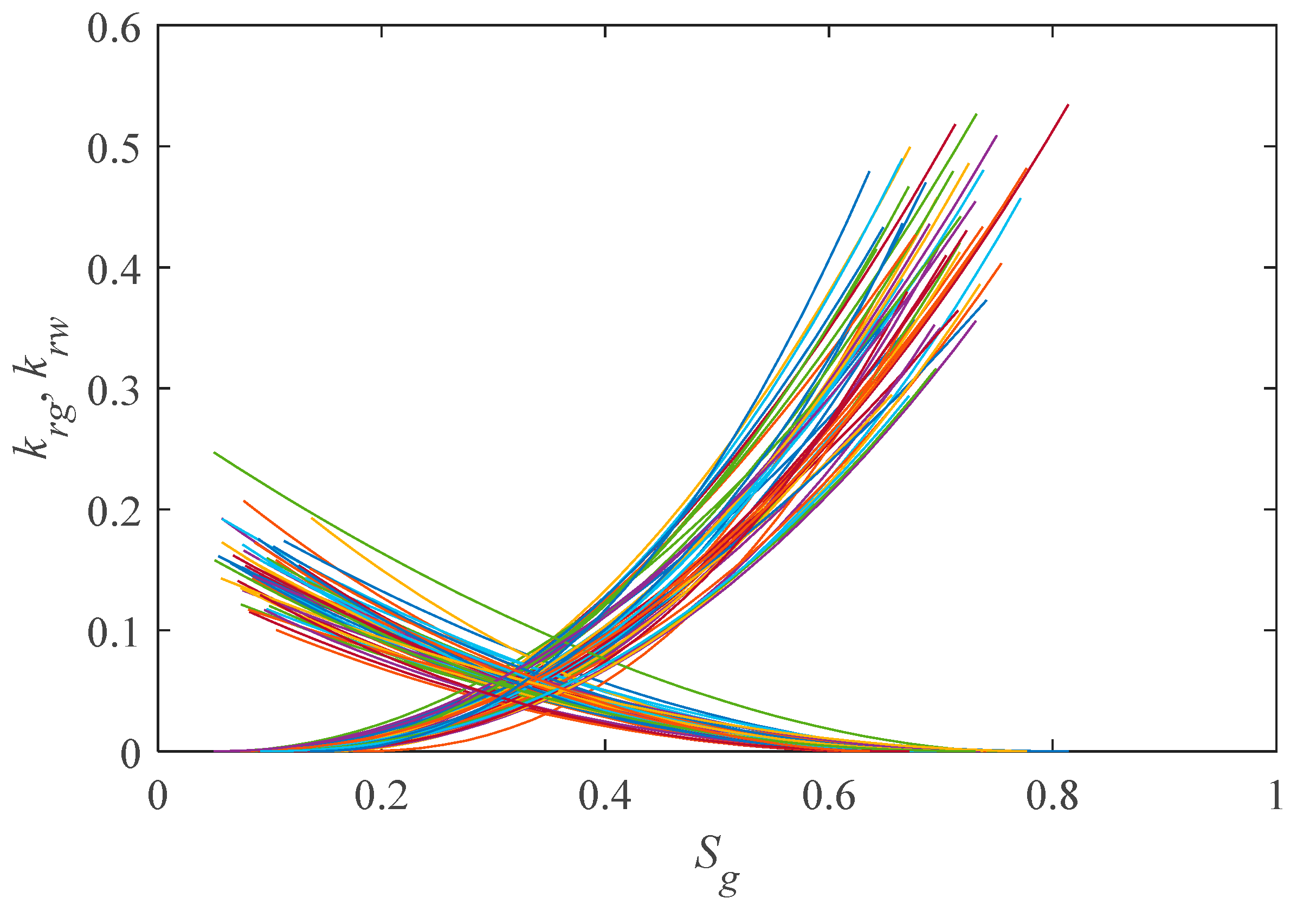
3.3. Uncertainty Quantification

The posterior distributions of the calibrated parameters after history matching are shown in Figure 7. An interesting phenomenon is that the posterior distributions of the model parameters exhibit a peak in Figure 7, although uniform distributions are assumed for all the parameters. A comparison between the range of the prior and posterior distributions are provided in Table 2. It is obvious that the distribution range has been significantly narrowed down after history matching, which shows that the uncertainties can be greatly reduced using the proposed RTA method. Because the influence of the pressure-dependent permeability on the RTA responses is not significant, the range of the permeability modulus is not significantly narrowed down. The calibrated relative permeability curves are provided in Figure 8. The relative curves are obtained using Equations (1)–(3) and the history matching results of two-phase flow parameters, including $S_{wc}$, $S_{gc}$, $k_{wr}$, $k_{gr}$, $n_w$, and $n_g$. Combining the posterior distributions in Table 2, it is obvious the uncertainties have been significantly reduced.

Future studies about reservoir evaluations should mainly include the mathematical model, the history matching method, and field cases. First, the proposed trilinear flow model is simple but practical in the RTA of fractured unconventional reservoirs, in which the nonlinear flow mechanisms are further considered compared to the classical trilinear flow model. The fracture networks can be considered in present discrete fracture models, but it is not widely used in making formation evaluations for large uncertainties in characterizing each fracture. However, the uncertainties in fracture characterization may be reduced if efficient monitoring and interpretation methods are proposed in the future. Second, the computational time of the EnKF in history matching is mainly spent on running the ensemble in each step. The history matching and uncertainty quantification method with the EnKF method in this study is computationally cheap, but this may not be the case in calibrating other complex and large-scale numerical reservoir models. In each forecasting step, no more than two seconds are needed to run a model in each step for the semi-analytical model in this paper. However, the computational efficiency of the EnKF for large-scale issues or sophisticated reservoir models should be further studied and compared to other history matching methods, like Monte Carlo simulations and Bayesian inference. Third, the field case in this study is focused on evaluating the tight gas formation based on RTA. To reduce the uncertainties, more real-world cases and multiple databases can be used in history matching. In addition, more studies should be conducted to test the history matching method for cases in different contexts, like oil reserves or geothermal systems.

4. Conclusions

This paper provides an efficient history matching and uncertainty quantification method in the RTA of multi-fractured horizontal wells in a tight gas formation with gas–water two-phase flow. The following conclusions can be drawn from this study:

• Fluid flow in the fractured tight gas formation is with multiple uncertainties because the flow is affected by numerous factors, including formation properties, fracture parameters, and nonlinear flow mechanisms in the formation and fracture system. These factors can be considered in the proposed mathematical model and RTA method.
• An efficient workflow is proposed to quantify the uncertainties in the RTA of fractured tight gas wells by combining the mathematical model, the RTA, and the EnKF method. Seven steps should be included in the workflow in total, including the theoretical model selection, inverse parameter and prior distribution determination, initial ensemble generation, making forecasts with the theoretical model, parameter updating with the EnKF, parameter correction of unreasonable parameters, and the RTA results and uncertainty quantification.
• The normalized rates and material balance times of water and gas production performances can be used in EnKF-based history matching. The EnKF can assimilate the data step by step and converges quickly in the first several steps. The proposed workflow works stably and efficiently in history matching to the rate transient responses of the fractured tight gas wells, and only several seconds are needed in the computation by incorporating parallel computation for a field case.
• The uncertainties in the RTA of multi-fractured tight gas wells can be quantified after obtaining the posterior distribution of the inversed model parameters in history matching. The ranges and uncertainties of the parameters can be significantly narrowed down, and the posterior distributions exhibit a peak in the PDF graphs, although wide and uniform prior distributions are given in history matching.