Abstract
Modelling at the basin scale offers crucial insights for policymakers as they make decisions regarding the optimal utilization of water resources. This study employed the MIKE HYDRO Basin model to analyse water demand and supply dynamics in the Parvati Basin of Rajasthan, India, for the period 2005–2020. The MIKE11 NAM model showcased strong alignment between simulated and observed runoff during both the calibration (NSE = 0.79, PBIAS = −2%, R2 = 0.79, RMSE = 4.95, RSR = 0.5, and KGE = 0.84) and validation (NSE = 0.67, PBIAS = −12.4%, R2 = 0.68, RMSE = 8.3, RSR = 0.62, and KGE = 0.67) phases. The MIKE HYDRO Basin model also exhibited excellent agreement between observed and simulated reservoir water levels, with R2, NSE, RMSE, PBIAS, RSR, and KGE values of 0.86, 0.81, 3.87, −2.30%, 0.43, and 0.88, respectively. The MIKE HYDRO Basin model was employed to create six distinct scenarios, considering conveyance efficiency, irrigation method, and conjunctive water use, to assess irrigation demands and deficits within the basin. In the initial simulation, featuring a conveyance efficiency of 45%, flood irrigation, and no groundwater utilization, the average water demand and deficit throughout the study period were estimated as 43.15 MCM and 3.45 MCM, respectively, resulting in a sustainability index of 0.506. Enhancing conveyance efficiency to 75% under flood irrigation and 5% conjunctive use could elevate the sustainability index to 0.92. Transitioning to sprinkler irrigation and a lift irrigation system could raise the system’s sustainability index to 1. These developed models hold promise for real-time reservoir operation and irrigation planning across diverse climatic conditions and varying cropping patterns.
1. Introduction
The discrepancy between water resource supply and demand largely stems from an insufficient understanding of climatic shifts and inadequate management practices. To effectively plan, develop, and manage water resources, a continuous collection of hydrological data is imperative, often lacking due to faulty instrumentation and human errors [1]. The high temporal and spatial variability of rainfall, coupled with limited rainfall and runoff gauge stations, heightens the complexity of hydrological modelling and poses challenges for stream flow predictions [2]. Hydrological models are essential for comprehending and managing water resources by analysing rainfall patterns, runoff generation, groundwater recharge, and stream flow behaviour. They enable predictions of floods, droughts, and water availability, guiding decisions in water resource management, flood risk assessment, irrigation planning, and infrastructure design [3,4,5,6,7,8].
Hydrologic models are categorized into ‘physical’, ‘conceptual’, and ‘black box’ models [9]. Physical hydrological models are founded on complex physical principles and require extensive computational resources and time. These models offer a detailed view of hydrological processes, enhancing understanding of the system. Notable examples include SCS [10], VIC [11], MIKE SHE [12,13], SWAT [12], etc. Black box models rely solely on mathematical relationships between input and output variables, often without considering catchment behaviour [14]. These models are adept at modelling specific areas using analysed data and include regression, fuzzy logic, and artificial neural network models. Conceptual hydrological models rely on empirical relationships among various hydrological variables. These models employ lumped-parameter techniques and mathematical equations to describe hydrological processes, reducing data requirements and computational complexity. Examples of conceptual models include the AWBM [15], SIMHYD [16], and the MIKE 11 NAM model, among others.
Estimating water demand and deficits is pivotal for ensuring efficient water resource management. Understanding the water demand enables the authorities to effectively plan and allocate resources, ensuring a sufficient supply to fulfil the requirements of diverse sectors like domestic, industry, and agriculture [17,18]. Through precise demand estimation, decision makers can deploy strategies to balance water supply and demand, thus preventing water shortages and ensuring equitable distribution. The authors of [19] calculated the demand and supply of water for optimized cropping planning in the Mandla district of Madhya Pradesh. The MIKE HYDRO Basin and Water Evaluation and Planning (WEAP) software is widely utilized for basin planning, ranging from large scales to field-level applications within command areas. The authors of [20] utilized the WEAP model to develop various management scenarios to achieve sustainable water resource management from 2015 to 2050. Their findings underscored the significance of adopting new irrigation techniques and promoting the reuse of purified water for irrigation purposes. Similarly, ref. [21] developed a decision support system based on MIKE BASIN to manage the Rangawan reservoir, governed by a water distribution agreement between two Indian states. Their study recommended several efficiency-enhancing measures to mitigate demand deficits within the command area. In [22], the MIKE HYDRO Basin model was utilized to conduct scenario analyses in the Tandula reservoir system. Their findings revealed an annual deficit of 6.36 MCM with 88% reliability, assuming 51% efficiency and no groundwater utilization. The overall performance index stood at 0.13 but could increase to 0.86 by enhancing efficiencies and consumptive use. The authors of [23] employed the MIKE 11 NAM and MIKE HYDRO Basin models to investigate the impacts of river diversion, on-stream dams, and river interlinking on water availability within the Shipra River basin. Their results demonstrated that water availability in the Shipra basin has improved, mainly owing to the Narmada–Shipra link, ensuring a minimum flow of 1.7 m3/s at Ujjain, even during low-flow periods. Similarly, numerous other researchers have utilized the MIKE HYDRO Basin for various purposes such as reservoir operation, irrigation planning, basin management, and scenario assessment [24,25,26,27].
The Parvati basin, located in the eastern part of Rajasthan, primarily depends on agricultural activities. It is imperative to accurately assess water demand and supply within the basin to sustainably manage water resources and foster socio-economic growth in the region. As a primarily agrarian region, agriculture dramatically depends on irrigation water from the Parvati River. Precise water demand estimation is vital for improving agricultural productivity, safeguarding food security, and supporting the livelihoods of local communities [28]. Comprehending the availability of water supply from the Parvati River and groundwater sources is crucial for the equitable distribution and effective utilization of water resources. Ultimately, maintaining a balance between water demand and supply through informed decision-making can foster the sustainable development of water resources within the basin [29]. Optimization may not always address complex real-world challenges for water resources and management. This encouraged the study to generate multiple scenarios involving the demand, supply, efficiencies, and conjunctive use of water. Therefore, in the present study, the MIKE 11 NAM and MIKE HYDRO Basin models were employed with the specific objectives: (i) to determine the water demand and deficit in the Parvati basin under multiple management scenarios and (ii) to conduct a performance assessment of multiple management plans for ensuring the sustainable management of water resources in the basin.
2. Study Area
Parvati Basin
The Parvati River Basin, located in the eastern part of Rajasthan, extends from 26°20′29.76″ to 26°58′05.87″ N latitude and from 77°08′33.59″ to 78°16′27.33″ E longitude, covering an area of approximately 1109.7 km2. Western hills characterize its topography, the source of the Parvati River, gradually descending towards the northeast. Exhibiting a semi-arid climate, the region maintains an average ambient temperature of 25.7 °C, fluctuating between 6 °C and 44.5 °C. Rainfall predominantly occurs during the monsoon season, averaging 704 mm annually. The soil composition varies across the basin, ranging from sandy to sandy-loam type. Additionally, land use within the basin majorly encompasses agriculture and range land. Agricultural practices in the area are predominantly rainfed, heightening the significance of water availability as a pivotal determinant of agricultural productivity and rural sustenance. The Parvati Reservoir is the primary source for meeting the demands of the surrounding areas’ domestic and irrigation water. The location map of the Parvati basin is presented in Figure 1.
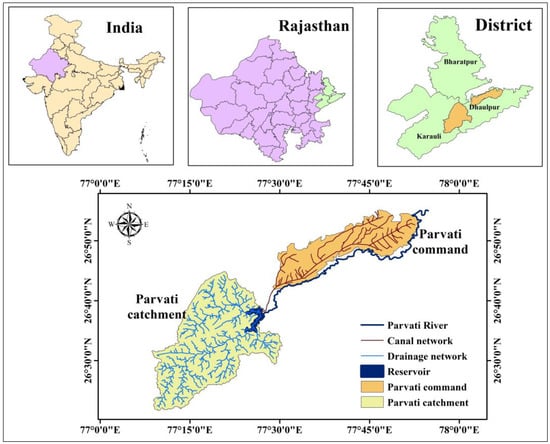
Figure 1.
Location map of the study area.
3. Methodology
3.1. Data Products Used in the Study
The present study requires comprehensive data, including meteorological, hydrological, reservoir, soil, and crop information as inputs. Daily rainfall and discharge data from 2005 to 2020 were sourced from the Water Resource Department (WRD), Dholpur. Daily temperature data were obtained from the India Meteorological Department (IMD), Pune. Additionally, reservoir-related data, including daily reservoir level, elevation-area-capacity tables, characteristics level, storage capacity, canal head releases, spillway information, reservoir type, and reservoir height, were collected from WRD, Dholpur. Soil and crop details pertinent to the study area were obtained from existing literature and the Food and Agriculture Organization (FAO) [30,31,32]. Throughout the study, continuous engagement with farmers, engineers, water resource managers, and technocrats facilitated the acquisition of new plans and strategies.
3.2. Rainfall–Runoff Modelling
This study utilized the MIKE 11 NAM model for rainfall–runoff (RR) modelling in the Parvati catchment. MIKE 11 NAM is a lumped, conceptual, and deterministic model that continuously tracks the moisture content across three interconnected storage representing overland flow, interflow, and base flow (DHI 2017). The NAM model necessitates three timeseries data inputs: rainfall, potential evapotranspiration (ET0), and observed discharge timeseries in .dfso format. Sensitivity analysis was performed to identify the model parameters that significantly influenced the hydrograph shape and peak runoff. It involved systematically adjusting each of the nine crucial parameters individually while keeping others constant. Each parameter was modified by ±20% from its initial value, and NSE values were graphed against each parameter for every model run. The sensitivity of parameters was assessed based on the impact of changes on the NSE value [33].
The calibration of the model was conducted from 2005 to 2013, while validation was performed for the years 2014–2020. Model performance during both the calibration and validation phases was assessed using six statistical indices: Coefficient of Determination (R2), Nash–Sutcliffe Efficiency (NSE), Root Mean Square Error (RMSE), and Percentage Bias (PBIAS), RMSE-observations standard deviation ratio (RSR), and Kling–Gupta Efficiency (KGE). R2 indicates the strength and direction of the linear relationship between two datasets, with values ranging from 0 to 1 [34]. NSE evaluates how well the model’s simulations match the observed data, considering both accuracy and timing, with values ranging from −∞ to 1 [35]. RMSE quantifies the magnitude of the error between the observed and simulated dataset [36]. PBIAS measures the model’s tendency to overestimate or underestimate observed data; negative PBIAS values indicate overestimation, while positive values indicate underestimation [37]. RSR is a statistical measure which combines both the error in model simulation and the variability in observed data into a single normalized metric, making it useful for model evaluation and comparison. The RSR is calculated by dividing the RMSE by the standard deviation of the observed data, with values ranging from 0 to ∞ [35]. KGE is a comprehensive statistical metric that combines correlation (r), variability (γ), and bias (β) into a single performance measure, with values ranging from −∞ to 1 [38]. The KGE not only assesses the accuracy of model simulation but also evaluates the model’s ability to capture the variability and timing of observed data. Table 1 presents various statistical indices formulas, range, and performance ratings.

Table 1.
Criteria for evaluating the performance of the climatic and hydrologic model.
3.3. Water Demand and Supply Analysis
The present study employed the MIKE HYDRO Basin model to analyse the water demand and deficit within the Parvati command area from 2005 to 2020. This model operates on a network of branches and nodes, which can be directly digitized using map view facilities or extracted from a digital elevation model. The river network and water transfer within the basin were delineated using the connected river segment, computational nodes, and module-specific features. Each river node was associated with catchments that contributed inflow data to the node. Moreover, the model integrated reservoirs as pivotal components, simulating single and multiple multipurpose reservoirs. These reservoirs could be configured with defined operational protocols, rights for resource allocation, or no-operation policy. In the MIKE HYDRO Basin framework, a water user is categorized as an ordinary user with a designated demand series or an irrigation water user. The model accounted for various factors affecting irrigation, including climate, soil, crop sequences, and irrigation techniques used by water users. The climate sub-model integrated rainfall and temperature data. The reference evapotranspiration (ET0) sub-model calculated evapotranspiration losses using climate data. The soil water sub-model incorporated soil types and properties such as the field capacity and wilting point. The crop sub-model included crop types, sowing dates, growth stages, and crop coefficients. Once all sub-models were configured, the model executed simulations and generated output files containing data such as total irrigation demand, individual user demands, net flow, deficits, reservoir storage levels, channel flows, etc., at predefined time intervals. The flowchart of the detailed methodology of the study is shown in Figure 2.
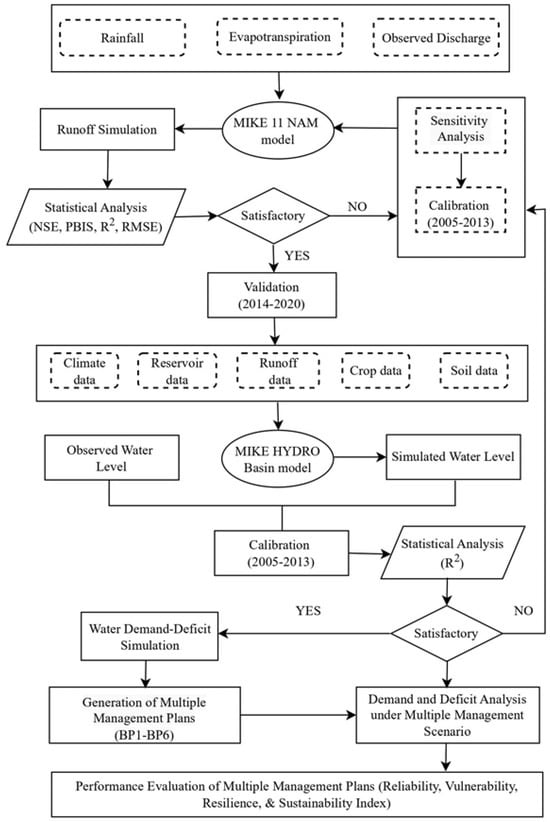
Figure 2.
The methodological framework of the study.
3.4. Scenarios Development
Effective management strategies must be adopted to ensure water resources’ sustainable use and prevent overexploitation. Climate change leads to erratic and severe weather shifts, exacerbating water scarcity across various areas. Additionally, water scarcity often creates resource disputes, highlighting the crucial need for equitable and transparent management approaches to mitigate social and geopolitical tensions. A well-designed management plan considers these changing conditions, assisting communities in adapting and stimulating themselves against the effects of water scarcity. With a focus on demand and deficit scenarios, various management strategies have been generated through continuous collaboration with stakeholders and experts to ensure the most efficient use of water resources.
3.5. Performance Indicators
Water resources management plans entail significant uncertainties, necessitating the development of multiple strategies for effective response. Evaluating the performance of these plans based on various indicators such as vulnerability (Vul), reliability (Rel), resilience (Res), and sustainability (Sus) is crucial for obtaining a comprehensive understanding of the system’s effectiveness under different scenarios [39]. Vulnerability (Vul) quantifies the fraction of time during which a shortage occurs, considering each event’s probability to be equal. According to [40], vulnerability defined as
where M represents the total failure events, and Defj and Demj denote the deficit and demand for the jth period. Reliability can be defined as the fraction of time during which the system fulfils all demands without any shortage. The computation of reliability can be performed using the formula given by [41]
NF represents the number of non-failure periods, and n denotes the total number. Resilience quantifies how fast the system is expected to recover to a satisfactory state following its transition into an unsatisfactory state. According to [40], resilience defined as
where d(j) represents the duration of the jth failure event, and M is the total number of failure events. The Sustainability Index (SI) quantifies the sustainability of water resource systems, serving as a tool for assessing and comparing sustainability across different water users. It aggregates various performance metrics into a single measure. The authors of [39] defined SI as the geometric mean of various performance indices as expressed by the following equation.
4. Results and Discussion
4.1. MIKE11 NAM Model Setup
The MIKE11 NAM Model was configured by inserting daily rainfall, ET0, and observed discharge data in .dfso format. Calibration of the model involved a sensitivity analysis of its parameters, which was crucial for refining the calibration process. Each parameter was adjusted within a reasonable range while holding other parameters as constant, and the resultant changes in model response were observed. In this study, parameters such as Lmax, CKOF, TOF, and CK12 emerged as particularly sensitive, requiring careful calibration. The model was calibrated for the timeframe spanning from 2005 to 2013. Initially, the model simulated runoff using the auto-calibration mode, followed by further calibration of parameters to optimize the match between observed and simulated runoff. Table 2 represents the range for each parameter and their best-fit value obtained during calibration of the NAM model.

Table 2.
Parameters used in the MIKE11-NAM model during simulation.
‘Lmax’ denotes the maximum soil moisture available to vegetation for transpiration within the root zone, with the best-fit value set at 250. A high ‘Lmax’ value suggests that the catchment soil may have higher infiltration rates, enabling deep percolation of rainwater to replenish soil moisture reserves. ‘TOF’ signifies the root zone threshold for overland flow, calibrated to 0.70, indicating enhanced infiltration in the lower zone. ‘CK12′, sensitive to runoff generation, was calibrated to 56.5 h, reflecting an extended duration required for overland flow initiation. ‘CQOF’ represents the portion of rainfall generating overland flow in the catchment, adjusted to 0.20. A lower ‘CQOF’ value indicates a gentler slope in the catchment terrain.
During model calibration, R2, NSE, RMSE, PBIAS, RSR, and KGE were estimated as 0.79, 0.79, 4.95, −2%, 0.5, and 0.84. respectively, indicating a good relation between simulated and observed runoff. A negative PBIAS denotes an underestimation in model-simulated runoff. The model parameter’s value obtained during calibration were kept unchanged for model validation. The validation results showed R2, NSE, RMSE, PBIAS, RSR, and KGE values as 0.68, 0.67, 8.3, −12.4%, 0.62, and 0.67, indicating a satisfactory agreement between simulated and observed runoff. During the calibration and validation phases, it was observed that model performed well in simulating average- and low-runoff events compared to high-runoff events, as shown in Figure 3A,B. This discrepancy could be due to the tendency of hydrological and mathematical models in general, to prioritize and represent average conditions over extreme events. Notably, extreme occurrences, such as peak floods or prolonged periods of low or no flow, pose challenges for accurate modelling due to the diverse nature of mathematical models, their underlying assumptions, and the inherent uncertainties associated with them [42]. Additionally, as a lumped model, MIKE11 NAM does not account for the variability in land use, soil saturation levels, and antecedent moisture conditions that can influence peak flow events [43]. Rainfall data for the present study were taken from only two rain gauge stations, though an assessment of the adequacy of rain gauge stations indicated that a minimum of three stations are required in the study area. The authors of [44] reported that a smaller number of rainfall gauging stations in the study area could impact the estimation of peak and low flows, suggesting incorporating additional rain gauge station data to enhance precision.
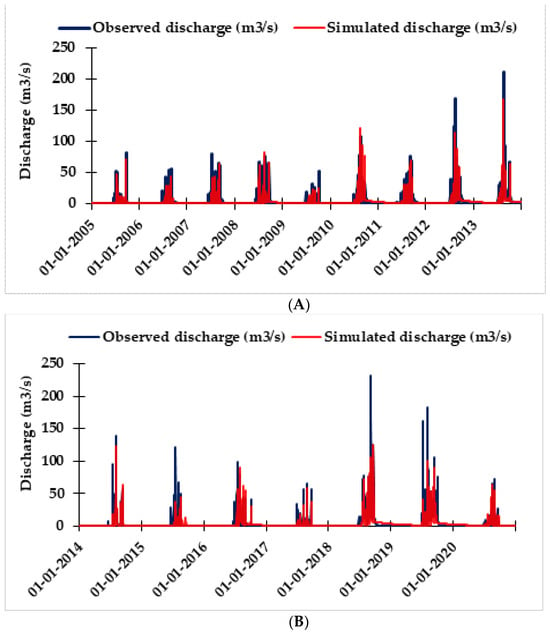
Figure 3.
(A) Comparison between observed and simulated discharge during calibration of the MIKE 11 NAM model. (B) Comparison between observed and simulated discharge during validation of the MIKE 11 NAM model.
Ref. [45] conducted a comparative analysis of the MIKE11 NAM, SWMM, WEC-FLOOD, and HEC-HMS models in the Mesima Torrent watershed in Italy. Their investigation indicated satisfactory prediction accuracy of the MIKE11-NAM model, suggesting its suitability for simulating runoff under climate change conditions. Similarly, ref. [46] utilized the MIKE 11 NAM model for RR modelling at the Shaya catchment (Ethiopia). The model exhibited good agreement between observed and simulated runoff during both the calibration (R = 0.93; NSE = 0.86; RMSE = 3.16; PBIAS = −1.58) and validation (R = 0.92; NSE = 0.83; RMSE = 4.04; PBIAS = −0.88) phases, indicating the effectiveness of the MIKE 11 NAM model in simulating runoff dynamics.
4.2. Water Management Model for Demand and Deficit Assessment
A network model using the MIKE HYDRO Basin was created for the Parvati Reservoir project to enhance water resources management and facilitate irrigation planning. This project involved 13 irrigation water users, namely Mudhik, Banora, Dopura, Salempur, Patipura, Makra, Nagla, Saipau, Piphera, Basai Nawab, Kolari, Knasil, and Nirdhara Kala. The MIKE HYDRO Basin model for the Parvati reservoir system is depicted in Figure 4.
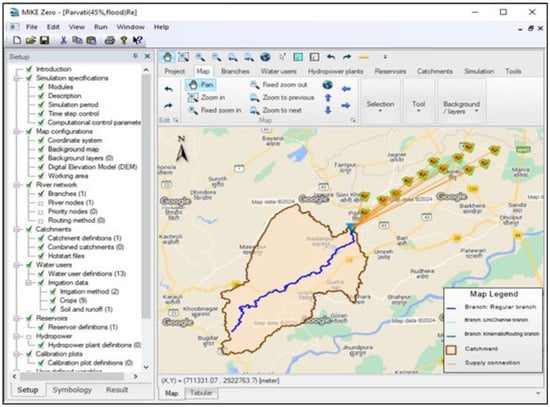
Figure 4.
Water management model for the Parvati reservoir system in the MIKE HYDRO Basin.
A comprehensive dataset regarding the reservoir was compiled to develop the model, encompassing various aspects such as elevation-area-capacity tables, reservoir characteristics, operational priorities, losses, efficiencies, and groundwater conditions. Detailed information on crop types and soil characteristics is also essential for effective irrigation planning. Therefore, data on the existing cropping pattern and soil profiles were collected and integrated into the model. The cropping pattern within the Parvati command consists primarily of three crops: wheat, mustard, and potato, all of which rely on water supplied by the reservoir system for irrigation. Due to the extensive agricultural area in the command, it was divided into three segments to individually represent the total areas under wheat, mustard, and potato. The cropping pattern in the command area is depicted in Figure 5.
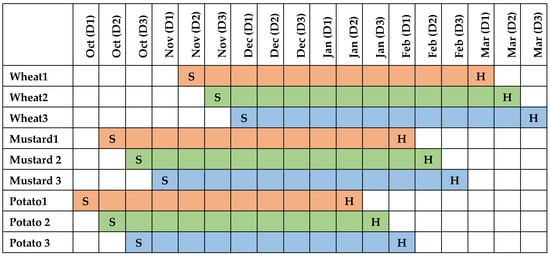
Figure 5.
Existing cropping pattern in Parvati command. D1: first 10-day period of a month (from the 1st to 10th day); D2: second 10-day period of a month (from the 11th to 20th day); D3: third 10-day period of a month (from the 21st to 28th/29th/30th/31st day); S: Planting period; H: harvesting period.
4.3. Calibration of MIKE HYDRO Basin Model
The calibration process of the MIKE HYDRO Basin model mainly depends on accurately calibrating the MIKE 11 NAM model. Runoff data obtained from the calibrated MIKE 11 NAM model serve as input for calibrating the MIKE HYDRO Basin model [47]. The calibration was carried out from 2005 to 2020. A comparison between the daily observed and simulated water level (WL) of the reservoir is depicted in Figure 6. Results showed a strong agreement between the observed and simulated water levels of the reservoir on a daily basis, with R2, NSE, RMSE, PBIAS, RSR, and KGE values of 0.86, 0.81, 3.87, −2.30%, 0.43, and 0.88, respectively. This high correlation indicates the model effectively replicates the behaviour of the reservoir system, providing reliable forecasts of water levels. Consequently, the model is a reliable tool for simulating reservoir operations and guiding water management decisions within the Parvati command area.
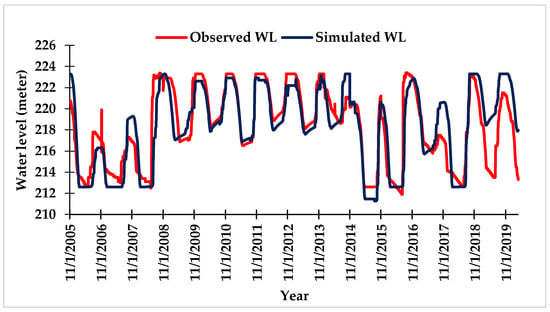
Figure 6.
Comparison between the observed and simulated water levels of the Parvati reservoir during calibration of the MIKE HYDRO Basin model.
4.4. Water Demand and Deficit Simulation
The irrigation water demand and deficit within the Parvati command area for the period from 2005 to 2020 were assessed using the MIKE HYDRO Basin model. The simulation outcomes of the model included various parameters, such as demand, supply, deficits, reservoir levels, and storage over a predefined timescale. Initially, the model was executed considering existing field conditions (BP-0), i.e., flood irrigation method, conveyance efficiency (ηc) of 45%, and no conjunctive use. The simulation results revealed significant challenges regarding water availability within the command area. Under the existing conditions, the average water demand and deficit were estimated at 42.79 MCM and 3.45 MCM, respectively. These findings highlight significant fluctuations in water demand and deficits during the study period. Notably, in 2006–2007 and 2019–2020, higher water demand was experienced, i.e., 48.50 MCM and 59.77 MCM, respectively. Conversely, 2006–2007 also saw the highest water deficit at 20.09 MCM (Figure 7), indicating substantial challenges in meeting irrigation requirements. Variations in water demand are anticipated due to various factors, such as shifts in agricultural practices, crop water needs, and effective water management strategies [48,49,50,51]. During the years 2008–2009, 2010–2011, and 2013–2014, minimal to no deficits were estimated despite varying levels of demand. This suggests the presence of efficient water conservation measures, cropping patterns, or favourable climatic conditions during those periods in the command area.
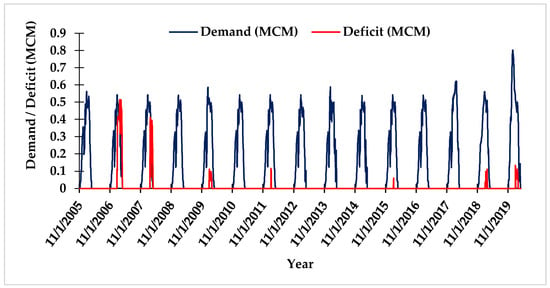
Figure 7.
Demand–deficit simulation under the BP-0 management scenario (ηc = 45%, flood irrigation, no GW use).
The irrigation method selection has a considerable impact on the water deficit [52,53]. Flood irrigation, in contrast to more efficient methods such as sprinkler and drip irrigation, results in greater water losses due to evaporation and runoff [54]. As a result, the available water for crops is reduced. Moreover, low ηc further exacerbated the water deficit in the study area by causing additional water losses.
4.5. Development of Management Scenarios
Using simulation-based methods proves effective under uncertainties originating from climate fluctuations and operational management strategies. This study employed a participatory approach involving farmers, engineers, and technocrats to devise six distinct management scenarios. These scenarios were generated considering factors such as irrigation methods, ηc, and the integration of conjunctive water usage. The specifics of management plans spanning the study period (2005–2020) are detailed in Table 3.

Table 3.
Statistics of water demand, deficit, and performance indices under different management scenarios during the study period (2005–2020).
4.6. Water Demand and Deficit Analysis under Management Scenarios
The water demand and deficit in the Parvati Basin are primarily driven by fluctuations in rainfall and runoff, with evapotranspiration playing a secondary but important role. Water demand in the basin remained relatively stable, with slight variations over the study period (2005–2020). It ranged from 38.67 MCM to 59.77 MCM, with a notable increase in demand in 2019, possibly due to expanded cultivation area [55,56,57]. Under the existing conditions (BP-0), the simulation showed seven years of deficit within the command area. Years with high rainfall and runoff, such as 2008, 2012, and 2013, showed no deficit, indicating that the available water was sufficient to meet the demand. However, in years of low rainfall, such as 2006, 2009, and 2017, deficits were observed. The most pronounced deficit occurred in 2006, reaching 20.09 MCM, largely attributed to the low rainfall of 526 mm and the resulting minimal runoff of 35.7 mm. High evaporation rates further compounded the problem by reducing the water available for supply. A similar pattern of water demand and deficit concerning rainfall and evaporation losses has been observed by other researchers [58,59,60]. To address these challenges, improving water management practices, such as enhanced irrigation methods, low conveyance losses, and exploring conjunctive use of groundwater (GW), are essential to mitigate the impact of water deficits and ensure sustainable water use in the basin [61,62,63].
Further analysis revealed that integrating 5% GW use (BP-1) demonstrated a significant reduction in the deficit to 1.81 MCM. Additionally, increasing ηc to 65% and 75% while maintaining 5% GW utilization (BP-3 and BP-5) yielded more promising outcomes, potentially reducing deficits to 0.64 and 0.05 MCM, respectively. Particularly, transitioning to sprinkler irrigation and raising ηc to 95% (BP-6) showed the optimum result, offering the possibility of achieving a zero deficit. The simulation outcomes derived from the MIKE HYDRO Basin under various management scenarios are illustrated in Figure 8A–F. The comparison of water demand and deficit simulations under different management scenarios is presented in Figure 9. These findings emphasize the significance of utilizing efficient irrigation methods, incorporating conjunctive water use, and improving ηc to address the water deficit within the Parvati command area successfully [64,65,66].
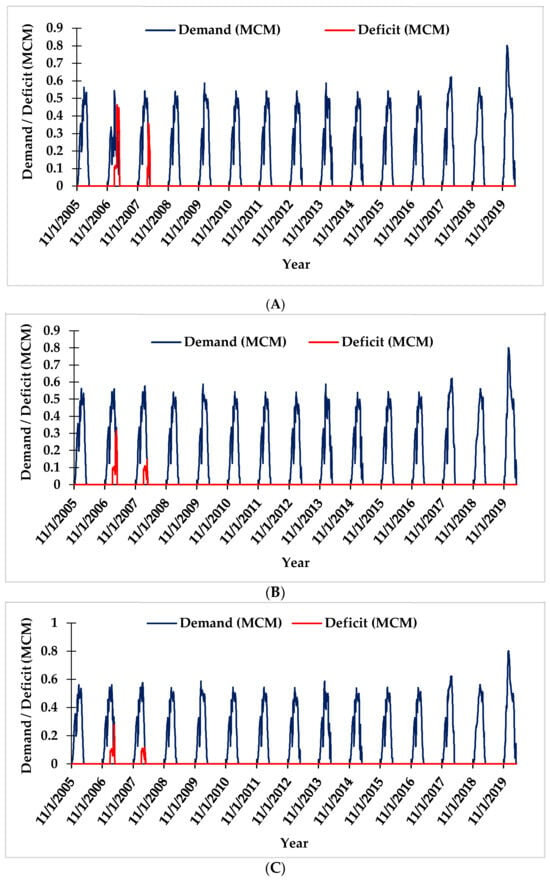
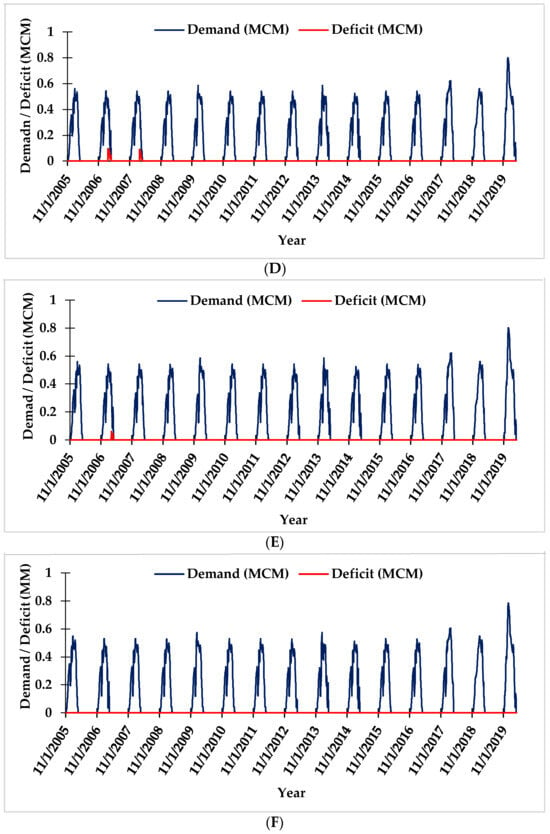
Figure 8.
(A) Demand–deficit simulations under the BP-1 management scenario (ηc = 45%, flood irrigation, 5% GW). (B) Demand–deficit simulation under the BP-2 management scenario (ηc = 65%, flood irrigation, no GW use). (C) Demand–deficit simulation under the BP-3 management scenario (ηc = 65%, flood irrigation, 5% GW use). (D) Demand–deficit simulation under the BP-4 management scenario (ηc = 75%, flood irrigation, no GW use). (E) Demand–deficit simulation under the BP-5 management scenario (ηc = 75%, flood irrigation, 5% GW use). (F) Demand–deficit simulation under the BP-6 management scenario (ηc = 95%, sprinkler irrigation, no GW use).
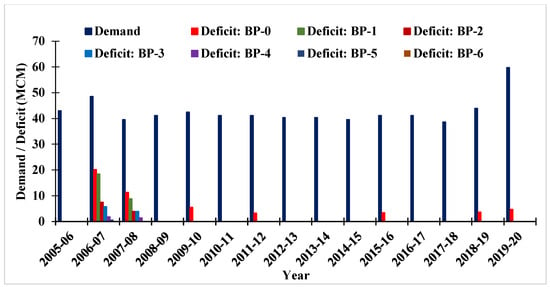
Figure 9.
Comparison of water demand and deficit simulations under different management scenarios.
4.7. Performance Evaluation of Parvati Reservoir System
The simulation outcomes generated by the MIKE HYDRO Basin model provide significant insights into demand and deficit estimation within the command area [41,67,68]. The performance of the Parvati Reservoir system was assessed under different management scenarios, using key performance indicators (PIs), namely reliability, vulnerability, resilience, and the sustainability index. These indicators provide a comprehensive evaluation of the system’s ability to meet water demand and manage deficit effectively. During the study period (2005–2020), it was observed that under the existing conditions i.e., ηc of 45% and flood irrigation without GW utilization, the system demonstrated reliability, vulnerability, resilience, and a sustainability index as 0.533, 0.467, 0.457, and 0.506, respectively. However, significant enhancements in these metrics were anticipated with increasing ηc. For instance, increasing the ηc to 65% led to enhanced reliability (0.812), reduced vulnerability (0.188), improved resilience (0.471), and a higher sustainability index (0.677). Further increasing the ηc to 75% resulted in greater improvement across all metrics, achieving reliability of 0.895, vulnerability of 0.105, resilience of 0.658, and a sustainability index of 0.807. Moreover, incorporating a 5% GW contribution along with 65% and 75% ηc further boosted system performance, yielding enhanced reliability (0.877, 0.957), vulnerability (0.123, 0.043), resilience (0.714, 0.857), and sustainability index (0.819, 0.922). Notably, adopting sprinkler irrigation with an ηc of 95% emerged as the most promising scenario, attaining optimal scores of 1 for reliability, resilience, and sustainability, while completely eliminating vulnerability. Values of performance indicators under different management scenarios are given in Table 3.
These findings underscore the critical role of enhancing ηc and adopting advanced irrigation methods in optimizing the performance of the water management system. The substantial improvement observed with the higher ηc value and efficient irrigation method demonstrates the potential for significantly boosting system reliability, resilience, sustainability, and reducing vulnerability. The results advocate for the implementation of such strategies in the Parvati command area to ensure a robust and sustainable water supply for agricultural needs [69,70,71,72]. The developed model showed significant potential for real-time reservoir operation and irrigation planning in the basin. Future research could expand the model’s application by incorporating multiple water users, including domestic, industrial, and hydropower, along with irrigation. The sustainable watershed is so important for the development of ecosystem system in the earth surface [73,74,75]. The drainage and hydraulic study is so important to maintain the watershed basin [76,77]. Furthermore, investigating alternative management strategies, such as varying cropping patterns, the combined use of drip and sprinkler systems, and optimizing water allocation across different sectors, could enhance the effectiveness of the model. Integrating advanced climate projections and remote sensing data will also boost predictive accuracy, making the model more adaptable to changing climate conditions and wider water management challenges in other river basins.
5. Conclusions
This study demonstrates the utility of basin-scale mathematical models as effective decision-support tools for sustainable water management. By integrating the MIKE 11 NAM and MIKE HYDRO Basin model, the performance of the Parvati Reservoir Project was evaluated under multiple management scenarios. The MIKE 11 NAM model showed strong capability in simulating runoff, with high R², NSE, KGE, and low PBIAS, RMSE, and RSR values, indicating accurate model calibration. Sensitivity analysis identified Lmax, CKOF, TOF, and CK12 as critical parameters, guiding the model calibration process. Furthermore, the MIKE HYDRO Basin model exhibited a strong relation between the observed and simulated reservoir water levels, with R2, NSE, RMSE, PBIAS, RSR, and KGE values of 0.86, 0.81, 3.87, −2.30%, 0.43, and 0.88 respectively, confirming its reliability in representing reservoir behaviour and its potential as a tool for strategic water management. Our findings revealed a significant irrigation water deficit in the Parvati River basin, with an average annual deficit of 3.45 MCM over the study period (2005–2020). Contributing factors include seasonal flow variations, inefficient water management practices, and inadequate water distribution infrastructure. The participatory approach involving farmers, engineers, and technocrats led to the development of six management scenarios, focusing on irrigation efficiency (ηc), water use methods, and conjunctive use strategies. Among these, improving ηc and implementing a 5% conjunctive groundwater use consistently enhanced the sustainability index. Moreover, adopting efficient irrigation methods, such as sprinkler irrigation combined with lift systems, further optimized the sustainability index. In conclusion, the MIKE HYDRO Basin model provides a comprehensive framework for addressing water scarcity, surplus, and distribution challenges in river basins. This model is not only valuable for current water management needs but also serves as a predictive tool for future water demand and deficit simulation, enabling proactive and informed decision-making for sustainable water resource management.
Author Contributions
A.A.: conceptualization, methodology, investigation, data collection, data interpretation, analysis, validation, and original draft preparation; M.K.: conceptualization, methodology, investigation, supervision, original draft preparation, writing—review and editing. R.K.J.: methodology, investigation, supervision, original draft preparation, writing—review and editing; V.K.G.: methodology, investigation, original draft preparation, writing—review and editing, formal analysis; C.B.P.: investigation, original draft preparation, writing—review and editing, formal analysis, and validation; K.O.A.: methodology, original draft preparation, writing—review and editing, formal analysis, and validation; S.S.R.: investigation, original draft preparation, writing—review and editing, formal analysis; M.Y.A.K.: investigation, original draft preparation, writing—review and editing, formal analysis; T.J.A.: investigation, data analysis, original draft preparation, writing—review and editing, and formal analysis; B.Đ.: investigation, data analysis, original draft preparation, writing—review and editing, and formal analysis. All authors have read and agreed to the published version of the manuscript.
Funding
This project was funded by the Deanship of Scientific Research (DSR) at King Abdulaziz University Jeddah, under grant no. GPIP: 88-246-2024. The author, therefore, acknowledge with thanks DSR for technical and financial support.
Data Availability Statement
The data are not publicly available due to further research.
Acknowledgments
This project was funded by the Deanship of Scientific Research (DSR) at King Abdulaziz University Jeddah, under grant no. GPIP: 88-246-2024. The author, therefore, acknowledge with thanks DSR for technical and financial support. The authors also thank the University North, Croatia, for providing help with their scientific project, “Hydrological and geodetic analysis of the watercourse’’.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Baig, M.A.A.; Mallikarjuna, P.; Krishna Reddy, T.V. Rainfall—Runoff modelling—A case study. ISH J. Hydraul. Eng. 2008, 14, 18–35. [Google Scholar] [CrossRef]
- Yatheendradas, S.; Wagener, T.; Gupta, H.; Unkrich, C.; Goodrich, D.; Schaffner, M.; Stewart, A. Understanding uncertainty in distributed flash flood forecasting for semiarid regions. Water Resour. Res. 2008, 1–17. [Google Scholar] [CrossRef]
- Alitane, A.; Essahlaoui, A.; Van Griensven, A.; Yimer, E.A.; Essahlaoui, N.; Mohajane, M.; Chawanda, C.J.; Van Rompaey, A. Towards a Decision-Making Approach of Sustainable Water Resources Management Based on Hydrological Modeling: A Case Study in Central Morocco. Sustainability 2022, 14, 10848. [Google Scholar] [CrossRef]
- Devia, G.K.; Ganasri, B.P.; Dwarakish, G.S. A Review on Hydrological Models. Aquat. Procedia 2015, 4, 1001–1007. [Google Scholar] [CrossRef]
- Mensah, J.K.; Ofosu, E.A.; Yidana, S.M.; Akpoti, K.; Kabo-bah, A.T. Integrated modeling of hydrological processes and groundwater recharge based on land use land cover, and climate changes: A systematic review. Environ. Adv. 2022, 8, 100224. [Google Scholar] [CrossRef]
- Singh, A.; Malik, A.; Kumar, A.; Kisi, O. Rainfall-runoff modeling in hilly watershed using heuristic approaches with gamma test. Arab. J. Geosci. 2018, 11, 261. [Google Scholar] [CrossRef]
- Ward, P.J.; de Ruiter, M.C.; Mård, J.; Schröter, K.; Van Loon, A.; Veldkamp, T.; von Uexkull, N.; Wanders, N.; AghaKouchak, A.; Arnbjerg-Nielsen, K.; et al. The need to integrate flood and drought disaster risk reduction strategies. Water Secur. 2020, 11, 100070. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, P.; Cheng, L.; Xie, K.; Han, D.; Zhou, L. The temporal variations in runoff-generation parameters of the Xinanjiang model due to human activities: A case study in the upper Yangtze River Basin, China. J. Hydrol. Reg. Stud. 2021, 37, 100910. [Google Scholar] [CrossRef]
- Jothiprakash, V.; Magar, R. Soft computing tools in rainfall-runoff modeling. ISH J. Hydraul. Eng. 2009, 15, 84–96. [Google Scholar] [CrossRef]
- Sahu, R.K.; Mishra, S.K.; Eldho, T.I. Performance evaluation of modified versions of scs curve number method for two watersheds of maharashtra, India. ISH J. Hydraul. Eng. 2012, 18, 27–36. [Google Scholar] [CrossRef]
- Abdulla, F.A.; Lettenmaier, D.P. Development of regional parameter estimation equations for a macroscale hydrologic model. J. Hydrol. 1997, 197, 230–257. [Google Scholar] [CrossRef]
- Venkatesh, B.; Chandramohan, T.; Purandara, B.K.; Jose, M.K.; Nayak, P.C. Modeling of a River Basin Using SWAT Model. In Hydrologic Modeling: Select Proceedings of ICWEES-2016; Springer: Singapore, 2018; pp. 707–714. [Google Scholar] [CrossRef]
- McMichael, C.E.; Hope, A.S.; Loaiciga, H.A. Distributed hydrological modelling in California semi-arid shrublands: MIKE SHE model calibration and uncertainty estimation. J. Hydrol. 2006, 317, 307–324. [Google Scholar] [CrossRef]
- Beven, K.; Bathurst, J.; O’connell, E.N.D.A.; Littlewood, I.; Blackie, J.; Robinson, M. Hydrological modelling. Prog. Mod. Hydrol. Past Present Future 2015, 216–239. [Google Scholar] [CrossRef]
- Boughton, W. The Australian water balance model. Environ. Model. Softw. 2004, 19, 943–956. [Google Scholar] [CrossRef]
- Chiew, F.H.S.; McMahon, T.A. Modelling the impacts of climate change on Australian streamflow. Hydrol. Process. 2002, 16, 1235–1245. [Google Scholar] [CrossRef]
- Gautam, V.K.; Awasthi, M.K. Evaluation of water resources demand and supply for the districts of central Narmada valley zone. Int. J. Curr. Microbiol. App. Sci. 2020, 9, 3043–3050. [Google Scholar] [CrossRef]
- Gautam, V.K.; Awasthi, M.K.; Trivedi, A. Optimum allocation of water and land resource for maximizing farm income of Jabalpur District, Madhya Pradesh. Int. J. Environ. Clim. Change 2020, 10, 224–232. [Google Scholar] [CrossRef]
- Gautam, V.K.; Trivedi, A. Optimal Water Resources Allocation and Crop Planning for Mandla District of Madhya Pradesh. Indian J. Soil Conserv. 2023, 51, 68–75. [Google Scholar]
- Zegait, R.; Bouznad, I.E.; Remini, B.; Bengusmia, D.; Ajia, F.; Guastaldi, E.; Lopane, N.; Petrone, D. Comprehensive model for sustainable water resource management in Southern Algeria: Integrating remote sensing and WEAP model. Model. Earth Syst. Environ. 2024, 10, 1027–1042. [Google Scholar] [CrossRef]
- Jaiswal, R.K.; Ghosh, N.C.; Guru, P.; Devakant. MIKE BASIN Based Decision Support Tool for Water Sharing and Irrigation Management in Rangawan Command of India. Adv. Agric. 2014, 2014, 924948. [Google Scholar] [CrossRef]
- Jaiswal, R.K.; Lohani, A.K.; Tiwari, H.L. A decision support system framework for strategic water resources planning and management under projected climate scenarios for a reservoir complex. J. Hydrol. 2021, 603, 127051. [Google Scholar] [CrossRef]
- Kumar, R.; Huda, M.B.; Maryam, M.; Lone, M.A. Rainfall runoff modeling using MIKE 11 NAM of the Jhelum river in Kashmir Valley, India. Mausam 2022, 73, 365–372. [Google Scholar] [CrossRef]
- Gabor, E.; Beilicci, E.; Beilicci, R. Advanced Hydroinformatic Tools for Modelling of Reservoirs Operation. IOP Conf. Ser. Mater. Sci. Eng. 2019, 471, 42002. [Google Scholar] [CrossRef]
- Pareta, K. Hydrological modelling of largest braided river of India using MIKE Hydro River software with rainfall runoff, hydrodynamic and snowmelt modules. J. Water Clim. Change 2023, 14, 1314–1338. [Google Scholar] [CrossRef]
- Santos, R.M.B.; Fernandes, L.F.S.; Cortes, R.M.V.; Pacheco, F.A.L. Development of a hydrologic and water allocation model to assess water availability in the Sabor river basin (Portugal). Int. J. Environ. Res. Public Health 2019, 16, 2419. [Google Scholar] [CrossRef]
- Yu, Y.; Disse, M.; Yu, R.; Yu, G.; Sun, L.; Huttner, P.; Rumbaur, C. Large-scale hydrological modeling and decision-making for agricultural water consumption and allocation in the main stem Tarim River, China. Water 2015, 7, 2821–2839. [Google Scholar] [CrossRef]
- Moharir, K.N.; Pande, C.B.; Gautam, V.K.; Singh, S.K.; Rane, N.L. Integration of hydrogeological data, GIS and AHP techniques applied to delineate groundwater potential zones in sandstone, limestone and shales rocks of the Damoh district,(MP) central India. Environ. Res. 2023, 228, 115832. [Google Scholar] [CrossRef]
- Gautam, V.K.; Pande, C.B.; Kothari, M.; Singh, P.K.; Agrawal, A. Exploration of groundwater potential zones mapping for hard rock region in the Jakham river basin using geospatial techniques and aquifer parameters. Adv. Space Res. 2023, 71, 2892–2908. [Google Scholar] [CrossRef]
- Allen, R.G.; Smith, M.; Pereira, L.S.; Raes, D.; Wright, J.L. Revised FAO procedures for calculating evapotranspiration: Irrigation and drainage paper no. 56 with testing in Idaho. In Proceedings of the Watershed Management and Operations Management 2000, Fort Collins, CO, USA, 20 June 2000; pp. 1–10. [Google Scholar]
- Jaiswal, R.K.; Kumari, C.; Galkate, R.V.; Lohani, A.K. Assessment of Productivity Based Efficiencies for Optimal Utilization of Water Resources in a Command. Sustain. Water Resour. 2022, 116, 262–282. [Google Scholar] [CrossRef]
- Kumar, A.; Mishra, A.R.; Denis, D.M.; Jeet, P.; Singh, U. Calibration and validation of FAO: Aqua crop model for wheat in Vindhyan region. J. Pharmacogn. Phytochem. 2020, 9, 299–305. [Google Scholar]
- Galkate, R.V.; Jaiswal, R.K.; Thomas, T.; Nayak, T.R. Rainfall runoff modelling using conceptual NAM model. In Proceedings of the International Conference on Sustainability and Management Strategy (ICSMS-2014), Nagpur, India, 21–22 March 2014; Institute of Management and Technology: Nagpur, India, 2014. [Google Scholar]
- Asuero, A.G.; Sayago, A.; González, A.G. The correlation coefficient: An overview. Crit. Rev. Anal. Chem. 2007, 36, 41–59. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Liew, M.W.; Van Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Willmott, C.J. Some comments on the evaluation of model performance. Bull. Am. Meteorol. Soc. 1982, 63, 1309–1313. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of automatic calibration for hydrologic models: Comparison with multilevel expert calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]
- Knoben, W.J.; Freer, J.E.; Woods, R.A. Inherent benchmark or not? Comparing Nash–Sutcliffe and Kling–Gupta efficiency scores. Hydrol. Earth Syst. Sci. 2019, 23, 4323–4331. [Google Scholar] [CrossRef]
- Sandoval-Solis, S.; McKinney, D.C.; Loucks, D.P. Sustainability index for water resources planning and management. J. Water Resour. Plan. Manag. 2011, 137, 381–390. [Google Scholar] [CrossRef]
- Hashimoto, T.; Stedinger, J.R.; Loucks, D.P. Reliability, Resiliency, and Vulnerability Criteria For Water Resource System Performance Evaluation. Water Resour. Res. 1982, 18, 14–20. [Google Scholar] [CrossRef]
- Kjeldsen, T.R.; Rosbjerg, D. Choice of reliability, resilience and vulnerability estimators for risk assessments of water resources systems/Choix d’estimateurs de fiabilité, de résilience et de vulnérabilité pour les analyses de risque de systèmes de ressources en eau. Hydrol. Sci. J. 2004, 49, 767. [Google Scholar] [CrossRef]
- Kahsay, K.D.; Pingale, S.M.; Hatiye, S.D. Impact of climate change on groundwater recharge and base flow in the sub-catchment of Tekeze basin, Ethiopia. Groundw. Sustain. Dev. 2018, 6, 121–133. [Google Scholar] [CrossRef]
- Vansteenkiste, T.; Tavakoli, M.; Van Steenbergen, N.; De Smedt, F.; Batelaan, O.; Pereira, F.; Willems, P. Intercomparison of five lumped and distributed models for catchment runoff and extreme flow simulation. J. Hydrol. 2014, 511, 335–349. [Google Scholar] [CrossRef]
- Odiyo, J.O.; Phangisa, J.I.; Makungo, R. Rainfall-runoff modelling for estimating Latonyanda River flow contributions to Luvuvhu River downstream of Albasini Dam. Phys. Chem. Earth 2012, 50–52, 5–13. [Google Scholar] [CrossRef]
- Filianoti, P.; Gurnari, L.; Zema, D.A.; Bombino, G.; Sinagra, M.; Tucciarelli, T. An evaluation matrix to compare computer hydrological models for flood predictions. Hydrology 2020, 7, 42. [Google Scholar] [CrossRef]
- Aredo, M.R.; Hatiye, S.D.; Pingale, S.M. Modeling the rainfall-runoff using MIKE 11 NAM model in Shaya catchment, Ethiopia. Model. Earth Syst. Environ. 2021, 7, 2545–2551. [Google Scholar] [CrossRef]
- DHI. MIKE 11-A Modelling System for Rivers and Channels: User Guide; Danish Hydraulic Institute: Horsholm, Denmark, 2017. [Google Scholar]
- Alotaibi, M.; Alhajeri, N.S.; Al-Fadhli, F.M.; Al Jabri, S.; Gabr, M. Impact of Climate Change on Crop Irrigation Requirements in Arid Regions. Water Resour. Manag. 2023, 37, 1965–1984. [Google Scholar] [CrossRef]
- Hatfield, J.L.; Dold, C. Water-use efficiency: Advances and challenges in a changing climate. Front. Plant Sci. 2019, 10, 103. [Google Scholar] [CrossRef] [PubMed]
- Iglesias, A.; Garrote, L. Adaptation strategies for agricultural water management under climate change in Europe. Agric. Water Manag. 2015, 155, 113–124. [Google Scholar] [CrossRef]
- Srivastav, A.L.; Dhyani, R.; Ranjan, M.; Madhav, S.; Sillanpää, M. Climate-resilient strategies for sustainable management of water resources and agriculture. Environ. Sci. Pollut. Res. 2021, 28, 41576–41595. [Google Scholar] [CrossRef]
- Fereres, E.; Soriano, M.A. Deficit irrigation for reducing agricultural water use. J. Exp. Bot. 2007, 58, 147–159. [Google Scholar] [CrossRef]
- Du, T.; Kang, S.; Zhang, J.; Davies, W.J. Deficit irrigation and sustainable water-resource strategies in agriculture for China’s food security. J. Exp. Bot. 2015, 66, 2253–2269. [Google Scholar] [CrossRef]
- Allen, L.N.; MacAdam, J.W. Irrigation and water management. Forages Sci. Grassl. Agric. 2020, 2, 497–513. [Google Scholar]
- Kumar, J.; Biswas, B.; Walker, S. Multi-temporal LULC classification using hybrid approach and monitoring built-up growth with Shannon’s entropy for a semi-arid region of Rajasthan, India. J. Geol. Soc. India 2020, 95, 626–635. [Google Scholar] [CrossRef]
- Mazahir, S.; Javed, A.; Khanday, M.Y. Assessing Spatio-Temporal Land Cover Changes in Dhund River Basin, Eastern Rajasthan (India), Using Multi-Temporal Landsat Data. J. Geogr. Inf. Syst. 2024, 16, 244–258. [Google Scholar] [CrossRef]
- Meraj, M.; Javed, A. Land Use/Land Cover (LULC) Dynamics in a Semi-Arid Watershed in Eastern Rajasthan, India Using Geospatial Tools. J. Geogr. Inf. Syst. 2022, 14, 612–633. [Google Scholar] [CrossRef]
- Hazbavi, Z.; Baartman, J.E.; Nunes, J.P.; Keesstra, S.D.; Sadeghi, S.H. Changeability of reliability, resilience and vulnerability indicators with respect to drought patterns. Ecol. Indic. 2018, 87, 196–208. [Google Scholar] [CrossRef]
- Malek, K.; Adam, J.C.; Stöckle, C.O.; Peters, R.T. Climate change reduces water availability for agriculture by decreasing non-evaporative irrigation losses. J. Hydrol. 2018, 561, 444–460. [Google Scholar] [CrossRef]
- Wada, Y.; van Beek, L.P.; Bierkens, M.F. Modelling global water stress of the recent past: On the relative importance of trends in water demand and climate variability. Hydrol. Earth Syst. Sci. 2011, 15, 3785–3808. [Google Scholar] [CrossRef]
- Yin, L.; Wang, L.; Keim, B.D.; Konsoer, K.; Zheng, W. Wavelet Analysis of Dam Injection and Discharge in Three Gorges Dam and Reservoir with Precipitation and River Discharge. Water 2022, 14, 567. [Google Scholar] [CrossRef]
- Zhou, G.; Tang, Y.; Zhang, W.; Liu, W.; Jiang, Y.; Gao, E.; Bai, Y. Shadow Detection on High-Resolution Digital Orthophoto Map Using Semantic Matching. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–20. [Google Scholar] [CrossRef]
- Li, J.; Pang, Z.; Liu, Y.; Hu, S.; Jiang, W.; Tian, L.; Tian, J. Changes in groundwater dynamics and geochemical evolution induced by drainage reorganization: Evidence from 81Kr and 36Cl dating of geothermal water in the Weihe Basin of China. Earth Planet. Sci. Lett. 2023, 623, 118425. [Google Scholar] [CrossRef]
- Dai, Z.; Peng, L.; Qin, S. Experimental and numerical investigation on the mechanism of ground collapse induced by underground drainage pipe leakage. Environ. Earth Sci. 2023, 83, 32. [Google Scholar] [CrossRef]
- Dai, Z.; Ritzi, R.W., Jr.; Dominic, D.F. Improving permeability semivariograms with transition probability models of hierarchical sedimentary architecture derived from outcrop analog studies. Water Resour. Res. 2005, 41, 1–13. [Google Scholar] [CrossRef]
- Dai, Z.; Samper, J. Inverse problem of multicomponent reactive chemical transport in porous media: Formulation and applications. Water Resour. Res. 2004, 40, 1–18. [Google Scholar] [CrossRef]
- Liu, C.; Shan, Y.; He, L.; Li, F.; Liu, X.; Nepf, H. Plant Morphology Impacts Bedload Sediment Transport. Geophys. Res. Lett. 2024, 51, e2024GL108800. [Google Scholar] [CrossRef]
- Li, Z.; He, M.; Li, B.; Wen, X.; Zhou, J.; Cheng, Y.; Deng, L. Multi-isotopic composition (Li and B isotopes) and hydrochemistry characterization of the Lakko Co Li-rich salt lake in Tibet, China: Origin and hydrological processes. J. Hydrol. 2024, 630, 130714. [Google Scholar] [CrossRef]
- Yin, L.; Wang, L.; Li, T.; Lu, S.; Yin, Z.; Liu, X.; Zheng, W. U-Net-STN: A Novel End-to-End Lake Boundary Prediction Model. Land 2023, 12, 1602. [Google Scholar] [CrossRef]
- Yin, L.; Wang, L.; Keim, B.D.; Konsoer, K.; Yin, Z.; Liu, M.; Zheng, W. Spatial and wavelet analysis of precipitation and river discharge during operation of the Three Gorges Dam, China. Ecol. Indic. 2023, 154, 110837. [Google Scholar] [CrossRef]
- Yin, L.; Wang, L.; Li, T.; Lu, S.; Tian, J.; Yin, Z.; Zheng, W. U-Net-LSTM: Time Series-Enhanced Lake Boundary Prediction Model. Land 2023, 12, 1859. [Google Scholar] [CrossRef]
- Zhou, G.; Lin, G.; Liu, Z.; Zhou, X.; Li, W.; Li, X.; Deng, R. An optical system for suppression of laser echo energy from the water surface on single-band bathymetric LiDAR. Opt. Lasers Eng. 2023, 163, 107468. [Google Scholar] [CrossRef]
- Zhou, G.; Xu, C.; Zhang, H.; Zhou, X.; Zhao, D.; Wu, G.; Zhang, L. PMT gain self-adjustment system for high-accuracy echo signal detection. Int. J. Remote Sens. 2022, 43, 7213–7235. [Google Scholar] [CrossRef]
- Zhang, K.; Li, Y.; Yu, Z.; Yang, T.; Xu, J.; Chao, L.; Lin, Z. Xin’anjiang Nested Experimental Watershed (XAJ-NEW) for Understanding Multiscale Water Cycle: Scientific Objectives and Experimental Design. Engineering 2022, 18, 207–217. [Google Scholar] [CrossRef]
- Hu, C.; Dong, B.; Shao, H.; Zhang, J.; Wang, Y. Toward Purifying Defect Feature for Multilabel Sewer Defect Classification. IEEE Trans. Instrum. Meas. 2023, 72, 5008611. [Google Scholar] [CrossRef]
- Ye, X.; Zhu, H.; Chang, F.; Xie, T.; Tian, F.; Zhang, W.; Catani, F. Revisiting spatiotemporal evolution process and mechanism of a giant reservoir landslide during weather extremes. Eng. Geol. 2024, 332, 107480. [Google Scholar] [CrossRef]
- Di, D.; Li, T.; Fang, H.; Xiao, L.; Du, X.; Sun, B.; Li, B. A CFD-DEM investigation into hydraulic transport and retardation response characteristics of drainage pipeline siltation using intelligent model. Tunn. Undergr. Space Technol. 2024, 152, 105964. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).