Drought Quantification in Africa Using Remote Sensing, Gaussian Kernel, and Machine Learning
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Dataset
2.3. Methodology
2.3.1. Key Drought Indicators and Indices and Their Trends
2.3.2. Drought Influencing Indicators and Drought Indices Used in the Study
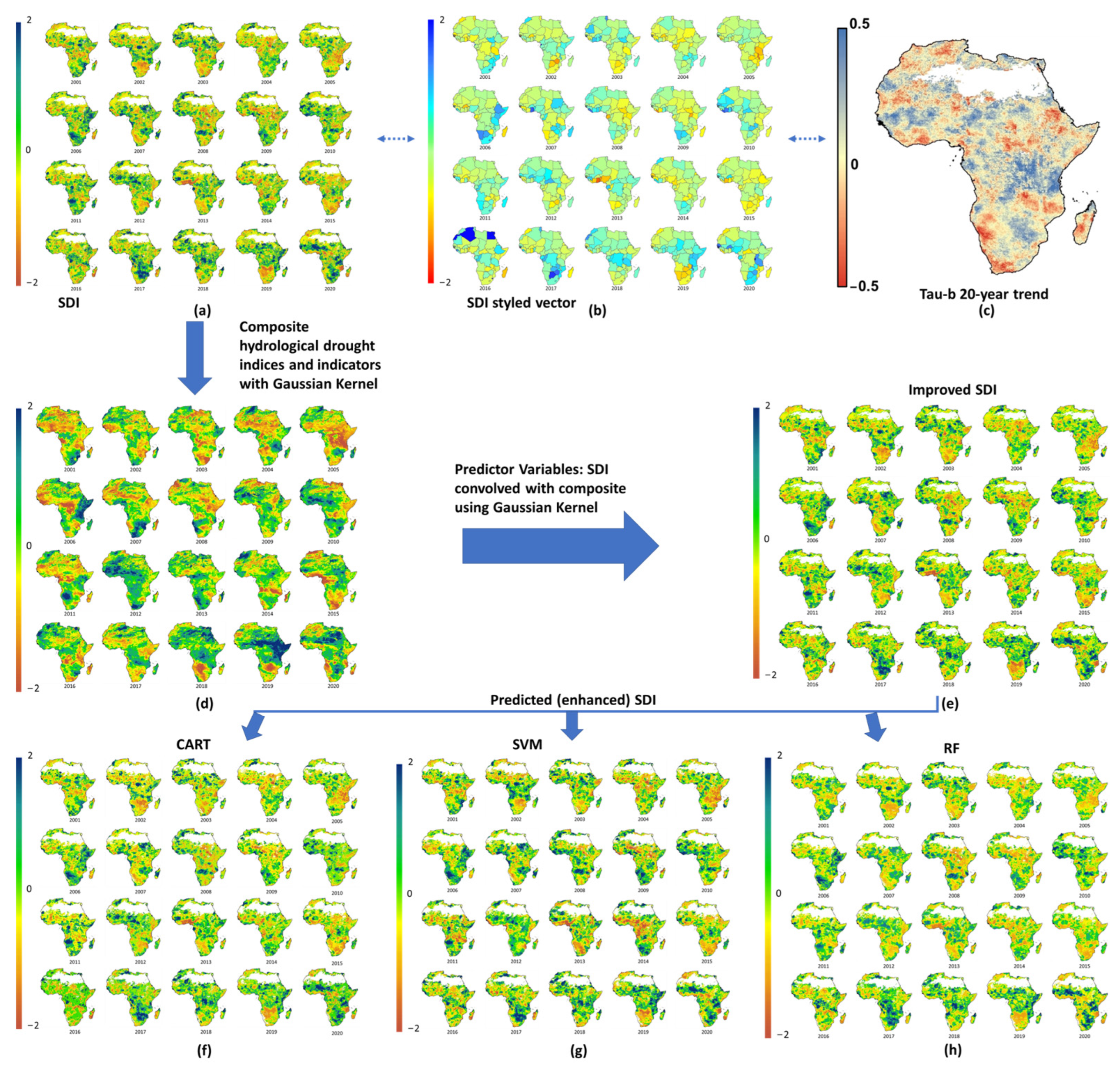
2.3.3. Blending Drought Indices and Indicators Using the Gaussian Kernel
2.3.4. Machine Learning Models
2.3.5. Model Performance
2.3.6. Model Parameter Settings and Validation
3. Results
3.1. Performance Evaluation
3.2. Drought Quantification Maps for Meteorological, Agricultural, and Hydrological Drought
3.2.1. Meteorological Drought Index
3.2.2. Agricultural Drought Index
3.2.3. Hydrological Drought Index
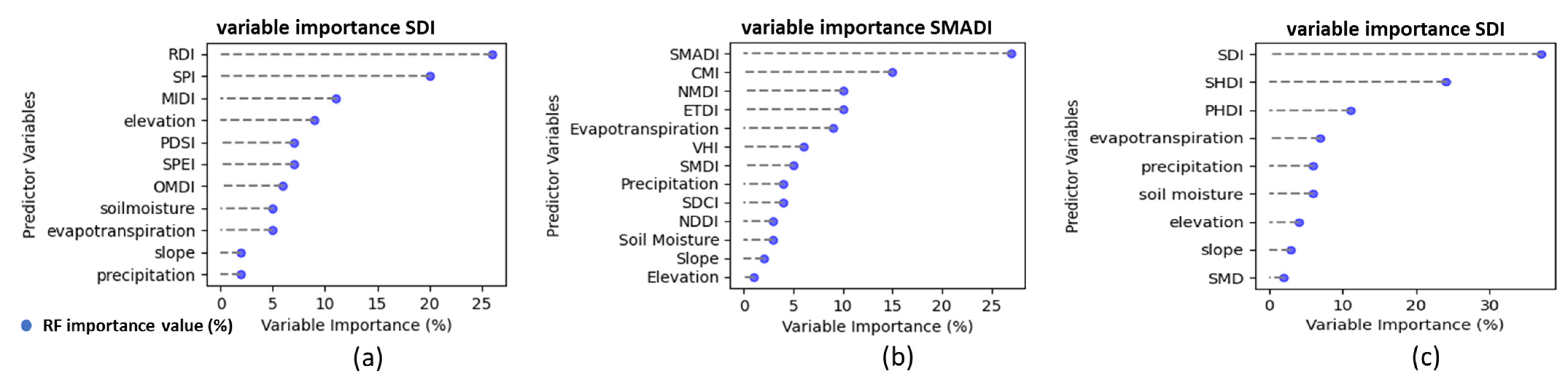
3.3. Ranking of Predictor Variable Importance for Meteorological, Agricultural, and Hydrological Drought in Africa
3.4. Evaluation of Meteorological, Agricultural, and Hydrological Percentage Drought Incidence in Africa from 2001 to 2020
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Masih, I.; Maskey, S.; Mussá, F.E.F.; Trambauer, P. A Review of Droughts on the African Continent: A Geospatial and Long-Term Perspective. Hydrol. Earth Syst. Sci. 2014, 18, 3635–3649. [Google Scholar] [CrossRef]
- Ding, Y.; Gong, X.; Xing, Z.; Cai, H.; Zhou, Z.; Zhang, D.; Sun, P.; Shi, H. Attribution of Meteorological, Hydrological and Agricultural Drought Propagation in Different Climatic Regions of China. Agric. Water Manag. 2021, 255, 106996. [Google Scholar] [CrossRef]
- Babaousmail, H.; Hou, R.; Ayugi, B.; Ojara, M.; Ngoma, H.; Karim, R.; Rajasekar, A.; Ongoma, V. Evaluation of the Performance of Cmip6 Models in Reproducing Rainfall Patterns over North Africa. Atmosphere 2021, 12, 475. [Google Scholar] [CrossRef]
- Bhaga, T.D.; Dube, T.; Shekede, M.D.; Shoko, C. Impacts of Climate Variability and Drought on Surface Water Resources in Sub-Saharan Africa Using Remote Sensing: A Review. Remote Sens. 2020, 12, 4184. [Google Scholar] [CrossRef]
- Siderius, C.; Gannon, K.E.; Ndiyoi, M.; Opere, A.; Batisani, N.; Olago, D.; Pardoe, J.; Conway, D. Hydrological Response and Complex Impact Pathways of the 2015/2016 El Niño in Eastern and Southern Africa. Earths Future 2018, 6, 2–22. [Google Scholar] [CrossRef]
- Chiang, F.; Mazdiyasni, O.; AghaKouchak, A. Evidence of Anthropogenic Impacts on Global Drought Frequency, Duration, and Intensity. Nat. Commun. 2021, 12, 2754. [Google Scholar] [CrossRef] [PubMed]
- Heydari Alamdarloo, E.; Khosravi, H.; Nasabpour, S.; Gholami, A. Assessment of Drought Hazard, Vulnerability and Risk in Iran Using GIS Techniques. J. Arid Land 2020, 12, 984–1000. [Google Scholar] [CrossRef]
- Xu, Z.; Wu, Z.; Shao, Q.; He, H.; Guo, X. From Meteorological to Agricultural Drought: Propagation Time and Probabilistic Linkages. J. Hydrol. Reg. Stud. 2023, 46, 101329. [Google Scholar] [CrossRef]
- Zhang, Q.; Miao, C.; Guo, X.; Gou, J.; Su, T. Human Activities Impact the Propagation from Meteorological to Hydrological Drought in the Yellow River Basin, China. J. Hydrol. 2023, 623, 129752. [Google Scholar] [CrossRef]
- Tladi, T.M.; Ndambuki, J.M.; Salim, R.W. Meteorological Drought Monitoring in the Upper Olifants Sub-Basin, South Africa. Phys. Chem. Earth Parts A/B/C 2022, 128, 103273. [Google Scholar] [CrossRef]
- Odongo, R.A.; De Moel, H.; Van Loon, A.F. Propagation from Meteorological to Hydrological Drought in the Horn of Africa Using Both Standardized and Threshold-Based Indices. Nat. Hazards Earth Syst. Sci. 2023, 23, 2365–2386. [Google Scholar] [CrossRef]
- Bahta, Y.T. Nexus between Coping Strategies and Households’ Agricultural Drought Resilience to Food Insecurity in South Africa. Land 2022, 11, 893. [Google Scholar] [CrossRef]
- Le Page, M.; Zribi, M. Analysis and Predictability of Drought In Northwest Africa Using Optical and Microwave Satellite Remote Sensing Products. Sci. Rep. 2019, 9, 1466. [Google Scholar] [CrossRef]
- Shoumik, B.A.A.; Khan, M.Z.; Islam, M.S. Spatio-Temporal Characteristics of Meteorological and Agricultural Drought Indices and Their Dynamic Relationships during the Pre-Monsoon Season in Drought-Prone Region of Bangladesh. Environ. Chall. 2023, 11, 100695. [Google Scholar] [CrossRef]
- Upadhyay, M.; Sherly, M.A. Multivariate Framework for Integrated Drought Vulnerability Assessment—An Application to India. Int. J. Disaster Risk Reduct. 2023, 85, 103515. [Google Scholar] [CrossRef]
- Lim Kam Sian, K.T.C.; Zhi, X.; Ayugi, B.O.; Onyutha, C.; Shilenje, Z.W.; Ongoma, V. Meteorological Drought Variability over Africa from Multisource Datasets. Atmosphere 2023, 14, 1052. [Google Scholar] [CrossRef]
- Ekolu, J.; Dieppois, B.; Sidibe, M.; Eden, J.M.; Tramblay, Y.; Villarini, G.; Peña-Angulo, D.; Mahé, G.; Paturel, J.E.; Onyutha, C.; et al. Long-Term Variability in Hydrological Droughts and Floods in Sub-Saharan Africa: New Perspectives from a 65-Year Daily Streamflow Dataset. J. Hydrol. 2022, 613, 128359. [Google Scholar] [CrossRef]
- Tsakiris, G.; Pangalou, D.; Vangelis, H. Regional Drought Assessment Based on the Reconnaissance Drought Index (RDI). Water Resour. Manag. 2007, 21, 821–833. [Google Scholar] [CrossRef]
- Domenikiotis, C.; Tsiros, E.; Dalezios, N.R.; Kanellou, E.; Domenikiotis, C.; Dalezios, N.R. Satellite-Based Drought Estimation in Thessaly. Eur. Water 2008, 23, 111–122. [Google Scholar]
- Zarei, A.R.; Shabani, A.; Moghimi, M.M. Accuracy Assessment of the SPEI, RDI and SPI Drought Indices in Regions of Iran with Different Climate Conditions. Pure Appl. Geophys. 2021, 178, 1387–1403. [Google Scholar] [CrossRef]
- Tian, Q.; Lu, J.; Chen, X. A Novel Comprehensive Agricultural Drought Index Reflecting Time Lag of Soil Moisture to Meteorology: A Case Study in the Yangtze River Basin, China. Catena 2022, 209, 105804. [Google Scholar] [CrossRef]
- Souza, A.G.S.S.; Ribeiro Neto, A.; Souza, L.L. de Soil Moisture-Based Index for Agricultural Drought Assessment: SMADI Application in Pernambuco State-Brazil. Remote Sens. Environ. 2021, 252, 112124. [Google Scholar] [CrossRef]
- Tareke, K.A.; Awoke, A.G. Comparing Surface Water Supply Index and Streamflow Drought Index for Hydrological Drought Analysis in Ethiopia. Heliyon 2022, 8, e12000. [Google Scholar] [CrossRef] [PubMed]
- Gumus, V.; Avsaroglu, Y.; Simsek, O.; Basak, A. Evaluating the Duration, Severity, and Peak of Hydrological Drought Using Copula. Theor. Appl. Climatol. 2023, 152, 1159–1174. [Google Scholar] [CrossRef]
- Ha, T.V.; Uereyen, S.; Kuenzer, C. Agricultural Drought Conditions over Mainland Southeast Asia: Spatiotemporal Characteristics Revealed from MODIS-Based Vegetation Time-Series. Int. J. Appl. Earth Obs. Geoinf. 2023, 121, 103378. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, Y.P.; Huang, G.H.; Wang, H.; Shen, Z.Y. Copula Function with Variational Bayesian Monte Carlo for Unveiling Uncertainty Impacts on Meteorological and Agricultural Drought Propagation. J. Hydrol. 2023, 622, 129669. [Google Scholar] [CrossRef]
- Zhang, J.; Bi, S.; Zhang, G. A Directional Gaussian Smoothing Optimization Method for Computational Inverse Design in Nanophotonics. Mater. Des. 2021, 197, 109213. [Google Scholar] [CrossRef]
- Park, S.; Im, J.; Park, S.; Rhee, J. Drought Monitoring Using High Resolution Soil Moisture through Multi-Sensor Satellite Data Fusion over the Korean Peninsula. Agric. For. Meteorol. 2017, 237–238, 257–269. [Google Scholar] [CrossRef]
- Rose, M.A.J.; Chithra, N.R. Tree-Based Ensemble Model Prediction for Hydrological Drought in a Tropical River Basin of India. Int. J. Environ. Sci. Technol. 2023, 20, 4973–4990. [Google Scholar] [CrossRef]
- Dibi-Anoh, P.A.; Koné, M.; Gerdener, H.; Kusche, J.; N’Da, C.K. Hydrometeorological Extreme Events in West Africa: Droughts. Surv. Geophys. 2023, 44, 173–195. [Google Scholar] [CrossRef]
- Shen, R.; Huang, A.; Li, B.; Guo, J. Construction of a Drought Monitoring Model Using Deep Learning Based on Multi-Source Remote Sensing Data. Int. J. Appl. Earth Obs. Geoinf. 2019, 79, 48–57. [Google Scholar] [CrossRef]
- Rakovec, O.; Samaniego, L.; Hari, V.; Markonis, Y.; Moravec, V.; Thober, S.; Hanel, M.; Kumar, R. The 2018–2020 Multi-Year Drought Sets a New Benchmark in Europe. Earths Future 2022, 10, e2021EF002394. [Google Scholar] [CrossRef]
- Dube, T.; Seaton, D.; Shoko, C.; Mbow, C. Advancements in Earth Observation for Water Resources Monitoring and Management in Africa: A Comprehensive Review. J. Hydrol. 2023, 623, 129738. [Google Scholar] [CrossRef]
- Zhang, M.; Gao, Y. Time of Emergence in Climate Extremes Corresponding to Köppen-Geiger Classification. Weather Clim. Extrem. 2023, 41, 100593. [Google Scholar] [CrossRef]
- Knight, J. The Last Glaciers in Africa and Their Environmental Implications. J. Afr. Earth Sci. 2023, 200, 104863. [Google Scholar] [CrossRef]
- Bello-Schünemann, J.; Donnenfeld, Z.; Aucoin, C. African Futures 2035: Key Trends. J. Futures Stud. 2018, 23, 127–140. [Google Scholar] [CrossRef]
- Chirachawala, C.; Shrestha, S.; Babel, M.S.; Virdis, S.G.P.; Wichakul, S. Evaluation of Global Land Use/Land Cover Products for Hydrologic Simulation in the Upper Yom River Basin, Thailand. Sci. Total Environ. 2020, 708, 135148. [Google Scholar] [CrossRef]
- Arregocés, H.A.; Rojano, R.; Pérez, J. Validation of the CHIRPS Dataset in a Coastal Region with Extensive Plains and Complex Topography. Case Stud. Chem. Environ. Eng. 2023, 8, 100452. [Google Scholar] [CrossRef]
- Aksu, H.; Taflan, G.Y.; Yaldiz, S.G.; Akgül, M.A. Evaluation of IMERG for GPM Satellite-Based Precipitation Products for Extreme Precipitation Indices over Turkiye. Atmos. Res. 2023, 291, 106826. [Google Scholar] [CrossRef]
- McNally, A.; Arsenault, K.; Kumar, S.; Shukla, S.; Peterson, P.; Wang, S.; Funk, C.; Peters-Lidard, C.D.; Verdin, J.P. A Land Data Assimilation System for Sub-Saharan Africa Food and Water Security Applications. Sci. Data 2017, 4, 170012. [Google Scholar] [CrossRef]
- Jung, H.C.; Getirana, A.; Policelli, F.; McNally, A.; Arsenault, K.R.; Kumar, S.; Tadesse, T.; Peters-Lidard, C.D. Upper Blue Nile Basin Water Budget from a Multi-Model Perspective. J. Hydrol. 2017, 555, 535–546. [Google Scholar] [CrossRef] [PubMed]
- Shirkey, G.; John, R.; Chen, J.; Dahlin, K.; Abraha, M.; Sciusco, P.; Lei, C.; Reed, D.E. Fine Resolution Remote Sensing Spectra Improves Estimates of Gross Primary Production of Croplands. Agric. For. Meteorol. 2022, 326, 109175. [Google Scholar] [CrossRef]
- Bari, E.; Nipa, N.J.; Roy, B. Association of Vegetation Indices with Atmospheric & Biological Factors Using MODIS Time Series Products. Environ. Chall. 2021, 5, 100376. [Google Scholar] [CrossRef]
- Gomis-Cebolla, J.; Rattayova, V.; Salazar-Galán, S.; Francés, F. Evaluation of ERA5 and ERA5-Land Reanalysis Precipitation Datasets over Spain (1951–2020). Atmos. Res. 2023, 284, 106606. [Google Scholar] [CrossRef]
- Li, L.; Zhan, W.; Hu, L.; Chakraborty, T.C.; Wang, Z.; Fu, P.; Wang, D.; Liao, W.; Huang, F.; Fu, H.; et al. Divergent Urbanization-Induced Impacts on Global Surface Urban Heat Island Trends since 1980s. Remote Sens. Environ. 2023, 295, 113650. [Google Scholar] [CrossRef]
- Qiao, L.; Will, R.; Wagner, K.; Zhang, T.; Zou, C. Improvement of Evapotranspiration Estimates for Grasslands in the Southern Great Plains: Comparing a Biophysical Model (SWAT) and Remote Sensing (MODIS). J. Hydrol. Reg. Stud. 2022, 44, 101275. [Google Scholar] [CrossRef]
- Liu, H.; Xin, X.; Su, Z.; Zeng, Y.; Lian, T.; Li, L.; Yu, S.; Zhang, H. Intercomparison and Evaluation of Ten Global ET Products at Site and Basin Scales. J. Hydrol. 2023, 617, 128887. [Google Scholar] [CrossRef]
- Ma, H.; Liang, S. Development of the GLASS 250-m Leaf Area Index Product (Version 6) from MODIS Data Using the Bidirectional LSTM Deep Learning Model. Remote Sens. Environ. 2022, 273, 112985. [Google Scholar] [CrossRef]
- Dong, G.; Huang, W.; Smith, W.A.P.; Ren, P. A Shadow Constrained Conditional Generative Adversarial Net for SRTM Data Restoration. Remote Sens. Environ. 2020, 237, 111602. [Google Scholar] [CrossRef]
- Das, P.K.; Dutta, D.; Sharma, J.R.; Dadhwal, V.K. Trends and Behaviour of Meteorological Drought (1901–2008) over Indian Region Using Standardized Precipitation-Evapotranspiration Index. Int. J. Climatol. 2016, 36, 909–916. [Google Scholar] [CrossRef]
- Corral-Pazos-de-Provens, E.; Rapp-Arrarás, Í.; Domingo-Santos, J.M. Estimating Textural Fractions of the USDA Using Those of the International System: A Quantile Approach. Geoderma 2022, 416, 115783. [Google Scholar] [CrossRef]
- Fassnacht, F.E.; Schiller, C.; Kattenborn, T.; Zhao, X.; Qu, J. A Landsat-Based Vegetation Trend Product of the Tibetan Plateau for the Time-Period 1990–2018. Sci. Data 2019, 6, 78. [Google Scholar] [CrossRef] [PubMed]
- Safanelli, J.L.; Poppiel, R.R.; Chimelo Ruiz, L.F.; Bonfatti, B.R.; de Oliveira Mello, F.A.; Rizzo, R.; Demattê, J.A.M. Terrain Analysis in Google Earth Engine: A Method Adapted for High-Performance Global-Scale Analysis. ISPRS Int. J. Geoinf. 2020, 9, 400. [Google Scholar] [CrossRef]
- Guo, M.; Li, J.; Wang, Y.; Long, Q.; Bai, P. Spatiotemporal Variations of Meteorological Droughts and the Assessments of Agricultural Drought Risk in a Typical Agricultural Province of China. Atmosphere 2019, 10, 542. [Google Scholar] [CrossRef]
- Palmer Meteorological Drought. Available online: https://www.droughtmanagement.info/literature/USWB_Meteorological_Drought_1965.pdf (accessed on 10 September 2024).
- Mckee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993. [Google Scholar]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Zhang, A.; Jia, G.; Wang, H. Improving Meteorological Drought Monitoring Capability over Tropical and Subtropical Water-Limited Ecosystems: Evaluation and Ensemble of the Microwave Integrated Drought Index. Environ. Res. Lett. 2019, 14, 044025. [Google Scholar] [CrossRef]
- Hao, C.; Zhang, J.; Yao, F. Combination of Multi-Sensor Remote Sensing Data for Drought Monitoring over Southwest China. Int. J. Appl. Earth Obs. Geoinf. 2015, 35, 270–283. [Google Scholar] [CrossRef]
- Gu, Y.; Brown, J.F.; Verdin, J.P.; Wardlow, B. A Five-Year Analysis of MODIS NDVI and NDWI for Grassland Drought Assessment over the Central Great Plains of the United States. Geophys. Res. Lett. 2007, 34, L06407. [Google Scholar] [CrossRef]
- Kogan, F. World Droughts in the New Millennium from Avhrr-Based Vegetation Health Indices. Eos Trans. Am. Geophys. Union 2002, 83, 557–563. [Google Scholar] [CrossRef]
- Narasimhan, B.; Srinivasan, R. Development and Evaluation of Soil Moisture Deficit Index (SMDI) and Evapotranspiration Deficit Index (ETDI) for Agricultural Drought Monitoring. Agric. For. Meteorol. 2005, 133, 69–88. [Google Scholar] [CrossRef]
- Sánchez, N.; González-Zamora, Á.; Piles, M.; Martínez-Fernández, J. A New Soil Moisture Agricultural Drought Index (SMADI) Integrating MODIS and SMOS Products: A Case of Study over the Iberian Peninsula. Remote Sens. 2016, 8, 287. [Google Scholar] [CrossRef]
- Wang, L.; Qu, J.J. NMDI: A Normalized Multi-Band Drought Index for Monitoring Soil and Vegetation Moisture with Satellite Remote Sensing. Geophys. Res. Lett. 2007, 34, L20405. [Google Scholar] [CrossRef]
- Rhee, J.; Im, J.; Carbone, G.J. Monitoring Agricultural Drought for Arid and Humid Regions Using Multi-Sensor Remote Sensing Data. Remote Sens. Environ. 2010, 114, 2875–2887. [Google Scholar] [CrossRef]
- Nalbantis, I.; Tsakiris, G. Assessment of Hydrological Drought Revisited. Water Resour. Manag. 2009, 23, 881–897. [Google Scholar] [CrossRef]
- Dehghani, M.; Saghafian, B.; Nasiri Saleh, F.; Farokhnia, A.; Noori, R. Uncertainty Analysis of Streamflow Drought Forecast Using Artificial Neural Networks and Monte-Carlo Simulation. Int. J. Climatol. 2014, 34, 1169–1180. [Google Scholar] [CrossRef]
- Mafi, M.; Martin, H.; Cabrerizo, M.; Andrian, J.; Barreto, A.; Adjouadi, M. A Comprehensive Survey on Impulse and Gaussian Denoising Filters for Digital Images. Signal Process. 2019, 157, 236–260. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Available online: www.stat.berkeley.edu/~breiman/randomforest2001.pdf (accessed on 10 September 2024).
- Cortes, C.; Vapnik, V.; Saitta, L. Support-Vector Networks Editor; Kluwer Academic Publishers: Alphen aan den Rijn, The Netherlands, 1995; Volume 20. [Google Scholar]
- Srivastava, D.; Bhambhu, L.; Srivastava, D.K. Data Classification Using Support Vector Machine. J. Theor. Appl. Inf. Technol. 2010, 12, 1–7. [Google Scholar]
- Breiman, L.; Friedman, H.J.; Olshen, A.R.; Stone, J.C. Classification and Regression Trees; Chapman & Hall/CRC: New York, NY, USA, 1984. [Google Scholar]
- Abedinia, A.; Seydi, V. Building Semi-Supervised Decision Trees with Semi-Cart Algorithm. Int. J. Mach. Learn. Cybern. 2024, 15, 4493–4510. [Google Scholar] [CrossRef]
- Biró, T.S.; Néda, Z. Gintropy: Gini Index Based Generalization of Entropy. Entropy 2020, 22, 879. [Google Scholar] [CrossRef]
- Bolouri, S.; Vafaeinejad, A.; Alesheikh, A.A.; Aghamohammadi, H. The Ordered Capacitated Multi-Objective Location-Allocation Problem for Fire Stations Using Spatial Optimization. ISPRS Int. J. Geo-Inf. 2018, 7, 44. [Google Scholar] [CrossRef]
- Noorunnahar, M.; Chowdhury, A.H.; Mila, F.A. A Tree Based EXtreme Gradient Boosting (XGBoost) Machine Learning Model to Forecast the Annual Rice Production in Bangladesh. PLoS ONE 2023, 18, e0283452. [Google Scholar] [CrossRef] [PubMed]
- Ebrahimi, M.A.; Khoshtaghaza, M.H.; Minaei, S.; Jamshidi, B. Vision-Based Pest Detection Based on SVM Classification Method. Comput. Electron. Agric. 2017, 137, 52–58. [Google Scholar] [CrossRef]
- Hodson, T.O. Root-Mean-Square Error (RMSE) or Mean Absolute Error (MAE): When to Use Them or Not. Geosci. Model. Dev. 2022, 15, 5481–5487. [Google Scholar] [CrossRef]
- Prasetyo, S.Y.J.; Hartomo, K.D.; Paseleng, M.C. Satellite Imagery and Machine Learning for Identification of Aridity Risk in Central Java Indonesia. PeerJ Comput. Sci. 2021, 7, e415. [Google Scholar] [CrossRef]
- Piao, Y.; Lee, D.; Park, S.; Kim, H.G.; Jin, Y. Multi-Hazard Mapping of Droughts and Forest Fires Using a Multi-Layer Hazards Approach with Machine Learning Algorithms. Geomat. Nat. Hazards Risk 2022, 13, 2649–2673. [Google Scholar] [CrossRef]
- Wu, J.; Zhou, L.; Liu, M.; Zhang, J.; Leng, S.; Diao, C. Establishing and Assessing the Integrated Surface Drought Index (ISDI) for Agricultural Drought Monitoring in Mid-Eastern China. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 397–410. [Google Scholar] [CrossRef]
- Zafar, Z.; Zubair, M.; Zha, Y.; Fahd, S.; Ahmad Nadeem, A. Performance Assessment of Machine Learning Algorithms for Mapping of Land Use/Land Cover Using Remote Sensing Data. Egypt. J. Remote Sens. Space Sci. 2024, 27, 216–226. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Liew, M.W.V.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 1983, 50, 885–900. [Google Scholar] [CrossRef]
- Thi, N.Q.; Govind, A.; Le, M.-H.; Linh, N.T.; Anh, T.T.M.; Hai, N.K.; Ha, T.V. Spatiotemporal Characterization of Droughts and Vegetation Response in Northwest Africa from 1981 to 2020. Egypt. J. Remote Sens. Space Sci. 2023, 26, 393–401. [Google Scholar] [CrossRef]
- Kasei, R.; Diekkrüger, B.; Leemhuis, C. Drought Frequency in the Volta Basin of West Africa. Sustain. Sci. 2010, 5, 89–97. [Google Scholar] [CrossRef]
- Ayugi, B.; Eresanya, E.O.; Onyango, A.O.; Ogou, F.K.; Okoro, E.C.; Okoye, C.O.; Anoruo, C.M.; Dike, V.N.; Ashiru, O.R.; Daramola, M.T.; et al. Review of Meteorological Drought in Africa: Historical Trends, Impacts, Mitigation Measures, and Prospects. Pure Appl. Geophys. 2022, 179, 1365–1386. [Google Scholar] [CrossRef] [PubMed]
- Chivangulula, F.M.; Amraoui, M.; Pereira, M.G. The Drought Regime in Southern Africa: A Systematic Review. Climate 2023, 11, 147. [Google Scholar] [CrossRef]
- Ntali, Y.M.; Lyimo, J.G.; Dakyaga, F. Trends, Impacts, and Local Responses to Drought Stress in Diamare Division, Northern Cameroon. World Dev. Sustain. 2023, 2, 100040. [Google Scholar] [CrossRef]
- Bhaga, T.D.; Dube, T.; Shekede, M.D.; Shoko, C. Investigating the Effectiveness of Landsat-8 OLI and Sentinel-2 MSI Satellite Data in Monitoring the Effects of Drought on Surface Water Resources in the Western Cape Province, South Africa. Remote Sens. Appl. 2023, 32, 101037. [Google Scholar] [CrossRef]
- Rulinda, C.M.; Dilo, A.; Bijker, W.; Stein, A. Characterising and Quantifying Vegetative Drought in East Africa Using Fuzzy Modelling and NDVI Data. J. Arid Environ. 2012, 78, 169–178. [Google Scholar] [CrossRef]
- Ndlovu, T.; Mjimba, V. Drought Risk-Reduction and Gender Dynamics in Communal Cattle Farming in Southern Zimbabwe. Int. J. Disaster Risk Reduct. 2021, 58, 102203. [Google Scholar] [CrossRef]
- Chen, J.; Shao, Z.; Huang, X.; Zhuang, Q.; Dang, C.; Cai, B.; Zheng, X.; Ding, Q. Assessing the Impact of Drought-Land Cover Change on Global Vegetation Greenness and Productivity. Sci. Total Environ. 2022, 852, 158499. [Google Scholar] [CrossRef]
- Henchiri, M.; Igbawua, T.; Javed, T.; Bai, Y.; Zhang, S.; Essifi, B.; Ujoh, F.; Zhang, J. Meteorological Drought Analysis and Return Periods over North and West Africa and Linkage with El Niño–Southern Oscillation (Enso). Remote Sens. 2021, 13, 4730. [Google Scholar] [CrossRef]
- Anderson, W.B.; Zaitchik, B.F.; Hain, C.R.; Anderson, M.C.; Yilmaz, M.T.; Mecikalski, J.; Schultz, L. Towards an Integrated Soil Moisture Drought Monitor for East Africa. Hydrol. Earth Syst. Sci. 2012, 16, 2893–2913. [Google Scholar] [CrossRef]
- Sorí, R.; Gimeno-Sotelo, L.; Nieto, R.; Liberato, M.L.R.; Stojanovic, M.; Pérez-Alarcón, A.; Fernández-Alvarez, J.C.; Gimeno, L. Oceanic and Terrestrial Origin of Precipitation over 50 Major World River Basins: Implications for the Occurrence of Drought. Sci. Total Environ. 2023, 859, 160288. [Google Scholar] [CrossRef]
- Hagenlocher, M.; Meza, I.; Anderson, C.C.; Min, A.; Renaud, F.G.; Walz, Y.; Siebert, S.; Sebesvari, Z. Drought Vulnerability and Risk Assessments: State of the Art, Persistent Gaps, and Research Agenda. Environ. Res. Lett. 2019, 14, 083002. [Google Scholar] [CrossRef]
- Bachmair, S.; Svensson, C.; Hannaford, J.; Barker, L.J.; Stahl, K. Appraising Drought Indicators and Modelling Drought Impacts A Quantitative Analysis to Objectively Appraise Drought Indicators and Model Drought Impacts Appraising Drought Indicators and Modelling Drought Impacts Appraising Drought Indicators and Modelling Drought Impacts. Hydrol. Earth Syst. Sci. Discuss. 2015, 12, 9437–9488. [Google Scholar] [CrossRef]
- Feng, G.; Chen, Y.; Mansaray, L.R.; Xu, H.; Shi, A.; Chen, Y. Propagation of Meteorological Drought to Agricultural and Hydrological Droughts in the Tropical Lancang–Mekong River Basin. Remote Sens. 2023, 15, 5678. [Google Scholar] [CrossRef]
- Anjali, C.V.; Pachore, A.; Remesan, R. Agricultural Drought Response to Meteorological Drought over Different Agro-Climatic Zones of the Ganga River Basin. J. Water Clim. Change 2024, 15, 998–1017. [Google Scholar] [CrossRef]
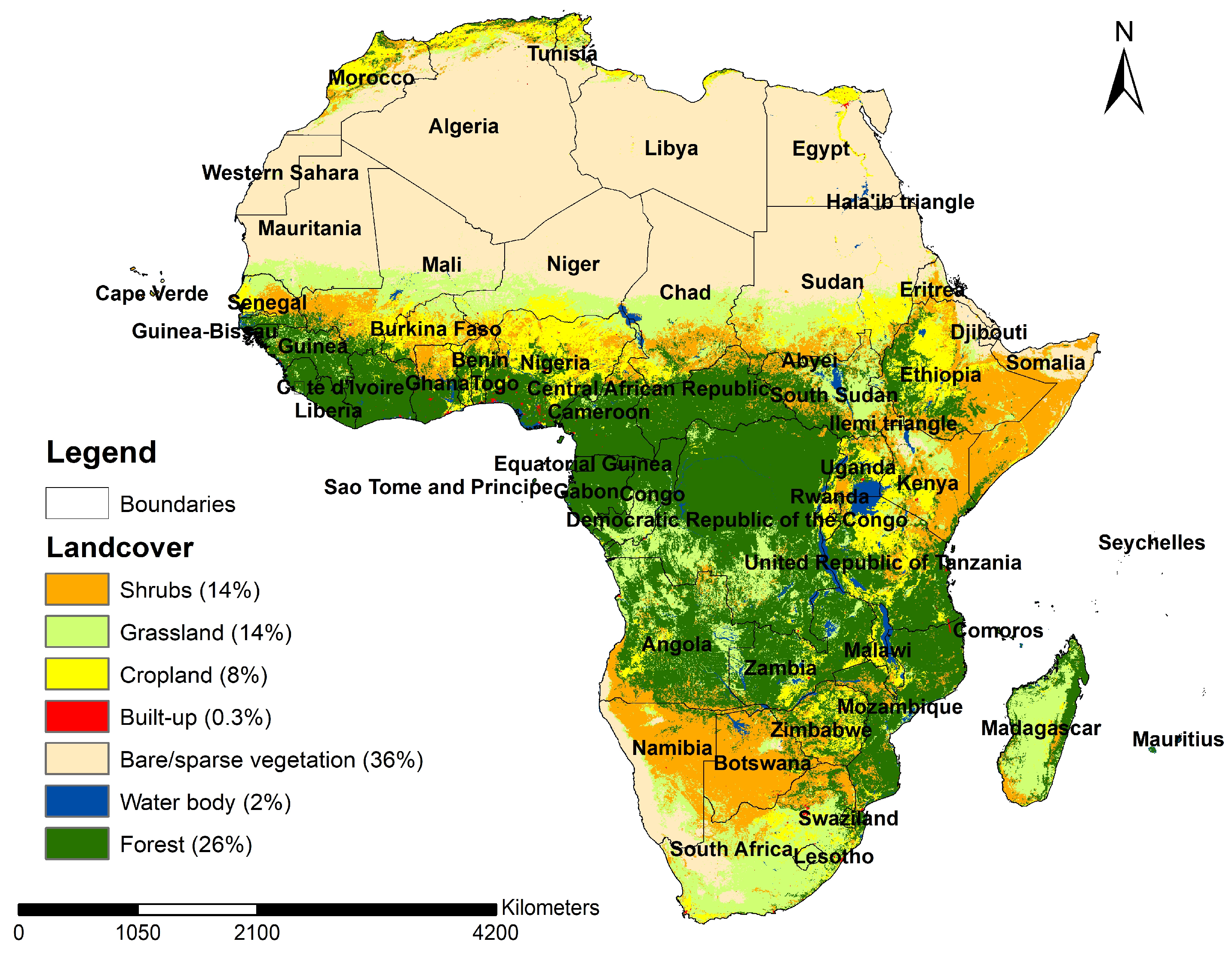





| Product | Variables | Spatiotemporal Resolution | Reference |
|---|---|---|---|
| CHIRPS IMERG-Final version “06” | Rainfall Rainfall | 0.05° × 0.05° (daily) 0.1° × 0.1° (monthly) | Arregocés et al. [38] Aksu et al. [39] |
| FLDAS FLDAS | Evapotranspiration Soil moisture | 0.1° × 0.1° (monthly) 0.1° × 0.1° (monthly) | McNally et al. [40] Jung et al. [41] |
| MOD17A2H V6 | GPP | 0.005° × 0.005° (8 day) | Shirkey et al. [42] |
| MOD13A2 V6.1 | NDVI | 0.01° × 0.01° (16 day) | Bari et al. [43] |
| ERA5 | Air temperature | 0.25° × 0.25° (monthly) | Gomis-Cebolla et al. [44] |
| MOD11A2 V6.1 | Land surface temp | 0.01° × 0.01° (8 day) | Li et al. [45] |
| MOD16A2 Version 6.1 | PET, ET | 0.004° × 0.004° (8 day) | Qiao et al. [46] |
| TerraClimate | PDSI | 0.04° × 0.04° (monthly) | Liu et al. [47] |
| MOD09A1 V6.1 | Surface reflectance | 0.001° × 0.001° (8 day) | Ma & Liang [48] |
| SRTM digital elevation data v4 | DEM | 0.0008° × 0.0008° | Dong et al. [49] |
| SPEIbase | SPEI | 0.5° × 0.5° (monthly) | Das et al. [50] |
| USDA system | Soil texture | 0.002° × 0.002° (yearly) | Corral-Pazos-de-Provens et al. [51] |
| MCD12Q1 V6.1 product | Land cover | 0.004° × 0.004° (yearly) | Chirachawala et al. [37] |
| Drought Index | Full Name | Formula | Reference |
|---|---|---|---|
| Meteorological Drought Indices | |||
| PDSI | Palmer Drought Severity Index | Palmer [55] | |
| SPI | Standardized Precipitation Index | McKee et al. [56] | |
| SPEI | Standardized Precipitation Evapotranspiration Index | Vicente-Serrano et al. [57] | |
| RDI | Reconnaissance drought index | Tsakiris et al. [18] | |
| MIDI | Microwave Integrated Drought Index | Zhang et al. [58] | |
| OMDI | Optimized Meteorological Drought Index | Hao et al. [59] | |
| Agricultural Drought Indices | |||
| NDDI | Normalized Difference Drought Index | Gu et al. [60] | |
| VHI | Vegetation Health Index | Kogan [61] | |
| SMDI | Soil Moisture Deficit Index | Narasimhan and Srinivasan [62] | |
| ETDI | Evapotranspiration Deficit Index | Narasimhan and Srinivasan [62] | |
| CMI | Crop Moisture Index | Palmer [55] | |
| SMADI | Soil Moisture Agricultural Drought Index | Sánchez et al. [63] | |
| NMDI | Normalized Multiband Drought Index | Wang and Qu [64] | |
| SDCI | Scaled Drought Condition Index | Rhee et al. [65] | |
| Hydrological Drought Indices | |||
| SDI | Stream flow Drought Index | Nalbantis and Tsakiris [66] | |
| PHDI | Palmer Hydrological Drought Index | PDSI, Palmer Drought Severity Index | Palmer [55] |
| SHDI | Standardized Hydrological Drought index | Dehghani et al. [67] |
| Meteorological Drought (RDI) | ||||
| Grid code | Classification | Area (km2) | Percentage of grid codes | Percentage of grid code 1 and 2 |
| 1 | Extreme drought | 3,729,089 | 16.8% | |
| 2 | Severe drought | 2,945,023 | 13.2% | |
| 3 | Moderate drought | 3,958,149 | 17.8% | |
| 4 | Mild drought | 3,986,207 | 17.9% | |
| 5 | Normal | 3,489,032 | 15.7% | 30% |
| 6 | Slightly wet | 2,105,593 | 9.4% | |
| 7 | Moderately wet | 1,068,267 | 4.8% | |
| 8 | Severely wet | 594,071 | 2.7% | |
| 9 | Extremely wet | 371,569 | 1.7% | |
| Agricultural Drought (SMADI) | ||||
| Grid code | Classification | Area (km2) | Percentage of grid codes | Percentage of grid code 2, 3, 4, and 5 |
| 1 | Near normal | 25,062,048 | 77.7% | |
| 2 | Mild drought | 5,027,211 | 15.6% | |
| 3 | Moderate drought | 1,646,027 | 5.1% | 22% |
| 4 | Severe drought | 379,880 | 1.2% | |
| 5 | Extreme drought | 138,697 | 0.4% | |
| Hydrological Drought (SDI) | ||||
| Grid code | Classification | Area (km2) | Percentage of grid codes | Percentage of grid code 1, 2, and 3 |
| 1 | Extreme drought | 150,067 | 0.5% | |
| 2 | Severe drought | 1,123,144 | 4.0% | |
| 3 | Moderate drought | 4,702,164 | 16.7% | |
| 4 | Mild drought | 5,089,351 | 18.1% | 21% |
| 5 | Mildly wet | 6,283,784 | 22.3% | |
| 6 | Moderately wet | 3,831,560 | 13.6% | |
| 7 | Severely wet | 3,029,034 | 10.7% | |
| 8 | Extremely wet | 3,981,002 | 14.1% |
| Drought Type | Region | Citation | Years | Remarks |
|---|---|---|---|---|
| Meteorological Drought | North Africa | Thi et al. [84] | 2001–2005, 2015–2017, 2019–2020 | Droughts detected in northeast Africa through the Standardized Precipitation Index (SPI). |
| West Africa | Kasei et al. [85] | 2001 | Droughts in Mali, Burkina Faso, Ghana, Togo, and the Volta Basin per SPI assessments. | |
| East Africa | Ayugi et al. [86] | 2005–2006, 2007–2009, 2011, 2017–2018 | Below-normal rainfall in Kenya, Tanzania, Somalia, Ethiopia. | |
| Southern Africa | Chivangulula et al. [87] | 2002–2004, 2015–2019 | Extreme droughts in southern Africa, influenced by El Niño. | |
| Central Africa | Ntali et al. [88] | Various years between 2002–2019 | Frequent droughts in northern Cameroon via SPI analysis. | |
| Agricultural Drought | North Africa | Thi et al. [84] | 2016–2017, 2019–2020 | Severe drought in Morocco and Algeria observed using NDVI data. |
| West Africa | Bhaga et al. [89] | 2018 | Crop failure in Senegal causing food insecurity for 245,000 people. | |
| East Africa | Rulinda et al. [90] | 2005–2006 | Drought across Burundi, Kenya, Rwanda, Tanzania, Uganda from September 2005 to January 2006. | |
| Southern Africa | Ndlovu & Mjimba [91] | 2019 | Approximately 70% drop in maize production in Zimbabwe due to drought. | |
| Central Africa | Chen et al. [92] | 2001–2020 | Declining productivity in the Congo rainforest with increasing drought frequency. | |
| Hydrological Drought | North Africa | Henchiri et al. [93] | 2001–2003, 2008–2010 | Hydrological droughts in Morocco and Algeria. |
| West Africa | Henchiri et al. [93] | 2000–2003, 2008–2010 | Hydrological droughts in Mali, Guinea, Ghana, Sierra Leone, Cote d’Ivoire, Niger, Burkina Faso, Nigeria. | |
| East Africa | Anderson et al. [94] | 2010–2011 | Hydrological drought in Ethiopia, Somalia, Kenya indicated by modeling. | |
| Southern Africa | Siderius et al. [5] | 2015–2016 | Hydrological droughts in southern Africa due to severe El Niño, affecting lake levels in Botswana, Zambia. | |
| Central Africa | Sorí et al. [95] | 2001–2020 | Drying trend in the Congo River Basin. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sseguya, F.; Jun, K.-S. Drought Quantification in Africa Using Remote Sensing, Gaussian Kernel, and Machine Learning. Water 2024, 16, 2656. https://doi.org/10.3390/w16182656
Sseguya F, Jun K-S. Drought Quantification in Africa Using Remote Sensing, Gaussian Kernel, and Machine Learning. Water. 2024; 16(18):2656. https://doi.org/10.3390/w16182656
Chicago/Turabian StyleSseguya, Fred, and Kyung-Soo Jun. 2024. "Drought Quantification in Africa Using Remote Sensing, Gaussian Kernel, and Machine Learning" Water 16, no. 18: 2656. https://doi.org/10.3390/w16182656
APA StyleSseguya, F., & Jun, K.-S. (2024). Drought Quantification in Africa Using Remote Sensing, Gaussian Kernel, and Machine Learning. Water, 16(18), 2656. https://doi.org/10.3390/w16182656







