1. Introduction
Freeze-up ice jams can cause significant flooding, damage to property, and loss of life. Floods caused by freeze-up ice jams can disrupt critical transportation routes and affect industries such as energy production ensuing substantial economic losses. Freeze-up ice jams can put significant pressure on existing infrastructure, including dams, levees, and flood control structures. In some cases, these structures may be overwhelmed or damaged during extreme flood events. Freeze-up ice jams can also significantly affect the environment with impacts to aquatic habitat and ecosystems.
The impacts of freeze-up ice-jam floods are often felt most strongly by local communities, which must respond to emergency situations while also dealing with the long-term consequences of flooding. Hence, freeze-up ice-jam flood forecasting is essential to ensure public safety, minimize economic losses, improve environmental management, and build community resilience in the face of climate change. Providing accurate forecasts can help mitigate the devastating consequences of these events and support more effective emergency response planning and mitigation strategies.
This article summarizes ice-jam flood forecasting methodologies that can be applied to rivers during freezing. The development of a freeze-up ice-jam flood forecasting system requires a thorough understanding of river ice processes, including the factors that influence freeze-up, such as frazil ice production, juxtapositioning, and ice-jam formation. The system must also take into account the characteristics of the fluvial geomorphology of the river, such as its slope, width, and depth, as well as any potential hazards or obstacles that may affect the flow of water and ice. One objective of this study is to provide a comprehensive overview of the requirements for a freeze-up ice-jam flood forecasting system in an operational context.
Another objective of this paper is to showcase a forecasting methodology that has gained much traction in recent years. It is a stochastic modelling approach, in which a deterministic river ice model is run many hundreds of times, with each simulation having a different set of parameter and boundary condition values chosen randomly from frequency distributions of the parameters and boundary conditions. The resulting ensemble of backwater flood stage profiles can be placed in a probabilistic context to predict the exceedance probabilities of flood threshold elevations. The Exploits River at Badger is used as a case study to illustrate the requirements for such a freeze-up ice-jam flood forecasting system based on the stochastic modelling approach. This river is located in Newfoundland, Canada, and has experienced several freeze-up ice-jam floods over the years.
Additional tools that could enhance the capabilities of forecasters by providing more accurate and timely information on weather conditions, river flow, and ice dynamics will also be highlighted. These include satellite imagery, in situ sensors, unmanned aerial vehicles, machine learning algorithms, hydrological and hydraulic modelling software, social media monitoring, and automated alert systems [
1,
2,
3,
4].
2. Freeze-Up Ice-Jam Flood Forecasting Approaches
Several approaches are available for the development, implementation, and operation of freeze-up ice-jam flood forecasting systems, including statistical, empirical, machine learning, and stochastic.
Statistical methods use historical data to establish correlations between hydrometeorological variables, such as air temperature, precipitation, and river ice conditions [
5,
6]. For example, a regression model could be used to predict the probability of occurrence of a freeze-up ice jam based on past observations of these variables. One advantage of empirical approaches is that they can be relatively simple to implement and do not require detailed knowledge of the underlying physical processes involved in ice cover formation and melting. However, they may not perform well if there are significant changes in the climate or other factors that affect river conditions. Empirical approaches also tend to be more site-specific and are difficult to transfer from one site to another.
Empirical approaches use analytical equations to calculate river ice hydraulic conditions. Algebraic solutions usually suffice to solve these equations, unlike numerical methods (described in the next paragraph), which require complex algorithms for execution. Empirical models need not be site-specific and have recently been applied to transfer river ice parameters along rivers to extrapolate the ice-jam flood hazard from gauged to ungauged communities [
7,
8].
Numerical models use mathematical equations to simulate the physical processes involved in frazil ice generation and freeze-up ice cover formation. Examples of numerical models include River2D [
9], HEC-RAS [
10] and RIVICE [
7]. These models can be used to predict the evolution of ice conditions over time by considering factors from the fluvial geomorphological, hydraulic, meteorological and river ice regimes. Compared to empirical approaches, numerical modelling requires significantly more computational resources necessitating their reduction in complexity if they are to be suitable for real-time flood forecasting.
Machine learning uses algorithms that learn from historical data to make predictions about future ice-jam events. For example, a decision tree or random forest model could be used to predict the probability of an ice jam occurring based on past observations of hydrometeorological variables and other factors such as river geometry and tributary inflows [
11]. Other methods include the k-nearest neighbour algorithm [
12], neural networks [
13,
14,
15] and fuzzy-logic models [
16,
17]. Machine learning methods can be very accurate if a vast amount of high-quality data is available for training the model, but they may not perform well if the relationships between variables are complex or if there are significant changes in the climate or other factors that affect river conditions.
Hybrid methods combine two or more of the above approaches and weigh their outcomes to yield more accurate forecasts [
1,
11,
18]. For example, a statistical model can be used to predict the locations of ice-jam lodgements based on fluvial geomorphological variables, while a numerical model could be used to simulate the generation of an ice cover stemming from those lodgements. Hybrid approaches can take advantage of the strengths of each method and may provide more accurate predictions than any single approach alone.
3. Examples of Freeze-Up Ice-Jam Flood Forecasting Systems
3.1. Deterministic Modelling System for the Kokemäenjoki River, Finland (Adapted from [19])
A freeze-up ice-jam flood forecasting system has been developed for the Kokemäenjoki River in Finland [
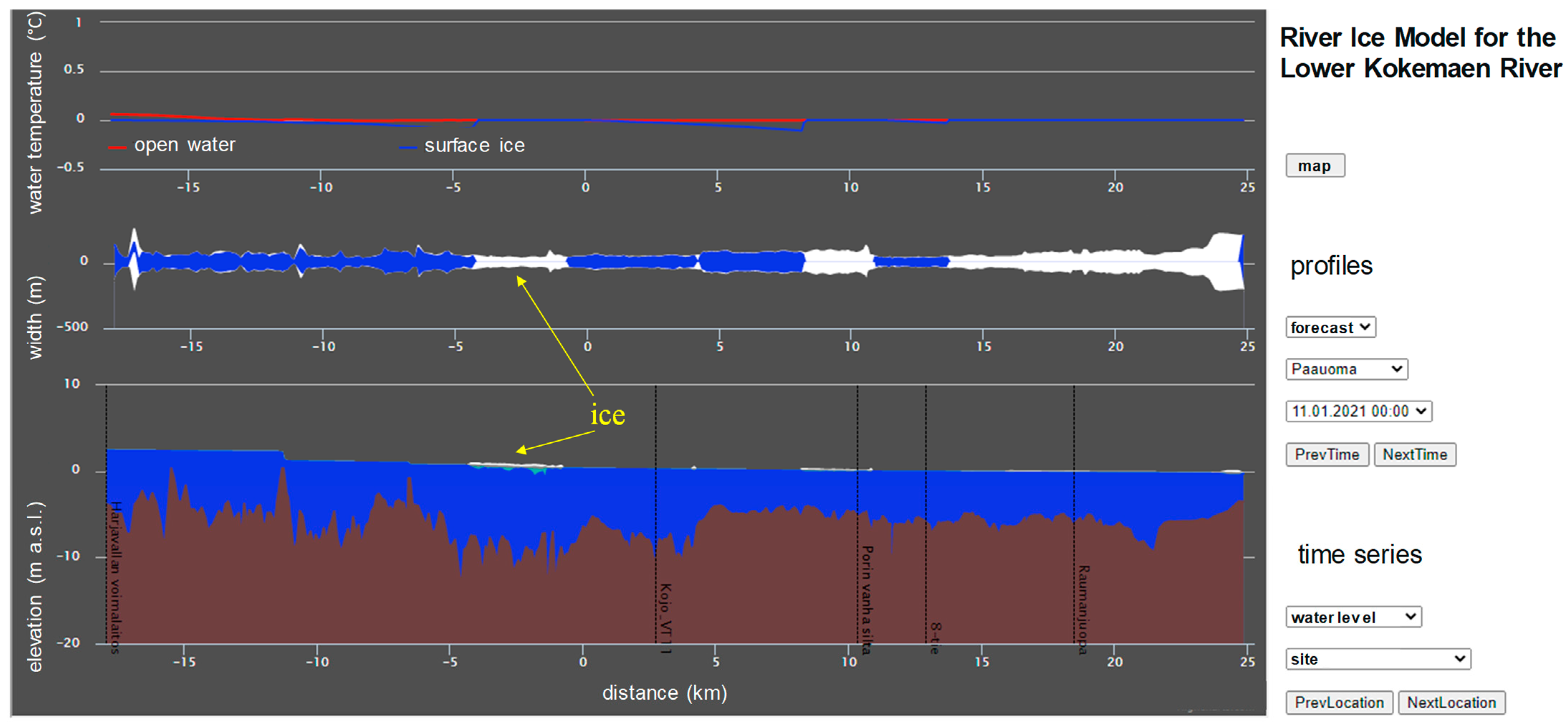
19]. It uses a numerical river ice model to simulate ice cover formation on the river. The system takes the hourly observed and forecasted (mean forecast) discharge from an upstream hydropower plant, hourly observed water temperatures from the same plant, and hourly observed and forecasted (mean forecast) sea level as input data. The ice model runs every six hours and yields results graphically through an HTML-based viewer on the internet, through an interface as shown in
Figure 1. “There are three different means of viewing the model results: longitudinal profiles, time series, and a map. On the map, only the locations of the points where time series data are available are presented with no ice cover information. It is possible, however, to display time series data (stage, discharge, water temperature) by clicking a point on the map. The profile output allows the selection of different model runs of mean and modified ice-extent forecasts with simulated open-water conditions” (pers. comm, Mikko Huokuna, Finnish Environment Agency).
The freeze-up ice-jam flood forecasting system is a combination of hydrological and hydrodynamic river ice models. It produces several forecasts based on different meteorological and hydrological forecasts and by using selected ranges for parameters controlling ice cover formation. The model runs in real-time, providing the latest information about ice cover formation on the river.
3.2. Stochastic Modelling System for the Saint John River, New Brunswick
Freeze-up ice-jam flood forecasting capabilities have also been developed for the Saint John River in Atlantic Canada [
20]. The Saint John River freeze-up ice-jam flood forecasting system uses a stochastic modelling approach to generate hundreds of potential backwater level profiles under various flow and ice conditions, using variables and parameters drawn from frequency distributions. The RIVICE hydrodynamic model is used to mimic the river ice processes, which include frazil ice production, the transport of slush ice, juxtapositioning of slush-ice pans to extend the ice cover in the upstream direction, shoving to thicken the ice cover and the formation of hanging dams. An important boundary condition at the upstream end of the model domain is the water discharge. The flows stem from the MESH hydrological model that was developed for the Saint John River, implemented for freeze-up and mid-winter ice-jam flood forecasting [
20] and spring breakup ice-jam flood forecasting [
21].
Within a Monte Carlo analysis (MOCA) framework, the modelling can simulate hundreds of ice-jam backwater level profiles yielded from simulations using input from a range of randomly selected parameters and boundary conditions. Hydraulic and river ice parameters and ice-jam toe locations are selected from uniform distributions and discharges and ice volumes stem from extreme value distributions (generalized extreme value and gamma distributions, respectively). MESH hydrological model outputs (3-day daily forecasts) are then used to constrain the distribution for discharge. The maximum and minimum range from the 3-day daily forecast are used to select the hundreds of discharge values for the stochastic framework. The volume of ice, also an influential boundary condition, can be extracted from an extreme value distribution. That study also used stochastic processes to simulate freeze-up conditions along the Saint John River. From that study, a cumulative distribution was developed to select the total volume of ice that could accumulate in a freeze-up ice jam for a particular toe location. Based on the toe location, random values of the ice volumes were selected from the distribution.
The stochastic modeling framework creates an ensemble of backwater level profiles as shown in
Figure 2. The ensembles can be summarized using profiles of the 5th, 50th, and 95th percentiles. The figure also includes the maximum water level that occurred in hindsight (green dot), which lies between the 50th and 95th percentile profiles, indicating a successful forecast of the ice-induced water level that occurred.
3.3. Stochastic Modelling System for the Churchill River, Labrador (Adapted from [22])
The Churchill River Flood Forecasting System (CRFFS) is an automated, operational flood forecasting system developed for the Churchill River in Labrador, Canada. The system predicts flows on the river using the hydrological model HEC-HMS and predicts water levels using the hydraulic models HEC-RAS (for open water) and RIVICE (for ice conditions). The forecasting system was developed using 4DM’s (
http://www.4dm-inc.com/; accessed on 10 September 2024) HydrologiX software as the backbone for the system, which gathers a wide variety of near real-time or forecast information from several different sources to generate a forecast of the river conditions. The near-real-time and forecast information includes forecast temperature and precipitation data from Environment and Climate Change Canada; near-real-time water level, water temperature, and flow data on the Churchill River and tributaries from both the Water Survey of Canada (
https://wateroffice.ec.gc.ca/, accessed on 10 September 2024) and the Water Resources Management Division of the Government of Newfoundland and Labrador (
https://www.gov.nl.ca/ecc/waterres/, accessed on 10 September 2024); ice thickness and ice coverage information from C-Core, near-real-time generating station outflows from Nalcor (
https://nlhydro.com/, accessed on 10 September 2024); and forecast tidal levels on Lake Melville from the Department of Fisheries and Oceans Canada (
https://www.dfo-mpo.gc.ca/, accessed on 10 September 2024). All the data are stored in a database in the system for future reference. Some of the data are used as inputs to the forecasting system, while other data are used to check the quality of the forecast on an ongoing basis.
The cycle of the freeze-up ice-jam flood forecast component of the system begins with the open water state in the fall prior to freezing conditions. Forecasted flows from the hydrological model are transformed into water levels using rating curve tables, which are defined using the open-water hydraulic model. Before the model cycle progresses to the ice formation state in autumn, the system starts collecting and verifying water temperature data from temperature sondes against threshold values that initiate ice formation modelling in the river ice hydraulics model. The retrieval of water temperature data is currently set to begin on 1 November, but this can be modified in the CRFFS configuration file. Water temperature thresholds are set to just above 0 °C based on a review of historical water temperature and freeze-up data. Once the water temperatures drop below the temperature threshold values, freeze-up modelling commences and the CRFFS no longer runs in open-water mode but continues to operate under the freeze-up state.
Freeze-up is simulated in the river ice hydraulics model by generating ice from the heat loss from the water to the freezing air temperatures (forecasted). The potential ice jam toe locations are restricted to only the reach posing a high flood risk, as any jams outside of this area will not impact any of the communities on the Churchill River. Once the CRFFS is forecasting in the freeze-up state, the system retrieves the ice coverage data and checks the coverage against a threshold condition of 50%. Once the threshold is exceeded, the forecast model cycle moves into a stable winter ice state where the river ice hydraulic model is used to simulate a stable intact ice cover.
Depending on the season, the flow forecast is converted to water levels at several locations on the Churchill River using either the open water forecasting model or the ice-affected forecasting model. The forecast water levels at key locations are then automatically compared by the forecasting system against reference levels at those key locations at which flooding is anticipated to start. If the forecast water levels are higher than the reference levels, the system automatically sends warnings to the Government of Newfoundland and Labrador. An example of such a comparison is given in
Figure 3. Reference threshold levels include the 1:20 AEP (annual exceedance probability) and 1:100 AEP levels; the highwater marks recorded during the 2012 and 2017 ice-jam flood events; and the left, right, and low bank point levels. An ensemble of forecasted backwater level profiles produces the 10th, 50th, and 90th percentile levels. The hydrograph of the observed water levels recorded until 5 December 2023 by the English Point gauge on the Churchill River are plotted for comparison with the reference thresholds. Erratic variations in water levels began at approximately midday on 4 December 2023, pointing to the consolidated ice cover reaching the gauge. At times, the water level elevations spike to exceed various flood thresholds (e.g., low bank point on 4 December 2023 and 100-year flood on 5 December 2024), but only temporarily, for the water levels do trend within the 10th to 90th percentile range of the forecasted ice-jam flood levels.
3.4. Machine Learning Extension for the Athabasca River, Alberta (Adapted from [23,24])
In the context of freeze-up ice-jam flood forecasting, machine learning refers to the use of algorithms and statistical models that enable computers to learn from historical data and make predictions about future events. Machine learning involves training artificial intelligence (AI) systems on large datasets containing information such as weather patterns, water levels, and ice conditions during river freezing. These AI systems can identify complex relationships between variables and develop predictive models for freeze-up ice-jam flood forecasting. By analyzing past occurrences of ice-jam floods or large amounts of data produced from other modelling systems, machine learning algorithms can learn to recognize patterns and make predictions about when and where future events are likely to occur. This enables the development of rapid warning systems that can alert authorities and communities in a timely manner, allowing them to take proactive measures to mitigate the impacts of ice-jam flooding.
Machine learning offers several advantages over traditional methods (e.g., empirical, statistical, or numerical) for forecasting freeze-up ice-jam floods. They can provide more accurate predictions by learning complex patterns in data. Machine learning models are well-suited to handle non-linear interactions between variables and adapt to changing river ice conditions or shifts in fluvial geomorphological settings. As datasets increase, machine learning algorithms can scale up easily, making them suitable for long-term forecasting applications. Real-time sensor data and weather forecasts can be used to train machine learning models, enabling the rapid prediction of ice-jam flood events as they occur during river freezing. Machine learning-based approaches are cost-effective and complement extensive field measurements or numerical modeling efforts. Modern algorithms provide insights into which variables most influence predictions, allowing for a better understanding of underlying processes. Combining multiple machine learning models can further improve forecasting accuracy and robustness. By integrating with various data sources like weather forecasts, satellite imagery, and social media feeds, machine learning-based approaches can provide a more comprehensive understanding of ice-jam flooding during freeze-up.
It is also important to note some shortcomings when used machine learning is used to forecast freeze-up ice-jam floods. Machine learning algorithms can be sensitive to noisy (e.g., highly fluctuating water levels as consolidated ice cover forms) or missing data (e.g., due to gauge failures), which may lead to inaccurate predictions. The models require large amounts of high-quality training data, which may not always be available in remote or under-resourced areas. Overfitting and underfitting are common issues that can occur when such algorithms are trained on limited datasets. The interpretability of complex machine learning models can be challenging, making it difficult to understand the underlying relationships between variables (e.g., the relationship between the rate of frazil ice production forming an ice cover and the resulting backwater levels). Machine learning approaches often rely heavily on historical data, which may not accurately represent future events or changes in river ice conditions. Additionally, machine learning models may struggle with handling rare and extreme events like severe ice-jam floods, as they are trained on more common patterns in the data. Such data may have also been filtered to remove such “outliers”.
Machine learning algorithms are increasingly being utilized to predict river ice phenomena. One such method for ice-jam flood prediction is currently being developed for a reach along the Athabasca River near Fort McMurray [
23,
24]. The method combines decision tree regressors (DTRs) with adaptive boosting (AdaBoost) regressor machine learning algorithms. A DTR is a type of machine learning algorithm that functions like a flowchart, where each step (or “node”) asks a question about the data and splits it into smaller groups based on the answer. The goal is to find the best way to predict an outcome by asking questions and narrowing down the possibilities until a final prediction is reached, which in our case is a forecasted ice-jam flood level. AdaBoost combines simpler models to create a new, more accurate model by giving each model a “weight” based on how well it performed. It uses these weights to amplify the strengths and minimize the weaknesses of each model. To forecast freeze-up ice-jam floods, the DTR creates multiple simple branches of the decision tree that predict flood levels based on different factors such as ice production and water levels. AdaBoost then takes these individual branches and combines them into a single, more accurate model by giving each branch a “weight” based on its performance.
A series of DTR models were trained using different subsets of available data features, including river flow rates, ice cover extent, and weather forecasts. Each tree was constructed by partitioning the feature space based on the most informative splits, allowing complex relationships between variables to be captured in a non-linear manner. AdaBoost was employed as an ensemble method to combine multiple DTR models into a single, more robust predictor. By iteratively reweighting the training data and updating model parameters, AdaBoost effectively identified the most important features for predicting ice-jam flood levels while reducing overfitting.
Shapley additive explanation (SHAP) was applied to identify the most influential parameters driving ice-jam flooding. SHAP assigns a value to each feature based on its contribution to the predicted outcome, allowing the relative importance of different variables in predicting flood levels to be quantified and visualized. Data from a stochastic modeling framework [
7] were used for training and testing purposes. The combined DTR-AdaBoost model was trained using 80% of available data for training and evaluated using the remaining 20%. The results showed that this approach achieves high skill in predicting ice-jam flood levels.
Insights into which features were most influential were gained by applying SHAP to the trained model. The results reveal that river flow rates and ice production play the most critical roles in determining ice-jam flood levels, with higher flows and volumes of ice accumulating in ice jams influencing the likelihood of flooding the most.
This approach has the potential to effectively leverage the strengths of different machine learning algorithms to develop robust and accurate freeze-up ice-jam flood forecasting systems. The resulting insights into the most influential parameters driving ice-jam flooding enabled more informed decisions for mitigating impacts on communities along ice jam-prone river reaches.
3.5. Comparison and Recommendations
Each method has its strengths and weaknesses, making it essential to consider the specific application and data availability when choosing an ice-jam flood forecasting approach. A deterministic-only modelling system is well-suited for rivers with relatively simple flow dynamics, while a stochastic modelling approach is more suitable for rivers with complex or uncertain flows. A machine learning extension offers an attractive combination of deterministic and stochastic approaches, allowing for more accurate predictions and better handling of unknowns. However, it requires significant computational resources and high-quality training data.
For freeze-up ice-jam flood forecasting, we recommend using a hybrid approach that combines the strengths of both deterministic and stochastic methods with machine learning algorithms. This allows for more accurate predictions while accounting for uncertainty and unknowns. Each method has its relative strengths and weaknesses, making it essential to consider the specific application and data availability when applying a freeze-up ice-jam flood forecasting approach.
A number of methods can be implemented to improve the computational efficiency of coupled hydrological–hydraulic modelling systems for freeze-up ice-jam flood forecasting. Parallel processing techniques in which the computational load is distributed across multiple CPU cores and GPUs, or even distributed computing architectures, can shorten computation times, particularly for ensemble forecasting. To optimize computational efficiency while maintaining accuracy, it may be possible to simplify the model structure by reducing variables, equations, and dimensions. Pre-processing and post-processing can be adapted to help manage computational load. Machine learning algorithms can be incorporated to enhance the forecasting accuracy and reduce the need for extensive simulations [
24].
4. Modelling River Freeze-Up Ice Processes (Adapted and Summarized from [25])
The river freezing processes simulated in RIVICE are depicted in
Figure 1 and described below.
During freeze-up, an ice cover that can form an ice jam relies on two primary sources of ice. The first source is frazil ice, which forms in the river when the air temperature drops below freezing, causing heat to be transferred from the river water to the atmosphere, lowering the water temperature slightly below 0 °C to supercool it (see ‘A’ in
Figure 4). The resulting frazil crystals cluster into flocs and then into slush pans that float to the surface and drift downstream to the leading edge of the ice cover. The second source is the inflow of ice (marked as ‘B’ in
Figure 4). This represents ice blocks that have broken off from upstream ice sheets or border ice, or additional slush pans formed from upstream frazil ice. This ice floats downstream at the river’s average flow speed until it reaches the leading edge of the downstream ice cover.
Once the ice reaches the leading edge, the ice accumulated in the ice jam can either shove or juxtapose. Shoving causes the ice cover to retract downstream (marked as ‘C’ in
Figure 4), which thickens the existing ice cover as it telescopes further in the downstream direction. Shoving happens when the combined external forces on the cover—the thrust of the flowing water against the leading edge
FT, the weight of the ice cover in the sloping direction
FW, and the drag force on the underside of the ice cover by the flowing water
FD—surpass the ice cover’s internal resistance
FI and the frictional force along the river banks
FF, i.e.,
FT +
FW +
FD >
FI +
FF. The frictional force and the thickening of the ice cover distribute longitudinal forces along the ice cover’s thickness. Shoving continues until
FT +
FW +
FD <
FI +
FF, at which point the ice cover progresses upstream (marked as ‘D’ in
Figure 4) through a process called juxtapositioning. The slush pans accumulate at the leading edge, stacking up against each other to extend the ice cover upstream. As more ice accumulates, the balance of forces anywhere along the juxtapositioned ice cover may shift again for the ice cover to shove again.
Ice under the cover can erode and be transported downstream as ice in transit. If the average flow speed drops below a certain threshold value
vdep, the ice will deposit on the underside of the ice cover (marked as ‘E’ in
Figure 4). If the average flow velocity underneath the ice cover increases and exceeds a threshold value
ver, the ice will erode from the underside (marked as ‘F’ in
Figure 4).
The roughness of the riverbed and the underside of the ice cover are crucial parameters controlling the hydraulics of the flow and ice regimes. Bed roughness is a constant value represented by Manning’s coefficient, while ice cover roughness is a function of ice cover thickness. Important boundary conditions include the upstream discharge of the water entering the modeled stretch of the river, the downstream water level elevation where the water exits the stretch, and the location of the ice-jam lodgement.
5. Stochastic Modelling for Freeze-Up Ice-Jam Flood Forecasting
The river ice hydraulics model can be integrated into a Monte Carlo analysis (MOCA) framework to facilitate automated, multiple simulations. This allows the model to be executed hundreds of times, with each simulation having a unique set of parameters and boundary conditions. These values are randomly drawn from probability density functions within specified ranges (uniform distribution) or location, scale, and shape factors (extreme value distribution).
Uniform distributions are generally implemented for parameters or boundary conditions where there is no prior knowledge about the shape of the probability density function. However, for certain boundary conditions such as flows and water levels, historical data are used to construct extreme value distributions such as Gumbel and generalized extreme value (GEV) functions.
The MOCA is depicted in
Figure 5. It shows histograms representing probability frequency distributions of the boundary conditions: upstream inflow
Qu/s, downstream water level elevation
Wd/s, location of the consolidated ice cover toe
x, and the inflowing volume of rubble ice reaching the ice cover front
Vice.
Multiple model runs are executed with parameter and boundary condition values randomly drawn from the probability frequency distributions. This results in an ensemble of backwater level profiles. This distribution can be compared to the stage frequency distribution derived from observed values. If the simulated and observed stage frequency distributions do not match, the histograms of the input parameters and boundary conditions (generally Vice) are adjusted, and multiple simulations are carried out again within the Monte Carlo framework. This process is repeated until there is a reasonable agreement between the simulated and observed stage frequency distributions. Once this point is reached, the stochastic modeling system is considered calibrated.
Once the stochastic modeling framework is calibrated, it can be utilized for forecasting purposes. As the freeze-up ice cover approaches the flood risk area and a potential freeze-up ice-jam flood event draws near, the ranges on boundary conditions become more precise, allowing the boundary condition distributions to be constrained (see
Figure 6). The confidence bands of the resulting distributions of the backwater profiles become narrower, increasing the certainty of flood level exceedances. Depending on the probability of exceeding flood water levels, flood advisories or warnings can be issued.
6. Freeze-Up Ice-Jam Flood Forecasting Example—The Exploits River
There are several requirements for freeze-up ice-jam flood forecasting. Firstly, a river ice model is needed to generate frazil ice, which accumulates at a lodgement to form an ice cover and an ice jam. Secondly, a hydrological model is required to predict flows, although this aspect of the forecasting will not be covered here and the reader is referred to Lindenschmidt [
7] for more detailed information. Lastly, data are required to drive the models, including meteorological and hydraulic data. Water level elevations and remote sensing imagery are useful for the model calibration of backwater level elevations and the progression of the ice cover. The coupling of a hydrological model with a river ice hydraulics model allows for a more comprehensive simulation of the hydrological–hydraulic processes involved in freeze-up ice-jam flooding. Such a coupling can simulate the interaction between water flow, ice cover, and fluvial geomorphology, although the coupling assumes that the ice jam lodges at a specific location along the river channel, which may not always be the case. Incorporating remote sensing data into the hydrological–hydraulic model coupling can improve the accuracy of the hydrological and hydraulic models by providing ground truth information on ice cover and flood extents. Drawing on remote sensing data to support the modeling process can enhance the predictive capabilities of freeze-up ice-jam flood forecasting systems. Additionally, remote sensing data can help reduce uncertainty in model predictions by providing a more comprehensive understanding of the hydrological–hydraulic processes involved in river freezing.
This example of ice-jam flood forecasting focuses on the forecasting of freeze-up ice jams along the Exploits River in Atlantic Canada, where freeze-up ice jamming significantly impacts many rivers. Two freeze-up ice-jam flood forecasting approaches are discussed: the first approach involves predicting the extent of the ice cover during river freezing, while the second employs an ensemble method to determine backwater flood level elevations.
The Exploits River is located in central Newfoundland with the river basin spanning an area of about 8000 km
2, with an upper subbasin of about 5000 km
2 and a lower subbasin of approximately 3000 km
2 (see
Figure 7). This basin has two dams: the Millertown Dam and the Goodyear Dam. The community of Badger, situated along the stretch between the two dams, faces a high flood risk from freeze-up ice jamming. From 2010 to 2019, the average annual outlet flows from these two dams were 155 m
3/s and 238 m
3/s, respectively. From 2000 to 2022, February was the coldest month, with an average air temperature of −8.2 °C and cumulative freezing degree days ranging from 522 to 1250 °C-days by the end of March. The average annual total precipitation for the same timeframe was 1118 mm.
The river is heavily regulated, as evidenced by the outflow from the Millertown Dam and the discharge at Badger (see
Figure 8), whose gauge is located 51.3 km downstream of the dam gauge. Flows generally increase in early fall (September/October) but, through regulation, the higher streamflows of the river in the lower subbasin are held back until late fall (November/December) to meet higher power demand. Although spring (April/May) flows are higher, they are open water flows and do not create the same flood severity as flows during freezing with the presence of an ice cover. In this case study, we are particularly interested in the ice cover formation along the lower subbasin’s reach during the 2018–2019 winter season and the freeze-up ice jamming at Badger which typically occurs in February.
The river ice model was first simulated for open water flows to calibrate the bed roughness coefficient. A longitudinal profile of the model is shown in
Figure 9, indicating the model domain between the Millertown Dam and the Goodyear Dam, the location of the gauges at Badger and Charlie Edwards Point, and the location of Badger Rough Waters, a particularly steep section of the river with many riffles (see photo in
Figure 10).
In December 2018, a lake ice cover formed between Charlie Edwards Point and the Goodyear Dam, in the reservoir established by the dam. A consolidated ice cover was then simulated by the river ice model by generating frazil ice during freezing conditions, which lodged at the reservoir ice cover at Charlie Edwards Point (starting on 28 December 2018) and extended upstream to reach Badger by 2 February 2019. A longitudinal profile of the consolidated ice cover on 2 February 2019 is shown in
Figure 11. The simulated ice cover was slightly further upstream than what was observed, and the simulated water level elevation was slightly underestimated when compared to the recorded maximum elevation attained that winter season at the Badger gauge. Adjusting the porosity of the ice cover and the rate of heat transfer from the open-water surface to the freezing air were found to be the most influential parameters and were adjusted to provide the optimum fit considering both the ice cover extent and the maximum water-level elevation attained at Badger. More details on the calibration of the model can be obtained from Lindenschmidt et al. [
7].
The first type of freeze-up forecasting is to predict the extent of the ice cover (domain is indicated by “ice-cover extent forecast” in
Figure 9). The model was first calibrated by adjusting the most impactful parameters: the porosity of the ice cover and the heat transfer coefficient. A total of 40 days of freezing were required for the ice cover to extend from Charlie Edwards Point to Badger. Space-borne remote sensing imagery was extensively used to track the ice cover (top panel of
Figure 12). C-Core provided a classification of the consolidated or non-consolidated ice cover (bottom panel of
Figure 12). More details on the calibration can be obtained from Lindenschmidt [
7].
After the model was calibrated for ice cover extent, the model was then used to forecast upcoming ice cover extents. Forecasted air temperatures and precipitation and anticipated discharges from the Millertown Dam were used to predict discharges at Badger (for the next three to ten days). The forecasted air temperatures were also required to predict the amount of ice generated to extend the ice cover in the upstream direction. Further details on this forecasting approach are provided in Lindenschmidt [
7].
Once the ice cover extent reached Badger, the second forecasting approach was implemented, which involved predicting the backwater level elevations at the Badger gauge. Only the reach at Badger is used for this forecasting (domain is indicated by “backwater level forecast” in
Figure 9), with the toe of the ice jam located along Badger Rough Waters. In this case, a distribution of the volume of ice generated and accumulated in the ice jam was utilized, not the frazil ice production, as was the case for the first forecasting approach. Many simulations were carried out (see [e] in
Figure 13), with each simulation’s input values chosen randomly from distributions of all parameters and boundary conditions (see [a], [b], [c], and [d] in
Figure 13) to create an ensemble of longitudinal profiles of backwater level elevations (domain inset location indicated in
Figure 9). The results of these simulations can be summarized using percentile profiles (see [f] in
Figure 13), which were then compared to the return periods of the observed values (see [g] in
Figure 13) recorded at the gauge at Badger. This method can also be used to create hazard maps and risk maps by extrapolating these water levels into the floodplain.
When an event is imminent and more confidence can be acquired in the forecasted flows (from hydrological modelling output) and ice volumes (from remote sensing data), we can constrain the distributions of flow and ice volumes to the ranges of these boundary conditions expected to occur within the next three to ten days (see [a], [b], and [c] in
Figure 14). The same probability for the ice-jam toe locations (see [d] in
Figure 14) remains unchanged. Again, many simulations are carried out (see [e] in
Figure 14) to produce an ensemble of longitudinal profiles of backwater level elevations at Badger (domain inset location indicated in
Figure 9). The ensemble can be summarized using the quartiles and median of the ensemble (see [f] in
Figure 14). A comparison of the actual water level elevation that was attained during the event (see [g] in
Figure 14) provides an indication of the skill of the forecast. Interestingly, the maximum water level elevation that was attained for this event almost matched the median of the ensemble, indicating a successful forecast.
Two forecasting methods have been presented here, as shown in
Figure 15, ice cover extent forecasting and backwater level forecasting. The two may be combined into a single approach; however, this comes with its own set of challenges. For one, it requires more computational time, which may not be feasible if daily forecasts are required in an operational context. One means of reducing the computational time is to leverage the correlation between the amount of ice produced from freezing upstream of Badger to the water level elevations attained at the Badger gauge (see
Figure 16). However, there is much scatter within the relationship, leading to a significant amount of uncertainty, which may reduce the skill of the forecasting. Balancing accuracy with computational efficiency is a key consideration when developing forecasting systems.
Another consideration, as we move forward in a changing climate, is that warmer conditions could affect the full distribution of the volume of ice being generated. Future patterns of precipitation may also shift distributions of upstream flows and downstream water level elevations.
7. Requirements for a Freeze-Up Ice-Jam Flood Forecasting System
Several key components are required for the successful development of freeze-up ice-jam flood forecasting. Real-time data collection is required to accurately predict the development of an ice jam, and real-time data on water temperature, flow rate, and other relevant factors are necessary. These data can be collected through a variety of methods such as sensors, gauging stations, or remote sensing technologies. For example, sensors placed along the river can measure the water temperature and flow rate at different locations in real time. Gauging stations can also provide information on water levels and discharges. Remote sensing technologies in both visible and microwave spectrum regions can be used to monitor ice cover extent.
In addition to real-time data collection, historical data on past ice jam events should also be analyzed to identify patterns and trends that may inform future forecasts. This can include information on the timing and duration of previous ice jams, as well as any associated flood events or damages. By analyzing historical data, it is possible to develop a better understanding of how ice jams form and evolve over time, which can help inform future forecasting efforts.
The implementation of numerical models is necessary to simulate the behavior of an ice jam under different meteorological, hydrological, and hydraulic conditions. These models use numerical algorithms to solve equations that describe the behavior of ice jams based on input parameters such as water temperature and flow rate.
An easy-to-use interface for displaying real-time data and forecasts can be helpful for operators and other stakeholders to quickly understand the status of the consolidated ice covers and ice jams and make informed decisions about potential risks or mitigation measures. This interface should provide clear visualizations of water levels and ice cover extents.
A system that automatically triggers alerts when certain conditions are met can help ensure timely response to potential ice jam events. For example, if certain thresholds are exceeded or conditions change drastically, the alert system should trigger an alarm to notify operators of the potential for ice-jam flooding.
The freeze-up ice-jam flood forecasting system should be integrated with other relevant systems, such as meteorological forecasting systems and hydrological models, to provide a comprehensive view of the conditions occurring within the river basin. This integration can help ensure that operators have access to all the information they need to make informed decisions about potential flood risks or mitigation measures.
Lindenschmidt et al. [
28] report on elements and processes required for the development of a spring breakup ice-jam flood forecasting system. In this paper, we have addressed those required for autumn freeze-up ice-jam flood forecasting systems. Breakup and freeze-up ice-jam floods refer to two distinct types of flooding events that occur when ice jams form in rivers during the process of either spring breakup or autumn freeze-up. The differences between these two systems lie in their underlying physical processes, data requirements, and forecasting approaches. By understanding these differences, more effective flood forecasting models that account for the unique characteristics of each type of event can be developed.
Spring breakup typically occurs in early spring or mid-spring in temperate regions. As snowmelt increases, water levels rise rapidly due to increased runoff. The increased air temperatures and solar irradiance also cause ice covers on rivers to weaken and eventually to break up. The broken-up ice pieces can accumulate at lodgements, causing the river waters to dam up (jam) and back up to potentially flood surrounding floodplains. Forecasting systems for spring breakup ice-jam floods rely heavily on observed data on the snowpack, forecasted data on air temperatures and precipitation, and historical and real-time data on water levels and flows. They rely heavily on the use of hydrological models to simulate snowmelt, runoff, and river stages based on weather forecast inputs and river ice models to capture the dynamics of ice jamming in the river channel. These models often require more complex representations of snowpack dynamics, including temperature-dependent melt rates and soil moisture interactions.
Freeze-up typically occurs from late November to early February in temperate regions. As air temperatures drop, rivers freeze over, and subsequent cold snaps can cause the ice cover to extend and jam, leading to rapid water level increases. Forecasting systems for freeze-up floods rely on air temperature forecasts and precipitation forecasts (to account for potential snowfall), as well as water temperature and river stage and flow data, historically and in real time. Again, hydrological and river ice hydraulic models are imperative to simulate runoff, river stages, and ice cover dynamics based on weather forecast inputs. However, models typically focus on the interaction between air temperatures, river flow, and ice growth/decay, with less emphasis on snowpack processes.
A key difference between the two ice-jam flood forecasting systems is that spring breakup involves snowmelt-driven runoff, while freeze-up is driven by cold temperatures. Spring breakup models typically rely on a combination of deterministic and probabilistic approaches to predict the timing and magnitude of peak flows. In contrast, freeze-up ice-jam flood forecasting needs to focus on capturing the complex interactions between atmospheric conditions, river flow, and ice dynamics. While both systems require air temperature forecasts, the importance of snowpack data is much higher in spring breakup forecasting. To account for uncertainty in both approaches, ensemble forecasting techniques can be employed, generating multiple forecasts using slightly different initial conditions or model parameters for each forecasting system. This allows forecasters to quantify the range of possible outcomes and provide probabilistic flood warnings. In addition, data assimilation techniques can be used to merge observed river stages with modeled predictions, providing a more accurate representation of current and future flow conditions. By incorporating real-time observations into the forecasting process, these approaches can help reduce uncertainty and improve forecast reliability.
Forecast horizons for spring breakup typically range from 1 to 5 days, as the timing of spring breakup is relatively well predicted. However, forecast horizons for freeze-up can be longer, from 3 to 10 days, as freeze-up events are often more predictable in terms of temperature and precipitation patterns.
Ultimately, effective spring breakup or freeze-up ice-jam flood forecasting requires a deep understanding of local hydrological processes, atmospheric dynamics, and ice cover behavior, as well as the ability to integrate multiple data sources and modeling techniques.
Hydro-meteorological data for freeze-up ice-jam flood forecasting is typically obtained from river gauges, hydroelectric power plants, and weather stations (e.g., precipitation and air temperature). Ice volume data can be extracted from satellite imagery, aerial photography, and field observations. Other inputs include weather forecasts and observations, fluvial geomorphological data, and archived freeze-up ice-jam histories. One needs to be aware of the limitations of these data sources. For instance, flow and water level data may be limited in spatial coverage, subject to measurement errors and biases, and affected by human activities (e.g., water withdrawals and dam operations). Forecasting outcomes may be inaccurate due to the limitations of remote sensing technologies, the coarse temporal and spatial resolution of the data, uncertainties and errors in weather forecasts, inaccurate and coarse representation of the river morphology, and incomplete or biased historical data. To mitigate these limitations and assure forecast accuracy and reliability, it is important to integrate multiple sources of data, calibrate models using historical data, and validate modelling exercises against real-time observations.
8. Uncertainty and Reliability of Freeze-Up Ice-Jam Flood Forecasting Systems
Uncertainty is an inherent component of the flood forecasting process. Understanding the sources of uncertainty and implementing mitigating strategies such as model calibration, data assimilation, and ensemble forecasting are essential to improving forecast reliability. By acknowledging and addressing these uncertainties, more accurate and reliable flood forecasts that better support decision-making in water resources management can be developed.
The choice of model formulation, including the physical laws used to describe river flow dynamics, can introduce significant uncertainties. Uncertainty in model formulations can impact reliability and lead to inaccurate predictions of ice cover backwater levels. Calibrating and validating models using historical data can help reduce these uncertainties. The estimation of parameters such as roughness coefficients can also be uncertain due to limited data availability or inconsistent measurement techniques. Inaccurate parameter estimation can result in biased forecasts that may not accurately capture the dynamics of the system. In general, the quality of input data, such as precipitation, snowmelt, and water flows, can impact the reliability of forecast results.
Initial conditions used to initialize the model can introduce uncertainty in the forecasting process. Uncertainty in initial conditions can propagate through the modelling system, resulting in uncertain forecast outcomes. In addition, boundary conditions, such as upstream flows or climatic conditions, can also contribute to uncertainty. Incorporating real-time observations into the forecasting process through data assimilation techniques may improve forecast reliability by reducing uncertainty in initial conditions and boundary conditions. Generating multiple forecasts using different initial conditions, parameters, or models (ensemble forecasting) can provide a range of possible outcomes, allowing for more accurate predictions and better handling of unknowns.
9. Conclusions
An effective freeze-up ice-jam flood forecasting system requires real-time data collection and analysis, historical data analysis, ice jam modeling, user interface design, alert systems, and integration with other relevant systems. By combining these elements, operators can better understand the behavior of ice jams and make informed decisions about potential risks or mitigation measures to protect people and property along rivers. Key findings of this freeze-up ice-jam flood forecasting review include the demonstration of improved forecast accuracy compared to traditional methods through a combination of modelling, remote sensing, and graphical interface tools. Ensemble forecasting techniques, which combine multiple models or scenarios to generate a range of possible outcomes, result in more accurate and reliable forecasts. The integration of real-time data from various sources into the forecasting process can further enhance forecast accuracy and reliability. Additionally, hybrid approaches that combine deterministic and stochastic methods with machine learning algorithms show promise for improving forecast skill.
This review suggests that operational flood forecasting systems can enhancing decision-making through the integration of real-time data, ensemble forecasting techniques, and hybrid approaches into user-friendly graphical interfaces. By incorporating these advanced methods and tools into larger operating systems, freeze-up ice-jam flood forecast accuracy is likely to improve, enabling more informed decision-making for emergency response efforts. Improved forecast accuracy and reliability will enable better resource allocation for emergency response efforts, reducing economic losses associated with flood events.
Future directions in freeze-up ice-jam flood forecasting research include extending methods to integrate real-time data from various sources (e.g., weather stations, radar, satellite imagery) into the forecasting process, exploring and refining ensemble forecasting techniques that combine multiple models or scenarios to generate a range of possible outcomes, and investigating hybrid approaches that combine deterministic and stochastic methods with machine learning algorithms for improved forecast accuracy and reliability. Leveraging high-performance computing architectures (e.g., GPUs, distributed systems) to accelerate simulations and enable more complex modeling scenarios, developing data assimilation techniques that incorporate real-time observations into the forecasting process to reduce uncertainty in initial conditions and boundary conditions, and improving our understanding of uncertainty sources and quantifying their impact on forecast reliability using advanced statistical methods (e.g., Bayesian inference) are also key areas of focus. Additionally, investigating human–machine collaboration approaches that leverage expert knowledge and machine learning algorithms to improve forecasting accuracy and decision-making is crucial.
To improve freeze-up ice-jam flood forecasting, policies should be implemented that focus on enhancing public awareness by educating the public on ice-jam flood risks and the importance of preparedness through regular updates, emergency alerts, and community outreach programs. Establishing early warning systems that can detect changes in river flow and ice conditions will enable timely evacuations and minimize damage to infrastructure and property. Improving infrastructure resilience by upgrading flood-control structures (e.g., dams, levees) to withstand extreme weather events and ice-jam floods is crucial. International cooperation should be fostered by collaborating with neighboring countries and international organizations to share best practices, research findings, and expertise in managing ice-jam flood risks. Comprehensive emergency response plans should be developed, including evacuation procedures, emergency shelters, and communication protocols for effective disaster management. Regular assessments of river flow, ice conditions, and weather patterns should be conducted to identify areas prone to freeze-up ice-jam floods. Implementing ice-jam mitigation measures such as dredging, channel widening, or installing ice detection systems can help manage flood risks. Developing floodplain management plans that include zoning regulations, building codes, and emergency response procedures for areas prone to freeze-up ice-jam floods is essential. Collaboration with local communities, emergency responders, and other stakeholders is necessary to develop these policies and strategies. Conducting cost–benefit analyses of proposed policy changes or infrastructure upgrades ensures they are economically viable and socially acceptable. Finally, developing training programs for emergency responders, community members, and policymakers on ice-jam flood risk management and response is vital.