Developing Collaborative Management Strategies for Flood Control and Drainage across Administrative Regions Using Game Theory
Abstract
1. Introduction
2. Study Domain and Conflicts of Interest
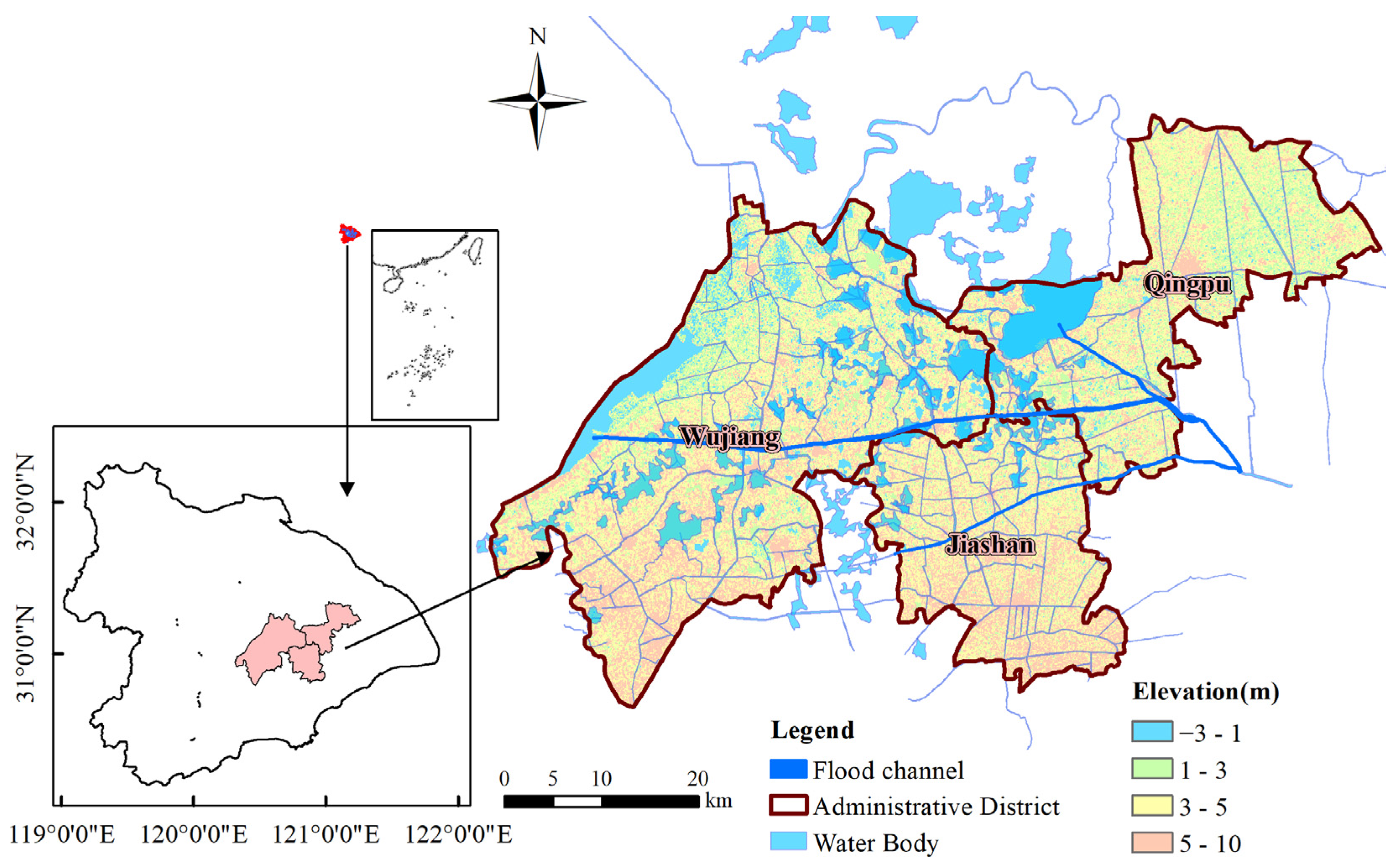
2.1. Study Domain
2.2. Conflicts of Interest for Flood Control and Drainage
3. Game Analysis
3.1. Game Model Scenario Assumptions
3.2. Analysis of the Game Stability Strategy
3.2.1. Strategy Stability in JQA
3.2.2. Strategy Stability in Wujiang
3.2.3. Strategy Stability in Wujiang and JQA
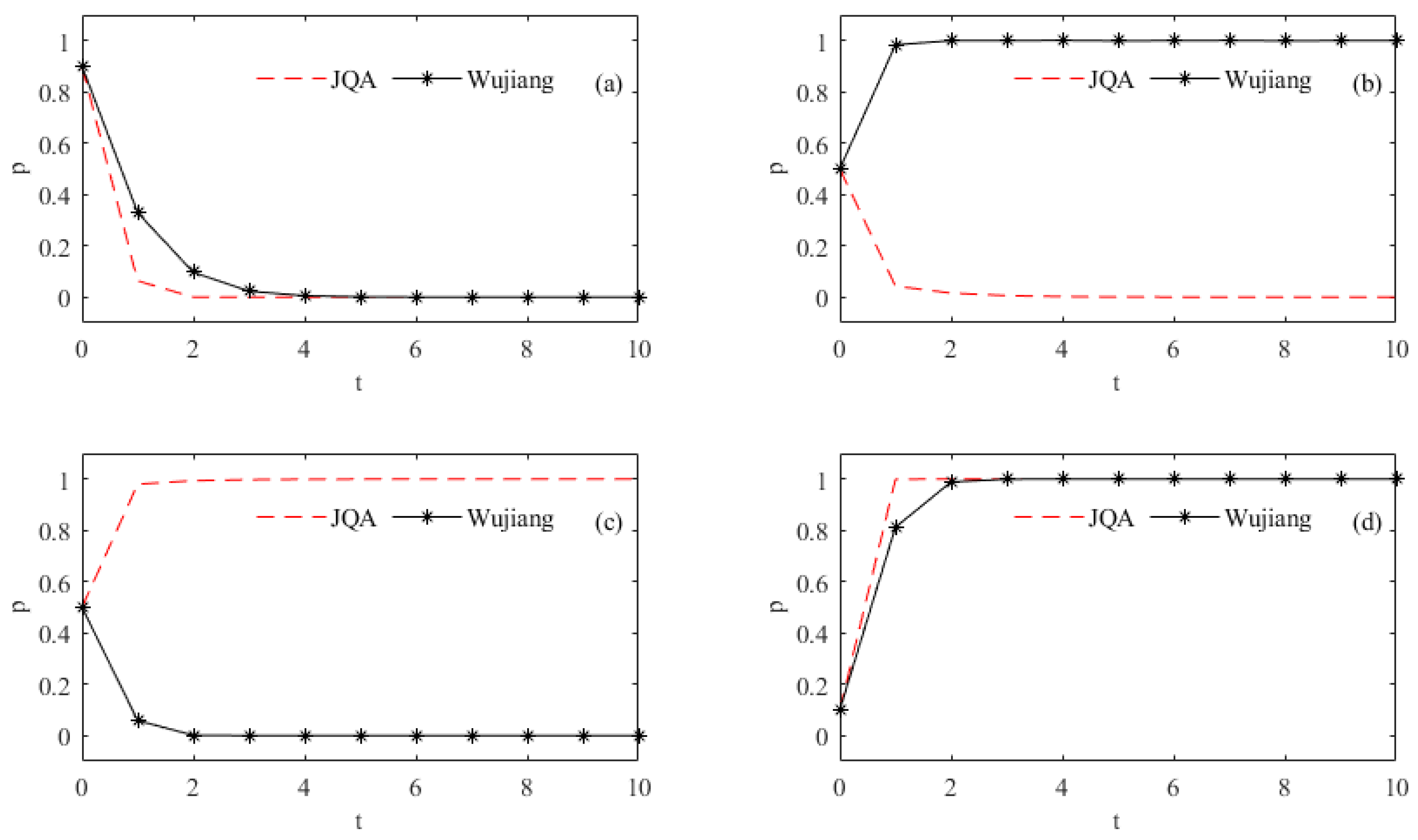
3.3. Simulation Analysis of the Strategy Evolution
4. Collaborative Governance Strategy
- (1)
- Unified planning and management of DZGIED, along with the coordinated integration of urban flood control and drainage planning within DZGIED
- (2)
- Enhance the reward and punishment mechanism to incentivize the cities in DZGIED to cooperate.
- (3)
- Introducing an internal equilibrium mechanism and a two-way compensation mechanism between cities.
5. Conclusions
- (1)
- Based on the game stability analysis, the strategy of the two parties in the game changes according to the strategy of the other. Five elements, namely the cost of conflict, the compensation of one party to the other, the additional benefits obtained by the two parties, the reward for the choices, and the punishment for the choices, are the main factors affecting the behavioral strategy of Wujiang and JQA.
- (2)
- The strategies of both parties will evolve towards those that are beneficial to themselves, thereby maximizing each party’s interest. To promote the game model towards a stable strategy (Reducing drainage capacity, Non-conflict), a reasonable two-way compensation mechanism and reward and punishment mechanism should be established. It can share the losses caused by the assumption of flood pressure upstream and alleviate the compensation pressure downstream.
- (3)
- The collaborative management strategy for flood control and drainage is proposed: for the external part, the agency of DZGIED is responsible for coordinating the conflicts; for the downstream and upstream, it should implement incentive and constraint policies with clear rewards and punishments; for the internal part, a two-way compensation mechanism should be established to compensate for the economic losses caused by the imbalanced capabilities of both parties.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Luo, Z.; Zuo, Q. Evaluating the coordinated development of social economy, water, and ecology in a heavily disturbed basin based on the distributed hydrology model and the harmony theory. J. Hydrol. 2019, 574, 226–241. [Google Scholar] [CrossRef]
- Jia, K.; Yuan, R. The impact of basin horizontal ecological compensation policies on carbon emissions: A case study of the Yangtze River economic Belt. Heliyon 2024, 10, e28858. [Google Scholar] [CrossRef] [PubMed]
- Wheeler, K.G.; Robinson, C.J.; Bark, R.H. Modelling to bridge many boundaries: The Colorado and Murray-Darling River basins. Reg. Environ. Chang. 2018, 18, 1607–1619. [Google Scholar] [CrossRef]
- Zhang, K. Study on Allocation Method of Flood Drainage Rights Based on Game Analysis. Ph.D. Thesis, Hohai University, Nanjing, China, 2020. [Google Scholar]
- Chen, S.; He, Y.; Tan, Q.; Hu, K.; Zhang, T.; Zhang, S. Comprehensive assessment of water environmental carrying capacity for sustainable watershed development. J. Environ. Manag. 2022, 303, 114065. [Google Scholar] [CrossRef]
- Huang, X.; Chen, X.; Huang, P. Research on Fuzzy Cooperative Game Model of Allocation of Pollution Discharge Rights. Water 2018, 10, 662. [Google Scholar] [CrossRef]
- Gorgoglione, A.; Crisci, M.; Kayser, R.H.; Chreties, C.; Collischonn, W. A New Scenario-Based Framework for Conflict Resolution in Water Allocation in Transboundary Watersheds. Water 2019, 11, 1174. [Google Scholar] [CrossRef]
- Bernauer, T.; Böhmelt, T. International conflict and cooperation over freshwater resources. Nat. Sustain. 2020, 3, 350–356. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, L.; Huang, C. A Tripartite Evolutionary Game and Simulation Analysis of Transportation Carbon Emission Reduction across Regions under Government Reward and Punishment Mechanism. Sustainability 2022, 14, 10562. [Google Scholar] [CrossRef]
- Kicsiny, R.; Varga, Z. Differential game model with discretized solution for the use of limited water resources. J. Hydrol. 2019, 569, 637–646. [Google Scholar] [CrossRef]
- Zhou, X.Y.; Zheng, B.; Khu, S.T. Validation of the hypothesis on carrying capacity limits using the water environment carrying capacity. Sci. Total Environ. 2019, 665, 774–784. [Google Scholar] [CrossRef]
- Tucker, C.M.; Hribar, M.Š.; Urbanc, M.; Bogataj, N.; Gunya, A.; Rodela, R.; Sigura, M.; Piani, L. Governance of interdependent ecosystem services and common-pool resources. Land Use Policy 2023, 127, 106575. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, J.; Feng, Z.; Li, S.; Cai, Y. Theoretical Framework for Sus-tainable Governance of Common-Pool Resource. J. Nat. Resour. 2012, 27, 1797–1807. [Google Scholar]
- Feng, J. Optimal allocation of regional water resources based on multi-objective dynamic equilibrium strategy. Appl. Math. Model 2021, 90, 1183–1203. [Google Scholar] [CrossRef]
- Fu, J.; Zhong, P.-A.; Xu, B.; Zhu, F.; Chen, J.; Li, J. Comparison of Transboundary Water Resources Allocation Models Based on Game Theory and Multi-Objective Optimization. Water 2021, 13, 1421. [Google Scholar] [CrossRef]
- Rogers, P. A Game Theory Approach to the Problems of International River Basins. Water Resour. Res. 2010, 5, 749–760. [Google Scholar] [CrossRef]
- Kucukmehmetoglu, M. An integrative case study approach between game theory and Pareto frontier concepts for the transboundary water resources allocations. J. Hydrol. 2012, 450–451, 308–319. [Google Scholar] [CrossRef]
- Wang, L.; Fang, L.; Hipel, K.W. Basin-wide cooperative water resources allocation. Eur. J. Oper. Res. 2008, 190, 798–817. [Google Scholar] [CrossRef]
- Shi, G.; Wang, J.; Dong, Z.; Zhang, Y. Pollution Prevention for Transboundary Watershed: Perspective from Cooperative Game Theory. J. Nat. Resour. 2015, 30, 549–559. [Google Scholar]
- Lin, N. Study on the Coordination Mechanism and Damage Assessment System of Domestic Transboundary Water Pollution Accidents. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2014. [Google Scholar]
- Roy, S.K.; Bhaumik, A. Intelligent Water Management:A triangular Type-2 Intuitionistic Fuzzy Matrix Games Approach. Water Resour. Manag. 2018, 32, 949–968. [Google Scholar] [CrossRef]
- Madani, K. Game theory and water resources. J. Hydrol. 2010, 381, 225–238. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, Z.; Botterud, A. An evolutionary game approach to an-alyzing bidding strategies in electricity markets with elastic demand. Energy 2011, 36, 3459–3467. [Google Scholar] [CrossRef]
- Lu, S.; Lian, Z.; Sun, H.; Wu, X.; Bai, X.; Wang, C. Simulating transboundary watershed water resources conflict. Resour. Policy 2021, 73, 102139. [Google Scholar] [CrossRef]
- Mirzaei-Nodoushan, F.; Bozorg-Haddad, O.; Singh, V.P.; Loaiciga, H.A. Analysis of long-term strategies of riparian countries in transboundary river basins. Sci. Rep. 2021, 11, 20199. [Google Scholar] [CrossRef]
- Biancardi, M.; Iannucci, G.; Villani, G. An evolutionary game on compliant and non-compliant firms in groundwater exploitation. Ann. Oper. Res. 2021, 318, 831–847. [Google Scholar] [CrossRef]
- Guo, L.; Wu, Y.; Huang, F.; Jing, P.; Huang, Y. An approach to complex transboundary water management in Central Asia: Evolutionary cooperation in transboundary basins under the water-energy-food-ecosystem nexus. J. Environ. Manag. 2024, 351, 119940. [Google Scholar] [CrossRef]
- Shen, J.; Gao, X.; He, W.; Sun, F.; Zhang, Z.; Kong, Y.; Wan, Z.; Zhang, X.; Li, Z.; Wang, J.; et al. Prospect theory in an evolutionary game: Construction of watershed ecological compensation system in Taihu Lake Basin. J. Clean Prod. 2021, 291, 125929. [Google Scholar] [CrossRef]
- Yuan, L.; Qi, Y.; He, W.; Wu, X.; Kong, Y.; Ramsey, T.S.; Degefu, D.M. A differential game of water pollution management in the trans-jurisdictional river basin. J. Clean Prod. 2024, 438, 140823. [Google Scholar] [CrossRef]
- Mahdevari, S.; Fazli Allah Abadi, A. A model based on the evolutionary game theory for implementing green mining principles in riverine sand and gravel resources. J. Clean. Prod. 2023, 428, 139501. [Google Scholar] [CrossRef]
- Liu, K.; He, S. Review and consideration of flood control and management practice in Taihu Lake Basin. Yangtze River 2024, 55, 9–17. [Google Scholar]
- Ma, K. Study on the Disaster Effects of Heavy Rain and Waterlogging Caused by Land Use/Cover Change: A Case Study of the Yangtze River Delta Eco-Green Integrated Development Demonstration Zone. Master’s Thesis, Shanghai Normal University Master of Science, Shanghai, China, 2021. [Google Scholar]
- Zhong, G.; Liu, S.; Hu, Z.; Zhang, X. Analysis of influence on region flood control due to polder waterlogging drainage in Yangcheng and Dianmao area. Yangtze River 2017, 48, 9–14. [Google Scholar]
- Zhang, K.; Shen, J. Research on China’s Drainage Rights Trading Management under the Quasi Market: Based on the Perspective of Evolutionary Game. J. Henan Univ. (Soc. Sci.) 2019, 59, 21–29. [Google Scholar]
- Hu, R. Analyse of the absurdity of the administration division and the river basin water pollution mending. Environ. Prot. 2006, 6, 65–68. [Google Scholar]
- Peng, K.; Dong, C.; Mi, J. Dynamic Research on the Collaborative Governance in Urban and Rural Black-Odorous Water: A Tripartite Stochastic Evolutionary Game Perspective. Systems 2024, 12, 307. [Google Scholar] [CrossRef]
| Parameter | Illustrate |
|---|---|
| q | The probability that JQA does not require Wujiang to limit its drainage capacity is q (0 < q < 1). |
| p | The probability that Wujiang will take the initiative to bear the regional flood pressure and limit its drainage capacity is p (0 < p < 1). |
| F1 | Conflict costs incurred by JQA due to conflicts. |
| F2 | The conflict costs incurred by the conflict caused by increasing drainage capacity in Wujiang. |
| M | The flood control benefit obtained by JQA due to Wujiang’s reduced drainage capacity is M. |
| x | Marginal benefits of unit drainage capacity change in Wujiang. |
| y | Marginal benefits of unit drainage capacity change in JQA. |
| Q | The drainage power of Wujiang to increase drainage capacity, and the drainage power obtained by JQA causing conflict. |
| B | Compensation to Wujiang when conflicts arise between JQA. |
| C | Wujiang increases drainage capacity to compensate for JQA. |
| G | Rewards from management agencies when cities in DZGIED adopt cooperative strategies (i.e., “Reducing drainage capacity” and “Non-conflict”). |
| T | Penalties from management agencies for non-cooperative strategies (i.e., “Increasing drainage capacity” and “Conflict”). |
| Wujiang Reduces Its Drainage Capacity (p) | Wujiang Increases Drainage Capacity (1 − p) | |
|---|---|---|
| JQA conflict (1 − q) | JQA: Wujiang: | JQA:
Wujiang: |
| JQA does not conflict (q) | JQA: M + G Wujiang: G | JQA:
Wujiang: |
| Balance Point | ||
|---|---|---|
| O (0,0) | ||
| A (1,0) | ||
| B (1,1) | ||
| C (0,1) | ||
| 0 |
| Balance Point | Scene | Symbol | Symbol | In Conclusion |
|---|---|---|---|---|
| (0,0) | , | + | − | ESS |
| , | + | + | Unstable | |
| , | − | ± | Saddle Point | |
| , | − | ± | Saddle Point | |
| (0,1) | , | + | − | ESS |
| , | + | + | Unstable | |
| , | − | ± | Saddle Point | |
| , | − | ± | Saddle Point | |
| (1,0) | , | + | − | ESS |
| , | + | + | Unstable | |
| , | − | ± | Saddle Point | |
| , | − | ± | Saddle Point | |
| (1,1) | , | + | − | ESS |
| , | + | + | Unstable | |
| , | − | ± | Saddle Point | |
| , | − | ± | Saddle Point | |
| none | + | 0 | Center |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shang, S.; Wang, L.; Guo, W.; Zhang, L.; Wang, Y.; Su, X.; Li, L.; Chen, Y. Developing Collaborative Management Strategies for Flood Control and Drainage across Administrative Regions Using Game Theory. Water 2024, 16, 2510. https://doi.org/10.3390/w16172510
Shang S, Wang L, Guo W, Zhang L, Wang Y, Su X, Li L, Chen Y. Developing Collaborative Management Strategies for Flood Control and Drainage across Administrative Regions Using Game Theory. Water. 2024; 16(17):2510. https://doi.org/10.3390/w16172510
Chicago/Turabian StyleShang, Shouwei, Leizhi Wang, Weijian Guo, Leilei Zhang, Yintang Wang, Xin Su, Lingjie Li, and Yuan Chen. 2024. "Developing Collaborative Management Strategies for Flood Control and Drainage across Administrative Regions Using Game Theory" Water 16, no. 17: 2510. https://doi.org/10.3390/w16172510
APA StyleShang, S., Wang, L., Guo, W., Zhang, L., Wang, Y., Su, X., Li, L., & Chen, Y. (2024). Developing Collaborative Management Strategies for Flood Control and Drainage across Administrative Regions Using Game Theory. Water, 16(17), 2510. https://doi.org/10.3390/w16172510






