Assessment of Human Errors in the Operation of the Water Treatment Plant
Abstract
1. Introduction
2. Materials and Methods
2.1. CREAM Framework
2.2. Use of Fuzzy Logic in CREAM
- -
- CV—crisp value–defuzzified value of fuzzy number,
- -
- x—element of the real set (R), x ∈ R,
- -
- μ(x)—membership function that assigns each element x ∈ R its degree of membership in the fuzzy set.
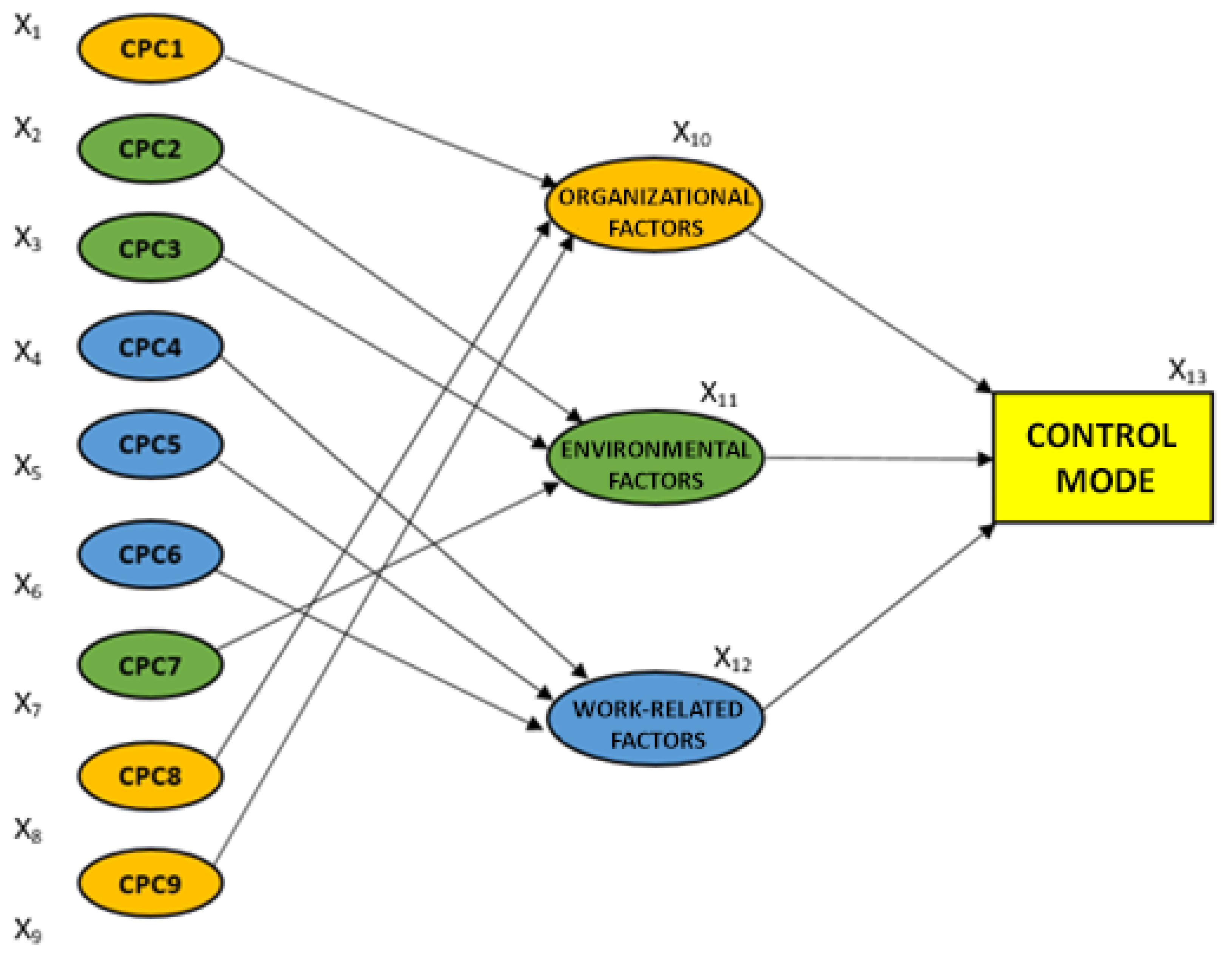
2.3. Use of Bayesian Networks in CREAM
- organizational factors–include training, experience, and skills of operators, organization, planning, supervision of work processes, enterprise administration, etc.,
- environmental factors–related to the work environment, e.g., lighting, noise, vibration, temperature, air humidity, ergonomics of the workplace,
- work-related factors–refer to the work process, e.g., length of shift, number of tasks to be performed simultaneously, characteristics of the task, and the stressful nature of the task.
2.4. Research Object
3. Results
4. Discussion
5. Conclusions
- The probability of making an error by the WTP operator varies in the range of 0.0005–0.0746 depending on the analyzed subsystem.
- The lowest average probability of making an error by the WTP operator occurs for the water treatment subsystem in the disinfection process (HEP WTSubS: D = 0.0122).
- Due to the nature of the operator’s work in the water treatment subsystem, where chemicals are used in the water treatment process and precise technological processes are performed, the operator is required to have high competence and care for the correct execution of tasks. The failure of this subsystem is mainly related to maintaining appropriate water quality and may pose a threat to the health or life of water consumers.
- The highest average probability of making an error by the WTP operator occurs for the water intake subsystem (HEP WISubS = 0.0148).
- Failures of the water intake, water pumping, or water storage subsystems are mainly related to maintaining the supply of an appropriate amount of water and may pose a threat to the continuity of its supply or maintaining appropriate hydraulic parameters of the network operation.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, W.; Song, Z. Review of studies on the resilience of urban critical infrastructure networks. Reliab. Eng. Syst. Saf. 2020, 193, 106617. [Google Scholar] [CrossRef]
- French, S.; Bedford, T.; Pollard, S.J.T.; Soane, E. Human reliability analysis: A critique and review for managers. Saf. Sci. 2011, 49, 753–763. [Google Scholar] [CrossRef]
- Zheng, X.; Bolton, M.L.; Daly, C.; Biltekoff, E. The development of a next-generation human reliability analysis: Systems analysis for formal pharmaceutical human reliability (SAFPH). Reliab. Eng. Syst. Saf. 2020, 202, 106927. [Google Scholar] [CrossRef]
- Żywiec, J.; Tchórzewska-Cieślak, B.; Rak, J. Safety of the Water Supply System from the System Operator Perspective. In Lecture Notes in Civil Engineering, Proceedings of the 18th International Conference Current Issues of Civil and Environmental Engineering Lviv—Košice—Rzeszów, CEE 2023, Rzeszów, Poland, 6–8 September 2023; Springer Nature: Cham, Switzerland, 2024; Volume 438, pp. 551–561. [Google Scholar] [CrossRef]
- Wu, S.; Hrudey, S.; French, S.; Bedford, T.; Soane, E.; Pollard, S. A role for human reliability analysis (HRA) in preventing drinking water incidents and securing safe drinking water. Water Res. 2009, 43, 3227–3238. [Google Scholar] [CrossRef][Green Version]
- Tang, Y.; Wu, S.; Miao, X.; Pollard, S.J.T.; Hrudey, S.E. Resilience to evolving drinking water contamination risks: A human error prevention perspective. J. Clean. Prod. 2013, 57, 228–237. [Google Scholar] [CrossRef]
- Dhillon, B.S. Human Reliability: With Human Factors; Elsevier: Oxford, UK, 1986. [Google Scholar]
- De Felice, F.; Petrillo, A. Human Factors and Reliability Engineering for Safety and Security. In Critical Infrastructures—Decision Making, Theory, and Practice; De Felice, F., Ed.; Springer International Publishing: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Dsouza, N.; Lu, L. A Literature Review on Human Reliability Analysis Techniques Applied for Probabilistic Risk Assessment in the Nuclear Industry. Adv. Intell. Syst. Comput. 2017, 495, 41–54. [Google Scholar] [CrossRef]
- Tao, J.; Qiu, D.; Yang, F.; Duan, Z. A bibliometric analysis of human reliability research. J. Clean. Prod. 2020, 260, 121041. [Google Scholar] [CrossRef]
- Williams, J.C. A data-based method for assessing and reducing human error to improve operational performance. In Proceedings of the IEEE Fourth Conference on Human Factors and Power Plants, Monterey, CA, USA, 5–9 June 1988; IEEE: New York, NY, USA, 1988. [Google Scholar] [CrossRef]
- Bello, G.C.; Colombari, V. The human factors in risk analyses of process plants: The control room operator model ‘TESEO’. Reliab. Eng. Syst. Saf. 1980, 1, 3–14. [Google Scholar] [CrossRef]
- US Nuclear Regulatory Commission. NUREG-1624: Technical Basis and Implementation Guidelines for a Technique for Human Event Analysis (ATHEANA); US Nuclear Regulatory Commission: Washington, DC, USA, 2000.
- Hollnagel, E. Cognitive Reliability and Error Analysis Method (CREAM); Elsevier Science: Amsterdam, The Netherlands, 1998. [Google Scholar] [CrossRef]
- Kirwan, B.; Gibson, H. CARA: A Human Reliability Assessment Tool for Air Traffic Safety Management—Technical Basis and Preliminary Architecture. In Safety of Systems, Proceedings of the 15th Safety-Critical Systems Symposium, Bristol, UK, 13–15 February 2007; Springer: London, UK, 2007. [Google Scholar] [CrossRef]
- Tu, J.; Lin, W.; Lin, Y. A Bayes-SLIM based methodology for human reliability analysis of lifting operations. Int. J. Ind. Ergon. 2015, 45, 48–54. [Google Scholar] [CrossRef]
- Li, D.; Li, L. Preliminary Study of Human Factor Reliability in Hydropower Station. Adv. Mat. Res. 2011, 422, 803–806. [Google Scholar] [CrossRef]
- Tavakoli, M.; Nafar, M. Modification of the FFTA method for calculating and analyzing the human reliability of maintenance groups in power transmission grids. Int. J. Syst. Assur. Eng. Manag. 2021, 12, 1221–1234. [Google Scholar] [CrossRef]
- Borgheipour, H.; Mohammadfam, I.; Narenji, M.A. Assessing and Comparing Human Errors in Technical operations in Petroleum Wells using Extended CREAM Technique. J. Occup. Hyg. 2017, 9, 132–141. [Google Scholar]
- Wang, X.; Zhang, W.; Pan, X.; Liu, T. Method for Crew Human Reliability Analysis Based on CREAM. In Advances in Human Error, Reliability, Resilience and Performance; Springer: Cham, Switzerland, 2019; pp. 225–234. [Google Scholar] [CrossRef]
- Guo, Y.; Sun, Y.; Yang, X.; Wang, Z. Flight Safety Assessment Based on a Modified Human Reliability Quantification Method. Int. J. Aerosp. Eng. 2019, 2019, 2812173. [Google Scholar] [CrossRef]
- Jin, J.; Li, K.; Yuan, L. A Fuzzy and Bayesian Network CREAM Model for Human Error Probability Quantification of the ATO System. In Proceedings of the 4th International Conference on Electrical and Information Technologies for Rail Transportation (EITRT), Qingdao, China, 25–27 October 2019; Springer: Singapore, 2020; pp. 567–576. [Google Scholar] [CrossRef]
- Akyuz, E.; Celik, E. A modified human reliability analysis for cargo operation in single point mooring (SPM) off-shore units. Appl. Ocean Res. 2016, 58, 11–20. [Google Scholar] [CrossRef]
- Sezer, S.I.; Akyuz, E.; Arslan, O. An extended HEART Dempster–Shafer evidence theory approach to assess human reliability for the gas freeing process on chemical tankers. Reliab. Eng. Syst. Saf. 2022, 220, 108275. [Google Scholar] [CrossRef]
- Zhou, Q.; Wong, Y.D.; Loh, H.S.; Yuen, K.F. A fuzzy and Bayesian network CREAM model for human reliability analysis—The case of tanker shipping. Saf. Sci. 2018, 105, 149–157. [Google Scholar] [CrossRef]
- He, C.; Söffker, D. Human reliability analysis in situated driving context considering human experience using a fuzzy-based clustering approach. In Proceedings of the 2021 IEEE 2nd International Conference on Human-Machine Systems (ICHMS), Magdeburg, Germany, 8–10 September 2021; IEEE: New York, NY, USA, 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Lin, Q.L.; Wang, D.J.; Lin, W.G.; Liu, H.C. Human reliability assessment for medical devices based on failure mode and effects analysis and fuzzy linguistic theory. Saf. Sci. 2014, 62, 248–256. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Kluska, J. Analytical Methods in Fuzzy Modeling and Control; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Zimmermann, H.J. Fuzzy Set Theory—And Its Applications; Springer: Dordrecht, The Netherlands, 2001. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Fuzzy Sets and Systems: Theory and Applications; Academic Press: Cambridge, MA, USA, 1980. [Google Scholar]
- Jensen, F.V. An Introduction to Bayesian Networks; UCL Press Ltd.: London, UK, 1996. [Google Scholar]
- Habier, D.; Fernando, R.L.; Kizilkaya, K.; Garrick, D.J. Extension of the bayesian alphabet for genomic selection. BMC Bioinform. 2011, 12, 186. [Google Scholar] [CrossRef]
- Nistal-Nuño, B. Tutorial of the probabilistic methods Bayesian networks and influence diagrams applied to medicine. J. Evid.-Based Med. 2018, 11, 112–124. [Google Scholar] [CrossRef]
- Tchórzewska-Cieślak, B.; Rak, J.; Szpak, D. Bayesian Inference in the Analysis of the Failure Risk of the Water Supply Network. J. KONBiN 2019, 49, 433–450. [Google Scholar] [CrossRef][Green Version]
- Bishop, C. Pattern Recognition and Machine Learning; Springer: Singapore, 2006. [Google Scholar]
- BayesFusion. Genie 3.0 Software. 2020. Available online: https://bayesfusion.com/2020/08/26/genie-3-0-released/ (accessed on 10 December 2023).
- Boryczko, K.; Szpak, D.; Żywiec, J.; Tchórzewska-Cieślak, B. The Use of a Fault Tree Analysis (FTA) in the Operator Reliability Assessment of the Critical Infrastructure on the Example of Water Supply System. Energies 2022, 15, 4416. [Google Scholar] [CrossRef]
- Żywiec, J.; Tchórzewska-Cieślak, B. Analysis of the impact of failures related to the operator’s actions on the functioning of the collective water supply system. In Problems of Reliability of Technical Systems: Theory and Applications; Oficyna Wydawnicza Politechniki Warszawskiej: Warsaw, Poland, 2021. (In Polish) [Google Scholar]
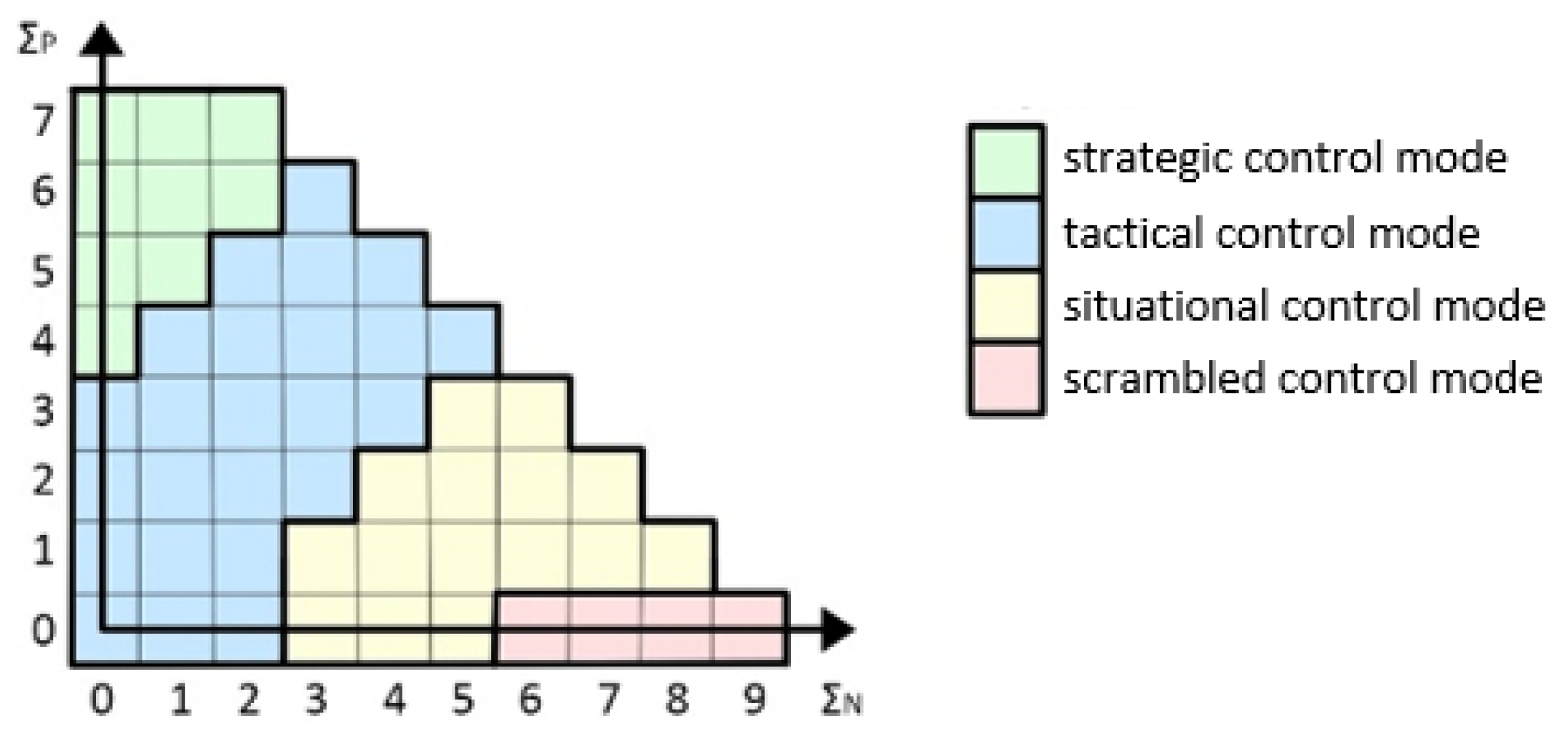


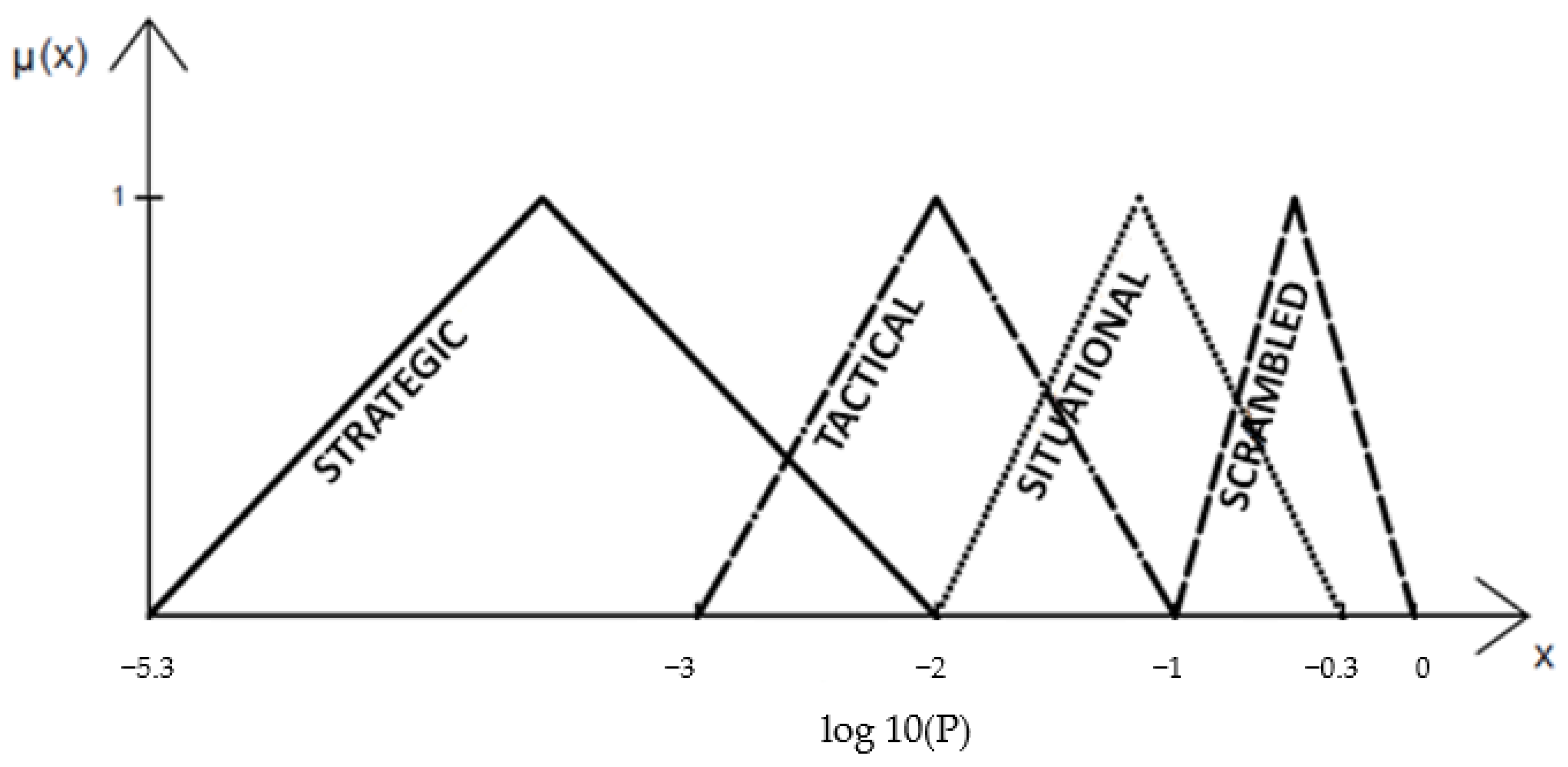
| Control Mode | Description | HEP Value |
|---|---|---|
| Scrambled (SC) | This mode characterizes situations in which the operator devotes little attention to the planning of subsequent actions or does not plan them at all. He takes action in a random, unplanned way. Most often, it concerns an unknown situation, when the operator loses the ability to think logically, does not analyze the possible solutions and effects of his actions. | 10−1 < P < 1 |
| Situational (ST) | The operator takes further actions based on the current state of the system, ignoring the achievement of the main task objective. Most often, this applies to situations in which there are time constraints, or the operator is unable to properly interpret the current state of the system. | 1 × 10−2 < P < 5 × 10−1 |
| Tactical (TT) | The operator takes subsequent actions according to procedures or plans known to him. In the event of an unknown situation, the next action is taken after analyzing the operating parameters of the system and the context of the situation. It is based on familiar patterns of action. | 1 × 10−3 < P < 1 × 10−1 |
| Strategic (SR) | The operator takes actions in a thoughtful and planned manner, knowing their consequences. His actions are directed toward achieving the main goal of the task. The operator relies on his knowledge and experience. | 5 × 10−6 < P < 1 × 10−2 |
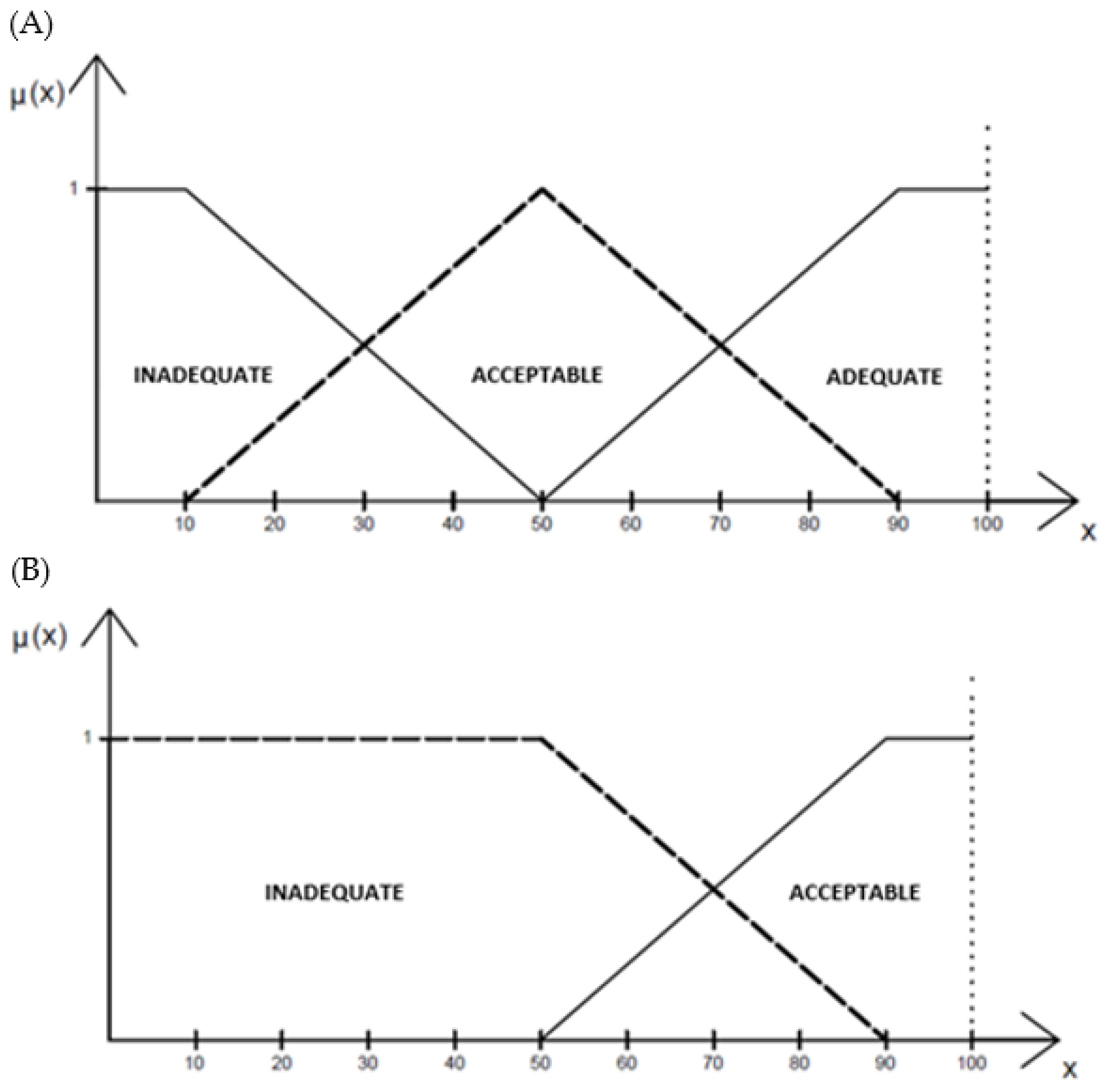
| No. | CPC Name | CPC Level | Effect | Membership Function Parameters |
|---|---|---|---|---|
| CPC1 | Adequacy of organization | adequate | positive | (50, 90, 100, 100) |
| acceptable | neutral | (10, 50, 90) | ||
| inadequate | negative | (0, 0, 10, 50) | ||
| CPC2 | Working conditions | adequate | positive | (50, 90, 100, 100) |
| acceptable | neutral | (10, 50, 90) | ||
| inadequate | negative | (0, 0, 10, 50) | ||
| CPC3 | Quality of the SCADA System | adequate | positive | (50, 90, 100, 100) |
| acceptable | neutral | (10, 50, 90) | ||
| inadequate | negative | (0, 0, 10, 50) | ||
| CPC 4 | Availability of procedures and plans | adequate | positive | (50, 90, 100, 100) |
| acceptable | neutral | (10, 50, 90) | ||
| inadequate | negative | (0, 0, 10, 50) | ||
| CPC 5 | Number of simultaneous tasks | acceptable | neutral | (50, 90, 100, 100) |
| inadequate | negative | (0, 0, 50, 90) | ||
| CPC 6 | Available time | adequate | positive | (50, 90, 100, 100) |
| acceptable | neutral | (10, 50, 90) | ||
| inadequate | negative | (0, 0, 10, 50) | ||
| CPC 7 | Time of day | acceptable | neutral | (50, 90, 100, 100) |
| inadequate | negative | (0, 0, 50, 90) | ||
| CPC 8 | Qualifications and training | adequate | positive | (50, 90, 100, 100) |
| acceptable | neutral | (10, 50, 90) | ||
| inadequate | negative | (0, 0, 10, 50) | ||
| CPC 9 | Team collaboration quality | adequate | positive | (50, 90, 100, 100) |
| acceptable | neutral | (10, 50, 90) | ||
| inadequate | negative | (0, 0, 10, 50) |
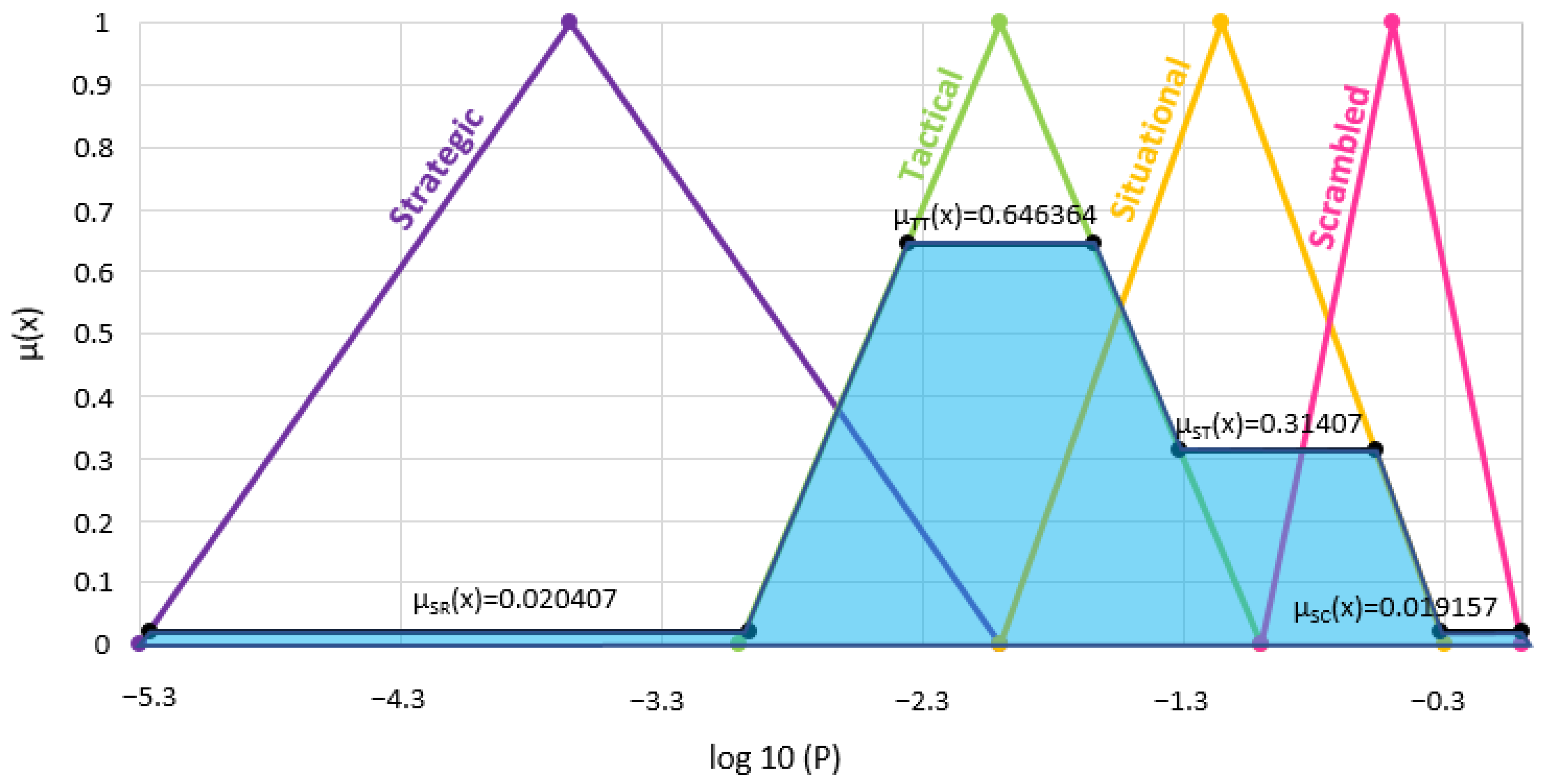
| Control Mode | Logarithmized HEP Value | Membership Function Parameters |
|---|---|---|
| Scrambled (SC) | 0 < log10 (P) < −1 | (−1; −0.5; 0) |
| Situational (ST) | −2 < log10 (P) < −0.3 | (−2; −1.15; −0.3) |
| Tactical (TT) | −3 < log10 (P) < −1 | (−3; −2; −1) |
| Strategic (SR) | −5.3 < log10 (P) < −2 | (−5.3; −3.65; −2) |
| CPC Factor | Score Scale: 0 Inadequate, 50 Acceptable, 100 Adequate | |
|---|---|---|
| CPC 1 | Adequacy of organization | (answer) |
| CPC 2 | Working conditions | (answer) |
| CPC 3 | Quality of the SCADA interface | (answer) |
| CPC 4 | Availability of procedures and plans | (answer) |
| CPC 5 | Number of simultaneous tasks | (answer) |
| CPC 6 | Available time | (answer) |
| CPC 7 | Time of day | (answer) |
| CPC 8 | Qualifications and training | (answer) |
| CPC 9 | Crew collaboration quality | (answer) |
| CPC Factor | Survey Score | Fuzzy Values |
|---|---|---|
| CPC1 | 50 | 0; 1; 0 |
| CPC2 | 60 | 0.25; 0.75; 0 |
| CPC3 | 50 | 0; 1; 0 |
| CPC4 | 50 | 0; 1; 0 |
| CPC5 | 60 | 0.25; 0,75 |
| CPC6 | 60 | 0.25; 0.75; 0 |
| CPC7 | 50 | 0; 1 |
| CPC8 | 70 | 0.5; 0.5; 0 |
| CPC9 | 60 | 0.25; 0.75; 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Żywiec, J.; Tchórzewska-Cieślak, B.; Sokolan, K. Assessment of Human Errors in the Operation of the Water Treatment Plant. Water 2024, 16, 2399. https://doi.org/10.3390/w16172399
Żywiec J, Tchórzewska-Cieślak B, Sokolan K. Assessment of Human Errors in the Operation of the Water Treatment Plant. Water. 2024; 16(17):2399. https://doi.org/10.3390/w16172399
Chicago/Turabian StyleŻywiec, Jakub, Barbara Tchórzewska-Cieślak, and Kateryna Sokolan. 2024. "Assessment of Human Errors in the Operation of the Water Treatment Plant" Water 16, no. 17: 2399. https://doi.org/10.3390/w16172399
APA StyleŻywiec, J., Tchórzewska-Cieślak, B., & Sokolan, K. (2024). Assessment of Human Errors in the Operation of the Water Treatment Plant. Water, 16(17), 2399. https://doi.org/10.3390/w16172399