Improving Urban Stormwater Management Using the Hydrological Model of Water Infiltration by Rain Gardens Considering the Water Column
Abstract
1. Introduction
2. Materials and Methods
2.1. Determination of the Main Parameters of Soil Mixtures
2.2. Rainfall Event
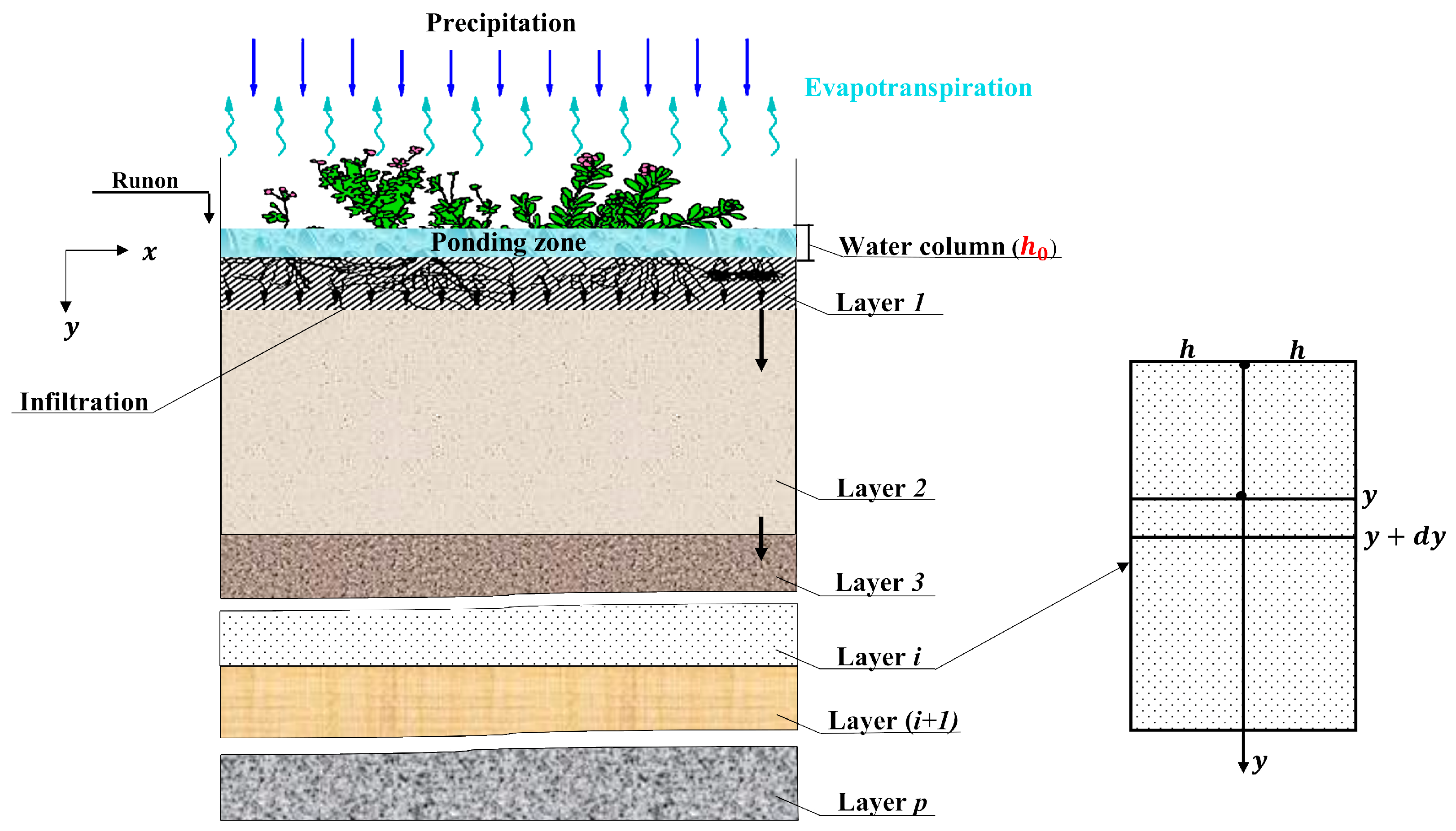
2.3. A Mathematical Hydrological Model Considering the Water Column Height and Filtration Coefficient
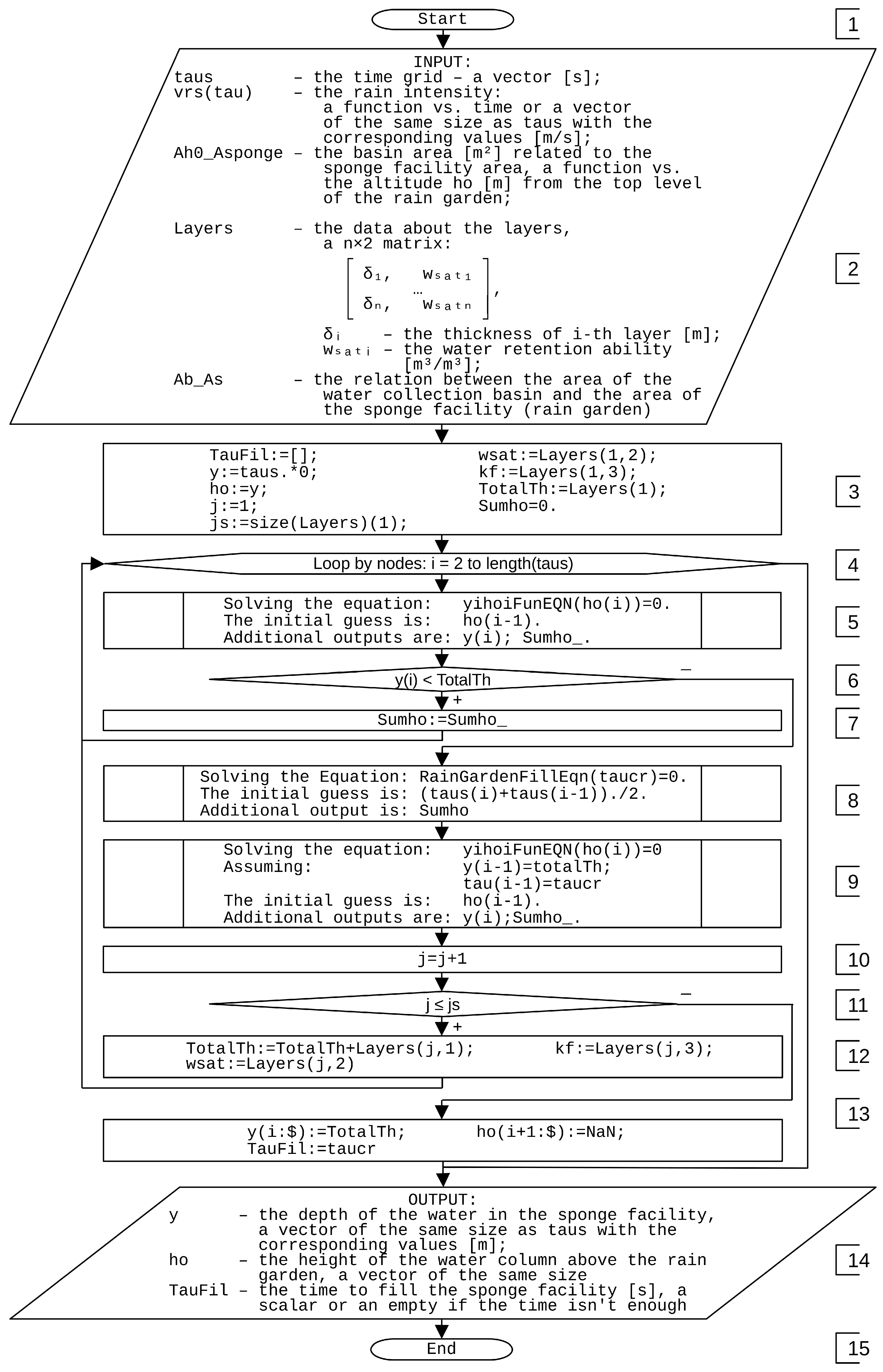
2.4. Algorithm and Software
- -
- grid approximation of the derivative of the free area of the horizontal water level at the HWC ho, m
- -
- analysis of water saturation in the system, m, while modelling the current layer without any constraints;
- -
- sum for calculating the depth of water saturation of the structure;
- -
- is the inviscid equation for the HWC, m;
3. Results
- topsoil layer: = 0.33 m3/m3; = 7.0 cm/h;
- intermediate/infiltration sand layer: = 0.31 m3/m3; = 45.0 cm/h;
- lower gravel layer: = 0.1 m3/m3; = 200.0 cm/h.
4. Discussion
5. Conclusions
- The enhanced universal hydrological model, which is based on Darcy’s law, effectively simulates the dynamic processes of rain garden layer saturation at a specific time. It takes into consideration the water column height on the structure’s surface. The model’s accuracy was confirmed using Scilab software, which assessed the rain garden’s performance under extreme conditions during a single excessive rainfall event (36 mm/h). The validated model was then used to simulate the water level on the rain garden surface (water column height) and the saturation depth of the structural layers.
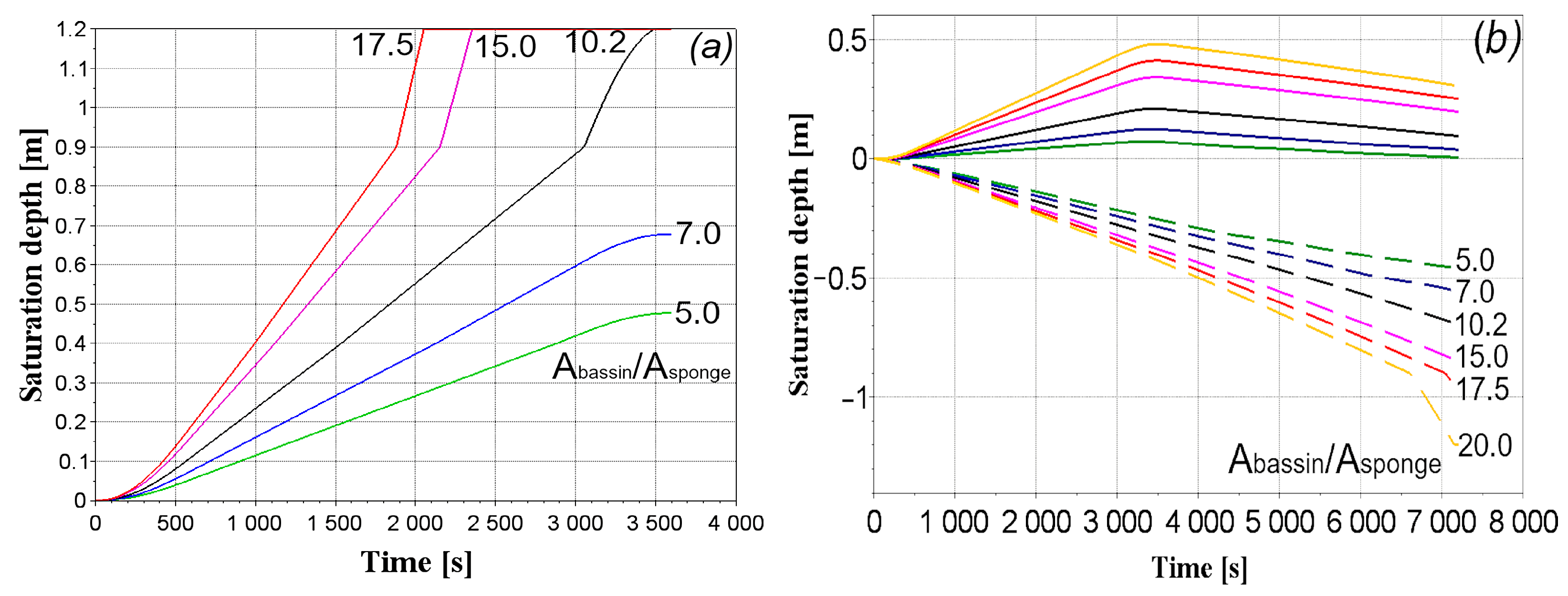
- In our model, the filtration coefficient and thickness of the upper and intermediate infiltration layers of the rain garden are the main parameters that influence the saturation depth of the structure layers and the water column height at the surface. The model is less sensitive to the model parameters associated with the lower gravel layer.
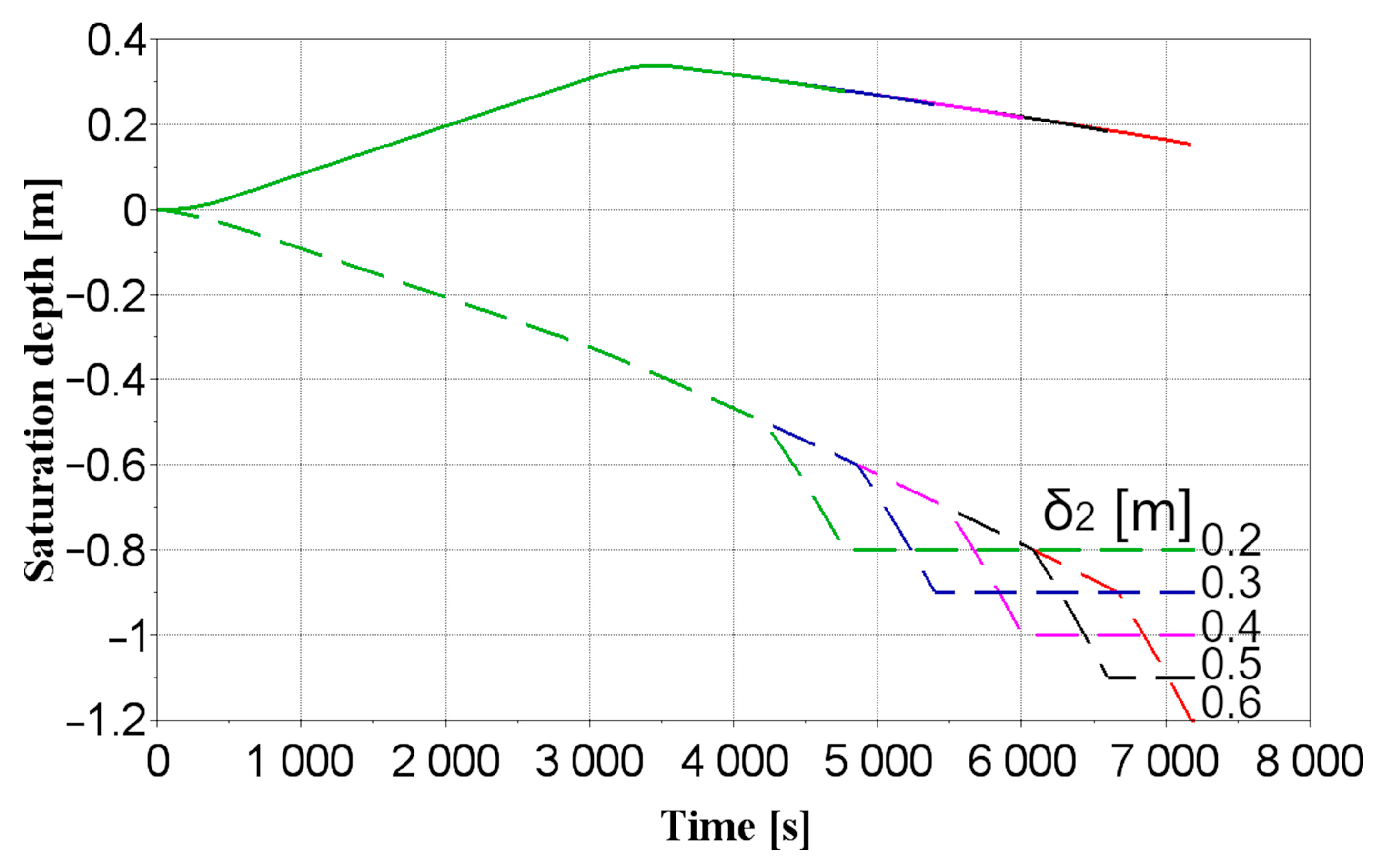
- Increasing the thickness of the top layer by 10 cm results in a longer filling time and a surface column height of 0.341 m. It is recommended to have a top layer thickness of at least 0.3 m. A top layer thickness of less than 0.3 m leads to uneven runoff distribution, reducing efficiency and delaying complete system filling. Adjusting the thickness of the infiltration and gravel layers increases the filling time by an average of 601.25 s and 158.3 s, respectively, with a resulting water column height of 0.34 m. The recommended thicknesses for the infiltration and gravel layers are 0.5–0.6 m and 0.3 m, respectively.
- Changes in the soil mixture’s filtration coefficient significantly affect the rain garden’s hydrological behaviour. Enhanced productivity occurs when the filtration coefficient of the upper layer reaches 7.0 cm/h. At this value, complete saturation and filling of the structure with rainwater takes 7200 s, and the water column height reaches 0.342 m. Increasing the filtration coefficient of the intermediate layer reduces the water column height by an average of 0.007 m and shortens the filling time. When modelling the saturation depth and water column height over time based on the gravel layer’s filtration coefficient, curves for different values overlap and exhibit the same behaviour.
- The depth of the depression zone on the surface of the rain garden is crucial for creating a water column and accumulating stormwater runoff. This allows water to saturate the entire structure vertically. The thicker the top layer of the rain garden and its filtration coefficient, the higher the resulting water column on the surface. The lower gravel layer has a minimal impact on the height of the water column and primarily functions as a drainage layer for water drainage.
- The tested model can predict the performance of rain gardens in stormwater infiltration based on the saturation depth, water column height, drainage area to basin area ratio, and soil filtration coefficient. The effectiveness of the rain garden design decreases when the thickness of the top layer is less than 0.3 m, the thickness of the intermediate infiltration layer is less than 0.5 m when the catchment area to rain garden area ratio falls below 15, or when the filtration coefficient of the top and intermediate infiltration layers surpasses 15 cm/h and 25 cm/h, respectively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A


References
- Guptha, G.C.; Swain, S.; Al-Ansari, N.; Taloor, A.K.; Dayal, D. Assessing the Role of SuDS in Resilience Enhancement of Urban Drainage System: A Case Study of Gurugram City, India. Urban Clim. 2022, 41, 101075. [Google Scholar] [CrossRef]
- Prayogi, L.; Yandri, S.; Schneider, V. Adaptation and Application of Low Impact Urban Design and Development (LIUDD) in Resistencia, Argentina. IOP Conf. Ser. Earth Environ. Sci. 2022, 1092, 012018. [Google Scholar] [CrossRef]
- Liu, Y.; Engel, B.A.; Flanagan, D.C.; Gitau, M.W.; McMillan, S.K.; Chaubey, I. A Review on Effectiveness of Best Management Practices in Improving Hydrology and Water Quality: Needs and Opportunities. Sci. Total Environ. 2017, 601–602, 580–593. [Google Scholar] [CrossRef] [PubMed]
- De Jesús Arce-Mojica, T.; Nehren, U.; Sudmeier-Rieux, K.; Miranda, P.J.; Anhuf, D. Nature-Based Solutions (NbS) for Reducing the Risk of Shallow Landslides: Where Do We Stand? Int. J. Disaster Risk Reduct. 2019, 41, 101293. [Google Scholar] [CrossRef]
- Joshi, P.; Leitão, J.P.; Maurer, M.; Bach, P.M. Not All SuDS Are Created Equal: Impact of Different Approaches on Combined Sewer Overflows. Water Res. 2021, 191, 116780. [Google Scholar] [CrossRef] [PubMed]
- Radinja, M.; Škerjanec, M.; Džeroski, S.; Todorovski, L.; Atanasova, N. Design and Simulation of Stormwater Control Measures Using Automated Modeling. Water 2021, 13, 2268. [Google Scholar] [CrossRef]
- Li, C.; Peng, C.; Chiang, P.-C.; Cai, Y.; Wang, X.; Yang, Z. Mechanisms and Applications of Green Infrastructure Practices for Stormwater Control: A Review. J. Hydrol. 2019, 568, 626–637. [Google Scholar] [CrossRef]
- Kaykhosravi, S.; Khan, U.; Jadidi, A. A Comprehensive Review of Low Impact Development Models for Research, Conceptual, Preliminary and Detailed Design Applications. Water 2018, 10, 1541. [Google Scholar] [CrossRef]
- Kravchenko, M.V.; Tkachenko, T.M. Problems of Improving the Terminology and Modern Classification of “Green” Constructions for the Creation of Ukrainian “Green” Standards. Collect. Sci. Publ. NUS 2023, 493, 194–204. [Google Scholar] [CrossRef] [PubMed]
- Lisenbee, W.A.; Hathaway, J.M.; Burns, M.J.; Fletcher, T.D. Modeling Bioretention Stormwater Systems: Current Models and Future Research Needs. Environ. Model. Softw. 2021, 144, 105146. [Google Scholar] [CrossRef]
- Morash, J.; Wright, A.; LeBleu, C.; Meder, A.; Kessler, R.; Brantley, E.; Howe, J. Increasing Sustainability of Residential Areas Using Rain Gardens to Improve Pollutant Capture, Biodiversity and Ecosystem Resilience. Sustainability 2019, 11, 3269. [Google Scholar] [CrossRef]
- Burszta-Adamiak, E.; Biniak-Pieróg, M.; Dąbek, P.B.; Sternik, A. Rain Garden Hydrological Performance—Responses to Real Rainfall Events. Sci. Total Environ. 2023, 887, 164153. [Google Scholar] [CrossRef] [PubMed]
- Greksa, A.; Blagojević, B.; Grabić, J. Nature-Based Solutions in Serbia: Implementation of Rain Gardens in the Suburban Community Kać. Environ. Process. 2023, 10, 41. [Google Scholar] [CrossRef]
- Zhang, L.; Ye, Z.; Shibata, S. Assessment of Rain Garden Effects for the Management of Urban Storm Runoff in Japan. Sustainability 2020, 12, 9982. [Google Scholar] [CrossRef]
- Ge, M.; Huang, Y.; Zhu, Y.; Kim, M.; Cui, X. Examining the Microclimate Pattern and Related Spatial Perception of the Urban Stormwater Management Landscape: The Case of Rain Gardens. Atmosphere 2023, 14, 1138. [Google Scholar] [CrossRef]
- Wanitchayapaisit, C.; Suppakittpaisarn, P.; Charoenlertthanakit, N.; Surinseng, V.; Yaipimol, E.; Rinchumphu, D. Rain Garden Design for Stormwater Management in Chiang Mai, Thailand: A Research-through-Design Study. NJEDP 2022, 21, 222. [Google Scholar] [CrossRef]
- Corrêa, C.J.P.; Nnadi, E.O.; Mbanaso, F.U.; Tonello, K.C. Urban Gardens’ Potential to Improve Stormwater Management: A Comparative Analysis among Urban Soils in Sorocaba, São Paulo, Brazil. Sustainability 2022, 14, 2965. [Google Scholar] [CrossRef]
- Tang, S.; Luo, W.; Jia, Z.; Liu, W.; Li, S.; Wu, Y. Evaluating Retention Capacity of Infiltration Rain Gardens and Their Potential Effect on Urban Stormwater Management in the Sub-Humid Loess Region of China. Water Resour Manag. 2016, 30, 983–1000. [Google Scholar] [CrossRef]
- Syafriana, A.; Arifin, H.S. Rain Garden Model for Stormwater Management in Sentul City, Bogor, Indonesia. IOP Conf. Ser. Earth Environ. Sci. 2020, 477, 012031. [Google Scholar] [CrossRef]
- Öhrn Sagrelius, P.; Blecken, G.; Hedström, A.; Ashley, R.; Viklander, M. Environmental Impacts of Stormwater Bioretention Systems with Various Design and Construction Components. J. Clean. Prod. 2022, 359, 132091. [Google Scholar] [CrossRef]
- Venvik, G.; Boogaard, F. Infiltration Capacity of Rain Gardens Using Full-Scale Test Method: Effect of Infiltration System on Groundwater Levels in Bergen, Norway. Land 2020, 9, 520. [Google Scholar] [CrossRef]
- Kravchenko, M.V.; Tkachenko, T.M.; Mileikovskyi, V.O. Study of the Influence of the Main Parameters of the Rain Garden on Its Hydrological Parameters by Modeling. Collect. Sci. Publ. NUS 2024, 1, 166–176. [Google Scholar] [CrossRef] [PubMed]
- Na Nagara, V.; Sarkar, D.; Boufadel, M.; Datta, R. Green Engineered Mulch for Phosphorus and Metal Removal from Stormwater Runoff in Bioretention Systems. Chemosphere 2023, 331, 138779. [Google Scholar] [CrossRef]
- Request Unavailable—Melbourne Water. Available online: https://www.melbournewater.com.au/media/446/download (accessed on 12 March 2024).
- Design Criteria for Bioretention—Minnesota Stormwater Manual. Available online: https://stormwater.pca.state.mn.us/index.php/Design_criteria_for_bioretention (accessed on 18 April 2024).
- Wisconsin Department of Natural Resources. Available online: https://dnr.wisconsin.gov/ (accessed on 18 April 2024).
- Paus, K.H.; Morgan, J.; Gulliver, J.S.; Hozalski, R.M. Effects of Bioretention Media Compost Volume Fraction on Toxic Metals Removal, Hydraulic Conductivity, and Phosphorous Release. J. Environ. Eng. 2014, 140, 04014033. [Google Scholar] [CrossRef]
- Davis, A.P.; Traver, R.G.; Hunt, W.F. Improving Urban Stormwater Quality: Applying Fundamental Principles. Contemp. Water Res. 2010, 146, 3–10. [Google Scholar] [CrossRef]
- Ren, X.W.; Santamarina, J.C. The Hydraulic Conductivity of Sediments: A Pore Size Perspective. Eng. Geol. 2018, 233, 48–54. [Google Scholar] [CrossRef]
- Carpenter, D.D.; Hallam, L. Influence of Planting Soil Mix Characteristics on Bioretention Cell Design and Performance. J. Hydrol. Eng. 2010, 15, 404–416. [Google Scholar] [CrossRef]
- Gregory, J.H.; Dukes Michael, D.; Jones Pierce, H.; Miller Grady, L. Effect of Urban Soil Compaction on Infiltration Rate. J. Soil Water Conserv. 2006, 3, 117–124. [Google Scholar]
- Ren, X.; Kang, J.; Ren, J.; Chen, X.; Zhang, M. A Method for Estimating Soil Water Characteristic Curve with Limited Experimental Data. Geoderma 2020, 360, 114013. [Google Scholar] [CrossRef]
- Boancă, P.; Dumitraș, A.; Luca, L.; Bors-Oprișa, S.; Laczi, E. Analysing Bioretention Hydraulics and RunoffRetention through Numerical Modelling UsingRECARGA: A Case Study in a RomanianUrban Area. Pol. J. Environ. Stud. 2018, 27, 1965–1973. [Google Scholar] [CrossRef] [PubMed]
- Le Coustumer, S.; Fletcher, T.D.; Deletic, A.; Barraud, S.; Poelsma, P. The Influence of Design Parameters on Clogging of Stormwater Biofilters: A Large-Scale Column Study. Water Res. 2012, 46, 6743–6752. [Google Scholar] [CrossRef]
- Zhou, Z.; Guo, Q. Drainage Alternatives for Rain Gardens on Subsoil of Low Permeability: Balance among Ponding Time, Soil Moisture, and Runoff Reduction. J. Sustain. Water Built Environ. 2022, 8, 05022002. [Google Scholar] [CrossRef]
- Jackisch, N.; Weiler, M. The Hydrologic Outcome of a Low Impact Development (LID) Site Including Superposition with Streamflow Peaks. Urban Water J. 2017, 14, 143–159. [Google Scholar] [CrossRef]
- Liu, J.; Sample, D.; Bell, C.; Guan, Y. Review and Research Needs of Bioretention Used for the Treatment of Urban Stormwater. Water 2014, 6, 1069–1099. [Google Scholar] [CrossRef]
- Gilchrist, S.; Borst, M.; Stander, E.K. Factorial Study of Rain Garden Design for Nitrogen Removal. J. Irrig. Drain Eng. 2014, 140, 04013016. [Google Scholar] [CrossRef]
- Goh, H.W.; Lem, K.S.; Azizan, N.A.; Chang, C.K.; Talei, A.; Leow, C.S.; Zakaria, N.A. A Review of Bioretention Components and Nutrient Removal under Different Climates—Future Directions for Tropics. Env. Sci Pollut Res 2019, 26, 14904–14919. [Google Scholar] [CrossRef]
- Payne, E.G.I.; Fletcher, T.D.; Cook, P.L.M.; Deletic, A.; Hatt, B.E. Processes and Drivers of Nitrogen Removal in Stormwater Biofiltration. Crit. Rev. Environ. Sci. Technol. 2014, 44, 796–846. [Google Scholar] [CrossRef]
- Clar, M.; Laramore, E.; Ryan, H. Rethinking Bioretention Design Concepts. In Proceedings of the Low Impact Development, Seattle, WA, USA, 16–19 November 2008; American Society of Civil Engineers: Wilmington, NC, USA, 2008; pp. 119–127. [Google Scholar]
- Hunt, W.F.; Davis, A.P.; Traver, R.G. Meeting Hydrologic and Water Quality Goals through Targeted Bioretention Design. J. Environ. Eng. 2012, 138, 698–707. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, J.; Babovic, V.; Gin, K.Y.H. A Comprehensive Integrated Catchment-Scale Monitoring and Modelling Approach for Facilitating Management of Water Quality. Environ. Model. Softw. 2019, 120, 104489. [Google Scholar] [CrossRef]
- Heasom, W.; Traver, R.G.; Welker, A. Hydrologic modeling of a bioinfiltration best management practice. J. Am. Water Resour. Assoc. 2006, 42, 1329–1347. [Google Scholar] [CrossRef]
- Kravchenko, M.; Trach, Y.; Trach, R.; Tkachenko, T.; Mileikovskyi, V. Improving the Efficiency and Environmental Friendliness of Urban Stormwater Management by Enhancing the Water Filtration Model in Rain Gardens. Water 2024, 16, 1316. [Google Scholar] [CrossRef]
- Eestimation of Infiltration Rate in the Vadose Zone: Compilation of Simple Mathematical Models—Volume I|Science Inventory|US EPA. Available online: https://cfpub.epa.gov/si/si_public_record_report.cfm?Lab=NRMRL&dirEntryId=99481 (accessed on 24 May 2024).
- Smith, R.E. The Infiltration Envelope: Results from a Theoretical Infiltrometer. J. Hydrol. 1972, 17, 1–22. [Google Scholar] [CrossRef]
- Horton RE The Rôle of Infiltration in the Hydrologic Cycle. Eos Trans. AGU 1933, 14, 446–460. [CrossRef]
- Heber Green, W.; Ampt, G.A. Studies on Soil Phyics. J. Agric. Sci. 1911, 4, 1–24. [Google Scholar] [CrossRef]
- Richards, L.A. Capillary conduction of liquids through porous mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Ali, M.H. Fundamentals of Irrigation and On-Farm Water Management: Volume 1; Springer: New York, NY, USA, 2010; ISBN 978-1-4419-6334-5. [Google Scholar]
- Gray, W.G.; Miller, C.T. Examination of Darcy’s Law for Flow in Porous Media with Variable Porosity. Environ. Sci. Technol. 2004, 38, 5895–5901. [Google Scholar] [CrossRef]
- Wang, J.; Song, J.; Lin, H.; Peng, L.; Li, K.; Wang, Z. Comparison of Infiltration Models to Describe Infiltration Characteristics of Bioretention. J. Hydro-Environ. Res. 2021, 38, 35–43. [Google Scholar] [CrossRef]
- Adoption Guidelines for Stormwater Biofiltration Systems: Cities as Water Supply Catchments—Sustainable Technologies—CRC for Water Sensitive Cities. Available online: https://watersensitivecities.org.au/content/stormwater-biofilter-design/ (accessed on 18 April 2024).
- Fassman, E.A.; Simcock, R.; Wang, S. Media Specification for Stormwater Bioretention Devices, Prepared by Auckland UniServices for Auckland Council. Auckland Council Technical Report, TR2013/011. 2013. Available online: https://knowledgeauckland.org.nz/media/1616/tr2013-011-media-specification-for-stormwater-bioretention-devices.pdf (accessed on 17 August 2024).
- Kravchenko, M.; Trach, Y.; Trach, R.; Tkachenko, T.; Mileikovskyi, V. Behaviour and Peculiarities of Oil Hydrocarbon Removal from Rain Garden Structures. Water 2024, 16, 1802. [Google Scholar] [CrossRef]
- Guo, J.C.Y.; Luu, T.M. Hydrologic Model Developed for Stormwater Infiltration Practices. J. Hydrol. Eng. 2015, 20, 06015001. [Google Scholar] [CrossRef]
- Azure, I.; Wiredu, J.K.; Musah, A.; Akolgo, E. AI-Enhanced Performance Evaluation of Python, MATLAB, and Scilab for Solving Nonlinear Systems of Equations: A Comparative Study Using the Broyden Method. AJCM 2023, 13, 644–677. [Google Scholar] [CrossRef]
- Rain Gardens. Available online: https://www.susdrain.org/delivering-suds/using-suds/suds-components/infiltration/rain-gardens.html (accessed on 12 March 2024).
- Rinchumphu, D.; Suriyanon, N.; Phichetkunbodee, N.; Munlikawong, S.; Wanitchayapaisit, C.; Sitthikankun, S. Economics and Cost Effectiveness of a Rain Garden for Flood-Resistant Urban Design. Glob. J. Environ. Sci. Manag. 2024, 10, 1–12. [Google Scholar] [CrossRef]
- Zhang, B.; Li, J.; Li, Y. Simulation and Optimization of Rain Gardens via DRAINMOD Model and Response Surface Methodology. Ecohydrol. Hydrobiol. 2020, 20, 413–423. [Google Scholar] [CrossRef]
- Li, H.; Sharkey, L.J.; Hunt, W.F.; Davis, A.P. Mitigation of Impervious Surface Hydrology Using Bioretention in North Carolina and Maryland. J. Hydrol. Eng. 2009, 14, 407–415. [Google Scholar] [CrossRef]
- Vijayaraghavan, K.; Biswal, B.K.; Adam, M.G.; Soh, S.H.; Tsen-Tieng, D.L.; Davis, A.P.; Chew, S.H.; Tan, P.Y.; Babovic, V.; Balasubramanian, R. Bioretention Systems for Stormwater Management: Recent Advances and Future Prospects. J. Environ. Manag. 2021, 292, 112766. [Google Scholar] [CrossRef]
- Rezaei, A.R.; Ismail, Z.; Niksokhan, M.H.; Dayarian, M.A.; Ramli, A.H.; Shirazi, S.M. A Quantity–Quality Model to Assess the Effects of Source Control Stormwater Management on Hydrology and Water Quality at the Catchment Scale. Water 2019, 11, 1415. [Google Scholar] [CrossRef]
- Skorobogatov, A.; He, J.; Chu, A.; Valeo, C.; Van Duin, B. The Impact of Media, Plants and Their Interactions on Bioretention Performance: A Review. Sci. Total Environ. 2020, 715, 136918. [Google Scholar] [CrossRef] [PubMed]
- Blecken, G.-T.; Zinger, Y.; Deletić, A.; Fletcher, T.D.; Viklander, M. Impact of a Submerged Zone and a Carbon Source on Heavy Metal Removal in Stormwater Biofilters. Ecol. Eng. 2009, 35, 769–778. [Google Scholar] [CrossRef]
- Winston, R.J.; Dorsey, J.D.; Hunt, W.F. Quantifying Volume Reduction and Peak Flow Mitigation for Three Bioretention Cells in Clay Soils in Northeast Ohio. Sci. Total Environ. 2016, 553, 83–95. [Google Scholar] [CrossRef]
- Jiang, C.; Li, J.; Li, H.; Li, Y. Experiment and Simulation of Layered Bioretention System for Hydrological Performance. J. Water Reuse Desalination 2019, 9, 319–329. [Google Scholar] [CrossRef]
- Baek, S.-S.; Ligaray, M.; Park, J.-P.; Shin, H.-S.; Kwon, Y.; Brascher, J.T.; Cho, K.H. Developing a Hydrological Simulation Tool to Design Bioretention in a Watershed. Environ. Model. Softw. 2019, 122, 104074. [Google Scholar] [CrossRef]
- Tansar, H.; Duan, H.-F.; Mark, O. Global Sensitivity Analysis of Bioretention Cell Design for Stormwater System: A Comparison of VARS Framework and Sobol Method. J. Hydrol. 2023, 617, 128895. [Google Scholar] [CrossRef]
- Wang, J.; Chua, L.H.C.; Shanahan, P. Hydrological Modeling and Field Validation of a Bioretention Basin. J. Environ. Manag. 2019, 240, 149–159. [Google Scholar] [CrossRef]
- Mangangka, I.R.; Liu, A.; Egodawatta, P.; Goonetilleke, A. Performance Characterisation of a Stormwater Treatment Bioretention Basin. J. Environ. Manag. 2015, 150, 173–178. [Google Scholar] [CrossRef] [PubMed]
- Dussaillant, A.R.; Wu, C.H.; Potter, K.W. Richards Equation Model of a Rain Garden. J. Hydrol. Eng. 2004, 9, 219–225. [Google Scholar] [CrossRef]
- Hatt, B.E.; Fletcher, T.D.; Deletic, A. Hydrologic and Pollutant Removal Performance of Stormwater Biofiltration Systems at the Field Scale. J. Hydrol. 2009, 365, 310–321. [Google Scholar] [CrossRef]
- Wang, J.; Song, Y.; Ma, T.; Raza, W.; Li, J.; Howland, J.G.; Huang, Q.; Shen, Q. Impacts of Inorganic and Organic Fertilization Treatments on Bacterial and Fungal Communities in a Paddy Soil. Appl. Soil Ecol. 2017, 112, 42–50. [Google Scholar] [CrossRef]
- Li, Y.; Wen, M.; Li, J.; Chai, B.; Jiang, C. Reduction and Accumulative Characteristics of Dissolved Heavy Metals in Modified Bioretention Media. Water 2018, 10, 1488. [Google Scholar] [CrossRef]
- Homepage—Water Sensitive Cities Australia. Available online: https://wscaustralia.org.au/ (accessed on 18 April 2024).
- Le Coustumer, S.; Fletcher, T.D.; Deletic, A.; Barraud, S.; Lewis, J.F. Hydraulic Performance of Biofilter Systems for Stormwater Management: Influences of Design and Operation. J. Hydrol. 2009, 376, 16–23. [Google Scholar] [CrossRef]
- Tahvonen, O. Adapting Bioretention Construction Details to Local Practices in Finland. Sustainability 2018, 10, 276. [Google Scholar] [CrossRef]
- Bratieres, K.; Fletcher, T.D.; Deletic, A.; Zinger, Y. Nutrient and Sediment Removal by Stormwater Biofilters: A Large-Scale Design Optimisation Study. Water Res. 2008, 42, 3930–3940. [Google Scholar] [CrossRef]
- Jiang, C.; Li, J.; Li, H.; Li, Y. An Improved Approach to Design Bioretention System Media. Ecol. Eng. 2019, 136, 125–133. [Google Scholar] [CrossRef]
- Kandel, S.; Vogel, J.; Penn, C.; Brown, G. Phosphorus Retention by Fly Ash Amended Filter Media in Aged Bioretention Cells. Water 2017, 9, 746. [Google Scholar] [CrossRef]
- Sang, M.; Huang, M.; Zhang, W.; Che, W.; Sun, H. A Pilot Bioretention System with Commercial Activated Carbon and River Sediment-Derived Biochar for Enhanced Nutrient Removal from Stormwater. Water Sci. Technol. 2019, 80, 707–716. [Google Scholar] [CrossRef]
- William, R.; Gardoni, P.; Stillwell, A.S. Reliability-Based Approach to Investigating Long-Term Clogging in Green Stormwater Infrastructure. J. Sustain. Water Built Environ. 2019, 5, 04018015. [Google Scholar] [CrossRef]
- Sharma, R.; Malaviya, P. Management of stormwater pollution using green infrastructure: The role of rain gardens. WIREs Water 2021, 8, e1507. [Google Scholar] [CrossRef]
- Meng, Y.; Wang, H.; Chen, J.; Zhang, S. Modelling Hydrology of a Single Bioretention System with HYDRUS-1D. Sci. World J. 2014, 2014, 1–10. [Google Scholar] [CrossRef]
- Paus, K.H.; Morgan, J.; Gulliver, J.S.; Leiknes, T.; Hozalski, R.M. Assessment of the Hydraulic and Toxic Metal Removal Capacities of Bioretention Cells After 2 to 8 Years of Service. Water Air Soil Pollut. 2014, 225, 1803. [Google Scholar] [CrossRef]
- Archer, N.A.L.; Quinton, J.N.; Hess, T.M. Below-Ground Relationships of Soil Texture, Roots and Hydraulic Conductivity in Two-Phase Mosaic Vegetation in South-East Spain. J. Arid Environ. 2002, 52, 535–553. [Google Scholar] [CrossRef]
- Lucas, W.C. Design of Integrated Bioinfiltration-Detention Urban Retrofits with Design Storm and Continuous Simulation Methods. J. Hydrol. Eng. 2010, 15, 486–498. [Google Scholar] [CrossRef]
- Lee, J.Y.; Moon, H.J.; Kim, T.I.; Kim, H.W.; Han, M.Y. Quantitative Analysis on the Urban Flood Mitigation Effect by the Extensive Green Roof System. Environ. Pollut. 2013, 181, 257–261. [Google Scholar] [CrossRef] [PubMed]
- Hlushchenko, R.; Tkachenko, T.; Mileikovskyi, V.; Kravets, V.; Tkachenko, O. “Green Structures” for Effective Rainwater Management on Roads. Prod. Eng. Arch. 2022, 28, 295–299. [Google Scholar] [CrossRef]
- Tkachenko, T.; Kravchenko, M.; Voloshkina, O.; Mileikovskyi, V.; Tkachenko, O.; Sipakov, R. Evaluating Rain-Garden Bands: Filtration Properties and Implications for Urban Water Management. In Proceedings of the World Environmental and Water Resources Congress 2024, Milwaukee, WI, USA, 19–22 May 2024; American Society of Civil Engineers: Milwaukee, WI, USA, 2024; pp. 960–968. [Google Scholar]
- Tkachenko, T.; Mileikovskyi, V.; Dziubenko, V.; Tkachenko, O. Improvement of the Safety of Multi-Floor Housing. IOP Conf. Ser. Mater. Sci. Eng. 2020, 907, 012064. [Google Scholar] [CrossRef]
- Tkachenko, T.; Voloshkina, O.; Mileikovskyi, V.; Sipakov, R.; Hlushchenko, R.; Tkachenko, O. Using Rain-Garden Bands for Rainwater Drainage from Roads. In Proceedings of the World Environmental and Water Resources Congress 2023, Henderson, NV, USA, 21–25 May 2023; American Society of Civil Engineers: Henderson, NV, USA, 2023; pp. 1207–1214. [Google Scholar]
- Tkachenko, T.; Mileikovskyi, V. Capturing Carbon Dioxide from Human-Driven Vehicles by Green Structures for Carbon Neutrality. IOP Conf. Ser. Earth Environ. Sci. 2022, 1111, 012056. [Google Scholar] [CrossRef]



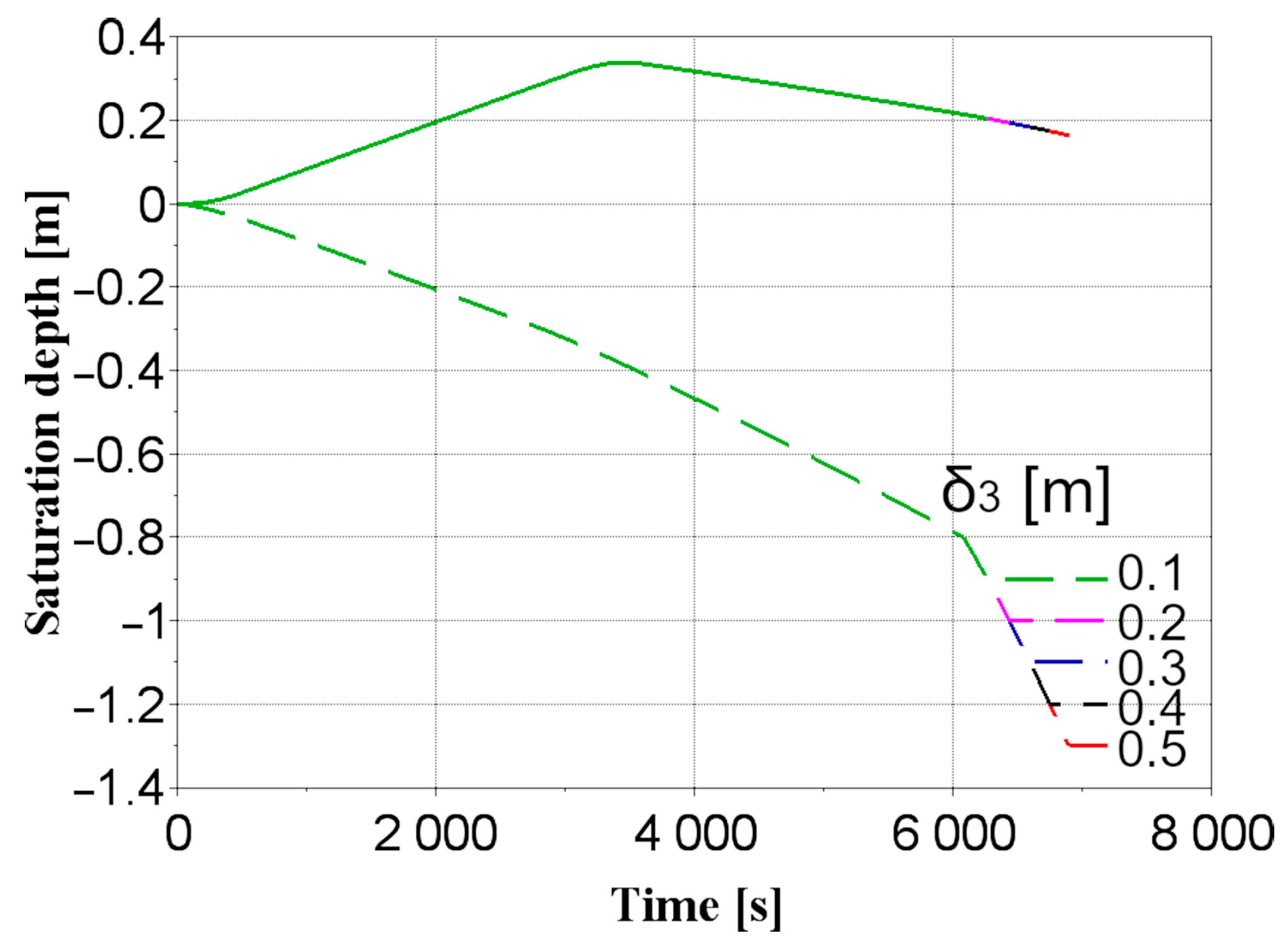

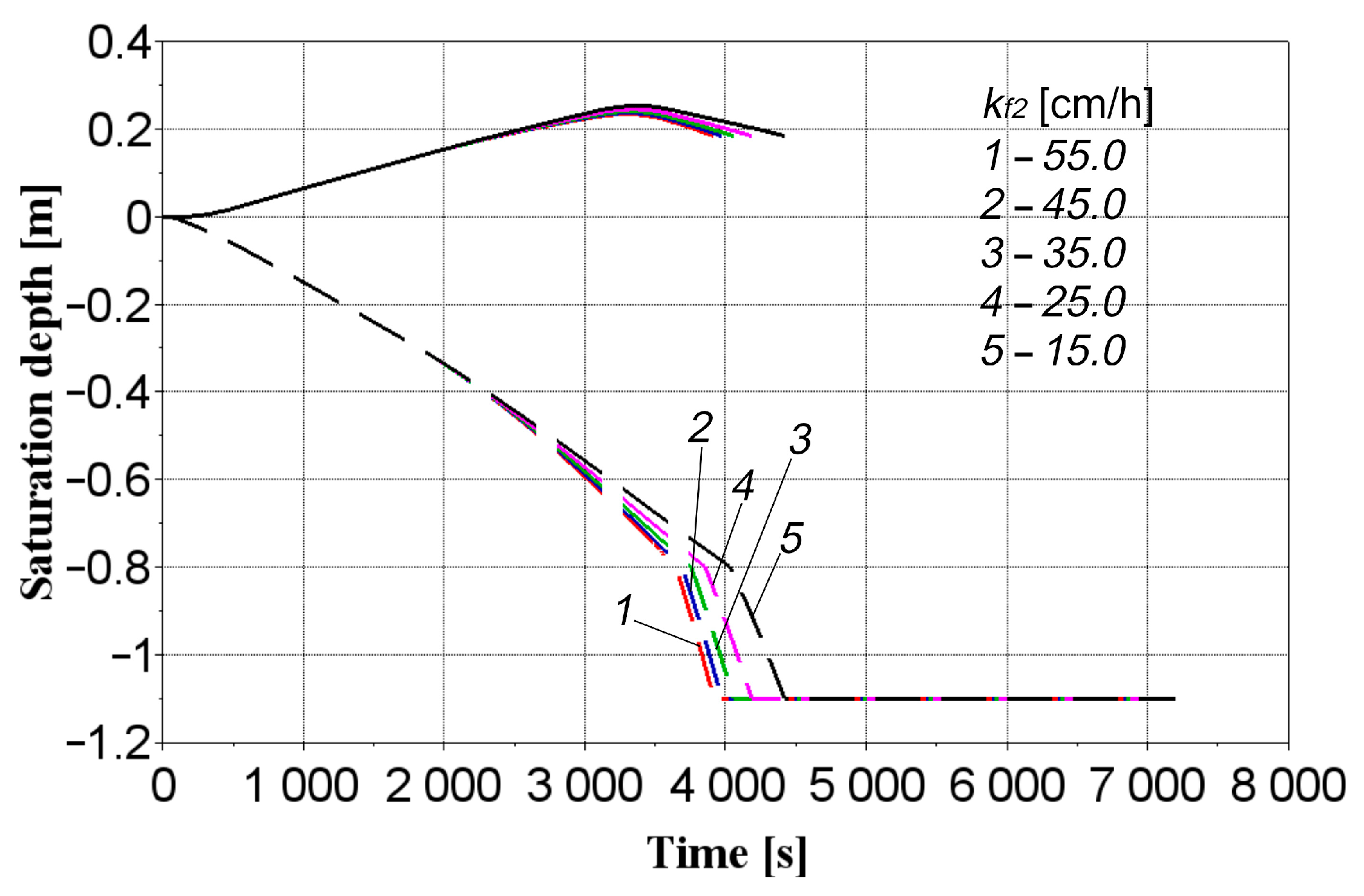

| Variable Parameters | Construction of a Rain Garden | ||||
|---|---|---|---|---|---|
| Sample 1 | Sample 2 | Sample 3 | Sample 4 | Sample 5 | |
| , m | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 |
| , m | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 |
| , m | 0.7 | 0.7 | 0.7 | 0.7 | 0.7 |
| , m | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 |
| , m | 0.262 | 0.321 | 0.338 | 0.341 | 0.341 |
| , s | 4202.5 | 5975 | - | - | - |
| Variable Parameters | Construction of a Rain Garden | ||||
|---|---|---|---|---|---|
| Sample 1 | Sample 2 | Sample 3 | Sample 4 | Sample 5 | |
| , m | 0.8 | 0.9 | 1.0 | 1.1 | 1.2 |
| , m | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 |
| , m | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 |
| , m | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 |
| , m | 0.34 | 0.34 | 0.34 | 0.34 | 0.34 |
| , s | 4769 | 5397 | 6005.5 | 6595.5 | 7174 |
| Variable Parameters | Construction of a Rain Garden | ||||
|---|---|---|---|---|---|
| Sample 1 | Sample 2 | Sample 3 | Sample 4 | Sample 5 | |
| , m | 0.9 | 1.0 | 1.1 | 1.2 | 1.3 |
| , m | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 |
| , m | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| , m | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 |
| , m | 0.338 | 0.338 | 0.338 | 0.338 | 0.338 |
| , s | 6264.5 | 6436 | 6596.5 | 6747.5 | 6898 |
| Variable Parameters | Construction of a Rain Garden | ||||
|---|---|---|---|---|---|
| Sample 1 | Sample 2 | Sample 3 | Sample 4 | Sample 5 | |
| , cm/h | 7.0 | 15.0 | 25.0 | 30.0 | 40.0 |
| , cm/h | 45.0 | 45.0 | 45.0 | 45.0 | 45.0 |
| , cm/h | 200.0 | 200.0 | 200.0 | 200.0 | 200.0 |
| , m | 0.342 | 0.257 | 0.165 | 0.127 | 0.063 |
| , s | - | 4800 | 3538.5 | 3212 | 2776 |
| Variable Parameters | Construction of a Rain Garden | ||||
|---|---|---|---|---|---|
| Sample 1 | Sample 2 | Sample 3 | Sample 4 | Sample 5 | |
| , cm/h | 7.0 | 7.0 | 7.0 | 7.0 | 7.0 |
| , cm/h | 15.0 | 25.0 | 35.0 | 45.0 | 55.0 |
| , cm/h | 200.0 | 200.0 | 200.0 | 200.0 | 200.0 |
| , m | 0.253 | 0.245 | 0.24 | 0.237 | 0.234 |
| , s | 4418.5 | 4185 | 4055.5 | 3972.5 | 3915.5 |
| Variable Parameters | Construction of a Rain Garden | ||||
|---|---|---|---|---|---|
| Sample 1 | Sample 2 | Sample 3 | Sample 4 | Sample 5 | |
| , cm/h | 7.0 | 7.0 | 7.0 | 7.0 | 7.0 |
| , cm/h | 45.0 | 45.0 | 45.0 | 45.0 | 45.0 |
| , cm/h | 100.0 | 150.0 | 200.0 | 250.0 | 300.0 |
| , m | 0.263 | 0.263 | 0.263 | 0.263 | 0.263 |
| , s | 4045.5 | 4045.5 | 4045.5 | 4045.5 | 4045.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kravchenko, M.; Wrzesiński, G.; Pawluk, K.; Lendo-Siwicka, M.; Markiewicz, A.; Tkachenko, T.; Mileikovskyi, V.; Zhovkva, O.; Szymanek, S.; Piechowicz, K. Improving Urban Stormwater Management Using the Hydrological Model of Water Infiltration by Rain Gardens Considering the Water Column. Water 2024, 16, 2339. https://doi.org/10.3390/w16162339
Kravchenko M, Wrzesiński G, Pawluk K, Lendo-Siwicka M, Markiewicz A, Tkachenko T, Mileikovskyi V, Zhovkva O, Szymanek S, Piechowicz K. Improving Urban Stormwater Management Using the Hydrological Model of Water Infiltration by Rain Gardens Considering the Water Column. Water. 2024; 16(16):2339. https://doi.org/10.3390/w16162339
Chicago/Turabian StyleKravchenko, Maryna, Grzegorz Wrzesiński, Katarzyna Pawluk, Marzena Lendo-Siwicka, Anna Markiewicz, Tetiana Tkachenko, Viktor Mileikovskyi, Olga Zhovkva, Sylwia Szymanek, and Konrad Piechowicz. 2024. "Improving Urban Stormwater Management Using the Hydrological Model of Water Infiltration by Rain Gardens Considering the Water Column" Water 16, no. 16: 2339. https://doi.org/10.3390/w16162339
APA StyleKravchenko, M., Wrzesiński, G., Pawluk, K., Lendo-Siwicka, M., Markiewicz, A., Tkachenko, T., Mileikovskyi, V., Zhovkva, O., Szymanek, S., & Piechowicz, K. (2024). Improving Urban Stormwater Management Using the Hydrological Model of Water Infiltration by Rain Gardens Considering the Water Column. Water, 16(16), 2339. https://doi.org/10.3390/w16162339









