Modification and Improvement of the Churchill Equation for Friction Factor Calculation in Pipes
Abstract
1. Introduction
2. Materials and Methods
2.1. Proposed Mathematical Model Based on Dimensional Parameters, Velocity, and Roughness: The Churchill B(V,ε) Function
Statistical Methodology
2.2. Proposed Mathematical Model Based on Dimensionless Parameters, Reynolds Number and Relative Roughness: The Churchill B(Re) Function
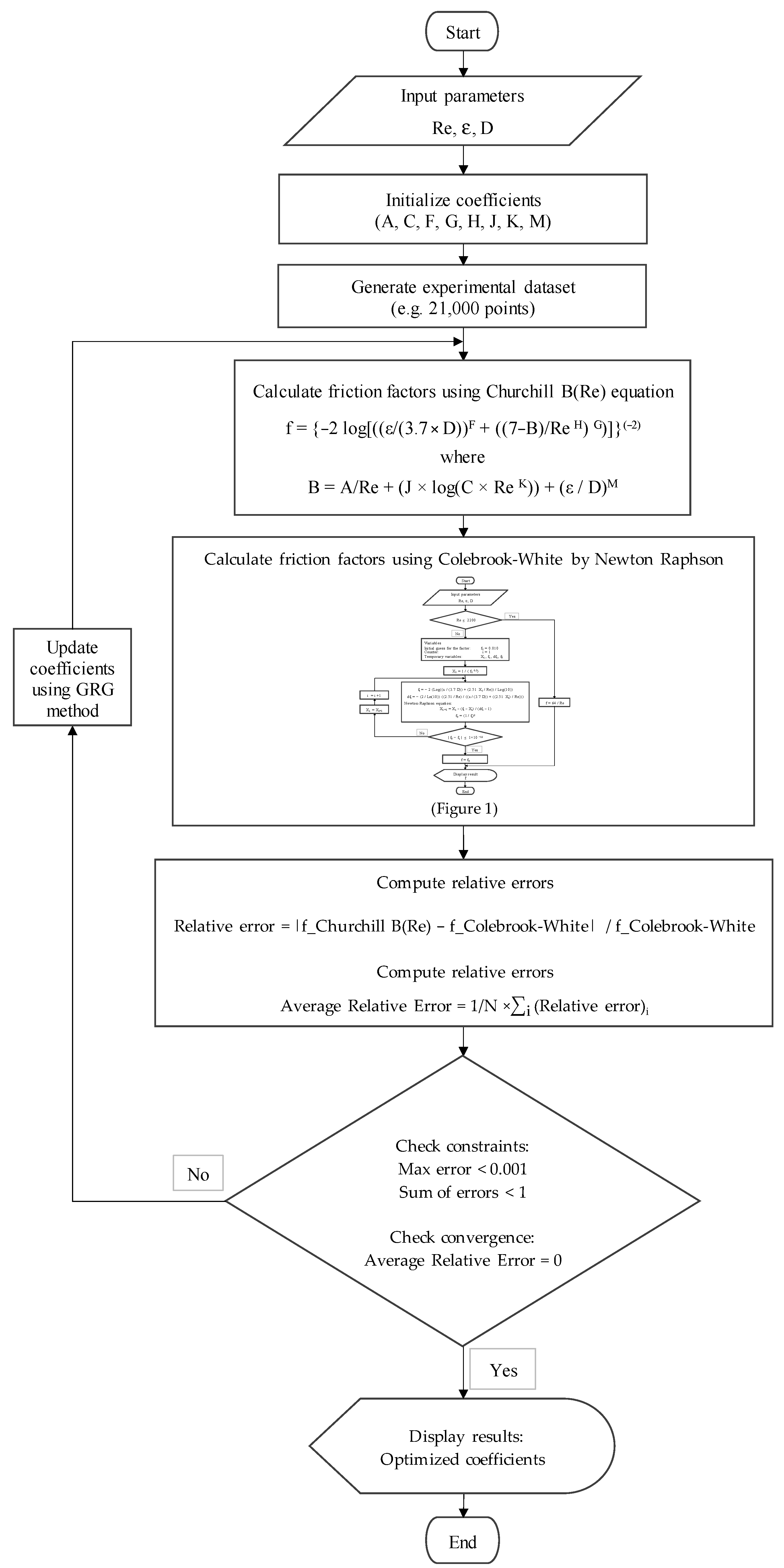
2.2.1. GRG Nonlinear Optimization
- Formulation of the Optimization Problem
- b.
- Concept of Reduced Gradients
- c.
- Feasible Direction
Jh(xk) d ≤ 0
- d.
- Lagrangian Function
- e.
- Karush–Kuhn–Tucker (KKT) ConditionsFor a point to be optimal, it must satisfy the KKT conditions:
- ○
- Stationarity Condition, Equation (18):
where is the gradient of the objective function with respect to the decision variables, which is a vector of partial derivatives of the objective function evaluated at the optimal point [45]. are the gradients of the equality constraints with respect to the decision variables, which are vectors of partial derivatives of the equality constraints evaluated at the optimal point . are the gradients of the inequality constraints with respect to the decision variables, which are vectors of partial derivatives of the inequality constraints evaluated at the optimal point .- ○
- Primal Feasibility Condition:
- ○
- Dual Feasibility Condition:
- ○
- Complementarity Condition:
- f.
- GRG Method Algorithm
- Initialization: Choose an initial feasible point x0. Set initial values for the Lagrange multipliers.
- Search Direction: Compute the search direction dk using the reduced gradient.
- Update: Update the current point: , where is the step size determined by a line search procedure.
- Convergence Check: Check if the KKT conditions are satisfied within a predefined tolerance.
- Iteration: If not converged, update the Lagrange multipliers and repeat from Step 2.
- g.
- Implementation Details
2.2.2. Optimization of Churchill B(Re)’s Friction Factor Equation Using Generalized Reduced Gradient Method
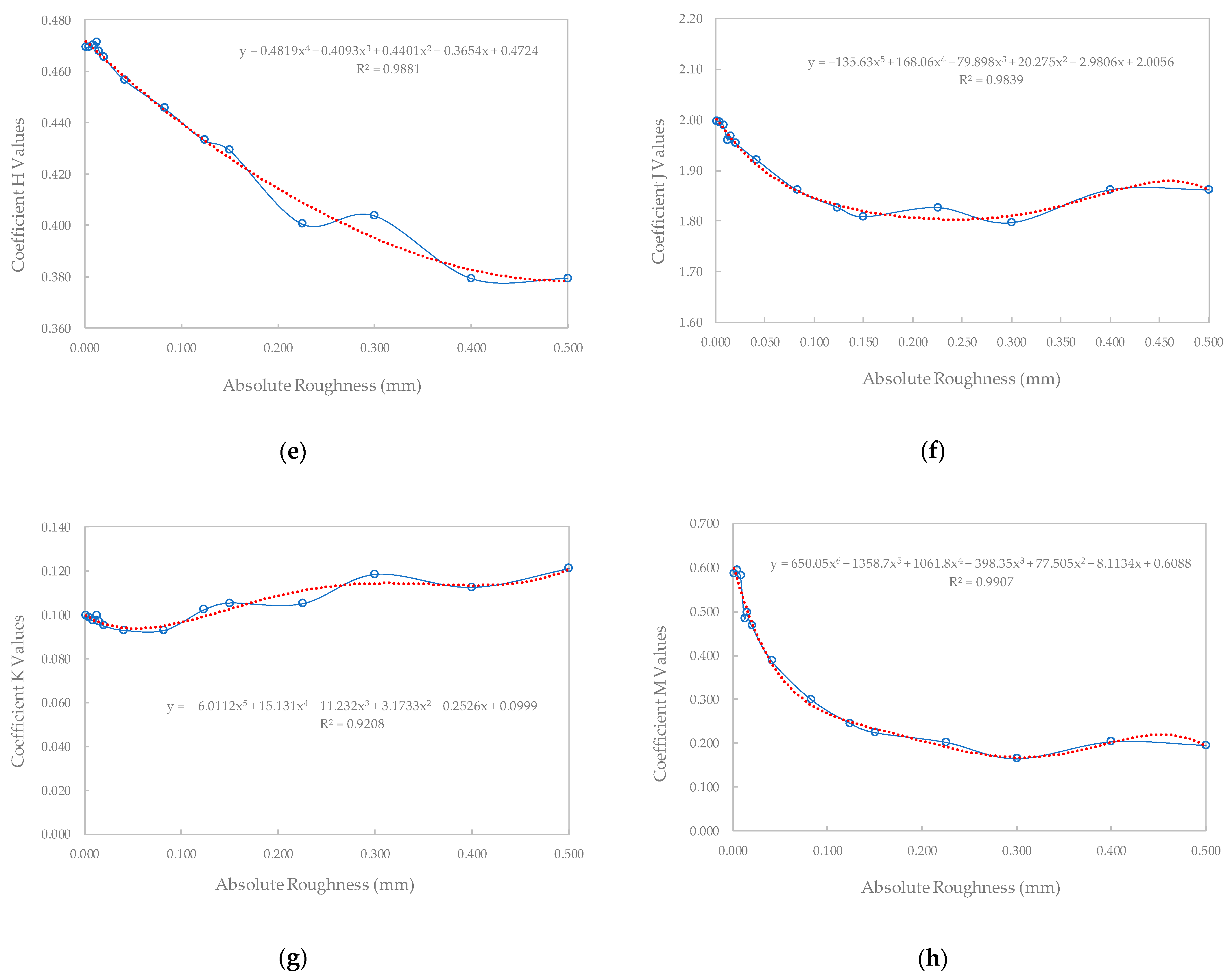
2.2.3. Proposed Function for the Churchill B(Re) Function
2.3. Other Equations Used for Comparative Analysis
2.4. Test Cases for the Validation of the Churchill Functions
2.4.1. Input Parameters and Calculation Method
2.4.2. Development of Churchill Functions through Test Case Generation
2.4.3. Test Case Generation for Validation of Churchill Functions
3. Results
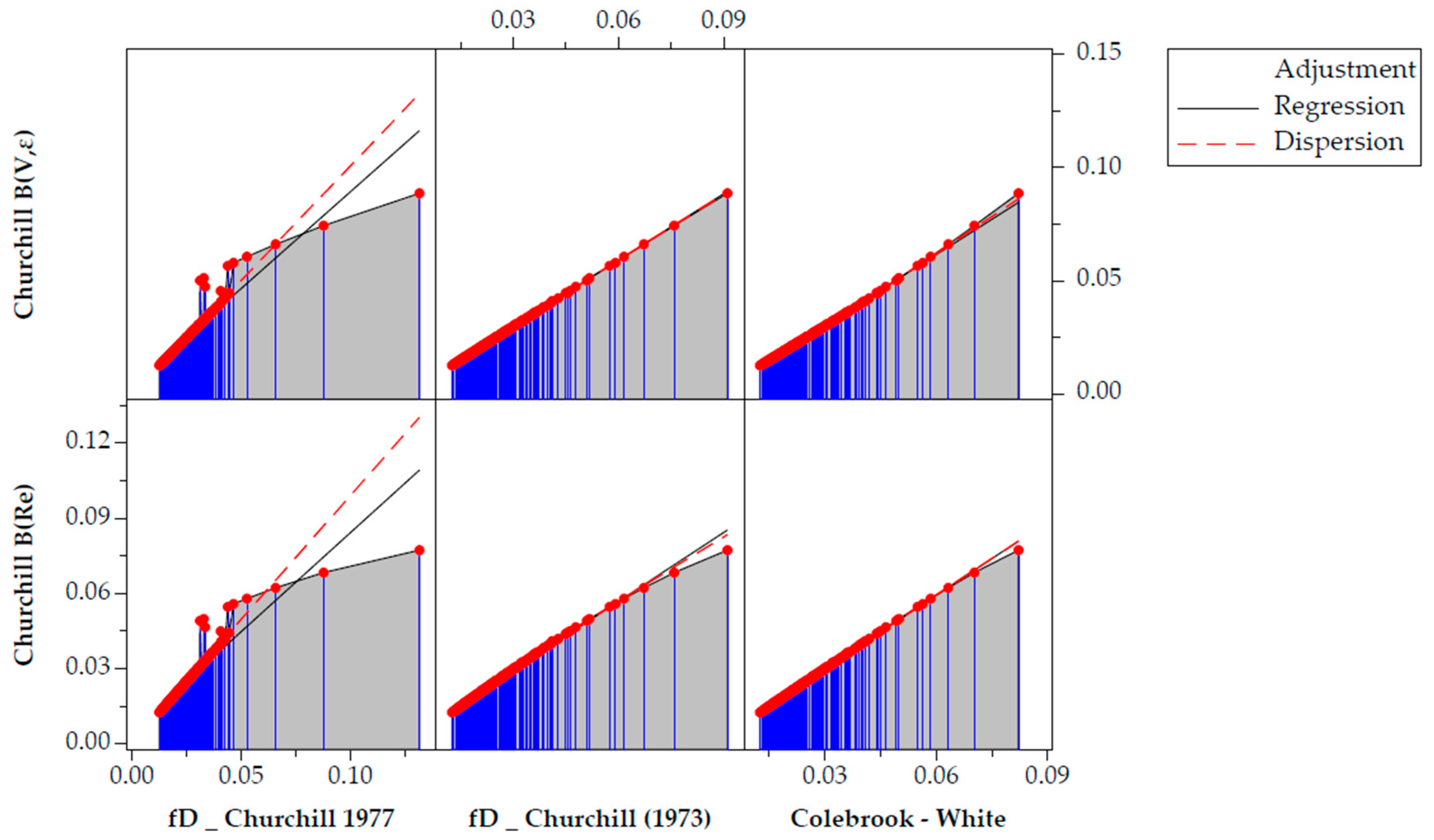
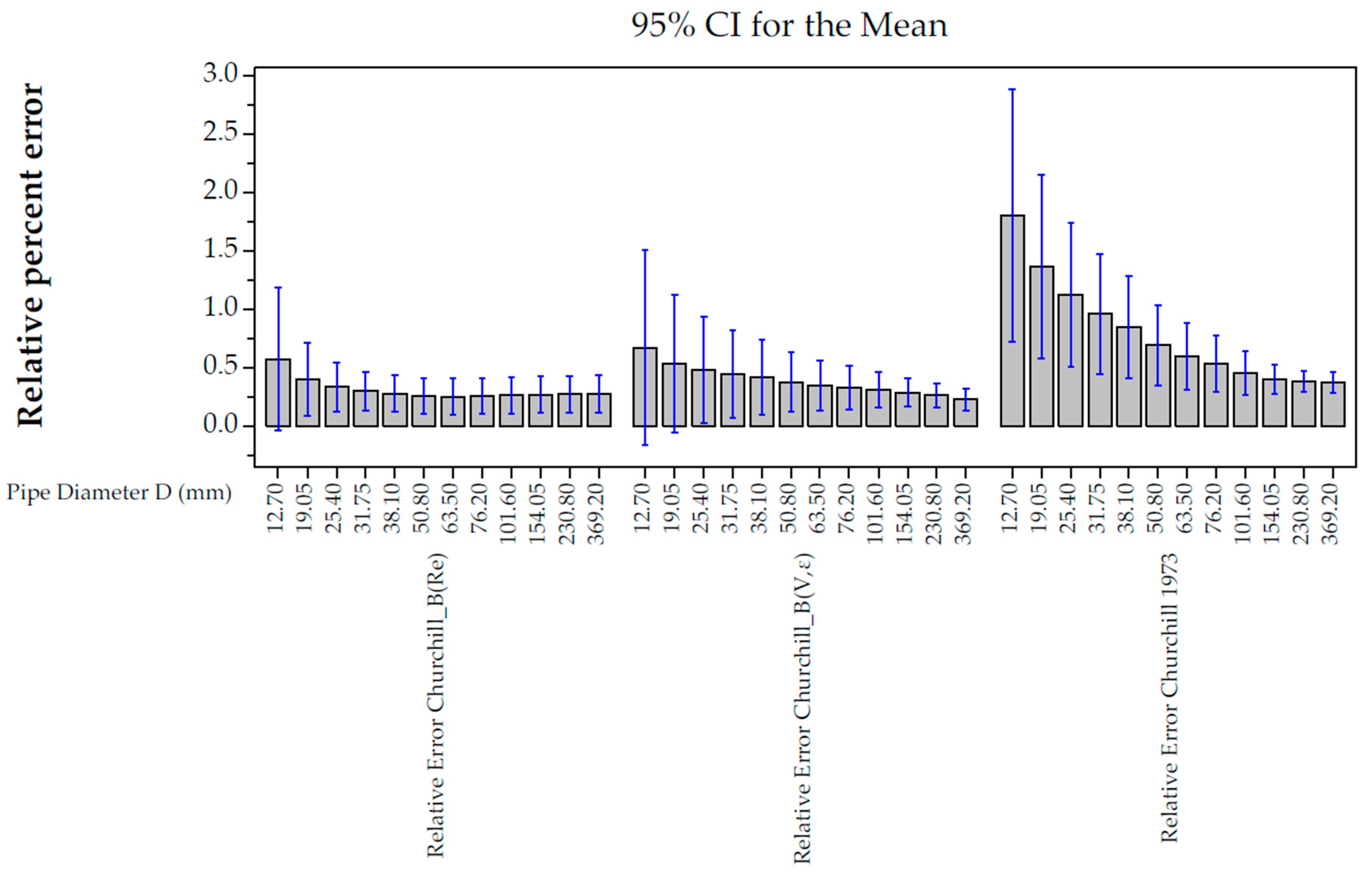
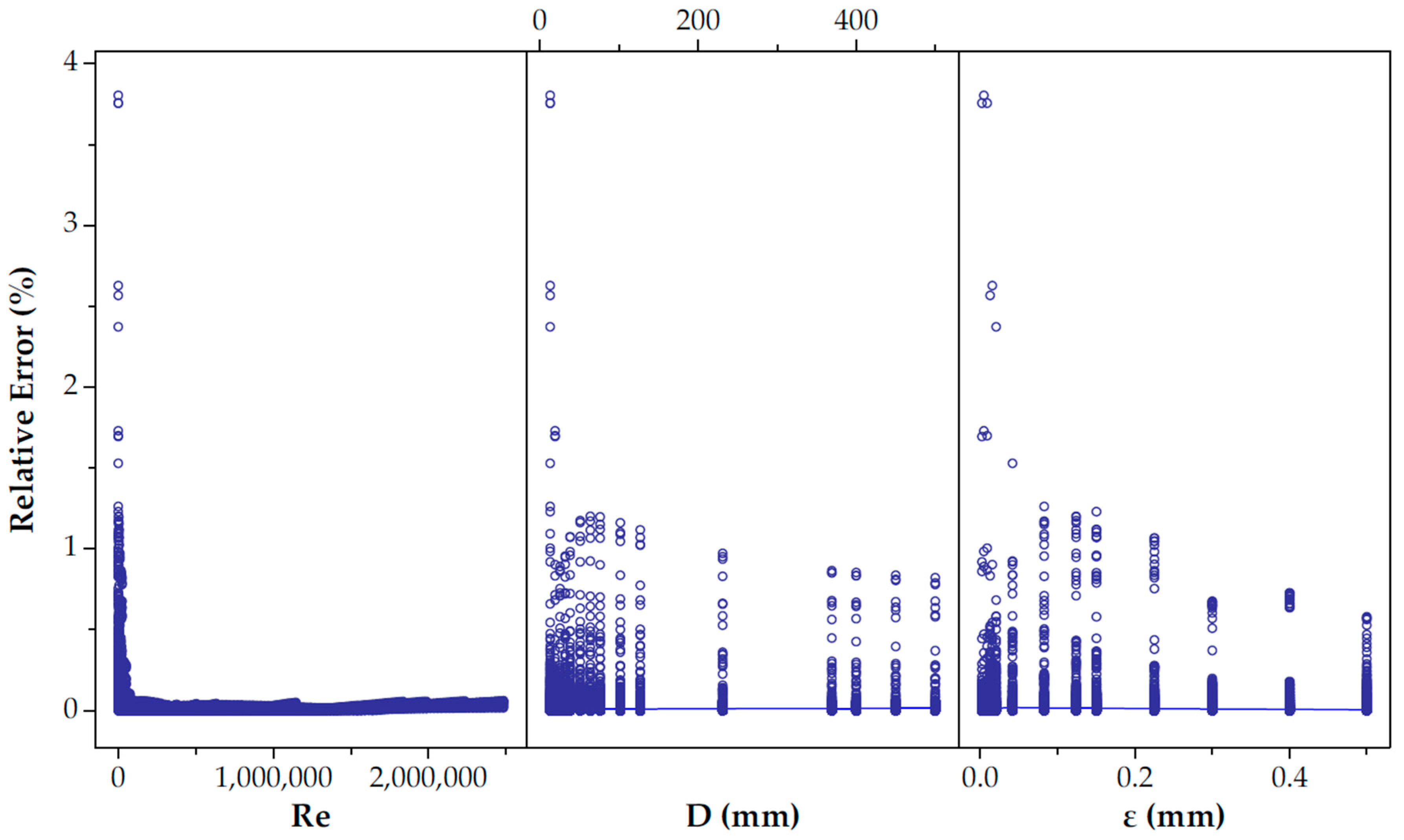
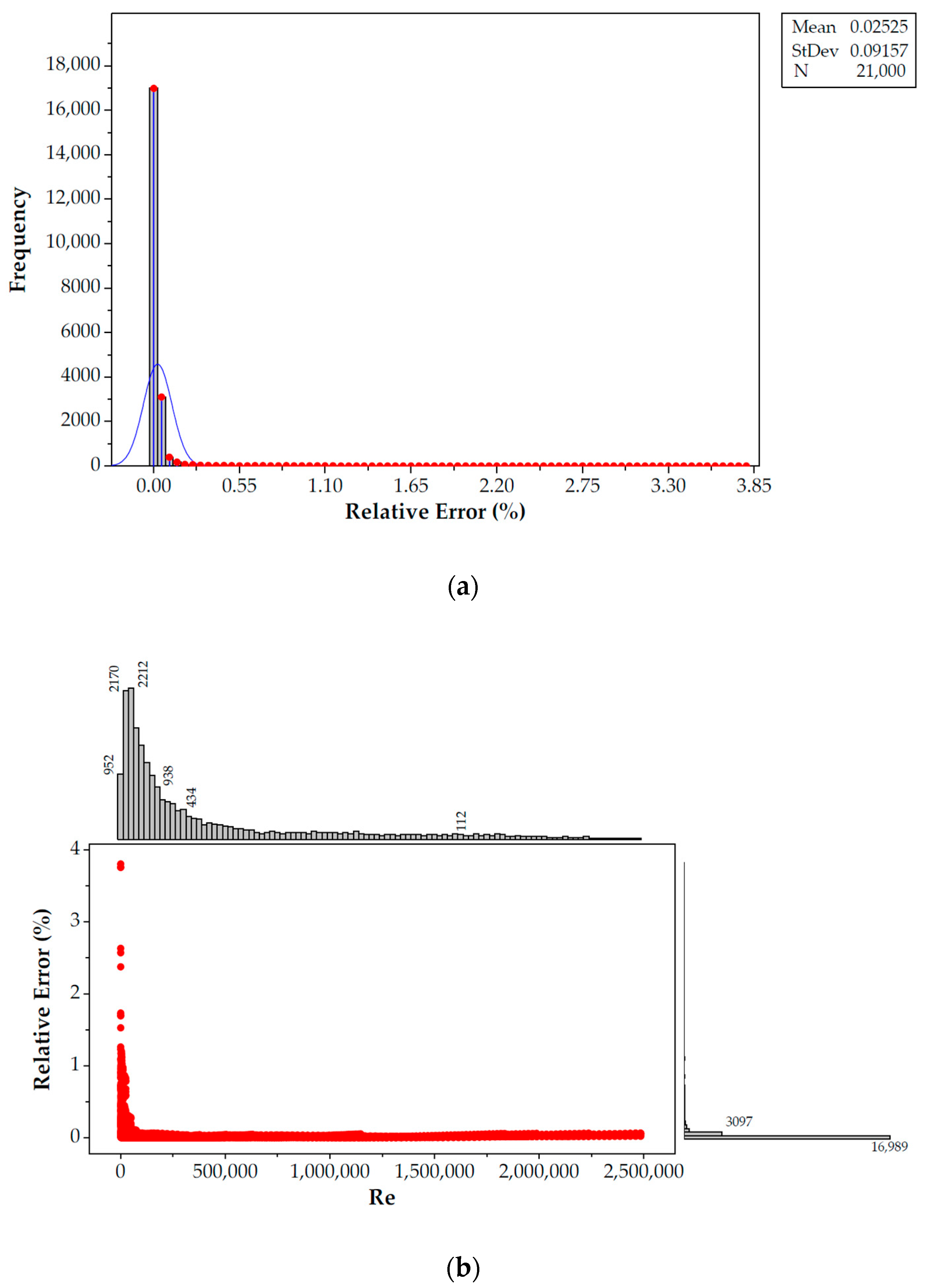
3.1. Precisions and Errors of the Selected Methods
3.1.1. Relative Errors
3.1.2. Absolute Errors
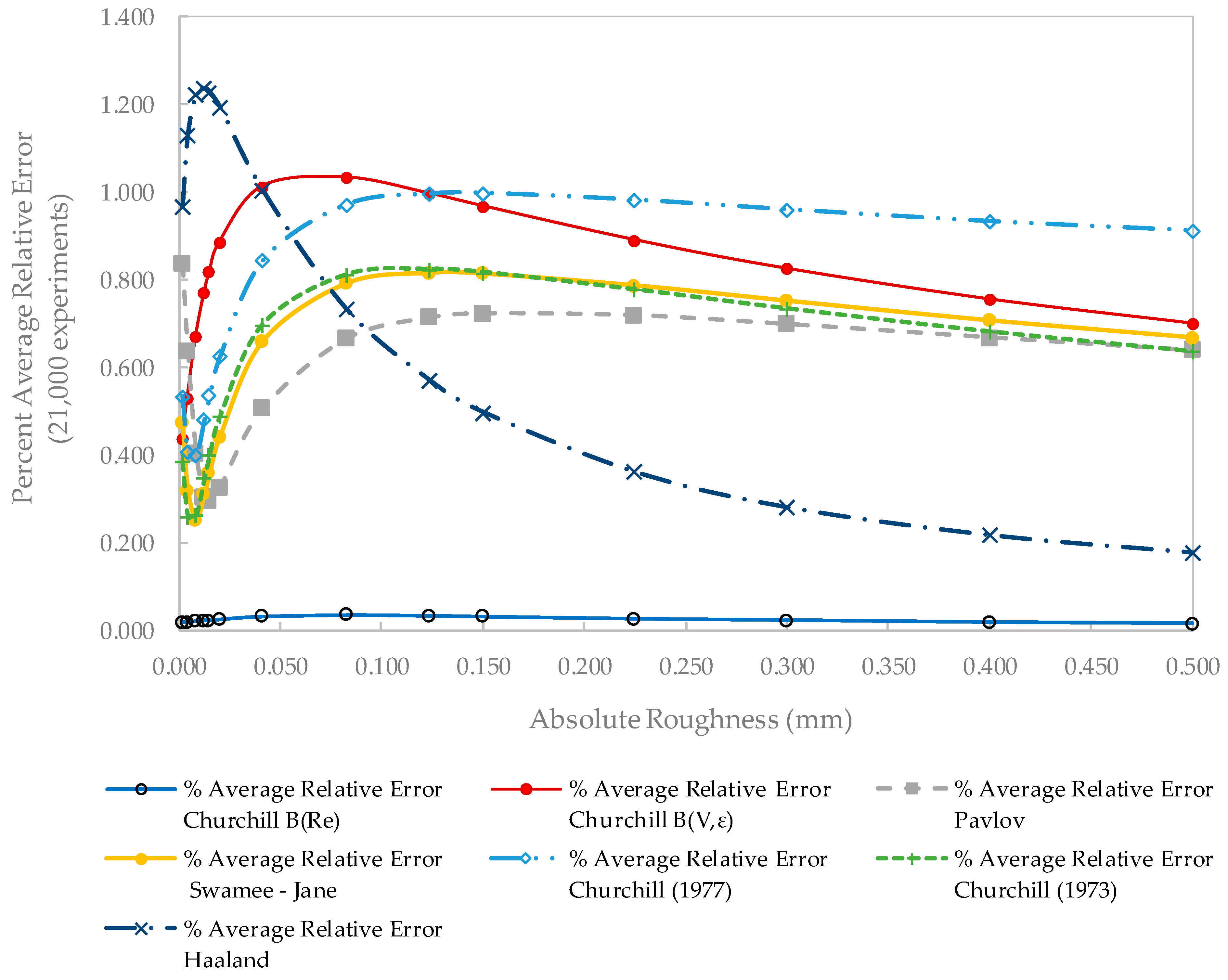
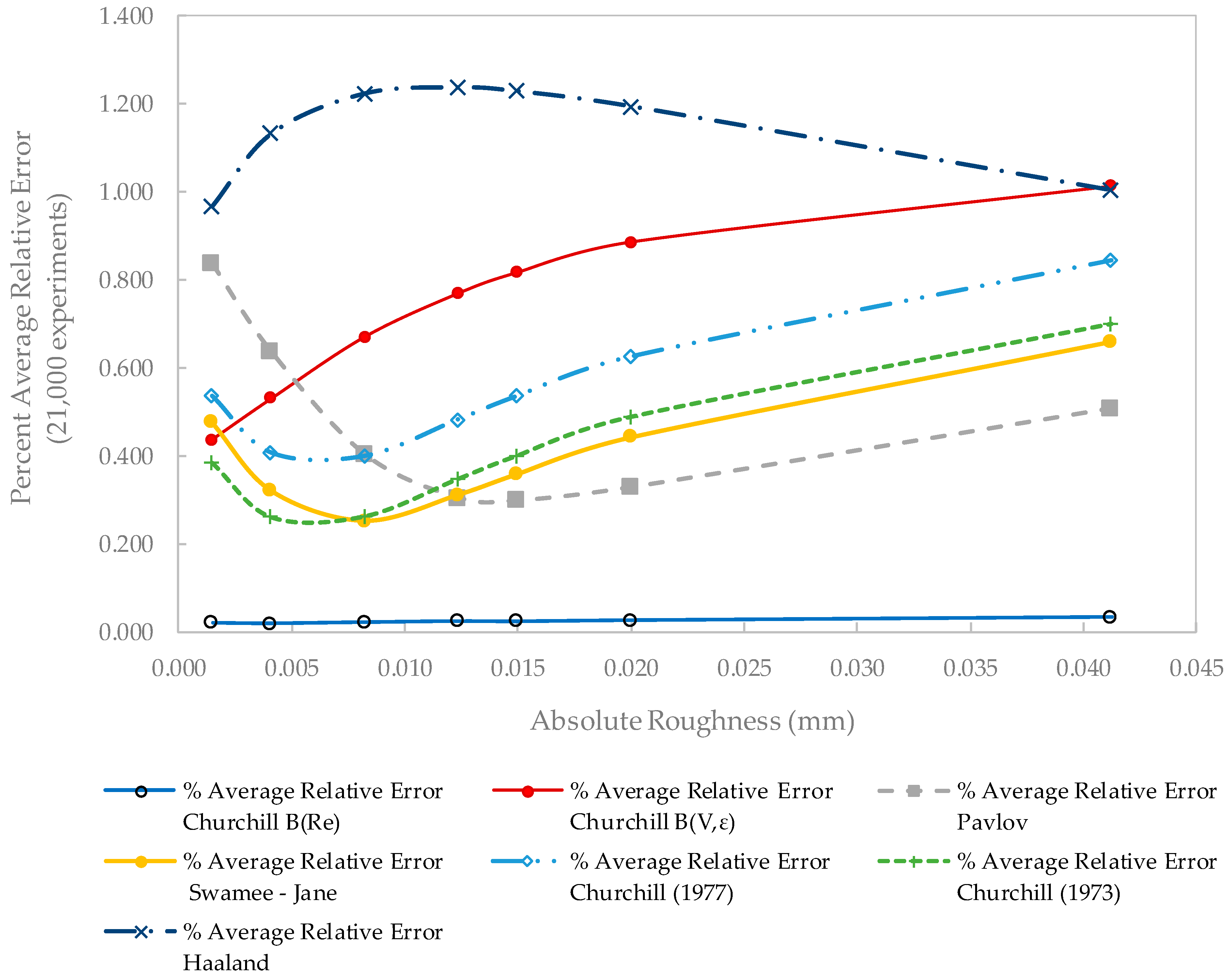
4. Discussion and Comparative Results
4.1. Normal Probability Plot
4.2. Histogram of the Residuals
4.3. Error Comparison
4.3.1. Absolute Error Comparison for Churchill B(V,ε) Function
4.3.2. Relative Error Comparison for Churchill B(Re) Function
4.4. Statistical Significance
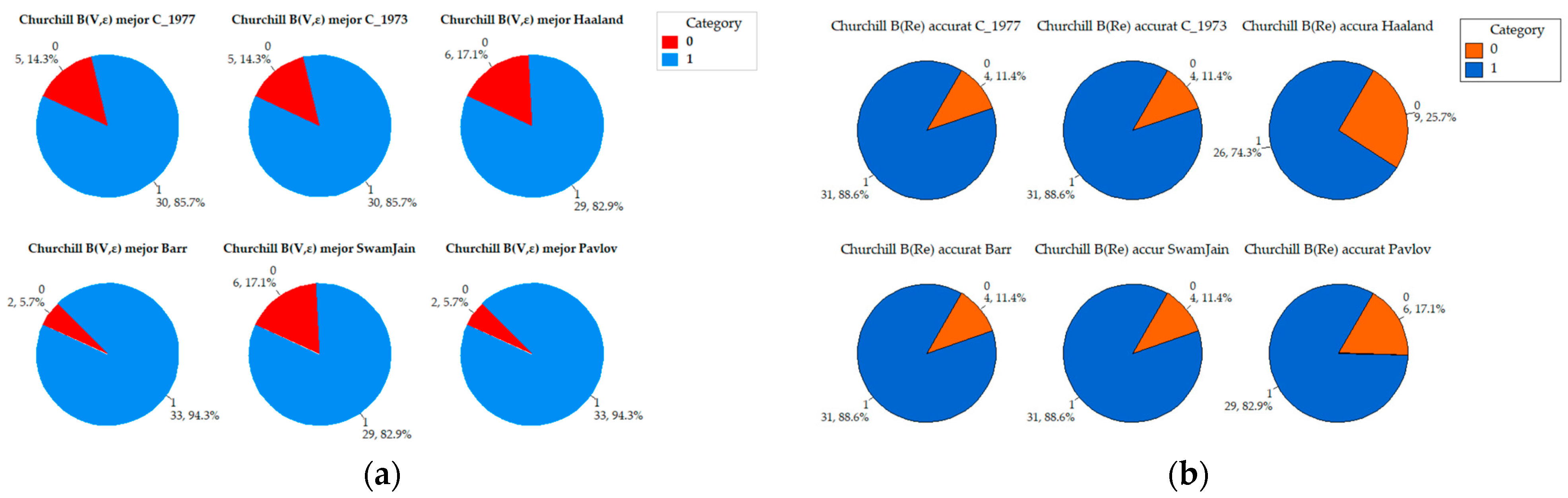
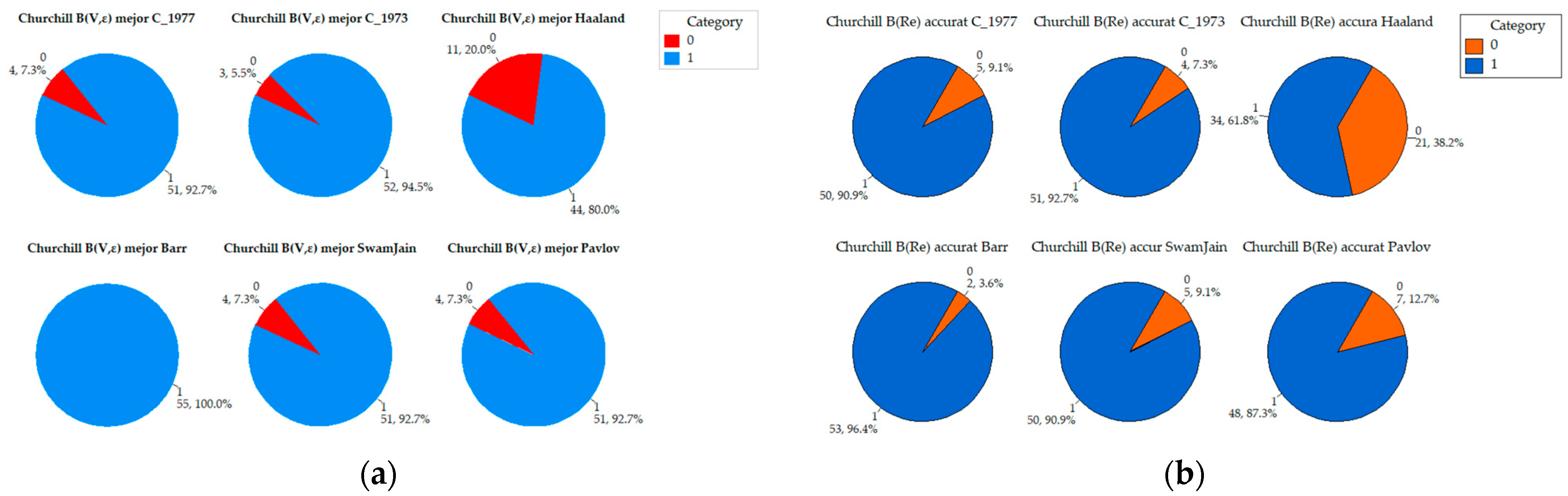
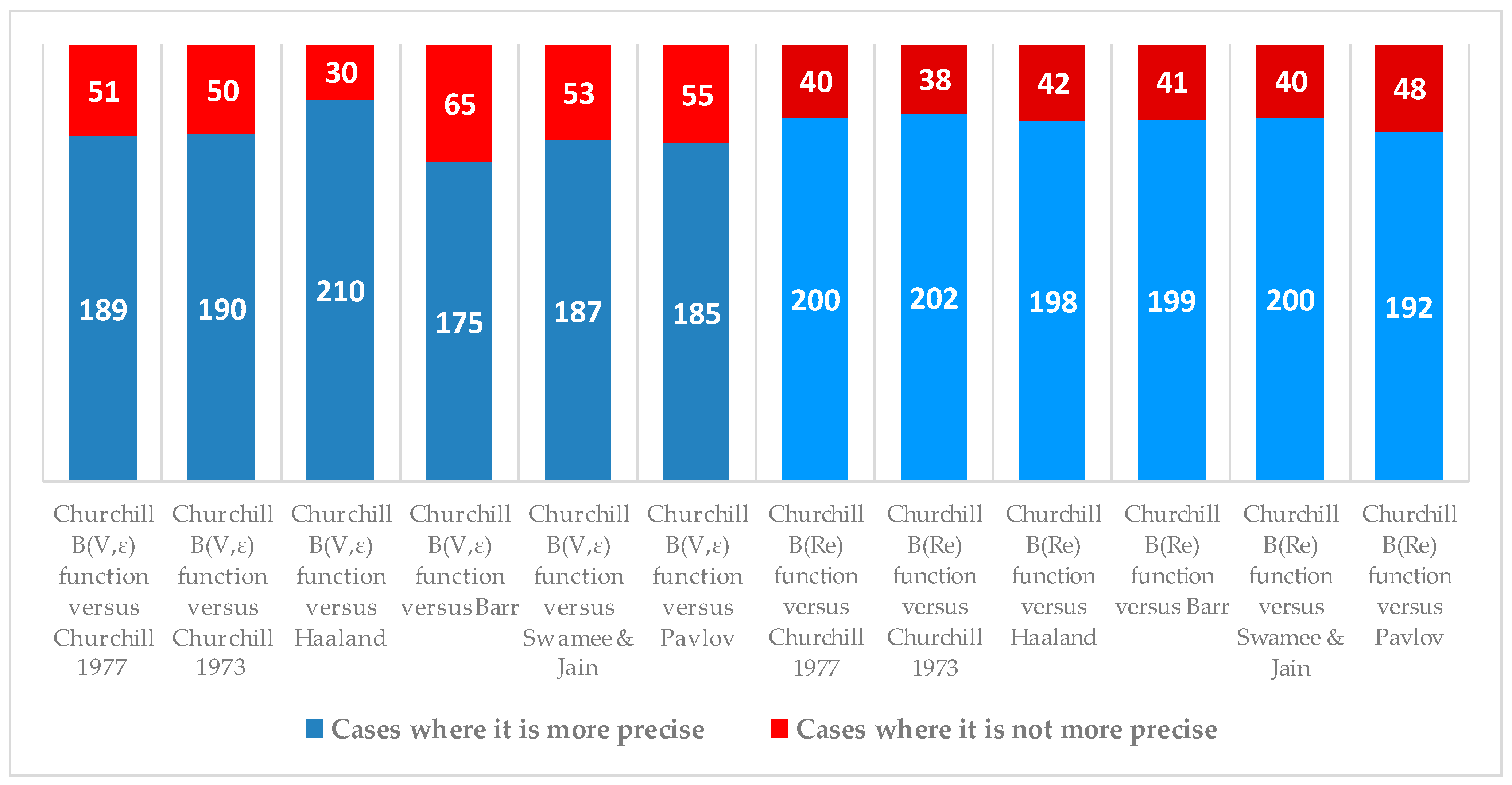
4.5. Analysis of Precision of the Churchill B(V,ε) Function in Comparative Cases
Comparative Analysis
5. Conclusions
5.1. Limitations of the Study
5.1.1. Sample Size and Flow Conditions
5.1.2. Fluid Properties
5.1.3. Comparison Scope
5.2. Future Work
5.2.1. Expand the Dataset and Flow Conditions
5.2.2. Explore Fluid Property Effects
5.2.3. Evaluating the Practicality and Impact of Incorporating the New Churchill B(V,ε) and Churchill B(Re) Expression in WDS Simulation Software (in the Most Current Version Available at the Time of the Future Evaluation)
5.2.4. Broaden the Comparison Scope
5.2.5. Experimentally Validate and Explore Advanced Techniques
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Comparative Analysis of the Precision of Friction Factor Estimation Methods: Evaluation of Absolute Error Grouped by Reynolds Number
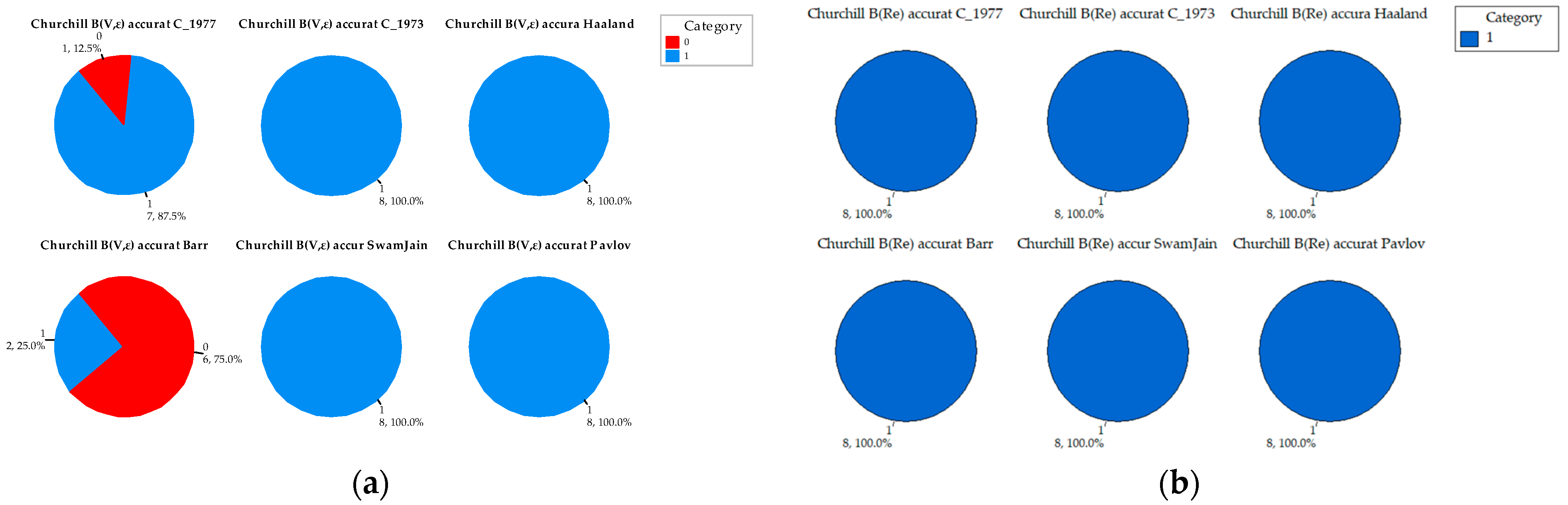
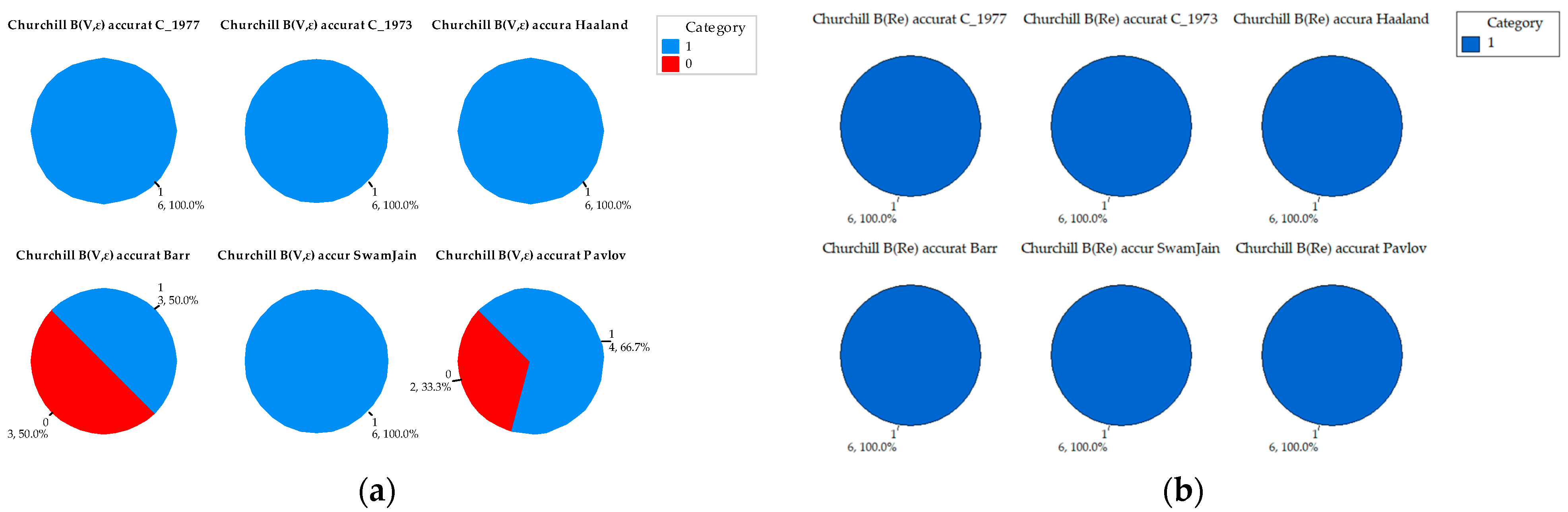
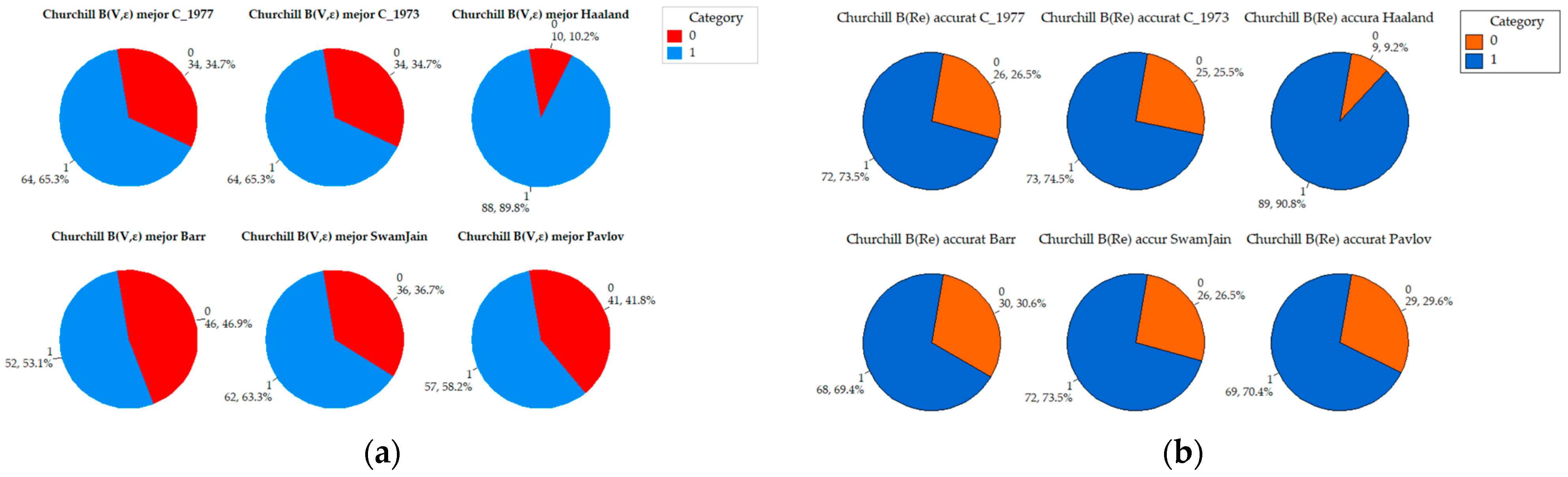
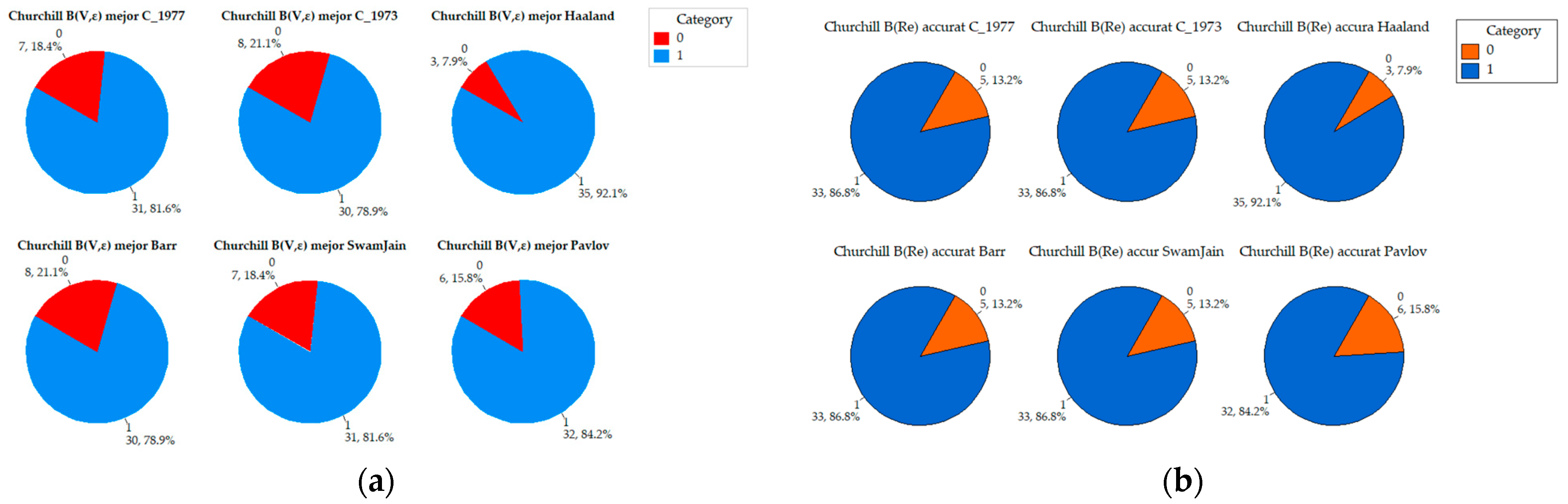
References
- Silverio, N.; Benavides-Muñoz, H.B. Determinación de pérdidas de carga en accesorios “k” de Sistemas Domiciliarios. Ecuadorian Sci. J. 2020, 4, 7–11. [Google Scholar] [CrossRef]
- Paloka, E.M.; Pažanin, I. Effects of boundary roughness and inertia on the fluid flow through a corrugated pipe and the formula for the Darcy–Weisbach friction coefficient. Int. J. Eng. Sci. 2020, 152, 103293. [Google Scholar] [CrossRef]
- Zierep, J.; Bühler, K. Principles of Fluid Mechanics: Fundamentals, Statics and Dynamics of Fluids; Springer Nature: Wiesbaden, Germany, 2022. [Google Scholar]
- Kundu, P.K.; Cohen, I.M.; Dowling, D.R. Fluid Mechanics, 6th ed.; Academic Press: Cambridge, MA, USA; Elsevier: Amsterdam, The Netherlands, 2016; p. 922. [Google Scholar]
- Wilkes, J.O. Fluid Mechanics for Chemical Engineers; Wilkes, J., Ed.; with contributions by Stacy G. Bike; Prentice Hall International Series in the Physical and Chemical Engineering Sciences; Prentice Hall PTR: Hoboken, NJ, USA, 1999; p. 599. [Google Scholar]
- Colebrook, C.F.; White, C.M. Experiments on turbulent flow in smooth pipes with particular reference to the transition region between smooth and rough pipe laws. Proc. R. Soc. Lond. A Math. Phys. Sci. 1937, 161, 391–418. [Google Scholar]
- Moody, L.F. Friction factors for pipe flow. Trans. ASME 1944, 66, 671–684. [Google Scholar] [CrossRef]
- Genić, S.; Aranđelović, I.; Kolendić, P.; Jarić, M.; Budimir, N.; Genić, V. A review of explicit approximations of Colebrook’s equation. FME Trans. 2011, 39, 67–71. [Google Scholar]
- Muzzo, L.E. Análise Comparativa de Correlações para o Fator de Atrito em Condutas. Ph.D. Thesis, Instituto Politecnico de Braganca (Portugal), Bragança, Portugal, 2019. [Google Scholar]
- Brkić, D.; Praks, P. Discussion of Approximate Analytical Solutions for the Colebrook Equation by Ali R. Vatankhah. J. Hydraul. Eng. 2020, 146, 07019011. [Google Scholar] [CrossRef]
- Plascencia, G.; Díaz–Damacillo, L.; Robles-Agudo, M. On the estimation of the friction factor: A review of recent approaches. SN Appl. Sci. 2020, 2, 163. [Google Scholar] [CrossRef]
- NACA. Laws of Flow in Rough Pipes; Technical Memorandum 1292. Translation of Strömungsgesetze in rauhen Rohren. VDI Forschungsheft 361. Beilage zu Forschung auf dem Gebiete des Ingenieurwesens. 1933. 1950. TM 1292; National Advisory Committee for Aeronautics: Washington, DC, USA, 1950. [Google Scholar]
- Wood, D.J. An explicit friction factor relationship. Civ. Eng. 1966, 36, 60–61. [Google Scholar]
- Churchill, S.W. Friction factor equations span all fluid flow regimes. Chem. Eng. 1977, 84, 91. [Google Scholar]
- Chen, N.H. An explicit equation for friction factor in pipe. Ind. Eng. Chem. Fundam. 1979, 18, 296–297. [Google Scholar] [CrossRef]
- Barr, D.I.H. Solutions of the Colebrook-White function for resistance to uniform turbulent flow. Proc. Inst. Civ. Eng. 1981, 71, 529–536. [Google Scholar]
- Churchill, S.W.; Chan, C. Improved correlating equations for the friction factor for fully turbulent flow in round tubes and between identical parallel plates, both smooth and naturally rough. Ind. Eng. Chem. Res. 1994, 33, 2016–2019. [Google Scholar] [CrossRef]
- Haaland, S.E. Simple and explicit formulas for the friction factor in turbulent pipe flow. J. Fluids Eng.-Trans. ASME 1983, 105, 243. [Google Scholar] [CrossRef]
- Swamee, P.K.; Jain, A.K. Explicit equations for pipe-flow problems. J. Hydraul. Div. 1976, 102, 657–664. [Google Scholar] [CrossRef]
- Nurudin, A.S. Error Review of Single Iteration Explicit Approximations of Colebrook’s Equation. Selangor Sci. Technol. Rev. (SeSTeR) 2021, 5, 22–30. [Google Scholar]
- Papaevangelou, G.; Evangelides, C.; Tzimopoulos, C. A new explicit relation for the friction factor coefficient in the Darcy–Weisbach equation. In Proceedings of the Tenth Conference on Protection and Restoration of the Environment, Corfu, Greece, 5–9 July 2010; Volume 166, pp. 5–9. [Google Scholar]
- Salmasi, F.; Khatibi, R.; Ghorbani, M. A study of friction factor formulation in pipes using artificial intelligence techniques and explicit equations. Turk. J. Eng. Environ. Sci. 2012, 36, 121–138. [Google Scholar]
- Bonakdari, H.; Zaji, A.H.; Shamshirband, S.; Hashim, R.; Petkovic, D. Sensitivity analysis of the discharge coefficient of a modified triangular side weir by adaptive neuro-fuzzy methodology. Measurement 2015, 73, 74–81. [Google Scholar] [CrossRef]
- Bemani, A.; Kazemi, A.; Ahmadi, M.; Yousefzadeh, R.; Moraveji, M.K. Rigorous modeling of frictional pressure loss in inclined annuli using artificial intelligence methods. J. Pet. Sci. Eng. 2022, 211, 110203. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Shiri, J.; Sadeghi, G.; Ghaemi, A. Prediction of the friction factor in pipes using model tree. ISH J. Hydraul. Eng. 2018, 24, 9–15. [Google Scholar] [CrossRef]
- Azizi, N.; Homayoon, R.; Hojjati, M.R. Predicting the Colebrook–White friction factor in the pipe flow by new explicit correlations. J. Fluids Eng. 2019, 141, 051201. [Google Scholar] [CrossRef]
- Olivares, A.; Guerra, R.; Alfaro, M.; Notte-cuello, E.; Puentes, L. Experimental evaluation of correlations used to calculate friction factor for turbulent flow in cylindrical pipes. Rev. Int. Métodos Numér. Cálculo Diseño Ing. 2019, 35, 15. [Google Scholar] [CrossRef]
- Churchill, S.W. Friction factor for laminar and turbulent flow of a fluid through a pipe. J. Fluid Mech. 1973, 52, 447–460. [Google Scholar]
- Jain, A.K. Accurate explicit equation for friction factor. J. Hydraul. Div. 1976, 102, 674–677. [Google Scholar] [CrossRef]
- Brkić, D. Review of explicit approximations to the Colebrook relation for flow friction. J. Pet. Sci. Eng. 2011, 77, 34–48. [Google Scholar] [CrossRef]
- Zigrang, D.J.; Sylvester, N.D. A review of explicit friction factor equations. J. Energy Resour. Technol. 1985, 107, 280–283. [Google Scholar] [CrossRef]
- Shacham, M. An Explicit Equation for Friction Factor in Pipe. Ind. Eng. Chem. Fundam. 1980, 19, 229–230. [Google Scholar] [CrossRef]
- Fang, X.P. Hydraulics of Pressurized Flow. In Water Encyclopedia; Lehr, J.H., Keeley, J., Eds.; Surface and Agricultural Water; Wiley Interscience: New York, NY, USA, 2005; Volume 3, pp. 196–199. [Google Scholar]
- Eck, B. Technische Stromungslehre. Springer-Verlag, 1973. Citado en: Cheng, N.-S. Simplified explicit equations for the Colebrook–White equation. J. Hydraul. Eng. 2011, 137, 1717–1719. [Google Scholar]
- Serghides, T.K. Estimate friction factor accurately. Chem. Eng. 1984, 91, 63–64. [Google Scholar]
- Sonnad, J.R.; Goudar, C.T. Turbulent flow friction factor calculation using a mathematically exact alternative to the Colebrook-White equation. J. Hydraul. Eng. 2006, 132, 863–867. [Google Scholar] [CrossRef]
- Avci, A.; Karagoz, I. A novel explicit equation for friction factor in smooth and rough pipes. J. Fluids Eng. 2009, 131, 061203. [Google Scholar] [CrossRef]
- Majid, N.; Nasser, T. Comparison of Explicit Relations for Calculating Colebrook Friction Factor in Pipe Network Analysis Using h-based Methods. Iran. J. Sci. Technol.-Trans. Civ. Eng. 2020, 44, 231–249. [Google Scholar] [CrossRef]
- Brkić, D. New explicit correlations for turbulent flow friction factor. Nucl. Eng. Des. 2011, 241, 4055–4059. [Google Scholar] [CrossRef]
- Asker, M.; Turgut, O.E.; Coban, M.T. A review of non-iterative friction factor correlations for the calculation of pressure drop in pipes. Bitlis Eren Univ. J. Sci. Technol. 2014, 4, 1–8. [Google Scholar]
- Vatankhah, A.R. Approximate analytical solutions for the Colebrook equation. J. Hydraul. Eng. 2018, 144, 06018007. [Google Scholar] [CrossRef]
- López-Silva, M.; Carmenates-Hernández, D.S.; Delgado-Hernández, N.; Chunga-Bereche, N. Explicit Pipe Friction Factor Equations: Evaluation, Classification, and Proposal. Rev. Fac. Ing. Univ. Antioq. 2024, 111, 38–47. [Google Scholar] [CrossRef]
- Narciso, D.A.; Pistikopoulos, E.N. Novel solution strategies for multiparametric nonlinear optimization problems with convex objective function and linear constraints. Optim. Eng. 2024, 1–29. [Google Scholar] [CrossRef]
- McWilliam, M.K.; Dicholkar, A.C.; Zahle, F.; Kim, T. Post-Optimum Sensitivity Analysis with Automatically Tuned Numerical Gradients Applied to Swept Wind Turbine Blades. Energies 2022, 15, 2998. [Google Scholar] [CrossRef]
- Rovnyak, S.M.; Chong, E.K.P.; Rovnyak, J. First-Order Conditions for Set-Constrained Optimization. Mathematics 2023, 11, 4274. [Google Scholar] [CrossRef]
- Chenche, L.E.P.; Mendoza, O.S.H.; Bandarra Filho, E.P. Comparison of Four Methods for Parameter Estimation of Mono- and Multi-Junction Photovoltaic Devices Using Experimental Data. Renew. Sustain. Energy Rev. 2018, 81, 2823–2838. [Google Scholar] [CrossRef]
- Brano, V.L.; Ciulla, G. An Efficient Analytical Approach for Obtaining a Five Parameters Model of Photovoltaic Modules Using Only Reference Data. Appl. Energy 2013, 111, 894–903. [Google Scholar] [CrossRef]
- Pavlov, K.F.; Romankov, P.G. Problemas y Ejemplos para el Curso de Operaciones Básicas y Aparatos en Tecnología Química; MIR: Moscú, Russia, 1981; pp. 19–548. [Google Scholar]
- Zeyu, Z.; Junrui, C.; Zhanbin, L.; Zengguang, X.; Peng, L. Approximations of the Darcy–Weisbach friction factor in a vertical pipe with full flow regime. Water Supply 2020, 20, 1321–1333. [Google Scholar] [CrossRef]
- Vatankhah, A.R.; Kouchakzadeh, S. Exact equations for pipe-flow problems. J. Hydraul. Res. 2009, 47, 537–538. [Google Scholar] [CrossRef]
- Montgomery, D.C.; Runger, G.C. Applied Statistics and Probability for Engineers; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Praks, P.; Brkić, D. Approximate flow friction factor: Estimation of the accuracy using Sobol’s quasi-random sampling. Axioms 2022, 11, 36. [Google Scholar] [CrossRef]
- Cardoso, F.C.; Berri, R.A.; Lucca, G.; Borges, E.N.; Mattos, V.L.D. Testes de Normalidade: Estudo dos Resíduos Obtidos na Modelagem da Tendência de Uma Série Temporal. Exacta 2023. accepted. [Google Scholar] [CrossRef]
- Law, M.; Jackson, D. Residual Plots for Linear Regression Models with Censored Outcome Data: A Refined Method for Visualizing Residual Uncertainty. Commun. Stat. Simul. Comput. 2017, 46, 3159–3171. [Google Scholar] [CrossRef] [PubMed]
- Qiu, M.; Ostfeld, A. A head formulation for the steady-state analysis of water distribution systems using an explicit and exact expression of the Colebrook–White equation. Water 2021, 13, 1163. [Google Scholar] [CrossRef]
- Rodriguez-Procel, W.; Benavides-Munoz, H. Hydraulic modeling and calibration of drinking water distribution networks. Tecnol. Cienc. Agua 2021, 12, 1–41. [Google Scholar]



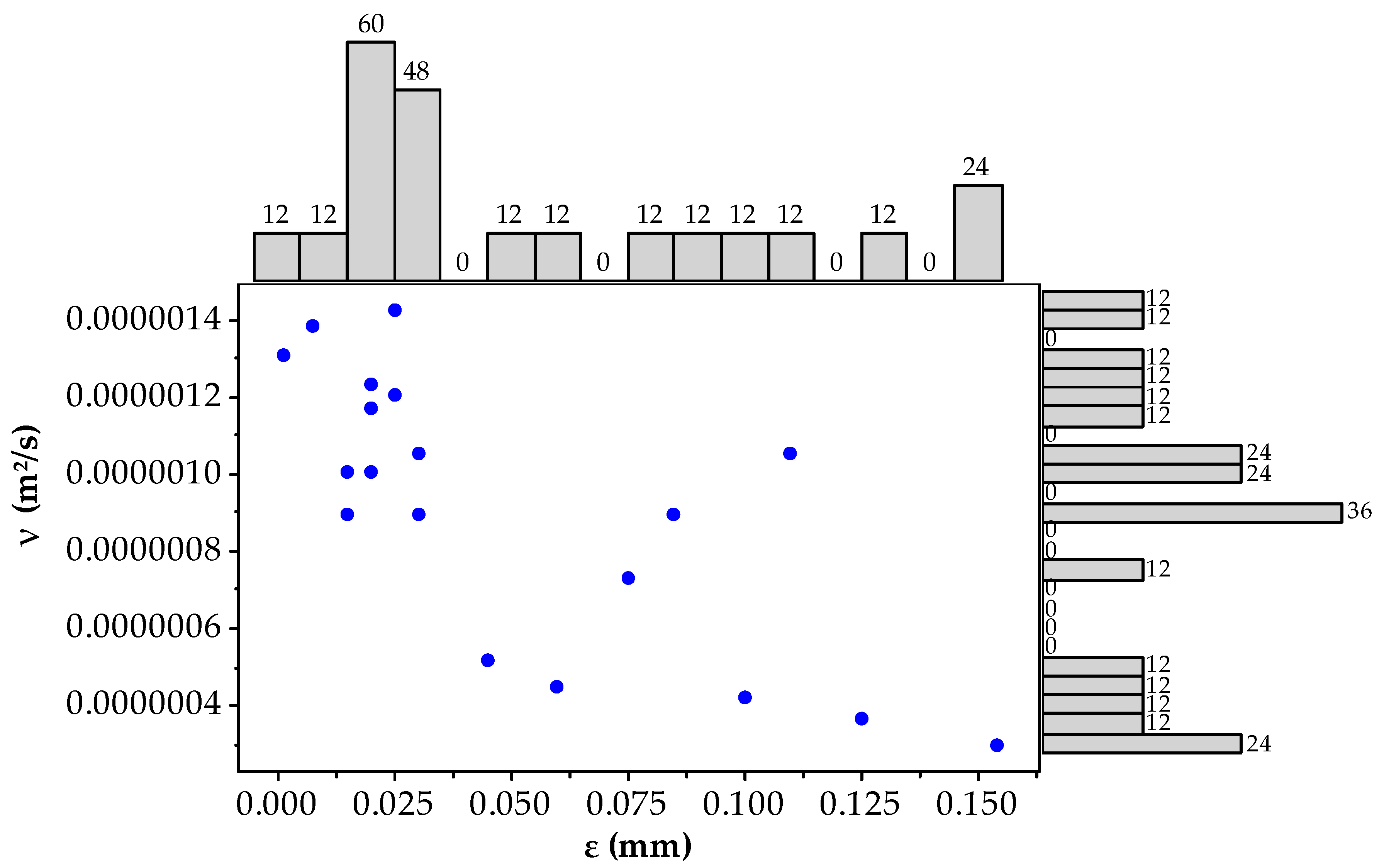
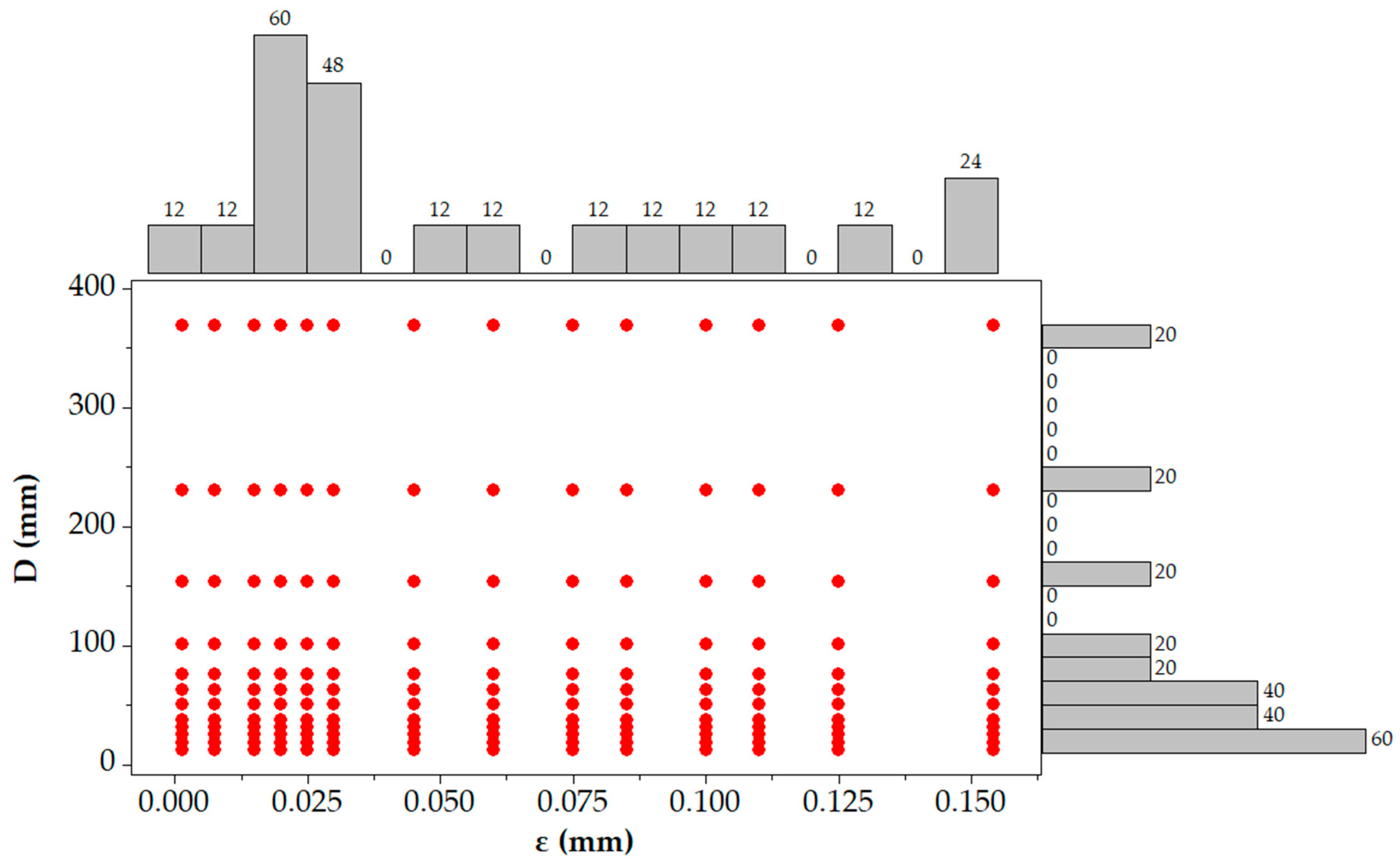
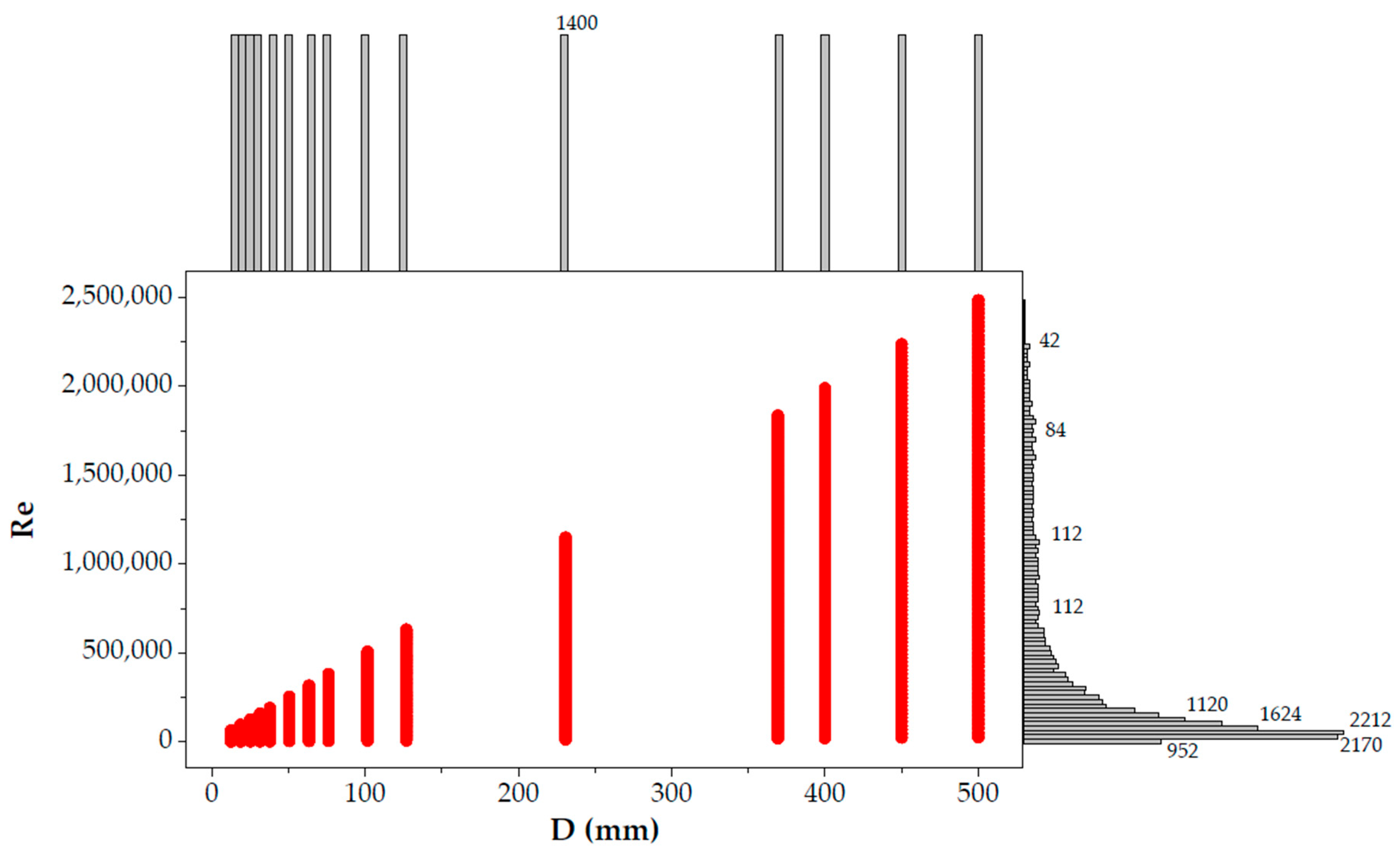
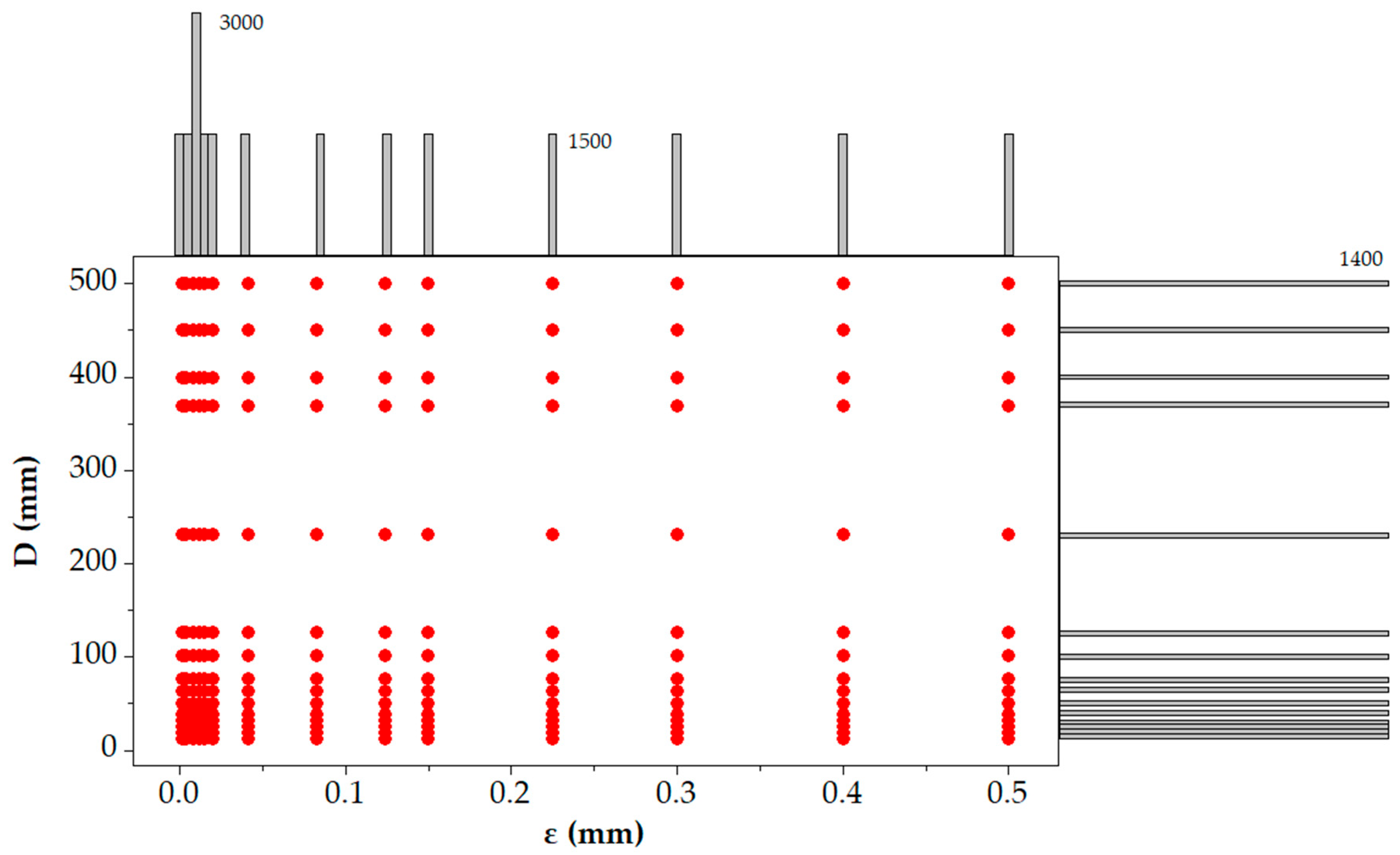




| ε (mm) | A | C | F | G | H | J | K | M |
|---|---|---|---|---|---|---|---|---|
| 0.001500 | 123.7852122 | 212.2573135 | 1.0055491 | 1.6833766 | 0.4692636 | 1.9972844 | 0.0997693 | 0.5860833 |
| 0.004125 | 123.7851978 | 212.2578596 | 1.0072233 | 1.6866568 | 0.4693298 | 1.9951957 | 0.0988583 | 0.5927161 |
| 0.008250 | 123.7610000 | 212.3220000 | 1.0073013 | 1.6916093 | 0.4700108 | 1.9885561 | 0.0975234 | 0.5808196 |
| 0.012375 | 113.0025564 | 212.8032189 | 1.0056746 | 1.6999204 | 0.4711697 | 1.9602235 | 0.0994546 | 0.4840345 |
| 0.015000 | 111.3241942 | 212.9999935 | 1.0059032 | 1.7143822 | 0.4679270 | 1.9670447 | 0.0967506 | 0.4961413 |
| 0.020000 | 110.3689523 | 213.2338135 | 1.0053641 | 1.7355369 | 0.4655973 | 1.9543190 | 0.0948980 | 0.4678421 |
| 0.041250 | 97.7282841 | 213.4999993 | 1.0036670 | 1.7961942 | 0.4565267 | 1.9213918 | 0.0928863 | 0.3869753 |
| 0.082500 | 93.3690383 | 214.0246813 | 1.0021490 | 1.8760483 | 0.4455154 | 1.8611599 | 0.0929679 | 0.2993959 |
| 0.123750 | 82.0499806 | 215.6486086 | 1.0013210 | 1.9256581 | 0.4330146 | 1.8263892 | 0.1023031 | 0.2445000 |
| 0.150000 | 81.7039696 | 215.6175947 | 1.0010905 | 1.9446166 | 0.4291668 | 1.8078201 | 0.1053104 | 0.2229616 |
| 0.225000 | 54.1653832 | 216.6564593 | 1.0006130 | 2.0735259 | 0.4004915 | 1.8259778 | 0.1050203 | 0.2008119 |
| 0.300000 | 36.9417419 | 217.8925943 | 1.0004194 | 2.0199180 | 0.4036004 | 1.7961138 | 0.1183420 | 0.1633125 |
| 0.400000 | 14.6831034 | 218.4900000 | 1.0002137 | 2.1366956 | 0.3792815 | 1.8614158 | 0.1124163 | 0.2019214 |
| 0.500000 | 14.6831034 | 219.5796607 | 1.0000903 | 2.0978096 | 0.3792815 | 1.8614158 | 0.1208657 | 0.1939013 |
| Variable | Symbol | SI Units |
|---|---|---|
| Absolute Roughness | ε | m |
| Internal Diameter | D | m |
| Velocity | V | m/s |
| Kinematic Viscosity | ν | m²/s |
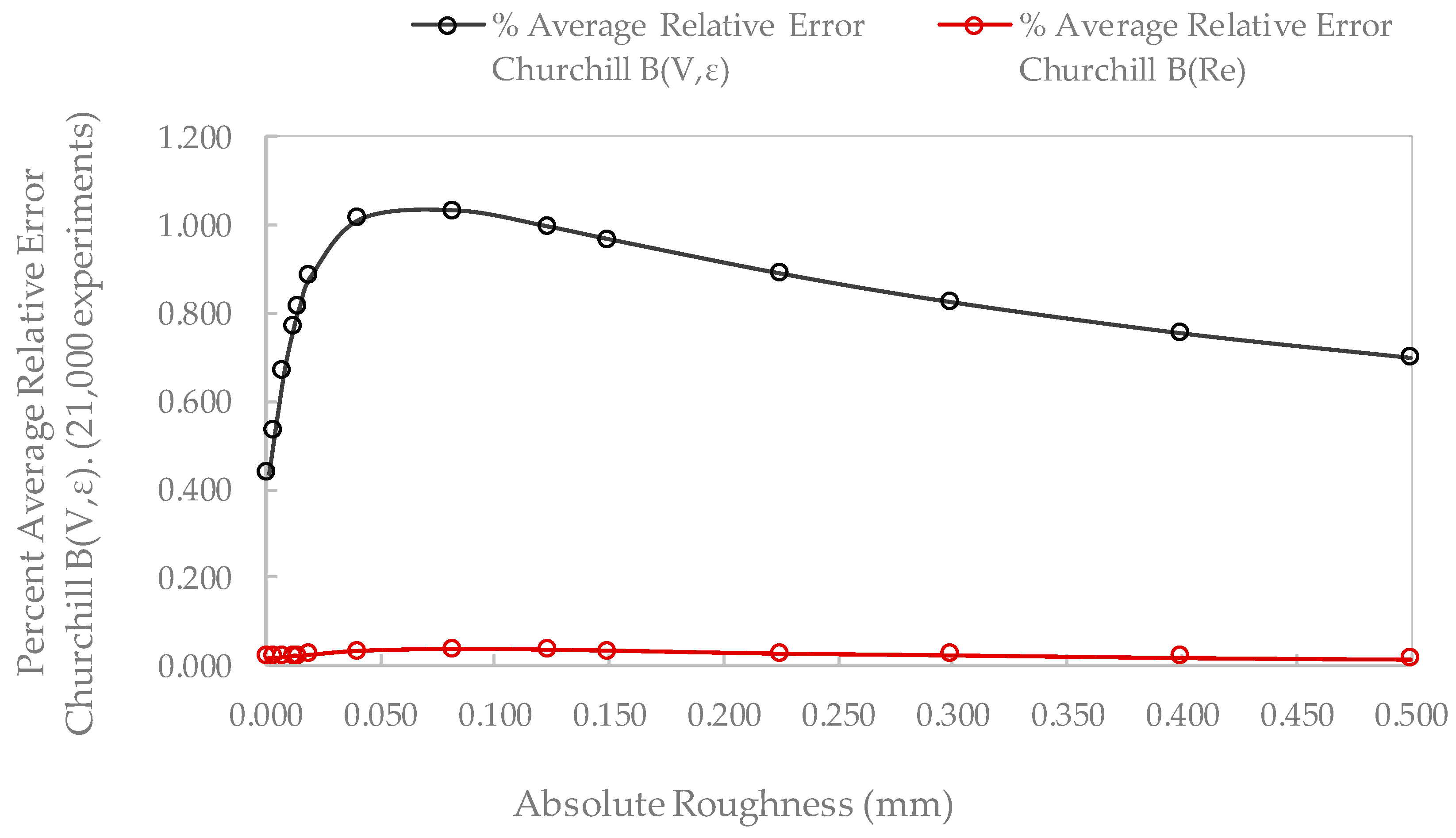
| Pipe Roughness ε (mm) | % Average Relative Error Churchill B(Re) | % Average Relative Error Churchill B(V,ε) |
|---|---|---|
| 0.001500 | 0.019808 | 0.437443 |
| 0.004125 | 0.018866 | 0.531191 |
| 0.008250 | 0.021176 | 0.671271 |
| 0.012375 | 0.023488 | 0.769550 |
| 0.015000 | 0.023097 | 0.817256 |
| 0.020000 | 0.025254 | 0.885935 |
| 0.041250 | 0.032443 | 1.013247 |
| 0.082500 | 0.036022 | 1.033179 |
| 0.123750 | 0.034340 | 0.996127 |
| 0.150000 | 0.032512 | 0.967613 |
| 0.225000 | 0.027243 | 0.889976 |
| 0.300000 | 0.023956 | 0.824762 |
| 0.400000 | 0.019154 | 0.754921 |
| 0.500000 | 0.016149 | 0.699515 |
| Model | Advantages | Disadvantages |
|---|---|---|
| Churchill B(Re) Function |
|
|
| Churchill B(V,ε) Function |
|
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benavides-Muñoz, H.M. Modification and Improvement of the Churchill Equation for Friction Factor Calculation in Pipes. Water 2024, 16, 2328. https://doi.org/10.3390/w16162328
Benavides-Muñoz HM. Modification and Improvement of the Churchill Equation for Friction Factor Calculation in Pipes. Water. 2024; 16(16):2328. https://doi.org/10.3390/w16162328
Chicago/Turabian StyleBenavides-Muñoz, Holger Manuel. 2024. "Modification and Improvement of the Churchill Equation for Friction Factor Calculation in Pipes" Water 16, no. 16: 2328. https://doi.org/10.3390/w16162328
APA StyleBenavides-Muñoz, H. M. (2024). Modification and Improvement of the Churchill Equation for Friction Factor Calculation in Pipes. Water, 16(16), 2328. https://doi.org/10.3390/w16162328







