The Contradictory Issue of the Impact of Antecedent Soil Moisture to Interrill Erosion in Clay Soil: A Two-Year Field Study
Abstract
1. Introduction
2. Materials and Methods
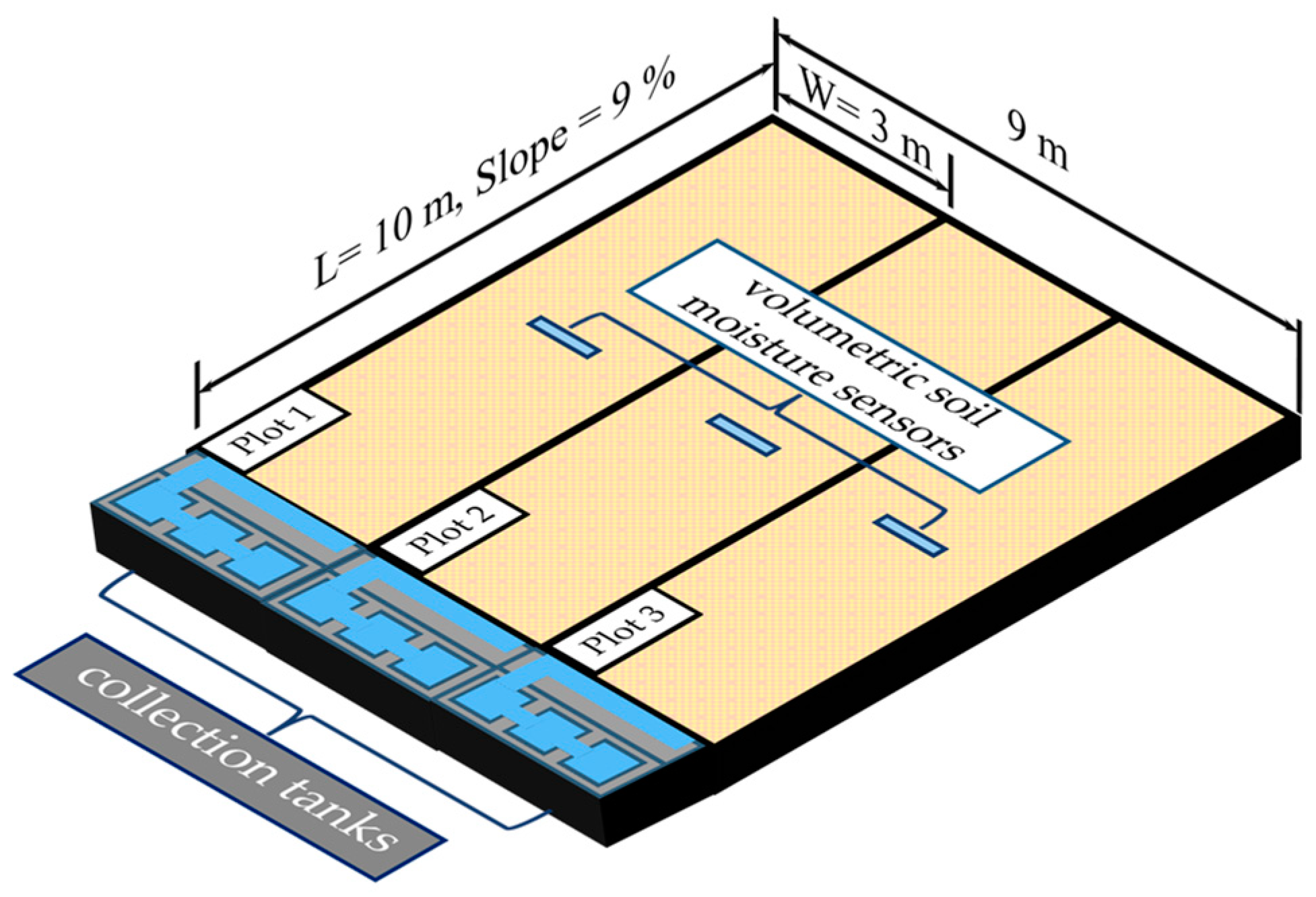
2.1. Experiment Site and Preparation
2.2. Data Collection and Analysis
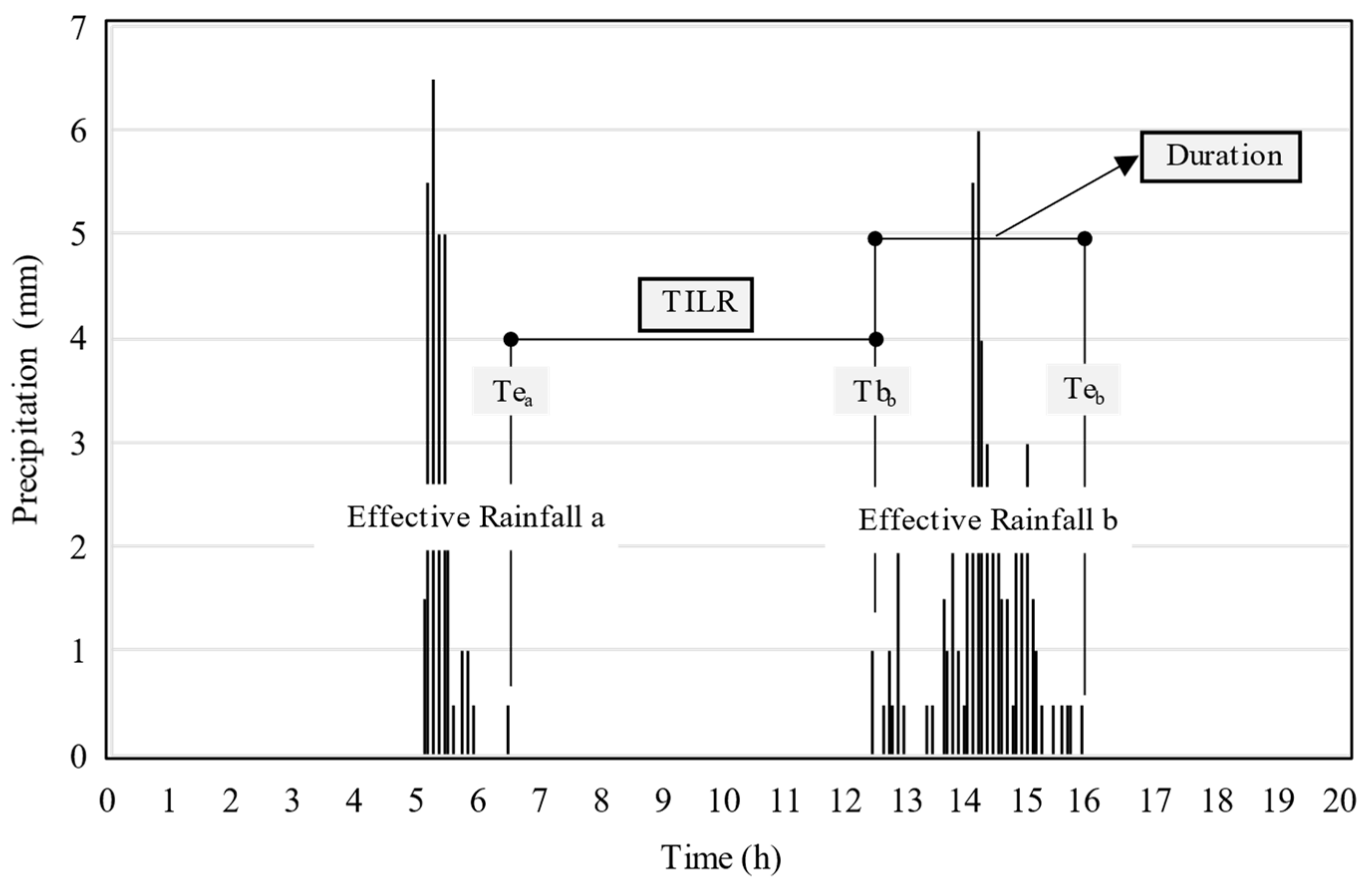
2.2.1. Rainfall
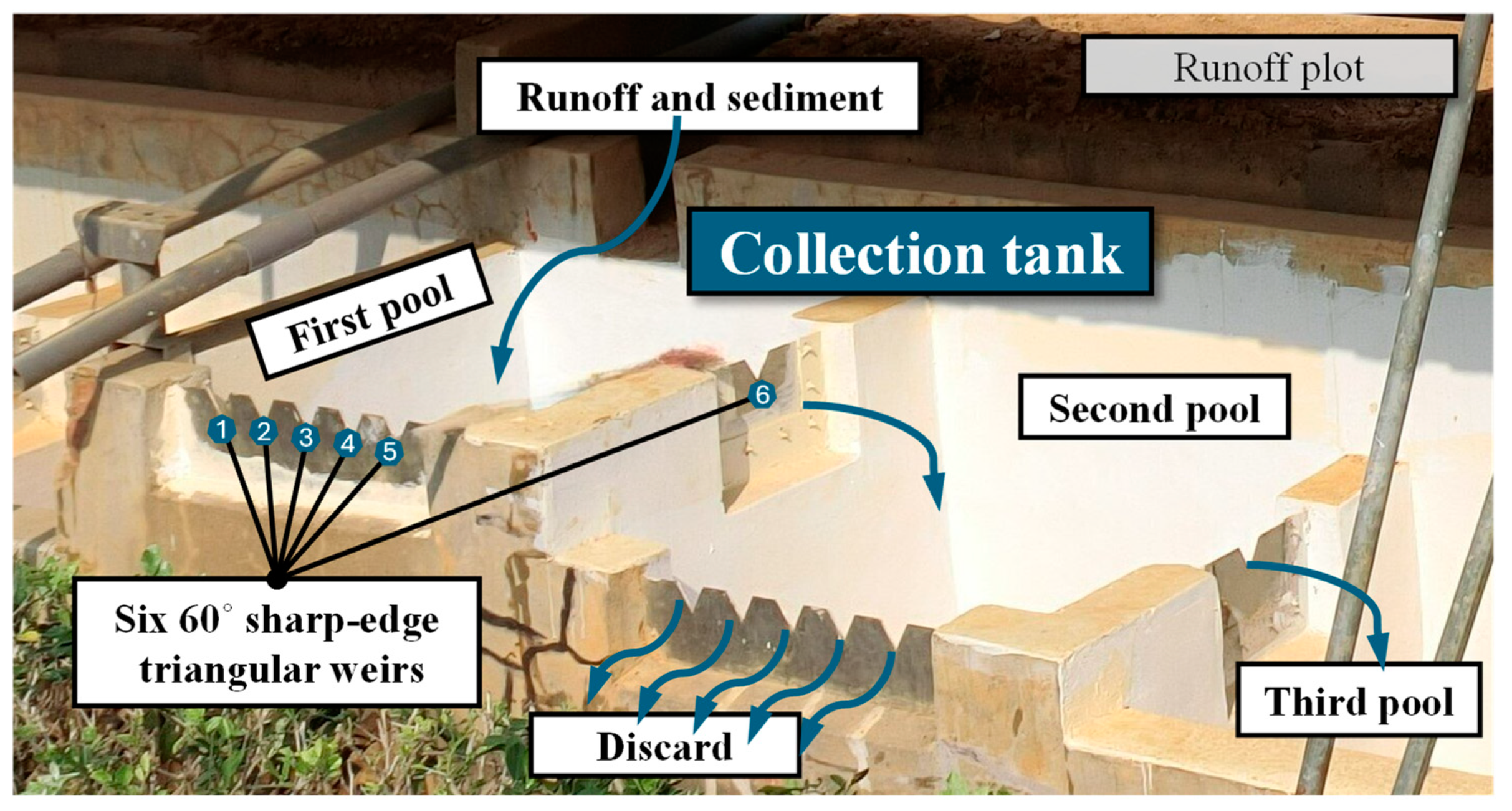
2.2.2. Runoff and Soil Loss
2.2.3. Antecedent Soil Moisture Content
3. Results and Discussion
4. Conclusions
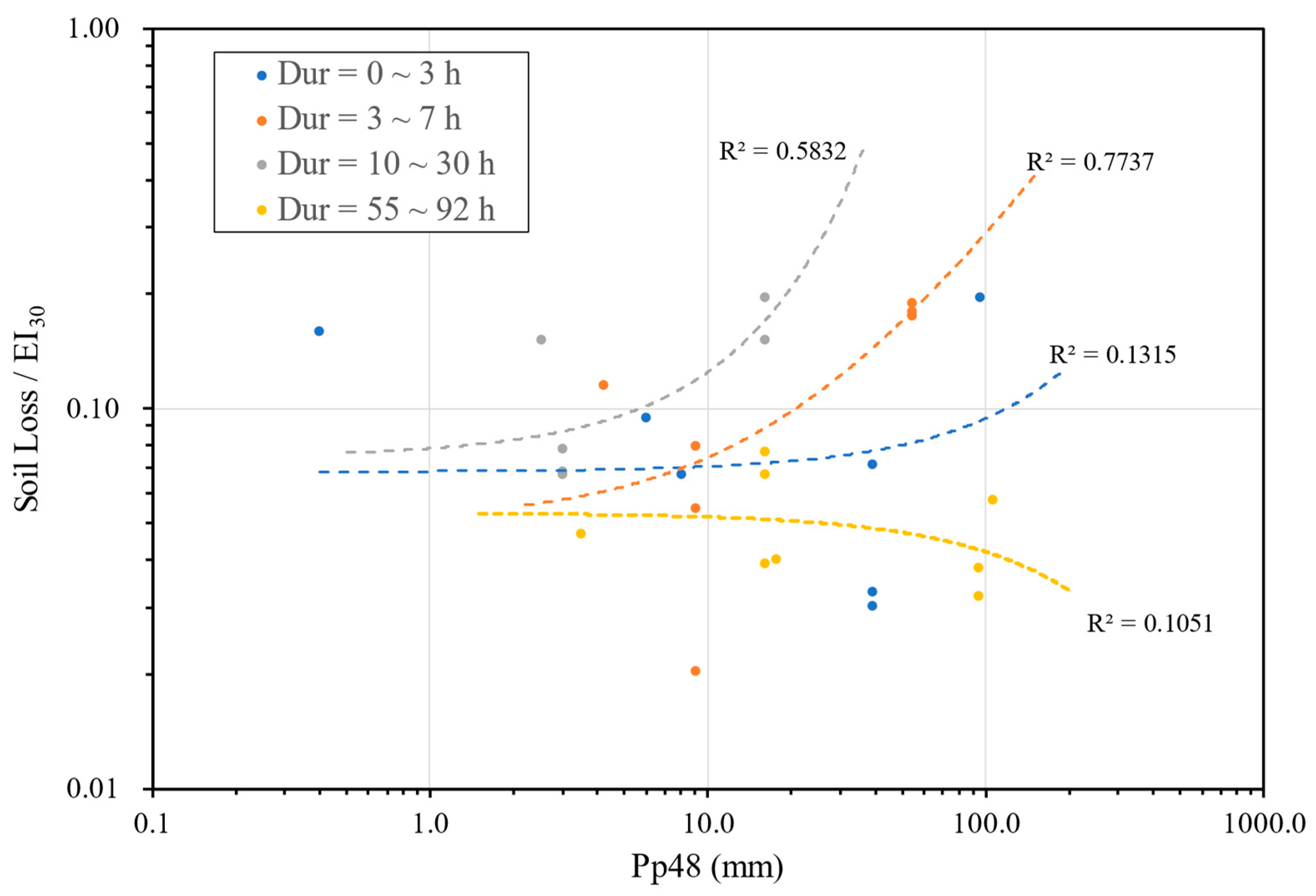
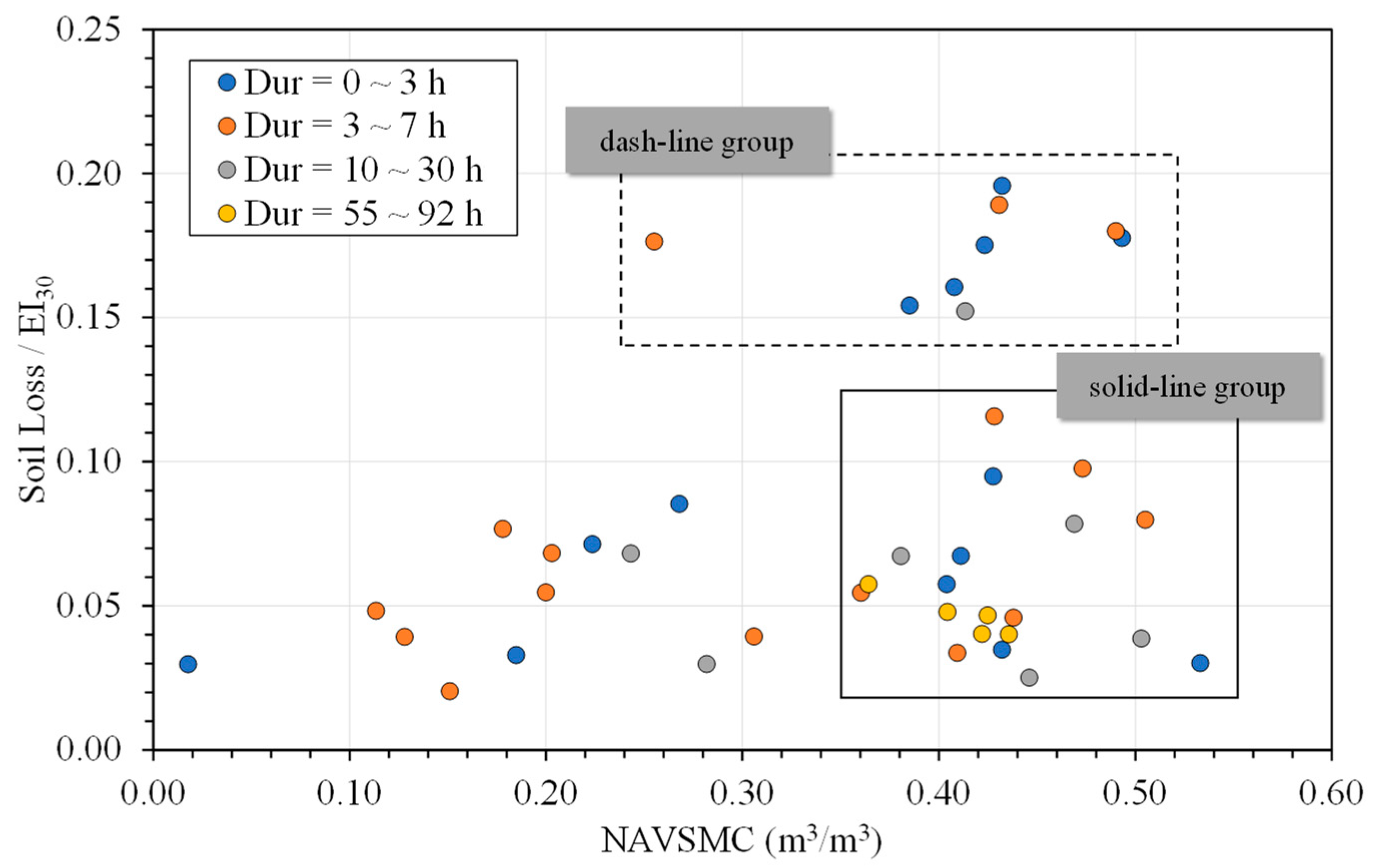
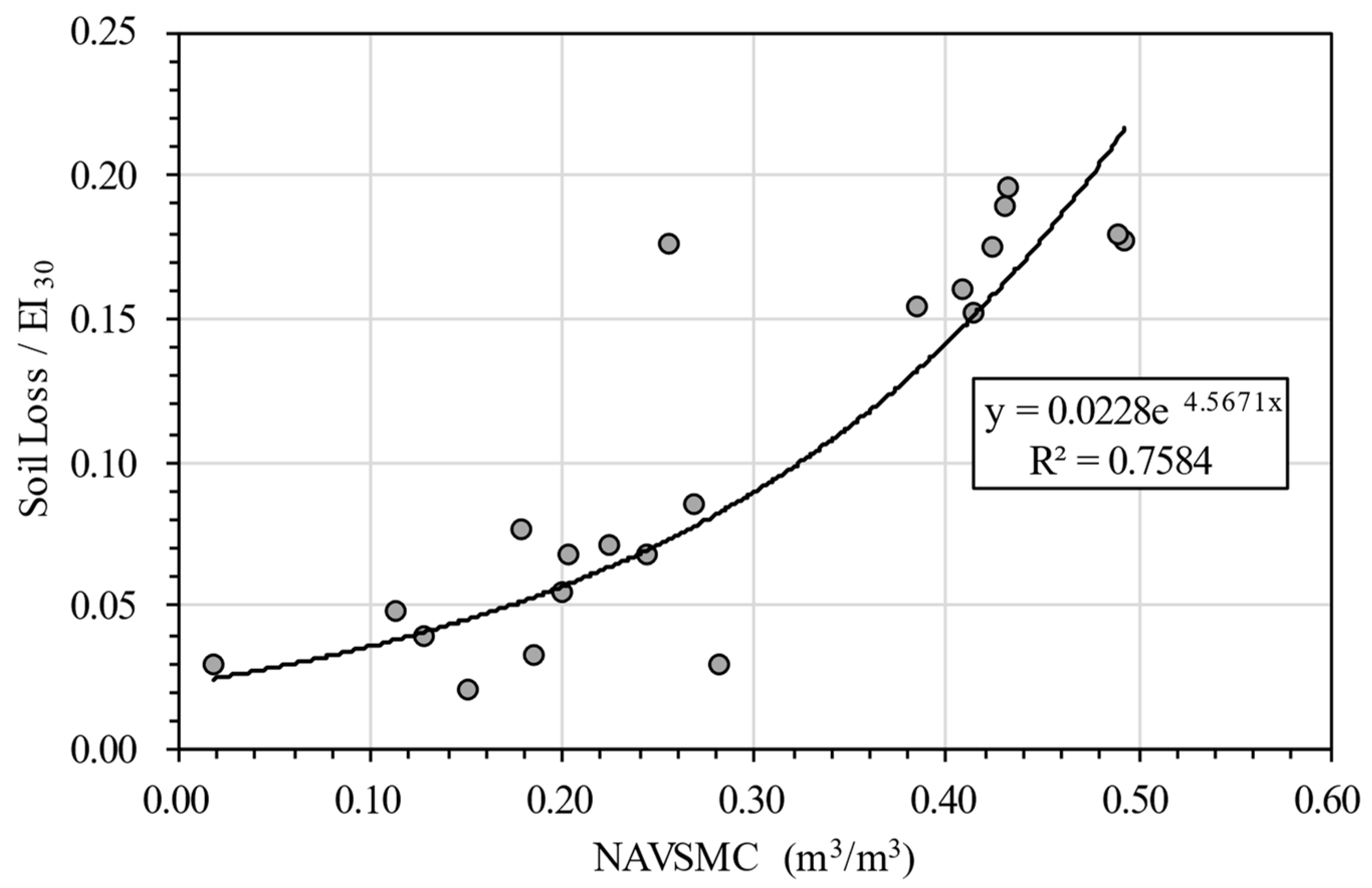
- Antecedent soil moisture content has an effect on unit area soil loss per EI30 (Soil Loss/EI30) in rainfall events with short durations, low rainfall amounts, and low Rainfall–Runoff Erosivity. When the average rainfall intensity is between 7.6 and 50 mm/h, which is classified into the heavy rain category by the World Meteorological Organization (2018), the impact of antecedent volumetric soil moisture content is negligible.
- There is a positive correlation between antecedent soil moisture content and unit area soil loss per EI30 (Soil Loss/EI30) for rainfall events with a 0~4 h duration. When the event duration exceeds 10 h, the impact of antecedent soil moisture on soil erosion can be ignored.
- The results of this field study on clay soil suggest that accumulative rain falling within 48 h (Pp48) prior to an effective erosion event is strongly correlated with unit area soil loss per Rainfall–Runoff Erosivity (Soil Loss/EI30). When the duration of an effective erosion event is less than 10 h, Pp48 makes a noticeable contribution to soil loss. However, when Pp48 is less than 20 mm, it does not affect soil loss in events with a 0~3 h duration.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bennett, H.H. Soil Conservation, 1st ed.; McGraw-Hill Book Company: New York, NY, USA, 1939. [Google Scholar]
- Kirkby, M.J.; Morgan, R.P.C. (Eds.) Soil Erosion; Wiley: Chichester, UK; New York, NY, USA, 1980; ISBN 978-0-471-27802-3. [Google Scholar]
- Wang, Y.; Liu, G.; Zhao, Z.; Wu, C.; Yu, B. Using Soil Erosion to Locate Nonpoint Source Pollution Risks in Coastal Zones: A Case Study in the Yellow River Delta, China. Environ. Pollut. 2021, 283, 117117. [Google Scholar] [CrossRef] [PubMed]
- Borah, D.K.; Bera, M. Watershed-Scale Hydrologic and Nonpoint-Source Pollution Models: Review of Mathematical Bases. Trans. Am. Soc. Agric. Eng. 2003, 46, 1553–1566. [Google Scholar] [CrossRef]
- An, J.; Zheng, F.L.; Han, Y. Effects of Rainstorm Patterns on Runoff and Sediment Yield Processes. Soil Sci. 2014, 179, 293–303. [Google Scholar] [CrossRef]
- Wischmeier, W.H.; Smith, D.D. Predicting Rainfall Erosion Losses: A Guide to Conservation Planning; Department of Agriculture, Science and Education Administration: Washington, DC, USA, 1978.
- Alewell, C.; Borrelli, P.; Meusburger, K.; Panagos, P. Using the USLE: Chances, Challenges and Limitations of Soil Erosion Modelling. Int. Soil Water Conserv. Res. 2019, 7, 203–225. [Google Scholar] [CrossRef]
- Renard, K.G.; Foster, G.R.; Weesies, G.A.; McCool, D.K.; Yoder, D.C. (Eds.) Predicting Soil Erosion by Water: A Guide to Conservation Planning with the Revised Universal Soil Loss Equation (RUSLE); Agricultural Handbook; USDA, Agricultural Research Service: Washington, DC, USA, 1997; ISBN 978-0-16-048938-9.
- Knisel, W.G. CREAMS: A Field Scale Model for Chemicals, Runoff, and Erosion from Agricultural Management Systems; Conservation Research Report; Department of Agriculture, Science and Education Administration: Washington, DC, USA, 1980.
- Young, R.; Onstad, C.; Bosch, D.; Anderson, W. AGNPS: A Non-Point-Source Pollution Model for Evaluating Agricultural Watersheds. J. Soil Water Conserv. 1989, 44, 168–173. [Google Scholar]
- Laflen, J.M.; Elliot, W.J.; Flanagan, D.C.; Meyer, C.R.; Nearing, M.A. WEPP-Predicting Water Erosion Using a Process-Based Model. J. Soil Water Conserv. 1997, 52, 96–102. [Google Scholar]
- Flanagan, D.; Gilley, J.; Franti, T. Water Erosion Prediction Project (WEPP): Development History, Model Capabilities, and Future Enhancements. Trans. ASABE 2007, 50, 1603–1612. [Google Scholar] [CrossRef]
- Arnold, J.G.; Fohrer, N. SWAT2000: Current Capabilities and Research Opportunities in Applied Watershed Modelling. Hydrol. Process. 2005, 19, 563–572. [Google Scholar] [CrossRef]
- Wischmeier, W.H.; Johnson, C.B.; Cross, B. Soil Erodibility Nomograph for Farmland and Construction Sites. J. Soil Water Conserv. 1971, 26, 5189. [Google Scholar]
- Knapen, A.; Poesen, J.; Govers, G.; Gyssels, G.; Nachtergaele, J. Resistance of Soils to Concentrated Flow Erosion: A Review. Earth Sci. Rev. 2007, 80, 75–109. [Google Scholar] [CrossRef]
- Kemper, W.D.; Rosenau, R.C. Soil Cohesion as Affected by Time and Water Content. Soil Sci. Soc. Am. J. 1984, 48, 1001–1006. [Google Scholar] [CrossRef]
- Shainberg, I.; Goldstein, D.; Levy, G.J. Rill Erosion Dependence on Soil Water Content, Aging, and Temperature. Soil Sci. Soc. Am. J. 1996, 60, 916–922. [Google Scholar] [CrossRef]
- Le Bissonnais, Y.; Bruand, A.; Jamagne, M. Laboratory Experimental Study of Soil Crusting: Relation between Aggregate Breakdown Mechanisms and Crust Structure. Catena 1989, 16, 377–392. [Google Scholar] [CrossRef]
- Holz, D.J.; Williard, K.W.J.; Edwards, P.J.; Schoonover, J.E. Soil Erosion in Humid Regions: A Review. J. Contemp. Water Res. Educ. 2015, 154, 48–59. [Google Scholar] [CrossRef]
- Wei, L.; Zhang, B.; Wang, M. Effects of Antecedent Soil Moisture on Runoff and Soil Erosion in Alley Cropping Systems. Agric. Water Manag. 2007, 94, 54–62. [Google Scholar] [CrossRef]
- Auerswald, K.; Mutchler, C.K.; McGregor, K.C. The Influence of Tillage-Induced Differences in Surface Moisture Content on Soil Erosion. Soil Tillage Res. 1994, 32, 41–50. [Google Scholar] [CrossRef]
- Fortesa, J.; Latron, J.; García-Comendador, J.; Company, J.; Estrany, J. Runoff and Soil Moisture as Driving Factors in Suspended Sediment Transport of a Small Mid-Mountain Mediterranean Catchment. Geomorphology 2020, 368, 107349. [Google Scholar] [CrossRef]
- Massari, C.; Pellet, V.; Tramblay, Y.; Crow, W.T.; Gründemann, G.J.; Hascoetf, T.; Penna, D.; Modanesi, S.; Brocca, L.; Camici, S.; et al. On the Relation between Antecedent Basin Conditions and Runoff Coefficient for European Floods. J. Hydrol. 2023, 625, 130012. [Google Scholar] [CrossRef]
- Jadidoleslam, N.; Hornbuckle, B.; Krajewski, W.; Mantilla, R.; Cosh, M. Analyzing Effects of Crops on SMAP Satellite-Based Soil Moisture Using a Rainfall-Runoff Model in the U.S. Corn Belt. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 15, 247–260. [Google Scholar] [CrossRef]
- Schoener, G.; Stone, M.C.; Thomas, C. Comparison of Seven Simple Loss Models for Runoff Prediction at the Plot, Hillslope and Catchment Scale in the Semiarid Southwestern U.S. J. Hydrol. 2021, 598, 126490. [Google Scholar] [CrossRef]
- Luk, S.-H.; Hamilton, H. Experimental Effects of Antecedent Moisture and Soil Strength on Rainwash Erosion of Two Luvisols, Ontario. Geoderma 1986, 37, 29–43. [Google Scholar] [CrossRef]
- Wang, L.; Zheng, F.; Hu, W.; Zhang, X.J.; Shi, H. Interactive Effects of Rainfall Intensity, Kinetic Energy and Antecedent Soil Moisture Regime on Splash Erosion in the Ultisol Region of South China. Catena 2023, 222, 106863. [Google Scholar] [CrossRef]
- Castillo, V.; Gomezplaza, A.; Martinezmena, M. The Role of Antecedent Soil Water Content in the Runoff Response of Semiarid Catchments: A Simulation Approach. J. Hydrol. 2003, 284, 114–130. [Google Scholar] [CrossRef]
- Truman, C.C.; Bradford, J.M.; Ferris, J.E. Antecedent Water Content and Rainfall Energy Influence on Soil Aggregate Breakdown. Soil Sci. Soc. Am. J. 1990, 54, 1385–1392. [Google Scholar] [CrossRef]
- Armenise, E.; Simmons, R.W.; Ahn, S.; Garbout, A.; Doerr, S.H.; Mooney, S.J.; Sturrock, C.J.; Ritz, K. Soil Seal Development under Simulated Rainfall: Structural, Physical and Hydrological Dynamics. J. Hydrol. 2018, 556, 211–219. [Google Scholar] [CrossRef] [PubMed]
- Auerswald, K. Influence of Initial Moisture and Time since Tillage on Surface Structure Breakdown and Erosion of a Loessial Soil. Catena Suppl. 1993, 24, 93–101. [Google Scholar]
- Ma, R.-M.; Li, Z.-X.; Cai, C.-F.; Wang, J.-G. The Dynamic Response of Splash Erosion to Aggregate Mechanical Breakdown through Rainfall Simulation Events in Ultisols (Subtropical China). Catena 2014, 121, 279–287. [Google Scholar] [CrossRef]
- Wu, C.-C.; Wang, A.-B. Drop Size Characteristics and Erosive Kinetic Energy of Natural Rainstorms in Pingtung Laopi Area. Chin. Soil Water Conserv. 1996, 27, 151–165. (In Chinese) [Google Scholar]
- Secretariat of the World Meteorological Organization. Guide to Meteorological Instruments and Methods of Observation; Secretariat of the World Meteorological Organization: Geneva, Switzerland, 2018; ISBN 978-92-63-16008-9. [Google Scholar]


| Event No. | Unit Area Soil Loss | Unit Area Runoff Volume | Precp. | EI30 | Soil Loss/EI30 | C | NAVSMC | Pp12 | Pp24 | Pp48 | Pp72 | Pp120 | Event Duration | TILR |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| kg/m2 | mm3/mm2 | mm | MJ-mm/ ha-h | (kg/m2)/ (MJ-mm/ha-h) | - | m3/m3 | mm | mm | mm | mm | mm | h | h | |
| 1 | 0.080 | 9.60 | 34.0 | 391.75 | 0.020 | 0.28 | 0.15 | 0.0 | 9.0 | 9.0 | 9.0 | 9.5 | 3.17 | 213.00 |
| 2 | 0.214 | 9.20 | 34.0 | 391.75 | 0.055 | 0.27 | 0.20 | 0.0 | 9.0 | 9.0 | 9.0 | 9.5 | 3.17 | 213.00 |
| 3 | 0.313 | 17.02 | 34.0 | 391.75 | 0.080 | 0.50 | 0.51 | 0.0 | 9.0 | 9.0 | 9.0 | 9.5 | 3.17 | 213.00 |
| 4 | 0.177 | 19.58 | 39.0 | 451.04 | 0.039 | 0.50 | 0.13 | 0.0 | 0.0 | 0.0 | 34.0 | 43.0 | 3.33 | 68.83 |
| 5 | 0.346 | 19.43 | 39.0 | 451.04 | 0.077 | 0.50 | 0.18 | 0.0 | 0.0 | 0.0 | 34.0 | 43.0 | 3.33 | 68.83 |
| 6 | 0.440 | 18.72 | 39.0 | 451.04 | 0.098 | 0.48 | 0.47 | 0.0 | 0.0 | 0.0 | 34.0 | 43.0 | 3.33 | 68.83 |
| 7 | 0.972 | 61.85 | 87.5 | 2951.65 | 0.033 | 0.71 | 0.18 | 0.0 | 39.0 | 39.0 | 39.0 | 82.0 | 2.42 | 20.25 |
| 8 | 2.109 | 39.19 | 87.5 | 2951.65 | 0.071 | 0.45 | 0.22 | 0.0 | 39.0 | 39.0 | 39.0 | 82.0 | 2.42 | 20.25 |
| 9 | 0.890 | 77.77 | 87.5 | 2951.65 | 0.030 | 0.89 | 0.53 | 0.0 | 39.0 | 39.0 | 39.0 | 82.0 | 2.42 | 20.25 |
| 10 | 0.178 | 19.40 | 23.0 | 117.47 | 0.151 | 0.84 | 0.27 | 0.5 | 3.5 | 16.0 | 21.5 | 114.0 | 10.83 | 104.00 |
| 11 | 0.230 | 16.90 | 23.0 | 117.47 | 0.196 | 0.73 | 0.34 | 0.5 | 3.5 | 16.0 | 21.5 | 114.0 | 10.83 | 104.00 |
| 12 | 1.335 | 91.31 | 117.5 | 1731.80 | 0.077 | 0.78 | 0.28 | 0.5 | 3.5 | 16.0 | 21.5 | 114.0 | 61.33 | 11.08 |
| 13 | 0.679 | 21.39 | 117.5 | 1731.80 | 0.039 | 0.18 | 0.34 | 0.5 | 3.5 | 16.0 | 21.5 | 114.0 | 61.33 | 11.08 |
| 14 | 1.166 | 48.37 | 117.5 | 1731.80 | 0.067 | 0.41 | 0.56 | 0.5 | 3.5 | 16.0 | 21.5 | 114.0 | 61.33 | 11.08 |
| 15 | 2.969 | 93.65 | 402.5 | 7811.82 | 0.038 | 0.23 | 0.29 | 0.5 | 2.0 | 94.5 | 117.5 | 144.0 | 91.50 | 10.50 |
| 16 | 2.511 | 53.17 | 402.5 | 7811.82 | 0.032 | 0.13 | 0.25 | 0.5 | 2.0 | 94.5 | 117.5 | 144.0 | 91.50 | 10.50 |
| 17 | 1.689 | 106.28 | 197.5 | 2476.39 | 0.068 | 0.54 | 0.24 | 0.0 | 0.0 | 3.0 | 3.0 | 25.0 | 28.00 | 133.58 |
| 18 | 1.666 | 45.95 | 197.5 | 2476.39 | 0.067 | 0.23 | 0.38 | 0.0 | 0.0 | 3.0 | 3.0 | 25.0 | 28.00 | 133.58 |
| 19 | 1.944 | 114.89 | 197.5 | 2476.39 | 0.078 | 0.58 | 0.47 | 0.0 | 0.0 | 3.0 | 3.0 | 25.0 | 28.00 | 133.58 |
| 20 | 0.256 | 32.20 | 41.5 | 374.80 | 0.068 | 0.78 | 0.20 | 0.0 | 0.0 | 0.0 | 0.0 | 176.5 | 4.33 | 97.08 |
| 21 | 0.205 | 20.68 | 41.5 | 374.80 | 0.055 | 0.50 | 0.36 | 0.0 | 0.0 | 0.0 | 0.0 | 176.5 | 4.33 | 97.08 |
| 22 | 0.172 | 24.73 | 41.5 | 374.80 | 0.046 | 0.60 | 0.44 | 0.0 | 0.0 | 0.0 | 0.0 | 176.5 | 4.33 | 97.08 |
| 23 | 0.320 | 48.77 | 54.0 | 1070.56 | 0.030 | 0.90 | 0.28 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 13.08 | 121.42 |
| 24 | 0.269 | 21.05 | 54.0 | 1070.56 | 0.025 | 0.39 | 0.45 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 13.08 | 121.42 |
| 25 | 0.414 | 52.16 | 54.0 | 1070.56 | 0.039 | 0.97 | 0.50 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 13.08 | 121.42 |
| 26 | 0.041 | 8.55 | 11.5 | 23.52 | 0.176 | 0.74 | 0.26 | 0.0 | 0.5 | 54.0 | 54.0 | 54.0 | 5.75 | 18.67 |
| 27 | 0.044 | 3.97 | 11.5 | 23.52 | 0.189 | 0.35 | 0.43 | 0.0 | 0.5 | 54.0 | 54.0 | 54.0 | 5.75 | 18.67 |
| 28 | 0.042 | 8.74 | 11.5 | 23.52 | 0.180 | 0.76 | 0.49 | 0.0 | 0.5 | 54.0 | 54.0 | 54.0 | 5.75 | 18.67 |
| 29 | 0.051 | 15.28 | 19.5 | 59.37 | 0.085 | 0.78 | 0.27 | 0.0 | 0.0 | 0.0 | 11.0 | 65.0 | 1.67 | 54.50 |
| 30 | 0.104 | 12.95 | 19.5 | 59.37 | 0.175 | 0.66 | 0.42 | 0.0 | 0.0 | 0.0 | 11.0 | 65.0 | 1.67 | 54.50 |
| 31 | 0.105 | 16.30 | 19.5 | 59.37 | 0.178 | 0.84 | 0.49 | 0.0 | 0.0 | 0.0 | 11.0 | 65.0 | 1.67 | 54.50 |
| 32 | 0.279 | 39.50 | 54.5 | 578.57 | 0.048 | 0.72 | 0.11 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 3.50 | 167.00 |
| 33 | 0.228 | 23.92 | 54.5 | 578.57 | 0.039 | 0.44 | 0.31 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 3.50 | 167.00 |
| 34 | 0.195 | 35.72 | 54.5 | 578.57 | 0.034 | 0.66 | 0.41 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 3.50 | 167.00 |
| 35 | 0.108 | 14.31 | 29.0 | 361.82 | 0.030 | 0.49 | 0.02 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.42 | 307.33 |
| 36 | 0.208 | 14.95 | 29.0 | 361.82 | 0.058 | 0.52 | 0.40 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.42 | 307.33 |
| 37 | 0.126 | 16.78 | 29.0 | 361.82 | 0.035 | 0.58 | 0.43 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.42 | 307.33 |
| 38 | 6.405 | 453.29 | 551.0 | 11,126.44 | 0.058 | 0.82 | 0.36 | 0.0 | 45.0 | 106.0 | 106.0 | 106.0 | 86.83 | 21.92 |
| 39 | 1.536 | 101.54 | 192.5 | 3204.80 | 0.048 | 0.53 | 0.40 | 0.0 | 0.0 | 0.0 | 18.0 | 538.0 | 58.50 | 52.58 |
| 40 | 1.099 | 51.77 | 62.0 | 1631.76 | 0.067 | 0.83 | 0.41 | 0.0 | 0.0 | 8.0 | 9.0 | 13.5 | 1.25 | 307.50 |
| 41 | 0.362 | 1.22 | 23.5 | 234.68 | 0.154 | 0.05 | 0.39 | 0.0 | 0.0 | 0.0 | 0.0 | 4.0 | 1.17 | 450.67 |
| 42 | 0.613 | 50.35 | 170.5 | 1311.07 | 0.047 | 0.30 | 0.42 | 0.0 | 0.0 | 3.5 | 6.0 | 46.5 | 55.92 | 107.27 |
| 43 | 0.413 | 18.75 | 24.5 | 211.19 | 0.196 | 0.77 | 0.43 | 0.0 | 16.0 | 95.5 | 140.5 | 172.5 | 2.25 | 20.17 |
| 44 | 0.012 | 0.85 | 6.0 | 7.96 | 0.152 | 0.14 | 0.41 | 0.0 | 1.5 | 2.5 | 2.5 | 12.0 | 22.00 | 91.83 |
| 45 | 0.058 | 11.14 | 12.5 | 61.42 | 0.095 | 0.89 | 0.43 | 0.0 | 0.5 | 6.0 | 16.5 | 19.0 | 0.75 | 49.25 |
| 46 | 0.131 | 20.47 | 58.0 | 325.25 | 0.040 | 0.35 | 0.42 | 0.0 | 0.0 | 0.0 | 14.0 | 31.5 | 61.00 | 72.08 |
| 47 | 0.717 | 97.78 | 198.8 | 1785.67 | 0.040 | 0.49 | 0.44 | 0.0 | 0.5 | 17.5 | 44.0 | 58.0 | 81.67 | 22.83 |
| 48 | 0.009 | 0.05 | 5.6 | 7.72 | 0.116 | 0.01 | 0.43 | 0.0 | 4.0 | 4.2 | 11.6 | 176.6 | 6.67 | 16.58 |
| 49 | 0.105 | 9.42 | 11.6 | 65.44 | 0.161 | 0.81 | 0.41 | 0.0 | 0.0 | 0.4 | 6.0 | 10.0 | 0.83 | 47.00 |
| Unit Area Soil Loss (kg/m2) | Unit Area Runoff Volume (mm3/ mm2) | Precp. (mm) | NAVSMC (m3/m3) | Pp12 (mm) | Pp24 (mm) | Pp48 (mm) | Pp72 (mm) | Pp120 (mm) | Duration (h) | TILR (h) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Unit area soil loss | 1.0 | ||||||||||
| Unit area runoff volume | 0.90 | 1.0 | |||||||||
| Precp. | 0.92 | 0.81 | 1.0 | ||||||||
| NAVSMC | −0.02 | 0.03 | −0.03 | 1.0 | |||||||
| Pp12 | 0.22 | 0.04 | 0.32 | −0.06 | 1.0 | ||||||
| Pp24 | 0.53 | 0.52 | 0.32 | −0.06 | −0.06 | 1.0 | |||||
| Pp48 | 0.61 | 0.46 | 0.60 | −0.01 | 0.31 | 0.51 | 1.0 | ||||
| Pp72 | 0.53 | 0.38 | 0.55 | −0.02 | 0.31 | 0.40 | 0.94 | 1.0 | |||
| Pp120 | 0.24 | 0.19 | 0.27 | 0.07 | 0.25 | 0.09 | 0.22 | 0.29 | 1.0 | ||
| Duration | 0.65 | 0.56 | 0.82 | 0.09 | 0.53 | 0.06 | 0.44 | 0.45 | 0.34 | 1.0 | |
| TILR | −0.23 | −0.20 | −0.26 | −0.13 | −0.28 | −0.26 | −0.44 | −0.50 | −0.41 | −0.38 | 1.00 |
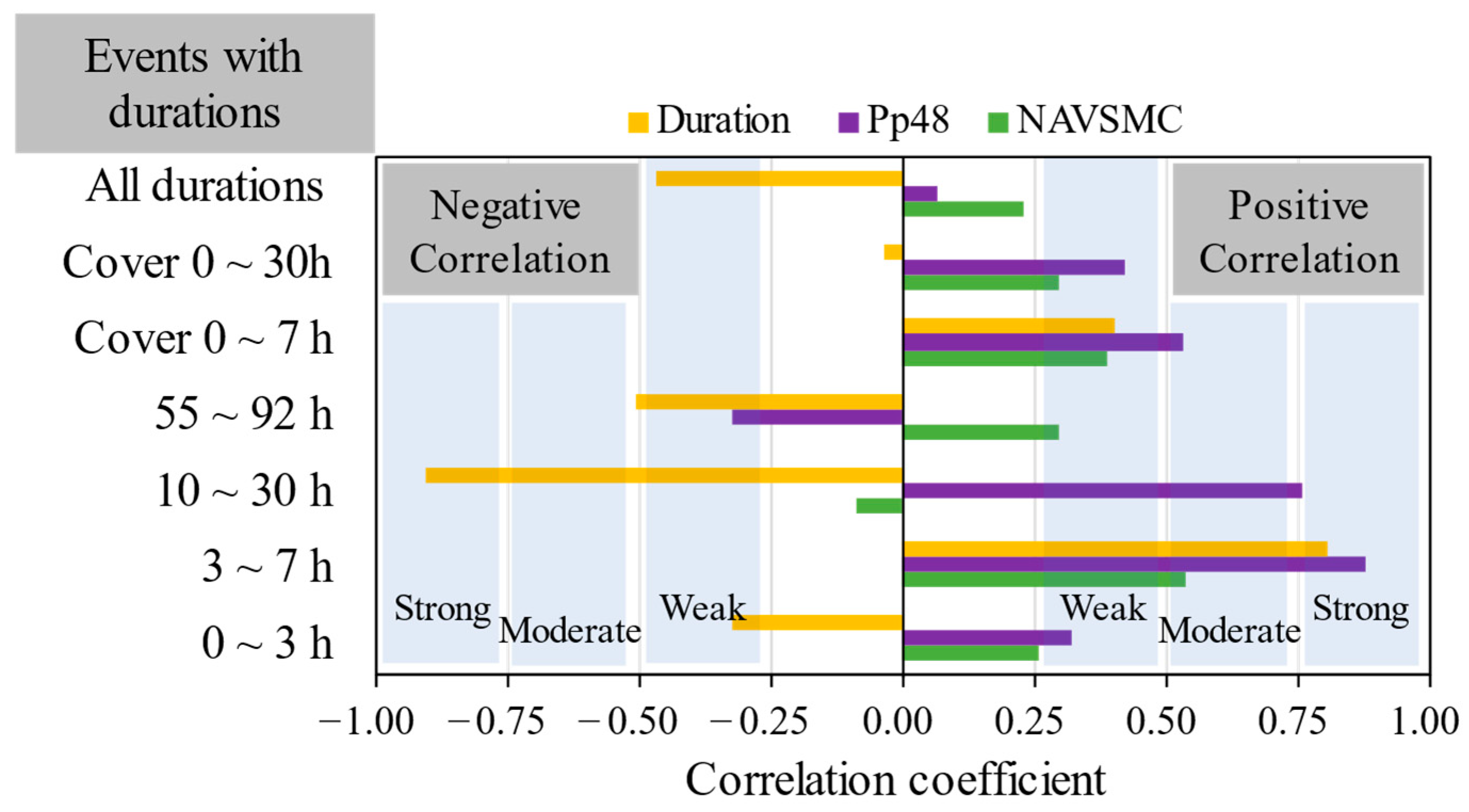
| Event with Durations | 0~3 h | 3~7 h | 10~30 h | 55~92 h | 0~7 h | 0~30 h | All Durations |
|---|---|---|---|---|---|---|---|
| NAVSMC | 0.256 | 0.538 | −0.086 | 0.296 | 0.386 | 0.295 | 0.230 |
| Pp48 | 0.319 | 0.880 | 0.759 | −0.323 | 0.532 | 0.423 | 0.064 |
| Duration | −0.325 | 0.808 | −0.903 | −0.508 | 0.402 | −0.034 | −0.466 |
| Total Event Counts | Duration Range (h) | NAVSMC | Pp12 | Pp24 | Pp48 | Pp72 | Pp120 | Duration (h) | TILR (h) |
|---|---|---|---|---|---|---|---|---|---|
| 49 | 0~91.5 | 0.259 | 0.035 | −0.125 | 0.164 | 0.179 | 0.030 | −0.302 | −0.170 |
| 39 | 0~30 | 0.318 | 0.342 | −0.155 | 0.451 | 0.476 | 0.283 | −0.015 | −0.323 |
| 30 | 0~10 | 0.438 | - | −0.215 | 0.465 | 0.495 | 0.172 | 0.140 | −0.344 |
| 26 | 0~5 | 0.435 | - | −0.163 | 0.242 | 0.379 | 0.174 | −0.433 | −0.199 |
| 23 | 0~4 | 0.473 | - | −0.196 | 0.222 | 0.359 | 0.447 | −0.430 | −0.226 |
| 14 | 0~3 | 0.419 | - | −0.347 | 0.131 | 0.312 | 0.343 | −0.186 | −0.218 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.-D.; Wu, C.-C. The Contradictory Issue of the Impact of Antecedent Soil Moisture to Interrill Erosion in Clay Soil: A Two-Year Field Study. Water 2024, 16, 2076. https://doi.org/10.3390/w16152076
Chen Y-D, Wu C-C. The Contradictory Issue of the Impact of Antecedent Soil Moisture to Interrill Erosion in Clay Soil: A Two-Year Field Study. Water. 2024; 16(15):2076. https://doi.org/10.3390/w16152076
Chicago/Turabian StyleChen, Yu-Da, and Chia-Chun Wu. 2024. "The Contradictory Issue of the Impact of Antecedent Soil Moisture to Interrill Erosion in Clay Soil: A Two-Year Field Study" Water 16, no. 15: 2076. https://doi.org/10.3390/w16152076
APA StyleChen, Y.-D., & Wu, C.-C. (2024). The Contradictory Issue of the Impact of Antecedent Soil Moisture to Interrill Erosion in Clay Soil: A Two-Year Field Study. Water, 16(15), 2076. https://doi.org/10.3390/w16152076






