Extension of Iber for Simulating Non–Newtonian Shallow Flows: Mine-Tailings Spill Propagation Modelling
Abstract
1. Introduction
2. Materials and Methods
2.1. Numerical Simulation Tool: IberNNF
2.2. Test Cases
3. Results
3.1. Idealised Dam-Break Problem for Viscous–Plastic Fluids
3.2. Fluid Detention on Sloping Terrain
3.3. Idealised Gypsum Spill (East Texas, USA)
3.4. Pond Failure of Los Frailes (Spain)
4. Discussion
4.1. On the Numerical Approach
4.2. On the Rheological Models
4.3. On the Performance of Iber in Simulating Mine-Tailings Spill Propagation
4.4. On the Code Optimization and Computing Time for GPU-Computing
4.5. On the Associated Risk of Mining Activities
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hudson-Edwards, K.A.; Macklin, M.G.; Jamieson, H.E.; Brewer, P.A.; Coulthard, T.J.; Howard, A.J.; Turner, J.N. The impact of tailings dam spills and clean-up operations on sediment and water quality in river systems: Rios Agrio–Guadiamar, Aznalcollar, Spain. Appl. Geochem. 2003, 18, 221–239. [Google Scholar] [CrossRef]
- Kheirkhah Gildeh, H.; Halliday, A.; Arenas, A.; Zhang, H. Tailings Dam Breach Analysis: A Review of Methods, Practices, and Uncertainties. Mine Water Environ. 2021, 40, 128–150. [Google Scholar] [CrossRef]
- Owen, J.R.; Kemp, D.; Lèbre, É.; Svobodova, K.; Pérez Murillo, G. Catastrophic tailings dam failures and disaster risk disclosure. Int. J. Disaster Risk Reduct. 2020, 42, 103361. [Google Scholar] [CrossRef]
- Roche, C.; Thygesen, K.; Baker, E. Mine Tailings Storage: Safety Is No Accident; United Nations Environment Programme: Nairobi, Kenya; GRID-Arendal: Arendal, Norway, 2017; ISBN 978-82-7701-170-7. [Google Scholar]
- Ngole-Jeme, V.M.; Fantke, P. Ecological and human health risks associated with abandoned gold mine tailings contaminated soil. PLoS ONE 2017, 12, e0172517. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Gomariz, E.; Barbero, C.; Sanchez-Juny, M.; Forero-Ortiz, E.; Sanz-Ramos, M. Dams or ponds classification based on a new criterion to assess potential flood damage to roads in case of failure. Nat. Hazards 2023, 117, 625–653. [Google Scholar] [CrossRef]
- Hudson-Edwards, K.A.; Jamieson, H.E.; Lottermoser, B.G. Mine wastes: Past, present, future. Elements 2011, 7, 375–380. [Google Scholar] [CrossRef]
- Kossoff, D.; Dubbin, W.E.; Alfredsson, M.; Edwards, S.J.; Macklin, M.G.; Hudson-Edwards, K.A. Mine tailings dams: Characteristics, failure, environmental impacts, and remediation. Appl. Geochem. 2014, 51, 229–245. [Google Scholar] [CrossRef]
- Bowker, L.N.; Chambers, D.M. The Risk, Public Liability and Economics of Tailings Storage Facility Failures. Earthwork Act 2015, 24, 56. [Google Scholar]
- Mudd, G.M. The Environmental sustainability of mining in Australia: Key mega-trends and looming constraints. Resour. Policy 2010, 35, 98–115. [Google Scholar] [CrossRef]
- Dong, L.; Deng, S.; Wang, F. Some developments and new insights for environmental sustainability and disaster control of tailings dam. J. Clean. Prod. 2020, 269, 122270. [Google Scholar] [CrossRef]
- López-Pamo, E.; Barettino, D.; Antón-Pacheco, C.; Ortiz, G.; Arránz, J.C.; Gumiel, J.C.; Martínez-Pledel, B.; Aparicio, M.; Montouto, O. The extent of the Aznalcollar pyritic sludge spill and its effects on soils. Sci. Total Environ. 1999, 242, 57–88. [Google Scholar] [CrossRef] [PubMed]
- Madejón, P.; Domínguez, M.; Madejón, E.; Cabrera, F.; Marañón, T.; Murillo, J. Soil-plant relationships and contamination by trace elements: A review of twenty years of experimentation and monitoring after the Aznalcóllar (SW Spain) mine accident. Sci. Total Environ. 2018, 625, 50–63. [Google Scholar] [CrossRef] [PubMed]
- Tornero, V.; Arias, A.M.; Blasco, J. Following the Aznalcóllar toxic spill. Environ. Res. 2011, 111, 1033–1036. [Google Scholar] [CrossRef] [PubMed]
- Sanz-Ramos, M.; Andrade, C.A.; Oller, P.; Furdada, G.; Bladé, E.; Martínez-Gomariz, E. Reconstructing the Snow Avalanche of Coll de Pal 2018 (SE Pyrenees). GeoHazards 2021, 2, 196–211. [Google Scholar] [CrossRef]
- Sanz-Ramos, M.; Bladé, E.; Oller, P.; Furdada, G. Numerical modelling of dense snow avalanches with a well-balanced scheme based on the 2D shallow water equations. J. Glaciol. 2023, 1–17. [Google Scholar] [CrossRef]
- Zugliani, D.; Rosatti, G. TRENT2D❄: An accurate numerical approach to the simulation of two-dimensional dense snow avalanches in global coordinate systems. Cold Reg. Sci. Technol. 2021, 190, 103343. [Google Scholar] [CrossRef]
- Medina, V.; Hürlimann, M.; Bateman, A. Application of FLATModel, a 2D finite volume code, to debris flows in the northeastern part of the Iberian Peninsula. Landslides 2008, 5, 127–142. [Google Scholar] [CrossRef]
- Xia, C.; Tian, H. A Quasi-Single-Phase Model for Debris Flows Incorporating Non–Newtonian Fluid Behavior. Water 2022, 14, 1369. [Google Scholar] [CrossRef]
- Hungr, O. A model for the runout analysis of rapid flow slides, debris flows, and avalanches. Can. Geotech. J. 1995, 32, 610–623. [Google Scholar] [CrossRef]
- Wu, T.; Vuong, T.; Wang, C.; Chu, C.; Lin, C. Model development for simulating mudslide and the case study of the failure of the gypsum tailings dam in East Texas in 1966. Nat. Hazards Earth Syst. Sci. Discuss. 2020. preprint. [Google Scholar] [CrossRef]
- Ding, W.; Wang, G.; Yang, Q.; Xu, Y.; Gao, Y.; Chen, X.; Xu, S.; Han, L.; Yang, X. Risk Assessment and Control of Geological Hazards in Towns of Complex Mountainous Areas Based on Remote Sensing and Geological Survey. Water 2023, 15, 3170. [Google Scholar] [CrossRef]
- Julien, P.Y.; Leon, C. Mudfloods, mudflows and debris flows, classification in rheology and structural design. In Proceedings of the International Workshop on the Debris Flow Disaster, Caracas, Venezuela, 14–16 December 1999. [Google Scholar]
- Hu, J.; Li, K.; Su, W.; Zhao, X. Numerical Simulation of Drilling Fluid Flow in Centrifugal Pumps. Water 2023, 15, 992. [Google Scholar] [CrossRef]
- Melo, M.; Eleutério, J. Probabilistic Analysis of Floods from Tailings Dam Failures: A Method to Analyze the Impact of Rheological Parameters on the HEC-RAS Bingham and Herschel-Bulkley Models. Water 2023, 15, 2866. [Google Scholar] [CrossRef]
- Bladé, E.; Gómez-Valentín, M.; Dolz, J.; Aragón-Hernández, J.L.; Corestein, G.; Sánchez-Juny, M. Integration of 1D and 2D finite volume schemes for computations of water flow in natural channels. Adv. Water Resour. 2012, 42, 17–29. [Google Scholar] [CrossRef]
- Bladé, E.; Gómez, M.; Sánchez-Juny, M.; Dolz, J. Source term treatment of SWEs using the surface gradient upwind method. J. Hydraul. Res. 2012, 50, 447–448. [Google Scholar] [CrossRef]
- Bermúdez, A.; Dervieux, A.; Desideri, J.-A.; Vázquez, M.E. Upwind schemes for the two-dimensional shallow water equations with variable depth using unstructured meshes. Comput. Methods Appl. Mech. Eng. 1998, 155, 49–72. [Google Scholar] [CrossRef]
- LeVeque, R.L. Finite Volume Methods for Hyperbolic Problems; Cambridge University Press: Cambridge, MA, USA, 2002; Volume 31. [Google Scholar]
- Toro, E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 2009; Volume 40, ISBN 978-3-540-25202-3. [Google Scholar]
- Vázquez-Cendón, M.E. Improved treatment of source terms in upwind schemes for the shallow water equations in channels with irregular geometry. J. Comput. Phys. 1999, 148, 497–526. [Google Scholar] [CrossRef]
- Chevrel, M.O.; Labroquère, J.; Harris, A.J.L.; Rowland, S.K. PyFLOWGO: An open-source platform for simulation of channelized lava thermo-rheological properties. Comput. Geosci. 2018, 111, 167–180. [Google Scholar] [CrossRef]
- Christen, M.; Kowalski, J.; Bartelt, P. RAMMS: Numerical simulation of dense snow avalanches in three-dimensional terrain. Cold Reg. Sci. Technol. 2010, 63, 1–14. [Google Scholar] [CrossRef]
- Eglit, M.; Yakubenko, A.; Zayko, J. A Review of Russian Snow Avalanche Models—From Analytical Solutions to Novel 3D Models. Geosciences 2020, 10, 77. [Google Scholar] [CrossRef]
- Pirulli, M.; Sorbino, G. Assessing potential debris flow runout: A comparison of two simulation models. Nat. Hazards Earth Syst. Sci. 2008, 8, 961–971. [Google Scholar] [CrossRef]
- Stefania, S.; Zugliani, D.; Rosatti, G. Dense snow avalanche modelling with Voellmy rheology: TRENT2D vs. RAMMS2D. In Proceedings of the Vistual Snow Science Workshop—VSSW 2020, Fernie, BC, Canada, 4–6 October 2020. [Google Scholar]
- Tan, W.Y. Shallow Water Hydrodynamics, 1st ed.; Elsevier Science: Amsterdam, The Netherlands, 1992; ISBN 9780080870939. [Google Scholar]
- Bladé, E.; Cea, L.; Corestein, G.; Escolano, E.; Puertas, J.; Vázquez-Cendón, E.; Dolz, J.; Coll, A. Iber: Herramienta de simulación numérica del flujo en ríos. Rev. Int. Métodos Numér. Cálc. Diseño Ing. 2014, 30, 1–10. [Google Scholar] [CrossRef]
- Bladé, E.; Cea, L.; Corestein, G. Modelización numérica de inundaciones fluviales. Ing. Agua 2014, 18, 68. [Google Scholar]
- Cea, L.; Bladé, E. A simple and efficient unstructured finite volume scheme for solving the shallow water equations in overland flow applications. Water Resour. Res. 2015, 51, 5464–5486. [Google Scholar] [CrossRef]
- Cea, L.; Legout, C.; Darboux, F.; Esteves, M.; Nord, G. Experimental validation of a 2D overland flow model using high resolution water depth and velocity data. J. Hydrol. 2014, 513, 142–153. [Google Scholar] [CrossRef]
- Uber, M.; Nord, G.; Legout, C.; Cea, L. How do modeling choices and erosion zone locations impact the representation of connectivity and the dynamics of suspended sediments in a multi-source soil erosion model? Earth Surf. Dyn. 2021, 9, 123–144. [Google Scholar] [CrossRef]
- Aranda, J.Á.; Sánchez-Juny, M.; Sanz-Ramos, M.; Beneyto, C. Design of Drainage Downspouts Systems over a Road Embankment. Water 2023, 15, 3529. [Google Scholar] [CrossRef]
- Aranda, J.Á.; Beneyto, C.; Sánchez-Juny, M.; Bladé, E. Efficient Design of Road Drainage Systems. Water 2021, 13, 1661. [Google Scholar] [CrossRef]
- Cea, L.; Bermúdez, M.; Puertas, J.; Bladé, E.; Corestein, G.; Escolano, E.; Conde, A.; Bockelmann-Evans, B.; Ahmadian, R. IberWQ: New simulation tool for 2D water quality modelling in rivers and shallow estuaries. J. Hydroinform. 2016, 18, 816–830. [Google Scholar] [CrossRef]
- Sañudo, E.; Cea, L.; Puertas, J. Modelling Pluvial Flooding in Urban Areas Coupling the Models Iber and SWMM. Water 2020, 12, 2647. [Google Scholar] [CrossRef]
- Sanz-Ramos, M.; Martí-Cardona, B.; Bladé, E.; Seco, I.; Amengual, A.; Roux, H.; Romero, R. NRCS-CN Estimation from Onsite and Remote Sensing Data for Management of a Reservoir in the Eastern Pyrenees. J. Hydrol. Eng. 2020, 25, 05020022. [Google Scholar] [CrossRef]
- Ruiz-Villanueva, V.; Gamberini, C.; Bladé, E.; Stoffel, M.; Bertoldi, W. Numerical Modeling of Instream Wood Transport, Deposition, and Accumulation in Braided Morphologies Under Unsteady Conditions: Sensitivity and High-Resolution Quantitative Model Validation. Water Resour. Res. 2020, 56, e2019WR026221. [Google Scholar] [CrossRef]
- Ruiz-Villanueva, V.; Mazzorana, B.; Bladé, E.; Bürkli, L.; Iribarren-Anacona, P.; Mao, L.; Nakamura, F.; Ravazzolo, D.; Rickenmann, D.; Sanz-Ramos, M.; et al. Characterization of wood-laden flows in rivers. Earth Surf. Process. Landf. 2019, 44, 1694–1709. [Google Scholar] [CrossRef]
- Sanz-Ramos, M.; López-Gómez, D.; Bladé, E.; Dehghan-Souraki, D. A CUDA Fortran GPU-parallelised hydrodynamic tool for high-resolution and long-term eco-hydraulic modelling. Environ. Model. Softw. 2023, 161, 105628. [Google Scholar] [CrossRef]
- Arbat-Bofill, M.; Bladé, E.; Sánchez-Juny, M.; Niñerola, D.; Dolz, J.; Sanchez-Juny, M.; Niñerola, D.; Dolz, J.; Arbat Bofill, M.; Bladé, E.; et al. Case studies of reservoir sedimentation as a consequence of soil erosion. In Reservoir Sedimentation; CRC Press: Boca Raton, FL, USA, 2014; pp. 83–92. ISBN 9781138026759. [Google Scholar]
- Bladé, E.; Sanz-Ramos, M.; Dolz, J.; Expósito-Pérez, J.; Sánchez-Juny, M. Modelling flood propagation in the service galleries of a nuclear power plant. Nucl. Eng. Des. 2019, 352, 110180. [Google Scholar] [CrossRef]
- Roe, P. A basis for upwind differentiating of the two dimensional unsteady Euler equations. In Numerical Methodes for Fluid Dynamics II; Morton, B., Ed.; Oxford University Press: Oxford, UK, 1986. [Google Scholar]
- Bingham, E.C. An investigation of the laws of plastic flow. Bull. Bur. Stand. 1916, 13, 309–353. [Google Scholar] [CrossRef]
- Pastor, M.; Haddad, B.; Sorbino, G.; Cuomo, S.; Drempetic, V. A depth-integrated, coupled SPH model for flow-like landslides and related phenomena. Int. J. Numer. Anal. Methods Geomech. 2009, 33, 143–172. [Google Scholar] [CrossRef]
- Chen, H.; Lee, C.F. Runout Analysis of Slurry Flows with Bingham Model. J. Geotech. Geoenviron. Eng. 2002, 128, 1032–1042. [Google Scholar] [CrossRef]
- Naef, D.; Rickenmann, D.; Rutschmann, P.; McArdell, B.W. Comparison of flow resistance relations for debris flows using a one-dimensional finite element simulation model. Nat. Hazards Earth Syst. Sci. 2006, 6, 155–165. [Google Scholar] [CrossRef]
- Voellmy, A. Über die Zerstörungskraft von Lawinen. Schweizerische Bauzeitung 1955, 73, 15. [Google Scholar]
- Bryant, S.M. Application of Tailings Flow Analyses to Field Conditions; University of California: Berkeley, CA, USA, 1983. [Google Scholar]
- de’ Michieli Vitturi, M.; Esposti Ongaro, T.; Lari, G.; Aravena, A. IMEX_SfloW2D 1.0: A depth-averaged numerical flow model for pyroclastic avalanches. Geosci. Model Dev. 2019, 12, 581–595. [Google Scholar] [CrossRef]
- Jeyapalan, J.K.; Duncan, J.M.; Seed, H.B. Investigation of Flow Failures of Tailings Dams. J. Geotech. Eng. 1983, 109, 172–189. [Google Scholar] [CrossRef]
- Gens, A.; Alonso, E.E. Aznalcóllar dam failure. Part 2: Stability conditions and failure mechanism. Géotechnique 2006, 56, 185–201. [Google Scholar] [CrossRef]
- Alonso, E.E.; Gens, A. Aznalcóllar dam failure. Part 1: Field observations and material properties. Géotechnique 2006, 56, 165–183. [Google Scholar] [CrossRef]
- Alonso, E.E.; Gens, A. Aznalcóllar dam failure. Part 3: Dynamics of the motion. Géotechnique 2006, 56, 203–210. [Google Scholar] [CrossRef]
- Ayala-Carcedo, J. La rotura de la balsa de residuos mineros de Aznalcóllar (España) de 1998 y el desastre ecológico consecuente del río Guadiamar: Causas, efectos y lecciones. Bol. Geol. Min. 2004, 115, 711–738. [Google Scholar]
- Sanz-Ramos, M.; Bladé, E.; Dolz, J.; Sánchez-Juny, M. Revisiting the Hydraulics of the Aznalcóllar Mine Disaster. Mine Water Environ. 2022, 41, 335–356. [Google Scholar] [CrossRef]
- Sanz-Ramos, M.; Bladé, E.; Dolz, J.; Sánchez-Juny, M. El desastre de Aznalcóllar: ¿lodos o aguas ácidas? Ing. Agua 2021, 25, 229–239. [Google Scholar] [CrossRef]
- Consultec Ingenieros SL. Calibración de las tres estaciones de aforo del río Guadiamar (EA no 56, EA no 90 y EA no 76) por métodos informáticos hidráulicos. Estud. Riada Tóxica 1999, 35. [Google Scholar]
- Antón-Pacheco, C.; Arranz, J.C.; Barettino, D.; Carrero, G.; Giménez, M.; Gómez, J.A.; Gumiel, J.C.; López-Pamo, E.; Martín Rubí, J.A.; Martínez-Pledel, B.; et al. Actuaciones para el reconocimiento y retirada de los lodos depositados sobre el terreno, y su restauración edáfica y morfológica. Bol. Geol. Min. 2001, 112, 93–122. [Google Scholar]
- CSIC Guadiamar. Ciencia, Técnicia y Restauración—El Accidente Minero Diez Años Después; Consejo Superior de Investigaciones Científicas (CSIC), Ministerio de Ciencia e Innovación: Madrid, Spain, 2008; ISBN 978-84-00-08644-2.
- Turner, J.N.; Brewer, P.A.; Macklin, M.G. Fluvial-controlled metal and As mobilisation, dispersal and storage in the Río Guadiamar, SW Spain and its implications for long-term contaminant fluxes to the Doñana wetlands. Sci. Total Environ. 2008, 394, 144–161. [Google Scholar] [CrossRef] [PubMed]
- Bladé, E.; Gómez-Valentín, M.; Sánchez-Juny, M.; Dolz, J. Preserving steady-state in one-dimensional finite-volume computations of river flow. J. Hydraul. Eng. 2008, 134, 1343–1347. [Google Scholar] [CrossRef]
- Dimitriadis, P.; Koutsoyiannis, D.; Iliopoulou, T.; Papanicolaou, P. A Global-Scale Investigation of Stochastic Similarities in Marginal Distribution and Dependence Structure of Key Hydrological-Cycle Processes. Hydrology 2021, 8, 59. [Google Scholar] [CrossRef]
- Ramos-Fuertes, A.; Marti-Cardona, B.; Bladé, E.; Dolz, J. Envisat/ASAR Images for the Calibration of Wind Drag Action in the Doñana Wetlands 2D Hydrodynamic Model. Remote Sens. 2013, 6, 379–406. [Google Scholar] [CrossRef]
- Sanz-Ramos, M.; Téllez-Álvarez, J.; Bladé, E.; Gómez-Valentín, M. Simulating the hydrodynamics of sewer-grates using a 2D-hydraulic model. In Proceedings of the 5th International Conference SimHydro, Nice, France, 20–22 November 2019; p. 8. [Google Scholar]
- Cea, L.; Puertas, J.; Vázquez-Cendón, M.-E. Depth averaged modelling of turbulent shallow water flow with wet-dry fronts. Arch. Comput. Methods Eng. 2007, 14, 303–341. [Google Scholar] [CrossRef]
- Sanz-Ramos, M.; Olivares, G.; Bladé, E. Experimental characterization and two-dimensional hydraulic-hydrologic modelling of the infiltration process through permeable pavements. Rev. Int. Métodos Numér. Cálc. Diseño Ing. 2022, 38, 1–12. [Google Scholar] [CrossRef]
- Msheik, K. Non–Newtonian Fluids: Modeling and Well-Posedness; Universite Grenoble Alpes: Saint-Martin-d’Hères, France, 2020. [Google Scholar]
- Takahashi, T. Debris flow: Mechanics and hazard mitigation. In Proceedings of the ROC-JAPAN Joint Seminar on Multiple Hazards Mitigation; National Taiwan Univerisity: Taipei, Taiwan, 1985; pp. 1075–1092. [Google Scholar]
- Laenen, A.; Hansen, R.P. Simulation of Three Lahars in the Mount St. Helens Area, Washington, Using a One-Dimensional, Unsteady-State Streamflow Model; U.S. Geological Survey Water-Resources Investigations Report 88-4004; U.S. Geological Survey: Portland, OR, UA, 1988.
- Syarifuddin, M.; Oishi, S.; Hapsari, R.I.; Legono, D. Empirical model for remote monitoring of rain-triggered lahar at Mount Merapi. J. Japan Soc. Civ. Eng. Ser. B1 (Hydraul. Eng.) 2018, 74, I_1483–I_1488. [Google Scholar] [CrossRef] [PubMed]
- Darnell, A.R.; Phillips, J.C.; Barclay, J.; Herd, R.A.; Lovett, A.A.; Cole, P.D. Developing a simplified geographical information system approach to dilute lahar modelling for rapid hazard assessment. Bull. Volcanol. 2013, 75, 713. [Google Scholar] [CrossRef]
- Macedonio, G.; Pareschi, M.T.T. Numerical simulation of some lahars from Mount St. Helens. J. Volcanol. Geotherm. Res. 1992, 54, 65–80. [Google Scholar] [CrossRef]
- O’Brien, J.S.; Julien, P.Y. Laboratory Analysis of Mudflow Properties. J. Hydraul. Eng. 1988, 114, 877–887. [Google Scholar] [CrossRef]
- Bartelt, P.; Valero, C.V.; Feistl, T.; Christen, M.; Bühler, Y.; Buser, O. Modelling cohesion in snow avalanche flow. J. Glaciol. 2015, 61, 837–850. [Google Scholar] [CrossRef]
- Kelfoun, K. Suitability of simple rheological laws for the numerical simulation of dense pyroclastic flows and long-runout volcanic avalanches. J. Geophys. Res. Solid Earth 2011, 116, 1–14. [Google Scholar] [CrossRef]
- Frattini, P.; Crosta, G.B.; Fusi, N.; Dal Negro, P. Shallow landslides in pyroclastic soils: A distributed modelling approach for hazard assessment. Eng. Geol. 2004, 73, 277–295. [Google Scholar] [CrossRef]
- de Bélizal, E.; Lavigne, F.; Hadmoko, D.S.; Degeai, J.-P.; Dipayana, G.A.; Mutaqin, B.W.; Marfai, M.A.; Coquet, M.; Le Mauff, B.; Robin, A.-K.; et al. Rain-triggered lahars following the 2010 eruption of Merapi volcano, Indonesia: A major risk. J. Volcanol. Geotherm. Res. 2013, 261, 330–347. [Google Scholar] [CrossRef]
- Dumaisnil, C.; Thouret, J.; Chambon, G.; Doyle, E.E.; Cronin, S.J.; Surono. Hydraulic, physical and rheological characteristics of rain-triggered lahars at Semeru volcano, Indonesia. Earth Surf. Process. Landf. 2010, 35, 1573–1590. [Google Scholar] [CrossRef]
- Pistolesi, M.; Cioni, R.; Rosi, M.; Cashman, K.V.; Rossotti, A.; Aguilera, E. Evidence for lahar-triggering mechanisms in complex stratigraphic sequences: The post-twelfth century eruptive activity of Cotopaxi Volcano, Ecuador. Bull. Volcanol. 2013, 75, 698. [Google Scholar] [CrossRef]
- van Westen, C.J.; Daag, A.S. Analysing the relation between rainfall characteristics and lahar activity at Mount Pinatubo, Philippines. Earth Surf. Process. Landf. 2005, 30, 1663–1674. [Google Scholar] [CrossRef]
- Manville, V.; Major, J.J.; Fagents, S.A. Modeling lahar behavior and hazards. In Modeling Volcanic Processes: The Physics and Mathematics of Volcanism; Fagents, S.A., Gregg, T.K.P., Lopes, R.M.C., Eds.; Cambridge University Press: Cambridge, UK, 2013; pp. 300–330. [Google Scholar]
- WISE. Chronology of Major Tailings Fam Failures. WISE Uranium Project Is Part of World Information Service on Energy. 2020. Available online: https://www.wise-uranium.org/mdaf.html (accessed on 15 July 2024).
- Penman, A.D.M.; Brook, D.; Martin, P.L.; Routh, D. Tailings Dams. Risk of Dangerous Occurrences. Lessons Learnt from Practical Experiences; Commission Internationale des UNEP/ICOLD: Paris, France, 2001; Volume 121, ISBN 9783540773405. [Google Scholar]
- Capart, H.; Eldho, T.I.; Huang, S.Y.; Young, D.L.; Zech, Y. Treatment of Natural Geometry in Finite Volume River Flow Computations. J. Hydraul. Eng. 2003, 129, 385–393. [Google Scholar] [CrossRef]
- Hou, J.; Liang, Q.; Simons, F.; Hinkelmann, R. A stable 2D unstructured shallow flow model for simulations of wetting and drying over rough terrains. Comput. Fluids 2013, 82, 132–147. [Google Scholar] [CrossRef]
- Pitman, E.B.; Nichita, C.C.; Patra, A.; Bauer, A.; Sheridan, M.; Bursik, M. Computing granular avalanches and landslides. Phys. Fluids 2003, 15, 3638–3646. [Google Scholar] [CrossRef]
- Mergili, M.; Fischer, J.T.; Krenn, J.; Pudasaini, S.P. r.avaflow v1, an advanced open-source computational framework for the propagation and interaction of two-phase mass flows. Geosci. Model Dev. 2017, 10, 553–569. [Google Scholar] [CrossRef]
- Courant, R.; Friedrichs, K.; Lewy, H. On the partial difference equations of mathematical physics. IBM J. Res. Dev. 1967, 11, 215–234. [Google Scholar] [CrossRef]
- Buttinger-Kreuzhuber, A.; Konev, A.; Horváth, Z.; Cornel, D.; Schwerdorf, I.; Blöschl, G.; Waser, J. An integrated GPU-accelerated modeling framework for high-resolution simulations of rural and urban flash floods. Environ. Model. Softw. 2022, 156, 105480. [Google Scholar] [CrossRef]
- Carlotto, T.; Borges Chaffe, P.L.; Innocente dos Santos, C.; Lee, S. SW2D-GPU: A two-dimensional shallow water model accelerated by GPGPU. Environ. Model. Softw. 2021, 145, 105205. [Google Scholar] [CrossRef]
- Dehghan-Souraki, D.; López-Gómez, D.; Bladé-Castellet, E.; Larese, A.; Sanz-Ramos, M. Optimizing sediment transport models by using the Monte Carlo simulation and deep neural network (DNN): A case study of the Riba-Roja reservoir. Environ. Model. Softw. 2024, 175, 105979. [Google Scholar] [CrossRef]
- Klose, C.D. Mine Water Discharge and Flooding: A Cause of Severe Earthquakes. Mine Water Environ. 2007, 26, 172–180. [Google Scholar] [CrossRef]



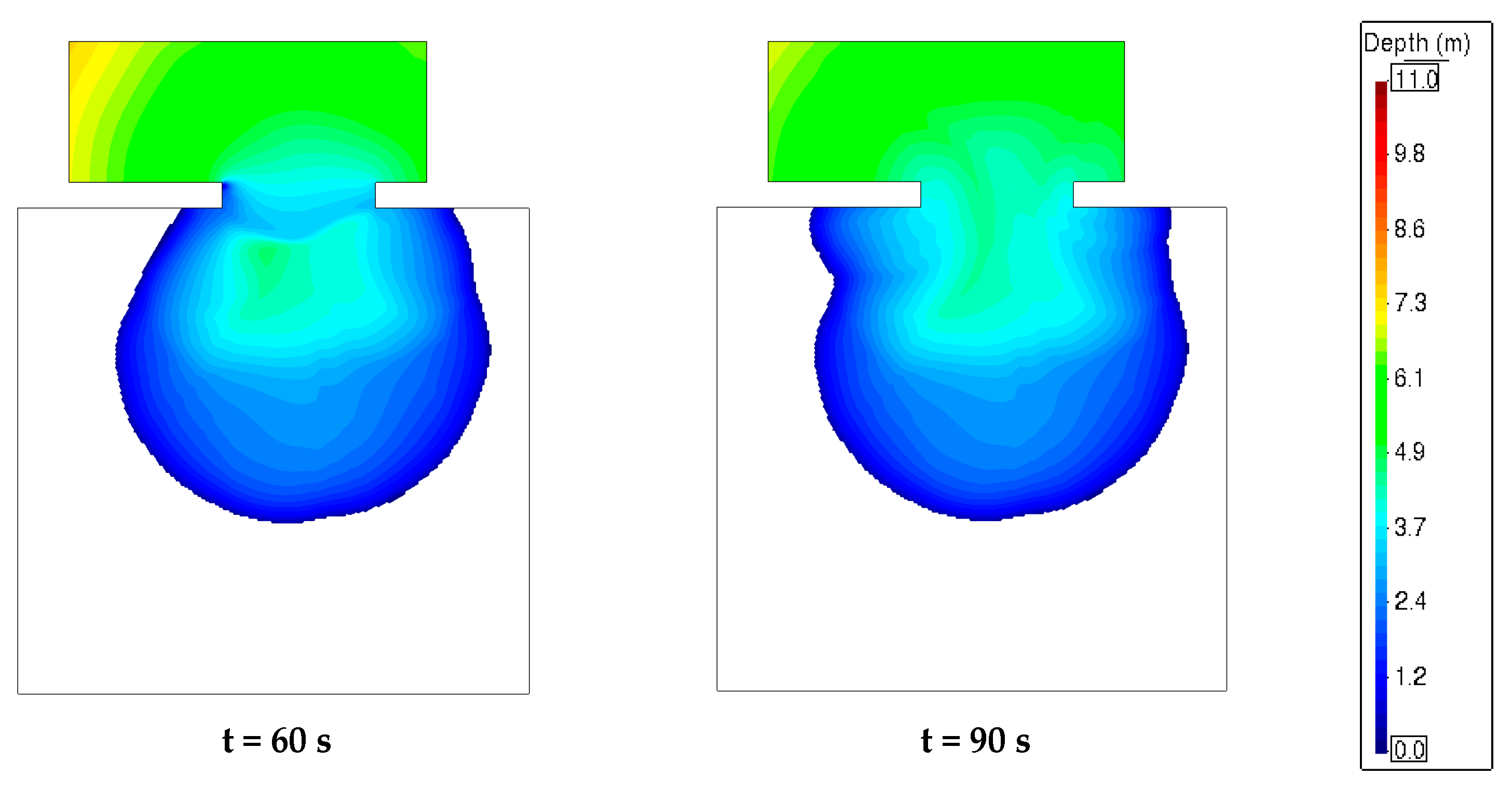
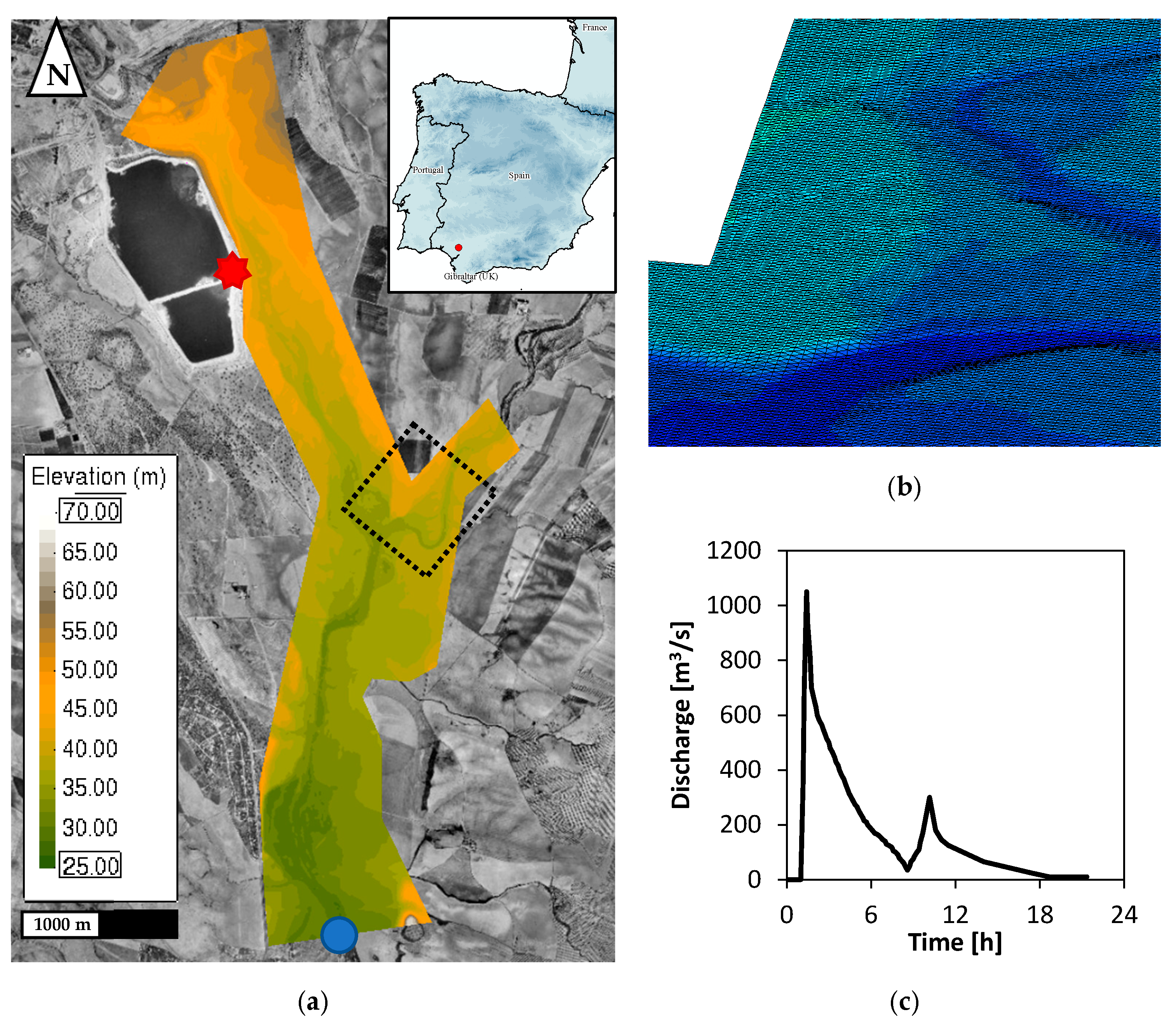


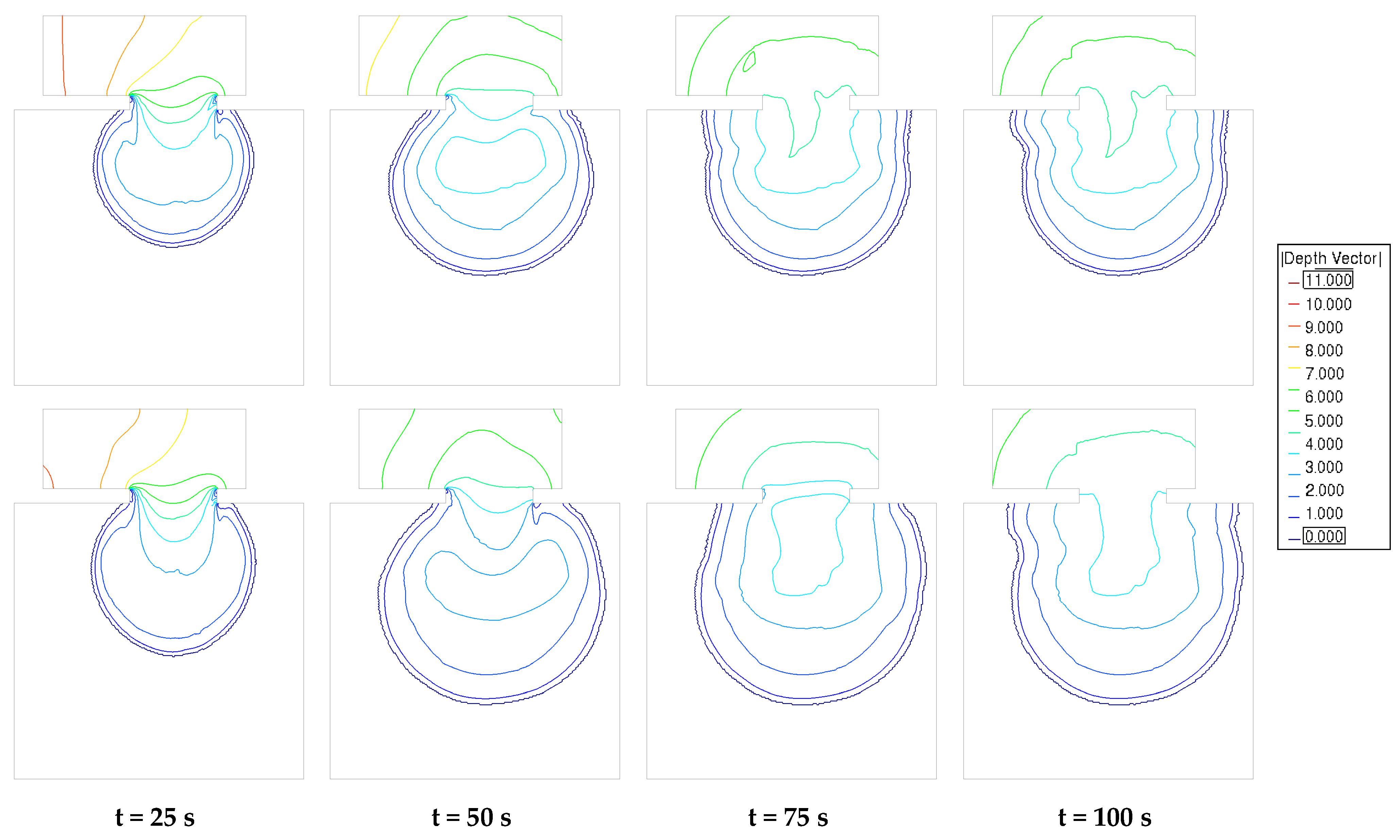
| Parameter | Range | Increments |
|---|---|---|
| Yield stress, [Pa] | 0–50 | 5 |
| Viscosity, [Pa·s] | 0–2000 | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sanz-Ramos, M.; Bladé, E.; Sánchez-Juny, M.; Dysarz, T. Extension of Iber for Simulating Non–Newtonian Shallow Flows: Mine-Tailings Spill Propagation Modelling. Water 2024, 16, 2039. https://doi.org/10.3390/w16142039
Sanz-Ramos M, Bladé E, Sánchez-Juny M, Dysarz T. Extension of Iber for Simulating Non–Newtonian Shallow Flows: Mine-Tailings Spill Propagation Modelling. Water. 2024; 16(14):2039. https://doi.org/10.3390/w16142039
Chicago/Turabian StyleSanz-Ramos, Marcos, Ernest Bladé, Martí Sánchez-Juny, and Tomasz Dysarz. 2024. "Extension of Iber for Simulating Non–Newtonian Shallow Flows: Mine-Tailings Spill Propagation Modelling" Water 16, no. 14: 2039. https://doi.org/10.3390/w16142039
APA StyleSanz-Ramos, M., Bladé, E., Sánchez-Juny, M., & Dysarz, T. (2024). Extension of Iber for Simulating Non–Newtonian Shallow Flows: Mine-Tailings Spill Propagation Modelling. Water, 16(14), 2039. https://doi.org/10.3390/w16142039








