Numerical Simulation of River Channel Change in the Suspended Sediment-Dominated Downstream Reach of the Sangu River
Abstract
1. Introduction
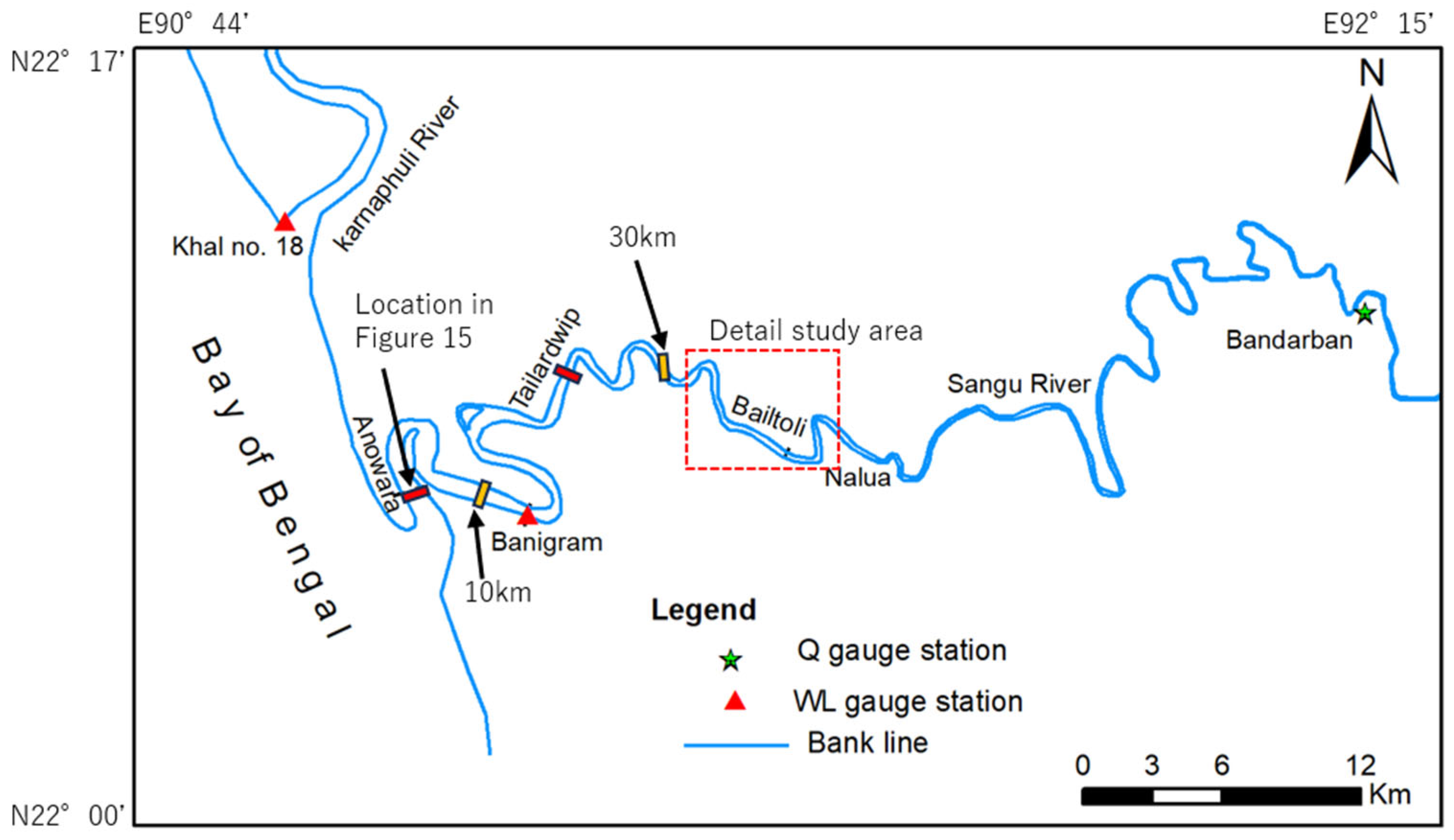
2. Study Sites
3. Methodology
3.1. Flow Calculation with Bed Deformations
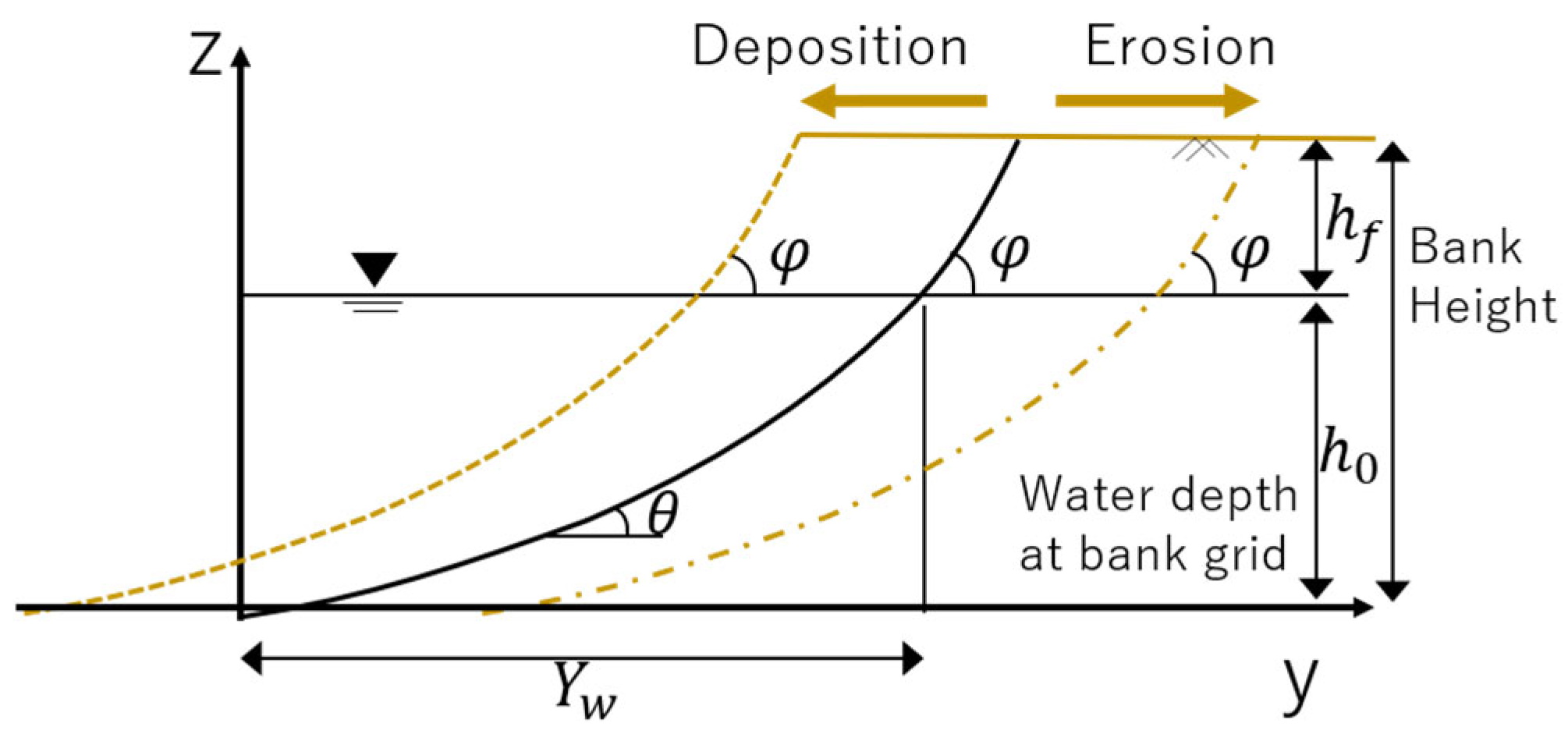
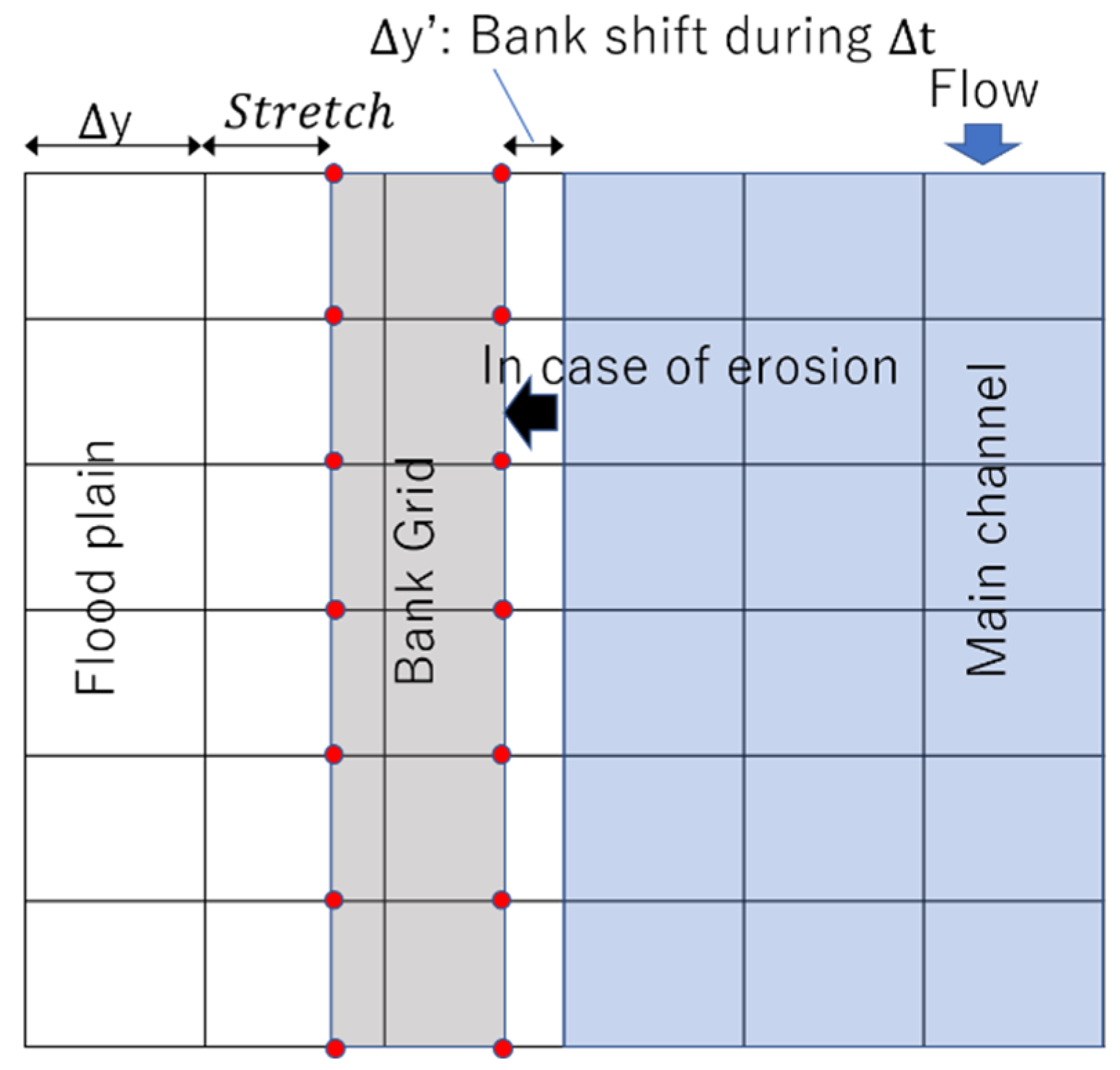
3.2. Bank Shift in the 2-D Depth-Averaged Framework
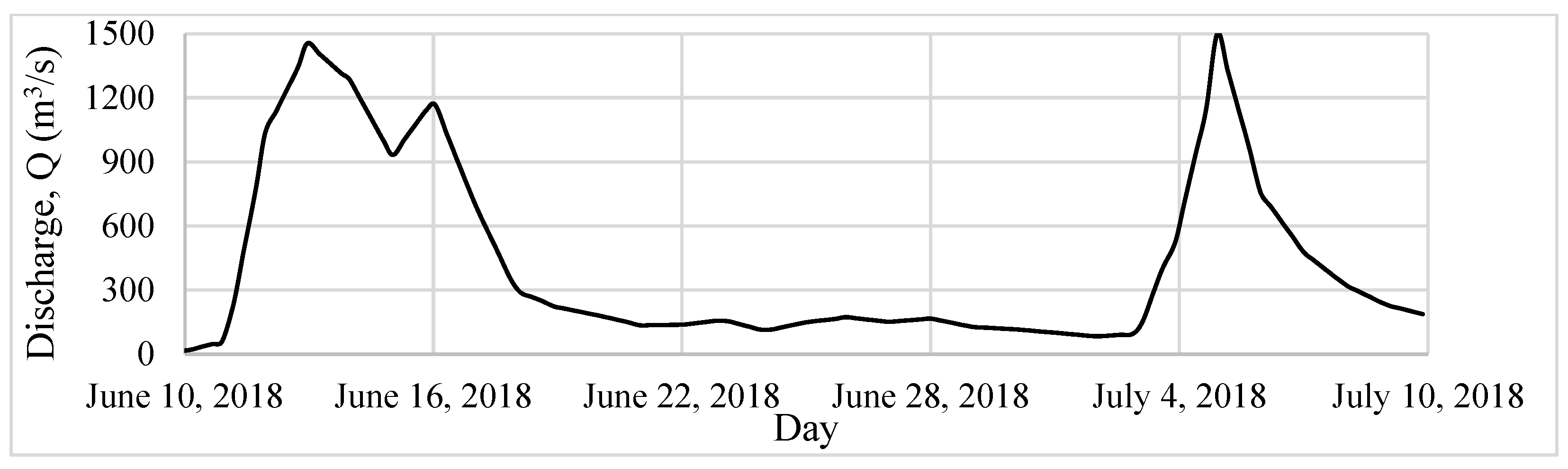
4. Calculation Conditions
5. Results
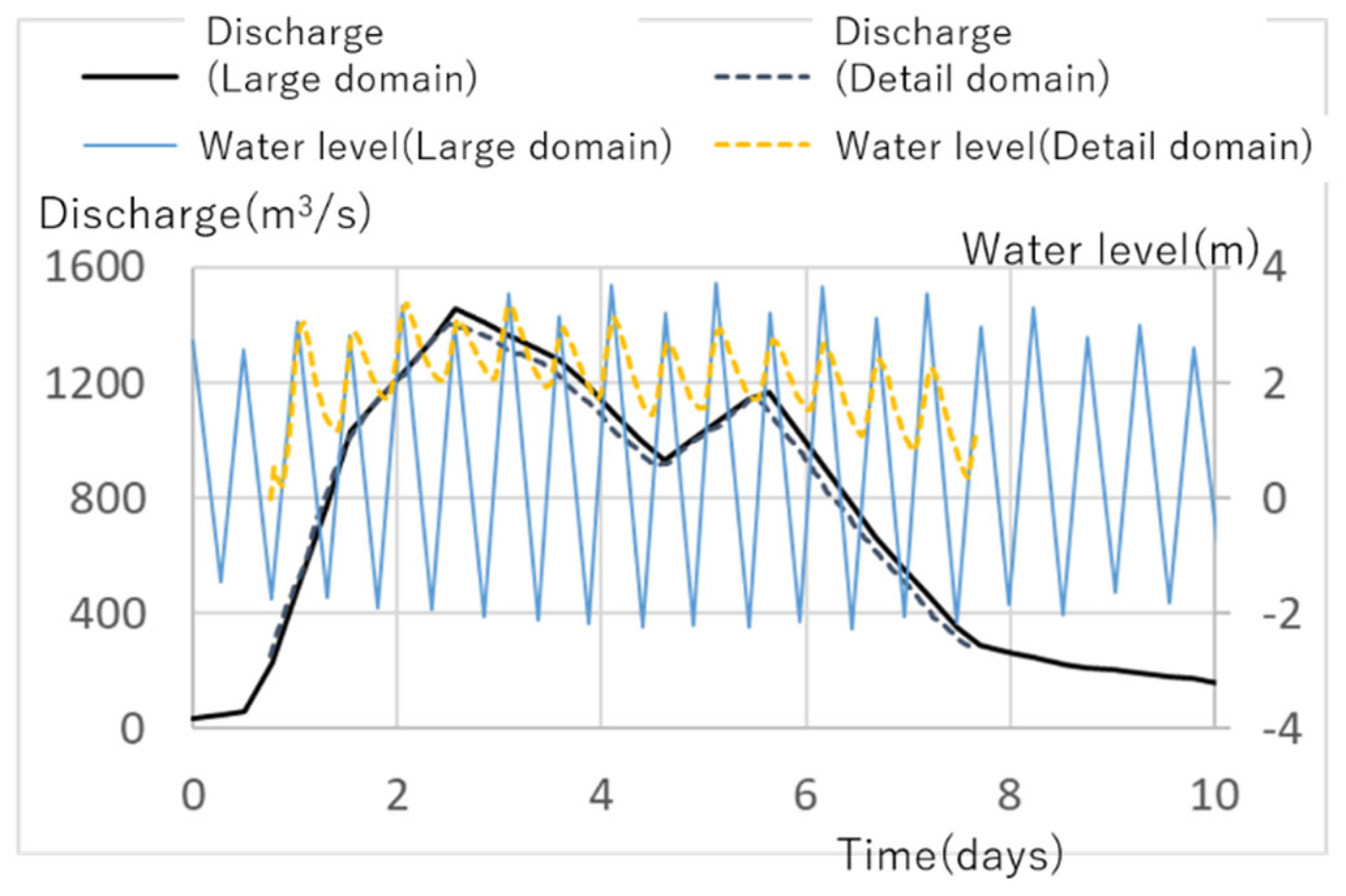
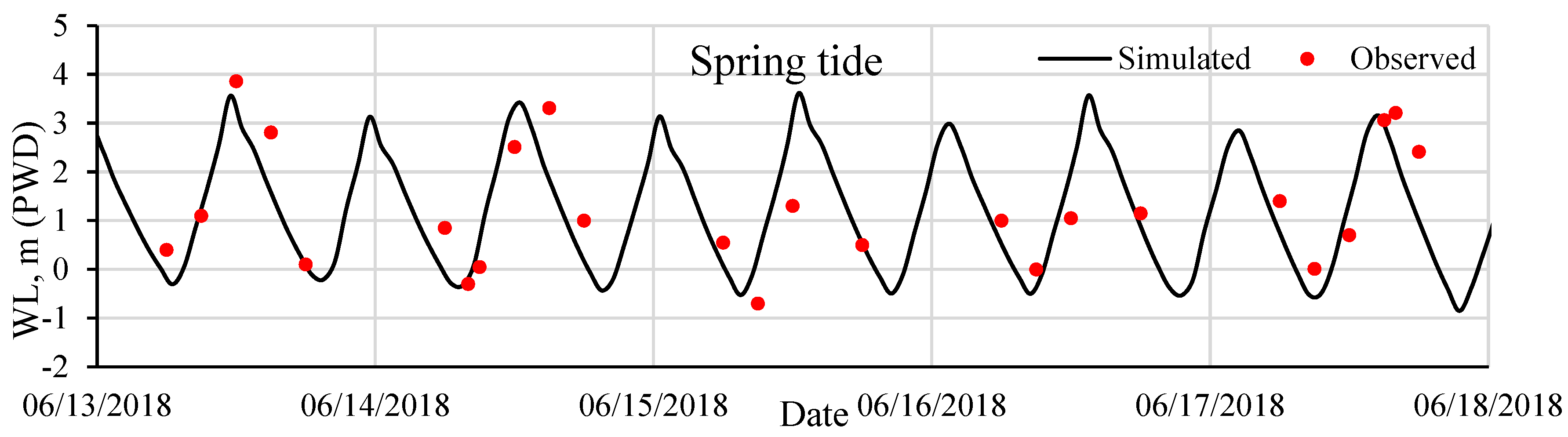
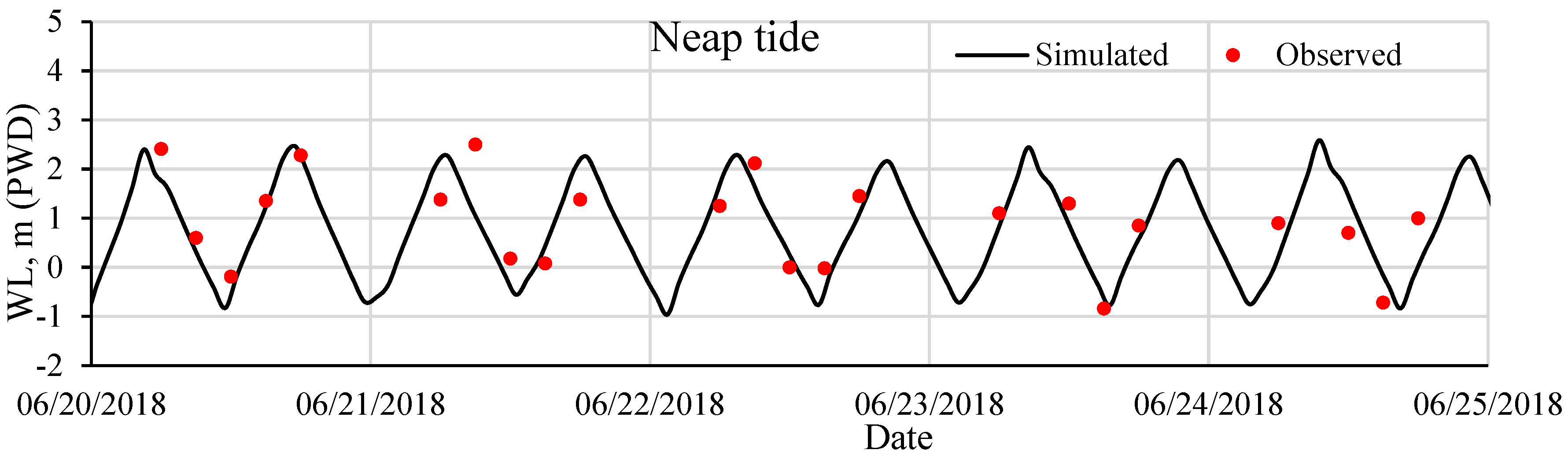
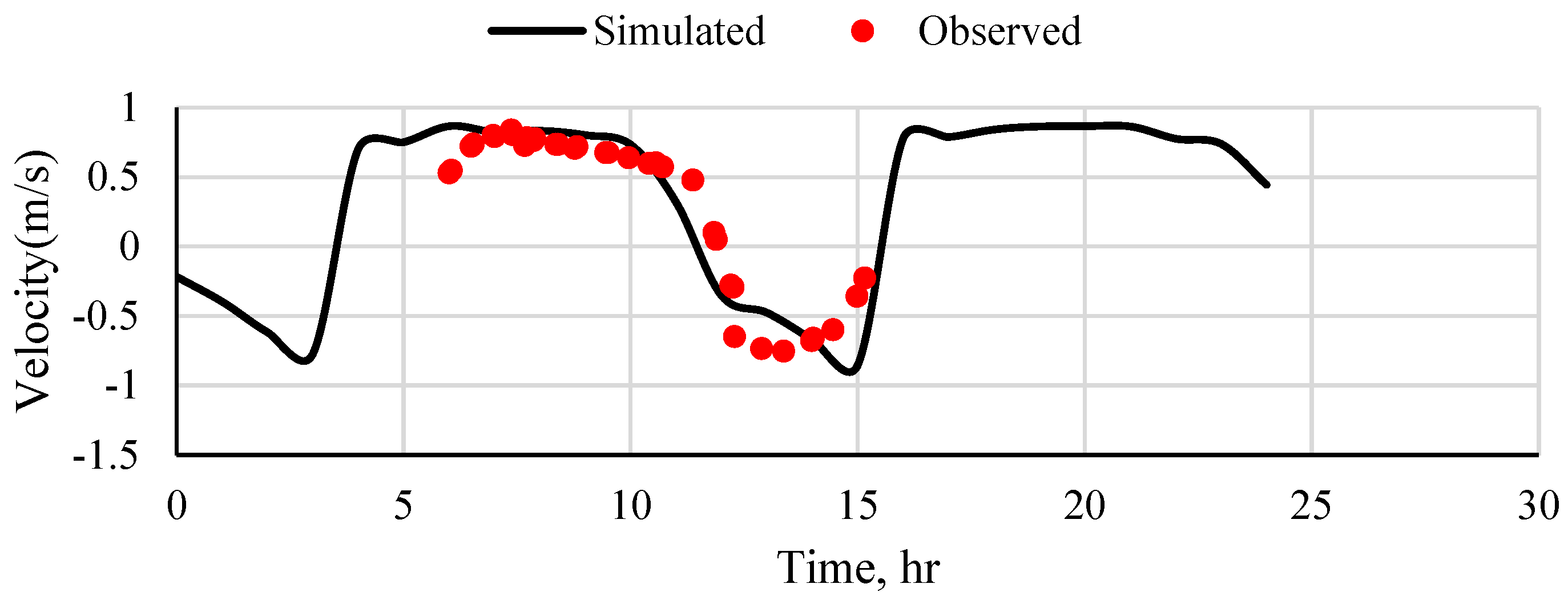
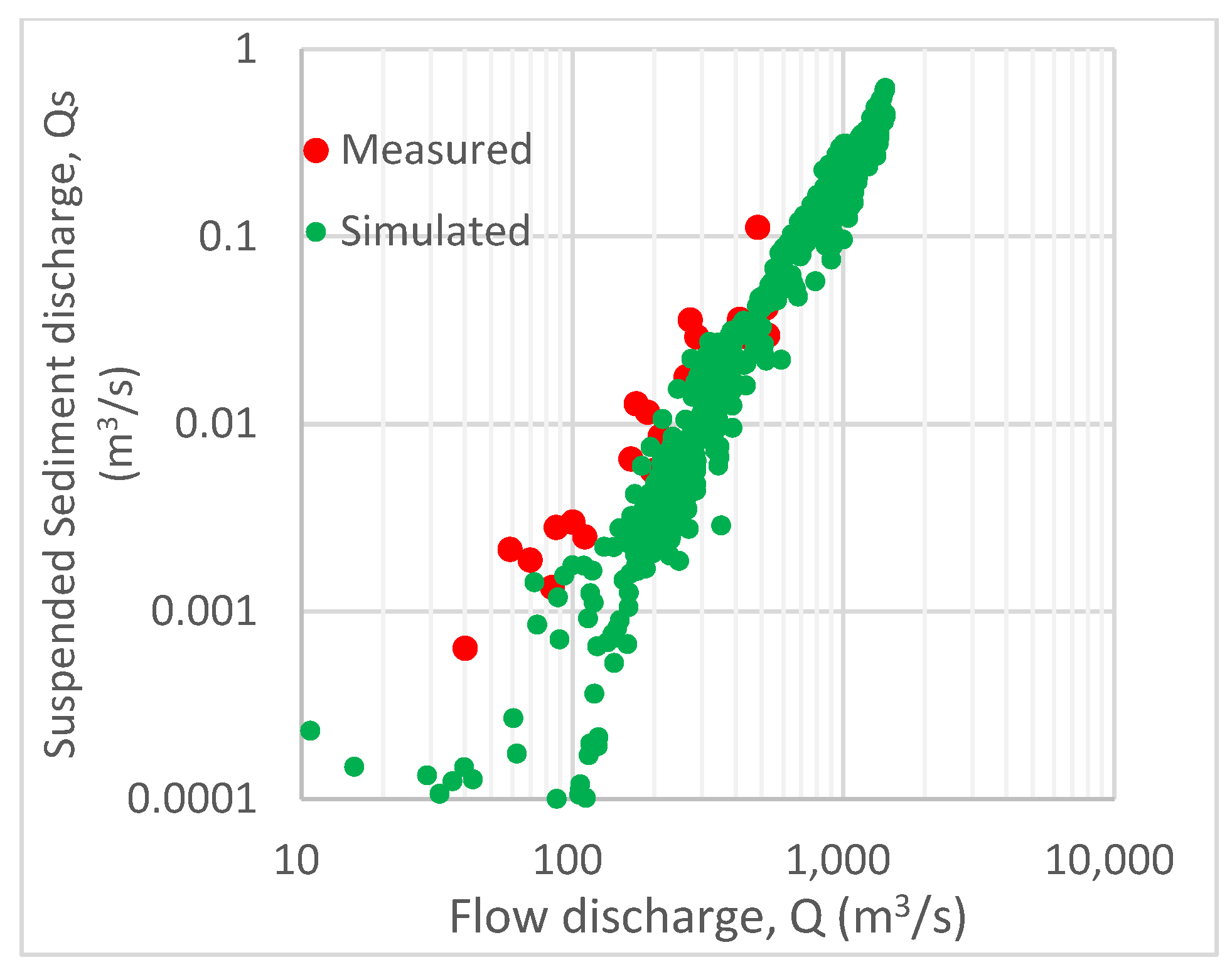
5.1. Computation Validation
5.2. Flow Characteristics for the Entire Domain
6. Discussions
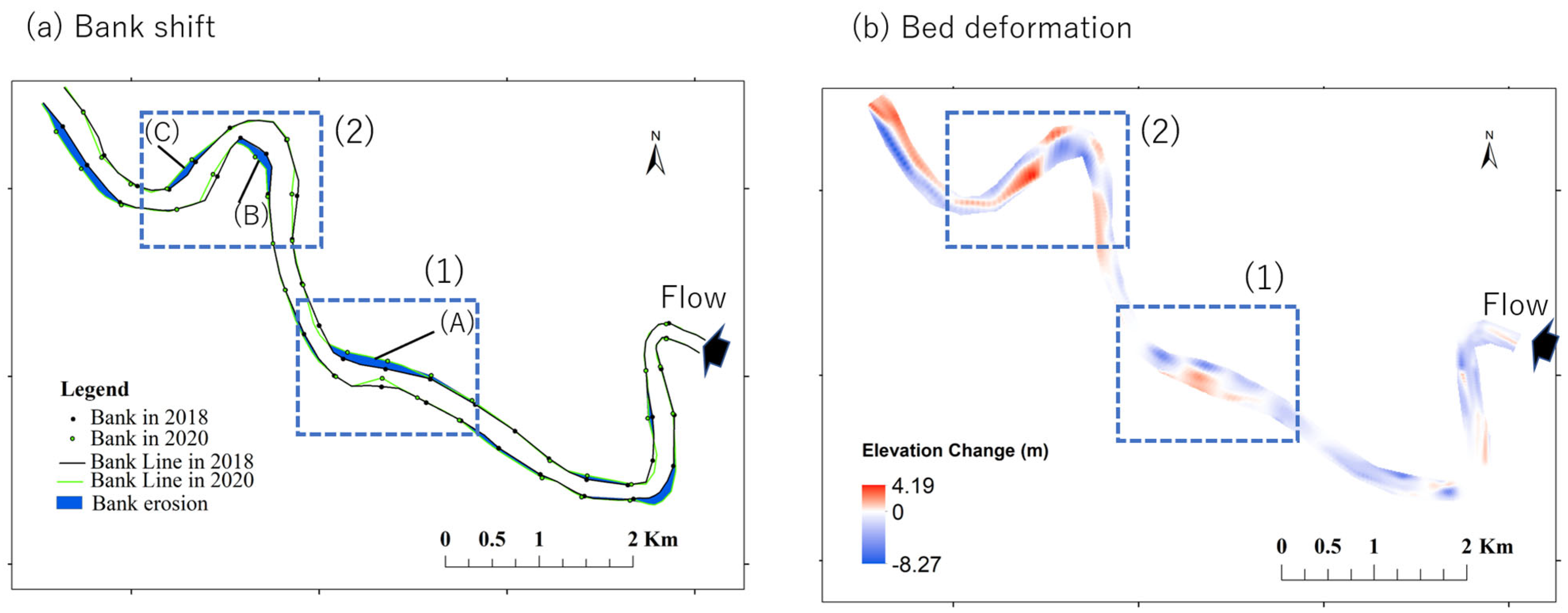
6.1. Characteristics of Bed Deformation and Bank Shift
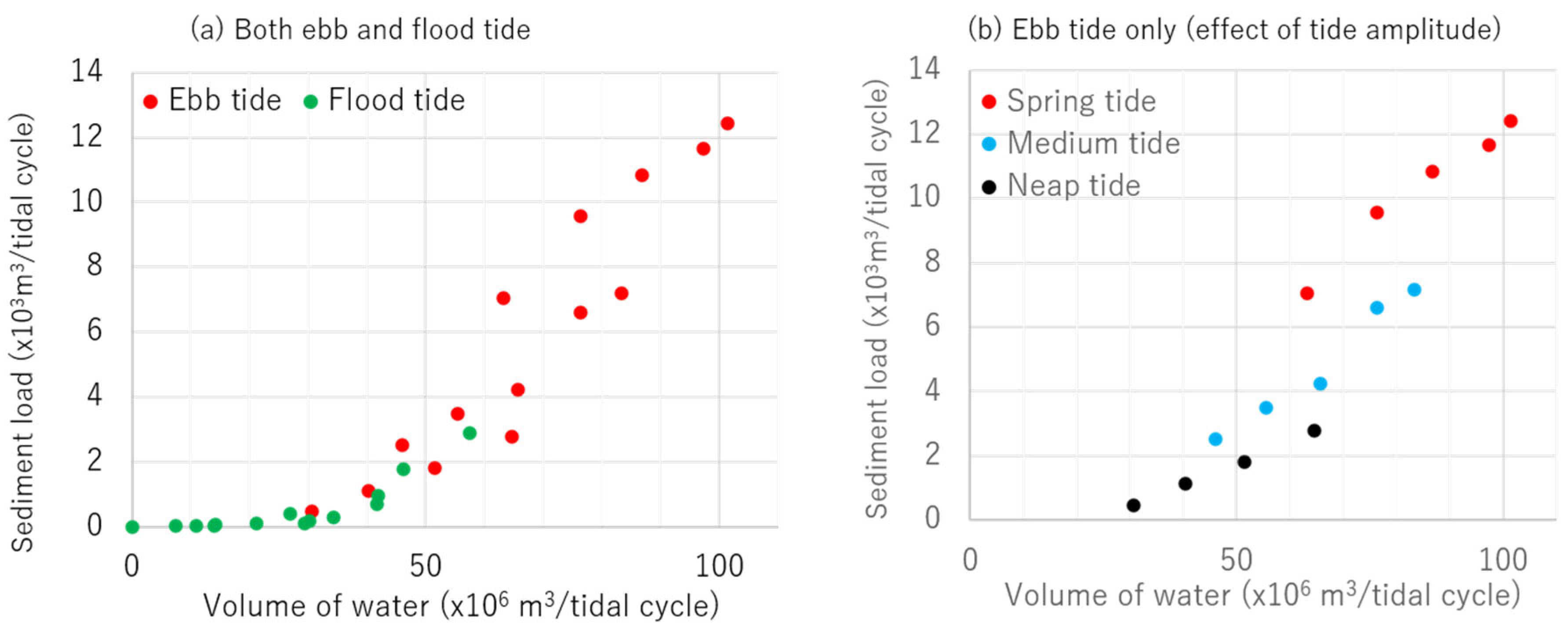
6.2. Characteristics of Sediment Transport and Channel Change in the Tide-Dominated Area
6.3. The Cause of Bank Migration and Channel Change Estimated by the Computation Results
7. Conclusions
- (1)
- The results of the large domain computations show that riverbed deformation is mainly caused by tides rather than river discharge in an area of about 10 km from the river mouth. In particular, a large amount of sediment is transported during the ebb tide period of the spring tide, resulting in active bed deformation and channel change in the downstream area.
- (2)
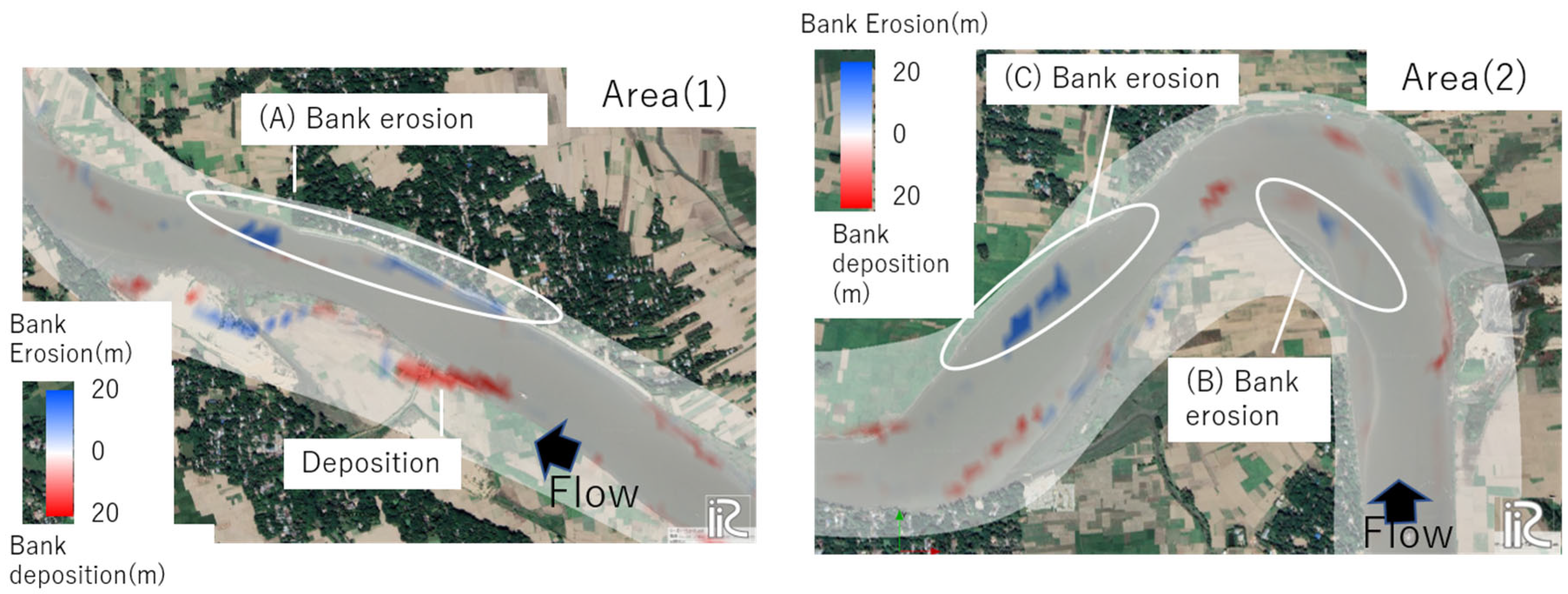
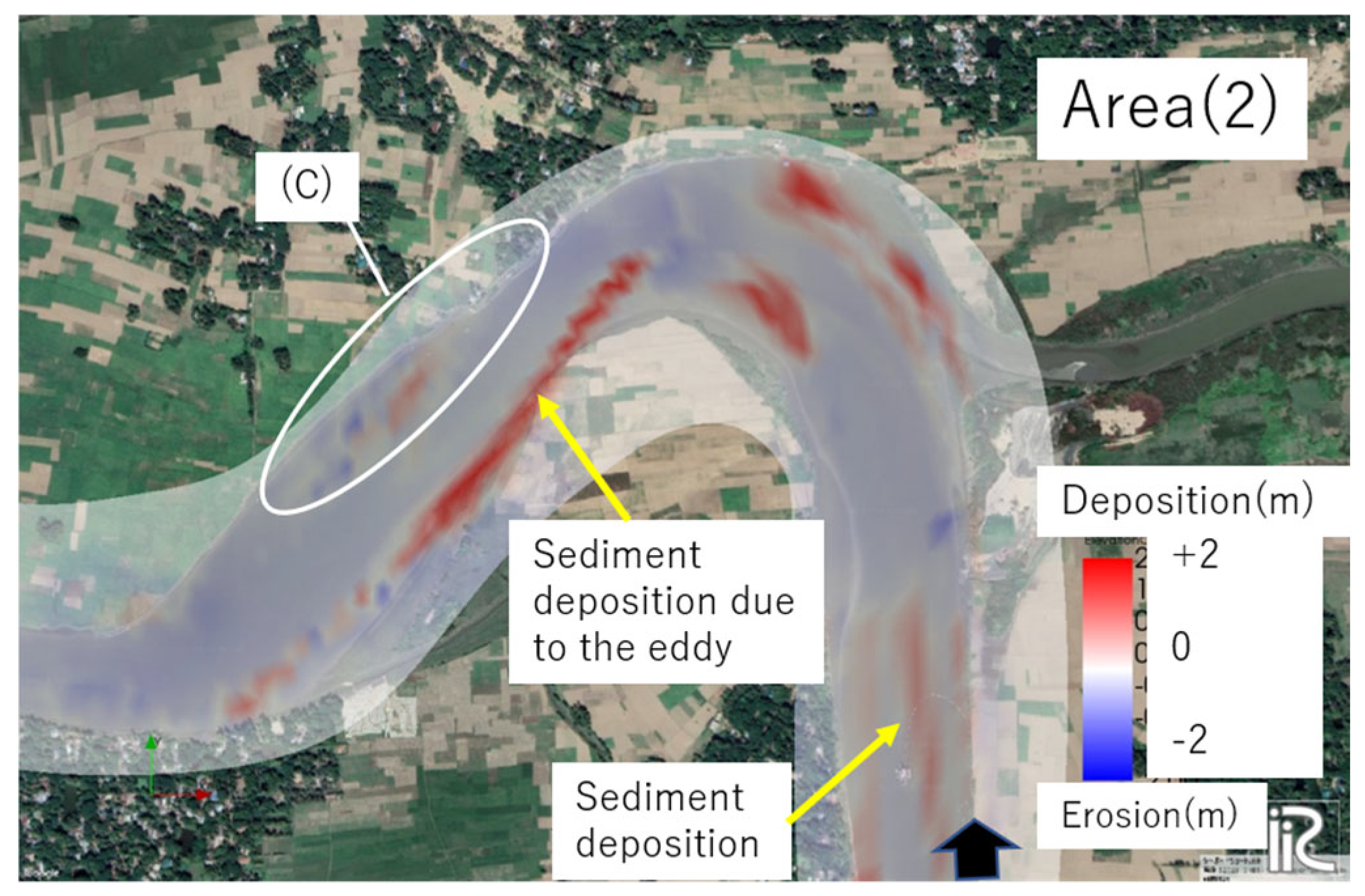
- According to the computation results in the detailed study area, flood flows cause active bed deformation. In these areas, sediment deposition on the inner bank and bank erosion on the outer bank are observed just downstream of the bend.
- (3)
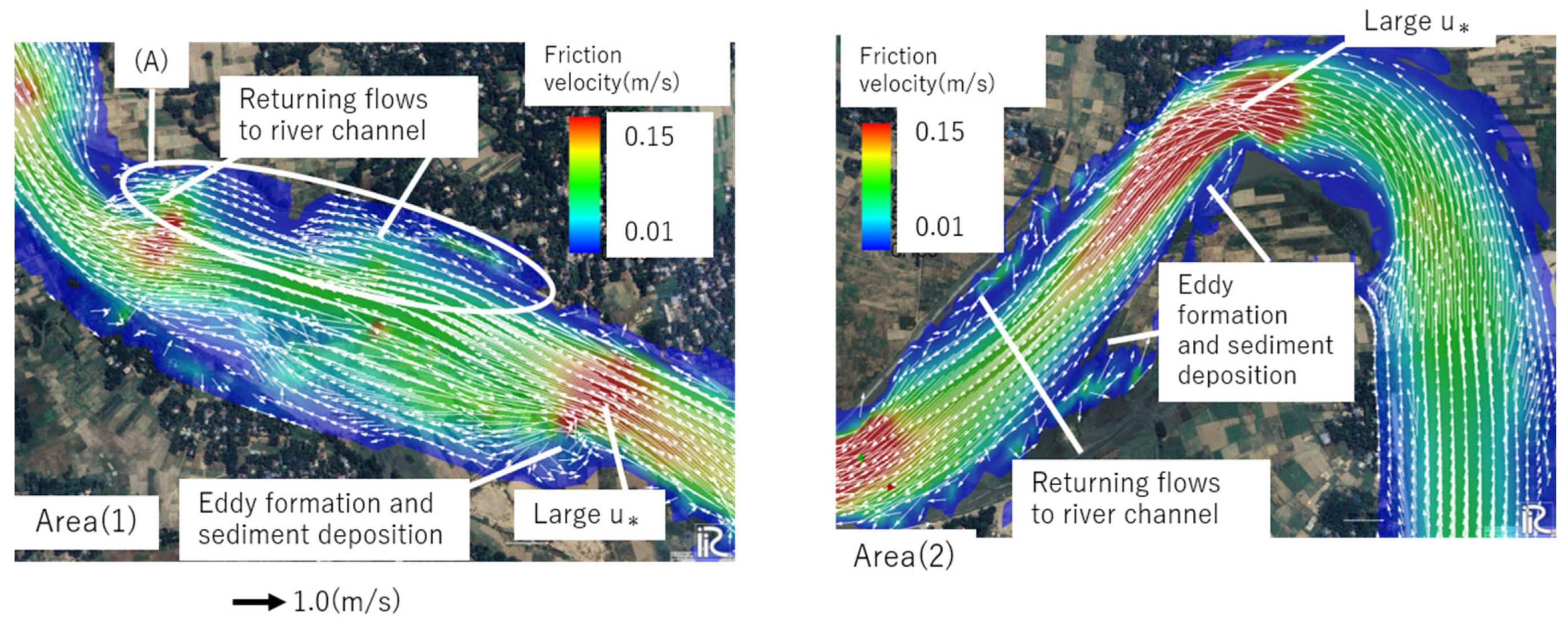
- A detailed study area computation with bank shifts shows that on the inner bank downstream of the flow concentration area, suspended sediment is deposited along with the eddy separated from the main stream. This eddy is not developed on the outer bank side, and bank erosion at the outer bank is caused when the overflow water returns to the river channel. Therefore, the process of bank migration and channel change due to sediment deposition on the inner bank and erosion on the outer bank caused by suspended sediment transport is demonstrated. Such channel change is particularly accelerated during the ebb tide period of the spring tide.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rahman, M.M.; Harada, D.; Egashira, S. Basin Scale Sediment Transport Processes Using Rainfall Sediment Runff Model—A Case Study of Sangu River Basin. J. Jpn. Soc. Civ. Eng. Ser. B1 (Hydraul. Eng.) 2022, 78, I_1099–I_1104. [Google Scholar] [CrossRef]
- Bangladesh Water Development Board (BWDB), Institute of Water Modelling (IWM), Feasibility Study for Restoration of Sangu and Matamuhuri River Basin. 2021. Available online: http://www.kmcltd.org/smrb_project.php (accessed on 28 November 2023).
- Ikeda, S.; Parker, G.; Sawai, K. Bend theory of river meanders. Part 1. Linear development. J. Fluid Mech. 1981, 112, 363–377. [Google Scholar] [CrossRef]
- Blondeaux, P.; Seminara, G. A unified bar–bend theory of river meanders. J. Fluid Mech. 1985, 157, 449–470. [Google Scholar] [CrossRef]
- Kuroki, M.; Kishi, T. Regime criteria on bars and braids in alluvial straight channels. Proc. Jpn. Soc. Civ. Eng. 1984, 1984, 87–96. [Google Scholar] [CrossRef] [PubMed]
- Struiksma, N.; Olsen, K.W.; Flokstra, C.; De Vriend, H.J. Bed deformation in curved alluvial channels. J. Hydraul. Res. 1985, 23, 57–79. [Google Scholar] [CrossRef]
- Shimizu, Y.; Itakura, T. Calculation of bed variation in alluvial channels. J. Hydraul. Eng. 1989, 115, 367–384. [Google Scholar] [CrossRef]
- Osman, A.M.; Thorne, C.R. Riverbank stability analysis. I: Theory. J. Hydraul. Eng. 1988, 114, 134–150. [Google Scholar] [CrossRef]
- Nagata, N.; Hosoda, T.; Muramoto, Y. Numerical analysis of river channel processes with bank erosion. J. Hydraul. Eng. 2000, 126, 243–252. [Google Scholar] [CrossRef]
- Darby, S.E.; Alabyan, A.M.; Van de Wiel, M.J. Numerical simulation of bank erosion and channel migration in meandering rivers. Water Resour. Res. 2002, 38, 2–1–2–21. [Google Scholar] [CrossRef]
- Bosa, S.; Petti, M.; Pascolo, S. Numerical modelling of cohesive bank migration. Water 2018, 10, 961. [Google Scholar] [CrossRef]
- Iwasaki, T.; Shimizu, Y.; Kimura, I. Numerical simulation of bar and bank erosion in a vegetated floodplain: A case study in the Otofuke River. Adv. Water Resour. 2016, 93, 118–134. [Google Scholar] [CrossRef]
- Micheli, E.R.; Kirchner, J.W. Effects of wet meadow riparian vegetation on streambank erosion. 1. Remote sensing measurements of streambank migration and erodibility. Earth Surf. Process. Landf. 2002, 27, 627–639. [Google Scholar] [CrossRef]
- Collins, D.B.G.; Bras, R.L.; Tucker, G.E. Modeling the effects of vegetation-erosion coupling on landscape evolution. J. Geophys. Res. Earth Surf. 2004, 109, 1–11. [Google Scholar] [CrossRef]
- Ahmed, T.S.; Egashira, S.; Harada, D.; Yorozuya, A. Sediment Transportation and Sand Bar Deformation Owing to Tidal Currents in Sittang River Estuary, Myanmar. J. Jpn. Soc. Civ. Eng. Ser. B1 (Hydraul. Eng.) 2019, 75, I_1027–I_1032. [Google Scholar] [CrossRef]
- Duan, J.G.; Nanda, S.K. Two-dimensional depth-averaged model simulation of suspended sediment concentration distribution in a groyne field. J. Hydrol. 2006, 327, 426–437. [Google Scholar] [CrossRef]
- Xie, Q.; Yang, J.; Lundström, T.S. Field Studies and 3D Modelling of Morphodynamics in a Meandering River Reach Dominated by Tides and Suspended Load. Fluids 2019, 4, 15. [Google Scholar] [CrossRef]
- Masbahul, I.M.; Yorozuya, A.; Harada, D.; Egashira, S. A Numerical Study on Bank Erosion of a Braided Channel: Case Study of the “Tangail and Manikganj Districts Along the Brahmaputra River”. J. Disaster Res. 2021, 17, 263–269. [Google Scholar] [CrossRef]
- Bangladesh Inland Water Transport Authority (BIWTA), Government of People’s Republic of Bangladesh Ministry of Shipping, Bangladesh Regional Waterway Transport Project 1. 2019. Available online: https://biwta.portal.gov.bd/sites/default/files/files/biwta.portal.gov.bd/page/f3ca1ff6_95b0_4606_849f_2c0844e455bc/Revised_Final%20Report%20%28Main%20Report%29.pdf (accessed on 28 November 2023).
- Uddin, M.; Alam, J.B.; Khan, Z.H.; Hasan, G.M.J.; Rahman, T. Two Dimensional Hydrodynamic Modelling of Northern Bay of Bengal Coastal Waters. Comput. Water Energy Environ. Eng. 2014, 3, 140–151. [Google Scholar] [CrossRef]
- Harada, D.; Egashira, S.; Ahmed, T.S.; Ito, H. Entrainment of bed sediment composed of very fine material. Earth Surf. Process. Landf. 2022, 47, 3051–3061. [Google Scholar] [CrossRef]
- van Rijn, L.C. Mathematical modeling of suspended sediment in nonuniform flows. J. Hydraul. Eng. 1986, 112, 433–455. [Google Scholar] [CrossRef]
- Itakura, T.; Kishi, T. Open channel flow with suspended sediments. J. Hydraul. Div. 1980, 106, 1325–1343. [Google Scholar] [CrossRef]
- Shimizu, Y.; Nelson, J.; Arnez Ferrel, K.; Asahi, K.; Giri, S.; Inoue, T.; Iwasaki, T.; Jang, C.L.; Kang, T.; Kimura, I.; et al. Advances in Computational Morphodynamics Using the International River Interface Cooperative (iRIC) Software. Earth Surf. Process. Landf. 2019, 45, 11–37. [Google Scholar] [CrossRef]
- Egashira, S.; Ashida, K. Studies on the structures of density stratified flows. Bull. Disaster Prev. Res. Inst. Kyoto Univ. 1980, 29, 165–198. [Google Scholar]
- Egashira, S.; Miyamoto, K.; Ito, T. Constitutive equations of debris flows and their applicabilities, Debris Flow Hazards Mitigation. In Proceedings of the First International Conference, Water Resources Engineering Division/ASCE, San Francisco, CA, USA, 7–9 August 1997; pp. 340–349. [Google Scholar] [CrossRef]
- Hasegawa, K. Universal bank erosion coefficient for meandering rivers. J. Hydraul. Eng. 1989, 115, 744–765. [Google Scholar] [CrossRef]
- Evangelista, S.; Greco, M.; Iervolino, M.; Leopardi, A.; Vacca, A. A new Algorithm for Bank-Failure Mechanisms in 2D Morphodynamic Models with Unstructured Grids. International J. Sediment Res. 2013, 30, 382–391. [Google Scholar] [CrossRef]
- Asahi, K.; Shimizu, Y.; Nelson, J.; Parker, G. Numerical simulation of river meandering with self-evolving banks. J. Geophys. Res. Earth Surf. 2013, 118, 2208–2229. [Google Scholar] [CrossRef]
- Biswas, R.K.; Yorozuya, A.; Egashira, S. Numerical Model for Bank Erosion in the Brahmaputra River. J. Disaster Res. 2016, 11, 1073–1081. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahman, M.M.; Harada, D.; Egashira, S. Numerical Simulation of River Channel Change in the Suspended Sediment-Dominated Downstream Reach of the Sangu River. Water 2024, 16, 1934. https://doi.org/10.3390/w16131934
Rahman MM, Harada D, Egashira S. Numerical Simulation of River Channel Change in the Suspended Sediment-Dominated Downstream Reach of the Sangu River. Water. 2024; 16(13):1934. https://doi.org/10.3390/w16131934
Chicago/Turabian StyleRahman, Md. Majadur, Daisuke Harada, and Shinji Egashira. 2024. "Numerical Simulation of River Channel Change in the Suspended Sediment-Dominated Downstream Reach of the Sangu River" Water 16, no. 13: 1934. https://doi.org/10.3390/w16131934
APA StyleRahman, M. M., Harada, D., & Egashira, S. (2024). Numerical Simulation of River Channel Change in the Suspended Sediment-Dominated Downstream Reach of the Sangu River. Water, 16(13), 1934. https://doi.org/10.3390/w16131934







