Abstract
Urban water systems worldwide are confronted with the dual challenges of dwindling water resources and deteriorating infrastructure, emphasising the critical need to minimise water losses from leakage. Conventional methods for leak and burst detection often prove inadequate, leading to prolonged leak durations and heightened maintenance costs. This study investigates the efficacy of logic- and machine learning-based approaches in early leak detection and precise location identification within water distribution networks. By integrating hardware and software technologies, including sensor technology, data analysis, and study on the logic-based and machine learning algorithms, innovative solutions are proposed to optimise water distribution efficiency and minimise losses. In this research, we focus on a case study area in the Sunbury region of Victoria, Australia, evaluating a pumping main equipped with Supervisory Control and Data Acquisition (SCADA) sensor technology. We extract hydraulic characteristics from SCADA data and develop logic-based algorithms for leak and burst detection, alongside state-of-the-art machine learning techniques. These methodologies are applied to historical data initially and will be subsequently extended to live data, enabling the real-time detection of leaks and bursts. The findings underscore the complementary nature of logic-based and machine learning approaches. While logic-based algorithms excel in capturing straightforward anomalies based on predefined conditions, they may struggle with complex or evolving patterns. Machine learning algorithms enhance detection by learning from historical data, adapting to changing conditions, and capturing intricate patterns and outliers. The comparative analysis of machine learning models highlights the superiority of the local outlier factor (LOF) in anomaly detection, leading to its selection as the final model. Furthermore, a web-based platform has been developed for leak and burst detection using a selected machine learning model. The success of machine learning models over traditional logic-based approaches underscores the effectiveness of data-driven, probabilistic methods in handling complex data patterns and variations. Leveraging statistical and probabilistic techniques, machine learning models offer adaptability and superior performance in scenarios with intricate or dynamic relationships between variables. The findings demonstrate that the proposed methodology can significantly enhance the early detection of leaks and bursts, thereby minimising water loss and associated economic costs. The implications of this study are profound for the scientific community and stakeholders, as it provides a scalable and efficient solution for water pipeline monitoring. Implementing this approach can lead to more proactive maintenance strategies, ultimately contributing to the sustainability and resilience of urban water infrastructure systems.
1. Introduction
Water is a precious resource that is vital for sustaining life and supporting critical sectors, including agriculture, industry, and urban infrastructure energy. However, one of the most pervasive and costly challenges faced by water utilities is the challenge of water leakages and bursts within municipal water distribution networks [1]. These leaks, whether minor and unnoticed or significant and catastrophic, result in substantial water losses, financial burdens, and environmental consequences. If leaks are small, flow from pipes generally does not disrupt the water supply. On the other hand, pipe bursts are created due to the rupture of pipes and will partly or fully disrupt the water supply in the area depending upon the location of the burst in the water supply network [1]. The Figure 1 shows leak and burst in the water pipeline.

Figure 1.
Showing (a) pipe leakage [3] and (b) pipe burst [4].
These leaks, whether unnoticed or catastrophic, result in substantial water losses, financial burdens, and environmental consequences. Addressing this issue is not just an economic imperative but also a moral obligation, considering the growing global concern over water scarcity and the need to optimise energy consumption. In response to this critical challenge, the adoption of smart systems driven by logic-based and machine learning (ML) techniques have emerged as transformative solutions [2].
Smart systems represent an integrated approach that combines sensor technologies, data analytics, automation, and system hydraulics to enhance the efficiency and sustainability of water distribution networks. This paper explores the multifaceted issue of water leakages and bursts and the urgent need for smart systems to mitigate their impacts. It also delves into the application of logic-based and ML techniques for early leak detection and precise identification, highlighting their pivotal role in optimising water and energy consumption while improving customer services.
The hydraulic characteristics of the pipeline, pressure sensors, and flow meters are integral components of a water network, working together to ensure efficient water distribution, pressure regulation, and accurate flow measurement. Pressure sensors are devices that measure the pressure of a fluid, such as water, and convert it into an electrical signal. Flow meters are devices that quantify the amount of fluid passing through a pipe or a channel. These technologies contribute to the overall functionality, sustainability, and management of water resources in urban and industrial settings.
The Intelligent Water Network (IWN) can be considered as a system that can predict/identify and inform about the likelihood of specific events or water network behaviours before their occurrence or immediately after their occurrence. This enables the service provider to be able to plan for, and mitigate, some of the possible outcomes or even prevent their occurrence [1]. Consequently, in the case of IWNs, asset management procedures can be planned for these events to mitigate possible practical consequences or prevent them completely [1]. Joseph et al. [5] presented comprehensive a literature examination review which underscores the global exploration and deployment of both software- and hardware-based technologies, showcasing their increase in adoption. These technologies confer advantages such as enhanced precision, speed, and cost-effectiveness in the identification and pinpointing of leaks and bursts. The evaluation encompasses various leak detection methods, and analysing factors like detection principle, sensitivity, accuracy, reliability, and user-friendliness. Software-driven technologies, artificial intelligence, and machine learning algorithms coupled with hydraulic models exhibit proficiency in the accurate prediction and early detection of water losses. On the other hand, hardware-based technologies, exemplified by acoustic sensors, pressure sensors, and flow meters, demonstrate efficacy in the real-time leak and burst detection and their localisation. Considering the characteristics of both software and hardware-based technologies, Joseph et al. [5] introduced a methodology integrating both software and hardware components for leak and burst identification. Below is a review of the literature on the challenges posed by water leakages and bursts in municipal water distribution networks and the emergence of smart systems integrating logic-based and machine learning techniques as transformative solutions. The work of Berardi and Giustolisi [6] presented a physically based approach for the calibration of water distribution network (WDN) hydraulic models aimed at supporting leakage management plans since the early stages. The application on two real networks and the experience carried on many real WDNs support pressure and flow monitoring to calibrate a design model to support early-stage leakage management [6]. Joseph et al. [7] described an integrated hardware and software framework tailored for an Intelligent Water Network (IWN) system. In this study [7], the water system established connectivity among flow meters, pressure sensors, and other monitoring devices through the SCADA system, linking them to the data analysis centre. Data from flow and pressure sensors are harnessed for calibrating the hydraulic model and for comparison with the real-time simulations of the water network. Water demand will increase in the future, resulting in the demand for rapid actions to improve resources, reduce demand, and increase treatment and transmission efficiency, further promoting the need for intelligent networks. Campos et al. [8] suggested an IoT framework with several layers for water supply networks. These layers are suggested for creating an Intelligent Water Network (IWN) framework: (i) the sensor layer; (ii) the communication layer; (iii) the water system and operation layer; and (iv) the application and prediction layer. SCADA receives data from sensors and flows metres for flow, pressure, and water quality characteristics. The best distribution of pressure sensors and flow metres will depend on the topography of the area, the size of the water delivery system, and historical data on water quantity changes brought on by the ageing infrastructure, environment, and several other factors. The SCADA system in a water system connects flow metres, pressure sensors, and other monitoring devices to the data analysis centre. Data from the flow and pressure sensors are utilised to calibrate the hydraulic mode and make comparisons with the water network’s real-time simulation. Fereidooni et al. [9] suggest a quick hybrid method for finding leaks and calculating the volume of material lost that combines hydraulic relations with AI algorithms. The suggested technique makes use of straightforward, reasonably priced flow sensors that are deployed at each pipeline network junction. By applying hydraulic equations like Hazen–Williams, Darcy–Weisbach, and pressure drop, Ref. [9] showed how influential features for leak identification would be produced. They constructed prediction models using decision tree, KNN, Random Forest, and Bayesian networks, and based on the topology of the pipeline, they identified leaks and their pressure. Gorenstein [10] demonstrated that the data-driven algorithms outperform the logic-based model in each metric by at least 5%. Additionally, as algorithms are trained with new data, their prediction becomes more accurate, but adding attributes that are connected to geography to the data does not increase the accuracy any further. The development of more complex prediction algorithms, such as Bayesian belief networks and deep neural networks, should be the focus of future efforts [10]. The purpose of developing the logic-based method lies in its structured approach to initial leak and burst detection. Logic-based algorithms efficiently capture straightforward anomalies that align with predefined conditions. They offer a clear and interpretable framework for identifying common patterns and straightforward deviations within the data. However, logic-based models may struggle with complex or evolving patterns that fall outside the scope of predefined rules. This limitation necessitates the integration of machine learning techniques, which excel in capturing intricate patterns and outliers that may not be apparent through fixed rules alone. In this paper, the relationship between the logic-based method and the machine learning-based approach is complementary. The logic-based method serves as a foundational framework for initial detection, providing a structured and efficient approach to identifying straightforward anomalies. On the other hand, the machine learning-based approach enhances the detection process by learning from historical data, adapting to changing conditions, and capturing complex patterns beyond the scope of the fixed rules. The research achieves a comprehensive and effective approach to leak and burst detection, leveraging the strengths of each method to enhance overall performance and reliability. Future research should focus on further refining these methodologies, developing algorithms with fewer false alarms, and optimising sensor deployment to enhance accuracy and reliability in leak and burst detection. This research aims to develop a methodology for water pipe leak and burst detection using logic- and machine learning-based approaches. The developed methodologies can be adopted on pumping mains using live SCADA data on pressure, flow, and pump speed for quick leak/burst detection.
2. Case Study Pumping Water System for the Detection of Leaks and Bursts
A water supply pumping main system in the Sunbury region, Victoria state, Australia, has been adopted as the case study system by considering the elevation, pipeline layout, and availability of data for developing the leak/burst detection methodology. Figure 2 shows the map of the case study area in the Sunbury region, Victoria, Australia, and Figure 3 presents the simplified detailed diagram of the case study pumping water supply system with a 450 mm pipeline to the water tank. Water is pumped directly from the trunk water main to a tank through an Asbestos–Cement pipeline of 450 mm diameter. There is a pressure sensor and flow meter sensor in the pipeline. The distance between the pumping station and the tank is 6.24 km. The research methodology was developed using data from a flow meter, pressure sensor, and pump speed recorder. The pumping station continuously monitors water flow, pressure, pump speed, and the water level in a tank with a capacity of 3.72 m (from the extracted SCADA information).
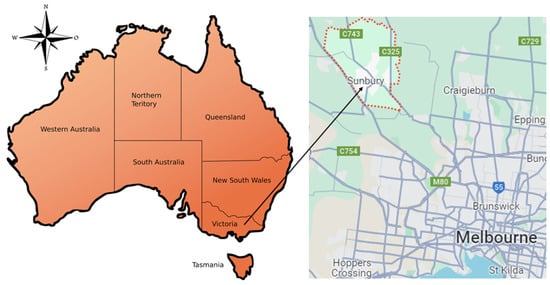
Figure 2.
Map of the location of the case study site in the Sunbury region, Victoria, Australia.
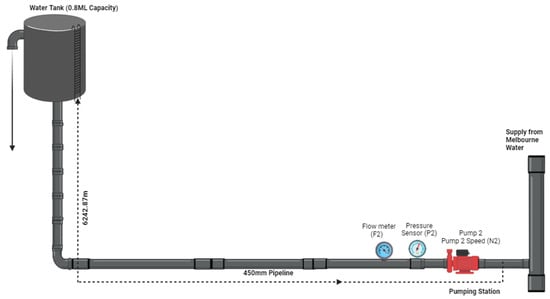
Figure 3.
Simplified detailed schematic diagram of the 6.24 km 450 mm pipeline.
2.1. Software- and Hardware-Based Methods for the Detection of Leaks and Bursts in the Water Pipeline
In this research, two methodologies are developed. One is the logic-based method, and the other is the machine learning-based approach. The overall study is shown in the flow chart below in Figure 4.
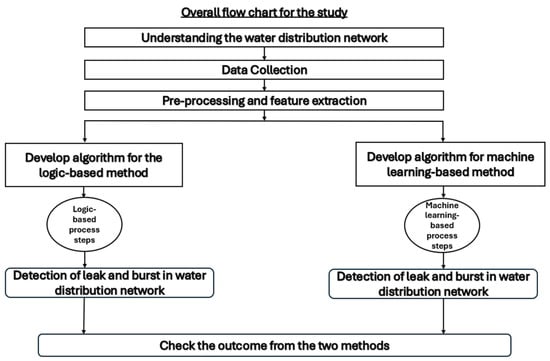
Figure 4.
An overall flow diagram of the leak and burst detection in the water distribution network.
The overall methodology includes understanding the water distribution system, SCADA data collection, the preprocessing of data for application, and finally developing algorithms for logic- and machine learning-based algorithms for leak and bust identification.
Table 1 shows an example of the extracted SCADA data points as attributed to the flow, pressure, and pump speed sensors illustrated in Figure 3. The measurements shown in Table 1 columns 2, 3, and 4 represent readings collected from the SCADA system at one-minute intervals. Once the pump reaches its maximum speed (1500 rpm), the pump speed remains constant. The pump speed increases gradually at the start of the pump until it reaches full speed, and decreases gradually when the pump is being shut down till it stops. Similar variations can be seen in other recorded parameters during pump start and shutdown operations.

Table 1.
Extracted SCADA per minute data from the flow meter, pressure sensor, and the pump speed sensor for the 450 mm pipeline.
A total of 20,000 data points based on per minute interval were collected for the methodology development. Using a part of the collected data set, leak and burst instances are created and these leak and burst instances are then integrated into the overall dataset, resulting in a modified dataset containing both normal, leak, and burst data points for training and testing the algorithms.
2.1.1. Logic-Based (If and Else If Conditions) Algorithm Design for the Detection of Leaks and Bursts in Water Pipelines Using Flow, Pressure, and Pump Speed Data
Logic-based methods involve defining explicit rules or conditions that, when met, indicate the presence of specific events or conditions, which are associated with a leak or burst in a pipeline.
The pressure drop rule is defined as if a sudden and significant pressure drop is detected in the pipeline over a short period of time, it may indicate a burst, or if the pressure drop is small over a long period of time in excess of the normal pressure variation during system operation. The rule could trigger an alarm when the pressure drop exceeds a predefined threshold. Pump speed variation occurs when the pump speed gradually increases from 0 to a normal operating speed once started and similarly decreases from the normal operating speed over a certain period under shutdown conditions.
Logic-based systems can analyse historical data to establish the patterns of normal behaviour. Deviations from these patterns can be flagged as potential leaks or bursts. The development of a logic-based algorithm using Python programming language for the detection of leaks and bursts in water pipelines is rooted in its interpretability, adaptability, and domain-specific applicability, which can help in addressing the challenges posed by leak and burst detection.
Figure 5 details the steps involved in the development of the algorithm for leak and burst identification. The following are the main considerations involved in the development of the algorithm: (a) collect SCADA data for flow in pumping main, pressure, and pump speed; (b) estimate variation in pressure and flow (delta ∆P and ∆Q) while the pump is running on its normal speed for the assessment of threshold values for leaks and burst conditions for algorithm development; (c) estimate pump speed variation during pump start to full speed and then decrease in pump speed during pump shutdown condition (identify pump start and shutdown stages); (d) develop an algorithm (coded in Python) for the identification of leak and burst conditions and to notify the operator for any leak and burst condition; and (e) in the case of burst condition, the estimation of approximate burst location.
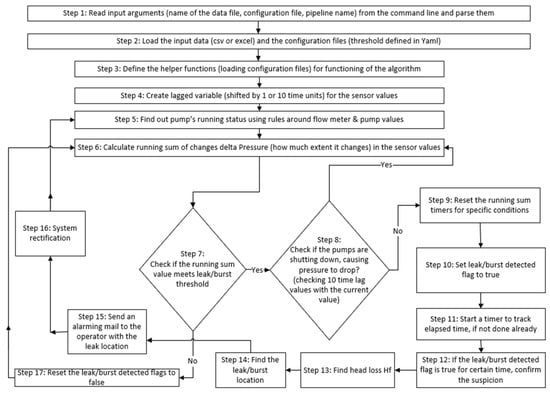
Figure 5.
A flow diagram of the leak and burst detection algorithm (logic-based).
The following identifications are essential for algorithm development:
Flow anomalies: Unusual flow patterns, such as unexpected increases or decreases in flow rates, can be indicative of leaks. It is determined by the percentage variations. Logic-based systems can flag such anomalies for further investigation.
Pump speed variation: The pump speed gradually increases from 0 to the normal operating speed of 1500 rpm once started and similarly decreases from the normal operating speed over a period of 10 min under shutdown conditions in the case study system. The operation time of the pumps is dependent on the water level in the 0.8 ML tank at the end of the pumping main.
Historical data analysis for algorithm development: Logic-based systems can analyse historical data to establish the patterns of normal behaviour. Deviations from these patterns can be flagged as potential leaks or bursts.
It is hoped that the algorithm developed herein will be used on pumping systems using live data to help water system operators with leak and burst identification in pipe networks quickly.
The main tasks in the diagram are from Step 6 to Step 10. The given specified algorithm outlines a series of steps for detecting leaks and bursts in a water distribution system. The process begins by reading per-minute input arguments from the command line for flow, pressure, and pump speed sensor values. Subsequently, threshold values for ∆P (delta pressure), ∆Q (delta flow), and ∆S (delta speed of the pump) are estimated using the recorded data; however, these values can be updated periodically.
The following main tasks are involved in the development of the algorithm for the identification of leaks and bursts:
- Task 1 (Steps 1–5): Collect SCADA data for flow in the pumping main, pressure, and pump speed.
Step 1: Read input arguments (name of the data file, configuration file, and pipeline name) from the command line and parse them. First, the program collects information about the pressure sensor, flow meter, and pump in the water pipeline. These data include the name of the data file, a configuration file, and the name of the pipeline.
Step 2: Load the input data (CSV or Excel) and the configuration files (threshold defined in Yaml), where Yaml is a human-readable data format commonly used for configuration files and data exchange between languages with different data structures. This enables the checking of the data file (in CSV or Excel format) and a configuration file that has a specific threshold in Yaml.
Step 3: Define the helper functions (loading configuration files) for the functioning of the algorithm. Helper functions in algorithms are small, specialised functions that are designed to perform a specific task or subtask within a larger algorithm. They are not the main components of the algorithm but rather an aid in achieving specific functionalities, making the algorithm more modular, readable, and easier to maintain.
Step 4: Create a lagged variable (shifted by 1 or 10 time units) for the sensor values. Lagged variables, also known as lag features, are a concept commonly used in time-series analysis and machine learning, where the past values of a variable are used as features in predictive modelling. Lagged variables are especially useful when dealing with time-dependent data.
Step 5: The final stage involves determining the pump’s running status using rules around the flow meter and pump values.
- Task 2 (Steps 6–8): Estimate variation in pressure ∆P, ∆S, and ∆Q while the pump is running at its normal speed for the assessment of threshold values for leaks and burst conditions. Any data point that is more than three times the standard deviation is likely a burst.
Step 6: Calculate the running sum of changes (to what extent it changes) in the sensor values over a certain period of time (during which the pump is running at its full speed). The running sum is the summing up of the differences between consecutive pressure readings (per minute) to check the anomalies over normal operating pressure.
Step 7: Check if the running sum value meets the leak or burst threshold. If “yes”, go to Step 8, and no go to Step 17.
Step 8: Check if the pumps are shutting down, causing pressure to drop by checking the 10 time lag values with the current value.
If the condition is “yes” from Step 8, go to Step 6 and calculate the running sum of changes in pressure values. If the condition is “no” then go to Step 9.
- Task 3 (Step 9): Estimate pump speed variation during pump start to full speed and then decrease in pump speed during pump shutdown condition (identify pump start and shutdown stages).
Step 9: Reset the running sum timers for specific conditions (if the pump is on or off).
- Task 4 (Steps 10–12): The identification of leak and burst conditions and notifying the operator of any leak and burst condition.
Step 10: If the leak/burst thresholds are met, set the leak/burst detected flag to true.
Step 11: Start a counter to track time for Step 10.
Step 12: If the burst detected flag is true for a certain time, confirm the suspicion.
Task 4 involves identifying the leak and burst conditions and notifying the operator accordingly.
- Task 5 (Steps 13–17): Estimate the appropriate leak location along the pressure water main
Step 13: Find head loss Hf in the pressure main based on the current pressure sensor readings under burst conditions and topography considerations (see Section 2.1.1.1).
Step 14: Find the burst location.
Step 15: Send an alarming mail to the operator with more information.
Step 16: Burst alerts at the start and end of the event.
Step 17: If the running sum value does not meet the burst threshold, reset the burst threshold values to false.
Task 5 involves estimating the appropriate leak location. In Step 13, the head loss (Hf) is calculated. Step 14 determines the burst location (Section 2.1.1.1). Following this, in Step 15, an alarming email containing additional information is sent to the operator. Step 16 ensures burst alerts are issued at the beginning and end of the event. Lastly, Step 17 resets the burst threshold values to false if the running sum value does not meet the burst threshold.
In case of live data availability, the process will check ongoing data to identify leaks or bursts based on system capabilities in terms of pressure/flow data availability across the pressure main.
2.1.1.1. Burst location Identification in a Pumping Main (Case Study System)
The algorithm can identify the approximate location of a leak or burst in pumping or gravity main systems, provided significant pressure and flow sensors are placed at regular intervals. In the absence of such an arrangement, the approximate location of a pipe burst can still be estimated with limited pressure and flow sensors. Using the change (drop) in pressure head reading at the pumping end, the location of burst LX can be estimated using any pipe head loss equation.
Darcy–Weisbach’s head loss equation for flow in pipes can be written as follows:
where f is the friction factor in the pipe, L is the pipe length in meters, D is the pipe diameter in meters, Q is the fluid flow in cubic m/s, and g is the gravitational constant.
The friction factor f can be estimated using Swamee equation (Swamee, 1993) [11]:
where ε is the average height of the roughness projection of the pipe wall and ν is the kinematic viscosity of the fluid. Kinematic viscosity can be obtained using Equation (3) (Swamee, 2004) [12]:
where T is the water temperature in degrees centigrade.
For known head loss in the pipeline, pipe length, and pipe diameter, friction factor f can be calibrated using Equation (1), and then ε the pipe wall roughness height can be calculated using Equation (2).
In the case of a pipe burst, the approximate location of the burst from the pumping station along the pipe can be estimated using the following equation.
where is the pressure at the sensor at the time of the leak, is the length of the leak location along the pumping main alignment, L is the length of the pumping main, is the elevation difference between the pumping main and the service tank. The topography of the pipe alignment has a uniform gradient in the case study; however, Equation (4) can be modified to incorporate various gradients at different lengths across the pumping main.
A simple system diagram for leak location detection is shown in Figure 5 below.
Pipe length for leak location can be estimated as follows:
As the pump system head (static head and head loss in pipe) will change due to pipe burst, and thus, in some pumps the pump characteristics will also change, which can also be incorporated in the algorithm specific to pump conditions. In Figure 6 below, a pipeline with a diameter of 0.45 m extends over a length of 6280 m, connecting the pump to a water tank. The pump is situated at an elevation of RL 138.3 m, while the tank stands at an increased level of 196.3 m.
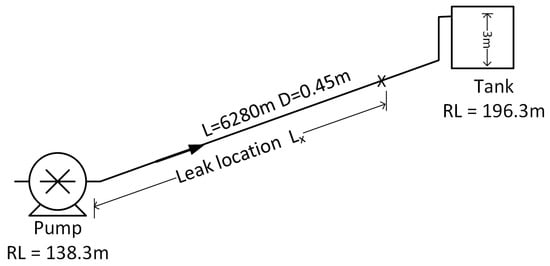
Figure 6.
Leak location at x.
Alert Generation
As the system operates, the algorithm continuously monitors the real-time pressure data from the sensors. It compares the current pressure readings with the established baseline to identify any deviations. The algorithm employs logic-based rules to identify patterns or anomalies in the pressure data that may indicate a leak. Common logic includes looking for sudden pressure drops, fluctuations outside expected ranges, or the patterns indicative of leaks. When the algorithm detects a deviation beyond the predefined thresholds or violates the established logic rules, it triggers an alert. The alert may include information about the burst occurrence time, the approximate distance of the burst location, and the potential cause of the detected anomaly including the pressure values, flow meter reading, and pump speed.
2.1.2. Machine Learning-Based Method for the Detection of Leaks and Bursts in Water Pipelines
Machine Learning is a subfield of artificial intelligence (AI) that focuses on the development of algorithms and models that enable computers to learn patterns from data.
Machine learning algorithms are suitable for detecting leaks and bursts in water pipelines due to their ability to provide early detection, analyse large datasets comprehensively, and monitor systems in real-time. These algorithms contribute to reducing false positives, adapting to changing conditions, and optimising maintenance strategies by predicting potential issues and prioritising areas at risk. The integration of machine learning with Internet of Things (IoT) devices and sensor networks enhances accuracy and efficiency, leading to significant cost savings through proactive intervention and efficient resource allocation. Overall, machine learning can play a crucial role in ensuring the sustainable management of water resources by improving the reliability and effectiveness of leak and burst detection in water pipeline systems.
Supervised machine learning requires labelled data, which means you need examples of both normal and leaky situations in the pipeline to train the model. However, obtaining labelled data for leaks can be challenging and expensive because leaks are relatively rare events and may not be readily available for training purposes. Unsupervised learning, on the other hand, does not require labelled data and can detect anomalies or deviations from normal behaviour without explicit examples of leaks. Unsupervised learning is a kind of machine learning in which algorithms are taught without explicit supervision or direction on unlabelled data.
Unsupervised learning: Unsupervised learning involves finding patterns in unlabelled data without predefined outcomes. These algorithms find patterns, structures, or correlations within the data. This allows them to do tasks like anomaly identification. Without the need for labelled examples, unsupervised learning is useful for analysing data, uncovering hidden patterns, and gaining important insights.
Prediction and classification: ML models can be used for forecasting (e.g., predicting future values) and classification (e.g., categorising data into classes).
Unsupervised machine learning focuses on identifying anomalies within unlabelled data, uncovering deviations from the normal pipeline behaviour that might indicate potential issues. Unsupervised learning, tailored for water pipeline monitoring, discovers patterns in the unlabelled data autonomously, contributing to the detection of leaks and bursts. Unlike supervised learning, it identifies inherent structures without predefined output labels, revealing hidden patterns. Its applications span anomaly detection in fraud and network security, as well as data preprocessing and feature engineering prior to supervised learning.
A total of 20,000 data points that represent the leak and non-leak scenarios are used for creating the machine learning model. The machine learning technique selection and application process is shown in Figure 7. The comparative studies of different machine learning models including K-Means, DBSCAN, One-Class SVM, Isolation Forest, and local outlier factor were conducted.
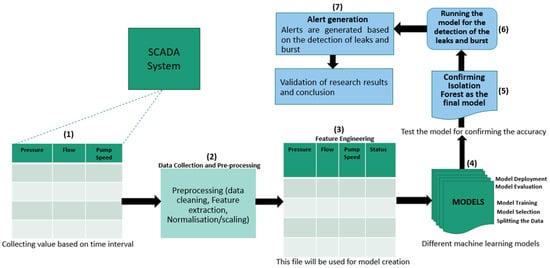
Figure 7.
Developed machine learning approach for leak and burst detection.
The steps (marked in Figure 6) in the machine learning approach for leak and burst detection are provided below:
- Step 1: Collect the data from the existing SCADA for pressure sensors, flow meters, and pump speeds in the time interval of 1 min for the 20,000 data points.
- Step 2: Preprocess the data for algorithm conditions by data cleaning and analysing the SCADA data.
- Step 3: The prepared data will be used for the machine learning algorithms.
- Step 4: Different machine learning models will be used for training and testing.
- Step 5: The selection of the highest-performing machine learning model with the machine learning parametric indices (anomaly F1 score and ROC curve—explained below).
- Step 6: Implementing the selected model for the detection of leaks and bursts.
- Step 7: Alert generation for the leaks and bursts in the pipeline.
As indicated, in the context of detecting leaks and bursts in water pipelines, machine learning algorithms can play a crucial role in analysing the complex data patterns indicative of such events. DBSCAN (Density-Based Spatial Clustering of Applications with Noise) can be applied to data from the sensors distributed along the pipeline network. By identifying the clusters of abnormal data points representing potential leaks or bursts, DBSCAN can effectively pinpoint the areas of interest for further investigation. On the other hand, KMEANS clustering can segment the data into distinct clusters, allowing for the detection of anomalies in the temporal behaviour of the pipeline, such as sudden pressure drops or irregular flow rates, which may indicate leaks or bursts [13]. One-Class SVM, trained on the historical data of normal pipeline operation, can detect deviations from this learned normal behaviour, signalling the presence of abnormalities like leaks or bursts [14]. Isolation Forest, by isolating anomalies in the data through random decision trees, can efficiently detect sudden changes or outliers indicative of leaks or bursts in the pipeline [15]. Lastly, the local outlier factor (LOF) can identify areas of low-density data points, which could signify abnormal conditions such as leaks or bursts in the pipeline network [16]. These machine learning algorithms, when applied judiciously to data collected from water pipeline systems, offer powerful tools for the early detection and mitigation of leaks and bursts, thereby enhancing the efficiency and reliability of water distribution networks [17].
Data imbalance in machine learning occurs when one category (usually the minority category) is significantly underrepresented compared to another category (usually the majority category) within a dataset. This can lead to biased models that perform poorly in predicting the minority category. In our case study, the minority category is the leak cases, and the majority category is the non-leak cases. To address the imbalance issue, several solutions can be employed, including resampling techniques such as oversampling the minority category, undersampling the majority category, or using a combination of both. Additionally, algorithmic approaches like cost-sensitive learning and ensemble methods can help mitigate the effects of data imbalance. Two widely used resampling techniques are ADASYN (Adaptive Synthetic Sampling) and SMOTE (Synthetic Minority Over-sampling Technique). ADASYN focuses on generating synthetic samples for the minority category based on their distribution density, while SMOTE creates synthetic instances along the line segments joining the k minority class nearest neighbours. By synthesising new instances from the minority category, both ADASYN and SMOTE aim to balance the distribution and improve the performance of machine learning models [15].
The effect of data imbalance for each ML algorithm is shown in Table 2, where it can be observed that the anomaly F1 score and ROC-AUC values of the algorithms are very low compared to balanced data. We use the oversampling methods ADASYN and SMOTE for improving the performance of machine learning algorithms in leak detection. In scenarios where positive instances (leaks) are significantly outnumbered by negative instances (non-leaks), these techniques address the data imbalance by generating synthetic samples for the minority category. By creating a more balanced training dataset, ADASYN and SMOTE help prevent bias and overfitting, and enhance the model’s generalisation to accurately identify leaks in water pipeline systems. These methods contribute to a more representative decision boundary, increased sensitivity to anomalies, and improved performance metrics, making them essential tools for building accurate and robust leak detection models.

Table 2.
The outcome depicted in Figure 8 is provided in Table below for further clarity.
The F1 score is the harmonic mean of precision and recall and is often used in binary classification and anomaly detection problems. It is calculated using the following Equation (6) [18,19]:
where precision is the proportion of data points identified as anomalies by the model that are anomalies and is calculated using Equation (7). True positive is the proportion of actual anomalies that are correctly identified as anomalies. False positive is the proportion of non-anomalous data points that are incorrectly classified as anomalies. Recall (sensitivity) is the proportion of actual anomalies that are correctly identified by the model and is calculated using Equation (8).
In evaluating the predictive models for leakage within the pipeline network, it is crucial to consider performance metrics such as the true positive rate and false positive rate. The true positive rate, also known as sensitivity or recall, measures the proportion of actual positive cases that are correctly identified by the model as positive. In the context of leak detection, it signifies the accuracy of the model in correctly identifying instances of leakage, ensuring timely intervention and maintenance. Conversely, the false positive rate measures the proportion of negative cases that are incorrectly classified as positive by the model. In leak detection, a high false positive rate could lead to unnecessary resource allocation and operational disruptions. Balancing these rates is essential for optimizing the efficiency and reliability of the predictive model in detecting and managing pipeline integrity issues.
The Receiver Operating Characteristic (ROC) curve is a graphical representation that illustrates the trade-off between the true positive rate (sensitivity) and the false positive rate across the different thresholds of a predictive model. The Area Under the ROC Curve (ROC AUC) quantifies the overall performance of the model across all the possible threshold values. It represents the probability that the model will rank a randomly chosen positive instance higher than a randomly chosen negative instance. Mathematically, ROC AUC is calculated as the integral of the true positive rate with respect to the false positive rate, ranging from 0 to 1. This integral captures the entire area under the ROC curve, providing a single scalar value that summarizes the model’s discriminatory power. A higher ROC AUC value indicates better overall performance of the model in distinguishing between positive and negative instances, with a value of 1 representing a perfect classifier.
The ROC AUC (Receiver Operating Characteristic Area Under the Curve) is a measure of the area under the ROC curve, which plots the true positive rate (sensitivity) against the false positive rate (1 − specificity) at various thresholds. The ROC AUC is calculated using Equation (9) [20,21]:
3. Results
3.1. Logic-Based Approach for Leak and Burst Detection
3.1.1. Estimation of Delta Pressure (∆P) and Delta Discharge (∆Q) for Case Study System
The values of ∆P and ∆Q can be estimated using the system running data (Table 1) for different time periods. Figure 7 below shows the variation in P and Q under the normal running conditions of the system. As can be seen from Figure 8a, the variation in pressure P at a time will be with ∆P and similarly, the variation in flow Q will be within a range of ∆Q. These can be written in the following form:
P = Paverage ± ∆P
Q = Qaverage ± ∆Q
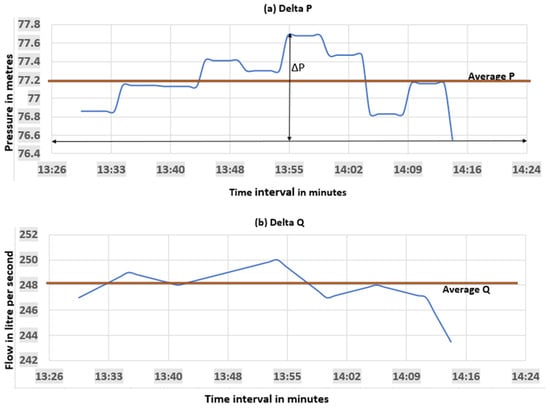
Figure 8.
(a) Estimation of delta pressure (∆P) and (b) delta discharge (∆Q) for case study system.
For the case study, ∆P was estimated as ± 0.6 m (1.3%) and ∆Q as ± 3.25 L/s (2.65%); and average P was 77.2 m and Q as 248 L/s.
Under no leak condition, the variation in pressure and flow at any time should be within ∆P and ∆Q. The pump start and shutdown conditions are also checked from the data. If the pump is running at normal speed and the variation in pressure and flow is two to three times the ∆P and ∆Q, a leak condition can be triggered. On the other hand, if there is a significant sudden change in pressure, a leak condition can be triggered. Developing the conditions for a leak would require a significant analysis of system data.
3.1.2. Estimation of Friction Factor in Pipe and Pipe Roughness
The friction factor for the pipeline can be calculated using Equation (12) and the known pumping main system values for flow, pipe length, pipe diameter, and headloss (Q = 248 L/s, L = 6240 m, D = 0.45 m, g = 9.81 and hf =16.3 m) as follows:
The estimated friction factor will be used in Equation (5) for the estimation of the approximate location of the pipe burst. For the estimation of potential leak location, a significant number of pressure and flow meters would be required at suitable intervals across the pipe.
3.1.3. Categories in the Detection of Leaks and Burst
Leakage severity within the pipeline network is categorised into distinct levels based on percentage thresholds (% pressure drop). Based on the % pressure drop, the following categories were developed:
- Minor leak: Instances where the percentage threshold falls below 15 (15% pressure drop from Paverage) are classified as minor leakage, indicating relatively minor disturbances in the system.
- Major leak: When the percentage thresholds range between 15% and 20%, the severity escalates to major leakage, signifying a more significant impact on the pipeline’s integrity and functionality.
- Burst: Any leakage surpassing the threshold of 20% is categorised as a burst, representing a critical burst in the pipeline system that requires immediate attention and intervention to prevent further damage or disruptions.
These categorisations provide a structured framework for assessing and prioritising responses to pipeline integrity issues, aiding in efficient maintenance and management strategies. Detailed system-specific assessment will be required to select the threshold values for these categories.
3.1.4. Leak and Burst Identification
Alerts are produced to detect bursts and leaks. The type of alert indicates whether it is a burst or a leak, along with details such as the time of occurrence, pressure, flow, pump speed readings, and the distance to the location of the burst. As indicated earlier, the leaks and bursts are grouped into three categories: minor leakage, major leakage, and burst. The screenshot of the outcome is shown in Figure 9. It shows the detection of minor leakage, major leakage, and burst detection outcomes using the logic-based approach.
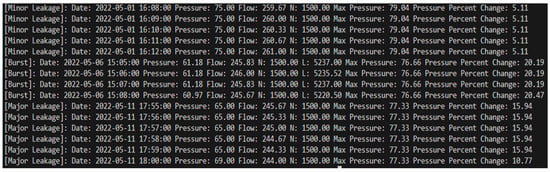
Figure 9.
Minor leakage, major leakage, and burst detection in the 450 mm pipeline using the logic-based approach.
Down below in Figure 10 is the graphical analysis of the pressure (P) data plotted using Python 3.12.4 in the 450 mm pipeline. Minor leaks, major leaks, and bursts are detected based on the three categories of alert systems.

Figure 10.
Graphical representation for pressure (P) in the 450 mm pipeline.
Any data point that is more than three times the standard deviation is almost certainly an anomaly or an outlier [22]. The detection of leakage is shown in a vertical red dotted line and burst is shown in a vertical black dotted line in Figure 9.
3.2. Machine Learning Approach
3.2.1. Selection of Suitable Machine Learning Techniques
The outcomes of a comprehensive comparison involving diverse machine learning models, namely DBSCAN, Isolation Forest, KMEANS, local outlier factor, and One-class SVM are discussed in this section. The criteria for selecting the machine learning models are as follows:
- KMeans: Used for clustering data into two clusters based on normalised and standardised features.
- Isolation Forest: Effective for anomaly detection with the ability to handle high-dimensional data.
- Local Outlier Factor: Computes the local deviation of the density of a sample with respect to its neighbors.
- DBSCAN: Good for identifying clusters of varying shapes and sizes and isolating points that do not belong to any cluster.
- One-Class SVM: Suitable for novelty detection (identifying anomalies) by mapping data to a higher-dimensional space.
- Data Preprocessing: Normalisation and standardisation were performed on both training and test data to ensure consistency in feature scaling.
- Evaluation: Models were evaluated using F1 score as a metric, considering both normal and anomaly classes.
In the Table 3 below, the hyper-parameter settings and the Python libraries used for implementation are provided.

Table 3.
Hyper-parameter settings and the Python libraries used for different machine learning models.
Following the initial analysis, various performance enhancement techniques, including ADASYN and SMOTE, were employed to refine the models. Notably, the local outlier factor emerged as the most effective among the examined models, exhibiting the highest anomaly F1 score and ROC curve Area Under the Curve (AUC) value. These findings underscore the superior performance of the local outlier factor in the context of anomaly detection, offering valuable insights for the advancement of robust and precise machine learning models in similar applications. The anomaly F1 score of the local outlier factor outperforms the other machine learning models. Local outlier factor, without resampling, is 0.12 and with SMOTE it is 0.67 and with ADASYN it is 0.69. The Receiver Operating Characteristic (ROC curve) of the local outlier factor with SMOTE and ADASYN are 0.71 and 0.72. The lowest anomaly F1 score is for DBSCAN with an F1 score of 0.02 after SMOTE analysis and 0.11 after the ADASYN analysis. It is shown in Table 4.

Table 4.
Performance comparison of different machine learning models with different techniques.
3.2.2. Web-Based Platform for Machine Learning Outcome
The local outlier factor algorithm selected in the previous step is employed to detect the leaks and bursts by developing a web-based platform as in Figure 10 and Figure 11. The pressure and flow data from the SCADA setup is collected in the form of a CSV file and is provided as input to the application; the application then predicts the leak or burst condition if any exists, pinpointing the time at which it occurred. Figure 10 shows the forecasted instances of leaks within the 450 mm pipeline network at a precise time point, providing valuable insights into potential vulnerabilities and areas requiring maintenance or monitoring. Meanwhile, Figure 11 depicts the anticipated occurrences of leakage and Figure 12 depicts the occurrences of bursts within the same pipeline network, offering crucial information for proactive maintenance strategies and risk mitigation measures.
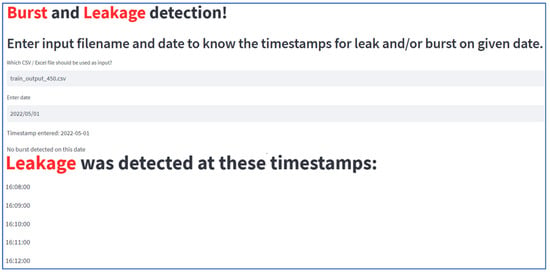
Figure 11.
Predicted leak occurrence within the 450 mm pipeline network at a specific time stamp.
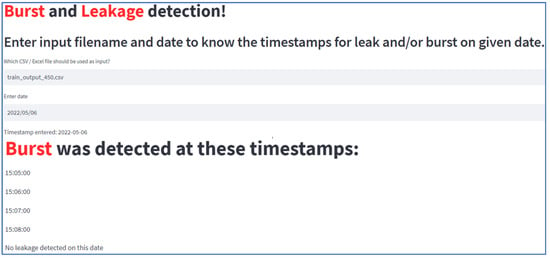
Figure 12.
Predicted burst occurrence within the 450 mm pipeline network at a specific time stamp.
These predictive models enable efficient resource allocation and proactive management, enhancing the resilience and reliability of the pipeline infrastructure.
4. Conclusions
In conclusion, this study presents a novel framework for leak and burst detection in water distribution networks. Through comprehensive modelling and analysis, our methodology has demonstrated promising results in identifying leaks and bursts within the network.
Logic-based and machine learning-based models have been developed and analysed/validated using the Melbourne metro area-based pumping water system’s modified historical SCADA data to detect the leaks and bursts. These models are based on system parameters such as flow, pressure, pump speeds, pump operating conditions, and system hydraulic characteristics.
The section on the most appropriate machine learning model was based on the identification of five models used recently in the literature, namely DBSCAN, Isolation Forest, KMEANS, local outlier factor, and One-class SVM. Following the initial analysis, various performance enhancement techniques, including ADASYN and SMOTE, were employed to refine the models. This analysis allows for the evaluation of different algorithms’ performance in detecting leaks and bursts within the water distribution system. It helps to assess each model’s strengths and weaknesses in handling the dataset, thereby providing insights into the suitability of various machine learning techniques for the task at hand.
A comparative study of multiple machine learning algorithms was conducted using the data obtained from the SCADA system. The findings indicate that the local outlier factor (LOF) algorithm achieved an F1 score of 0.69 and an ROC-AUC of 0.72 in predicting leakages. This trained LOF model has been integrated into a web-based platform designed to predict leakages for new data inputs. The platform processes real-time data and determines the presence of leaks through a user-friendly web interface.
Logic-based and machine learning-based methodologies have been developed and analysed through their application to aid a Melbourne metro area-based case study system to detect the leaks and bursts in the water pumping main. The logic-based algorithm for the detection of leaks and bursts in the water pipeline is based on parameters such as flow, pressure, pump speeds, pump operating conditions, and system hydraulic parameters. The relationship between the logic-based and machine learning approaches is complimentary. Logic-based algorithms provide a structured method for initial leak and burst detection. They are efficient in capturing straightforward anomalies that match predefined conditions. However, they might struggle with identifying complex or evolving patterns that fall outside the scope of the predefined rules. Machine learning algorithms enhance the detection process by learning from historical data and adapting to changing conditions. They excel in capturing complex patterns and outliers that might not be apparent through the fixed rules alone. Machine learning can also assist in refining logic-based rules by providing insights into new conditions or scenarios that are not initially considered. There exist various machine learning approaches in the literature and to select a suitable machine learning technique, a comparative analysis of different machine models has been conducted.
Further, a web-based platform has been developed for leak and burst detection using a selected machine learning model, thus demonstrating the automation of the process of leak and burst detection using the machine learning approach. The fact that LOF and other machine learning models outperform this logic-based approach highlights the effectiveness of data-driven, probabilistic methods in handling complex patterns and variations within the data. It is worth noting that machine learning models, such as LOF, leverage statistical and probabilistic techniques to identify patterns and anomalies in data, learning from the inherent structures present in the dataset. This adaptability allows them to potentially outperform logic-based systems in scenarios where the relationships between variables are intricate or dynamic.
By utilising real-time sensor data and historical operational information, our approach has shown significant improvements in detecting subtle deviations indicative of leaks or bursts, thereby minimising water loss and infrastructure damage. Furthermore, the scalability and robustness of our framework make it well suited for practical implementation across diverse water distribution network environments. Compatibility with the existing infrastructure, coupled with efficient data acquisition and processing mechanisms, ensures seamless integration into operational workflows. To support our conclusions, we provide quantitative data from extensive experimentation conducted on real-world datasets, showcasing the efficacy and reliability of our methodology in detecting and mitigating network anomalies. Looking ahead, future research endeavours could focus on further refining our framework through the incorporation of advanced machine learning techniques with live data from the water distribution network. Additionally, they could focus on finding out the optimal allocation of sensors in the water network.
In summary, our study contributes to advancing the state-of-the-art in leak and burst detection methodologies, offering a robust and scalable solution that holds promise for improving the efficiency and reliability of water distribution network management in the years to come.
5. Future Recommendations
The performance of machine learning can be further improved by conducting the study in real-time situations using system live data and significant historical data points for leak and burst conditions.
Author Contributions
Writing—original draft, K.J., J.S. and A.K.S.; Writing – review & editing, R.v.S., P.L.P.W., S.S. and N.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research is funded by Victoria University, Melbourne, Australia, and Greater Western Water, Melbourne, Australia.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
Authors Kiran Joseph, Sharna Small and Nathan Bennett were employed by the company Greater Western Water. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Mitchell Plumbing and Gas. The Difference between Leaking and Burst Pipes. 2021. Available online: https://www.mitchellplumbinggas.com/blog-post/the-difference-between-leaking-and-burst-pipes (accessed on 12 December 2023).
- Sharma, A.; Marney, D. The Application and Utility of ‘Smarts’ for Monitoring Water and its Infrastructure. Water J. Aust. Water Assoc. 2012, 39, 86–92. [Google Scholar]
- Rapid Service Plumbing. Burst Pipes Sydney. Available online: https://rapidserviceplumbing.com.au/services/burst-pipes-sydney/ (accessed on 4 January 2024).
- Water Leak Detection. How To Detect Burst Pipes. 2020. Available online: https://www.waterleakdetection.net.au/how-to-detect-burst-pipes/ (accessed on 4 January 2024).
- Joseph, K.; Sharma, A.K.; van Staden, R.; Wasantha, P.L.P.; Cotton, J.; Small, S. Application of Software and Hardware-Based Technologies in Leaks and Burst Detection in Water Pipe Networks: A Literature Review. Water 2023, 15, 2046. [Google Scholar] [CrossRef]
- Berardi, L.; Giustolisi, O. Calibration of Design Models for Leakage Management of Water Distribution Networks. Water Resour. Manag. 2021, 35, 2537–2551. [Google Scholar] [CrossRef]
- Joseph, K.; Sharma, A.K.; Van Staden, R. Development of an Intelligent Urban Water Network System. Water 2022, 14, 1320. [Google Scholar] [CrossRef]
- Campos, J.A.; Jiménez-Bello, M.A.; Alzamora, F.M. Real-time energy soptimisation of irrigation scheduling by parallel multi-objective genetic algorithms. Agric. Water Manag. 2020, 227, 105857. [Google Scholar] [CrossRef]
- Fereidooni, Z.; Tahayori, H.; Bahadori-Jahromi, A. A hybrid model-based method for leak detection in large scale water distribution networks. J. Ambient. Intell. Humaniz. Comput. 2021, 12, 1613–1629. [Google Scholar] [CrossRef]
- Gorenstein, A.; Kalech, M.; Hanusch, D.F.; Hassid, S. Pipe fault prediction for water transmission mains. J. Water 2020, 12, 2861. [Google Scholar] [CrossRef]
- Swamee, P.K. Improving design guidelines for class-I circular sedimentation tanks. Urban Water J. 2004, 1, 309–314. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996. [Google Scholar]
- MacQueen, J. Some methods for classification and analysis of multivariate observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability; University of California Press; Berkeley, CA, USA, 1967.
- Schölkopf, B.; Platt, J.C.; Shawe-Taylor, J.; Smola, A.J.; Williamson, R.C. Estimating the support of a high-dimensional distribution. Neural Comput. 2001, 13, 1443–1471. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.T.; Ting, K.M.; Zhou, Z.-H. Isolation forest. In Proceedings of the 2008 Eighth IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008. [Google Scholar]
- Breunig, M.M.; Kriegel, H.P.; Ng, R.T.; Sander, J. LOF: Identifying density-based local outliers. In Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data, Dallas, TX, USA, 16–18 May 2000. [Google Scholar]
- He, H.; Bai, Y.; Garcia, E.A.; Li, S. ADASYN: Adaptive synthetic sampling approach for imbalanced learning. In Proceedings of the 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–6 June 2008. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J.H.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: New York, NY, USA, 2009; Volume 2. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: New York, NY, USA, 2013; Volume 112. [Google Scholar]
- Fawcett, T. An Introduction to ROC Analysis. J. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Hand, D.J.; Till, R.J. A simple generalisation of the area under the ROC curve for multiple class classification problems. J. Mach. Learn. 2001, 45, 171–186. [Google Scholar] [CrossRef]
- Lewis, R.E. Determining Outliers Using Standard Deviation. Study.com. 2024. Available online: https://study.com/skill/learn/determining-outliers-using-standard-deviation-explanation.html#:~:text=deviation%20of%201.3.-,Step%202%3A%20Determine%20if%20any%20results%20are%20greater%20than%20%2B%2F%2D,3.9)%20or%203.5%20to%2011.3 (accessed on 25 April 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).