Abstract
The safety of mines is a top priority in the mining industry, and a precise assessment of aquifer water levels is crucial for conducting a risk analysis of water-related disasters. Among them, the GIS-based water abundance index method is widely used in water-richness evaluation. However, the existing research lacks sufficient determination of evaluation indicator weights, specifically in the following aspects: (1) failure to consider the information differences between indicators and (2) inadequate differentiation of the relative importance of each indicator and their importance to the evaluation target. Taking the No.3 coal roof of Dananhu No.7 coal mine as the research object, six factors are selected as the main indexes for evaluating water richness. The weights were calculated using an improved entropy method and the scatter degree method, with the principle of information entropy used to reconcile the competitive and consistent relationship between the two evaluation methods. This approach resulted in the determination of combination weights for each influencing factor, highlighting the information differences between indicators and the importance of each indicator. Finally, the evaluation of aquifer water richness is partitioned by combining the GIS analysis function. The findings suggest that the Ⅰ division has low water richness, while the Ⅱ division is primarily medium-to-high water rich. The accuracy of the evaluation results exceeds 80%, providing valuable insights for hydrophobic programs for other coal-seam roofs.
1. Introduction
Coal is a crucial energy source and irreplaceable natural resource that plays a vital role in sustaining economic and social development globally [1,2]. With the increase of mining depth and the mining of multiple coal seams, geological conditions tend to be complicated, and accidents, such as water inrush and gas explosion, occur frequently [3,4]. According to statistics, from 2001 to 2021, the death toll of mine accidents in China reached 55,632, of which roof-water inburst accounted for a relatively large proportion, posing a major threat to the safety of underground operators (China Statistical Yearbook 2020) [5]. Therefore, the accurate and objective prediction of water-rich characteristics of a coal-seam roof aquifer is a necessary preparation to ensure safe deep mining.
The traditional methods for determining aquifer richness include pumping tests and geophysical methods [6,7,8,9]. Although these methods are widely used to assess the water-resource abundance of aquifers, they are often expensive and time consuming, and their accuracy is reduced due to single influencing factors or the influence of terrain and insufficient exploration data. The multi-factor composite prediction method, on the other hand, is based on identifying multiple geoscientific factors that influence the water richness of the target aquifer. It combines and integrates earth-science information, such as aquifer thickness, bedrock fracture distribution, temperature, etc., using a specific method to predict and assess the water richness of aquifers [10,11,12]. Wu et al. [13,14] collected data on various key controlling factors influencing water abundance in aquifers and constructed thematic maps. They overlaid the geological information from these thematic maps, utilizing modern information fusion techniques, to propose a model for evaluating aquifer water abundance using a water-richness index. Han et al. [15] used the set pair analysis–variable fuzzy set coupling evaluation method to establish a hydrophobicity evaluation model for the roof sandstone based on lithology and structural characteristics in the study area and predicted the hydrophobicity of the Zhiluo Formation sandstone aquifer. The key aspect of employing the multi-factor composite prediction method lies in determining the weights of each influencing factor in a reasonable manner. The commonly used methods for determining weights include the entropy weight method (EWM) [16,17], backpropagation (BP) neural network method [18,19], sum of squared deviations (SSD) [20], analytic hierarchy process (AHP) [21,22,23], fuzzy analytic hierarchy process (FAHP) [24,25], variation coefficient method, triangular fuzzy number (TFN) [26], and fuzzy Delphi analytic hierarchy process (FDAHP) [27]. Subjective methods such as expert scoring or the AHP are often used. But, they suffer from inherent randomness, and the weighting is often based on equal weights, which lacks research on cases with significant variations in indicator values. To overcome the errors caused by a single weighting approach, many scholars have adopted combined weighting methods, aiming to organically combine subjective and objective weights, thus leveraging the advantages of both approaches.
Existing studies have primarily focused on considering the information differences within evaluation indicators while neglecting the information differences between indicators and the relative importance of distinguishing various indicators in terms of the importance of the evaluation target. In this study, the No.3 coal roof of the Dananhu No.7 coal mine in China is taken as the research object. The use of an improved entropy method and the scatter degree method, combined with the principle of information entropy, can effectively predict roof-water richness by determining weights for each influencing factor.
2. Study Area and Mining Conditions
The Dannanhu No.7 coal mine is a new mine located in Hami City, Xinjiang, China. The mine has a field area of 85.73 km2, a geological reserve of 1508.90 mt, a production capacity of 6.0 mt/a, and a service life of 97.65 a. The No.7 coal seam is the main coal seam, with an average thickness of 10 m (see Figure 1).
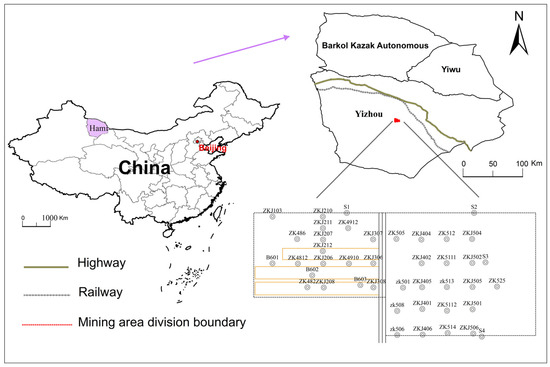
Figure 1.
Sketch map of the study area.
The mine site is located in the Dananhu Depression area of the Tuha Basin, with a relatively simple well field structure and gentle stratigraphic dip angle, generally 5°~15°. The basin is long in shape, wide in the west, and narrow in the east, with good exposure in the middle, covered by the Paleogene, Neogene, and Quaternary, and generally showing a compound oblique structure. The exploration thus far has revealed the presence of gentle folding in the area, with no significant faults or magmatic rocks. Only a few high-angle faults in the northeast direction have been identified, along with some small faults exposed during shaft and roadway construction [28,29].
According to the lithology of each stratum and its water-rich characteristics, the Dannanhu No.7 coal mine contains one permeable layer, three water-bearing layers, and five water-isolating layers. The aquifer as a whole, including the Quaternary permeable layer, the Neogene–Putaogou Formation fissure pore aquifer, the Jurassic Mesozoic Toutunhe Formation fissure pore aquifer, and the Jurassic Mesozoic Xishanyao Formation fissure pore aquifer, has a relatively low water richness (see Figure 2). Among them, the middle part of the Xishanyao Formation fissure pore aquifer is the direct water-filling aquifer of the mine, and the fracture pore brittle aquifer of the Toutunhe Formation is the relative water-insulating layer. The main lithology consists of sandstone, mudstone, sandy mudstone, and coal seams, with a small amount of medium conglomerate present.
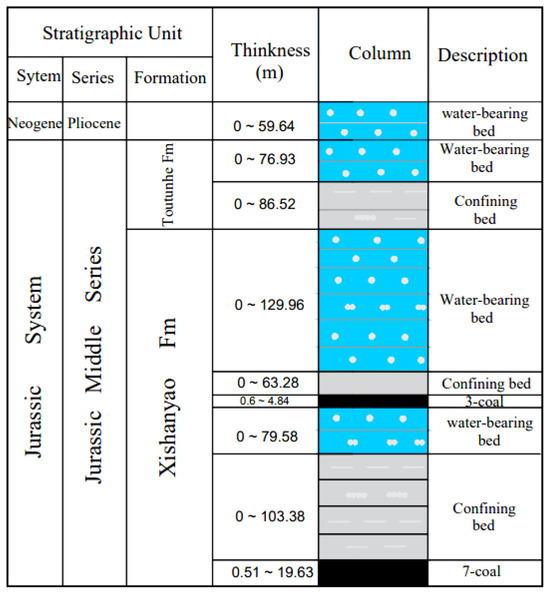
Figure 2.
Typical geological log profile of the Dananhu No.7 coal mine.
3. Methodology
The evaluation of coal-roof water richness consists of four steps: (1) conducting regional geological surveys and analysis to identify factors that influence coal-roof water richness; (2) normalizing data and determining weights for each indicator; (3) establishing indicator evaluation models; and (4) describing and validating the results. This process is illustrated in Figure 3.
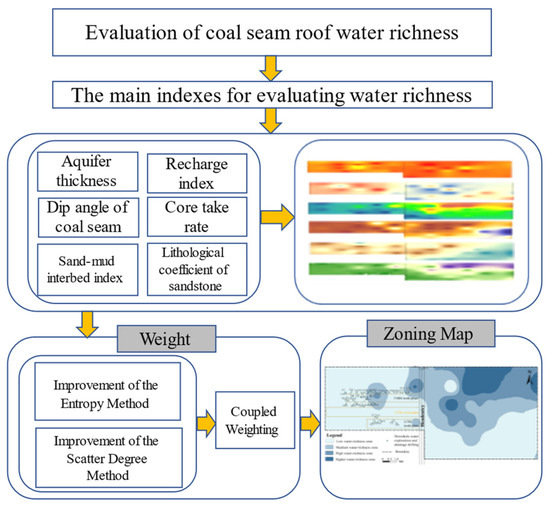
Figure 3.
Flowchart of the methodology used in this study.
3.1. Factors Influencing the Coal-Seam Roof Water Richness
For aquifer thickness (Figure 4a), the thickness of the aquifer is a critical factor in the occurrence of groundwater, with a greater thickness indicating a higher water richness [30]. Due to its good permeability and high porosity, sandstone layers are commonly considered as the cumulative thickness of the aquifer.
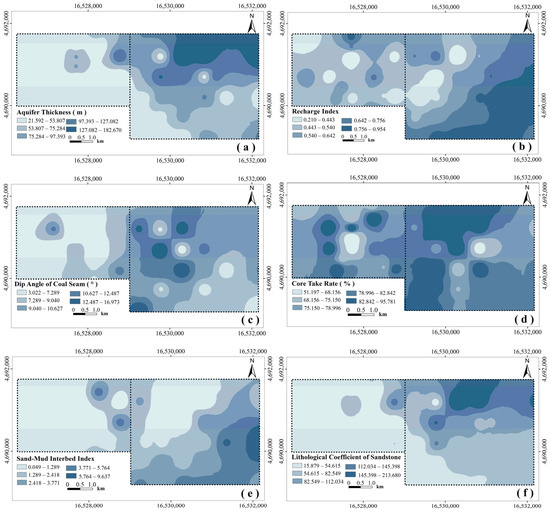
Figure 4.
Thematic map of water-richness influencing factors. (a) Aquifer thickness; (b) recharge index; (c) dip angle of coal seam; (d) core take rate; (e) sand–mud interbed index; (f) lithological coefficient of sandstone.
For the recharge index (Figure 4b), the recharge index is defined as the ratio of the cumulative thickness of the overlying aquifuge to the burial depth of the aquifer top. A higher recharge index indicates that the aquifer receives less replenishment from surface-water sources, such as groundwater and atmospheric precipitation, suggesting a lower water richness in the aquifer. The calculation is as follows:
In the equation, ‘r’ is the aquifuge thickness of the overlying diaphragm; and ‘H’ is the buried depth of the top plate of this aquifer.
For the dip angle of the coal seam (Figure 4c), in general, as the dip angle of a coal seam increases, the overlying rock strata experience greater induced stress, leading to increased recharge of the aquifer and the consequent enhancement of the water-richness of the rock strata.
For the core take rate (Figure 4d), the core take rate is the ratio of the actual length of the core obtained during drilling to the length of the drill [31]. By observing the core, we can understand its completeness and the change of lithology combination. In general, the lower core take rate indicates that the top plate structure is complex, the stability is poor, the rock is more broken, the connectivity is better, and the water-richness is higher.
For the sand–mud interbed index (Figure 4e), when considering the content of sand, gravel, clay, and silt particles within rock formations, further assessment is made regarding the vertical distribution of sand–mud interbeds and their impact on the water richness of the aquifer [32]. In this context, a specific group consisting of an overlying sand layer and an underlying clay layer is considered a sand–mud interbed. By assigning values based on the proportion of clay and silt particles within each individual interbed, the sum of the calculated thickness values for all interbeds composed of clay and silt particles is divided by the sum of thickness values for sand and gravel particles, defining it as the sand–mud interbed index. When the thickness of the aquifer is similar, a higher number of interbeds and a larger clay ratio within each interbed indicates a lower porosity and permeability within the layer, resulting in weaker hydrophobicity between the gravel layers and the weaker the water richness. A higher index indicates weaker hydraulic connectivity within the layers and a lower water richness.
In the equation, ‘pi’ is the assigned value (see Table 1), ‘li’ is the thickness of mudstone in the i interbed, and ‘S’ is the thickness of the sandstone conglomerate in the whole interbeds.

Table 1.
Results of assigning the proportion of mudstone thickness in a single interbed.
For the lithological coefficient of sandstone (Figure 4f), in general, within rock formations of the same thickness, larger grain sizes of sandstone indicate better water storage and permeability. The calculation method is to multiply the thickness of siltstone, fine sandstone, medium sandstone, and gritstone in the aquifer by an equivalent coefficient, then convert the thickness of gritstone, and multiply the structural coefficient to obtain the lithologic coefficient of sandstone. The equivalent coefficient is obtained by an engineering geological survey and statistics on the porosity of sandstone in the roof of the coal seam, based on gritstone (agreed as one) and converted into medium, fine, and siltstone. The structural coefficient is determined by the combined structure of rock sand and mud after conversion [33]. The lithological coefficient of sandstone is used to characterize the specific water storage and conductivity properties of the sandstone within a particular aquifer segment. It is calculated as follows:
In the equation, ‘K’ represents the lithologic structure index; ‘a’, ‘b’, ‘c’, and ‘d’ represent the thicknesses (m) of siltstone, fine sandstone, medium sandstone, and gritstone, respectively; and ‘e’ is the structural coefficient, with specific values provided in Table 2.

Table 2.
Value of structure coefficient e.
Considering the difference in the order of magnitude of each index, the aquifer thickness, the dip angle of the coal seam, and the lithological coefficient of sandstone are normalized in the forward direction, and the recharge index, the core take rate, and the sand-mud interbed index are normalized in the reverse direction (Table 3). The inverse distance weighting method, in ArcGIS, was used to interpolate the data for the six influencing factors and create thematic maps. All the data used in this paper are revealed by drilling in the mining area.

Table 3.
Water-richness influencing factors data (standardization).
3.2. The Determination of Indicator Weights
3.2.1. Improvement of the Entropy Method
The entropy method is a multi-attribute decision-making approach based on the principle of information entropy. Smaller entropy values indicate a higher information content and lower uncertainty, while larger entropy values indicate a lower information content and higher uncertainty. This method provides a relatively objective, scientific, and effective way to handle multi-attribute decision-making problems. The specific calculation steps are as follows [34].
(1) If there are n implementation hair cases and m indicators to be evaluated, the original data matrix X = (xij)n×m is constructed, and the matrix X is normalized to obtain the matrix R = (rij)n×m, rij ∈ [0,1];
(2) The relative column of the jth indicator is calculated for the ith object;
(3) The information entropy ej is calculated for the jth indicator;
In general,
(4) The information entropy redundancy dj is calculated for the jth indicator;
(5) The weight of the ith indicator is calculated.
However, the traditional entropy method only considers the information content of each indicator while ignoring the variability of the data and the subjective preferences of the decision-makers [35]. This may lead to unstable and unreasonable evaluation results, making it unsuitable for long-term dimensions and multi-objective comprehensive evaluations.
Therefore, to address the limitations of the entropy method, which focuses on local differences and lacks inheritability and transmissibility, we propose considering the use of the indicator conflict correlation coefficient to weigh the information entropy. While the entropy-based method calculates the information entropy horizontally, primarily considering the information differences within each indicator, the conflict coefficient is a vertical calculation method that primarily considers the information differences between indicators. The calculation method for indicator conflict is:
where kij represents the correlation coefficient between indicators i and j. The Pearson correlation coefficient method is chosen to calculate this correlation coefficient:
By combining the conflict coefficient with the entropy-based method, we obtain an improved measure of information utility:
The improved weight hj′ for the j-th indicator is calculated as:
3.2.2. Improvement of the Scatter Degree Method
The principle of the scatter degree method is to select weight coefficients for the indicators in such a way that the differences between the evaluated objects are maximized. However, it does not distinguish the relative importance of each indicator or the importance of each indicator to the evaluation objective [36]. Therefore, before applying the scatter degree method, it is necessary to weigh the numerical values xij of each indicator based on their importance. This can be achieved through subjective optimization methods to obtain weight coefficients rj for each indicator. In this study, a subjective optimization-based constrained weighting method using object serial preference is employed to generate the initial weights rj. The basic principle and model are as follows.
Let O be the set of evaluation objects O = {o1, o2, …, on} and P be the set of indicators P = {x1, x2, …, xm}. Where, xij = xj(oj) (i = 1, 2, …, n; j = 1, 2, …, m) represents the value information of object oi regarding indicator xj. An indicator value matrix A is constructed for the solution set O with respect to indicator set P.
Assuming that the values in matrix A have undergone standardization preprocessing to obtain normalized indicators, let yi denote the comprehensive evaluation value of object oi. By employing a linear weighting model to integrate the information, we can obtain:
In the formula, x = (xi1, xi2, …, xim)T is the index value vector of oj, and r = (r1, r2, …, rm)T is the weight vector of the index.
If object oa > ob (a,b = 1, 2, …, n, a ≠ b), then,
Here, c is any positive constant.
Equation (13) indicates that, for any two objects oa and ob, with corresponding indicator vectors xa and xb, selecting a weight vector r parallel to the direction of xa-xb emphasizes the differences between objects the most. Therefore, if object oa > ob (a,b = 1, 2, …, n, a ≠ b), then rT(xa − xb) > 0.
For any two solutions oa, ob (a,b = 1, 2, …, n, a ≠ b) in the object set O = {o1, o2, …, on}, if the evaluator perceives oa > ob, this superiority relationship can be described as an ordered pair (oa, ob), and the collection of all ordered pairs is denoted as Ψ = {(oa, ob)| a,b = 1, 2, …, n, a ≠ b}. It is required that all ordered pairs in Ψ satisfy transitivity.
Therefore, for the ordered pair set Ψ, the overall consistency of the evaluator’s preference judgments can be obtained as:
Rational decision-makers aim to achieve the highest level of consistency. Therefore, a subjective preference weight vector w optimization model can be constructed as follows:
Here, e = [1, 1, 1, …, 1]T; α and β represent the upper and lower bounds for weight setting, aiming to increase weight tolerance and better align with the evaluator’s preference.
The calculated rj is put into formula (16) to begin the weighting of the scatter degree method.
By weighting the initial values xi1, xi2, …, xim of the ith evaluation object by r’, we can get the evaluation merit of this evaluation object.
Then, it can also be transformed into a matrix.
The criterion for determining the vector of weight coefficients r′ is to maximize the difference between the evaluated objects with different attributes. And, the evaluation value score y′ by n evaluation objects to take the value of the composition of the sample of the variance is:
By substituting into Equation (19) and normalizing the indicators, it can be observed that . Hence, the following relationship holds:
If r is not constrained, ns2 can take any arbitrary large value. To address this, we impose the constraint of rTr = 1. In conclusion, the scatter degree method seeks the optimal solution under the constraints mentioned above.
Finally, the weight of the jth index obtained by the improved scatter degree method is changed to rj′.
The weights obtained by the improvement of the entropy method and the scatter degree method are shown in Table 4.

Table 4.
The weight of each main control factor was obtained by the improved entropy method (h′) and the improvement of the scatter degree method (r′).
3.2.3. Coupled Weighting
In order to eliminate any potential subjective bias and improve the objectivity of attribute weight assignment, this study employs both subjective weighting and objective weighting methods [37]. The principle of relative entropy is applied to aggregate their weight sets, investigating the harmonious relationship among conflicting evaluation conclusions corresponding to different evaluation methods.
By applying the Lagrange multiplier method to solve the optimization problem in Equation (22), the optimal solution for the coupled weights can be obtained (Table 5).
where hj′, rj′ are the weight obtained by improving the entropy weight method and the scatter degree method.

Table 5.
Comprehensive weight values (wj) of main controlling factors.
4. Results and Discussion
4.1. Results
Using the spatial overlay function of ArcGIS, the following evaluation model is constructed by combining the determined weights and normalized data of each indicator:
where ξ is the water inrush index. C1, C2, C3, C4, C5, and C6 represent the standardized data for various factors, and ω represents the standardized weight within different ranges.
The evaluation model was further classified using the natural breaks method. This method first sorts the data and then calculates the within-group variance and between-group variance for each possible classification scheme, ultimately selecting the scheme with the lowest variance as the final classification scheme. Based on the classification thresholds, the study area was divided into four regions: Class I, low water-rich area (0.0708–0.2636); Class II, medium water-rich area (0.2636–0.3728); Class III, high water-rich area (0.3728–0.5366); and Class IV, higher water-rich area (0.5366–0.8898). Figure 5 shows the water inrush risk zoning map.
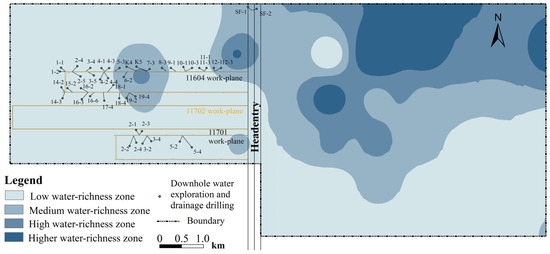
Figure 5.
Comprehensive zoning map of water richness of aquifers in the roofs of coal seams.
From the figure, it can be observed that the low water-richness zone in the mining area is mainly distributed in the western and southeastern parts of the research area, accounting for approximately 55% of the research area’s total area. The medium water-richness zone, high water-richness zone, and higher water-richness zone are primarily distributed in the northeastern part of the research area, accounting for 22%, 11%, and 12% of the research area’s total area, respectively. The evaluation model reveals that the northeastern part of the research area exhibits relatively higher water-richness. Through the analysis of factors influencing water abundance, it is evident that the maximum thickness of the overlying sandstone and the lithological coefficient of the sandstone in the northeastern part of the mining area, along with a relatively high core take rate, are significant factors contributing to the higher water richness in the roof of the coal seam. Therefore, it is recommended that the personnel in this mining area take effective measures to prevent water inrush in this particular region.
4.2. Discussion
To validate the accuracy of the water-richness zoning results, the observed water inflow data from boreholes 11604 and 11701 on the roof of the working faces were used for verification. These downhole water-exploration and drainage drillings were constructed prior to mining in order to detect and drain the high-risk areas of the roof with abnormally high water levels, and the drilling depth was within the range of the roof’s water-conducting fractures. Based on the distribution of water inflow data, the area with a water inflow ranging from 0 to 20 m3/h was classified as low water richness and medium water richness, while the area with an inflow exceeding 20 m3/h was classified as high water richness and higher water richness. The validation revealed a consistency rate of over 80% between the observed data and the water-richness zoning (Table 6). Therefore, the water-richness zoning obtained by combining the six evaluation indicators with suitable weights for the mining area accurately reflects the actual conditions, demonstrating a high level of accuracy in the evaluation results.

Table 6.
Validation between prediction results and actual data.
5. Summary
- The middle section of the Xishangyao Group is a water-bearing layer composed of fractured and porous conglomerate sandstone, which directly inundates the roof of the third coal seam, posing a threat to mining safety. Six factors, including the aquifer thickness, recharge index, dip angle of the coal seam, core take rate, sand–mud interbed index, and lithological coefficient of sandstone, were selected as the main indicators for evaluating the water abundance of the roof of the third coal seam;
- To address the limitations of the entropy method, which focuses on local differences and lacks inheritability and transitivity, the indicator conflict correlation coefficient was employed to weigh the information entropy, thus improving the entropy method to obtain the weights of individual indicators;
- Before obtaining the weights of each indicator using the scatter degree method, a subjective optimization method was employed to pre-weigh the original values of each indicator, thereby enhancing the method. The resulting weight coefficients can better differentiate the relative importance of each indicator and their significance in evaluating the target, enabling a more comprehensive assessment;
- The combination weighting of each indicator was performed, and a water-richness zoning model was established using GIS software. The evaluation model predicted a higher water richness in the northeastern part of the mining area. The prediction was validated to be consistent with the actual conditions, thus providing a reference for hydrological measures in other coal-seam roofs.
Author Contributions
Conceptualization, Q.W., Y.Z., W.L. and X.L.; Data curation, Y.Z.; Methodology, J.X. and Q.W.; Resources, Y.Z.; Software, J.X.; Writing—original draft, J.X.; Writing—review & editing, Q.W., W.L. and X.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (Grant No. 42007240) and the project “Enlisting and Leading” of China Coal (No. 2022JB01).
Data Availability Statement
The datasets used or analyzed during the current study are available from the corresponding author on reasonable Request.
Acknowledgments
The authors express their gratitude to everyone who provided assistance with the present study. The study was jointly supported by the National Natural Science Foundation of China (Grant No. 42007240) and the project “Enlisting and Leading” of China Coal (No. 2022JB01).
Conflicts of Interest
Author Yuguang Zhang was employed by the company China Coal Group Xinjiang Energy Co., Ltd. The remaining authors declare no conflicts of interest.
References
- Govindaraju, V.; Tang, C. The dynamic links between CO2 emissions, economic growth and coal consumption in China and India. Appl. Energy 2013, 104, 310–318. [Google Scholar] [CrossRef]
- Renn, O.; Marshall, J. Coal, nuclear and renewable energy policies in Germany: From the 1950s to the “Energiewende”. Energy Policy 2016, 99, 224–232. [Google Scholar] [CrossRef]
- Maiti, J.; Khanzode, V.; Ray, P. Severity analysis of Indian coal mine accidents—A retrospective study for 100 years. Saf. Sci. 2009, 47, 1033–1042. [Google Scholar] [CrossRef]
- Ismail, S.; Ramli, A.; Aziz, H. Research trends in mining accidents study: A systematic literature review. Saf. Sci. 2021, 143, 105438. [Google Scholar] [CrossRef]
- Zhang, P.; Dong, Y.; Zhang, X.; Xu, D. Statistical law analysis and forecast of coal mine water disaster accidents in China from 2008 to 2021. Coal Eng. 2022, 54, 131–137. [Google Scholar]
- Dhakate, R.; Chowdhary, D.; Rao, V.; Tiwary, R.; Sinha, A. Geophysical and geomorphological approach for locating groundwater potential zones in Sukinda chromite mining area. Environ. Earth Sci. 2012, 66, 2311–2325. [Google Scholar] [CrossRef]
- Hu, X.; Xu, H.; Peng, S.; Zhang, P.; Fu, M. Dynamic monitoring of water abundance of overlying strata in coal seam by transient electromagnetic method. J. China Coal Soc. 2021, 46, 1576–1586. [Google Scholar] [CrossRef]
- Meju, M.; Fontes, S.; Ulugergerli, E.; La Terra, E.; Germano, C.; Carvalho, R. A joint TEM-HLEM geophysical approach to borehole siting in deeply weathered granitic terrains. Ground Water 2001, 39, 554–567. [Google Scholar] [CrossRef] [PubMed]
- Ma, B.; Chen, J.; Wang, X. Application of transient electromagnetic method in coal mine water-rich detection: Taking the fifth and sixth panels of Daliuta Coal Mine in Shendong Mining Area as an example. Coal Sci. Technol. 2022, 50 (Suppl. S2), 223230. [Google Scholar] [CrossRef]
- Mojiri-Khozani, A.; Nassery, H.; Nikpeyman, Y.; Abedian, H. Assessing the impact of Koohrang III tunnel on the hydrogeological settings using stable isotopes and hydrochemical methods. Bull. Eng. Geol. Environ. 2023, 82, 219. [Google Scholar] [CrossRef]
- Lawrence, J.; Alagarsamy, V.K.; Mohanadhas, B.; Natarajan, N.; Vasudevan, M.; Govindarajan, S.K. Nitrate transport in a fracture-skin-matrix system under non-isothermal conditions. Environ. Sci. Pollut. Res. 2023, 30, 18091–18112. [Google Scholar] [CrossRef] [PubMed]
- Nampak, H.; Pradhan, B.; Abd Manap, M. Application of GIS based data driven evidential belief function model to predict groundwater potential zonation. J. Hydrol. 2014, 513, 283–300. [Google Scholar] [CrossRef]
- Wu, Q.; Fan, Z.; Liu, S.; Zhang, Y.; Sun, W. Water-richness evaluation method of water-filled aquifer based on the principle of information fusion with GIS: Water-richness index method. J. China Coal Soc. 2011, 36, 1124–1128. [Google Scholar] [CrossRef]
- Wu, Q.; Xu, K.; Zhang, W.; Wei, Z. Roof aquifer water abundance evaluation: A case study in Taigemiao, China. Arab. J. Geosci. 2017, 10, 254. [Google Scholar] [CrossRef]
- Han, C.; Wei, J.; Xie, D.; Xu, J.; Zhang, W.; Zhao, Z. Water-richness evaluation of sandstone aquifer based on set pair analysisvariable fuzzy set coupling method: A case from Jurassic Zhilyo formation of Jiniiagu coal mine in Ningdong mining area. J. China Coal Soc. 2020, 45, 2432–2443. [Google Scholar] [CrossRef]
- Sun, Z.; Bao, W.; Li, M. Comprehensive Water Inrush Risk Assessment Method for Coal Seam Roof. Sustainability 2022, 14, 10475. [Google Scholar] [CrossRef]
- Delgado, A.; Romero, I. Environmental conflict analysis using an integrated grey clustering and entropy-weight method: A case study of a mining project in Peru. Environ. Model. Softw. 2016, 77, 108–121. [Google Scholar] [CrossRef]
- Yan, P.; Shang, S.; Zhang, C.; Yin, N.; Zhang, X.; Yang, G.; Zhang, Z.; Sun, Q. Research on the Processing of Coal Mine Water Source Data by Optimizing BP Neural Network Algorithm With Sparrow Search Algorithm. IEEE Access 2021, 9, 108718–108730. [Google Scholar] [CrossRef]
- Wang, Q.; Han, Y.; Zhao, L.; Li, W. Water Abundance Evaluation of Aquifer Using GA-SVR-BP: A Case Study in the Hongliulin Coal Mine, China. Water 2023, 15, 3204. [Google Scholar] [CrossRef]
- Qiu, M.; Yin, X.; Shi, L.; Zhai, P.; Gai, G.; Shao, Z. Multifactor Prediction of the Water Richness of Coal Roof Aquifers Based on the Combination Weighting Method and TOPSIS Model: A Case Study in the Changcheng No. 1 Coal Mine. ACS Omega 2022, 7, 44984–45003. [Google Scholar] [CrossRef] [PubMed]
- Ruan, Z.; Li, C.; Wu, A.; Wang, Y. A New Risk Assessment Model for Underground Mine Water Inrush Based on AHP and D-S Evidence Theory. Mine Water Environ. 2019, 38, 488–496. [Google Scholar] [CrossRef]
- Biswas, S.; Mukhopadhyay, B.; Bera, A. Delineating groundwater potential zones of agriculture dominated landscapes using GIS based AHP techniques: A case study from Uttar Dinajpur district, West Bengal. Environ. Earth Sci. 2020, 79, 302. [Google Scholar] [CrossRef]
- Bogdanovic, D.; Nikolic, D.; Ilic, I. Mining method selection by integrated AHP and PROMETHEE method. An. Acad. Bras. Cienc. 2012, 84, 219–233. [Google Scholar] [CrossRef]
- Asghari, M.; Nassiri, P.; Monazzam, M.; Golbabaei, F.; Arabalibeik, H.; Shamsipour, A.; Allahverdy, A. Weighting Criteria and Prioritizing of Heat stress indices in surface mining using a Delphi Technique and Fuzzy AHP-TOPSIS Method. J. Environ. Health Sci. Eng. 2017, 15, 1. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Zheng, Q.; Pang, L.; Dou, W.; Meng, X. Study of roof water inrush forecasting based on EM-FAHP two-factor model. Math. Biosci. Eng. 2021, 18, 4987–5005. [Google Scholar] [CrossRef] [PubMed]
- Qu, X.; Han, J.; Shi, L.; Qu, X.; Bilal, A.; Qiu, M.; Gao, W. An extended ITL-VIKOR model using triangular fuzzy numbers for applications to water-richness evaluation. Expert Syst. Appl. 2023, 222, 119793. [Google Scholar] [CrossRef]
- Hoseinie, S.; Ataei, M.; Osanloo, M. A new classification system for evaluating rock penetrability. Int. J. Rock Mech. Min. Sci. 2009, 46, 1329–1340. [Google Scholar] [CrossRef]
- Xu, Z.; Gao, S.; Cui, S.; Sun, Y.; Sun, Y.; Chen, Z. Hydro-geological basic and practice for water-preserved mining in ecologically vulnerable area: A case study in Hami coalfield. J. China Coal Soc. 2017, 42, 80–87. [Google Scholar] [CrossRef]
- Yan, Z.; Wang, J.; Wang, X. Sedimentary Environments and Coal Accumulation of the Middle Xishanyao Formation, Jurassic, in the Western Dananhu Coalfield, Turpan-Hami Basin. Geofluids 2021, 2021, 6034055. [Google Scholar] [CrossRef]
- Li, Q.; Sui, W. Risk evaluation of mine-water inrush based on principal component logistic regression analysis and an improved analytic hierarchy process. Hydrogeol. J. 2021, 29, 1299–1311. [Google Scholar] [CrossRef]
- Feng, S.; Wu, Q. Research on water—richness of aquifer using comprehensive weight method based on AHP and variation coefficient. Coal Eng. 2016, 48 (Suppl. S2), 138–140. [Google Scholar]
- Li, S.; Yang, Z.; Ma, X.; Liu, S.; Fang, C.; Zhang, A. Influence of water yield property of Yan’an Formation aquifer on water yield of mines in southern Shenmu-Fugu mining area. Coal Geol. Explor. 2023, 51, 92–102. [Google Scholar]
- Dai, G.; Zhou, Y.; Yang, T.; Liu, M.; Gao, Z.; Niu, C. Study on multi-factor complex analysis method applied to watery of sandstone in ZhiluoFormation. Coal Sci. Technol. 2016, 44, 186–190. [Google Scholar] [CrossRef]
- Huang, D.; Wang, X.; Chang, X.; Qiao, S.; Zhu, Y.; Xing, D. A safety assessment model of filling mining based on comprehensive weighting-set pair analysis. Environ. Sci. Pollut. Res. 2023, 30, 60746–60759. [Google Scholar] [CrossRef] [PubMed]
- Cui, W.; Ye, J. Improved Symmetry Measures of Simplified Neutrosophic Sets and Their Decision-Making Method Based on a Sine Entropy Weight Model. Symmetry 2018, 10, 225. [Google Scholar] [CrossRef]
- Guo, Y.; Ma, F.; Dong, Q. Analysis of influence of dimensionless methods on deviation maximization method. J. Manag. Sci. China 2011, 14, 19–28. [Google Scholar]
- Chen, J.; Li, W.; Xue, F.; Wang, K.; Zhang, C.; Song, T. Comprehensive evaluation of TOPSIS-RSR grouting effect based on subjective and objective combined weights. Coal Sci. Technol. 2022, 51, 191–199. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).