Optimal Coordinated Operation for Hydro–Wind Power System
Abstract
1. Introduction
2. Model
2.1. Wind Power System
2.1.1. Wind Turbine
2.1.2. PMSG
2.1.3. Full-Size Converter
2.2. Hydropower System
2.2.1. Pipe Characteristic
2.2.2. Hydraulic Generator
2.2.3. Hydro-Turbine and Frequency Regulation System
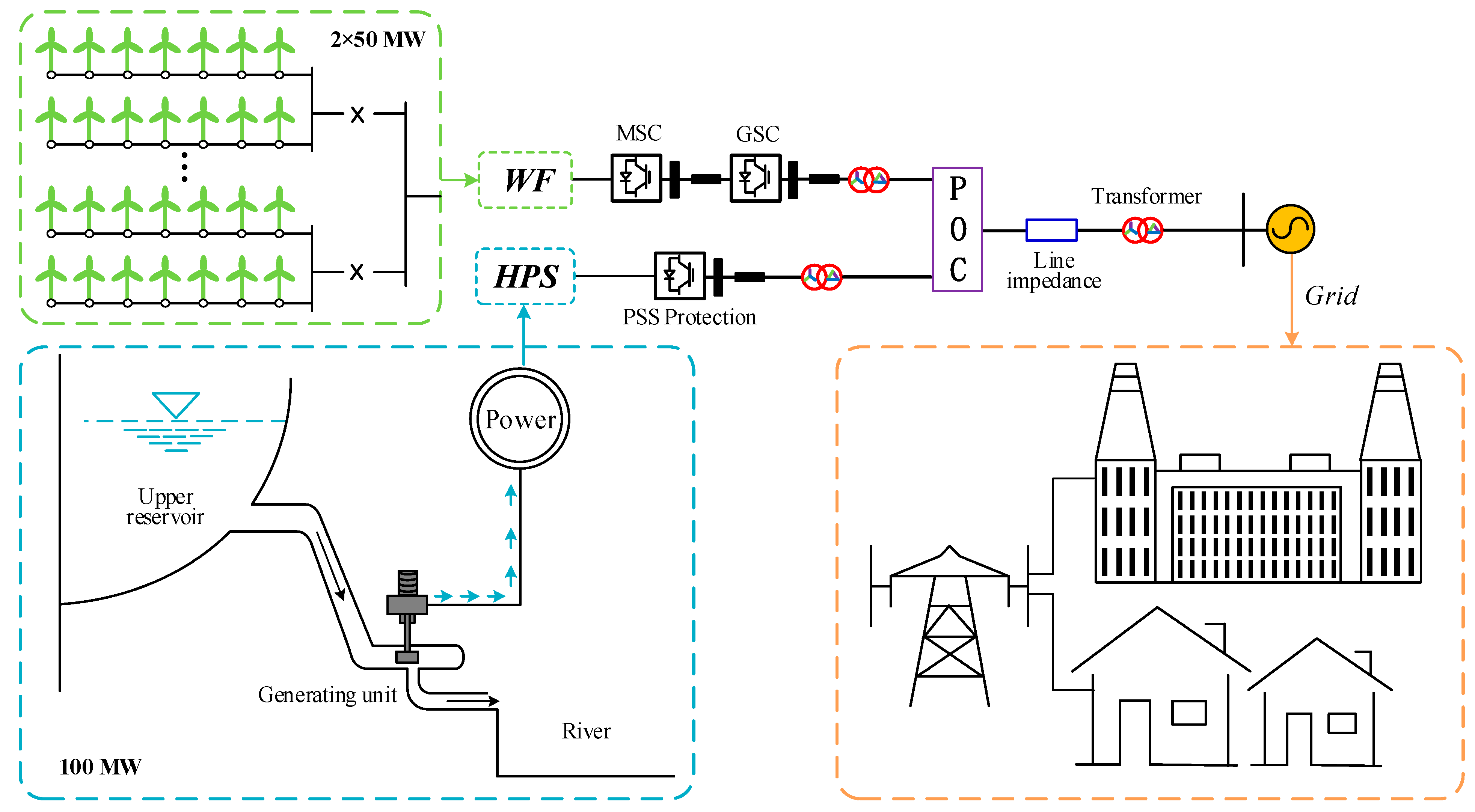
2.3. Hybrid Power System
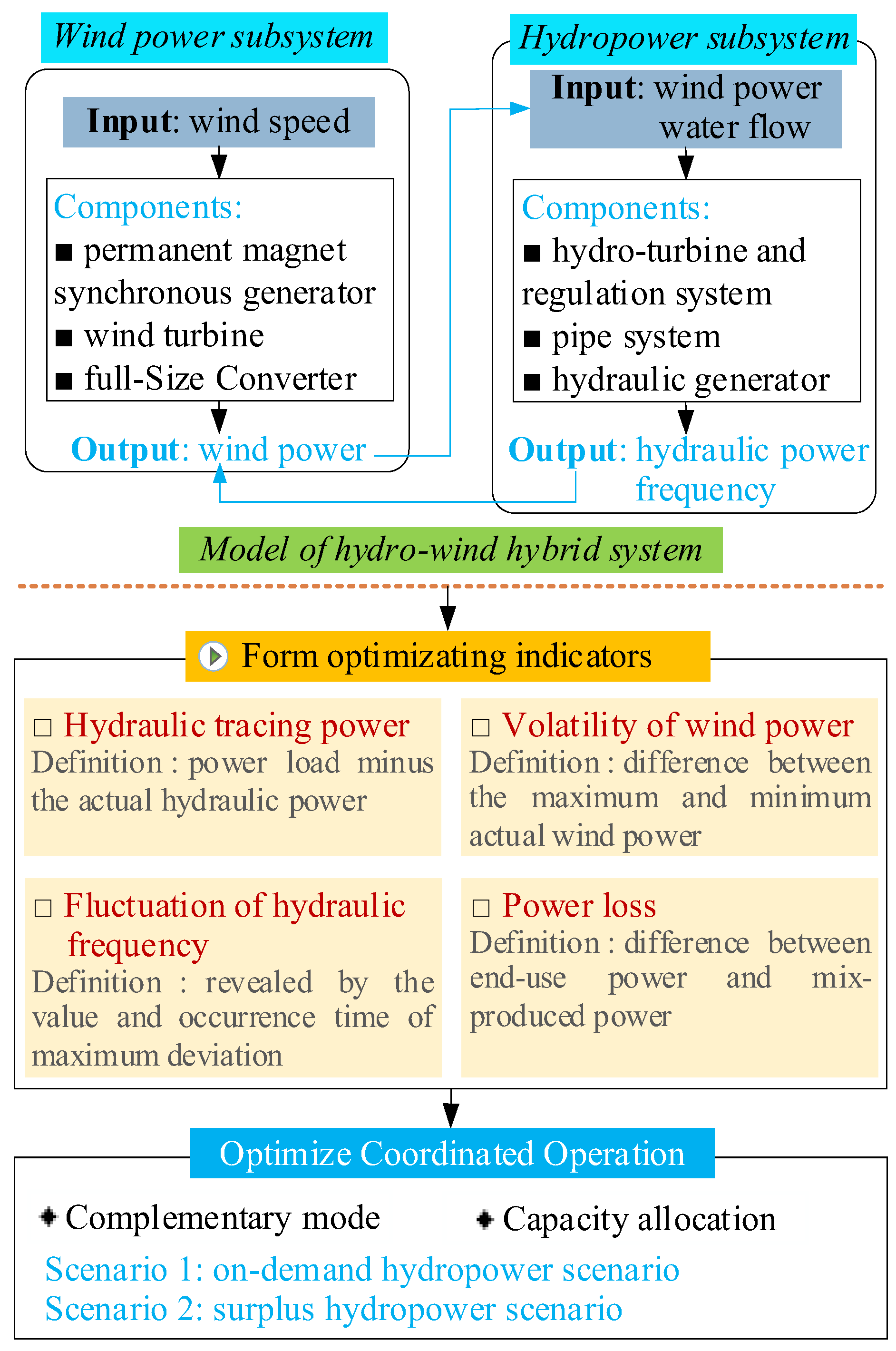
3. Methodology
4. Optimization of Complementary Mode
4.1. Scenario 1: On-Demand Hydropower Operation
4.2. Scenario 2: Surplus Hydropower Operation
5. Optimization of Capacity Allocation
6. Conclusions and Discussion
- (1)
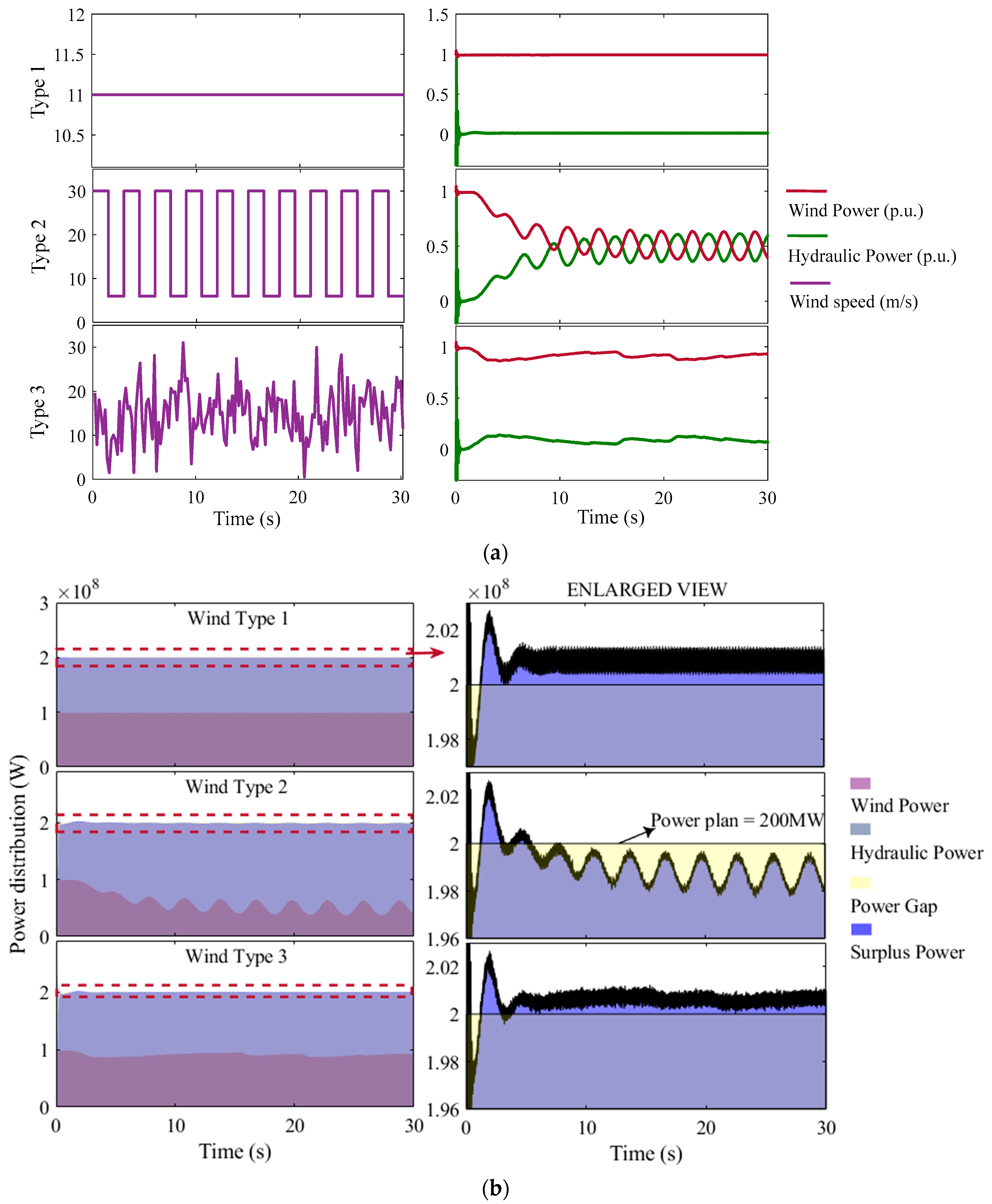
- The effect of wind speeds on the complementary mode: The mutational wind speed causes the worst complementary mode of the power system because there is an increasing burden of hydro regulation to cope with frequently drastic changes in wind speed. On the contrary, the complementary mode is the best under the random wind speed, since the power system makes full use of the regulation capability of hydropower in this situation.
- (2)
- The effect of application scenarios on the complementary mode: The most distinctive feature of complementarity for both real application scenarios lies in the power loss. The mean power loss for the on-demand hydropower scenario is 6 MW, while that for the surplus hydropower scenario is around 4 MW. Thus, the on-demand hydropower scenario is a better choice for the economic operation of power stations from the perspective of power loss.
- (3)
- The necessity for multiple indicators: When the hybrid power system is close to instability with the increasing wind power permeation, the marginal permeation of the installed wind capacity cannot be determined by a single indicator. For instance, the system loses stability when the hydraulic power and wind power still have good complementary tracking effects. In this situation, the indicators of power loss and hydraulic frequency are able to reveal this instability.
- (4)
- The optimal capacity allocation: Based on the comprehensive evaluation of multiple indicators, the marginal permeations of the installed wind capacity for a 100 MW hydropower system are approximatively 326 MW, 120 MW, and 250 MW under constant, mutational, and random wind speeds.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | swept area of blades |
| Cp | wind power coefficient |
| E0 | excitation electromotive force |
| egd | synchronous angular speed of grid voltage in d-axis |
| ΔF(s) | Laplace transform of frequency |
| GD(s) | transfer function between turbine head and flow |
| h | relative value of turbine head |
| hf | hydraulic friction loss |
| hw | pipe characteristic coefficient |
| is | current of the generator |
| igd | d-axis current in grid-side |
| igq | q-axis current in grid-side |
| Kp | proportional adjustment coefficient |
| Ki | integral adjustment coefficient |
| Kd | differential adjustment coefficient |
| Lg | line inductance |
| Ld | d-axis inductance |
| Lq | q-axis inductance |
| Mt | mechanical torque |
| m | phase number of stator |
| n | rotational speed |
| PCu | armature copper loss |
| Pem | difference between electromagnetic power |
| Pin | input power of the generator |
| P0 | no-load loss |
| Pl | total active power loss |
| Qt | turbine flow |
| q0 | relative value of initial flow |
| R | radius of the blade |
| Rg | line resistance |
| Rs | stator resistance |
| ra | armature resistance |
| Tn | acceleration time constant |
| Tr | water-hammer time constant |
| U | terminal voltage |
| us | voltage of the generator |
| udc | DC link voltage |
| ugq | q-axis voltage in grid-side |
| ugd | d-axis voltage in grid-side |
| v | wind speed |
| xσ | magnetic flux leakage |
| xad | d-axis armature reactance |
| xaq | q-axis armature reactance |
| xd | d-axis synchronous reactance |
| xq | q-axis synchronous reactance |
| Ypid(s) | Laplace transform of guide vane opening |
| y | relative value of guide vane opening |
| β | blade pitch angle |
| λ | tip–speed ratio |
| ρ | air density |
| φ | power factor angle |
| φi | phase angle between air gap voltage and armature current |
| ψ0 | magnetic flux of permanent magnet |
| ψs | magnetic flux of generator |
| Ω | mechanical rotor speed |
| ωg | synchronous angular speed of grid |
| ωt | rotational speed of wind turbine |
| ωe | rotor speed of generator |
Appendix A. Block Diagram of Simulink Models
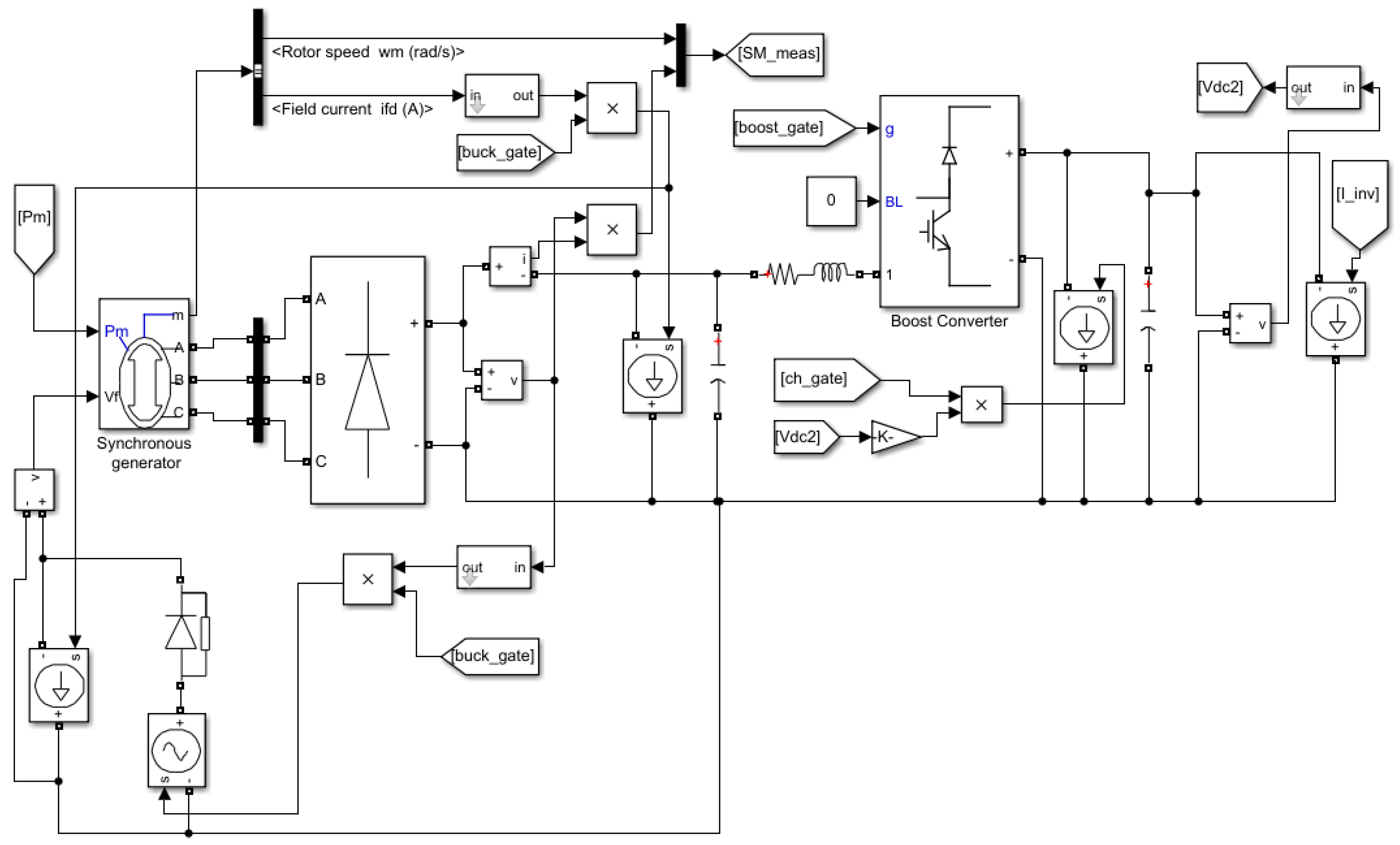
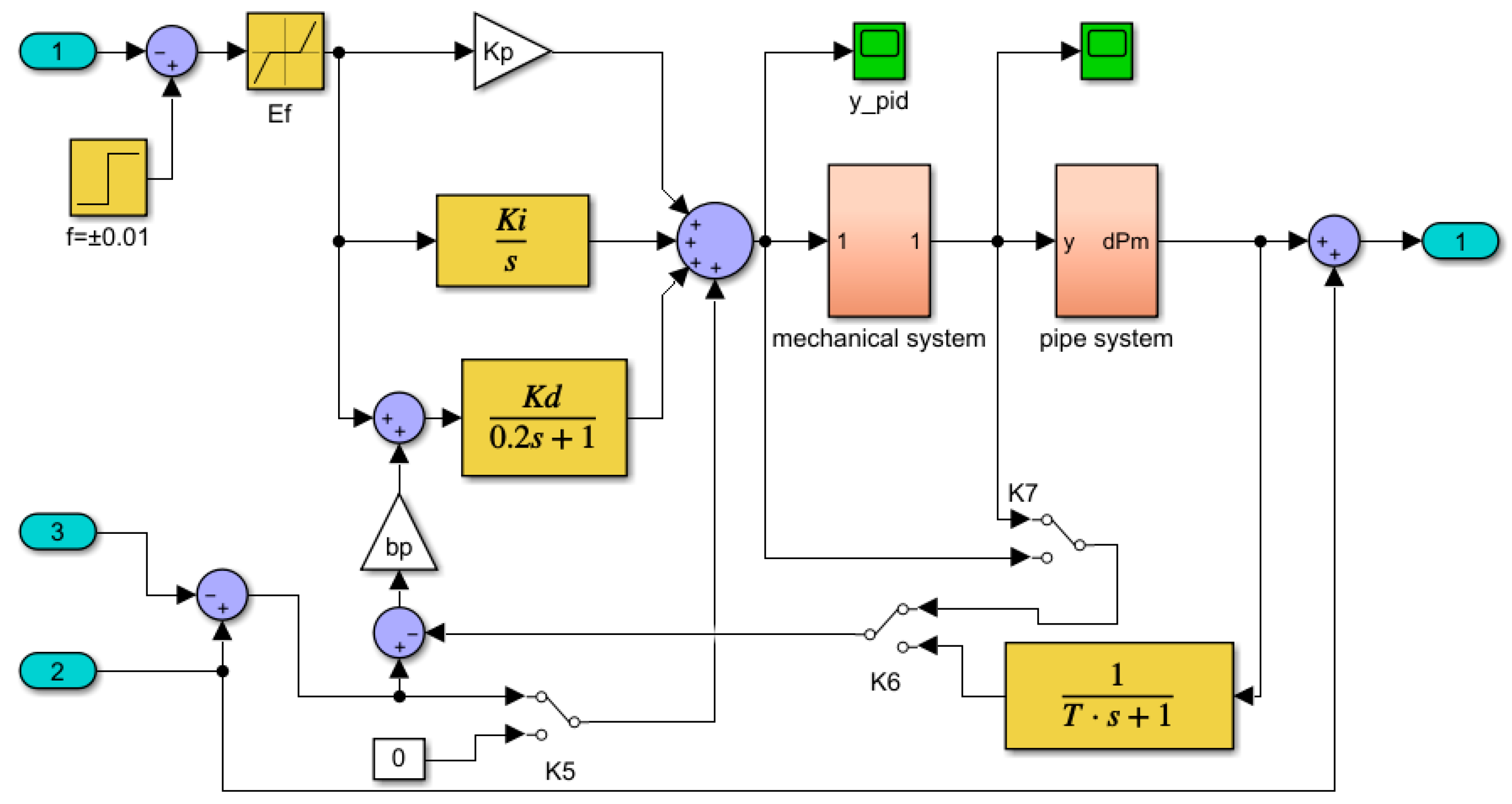
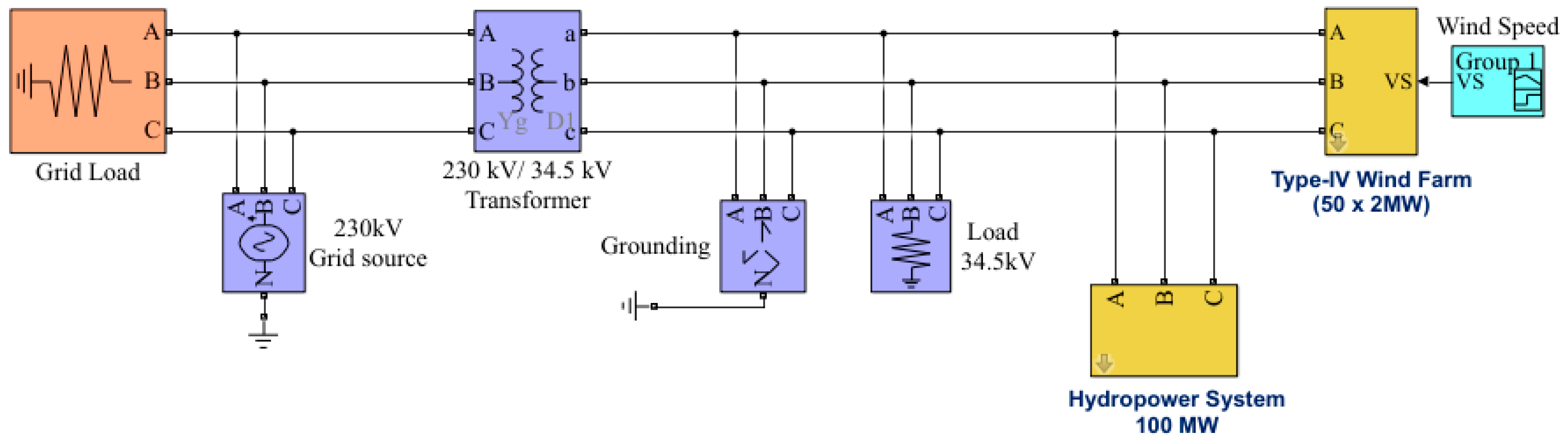
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Proportional gain of wind turbine | 2 pu | Online impedance of device | 1 × 10−3 ohms |
| Maximum protection voltage | 1.25 pu | Maximum protection frequency | 1.05 pu |
| Minimum protection voltage | 0.8 pu | Minimum protection frequency | 0.95 pu |
| Delay time of maximum protection voltage | 0.1 s | Lower limit of power input saturation | −1 pu |
| Delay time of minimum protection voltage | 5 s | Upper limit of power input saturation | 1 pu |
| Snubber resistor of current source | 1 × 105 ohms | Boost forward voltage | 0 V |
| Snubber resistor of boost converter | 1 × 106 ohms | Lower limit of input saturation of wind speed | 3 m/s |
| Delay time of protection frequency | 1 s | Upper limit of input saturation of wind speed | 27 m/s |
Appendix B. Description of the Setting of PID Control Parameter

Appendix C. Comparison of Models and Complementary Results

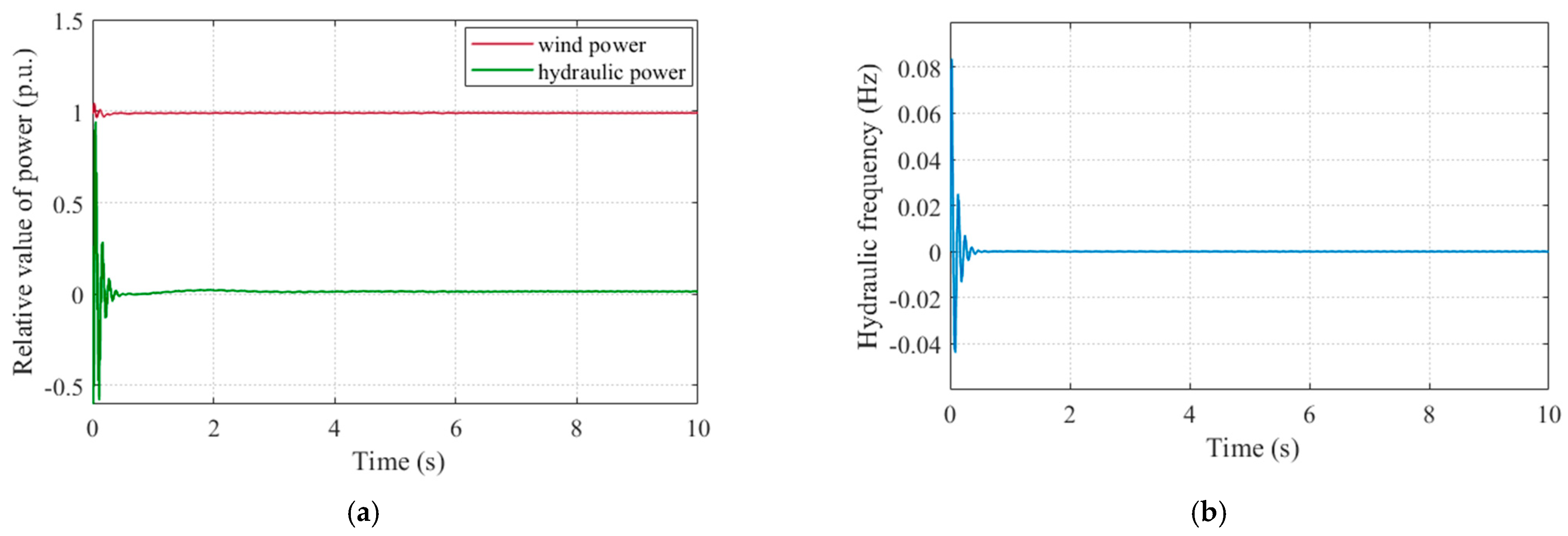
References
- Routray, A.; Mistry, K.D.; Arya, S.R.; Chittibabu, B. Power output evaluation of a wind-solar farm considering the influence parameters. IET Renew. Power Gener. 2021, 15, 1613–1623. [Google Scholar] [CrossRef]
- Zhou, B.Z.; Lin, C.S.; Huang, X.; Zhang, H.M.; Zhao, W.H.; Zhu, S.Y.; Jin, P. Experimental study on the hydrodynamic performance of a multi-DOF WEC-type floating breakwater. Renew. Sust. Energy. Rev. 2024, 202, 114694. [Google Scholar] [CrossRef]
- Zhang, H.; Wu, S.; Li, H.; Zhang, J.; Zhu, C.; Zhou, H.; Jia, Y. Multi-scheme optimal operation of pumped storage wind-solar-thermal generation system based on tolerable energy abandonment. Water 2024, 16, 576. [Google Scholar] [CrossRef]
- Li, B.; Wang, J.; Nassani, A.A.; Binsaeed, R.H.; Li, Z. The future of Green energy: A panel study on the role of renewable resources in the transition to a Green economy. Energy Econ. 2023, 127, 107026. [Google Scholar] [CrossRef]
- Ju, C.; Ding, T.; Jia, W.; Mu, C.; Zhang, H.; Sun, Y. Two-stage robust unit commitment with the cascade hydropower stations retrofitted with pump stations. Appl. Energy 2023, 334, 120675. [Google Scholar] [CrossRef]
- Gunturu, U.B.; Hallgren, W. Asynchrony of wind and hydropower resources in Australia. Sci. Rep. 2017, 7, 8818. [Google Scholar] [CrossRef]
- Eising, M.; Hobbie, H.; Most, D. Future wind and solar power market values in Germany—Evidence of spatial and technological dependencies? Energy Econ. 2020, 86, 104638. [Google Scholar] [CrossRef]
- Guo, P.C.; Zhang, H.; Gou, D.M. Dynamic characteristics of a hydro-turbine governing system considering draft tube pressure pulsation. IET Renew. Power Gener. 2020, 14, 1210–1218. [Google Scholar] [CrossRef]
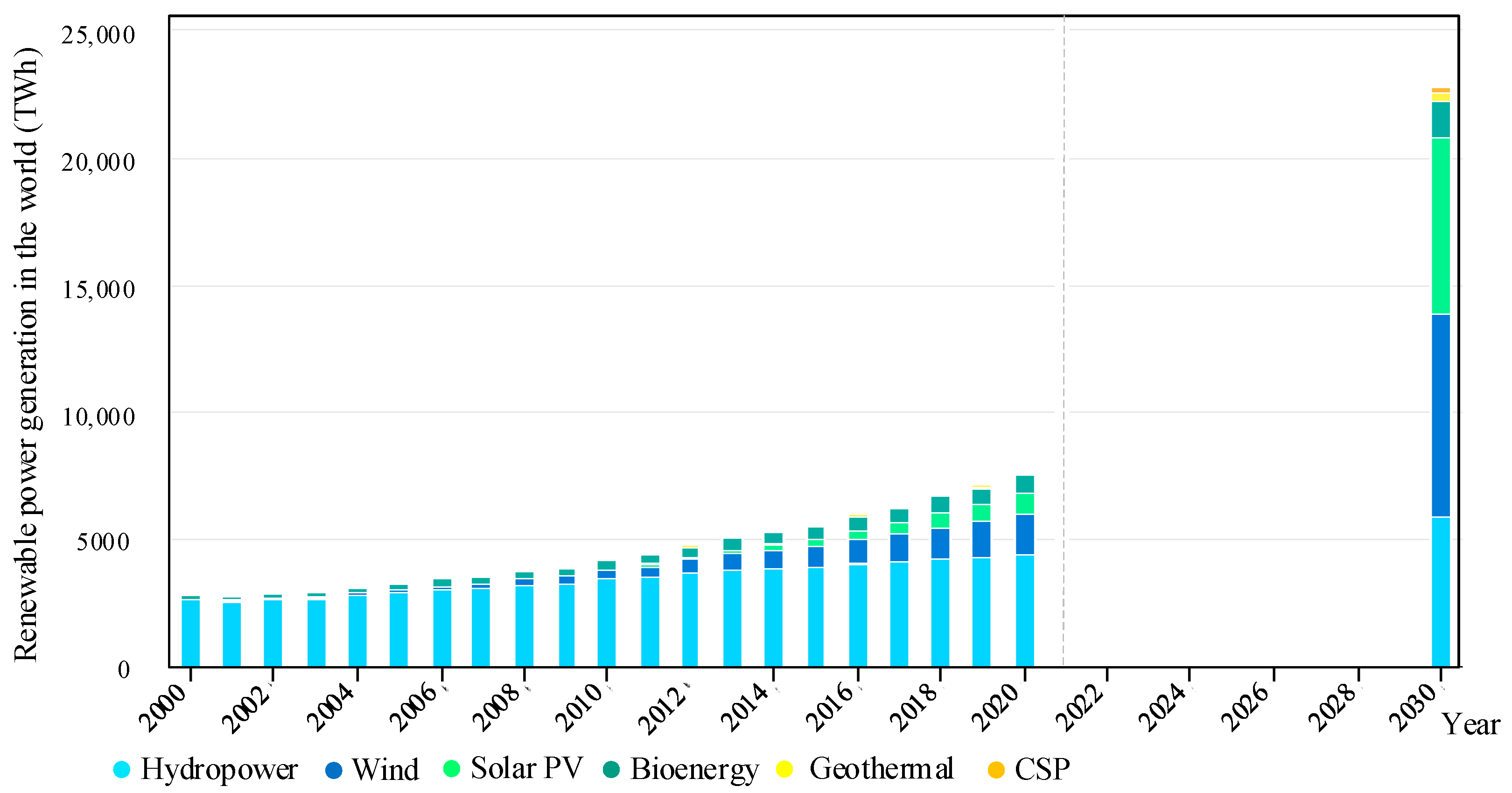
- IEA. Renewable Power Generation by Technology, Historic and in the Net Zero Scenario, 2000–2030; IEA: Paris, France, 2021; Available online: https://www.iea.org/data-and-statistics/charts/renewable-power-generation-by-technology-historic-and-in-the-net-zero-scenario-2000-2030 (accessed on 1 January 2023).
- Zhang, H.X.; Lu, Z.X.; Hu, W.; Wang, Y.T.; Dong, L.; Zhang, J.T. Coordinated optimal operation of hydro-wind-solar integrated systems. Appl. Energy 2019, 242, 883–896. [Google Scholar] [CrossRef]
- Ju, Y.T.; Liu, W.W.; Zhang, Z.F.; Zhang, R.S. Distributed three-phase power flow for AC/DC hybrid networked microgrids considering converter limiting constraints. IEEE Trans. Smart Grid 2022, 13, 1691–1708. [Google Scholar] [CrossRef]
- Simiao, M.; Ramos, H.M. Hybrid pumped hydro storage energy solutions towards wind and PV integration: Improvement on flexibility, reliability and energy costs. Water 2020, 12, 2457. [Google Scholar] [CrossRef]
- Mou, J.H.; Duan, P.Y.; Gao, L.; Pan, Q.K.; Gao, K.Z.; Singh, A.K. Biologically inspired machine learning-based trajectory analysis in intelligent dispatching energy storage system. IEEE Trans. Intell. Transp. Syst. 2023, 24, 4509–4518. [Google Scholar] [CrossRef]
- Alvarez, M.; Ronnberg, S.K.; Bermudez, J.; Zhong, J.; Bollen, M.H.J. Reservoir-type hydropower equivalent model based on a future cost piecewise approximation. Electr. Power Syst. Res. 2018, 155, 184–195. [Google Scholar] [CrossRef]
- Meng, Q.; Jin, X.; Luo, F.; Wang, Z.; Hussain, S. Distributionally robust scheduling for benefit allocation in regional integrated energy system with multiple stakeholders. J. Mod. Power Syst. Clean Energy 2024, 1–12. [Google Scholar] [CrossRef]
- Zhu, C.Y.; Wang, M.X.; Guo, M.X.; Deng, J.X.; Du, Q.P.; Wei, W.; Zhang, Y.X.; Talesh, S.S.A. Optimizing solar-driven multi-generation systems: A cascade heat recovery approach for power, cooling, and freshwater production. Appl. Therm. Eng. 2024, 240, 122214. [Google Scholar] [CrossRef]
- Zhu, C.Y.; Wang, M.X.; Guo, M.X.; Deng, J.X.; Du, Q.P.; Wei, W.; Zhang, Y.X.; Mohebbi, A. An innovative process design and multi-criteria study/optimization of a biomass digestion-supercritical carbon dioxide scenario toward boosting a geothermal-driven cogeneration system for power and heat. Energy 2024, 292, 130408. [Google Scholar] [CrossRef]
- Zhu, C.Y.; Zhang, Y.X.; Wang, M.X.; Deng, J.X.; Cai, Y.W.; Wei, W.; Guo, M.X. Optimization, validation and analyses of a hybrid PV-battery-diesel power system using enhanced electromagnetic field optimization algorithm and ε-constraint. Energy Rep. 2024, 11, 5335–5349. [Google Scholar] [CrossRef]
- Zhu, C.Y.; Zhang, Y.X.; Wang, M.X.; Deng, J.X.; Cai, Y.W.; Wei, W.; Guo, M.X. Simulation and comprehensive study of a new trigeneration process combined with a gas turbine cycle, involving transcritical and supercritical CO2 power cycles and Goswami cycle. J. Therm. Anal. Calorim. 2024, 149, 6361–6384. [Google Scholar] [CrossRef]
- Li, P.; Hu, J.P.; Qiu, L.; Zhao, Y.Y.; Ghosh, B.K. A distributed economic dispatch strategy for power-water networks. IEEE Trans. Control Netw. Syst. 2022, 9, 356–366. [Google Scholar] [CrossRef]
- Guo, Y.; Ming, B.; Huang, Q.; Wang, Y.M.; Zheng, X.D.; Zhang, W. Risk-averse day-ahead generation scheduling of hydro-wind-photovoltaic complementary systems considering the steady requirement of power delivery. Appl. Energy 2022, 309, 118467. [Google Scholar] [CrossRef]
- Majumdar, K.; Roy, P.K.; Banerjee, S. Implementation of multi-objective chaotic mayfly optimization for hydro-thermal- solar-wind scheduling based on available transfer capability problem. Int. Trans. Electr. Energy Syst. 2021, 31, e13029. [Google Scholar] [CrossRef]
- Wang, C.; Wang, Y.; Wang, K.S.; Dong, Y.; Yang, Y. An improved hybrid algorithm based on biogeography/complex and metropolis for many-objective optimization. Math. Probl. Eng. 2017, 2017, 2462891. [Google Scholar] [CrossRef]
- Zhang, Y.; Cheng, C.T.; Cao, R.; Li, G.; Shen, J.J.; Wu, X.Y. Multivariate probabilistic forecasting and its performance’s impacts on long-term dispatch of hydro-wind hybrid systems. Appl. Energy 2021, 283, 116243. [Google Scholar] [CrossRef]
- Shirkhani, M.; Tavoosi, J.; Danyali, S.; Sarvenoee, A.K.; Abdali, A.; Mohammadzadeh, A.; Zhang, C.W. A review on microgrid decentralized energy/voltage control structures and methods. Energy Rep. 2023, 10, 368–380. [Google Scholar] [CrossRef]
- Saidi, S.; Abbassi, R.; Amor, N.; Chebbi, S. Passivity-based direct power control of shunt active filter under distorted grid voltage conditions. Automatika 2016, 57, 361–371. [Google Scholar] [CrossRef]
- Saidi, S.; Abbassi, R.; Chebbi, S. Quality improvement of shunt active power filter with direct instantaneous power estimator based on Virtual Flux. Int. J. Control Autom. Syst. 2016, 14, 1309–1321. [Google Scholar] [CrossRef]
- Saidi, S.; Chebbi, S.; Jouini, H. Harmonic and reactive power compensations by shunt active filter controlled by adaptive fuzzy logic. Int. Rev. Model. Simul. 2011, 4, 1487–1492. [Google Scholar]
- Avila, L.; Mine, M.R.M.; Kaviski, E.; Detzel, D.H.M. Evaluation of hydro-wind complementarity in the medium-term planning of electrical power systems by joint simulation of periodic stream fl ow and wind speed time series: A Brazilian case study. Renew. Energy 2021, 167, 685–699. [Google Scholar] [CrossRef]
- Liu, S.; Han, W.Z.; Zhang, Z.; Chan, F.T.S. An analysis of performance, pricing, and coordination in a supply chain with cloud services: The impact of data security. Comput. Ind. Eng. 2024, 192, 110237. [Google Scholar] [CrossRef]
- Fayek, H.H.; Kotsampopoulos, P. Central tunicate swarm NFOPID-based load frequency control of the Egyptian power system considering new uncontrolled wind and photovoltaic farms. Energies 2021, 14, 3604. [Google Scholar] [CrossRef]
- Ren, Y.; Yao, X.H.; Liu, D.; Qiao, R.Y.; Zhang, L.L.; Zhang, K.; Jin, K.Y.; Li, H.W.; Ran, Y.L.; Li, F. Optimal design of hydro-wind-PV multi-energy complementary systems considering smooth power output. Sustain. Energy Technol. Assess. 2022, 50, 101832. [Google Scholar] [CrossRef]
- Tang, Y.J.; Fang, G.H.; Tan, Q.F.; Wen, X.; Lei, X.H.; Ding, Z.Y. Optimizing the sizes of wind and photovoltaic power plants integrated into a hydropower station based on power output complementarity. Energy Conv. Manag. 2020, 206, 112465. [Google Scholar] [CrossRef]
- Li, H.H.; Mahmud, M.A.; Arzaghi, E.; Abbassi, R.; Chen, D.Y.; Xu, B.B. Assessments of economic benefits for hydro-wind power systems: Development of advanced model and quantitative method for reducing the power wastage. J. Clean Prod. 2020, 277, 123823. [Google Scholar] [CrossRef]
- Karaagac, U.; Mahseredjian, J.; Gagnon, R.; Gras, H.; Saad, H.; Cai, L.J.; Kocar, I.; Haddadi, A.; Farantatos, E.; Bu, S.Q.; et al. A generic EMT-type model for wind parks with permanent magnet synchronous generator full size converter wind turbines. IEEE Power Energy Technol. Syst. J. 2020, 6, 131–141. [Google Scholar] [CrossRef]
- Gao, D.W.; Wu, Z.P.; Yan, W.H.; Zhang, H.G.; Yan, S.J.; Wang, X. Comprehensive frequency regulation scheme for permanent magnet synchronous generator-based wind turbine generation system. IET Renew. Power Gener. 2019, 13, 234–244. [Google Scholar] [CrossRef]
- Li, J.; Wang, N.; Zhou, D.; Hu, W.H.; Huang, Q.; Chen, Z.; Blaabjerg, F. Optimal reactive power dispatch of permanent magnet synchronous generator-based wind farm considering levelised production cost minimization. Renew. Energy 2020, 145, 1–12. [Google Scholar] [CrossRef]
- Banu, J.B.; Moses, M.B.; Ganapathy, S. Maximum Power Point Tracking of Direct-Drive PMSG with High-Efficiency Boost Converter. In Proceedings of the International Conference on Emerging Trends and Advances in Electrical Engineering and Renewable Energy (ETAEERE), Munich, Germany, 26–27 September 2018. [Google Scholar] [CrossRef]
- Soufyane, B.; Abdelhamid, R.; Smail, Z.; Elhafyani, M.L.; El Hajjaji, A. Fully Robust Sensorless Control of Direct-Drive PMSG Wind Turbine Feeding a Water Pumping System. Fully Robust Sensorless Control of Direct-Drive PMSG Wind Turbine Feeding a Water Pumping System. IFAC-PapersOnLine 2020, 53, 12797–12802. [Google Scholar] [CrossRef]
- Trevisan, A.S. Type-IV Wind Turbine. MATLAB Central File Exchange. 2022. Available online: https://www.mathworks.com/matlabcentral/fileexchange/71235-type-iv-wind-turbine (accessed on 1 December 2023).
- Trevisan, A.S.; El-Deib, A.A.; Gagnon, R.; Mahseredjian, J.; Fecteau, M. Field Validated Generic EMT-Type Model of a Full Converter Wind Turbine Based on a Gearless Externally Excited Synchronous Generator. IEEE Trans. Power Deliv. 2018, 33, 2284–2293. [Google Scholar] [CrossRef]
- Ling, D.J. Bifurcation and Chaos of Hydraulic Turbine Governor. Ph.D. Thesis, Hohai University, Nanjing, China, 2007. Available online: http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1241732 (accessed on 1 December 2023).
- Cheng, C.T.; Wu, H.J.; Wu, X.Y.; Shen, J.J.; Wang, J. Power generation scheduling for integrated large and small hydropower plant systems in southwest China. J. Water Resour. Plan. Manag. ASCE 2017, 143, 04017027. [Google Scholar] [CrossRef]
- Wang, P.F.; Deng, Y.W.; Li, H.N.; Chen, D.Y. Making connections: Information transfer in hydropower generation system during the transient process of load rejection. Sustain. Energy Technol. Assess. 2022, 50, 101766. [Google Scholar] [CrossRef]
- Zeng, Y.; Qian, J.; Guo, Y.K.; Yu, S.G. Differential equation model of single penstock multi-machine system with hydraulic coupling. IET Renew. Power Gener. 2019, 13, 1153–1159. [Google Scholar] [CrossRef]
- Li, H.H.; Zhang, R.F.; Mahmud, A.M.; Hredzak, B. A novel coordinated optimization strategy for high utilization of renewable energy sources and reduction of coal costs and emissions in hybrid hydro-thermal-wind power systems. Appl. Energy 2022, 320, 119019. [Google Scholar] [CrossRef]
- Wang, J.Z.; Qin, S.S.; Zhou, Q.P.; Jiang, H.Y. Medium-term wind speeds forecasting utilizing hybrid models for three different sites in Xinjiang, China. Renew. Energy 2015, 76, 91–101. [Google Scholar] [CrossRef]
- Qawaqzeh, M.Z.; Szafraniec, A.; Halko, S.; Miroshnyk, O.; Zharkov, A. Modelling of a household electricity supply system based on a wind power plant. Prz. Elektrotech. 2020, 96, 36–40. [Google Scholar] [CrossRef]
- Wu, Y.Y.; Li, Q.L.; Li, G.X.; He, B.; Dong, L.; Lang, H.N.; Zhang, L.J.; Chen, S.P.; Tang, X.X. Vertical wind speed variation in a metropolitan city in South China. Earth Space Sci. 2022, 9, e2021EA002095. [Google Scholar] [CrossRef]
- Basker, I.; Venkatesan, M.N. 3D-CFD flow driven performance analysis of new non-cylindrical helical vertical axis wind turbine for fluctuating urban wind conditions. Energy Sources Part A-Recovery Util. Environ. Eff. 2022, 44, 2186–2207. [Google Scholar] [CrossRef]
- Xu, B.B.; Li, H.H.; Campana, P.E.; Hredzak, B.; Chen, D.Y. Dynamic regulation reliability of a pumped-storage power generating system: Effects of wind power injection. Energy Conv. Manag. 2020, 222, 113226. [Google Scholar] [CrossRef]
- Abbassi, R.; Saidi, S.; Urooj, S.; Alhasnawi, B.N.; Alawad, M.A.; Premkumar, M. An Accurate Metaheuristic Mountain Gazelle Optimizer for Parameter Estimation of Single- and Double-Diode Photovoltaic Cell Models. Mathematics 2023, 11, 4565. [Google Scholar] [CrossRef]

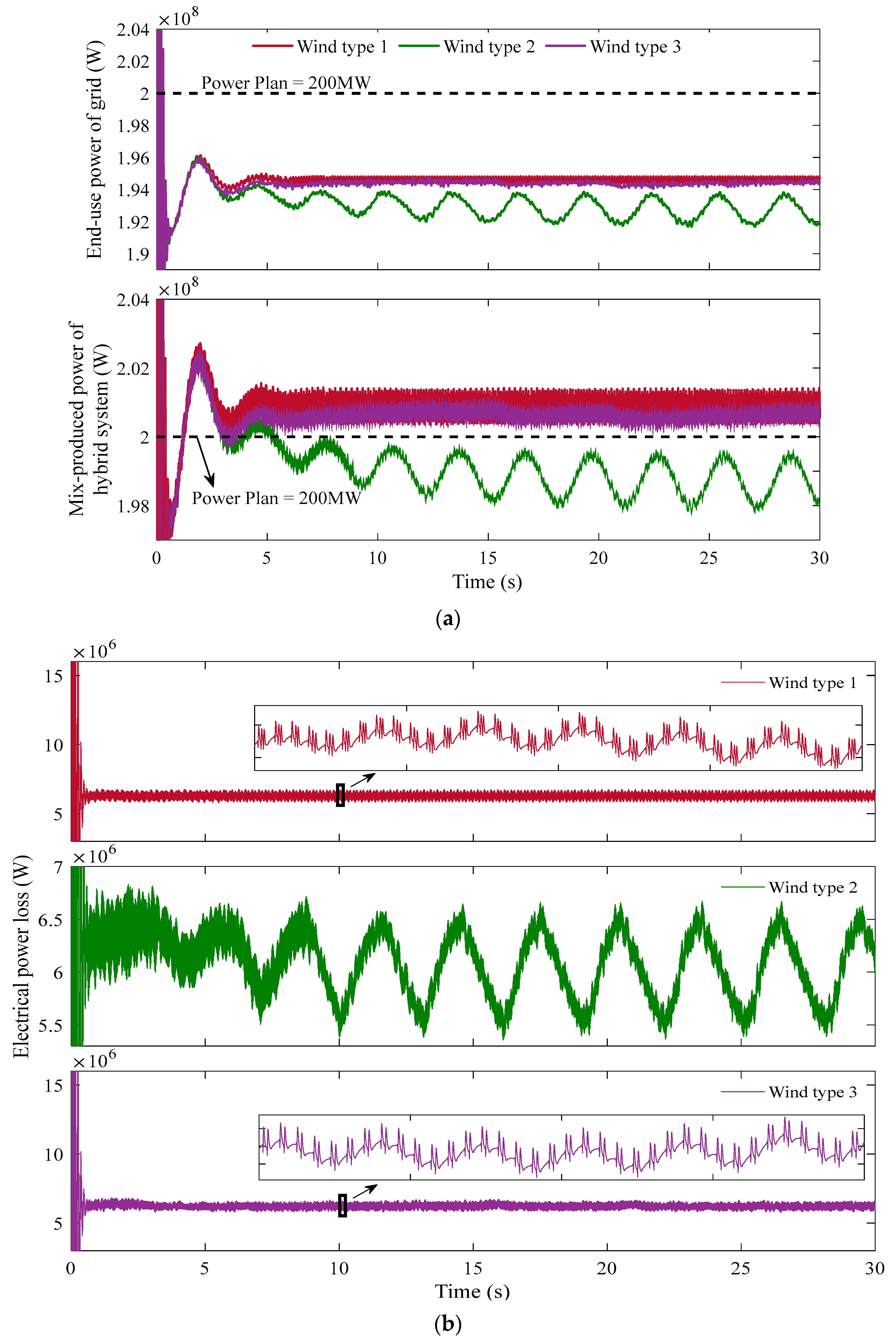
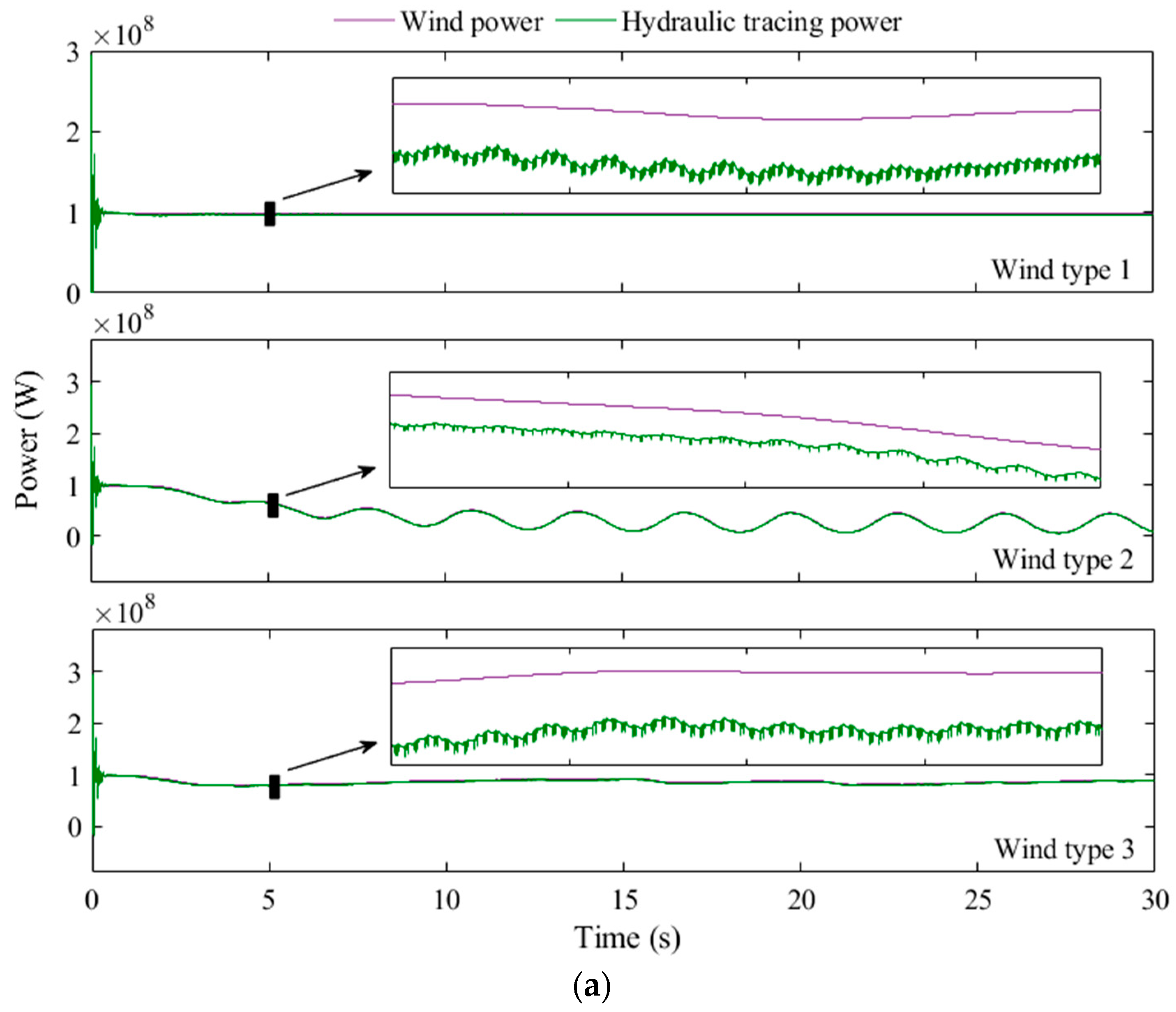
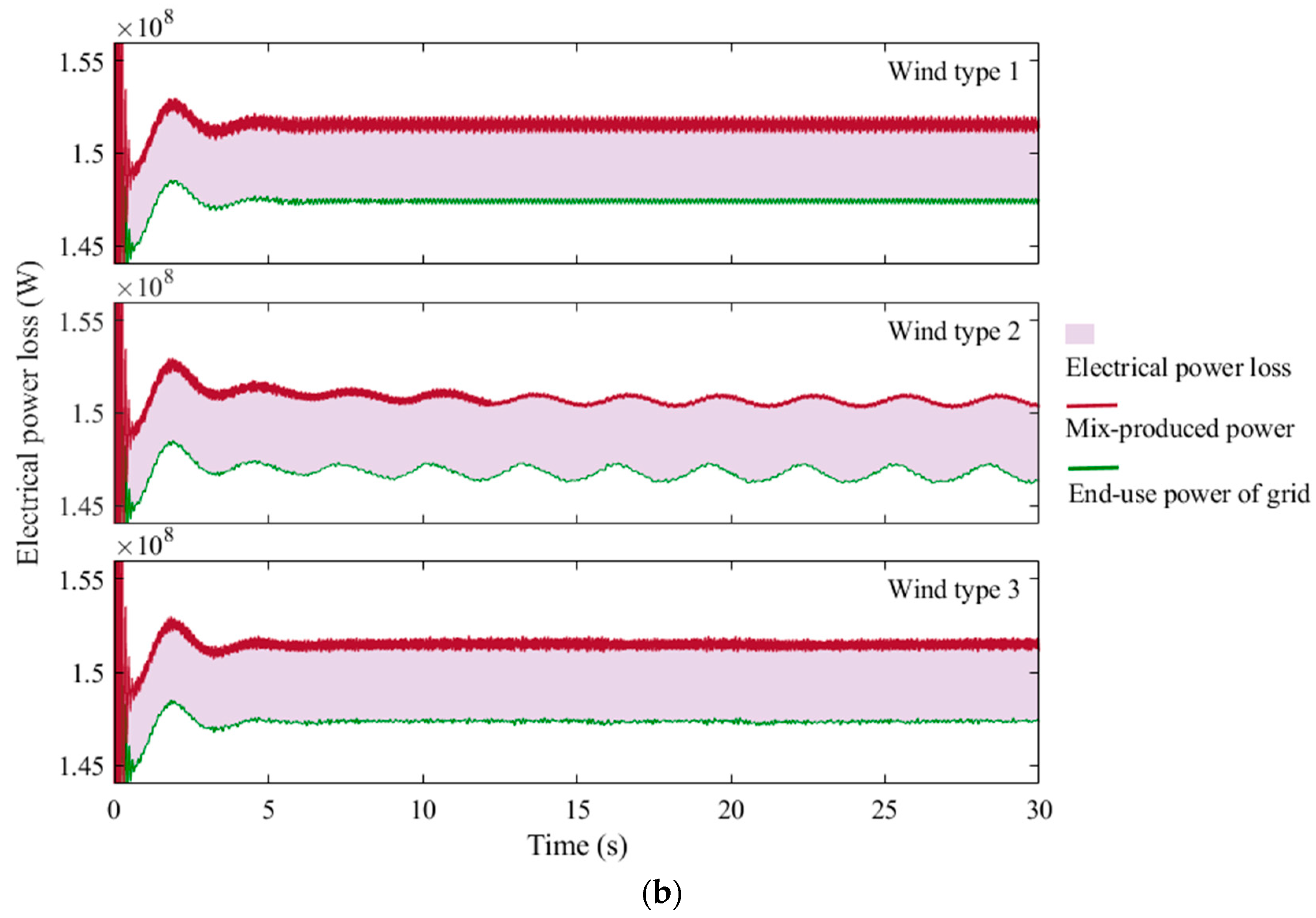


| Summary | Classification of Optimization Ways | |||
|---|---|---|---|---|
| Way 1 | Way 2 | Way 3 | ||
| Description | Establish an optimization model to optimize the operating coefficients. | Design an operational optimization method or scheduling method to maximize the benefits of operation goals. | Optimize the complementary performance of the fluctuations in output power or frequency. | |
| Common characteristic | The calculation process is reasonable and the optimization results are reliable. | |||
| Differences | (i) Key step | Establish a model that reflects the coupling characteristics of each component or subsystem. | Present a linear/nonlinear programming method. | Emphasize in-depth excavation from a certain research perspective. |
| (ii) Key factor that is related to the reliability of results | Model outputs. | Objective functions and constraints. | Controllers, operation variables, or operation scenarios. | |
| (iii) The literature involved | References [10,11,12,13,14] | References [15,16,17,18,19,20,21,22,23,24] | References [25,26,27,28,29,30,31,32,33] | |
| Indicator | Definition |
|---|---|
|
|
|
|
|
|
|
|
| Scenario | Characteristics |
|---|---|
| Scenario 1: on-demand hydropower scenario | The planned power generation is equivalent to the load demand. The installed hydropower capacity that can participate in regulation is prone to shortages if there is a prolonged period of extreme wind speed. It is not easy to produce surplus water for the hydropower system. |
| Scenario 2: surplus hydropower scenario | The planned power generation is larger than the load demand. When the fluctuation in wind power is large, the installed hydropower capacity that can participate in regulation is sufficient. More surplus water is produced. |
| Wind Type | WT Number | Wind Capacity (MW) | Complementary Characteristic | Hydraulic Frequency | Power Loss | ||||
|---|---|---|---|---|---|---|---|---|---|
| Wind Volatility (p.u.) | Hydraulic Tracing Effect | Maximum Deviation (Hz) | Occurrence Time (s) | Mean (MW) | Maximum (MW) | Peak Time (s) | |||
| 1 | 51 | 102 | 0.0121 | Excellent | 0.123 | 5.17 | 6.82 | 7.00 | 0.95 |
| 75 | 150 | 0.0174 | Excellent | 0.198 | 1.45 | 9.00 | 10.79 | 0.6 | |
| 100 | 200 | 0.0244 | Good | 0.2686 | 4.93 | 11.80 | 14.80 | 0.62 | |
| 125 | 250 | 0.0297 | Good | 0.3095 | 4.10 | 15.50 | 19.00 | 0.8 | |
| 150 | 300 | 0.0379 | Good | 0.432 | 1.12 | 19.00 | 24.00 | 0.76 | |
| 163 | 326 | 0.0413 | Good | 0.4297 | 1.38 | 21.80 | 27.50 | 0.79 | |
| 164 | 328 | -- | -- | -- | 0 | -- | -- | -- | |
| 2 | 51 | 102 | 0.6352 | Excellent | 0.0776 | 23.56 | 6.90 | 7.50 | 0.47 |
| 55 | 110 | 0.686 | Excellent | 0.0957 | 26.76 | 7.20 | 7.75 | 0.46 | |
| 60 | 120 | 0.7505 | Good | 0.3568 | 27.64 | 7.75 | 8.80 | 0.47 | |
| 61 | 122 | -- | -- | -- | 21.55 | -- | -- | -- | |
| 3 | 51 | 102 | 0.1397 | Excellent | 0.2329 | 1.60 | 6.86 | 7.43 | 0.46 |
| 75 | 150 | 0.208 | Good | 0.3219 | 15.98 | 9.38 | 11.21 | 0.49 | |
| 100 | 200 | 0.2744 | Good | 0.4761 | 2.62 | 13.50 | 16.56 | 0.49 | |
| 125 | 250 | 0.3427 | Good | 0.5000 | 2.31 | 19.50 | 23.91 | 0.57 | |
| 127 | 254 | -- | -- | -- | -- | -- | -- | -- | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Jia, H.; Zhang, Z.; Lan, T. Optimal Coordinated Operation for Hydro–Wind Power System. Water 2024, 16, 2256. https://doi.org/10.3390/w16162256
Li H, Jia H, Zhang Z, Lan T. Optimal Coordinated Operation for Hydro–Wind Power System. Water. 2024; 16(16):2256. https://doi.org/10.3390/w16162256
Chicago/Turabian StyleLi, Huanhuan, Huiyang Jia, Zhiwang Zhang, and Tian Lan. 2024. "Optimal Coordinated Operation for Hydro–Wind Power System" Water 16, no. 16: 2256. https://doi.org/10.3390/w16162256
APA StyleLi, H., Jia, H., Zhang, Z., & Lan, T. (2024). Optimal Coordinated Operation for Hydro–Wind Power System. Water, 16(16), 2256. https://doi.org/10.3390/w16162256






