Abstract
In the current implementation process for dredging projects, due to the lack of an accurate understanding of underwater soil characteristics, construction teams often find it difficult to accurately understand the soil condition. Not only does this lead to a reduced dredger operation efficiency, but it may also cause delays to the project’s progress, as well as increasing its cost. Therefore, there is an urgent need to closely integrate soil analysis technology with dredging construction to ensure that projects can be completed efficiently and to a high standard. Therefore, this paper proposes a soil modeling and prediction method based on a three-dimensional point cloud model. The research objective is to propose a new method of soil mass identification with a strong generalization ability and function, which can not only be applied to dredging engineering but can also identify and analyze statistics of land soil and its mass. The accuracy of this method, based on a convergent grid, can reach 95%.
1. Introduction
Due to the development of dredging processes worldwide, as well as the continuous progression of science and technology, and in order to meet the needs of different working conditions and the requirements of underwater dredging construction, there has been an increase in the different types of modern dredgers that are available. Dredging is no longer limited to general soil and sand, but can also include the digging of underwater rocks, minerals, and so on [1]. With the large scale of dredging engineering nowadays, the depth of underwater construction areas, and the high efficiency of construction processes, more stringent requirements are being put forward for the future of dredging construction.
Dredging works mostly take place on the seabed or river beds, and the soil distribution in the area is often complex, with characteristics of uncertainty, anisotropy, dynamic change, etc. Without clear information about the soil, huge difficulties in the construction of dredging works can arise. Therefore, in order to improve the construction efficiency of a dredger, it is necessary to understand the soil distribution of the dredged area before construction.
At present, it is often the case that only the soil quality information of the dredged area is considered in the construction process, while the amount of the various types of soil in the dredged area is ignored. Since the soil recovered from dredging may have an impact on the environment [2], and in order to facilitate people’s secondary use of the recovered soil, it is particularly important to calculate the amounts of the various types of soil.
In order to improve the construction efficiency of a dredger and to determine the amount of earthwork in all the different types of soil, this paper proposes a soil modeling and prediction method based on Python. This method is based on the extracted borehole location data and the soil layer data in the borehole, in combination with the geological point cloud generated using terrain files, and has the ability to identify each point of soil information. The distribution of soil in the construction area of a dredger can be predicted, and the amount of soil in the construction area can be calculated statistically.
Ghaderi et al. [3] proposed a new and optimized multi-output generalized feedforward neural network (GFNN) structure to generate a digital map of the soil types of southwest Sweden using 58 piezoelectric cone penetration test points (CPTus). Moreover, Cao et al. [4] established a Bayesian framework for probabilistic soil stratification to identify soil, while Wise et al. [5] proposed the use of a combination of 3D points and acoustics to predict soil erosion, aimed at three-dimensional point clouds. For noisy points in point cloud models, Zeng et al. [6] used a point cloud adaptive weighted guided filtering algorithm to smooth out noise based on its characteristics, which can effectively preserve the key points of the point cloud. In order to accurately predict the local details of point clouds, Hao et al. [7] proposed a new adaptive point cloud growth grid, MapGNET, to generate higher-quality point clouds.
Urbancic et al. [8] analyzed the influence of different surface interpolation methods and mesh element sizes on the calculation of earthwork volume. By comparing the volume of mesh and the triangulated irregular network (TIN) surface, they determined a good interpolation method and a suitable mesh element size and identified that the volume difference should not exceed 5%. Lee et al. [9] used unmanned aerial vehicles (UAVs) and RGB cameras to perform earthwork calculations. Meanwhile, Slattery et al. [10] used ground-based laser scanning (TLS) technology to develop an algorithm based on the finite element method to create a surface through the lowest scan point and to convert that surface into a TIN file; the amount of earthwork was calculated by comparing the TIN of the original terrain with the TIN of a completed project. Lee et al. [11] used the point cloud data obtained using unmanned aerial vehicle (UAV) photogrammetry as the basis for creating a 3D model and calculated the volume of earthwork using the 3D model based on the cloud data of a construction site. Compared with the traditional measurement method, the amount of earth calculated using UAV photogrammetry was 2.36–2.51% larger than that calculated using TSM.
At present, research mainly focuses on the optimization calculation of earthwork quantity. However, relevant research related to the simultaneous calculation of soil quality and earthwork quantity is lacking, and there is a seriously insufficient amount of research in the dredging industry. At present, the prediction of earthwork quantity in the industry mainly focuses on its measurement and calculation using UAVs. Researchers have also discussed the calculation of the earthwork quantity of soil of various qualities by using the projection axis method, the similar section method [12], and measurement software. However, for the projection axis and similar section methods, the soil layer order will be reversed, and the soil layer will be missing. The method of calculating soil mass using software usually requires a regular distribution of geological drilling points and an equal spacing of drilling holes.
The traditional soil type prediction methods mainly rely on the theoretical guidance of soil geography, through field investigations, as well as the observation and description of the morphology of soil profiles and their surrounding geographical environment. This includes analyzing, classifying, and evaluating both the physical and chemical properties of soil and then comparing and analyzing its occurrence, evolution, classification, distribution, and function. This method usually involves a large amount of fieldwork, with a long cycle, high cost, and complex process, especially in areas with complex terrain. With the development of technology, these traditional methods are gradually being supplemented or replaced by the digital soil mapping method. Also known as digital soil mapping (DSM) or predictive soil mapping, it is a modern method that utilizes geographic information systems (GISs), remote sensing technology, and statistical methods to predict and map soil types and their spatial distribution. This method can more efficiently process and analyze soil data, improving the accuracy and efficiency of soil mapping. Although DSM has significant advantages in obtaining and expressing soil spatial distribution information, it still has some shortcomings. The acquisition of high-quality soil data requires a lot of fieldwork and is time-consuming, especially in areas with complex geographical environments. Moreover, the generalization ability of this model is poor, and digital soil mapping models at different regions and scales need to be recalibrated; further research and exploration are needed to effectively display soil maps and apply them to practical soil management and environmental monitoring.
Therefore, this paper proposes a soil quality modeling and prediction method based on a three-dimensional point cloud that is determined using Python tools. This method can reconstruct a dredging construction area with a three-dimensional point cloud model. Compared with traditional modeling methods, the three-dimensional point cloud model proposed in this paper can effectively solve problems such as soil layer order reversal and soil layer loss. Additionally, because the point cloud model is composed of a series of discrete points, it can identify the soil quantity in the specified area, thus reducing the time spent on the calculation. Moreover, by using the visualization function in Python, the distribution of soil layers inside the model can be observed.
The soil quality identification and prediction method based on three-dimensional point clouds involves inserting holes into the point cloud and determining the soil quality status at each point through probabilistic methods that are based on borehole formation data. This method can accurately predict the soil type at each coordinate point of the three-dimensional point cloud model and can calculate the amount of various different types of soil. At the same time, it can effectively solve problems such as soil layer loss and the requirements for the location of the borehole. Not only can this method rapidly predict the whole dredging construction area, but it can also accurately predict the soil quantity.
The research objective of this paper is to put forward a new, innovative method of soil quantity identification. This method has a strong generalization ability and user-friendliness, and it can not only be applied to dredging engineering, but also identify and analyze statistics of land soil and its quantity.
2. Materials and Methods
2.1. Geological Survey Report and Format Data Processing
The technical solution described in this paper is primarily based on the relevant data extracted from geological survey reports provided by surveying companies. The geological survey reports for dredging may include data such as geological conditions within the construction area—such as soil types, rock types, geological structures, and hydrogeological conditions—and engineering geological survey reports, comprising topography, lithology, geological structures, hydrogeological conditions, and the geological environment within the dredging project’s impact area. Faced with abundant content in these reports, it is important to extract and organize the relevant data.
2.1.1. Geological Survey Report Data Processing
In order to meet the actual needs of dredging engineering, according to the “Soil Classification Standards for Guangzhou Shipping Bureau (Draft Proposal)” provided by China Communications Guangzhou Shipping Bureau Co, Ltd. located at 298 Lijiao Road, Zhuhai District, Guangzhou City, Guangdong Province, China, soil can be divided into organic soil and peat, silt, silt soil, cohesive soil, clay sand, fine sand, medium sand, and coarse sand based on particle composition and characteristics, natural weight, standard inertial impact times, shear strength, and compressive strength [13]. According to the “Guangzhou Navigation Bureau Soil Classification Standard (Suggested Draft)”, the classification indicators of dredging rock and soil can be extracted, as shown in Table 1.

Table 1.
Dredging classification geotechnical table.
The drilling and stratigraphic data are sourced from the Borehole Factual Report of Bucao River. The overall drilling data are shown in Table 2. According to Table 1, the soil layers under each drilling hole are graded, and the soil distribution of the corresponding soil category is obtained based on the classification criteria. Taking zk1 as an example, the classification of the soil layers at different depths in the drilling hole is mainly based on the standard penetration rate provided in Figure 1, in addition to the d50 data provided in Figure 2, combined with Table 1. In the case of missing d50 data, the soil layers are classified based on the percentage of particle size composition provided in Figure 2 and the soil layer description provided in Figure 1. The final data obtained are shown in Table 1. The distribution data of zk1 formation is shown in Table 3.

Table 2.
Summary of drilling data.
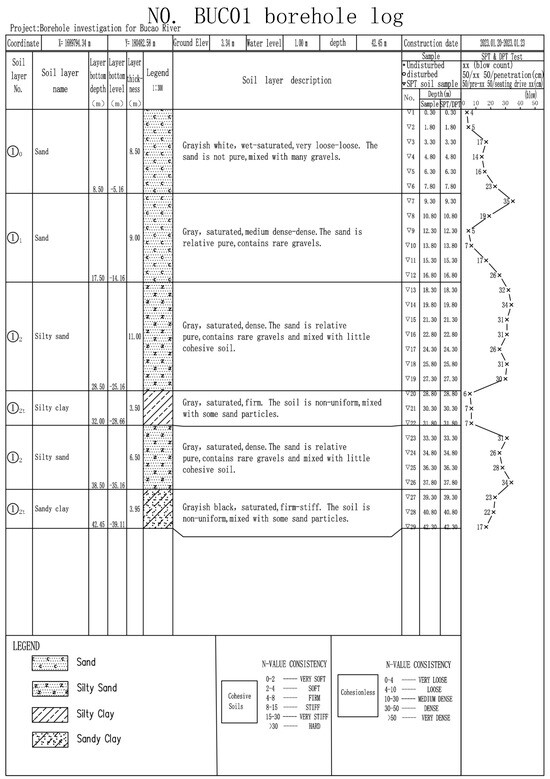
Figure 1.
BUC01 borehole log.
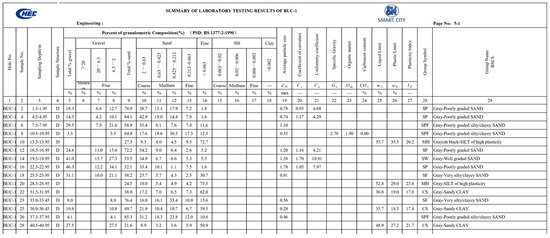
Figure 2.
Statistical chart of depth data for different layers of BUC-1.

Table 3.
The zk1 stratigraphic data distribution.
2.1.2. Reading MDB Format Data
In order to facilitate the processing of the data, previously entered data such as drilling holes, soil parameters, and formation distribution were exported in the standard MDB format. Then, the exported MDB format file was analyzed, and the drilling parameters and some formation distribution data that needed further analysis were extracted in batches. The drilling parameters are delineated in the first four columns of Table 2, with the ID of the drilling hole in the first column and the X, Y, Z coordinates in the last three columns, respectively. Some formation distribution data are shown in Table 4.

Table 4.
Partial stratigraphic distribution data.
2.2. Prediction of Soil Conditions
This article mainly establishes a prediction model by presenting the dredging area as an original point cloud. Based on this model, each coordinate point in the original point cloud, i.e., the X and Y coordinates of the queried point, is used to identify its adjacent boreholes and to calculate the distance between the query point and multiple adjacent boreholes. We determined the soil condition and probability based on the intersection between the set query point depth interval and the known drilling soil depth, and weighted the distance parameter to determine the soil condition of the query point, achieving recognition of the soil information for each point in the point cloud.
The process of predicting the soil condition in the designated construction area is shown in Figure 3.

Figure 3.
Flow chart of soil modeling and prediction.
2.2.1. Voronoi Diagram Division of the Drilling Area
Before judging the soil information, it is necessary to divide the terrain of the construction area into grids and also to divide the adjacent areas of the borehole. Because batch point state estimation is based on the analysis of drilling data and soil layer distribution data, to facilitate the analysis of a specific point, it is necessary to divide the given drilling plane area.
The advantages of the Voronoi diagram partitioning algorithm are as follows: a high algorithm efficiency, a wide adaptability, a simple data structure, and a good visualization effect [14,15,16]. Given the advantages of the Voronoi plot division, it was used for the drilling plane area. By importing drilling data and using the Voronoi plot partitioning algorithm, the planar region partitioning results can be obtained, as shown in the figure, and the partitioning area of each drilling hole can be intuitively obtained from the graph.
This article divides the drilling plane area using Delaunay triangulation [17] to generate the Voronoi diagram. By putting all the drilling points into a point set, creating an empty set of edges and triangles, finding a super triangle containing all the points, and adding them to the triangle set, it is possible to find the position of each point in the current triangulation. Based on this, the triangle can be updated and reconstructed, and subsequently, a Voronoi diagram can be generated, and any additional triangles added during the construction of the super triangle can be removed, producing the final Voronoi diagram, as shown in Figure 4.
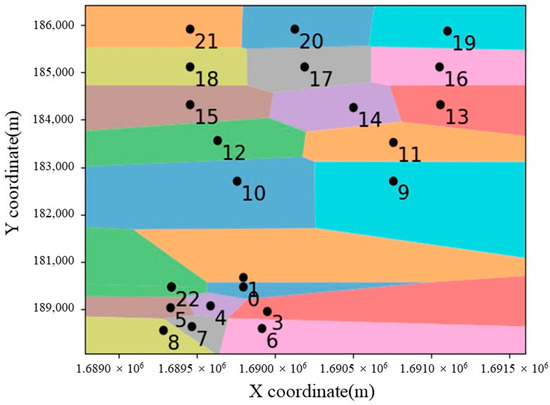
Figure 4.
Results of Voronoi diagram division in the drilling plane area.
Based on the queried coordinates of the point in terms of X and Y, its adjacent boreholes can be identified, and the distances between the query point and multiple adjacent boreholes can be calculated. The soil condition and the probability of the query point can be determined based on the intersection of the set depth interval for the query point and the known depth of the borehole soil layers. Distance parameter weighting can be performed to determine the soil condition of the query point.
According to the above algorithm, input test datasets are used to validate the software estimation effect. The dataset selects the coordinates of borehole points, and a certain random offset is added. Since the points after the addition of the offset deviate little from the positions of the boreholes, it is considered that the soil condition at the points after the offset is the same as that at the original position. The calculation results are as shown. With an input of 130 data points, the algorithm’s recognition accuracy is higher than 95%. Therefore, this soil condition estimation algorithm has good practical value. Some of the calculation results are shown in Table 5.

Table 5.
Partial test dataset and validation results.
2.2.2. Point Cloud Plane Resampling Method
Based on the mudline and dredging area point cloud data, as shown in Figure 5, this paper divides the terrain of the construction area into a grid. To facilitate the statistical calculation of earthwork volume for various soil types, rectangular prism grids are used as grid units, ensuring orthogonality between them; this is illustrated in Figure 6.
Figure 5.
Point cloud data map of dredging area.
Figure 6.
Rectangular grid.
To improve the computational efficiency while ensuring the regularity of the triangulated mesh on the 3D point cloud plane, this paper employs the ray casting method for resampling. The ray casting algorithm [18] is a geometric algorithm used to determine whether or not a point is inside a polygon. It works by emitting a ray from a point outside the polygon and then calculating the number of intersections between the ray and the polygon boundaries to determine whether the point is inside the polygon. The principle diagram of using the ray method to determine a point inside and outside a polygon is shown in Figure 7. If the number of intersections is odd, then the point is inside the polygon; if the number of intersections is even, then the point is outside the polygon.
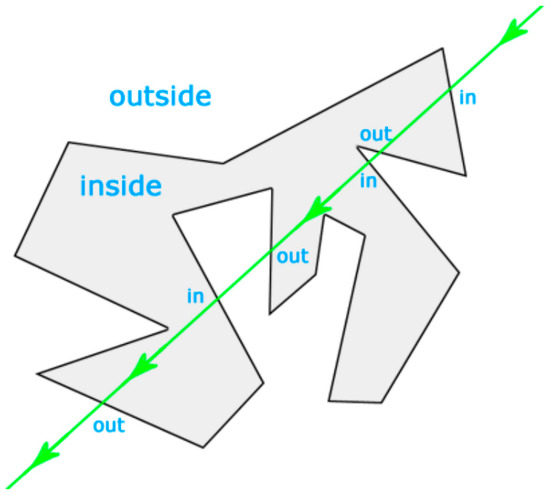
Figure 7.
Principle diagram of using the ray method to determine a point inside and outside a polygon.
Based on manually provided boundary feature points on the 3D point cloud plane, the ray casting method is used for resampling within the polygon enclosed by these boundary feature points. The resampled plane point cloud generated with a sampling point interval of 64 m is illustrated in Figure 8.
Figure 8.
The result of resampling the plane point cloud.
2.2.3. Three-Dimensional Model Contour Generation Method
Due to the substantial volume of data in the resampled point cloud, this paper aims to enhance the computational efficiency by employing the KD-tree algorithm based on the known resampling method for the plane point cloud. The KD-tree algorithm is a data structure used to efficiently search for the nearest neighbors in a multi-dimensional space, doing so by recursively partitioning the space, thereby reducing the time complexity of searching and enhancing the search efficiency [19]. The recursive process of the KD tree is shown in Figure 9.
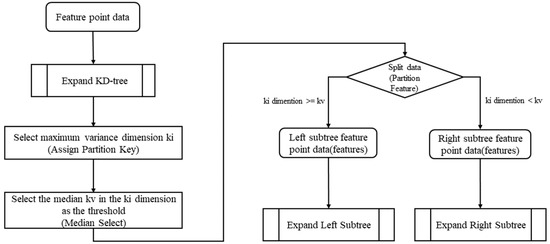
Figure 9.
KD tree recursive process.
The resampled point cloud is projected onto the design depth and mudline data using the KD-tree algorithm. By indexing the four nearest z-values, the elevation of the projection point is determined, representing the design depth and mudline elevation. This process generates the contour of the 3D model.
The contour of the resampled point cloud after design depth and mudline data resampling is shown in Figure 10.
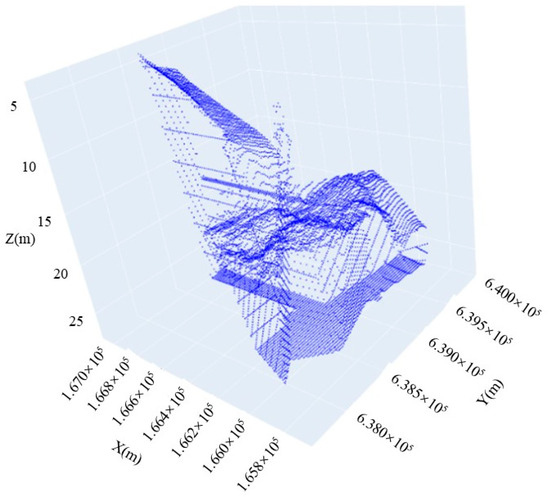
Figure 10.
Point cloud contour map of the dredging area.
2.2.4. Calculation of the Earthwork Volume Difference
To ensure the accuracy and reliability of the calculation results, the size of the grid unit depends on known terrain data and is determined based on the magnitude of earthwork volume change in the dredging construction area, controlled within half the range of typical commercial software variations, i.e., within 1%. Additionally, to handle the grid after fine resampling, the earthwork volume change of the XYZ data after two resamples needs to be controlled within 0.5%.
Since the spacing between each coordinate point in the XY direction of the terrain data is uniform, the volumetric data of the terrain for a certain reference surface can be obtained. By summing up these volumes, the total volume of the entire point cloud for the reference surface can be obtained. Taking the difference between the two sets of volumes, the earthwork volume of the dredging construction area can be obtained. The refined grid size determined by the difference in calculation results is shown in Table 6, Table 7 and Table 8.

Table 6.
Preliminary determination of grid spacing between 27m design depth and mudline.

Table 7.
Refinement of grid spacing for filling volume between 27m design depth and mudline.

Table 8.
Refinement of grid spacing for excavation volume between 27 m design depth and mudline.
2.2.5. Batch Prediction of Soil Conditions at Point Locations
Based on the method of generating planar point clouds, the model contours are determined using the KD-tree algorithm. The points are then evenly spaced in the z-direction to generate a point cloud, thus creating a preliminary three-dimensional point cloud model.
Based on the calculation results of earthwork volume differences, the minimum spacing of the model is iterated to determine the minimum grid spacing under the convergence condition of the earthwork volume differences. This process generates the final soil condition prediction point cloud model, as shown in Figure 11.
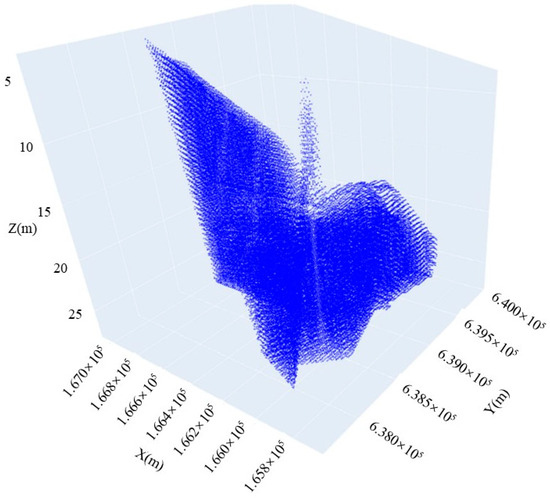
Figure 11.
Soil quality prediction point cloud model diagram.
By importing stratigraphic data, borehole data, and geological point cloud coordinates, the process involves locating adjacent boreholes based on the X, Y coordinates of the queried point and calculating the distance between the queried point and multiple adjacent boreholes. Then, based on the intersection of the set depth interval for the queried point and the known soil layer depths of the boreholes, the soil condition and probability at the queried point are determined. Finally, the soil condition at the queried point is determined using weighted distance parameters. The calculated soil conditions are illustrated in Figure 12. The distribution of soil is shown in Figure 13.
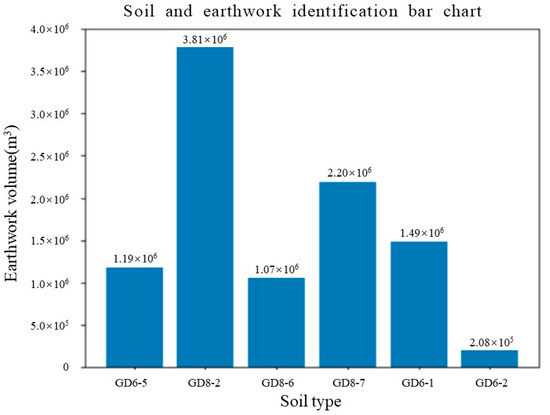
Figure 12.
Soil condition assessment and prediction chart.
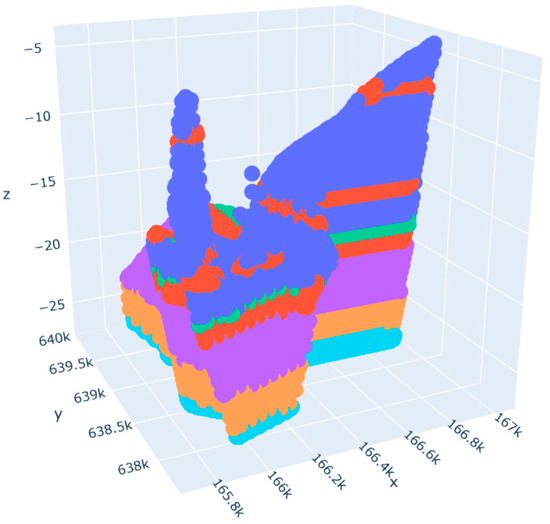
Figure 13.
Visualization of soil layers in dredged areas.
3. Results and Discussion
Firstly, the borehole data and the corresponding soil data in the geological prospecting report are classified according to the corresponding soil classification standard; geological investigation software is used for processing and analysis. Secondly, the borehole data and soil layer data are combined with the Voronoi diagrams to obtain the responsible area of the borehole under the same plane. Then, a geological point cloud is generated based on the known mud surface line point cloud and the dredged area point cloud. Finally, by dividing regions and geological point cloud regions based on the Voronoi diagrams, the node of the geological point cloud responsible for each borehole under the Voronoi diagrams can be obtained, and the soil state estimation and earth quantity calculation can be carried out using the borehole information and node information. The results show the following:
- (1)
- Firstly, this paper classifies the boreholes and the corresponding soil data in the geological prospecting report and processes them according to the corresponding soil classification standards (Part II). Data processing and analysis are carried out using geological prospecting software, which provides basic data for subsequent analysis. Since the data are divided according to the classification standard, they have a certain accuracy. However, some soil data with incomplete information and the influence of the screening method on sand particle size parameters [20] often cause some deviations in the determination of soil type, which is greatly interfered with by human factors. Moreover, it can be seen from Figure 2 that discontinuity exists between each sample depth; it is extremely important to control the information of the sample under missing depth. In this paper, the maximum depth of the previous sample depth interval and the minimum depth of the next sample depth interval are adopted as the dividing line, and an average of the two is taken as the dividing line. The unknown soil layer information on both sides of the boundary line is divided into the known soil layer data on the upper and lower samples. Therefore, the accuracy of the data partitioning method needs to be studied.
- (2)
- The planar division of the borehole area is determined using the Voronoi diagram partitioning algorithm (Section 1 of Part III); the high recognition accuracy of the soil state estimation algorithm (more than 95%) is verified using the test dataset, which shows the potential of the algorithm in practical applications. Although the Voronoi diagram partitioning algorithm can achieve a high recognition accuracy, the construction and computation of Voronoi diagrams are still quite complex, especially for large-scale datasets. The order of magnitude of the point cloud model starts from 1 × 105, and the calculation degree is quite complex.
- (3)
- The geological prediction model of a 3D point cloud in dredging construction areas is established by calculating the difference in earthwork quantity. The model is based on the grid size after the convergence of the calculation of earthwork difference, which can ensure the reliability of the earthwork calculation. The grid result is based on the two converging results and must meet the requirement that with the change in grid size, the overall change amplitude of earthwork volume is less than 0.1%, and the change amplitude of excavation and fill volume is less than 0.05% (Section 4 of Part III). Therefore, the calculation result of the earthwork is reliable. With the progress of the dredging construction process, the obtained soil is mixed with various types of soil, such as silt and yarn, and their separation often requires elevated costs; therefore, in the actual construction process, accurately obtaining the amount of soil of the various different soil types is extremely difficult. Therefore, at present, only the collected point cloud data are missing the actual data of various types of soil volume, and it is difficult to compare the predicted results with the actual results to verify their accuracy.
- (4)
- This paper presents an innovative method for modeling and forecasting soil quality in dredging construction areas. By combining 3D point cloud models with borehole data, the soil quality and the amount of soil in each part of the model can be predicted quickly and accurately. The method has a strong generalization ability; to identify the soil quality and the volume of the construction area, only the point cloud contour data and a series of point depth soil data in the construction area need to be provided.
- (5)
- There are five types of input data in this paper, including mud surface line data, dredging depth data, point cloud data, borehole data, and formation data, which come from the Borehole Factual Report of Bucao River provided by CCCC Guangzhou Waterway Bureau Co., LTD. In order to improve the accuracy of the model, the boundary feature points of the 3D point cloud plane are used to reduce the generation of invalid triangulation networks. Taking the initial mesh size as the starting point, the new mesh size = original mesh size *1/2 speed convergence is used to control the accuracy of the model, and the soil and its earthwork volume are finally predicted. In this paper, a point cloud model is adopted to control various types of earth quantities. The idea comes from the division of the grid in computer fluid mechanics, and a geometric parameter of the grid is controlled by artificially controlling the distance between each node, so as to effectively count the earth quantity of various types of soil.
4. Conclusions
A soil modeling and prediction method for dredging construction areas based on 3D point clouds is proposed in this paper. By combining drilling data and a geological point cloud, the problems of soil layer sequence reversal and soil layer loss in traditional methods are effectively solved, as are the problems of soil management and monitoring that are caused by digital soil mapping. The research method in this paper not only improves the construction efficiency of a dredger, but also rapidly and accurately predicts the amount of all types of soil in a construction area, ensuring reliability of the amount of earth. In addition, the method has a strong generalization ability and personnel operability, which is suitable not only for dredging engineering, but also for land soil identification. The research results show that the method is highly innovative; compared with the traditional soil quality identification method, the proposed method can achieve more functions and can freely add the profile, pile map, and other functions, which have important practical application values in improving the quality and efficiency of dredging engineering construction.
Author Contributions
Methodology, software, and writing—original draft preparation, Q.G.; validation, software, and data curation, W.W. (Wangming Wang); software and validation, Z.Y.; methodology and formal analysis, Z.W.; writing—review and editing and supervision, W.W. (Wei Wei); conceptualization, methodology, and project administration, P.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
Authors Qi Guo, Wangming Wang, and Zihao Yuan were employed by the company CCCC South China Communications Construction Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as potential conflicts of interest.
References
- Soliwoda, J.; Kaizer, A.; Neumann, T. Possibility of Capsizing of a Dredger during Towing. Water 2021, 13, 3027. [Google Scholar] [CrossRef]
- Smith, E.R.; D’Alessandro, F.; Tomasicchio, G.R.; Gailani, J.Z. Nearshore placement of a sand dredged mound. Coast. Eng. 2017, 126, 1–10. [Google Scholar] [CrossRef]
- Ghaderi, A.; Shahri, A.A.; Larsson, S. An artificial neural network based model to predict spatial soil type distribution using piezocone penetration test data (CPTu). Bull. Eng. Geol. Environ. 2019, 78, 4579–4588. [Google Scholar] [CrossRef]
- Cao, Z.-J.; Zheng, S.; Li, D.-Q.; Phoon, K.-K. Bayesian Identification of Soil Stratigraphy based on Soil Behaviour Type Index. Can. Geotech. J. 2019, 56, 570–586. [Google Scholar] [CrossRef]
- Wise, J.; Al Dushaishi, M.F. Prediction of Soil Erosion Using 3D Point Scans and Acoustic Emissions. Water 2024, 16, 1009. [Google Scholar] [CrossRef]
- Zeng, N.; Li, J.; Zhang, Y.; Gao, X.; Luo, L. Scattered Train Bolt Point Cloud Segmentation Based on Hierarchical Multi-Scale Feature Learning. Sensors 2023, 23, 2019. [Google Scholar] [CrossRef] [PubMed]
- Hao, R.; Wei, Z.; He, X.; Zhu, K.; Wang, J.; He, J.; Zhang, L. Multistage Adaptive Point-Growth Network for Dense Point Cloud Completion. Remote Sens. 2022, 14, 5214. [Google Scholar] [CrossRef]
- Urbančič, T.; Grahor, V.; Koler, B. Impact of the Grid Cell Size and Interpolation Methods on Earthwork Volume Calculation. Geod. Vestn. 2015, 59, 231–245. [Google Scholar] [CrossRef]
- Lee, K.; Lee, W.H. Earthwork Volume Calculation, 3D Model Generation, and Comparative Evaluation Using Vertical and High-Oblique Images Acquired by Unmanned Aerial Vehicles. Aerospace 2022, 9, 606. [Google Scholar] [CrossRef]
- Slattery, K.T.; Slattery, D.K.; Peterson, J.P. Road Construction Earthwork Volume Calculation Using Three-Dimensional Laser Scanning. J. Surv. Eng. 2012, 138, 96–99. [Google Scholar] [CrossRef]
- Lee, S.B.; Han, D.; Song, M. Calculation and Comparison of Earthwork Volume Using Unmanned Aerial Vehicle Photogrammetry and Traditional Surveying Method. Sensors Mater. 2022, 34, 4737–4753. [Google Scholar] [CrossRef]
- Wang, K.; Guo, B.; Yan, J. Discussion on Calculation Methods for Different Soil Mass in Dredging Engineering. Yangtze River 2012, 43, 21–23+50. [Google Scholar]
- Duan, M.; Song, X.; Li, Z.; Zhang, X.; Ding, X.; Cui, D. Identifying soil groups and selecting a high-accuracy classification method based on multi-textural features with optimal window sizes using remote sensing images. Ecol. Informatics 2024, 81, 102563. [Google Scholar] [CrossRef]
- Lu, X.; Yan, H. An Algorithm to Generate a Weighted Network Voronoi Diagram Based on Improved PCNN. Appl. Sci. 2022, 12, 6011. [Google Scholar] [CrossRef]
- Dhar, S.; Pal, S.; Bhattacharjee, G.; Pandey, A. A digital geometric approach for discrete Voronoi diagram construction using GPU. Concurr. Comput. Pr. Exp. 2024, 36, e8018. [Google Scholar] [CrossRef]
- Nielsen, F. On Voronoi Diagrams on the Information-Geometric Cauchy Manifolds. Entropy 2020, 22, 713. [Google Scholar] [CrossRef] [PubMed]
- Elshakhs, Y.S.; Deliparaschos, K.M.; Charalambous, T.; Oliva, G.; Zolotas, A. A Comprehensive Survey on Delaunay Triangulation: Applications, Algorithms, and Implementations Over CPUs, GPUs, and FPGAs. IEEE Access 2024, 12, 12562–12585. [Google Scholar] [CrossRef]
- Lu, X.; Lin, H. Improved quantum supersampling for quantum ray tracing. Quantum Inf. Process. 2023, 22, 359. [Google Scholar] [CrossRef]
- Bereczky, N.; Duch, A.; Németh, K.; Roura, S. Quad-kd trees: A general framework for kd trees and quad trees. Theor. Comput. Sci. 2016, 616, 126–140. [Google Scholar] [CrossRef]
- Poullet, P.; Muñoz-Perez, J.J.; Poortvliet, G.; Mera, J.; Contreras, A.; Lopez, P. Influence of Different Sieving Methods on Estimation of Sand Size Parameters. Water 2019, 11, 879. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).